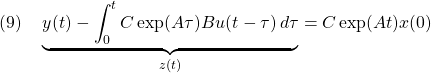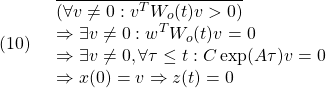LQI制御…Homework
[1] 次の可制御かつ可観測な 次系を考えます。
次系を考えます。
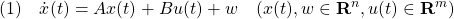
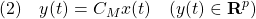
ここで、状態方程式には、操作入力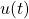 のほかに、定値外乱
のほかに、定値外乱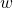 が加わっていること、出力方程式における行列
が加わっていること、出力方程式における行列 を
を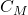 と書いたことに注意します。いま、出力変数の一部やそれらの組合せからなる新しい
と書いたことに注意します。いま、出力変数の一部やそれらの組合せからなる新しい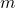 個の被制御変数(controlled variables)を
個の被制御変数(controlled variables)を
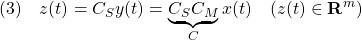
のように選び(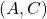 は可観測対)、定値外乱があるにも拘わらず、制御目的
は可観測対)、定値外乱があるにも拘わらず、制御目的
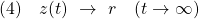
を達成したいとします。ここで、定数ベクトル は
は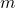 個の設定値からなる。もし制御目的(4)が物理的に可能とすると、ある状態
個の設定値からなる。もし制御目的(4)が物理的に可能とすると、ある状態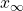 と入力
と入力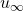 が確定し
が確定し
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \boxed{\left[\begin{array}{c} -w \\ r \end{array}\right] = \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] \left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5a63c22e2c20de8035fdefcbe9d60119_l3.png)
の関係を満足しているはずです。したがって、どのような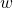 と
と に対しても、
に対しても、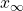 と
と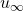 が定まるように、被制御変数(3)を
が定まるように、被制御変数(3)を
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \boxed{{\rm rank}\, \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S}=n+m} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b2fcb8d3d07f55b008eda2e6a5836e50_l3.png)
が成り立つように選ぶものとします。
 図1 積分動作を加えた状態フィードバックによる閉ループ系
図1 積分動作を加えた状態フィードバックによる閉ループ系
[2] さて、制御目的(4)を達成するために、図1に示すような、つぎの積分動作を加えた状態フィードバックを考えます。
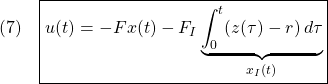
ここで、第2項は積分動作を表しています。このように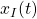 を定義すると
を定義すると
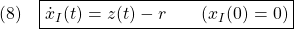
を得ます。(1)と(8)を合わせて
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad %\underbrace{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] %}_{\dot{x}_E(t)} = %\underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] %}_{A_E} %\underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] %}_{x_E(t)} + %\underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] %}_{B_E} u(t) + %\underbrace{ \left[\begin{array}{c} w \\ -r \end{array}\right] %}_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1785760af8b102a8103e05fb37ae732f_l3.png)
を得ます。(9)に、(7)すなわち
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad u(t)=- %\underbrace{ \left[\begin{array}{cc} F & F_I \end{array}\right] %}_{F_E} %\underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] %}_{x_E(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eb0405ede1ae694fbd79fe4f81577fa0_l3.png)
を代入すると、閉ループ系は、つぎのように表されます。
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \boxed{ %\underbrace{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] %}_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} A-BF & -BF_I \\ C & 0 \end{array}\right] }_{A_{EF}} %\underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] %}_{x_E(t)} + %\underbrace{ \left[\begin{array}{c} w \\ -r \end{array}\right] %}_{w_E} }}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a13e4e217df7e1cd4a8873612c945fbd_l3.png)
いま、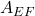 は安定行列であるとします。このとき、
は安定行列であるとします。このとき、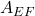 は正則であり、つぎのように書けます。
は正則であり、つぎのように書けます。
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad A_{EF} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} - \left[\begin{array}{cc} B \\ 0 \end{array}\right] \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ae3e582f261444dac1f56aa447ce0eaa_l3.png)
よって、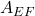 の逆行列は、公式
の逆行列は、公式
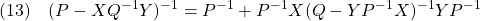
を用いて
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \begin{array}{ll} A_{EF}^{-1} =& S^{-1}+ S^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] \left(I_m- \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] S^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] \right)^{-1} \\[5mm] &\times \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] S^{-1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e0f009cac08e772a5836cd7f89991b53_l3.png)
ここで、
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad S^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] = \left[\begin{array}{cc} 0 \\ I_m \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e4fb7474d8aeb460f97a6d747dfe7496_l3.png)
に注意して、整理すると
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \boxed{A_{EF}^{-1} = \left[\begin{array}{cc} I_n & 0 \\ -F_I^{-1}F & -F_I^{-1} \end{array}\right] S^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0b2df9b56c6c85b1e3bfe245468fe652_l3.png)
のように計算されます。ところで、(11)から
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] \ \rightarrow\ A_{EF}^{-1} \left[\begin{array}{c} -w \\ r \end{array}\right] \quad (t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-51d8a32589cae65d1ed10918b3a56bbe_l3.png)
を得ます。この第1ブロック行は、(5)より
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad x(t)\ \rightarrow\ \left[\begin{array}{cc} I_n & 0 \end{array}\right] S^{-1} \left[\begin{array}{c} -w \\ r \end{array}\right] =x_\infty \quad (t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-77e29d2d337ccf720890ee35fdd3fd4b_l3.png)
となって、(5)の第2ブロック行から制御目的(4)が成り立ちます。また、(17)の第2ブロック行から
![Rendered by QuickLaTeX.com \displaystyle{(19)\quad -F_Ix_{I}(t)\ \rightarrow\ \left[\begin{array}{cc} F & I_m \end{array}\right] S^{-1} \left[\begin{array}{c} -w \\ r \end{array}\right] = Fx_\infty+u_\infty \quad (t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a35b0448666d5b653cbe384ef9fef451_l3.png)
を得ます。ここで、設定値 は既知だから、
は既知だから、 に関係した項
に関係した項![Rendered by QuickLaTeX.com \left[\begin{array}{cc} F & I_m \end{array}\right] S^{-1} \left[\begin{array}{c} 0 \\ r \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bfab95a9c3c8e2e87748e99de2083e61_l3.png) をフィードフォワードして、速応性を改善できます。すなわち、制御目的(4)を達成する制御方式は
をフィードフォワードして、速応性を改善できます。すなわち、制御目的(4)を達成する制御方式は
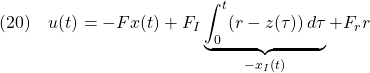
のように表され、ここで、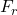 はつぎのように決定できます。
はつぎのように決定できます。
![Rendered by QuickLaTeX.com \displaystyle{(21)\quad F_r= \left[\begin{array}{cc} F & I_m \end{array}\right] S^{-1} \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4b063406fee042d23910d4d18edee04b_l3.png)
[3] これまで、閉ループ系(11)において、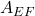 は安定行列であるとしていました。ここでは、これを満足させるための具体的手段として、先に学んだLQ制御を使うことを考えます。LQ制御の議論における閉ループ系は自励系(入力をもたない系)を前提にしていましたが、本章における閉ループ系は入力をもつことに注意が必要です。この前提を満足させるために、定常状態との差をとって得られる偏差系(error system)が用いられます。
は安定行列であるとしていました。ここでは、これを満足させるための具体的手段として、先に学んだLQ制御を使うことを考えます。LQ制御の議論における閉ループ系は自励系(入力をもたない系)を前提にしていましたが、本章における閉ループ系は入力をもつことに注意が必要です。この前提を満足させるために、定常状態との差をとって得られる偏差系(error system)が用いられます。
制御目的(4)が達成されたとき成り立つ(5)より
![Rendered by QuickLaTeX.com \displaystyle{(22)\quad \left[\begin{array}{c} 0 \\ 0 \end{array}\right] = \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] \left[\begin{array}{c} x_\infty \\ x_{I\infty} \end{array}\right] + \left[\begin{array}{c} B \\ 0 \end{array}\right] u_\infty + \left[\begin{array}{c} w \\ -r \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ff71f59b3e81ebeea81e30ac9c2aa0f4_l3.png)
を得ます(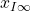 は定数ベクトル)。まず、(9)から(22)を引いて、つぎの偏差系を得ます。
は定数ベクトル)。まず、(9)から(22)を引いて、つぎの偏差系を得ます。
偏差系E1:
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \boxed{\frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] %}_{x_E(t)-x_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E1}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] %}_{x_E(t)-x_{E\infty}} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E1}} (u(t)-u_\infty)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2bcd3f36f880707fe8bc60b89fa6dbb6_l3.png)
この両辺を微分すれば、状態変数の中の定数ベクトルを除くことができて
偏差系E2:
![Rendered by QuickLaTeX.com \displaystyle{(24)\quad \boxed{\frac{d}{dt} %\underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] %}_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} %\underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] %}_{\dot{x}_E(t)} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} {\dot u}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-acdd13f2ef2c1d92a0004a5f47cda17a_l3.png)
を得ます。さらに、(1)と(3)をまとめた
![Rendered by QuickLaTeX.com \displaystyle{(25)\quad \left[\begin{array}{c} {\dot x}(t)-w \\ z(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-73ee9071a72e5208f32daf364e891bb9_l3.png)
から(5)を引いて、つぎの関係式が成り立ちます。
![Rendered by QuickLaTeX.com \displaystyle{(26)\quad \boxed{\left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-429e0ebfec7903d5dc5ce87f5046bed1_l3.png)
これに基づいて、偏差系E2に座標変換を行えば
偏差系E3:
![Rendered by QuickLaTeX.com \displaystyle{(27)\quad \boxed{\frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-69dd980e629d5d4d9cf34dc90dbc246d_l3.png)
を得ます。ここで、つぎの関係式を用いました。
![Rendered by QuickLaTeX.com \displaystyle{(28)\quad \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cc8034db5edc1a000b2f2add912d9e66_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(29)\quad \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e7784673b16ee3dc6fc71b2e2e461a8c_l3.png)
●これら3つの偏差系E1,E2,E3はすべて可制御ですが、どれを用いるのがよいのでしょう?
偏差系E1に対する安定化状態フィードバックを
![Rendered by QuickLaTeX.com \displaystyle{(30)\quad u(t)-u_\infty=- \underbrace{\left[\begin{array}{cc} F & F_I \end{array}\right] }_{F_{E1}} \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-49e57cd33d9728f3bb2e32ce3cc5341c_l3.png)
とします。これにより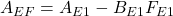 を安定行列とすることはできますが、(30)は実装上の難があります。
を安定行列とすることはできますが、(30)は実装上の難があります。
偏差系E2に対する安定化状態フィードバックを
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad {\dot u}(t)=- \underbrace{\left[\begin{array}{cc} F & F_I \end{array}\right] }_{F_{E2}} \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-38d968135e7c7820854f8a99e80ed705_l3.png)
とします。これにより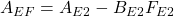 を安定行列とすることはできますが、LQ設計時の重み係数の決定に難があります。
を安定行列とすることはできますが、LQ設計時の重み係数の決定に難があります。
偏差系E3に対する安定化状態フィードバックを
![Rendered by QuickLaTeX.com \displaystyle{(32)\quad {\dot u}(t)=- \underbrace{\left[\begin{array}{cc} K & K_I \end{array}\right] }_{K_{E3}} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a0dd224c0271441aad07fc15b5834f36_l3.png)
とします。これにより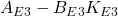 を安定行列とできます。一方、(32)は(26)を用いると
を安定行列とできます。一方、(32)は(26)を用いると
![Rendered by QuickLaTeX.com \displaystyle{(33)\quad {\dot u}(t)=- \underbrace{\left[\begin{array}{cc} K & K_I \end{array}\right] \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]^{-1} }_{K_{E3}S^{-1}} \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9efa6f3fc30539bde922fde97f38394c_l3.png)
と書けます。したがって
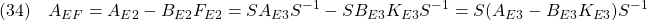
も安定行列となります。そして、
![Rendered by QuickLaTeX.com \displaystyle{(35)\quad \boxed{\left[\begin{array}{cc} F & F_I \end{array}\right] = \left[\begin{array}{cc} K & K_I \end{array}\right] \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-effa6673748e4582607e705f8cec8e0b_l3.png)
とおいて、(33)の両辺を積分すれば、制御測(7)が得られます。このことは偏差系E3の優位性を示唆しているといえます。
[4] 以下に、偏差系E3をLQ制御により安定化して、積分動作を加えた状態フィードバックを構成する手順を示します。
アルゴリズム <LQI制御>
ステップ1 被制御変数の決定
![Rendered by QuickLaTeX.com \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-103603de7e6651c35cea91693aeddce8_l3.png) が正則となるように(
が正則となるように(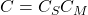 )、セレクタ行列
)、セレクタ行列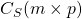 を決めます(一般に、多入力多出力系の場合、どの操作変数でどの被制御変数を制御するのかについて、物理的に実現可能な1対1対応を考えることが重要です。その際、被制御変数はフィードバックされるので観測量の中から選ばれなけばなりません)。
を決めます(一般に、多入力多出力系の場合、どの操作変数でどの被制御変数を制御するのかについて、物理的に実現可能な1対1対応を考えることが重要です。その際、被制御変数はフィードバックされるので観測量の中から選ばれなけばなりません)。
ステップ2 偏差系の安定化
偏差系
![Rendered by QuickLaTeX.com \displaystyle{(36)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-09c7b450fba91ff4da2925235911deb2_l3.png)
を、状態フィードバック
![Rendered by QuickLaTeX.com \displaystyle{(37)\quad {\dot u}(t)=- \left[\begin{array}{cc} K & K_I \end{array}\right] \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f8128bb5d21ddc8470649122fe45967a_l3.png)
によるLQ制御で安定化します。その際、評価関数としては
![Rendered by QuickLaTeX.com \displaystyle{(38)\quad \int_0^\infty \left( \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right]^T Q_E \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] +{\dot u}^T(t)R_E{\dot u}(t)\right)\,dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c670e9177dbb8cc950866876198e2e52_l3.png)
を用います。ただし、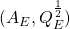 は可観測対とします。
は可観測対とします。
ステップ3 積分動作を加えた状態フィードバックの構成
つぎの積分動作を加えた状態フィードバックを構成します。
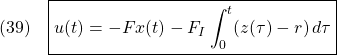
ただし
![Rendered by QuickLaTeX.com \displaystyle{(40)\quad \boxed{\left[\begin{array}{cc} F & F_I \end{array}\right] = \left[\begin{array}{cc} K & K_I \end{array}\right] \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bbcfc692f32dddd6063c223f23f96d7e_l3.png)
この手順で設計された積分動作を加えた状態フィードバックによる制御方式をLQI制御(LQ control with integral action)と呼びます。
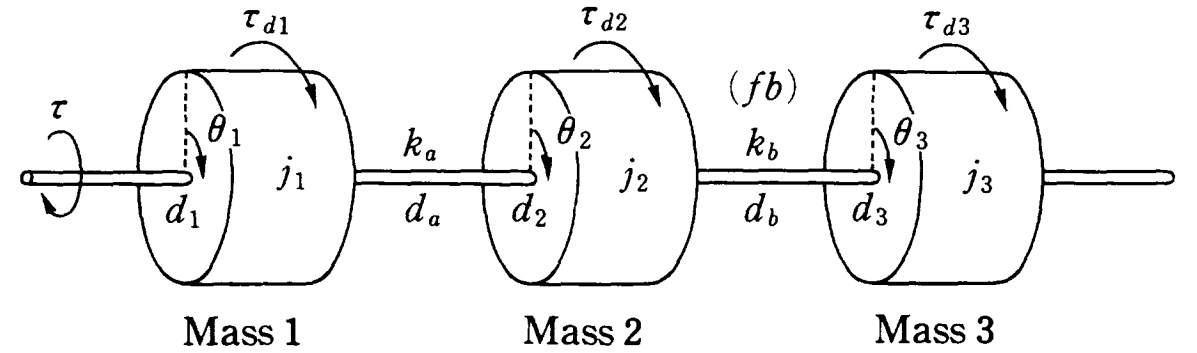
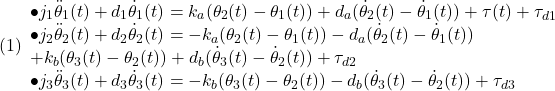
![]() の3つのパラメータ誤差を考慮して、回転体3に対してインパルス外乱が加わるときのシミュレーションを行ってみます。
の3つのパラメータ誤差を考慮して、回転体3に対してインパルス外乱が加わるときのシミュレーションを行ってみます。![]()
![]() とします。
とします。![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{ccc} j_1 & 0 & 0\\ 0 & j_2 & 0\\ 0 & 0 & j_3 \end{array}\right] }_{J} \underbrace{ \left[\begin{array}{ccc} \ddot{\theta}_1(t)\\ \ddot{\theta}_2(t)\\ \ddot{\theta}_3(t) \end{array}\right] }_{\ddot{\xi}(t)} +\underbrace{ \left[\begin{array}{ccc} d_1+d_a & -d_a & 0\\ -d_a & d_2+d_a+d_b & -d_b\\ 0 & -d_b & d_3+d_b \end{array}\right] }_{D} \underbrace{ \left[\begin{array}{ccc} \dot{\theta}_1(t)\\ \dot{\theta}_2(t)\\ \dot{\theta}_3(t) \end{array}\right] }_{\dot{\xi}(t)}\\ +\underbrace{ \left[\begin{array}{ccc} k_a & -k_a & 0\\ -k_a & k_a+k_b & -k_b\\ 0 & -k_b & k_b \end{array}\right] }_{K} \underbrace{ \left[\begin{array}{ccc} {\theta}_1(t)\\ {\theta}_2(t)\\ {\theta}_3(t) \end{array}\right] }_{{\xi}(t)} = \underbrace{ \left[\begin{array}{ccc} 1\\ 0\\ 0 \end{array}\right] }_{E_{3\times1}}\tau(t) +\underbrace{ \left[\begin{array}{ccc} \tau_{d1}\\ \tau_{d2}\\ \tau_{d3} \end{array}\right] }_{\tau_{d}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f503c942853f86278fa2c1b5860489f2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \left[\begin{array}{c} \dot{\xi}(t)\\ \ddot{\xi}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} 0_{3\times3} & I_3\\ -J^{-1}K & -J^{-1}D \end{array}\right] }_{A(d_3/j_3,k_b/j_3)} \left[\begin{array}{c} {\xi}(t)\\ \dot{\xi}(t) \end{array}\right] + \left[\begin{array}{c} 0\\ J^{-1}E_{3\times1} \end{array}\right]\tau(t) + \left[\begin{array}{c} 0\\ J^{-1} \end{array}\right]\tau_d \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b27ed5b2207cc572494ae4bfcb986605_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \begin{array}{l} J^{-1}D={ \left[\begin{array}{ccc} d_1/j_1+d_a/j_1 & -d_a/j_1 & 0\\ -d_a/j_2 & d_2/j_2+d_a/j_2+d_b/j_2 & -d_b/j_2\\ 0 & -d_b/j_3 & d_3/j_3+d_b/j_3 \end{array}\right]\\ =(d_1/j_1)D_1+(d_2/j_2)D_2+(d_3/j_3)D_3\\ +(d_a/j_1)D_4+(d_a/j_2)D_5+(d_b/j_2)D_6+(d_b/j_3)D_7\\ J^{-1}K= \left[\begin{array}{ccc} k_a/j_1 & -k_a/j_1 & 0\\ -k_a/j_2 & k_a/j_2+k_b/j_2 & -k_b/j_2\\ 0 & -k_b/j_3 & k_b/j_3 \end{array}\right]\\ =(k_a/j_1)K_1+(k_a/j_2)K_2+(k_b/j_2)K_3+(k_b/j_3)K_4\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e79c3e7ebe83b4bd6c5f805aa18b7707_l3.png)
![]()
![]() 、
、![]() に対する次の内分式に注目します。
に対する次の内分式に注目します。![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \left[\begin{array}{c} \alpha\\ \beta \end{array}\right]= \underbrace{\frac{\alpha_2-\alpha}{\alpha_2-\alpha_1}\frac{\beta_2-\beta}{\beta_2-\beta_1}}_{p_{11}(\alpha,\beta)}\left[\begin{array}{c} \alpha_1\\ \beta_1 \end{array}\right]+ \underbrace{\frac{\alpha_2-\alpha}{\alpha_2-\alpha_1}\frac{\beta-\beta_1}{\beta_2-\beta_1}}_{p_{12}(\alpha,\beta)}\left[\begin{array}{c} \alpha_1\\ \beta_2 \end{array}\right]\\+ \underbrace{\frac{\alpha-\alpha_1}{\alpha_2-\alpha_1}\frac{\beta_2-\beta}{\beta_2-\beta_1}}_{p_{21}(\alpha,\beta)}\left[\begin{array}{c} \alpha_2\\ \beta_1 \end{array}\right]+ \underbrace{\frac{\alpha-\alpha_1}{\alpha_2-\alpha_1}\frac{\beta-\beta_1}{\beta_2-\beta_1}}_{p_{22}(\alpha,\beta)}\left[\begin{array}{c} \alpha_2\\ \beta_2 \end{array}\right] \\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-484fd6de8261d6cb87bf54fb54115386_l3.png)
![]()
![]() のとき上の状態方程式は、端点モデル
のとき上の状態方程式は、端点モデル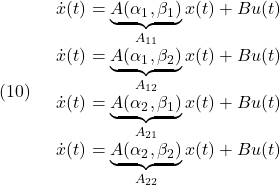
![]() によって重み付けして、LPVモデル
によって重み付けして、LPVモデル![]()
![]() 図1
図1![]() 図2
図2![]() 図3
図3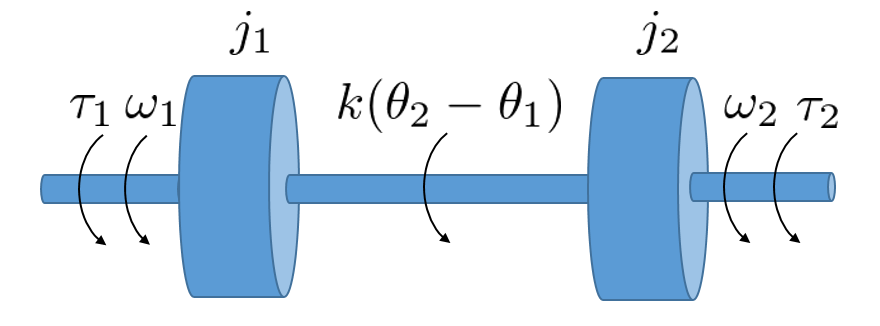
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \boxed{ \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\tau}_s(t)\\ \dot{\omega}_1(t)\\ \dot{\omega}_2(t) \end{array}\right] }_{\dot{\xi}(t)} = \underbrace{ \left[\begin{array}{cccc} 0 & k & -k\\ -1/j_1 & 0 & 0\\ 1/j_2 & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \tau_s(t)\\ \omega_1(t)\\ \omega_2(t) \end{array}\right] }_{\xi(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ 1/j_1 \\ 0 \end{array}\right] }_{B} \tau_1(t) + \underbrace{ \left[\begin{array}{c} 0\\ 0\\ 1/j_2 \end{array}\right] }_{w} \\ \omega_1(t)= \underbrace{ \left[\begin{array}{cccc} 0 & 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \tau_s(t)\\ \omega_1(t)\\ \omega_2(t) \end{array}\right] }_{\xi(t)}\\ \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c25f6b237c7c2e6cd097ce7e72e81495_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \left[\begin{array}{c} 0\\ 0\\ -1/j_2\\ \omega^* \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} 0 & k & -k & 0\\ -1/j_1 & 0 & 0 & 1/j_1\\ 1/j_2 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \end{array}\right] }_{S= \left[\begin{array}{cc} A & B\\ C & 0 \end{array}\right] } \left[\begin{array}{c} \tau_s(\infty)\\ \omega_1(\infty)\\ \omega_2(\infty)\\ \tau_1(\infty) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-200a8504b885306bfa297096ead9dcfa_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \underbrace{ \left[\begin{array}{c} \tau_s(\infty)\\ \omega_1(\infty)\\ \omega_2(\infty)\\ \tau_1(\infty) \end{array}\right] }_{\left[\begin{array}{c} \xi_\infty \\ \tau_{1,\infty} \end{array}\right]} = \underbrace{ \left[\begin{array}{cccc} 0 & 0 & j_2 & 0\\ 0 & 0 & 0 & 1\\ -1/k & 0 & 0 & 1\\ 0 & j_1 & j_2 &0\end{array}\right] }_{S^{-1}} \left[\begin{array}{c} 0\\ 0\\ -1/j_2\\ \omega^* \end{array}\right] = \left[\begin{array}{c} -1\\ \omega^*\\ \omega^*\\ -1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f0d4e810a55a6a882407932aaab00e86_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \left[\begin{array}{c} \dot{\xi}(t) \\ \omega_1(t)-\omega^* \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_{1,\infty} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-47d30f4e17805a9a2ebaefe39021995e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \frac{d}{dt} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_{1,\infty} \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_{1,\infty} \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_{E3}} \dot{\tau}_1(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a0ff98500da4e2f52af6872960bbcfc1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \dot{\tau}_1(t) = K_{E3} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_{1,\infty} \end{array}\right] = \underbrace{ K_{E3}S^{-1} }_{ \left[\begin{array}{cccc} F_1 & F_2 & F_3 & F_4 \end{array}\right]} \left[\begin{array}{c} \dot{\xi}(t) \\ \omega_1(t)-\omega^* \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-20938eef1ea9c03b40aa65e259fc059d_l3.png)
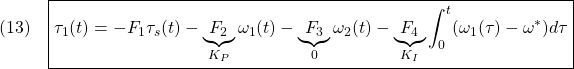
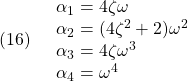
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \begin{array}{l} K_{E3}= \left[\begin{array}{cccc} 0 & 0 & 0 & 1 \end{array}\right]\\ \times \left[\begin{array}{cccc} B_{E3} & A_{E3}B_{E3} & A_{E3}^2B_{E3} & A_{E3}^3B_{E3} \end{array}\right]^{-1}\\ \times (A_{E3}^4+\alpha_1 A_{E3}^3+\alpha_2 A_{E3}^2+\alpha_3 A_{E3}+\alpha_4 I_4) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-753bbdf4eade430b3af666ccdd104bc1_l3.png)
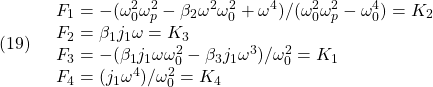
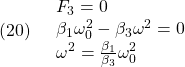
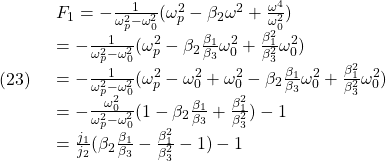
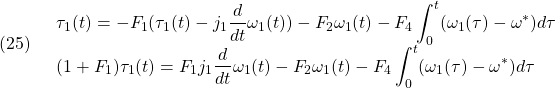
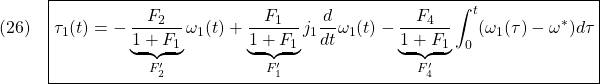
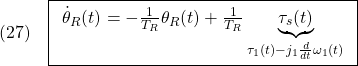
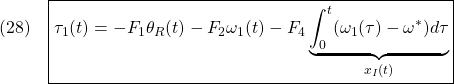
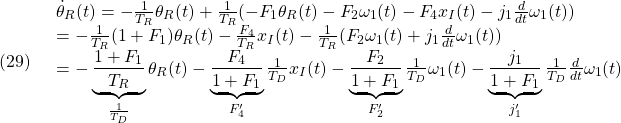
![Rendered by QuickLaTeX.com \displaystyle{(30)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_I(t)\\ \dot{\theta}_R(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} 0 & 0\\ -\frac{F'_4}{T_D} & -\frac{1}{T_D} \end{array}\right] }_{A_F} \left[\begin{array}{c} x_I(t)\\ \theta_R(t) \end{array}\right] + \underbrace{ \left[\begin{array}{cc} 1\\ -\frac{1}{T_D}(F'_2+j'_1\frac{d}{dt}) \end{array}\right] }_{B_F}\omega_1(t)\\ \tau_1(t)= \underbrace{ \left[\begin{array}{cccc} -F_4 & -F_1 \end{array}\right] }_{C_F} \left[\begin{array}{c} x_I(t)\\ \theta_R(t) \end{array}\right] +\underbrace{(-F_2)}_{D_F}\omega_1(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7e6311a39c4f39d2f6000e395385fed2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad \begin{array}{l} K(s)=\underbrace{ \left[\begin{array}{cccc} -F_4 & -F_1 \end{array}\right] }_{C_F} \underbrace{ \left[\begin{array}{cccc} s & 0\\ \frac{F'_4}{T_D} & s+\frac{1}{T_D} \end{array}\right]^{-1} }_{(sI-A_F)^{-1}} \underbrace{ \left[\begin{array}{cc} 1\\ -\frac{1}{T_D}(F'_2+j'_1s) \end{array}\right] }_{B_F} + \underbrace{(-F_2)}_{D_F}\\ = \left[\begin{array}{cccc} -F_4 & -F_1 \end{array}\right] \underbrace{ \left[\begin{array}{cccc} s & 0\\ \frac{F'_4}{T_D} & s+\frac{1}{T_D} \end{array}\right]^{-1} }_{ \frac{1}{s(s+\frac{1}{T_D})} \left[\begin{array}{cccc} s+\frac{1}{T_D} & 0\\ -\frac{F'_4}{T_D} & s \end{array}\right] } \left[\begin{array}{cc} 1\\ -\frac{1}{T_D}(F'_2+j'_1s) \end{array}\right] -F_2\\ =-F_4\frac{1}{s}+F_1 \frac{F'_4}{T_D}\frac{1}{s(s+\frac{1}{T_D})} +F_1 \frac{1}{s+\frac{1}{T_D}}\frac{1}{T_D}(F'_2+j'_1s)-F_2\\ =-(1+F_1 )(F'_2+F'_4\frac{1}{s})+F_1 \frac{1}{T_Ds+1}(F'_4\frac{1}{s}+F'_2+j'_1s)\\ =(-1-F_1 +F_1 \frac{1}{T_Ds+1}})(F'_2+F'_4\frac{1}{s})+F_1'\frac{j_1s}{T_Ds+1}}\\ =(-1-F_1 \frac{T_Ds}{T_Ds+1}})(F'_2+F'_4\frac{1}{s})+F_1'\frac{j_1s}{T_Ds+1}}\\ =(-1-F'_1\frac{T_Rs}{T_Ds+1}})(F'_2+F'_4\frac{1}{s})+F_1'\frac{j_1s}{T_Ds+1}}\\ =-F'_2-F'_4\frac{1}{s}-\frac{T_Rs}{T_Ds+1}}F'_1F'_2-\frac{T_Ds+1-T_Ds}{T_Ds+1}}T_RF'_1F'_4+F_1'\frac{j_1s}{T_Ds+1}}\\ =-F'_2-T_RF'_1F'_2-F'_4\frac{1}{s}-\frac{T_Rs}{T_Ds+1}}F'_1F'_2+\frac{T_Ds}{T_Ds+1}}T_RF'_1F'_4+F_1'\frac{j_1s}{T_Ds+1}}\\ =-\underbrace{(F'_2+T_RF'_1F'_2)}_{K_P}-\underbrace{F'_4}_{K_I}\frac{1}{s}-\frac{s}{T_Ds+1}}\underbrace{(T_RF'_1F'_2-T_DT_RF'_1F'_4-F_1'j_1)}}_{K_D}\\ %=F_P+F_I\frac{1}{s}+\frac{F_Ds}{Ts+1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4e1fa43bfe67aa01b18fdbf7cf206bd5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(33)\quad \boxed{ \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\tau}_s(t)\\ \dot{\omega}_1(t)\\ \dot{\omega}_2(t)\\ \dot{\tau}_1(t) \end{array}\right] }_{\dot{\xi}(t)} = \underbrace{ \left[\begin{array}{cccc} 0 & k & -k & 0\\ -1/j_1 & 0 & 0& 1/j_1\\ 1/j_2 & 0 & 0& 0\\ 0 & 0 & 0 & -1/T \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \tau_s(t)\\ \omega_1(t)\\ \omega_2(t)\\ \tau_1(t) \end{array}\right] }_{\xi(t)}\\ + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ 1/T \end{array}\right] }_{B} u(t) + \underbrace{ \left[\begin{array}{c} 0\\ 0\\ 1/j_2\\ 0 \end{array}\right] }_{w}\\ \dot{\theta}_1(t)= \underbrace{ \left[\begin{array}{cccc} 0 & 1 & 0& 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \tau_s(t)\\ \omega_1(t)\\ \omega_2(t)\\ \tau_1(t) \end{array}\right] }_{\xi(t)}\\ \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0face941bc9b742fd8c1a39a6ab8905e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(34)\quad \left[\begin{array}{c} 0\\ 0\\ -1/j_2\\ 0\\ \omega^* \end{array}\right] = \underbrace{ \left[\begin{array}{ccccc} 0 & k & -k & 0& 0\\ -1/j_1 & 0 & 0 & 1/j_1& 0\\ 1/j_2 & 0 & 0 & 0& 0\\ 0 & 0 & 0 & -1/T& 1/T\\ 0 & 1 & 0 & 0& 0 \end{array}\right] }_{S} \left[\begin{array}{c} \tau_s(\infty)\\ \omega_1(\infty)\\ \omega_2(\infty)\\ \tau_1(\infty)\\ u(\infty) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3bb52aeb5920c21402cde26565f91792_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(35)\quad \underbrace{ \left[\begin{array}{c} \tau_s(\infty)\\ \omega_1(\infty)\\ \omega_2(\infty)\\ \tau_1(\infty)\\ u(\infty) \end{array}\right] }_{\left[\begin{array}{c} \xi_\infty \\ u_\infty \end{array}\right]} = \underbrace{ \left[\begin{array}{ccccc} 0 & 0 & j_2 & 0& 0\\ 0 & 0 & 0 & 0& 1\\ -1 & 0 & 0 & 0& 1\\ 0 & j_1 & j_2 &0& 0\\ 0 & j_1 & j_2 &T& 0 \end{array}\right] }_{S^{-1}} \left[\begin{array}{c} 0\\ 0\\ -1/j_2\\ 0\\ \omega^* \end{array}\right] = \left[\begin{array}{c} -1\\ \omega^*\\ \omega^*\\ -1\\ -1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-384becd060fafe8dca8773e3c0ab725e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(36)\quad \left[\begin{array}{c} \dot{\xi}(t) \\ \omega_1(t)-\omega^* \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ u(t)-u_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-428e35cc70942d6dbf93edd87c4e25db_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(37)\quad \frac{d}{dt} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ u(t)-u_\infty \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ u(t)-u_\infty \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_{E3}} \dot{u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-06337a8f4ce7e3b2bf148980a4060511_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(38)\quad \dot{u}(t) = K_{E3} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ u(t)-u_\infty \end{array}\right] =\underbrace{ K_{E3}S^{-1} }_{ \left[\begin{array}{ccccc} K_2 & K_3 & K_1 & K_0& K_4 \end{array}\right]} \left[\begin{array}{c} \dot{\xi}(t) \\ \omega_1(t)-\omega^* \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c3735afe885bab43cef461836c34db22_l3.png)
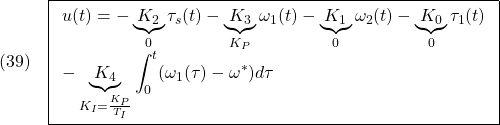
![Rendered by QuickLaTeX.com \displaystyle{(43)\quad \begin{array}{l} K_{E3}= \left[\begin{array}{ccccc} 0 & 0 & 0 & 0 &1 \end{array}\right]\\ \times \left[\begin{array}{ccccc} B_{E3} & A_{E3}B_{E3} & A_{E3}^2B_{E3} & A_{E3}^3B_{E3}& A_{E3}^4B_{E3} \end{array}\right]^{-1}\\ \times (A_{E3}^5+\alpha_1A_{E3}^4+\alpha_2A_{E3}^3+\alpha_3A_{E3}^2+\alpha_4A_{E3}+\alpha_5I_n) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c88f5d511bc275540dd02784c3de1ec1_l3.png)
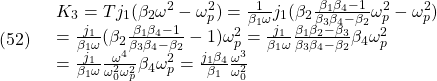
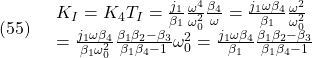
![Rendered by QuickLaTeX.com \displaystyle{(57)\quad \boxed{ \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\tau}_s(t)\\ \dot{\omega}_1(t)\\ \dot{\omega}_2(t)\\ \dot{x}_{D}(t)\\ \end{array}\right] }_{\dot{\xi}(t)} = \underbrace{ \left[\begin{array}{cccc} 0 & k & -k & 0\\ -1/j_1 & 0 & 0& 0\\ 1/j_2 & 0 & 0& 0\\ 0 & 1/T_D & 0 & -1/T_D \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \tau_s(t)\\ \omega_1(t)\\ \omega_2(t)\\ x_{D}(t)\\ \end{array}\right] }_{\xi(t)}\\ + \underbrace{ \left[\begin{array}{c} 0 \\ 1/j_1 \\ 0 \\ 0 \end{array}\right] }_{B} \tau_1(t) + \underbrace{ \left[\begin{array}{c} 0\\ 0\\ 1/j_2\\ 0 \end{array}\right] }_{w}\\ \omega_1(t)= \underbrace{ \left[\begin{array}{cccc} 0 & 1 & 0& 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \tau_s(t)\\ \omega_1(t)\\ \omega_2(t)\\ x_{D}(t)\\ \end{array}\right] }_{\xi(t)}\\ \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-43c48213c969f1206fa859c02ec68ff6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(58)\quad \left[\begin{array}{c} 0\\ 0\\ -1/j_2\\ 0\\ \omega^* \end{array}\right] = \underbrace{ \left[\begin{array}{ccccc} 0 & k & -k & 0& 0\\ -1/j_1 & 0 & 0& 0& 1/j_1 \\ 1/j_2 & 0 & 0& 0& 0\\ 0 & 1/T_D & 0 & -1/T_D& 0\\ 0 & 1 & 0 & 0& 0 \end{array}\right] }_{S} \left[\begin{array}{c} \tau_s(\infty)\\ \omega_1(\infty)\\ \omega_2(\infty)\\ x_{D}(\infty)\\ \tau_1(\infty) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-32cb895bdb660d3f9a735af3dc6e1f03_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(59)\quad \underbrace{ \left[\begin{array}{c} \tau_s(\infty)\\ \omega_1(\infty)\\ \omega_2(\infty)\\ x_{D}(\infty)\\ \tau_1(\infty) \end{array}\right] }_{\left[\begin{array}{c} \xi_\infty \\ \tau_\infty \end{array}\right]} = \underbrace{ \left[\begin{array}{ccccc} 0 & 0 & j_2 & 0& 0\\ 0 & 0 & 0 & 0& 1\\ -1/k & 0 & 0 & 0& 1\\ 0 & 0 & 0 &-1/T_D& 0\\ 0 & j_1 & j_2 &0& 0 \end{array}\right] }_{S^{-1}} \left[\begin{array}{c} 0\\ 0\\ -1/j_2\\ 0\\ \omega^* \end{array}\right] = \left[\begin{array}{c} -1\\ \omega^*\\ \omega^*\\ \omega^*\\ -1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-42e9671105c1457bff74113d4e882b97_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(60)\quad \left[\begin{array}{c} \dot{\xi}(t) \\ \omega_1(t)-\omega^* \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-451065a42216db1d57dd41f1a3b608e4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(61)\quad \frac{d}{dt} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_\infty \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_\infty \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_{E3}} \dot{u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f08c8362eba9a30ffbce176f269d3428_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(62)\quad \begin{array}{l} \dot{\tau}_1(t)(t) = K_{E3} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_\infty \end{array}\right]\\ =\underbrace{ K_{E3}S^{-1} }_{ \left[\begin{array}{ccccc} F_1(K_2) & F_2(K_3) & F_3(K_1) & F_4(K_0)& F_5(K_4) \end{array}\right]} \left[\begin{array}{c} \dot{\xi}(t) \\ \omega_1(t)-\omega^* \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-12a082ac3aaa6fa25b693f8371e7cdad_l3.png)
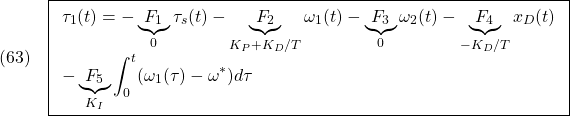
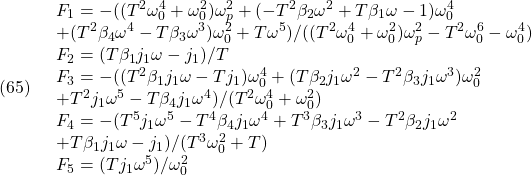
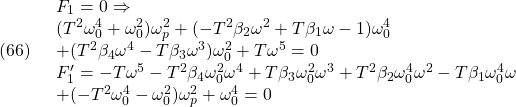
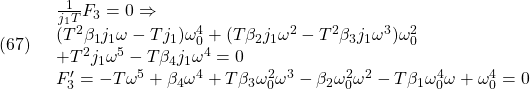
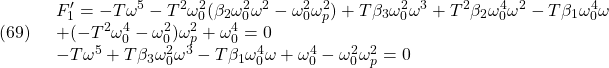
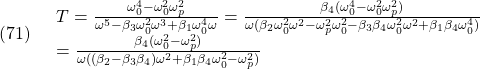
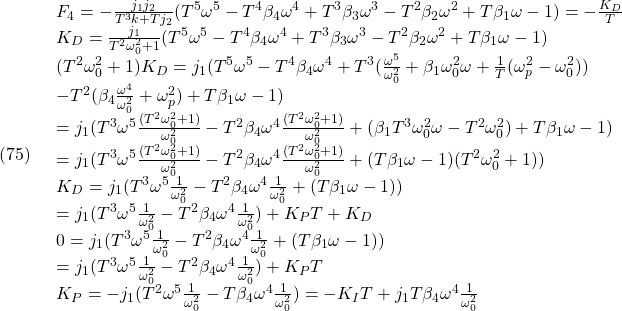
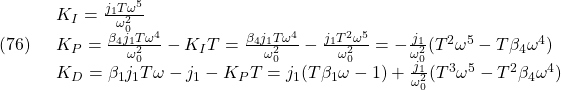
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad {\rm rank}\, \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S}=n+m }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2069deace994eb41f10ff0a9f788d3e6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \boxed{\begin{array}{rl} \left[\begin{array}{c} \dot{\hat{x}}(t) \\ \dot{x}_I(t) \end{array}\right] =& \underbrace{ \left[\begin{array}{cc} A-HC_M-BF & -BF_I \\ 0 & 0 \end{array}\right] }_{A_K} \left[\begin{array}{c} \hat{x}(t) \\ x_I(t) \end{array}\right]\\[10mm] &+ \underbrace{ \left[\begin{array}{cc} H & 0\\ C_S & -I_m \end{array}\right] }_{B_K} \left[\begin{array}{c} y(t) \\ r \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-977bf81afcea851483203c10814c5622_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \boxed{u(t)= \underbrace{- \left[\begin{array}{cc} F & F_I \end{array}\right] }_{C_K} \left[\begin{array}{c} \hat{x}(t) \\ x_I(t) \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d9ac340745aed0b88493ebd6fef302af_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \boxed{\left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \\ \dot{\hat{x}}(t) \end{array}\right] = \left[\begin{array}{ccc} A & -BF_I & -BF \\ C & 0 & 0 \\ HC_M & -BF_I & A-HC_M-BF \end{array}\right] \left[\begin{array}{c} x(t) \\ x_I(t) \\ \hat{x}(t) \end{array}\right] + \left[\begin{array}{c} w \\ -r \\ 0 \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-80e9ab84b8746522c22673f66ba84dda_l3.png)
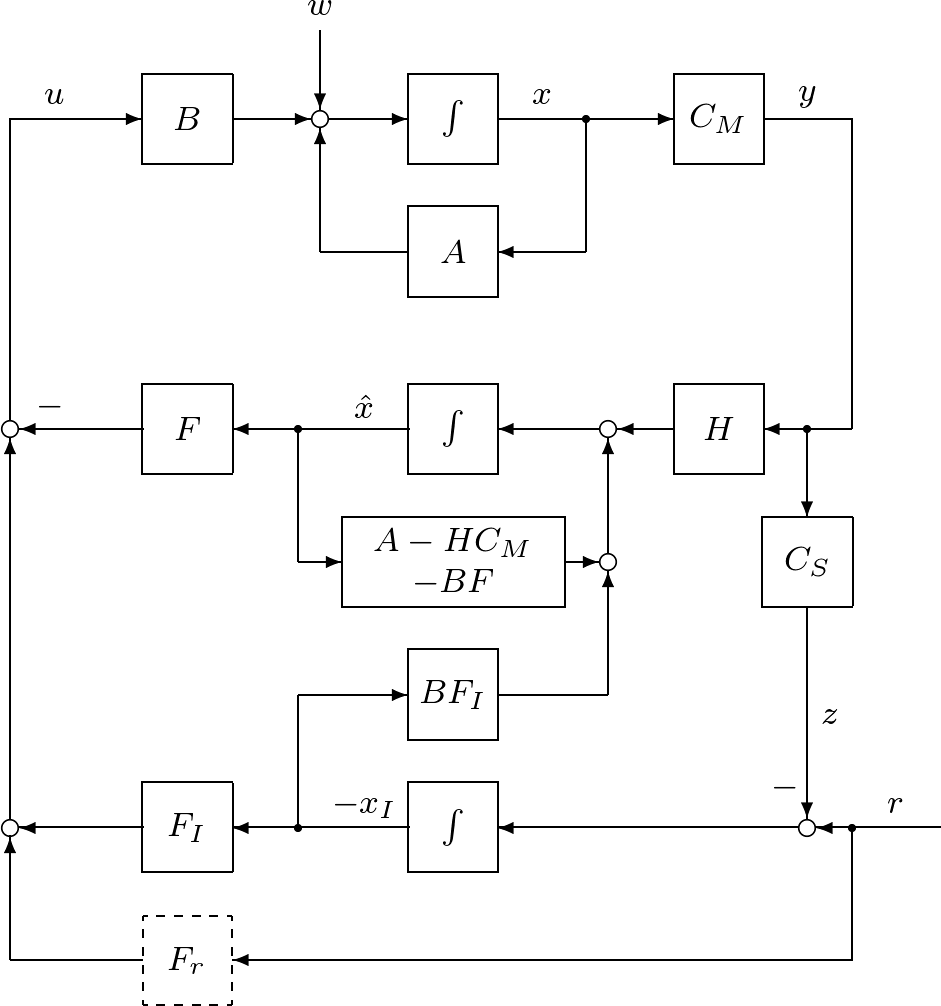 図1 積分動作を加えたオブザーバベースコントローラによる閉ループ系
図1 積分動作を加えたオブザーバベースコントローラによる閉ループ系![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \\ e(t) \end{array}\right] = \left[\begin{array}{ccc} I_n & 0 & 0 \\ 0 & I_m & 0 \\ -I_n & 0 & I_n \end{array}\right] \left[\begin{array}{c} x(t) \\ x_I(t) \\ \hat{x}(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b5d9f1751dc5c2977110972aa9b6df51_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \boxed{\left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \\\hline \dot{e}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc|c} A-BF & -BF_I & -BF \\ C & 0 & 0 \\\hline 0 & 0 & A-HC_M \end{array}\right] }_{ A_{EF}'= \left[\begin{array}{c|c} A_{EF} & - \left[\begin{array}{cc} B \\ 0 \end{array}\right] F \\[5mm] \hline 0 & \widehat{A} \end{array}\right] } \left[\begin{array}{c} x(t) \\ x_I(t) \\\hline e(t) \end{array}\right] + \left[\begin{array}{c} w \\ -r \\\hline -w \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e7fd58fcda89d55aeef7eae502bf33d5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \\\hline e(t) \end{array}\right] \ \rightarrow\ \underbrace{ \left[\begin{array}{c|c} A_{EF}^{-1} & -A_{EF}^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] F\widehat{A}^{-1} \\[5mm]\hline 0 & \widehat{A}^{-1} \end{array}\right] }_{A_{EF}'\,^{-1}} \left[\begin{array}{c} -w \\ r \\\hline w \end{array}\right] \quad (t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7dbdd90fdb25b174ea756263881e7ad1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(24)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0d41396e25f50798302fa74e0fcc7e0c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(26)\quad \int_0^\infty \left( \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right]^T Q_E \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] +{\dot u}^T(t)R_E{\dot u}(t)\right)\,dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e8a6e5b1e487b8f7d4c66618190de067_l3.png)
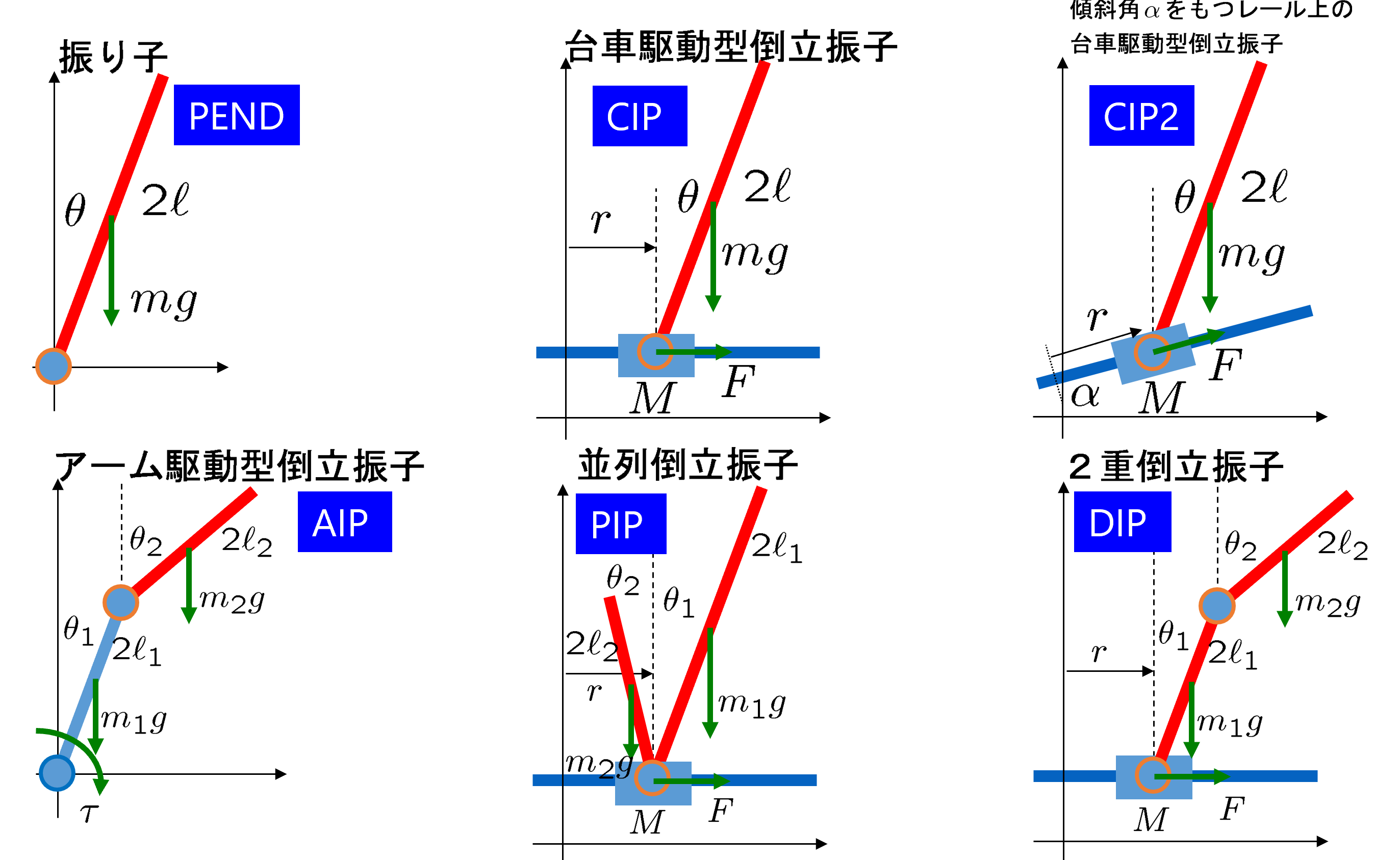 図1 様々な倒立振子
図1 様々な倒立振子![Rendered by QuickLaTeX.com \displaystyle{(2.1)\quad \frac{d}{dt}\left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & -\frac{3gm}{4M+m} & 0 & 0\\ 0 & \frac{3(M+m)g}{(4M+m)\ell} & 0 & 0\\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ 0\\ \frac{4}{4M+m}\\ \frac{3}{(4M+m)\ell} \end{array}\right] }_{B} \underbrace{F(t)}_{u(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-84a6ca484c9323a3fd95f4660cfea7d9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccc} f_1 & f_2 & f_3 & f_4 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (r(t)-r_c)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c730ca98f152a46bbeb44247cb831a1a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2.3)\quad \underbrace{r(t)}_{z(t)}= \underbrace{ \left[\begin{array}{cccc} 1 & 0 & 0 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b3d58870882b86ba47d53ab648e41923_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2.4)\quad \underbrace{\left[\begin{array}{c} 0\\ 0\\ 0\\ 0\\\hline r_c \end{array}\right] }_{\left[\begin{array}{c} -w \\ r_c \end{array}\right]} = \underbrace{\left[\begin{array}{cccc|c} 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & -\frac{3gm}{4M+m} & 0 & 0 & \frac{4}{4M+m}\\ 0 & \frac{3(M+m)g}{(4M+m)\ell} & 0 & 0 & \frac{3}{(4M+m)\ell}\\\hline 1 & 0 & 0 & 0 & 0 \end{array}\right] }_{S=\left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]} \underbrace{\left[\begin{array}{c} r_c\\ 0\\ 0\\ 0\\\hline 0 \end{array}\right] }_{\left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6e862f5ab4dc45e7e238f3e42b3b277a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2.5)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_{E}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c7d0b3f0821d3f8401967d391989d5f3_l3.png)
![Rendered by QuickLaTeX.com (3.1)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] = \underbrace{\left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & -\frac{6\cos\alpha mg}{8M+(5-3\cos2\alpha)m} & 0 & 0\\ 0 & \frac{6(M+m)g}{(8M+(5-3\cos2\alpha)m)\ell} & 0 & 0\\ \end{array}\right] }_{A(\alpha)} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)}}\\ \displaystyle{+ \underbrace{\left[\begin{array}{c} 0\\ 0\\ \frac{8}{8M+(5-3\cos2\alpha)m}\\ \frac{6\cos\alpha}{(8M+(5-3\cos2\alpha)m)\ell} \end{array}\right] }_{B(\alpha)} \underbrace{(F(t)-F^*)}_{u(t)}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e1dd7f9098a60203914c3ec06dcf5e98_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccc} f_1 & f_2 & f_3 & f_4 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (r(t)-r_c)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3a4cfa12b94bd29a0a664260285d99b8_l3.png)
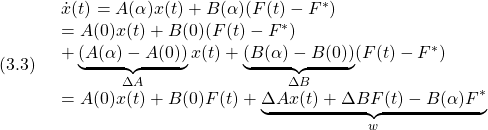
![Rendered by QuickLaTeX.com (4.1)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} \theta_1(t)\\ \theta_2(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] =}\\ \displaystyle{\underbrace{(\left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \frac{3(m_1+2m_2)g}{(4m_1+3m_2)\ell_1} & -\frac{9m_2g}{2(4m_1+3m_2)\ell_1} & 0 & 0\\ -\frac{9(m_1+2m_2)g}{2(4m_1+3m_2)\ell_1} & \frac{9m_2g}{(4m_1+3m_2)\ell_2} & 0 & 0\\ \end{array}\right]+\Delta A) }_{A(\alpha)=A+\Delta A} \underbrace{\left[\begin{array}{c} \theta_1(t)\\ \theta_2(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] }_{x(t)}\\ \displaystyle{+ \underbrace{(\left[\begin{array}{c} 0\\ 0\\ \frac{6}{2(4m_1+3m_2)\ell_1^2}\\ -\frac{9}{2(4m_1+3m_2)\ell_1\ell_2} \end{array}\right]+\Delta B) }_{B(\alpha)=B+\Delta B} \underbrace{(\tau(t)-\tau^*)}_{u(t)}}\\ =Ax(t)+B\tau(t)+\underbrace{\Delta Ax(t)+\Delta B\tau(t)-B(\alpha)\tau^*}_{w} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6e5d5f40649f7ccecd6e3e7aea53bb6f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4.2)\quad \tau(t)= \underbrace{- \left[\begin{array}{cccc} f_1 & f_2 & f_3 & f_4 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} \theta_1(t)\\ \theta_2(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (\theta_1(t)-\alpha)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5a9d737b654d24c373c67149fdb430f1_l3.png)
![Rendered by QuickLaTeX.com (5.1)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] =}\\ \displaystyle{\underbrace{\left[\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ 0 & -\frac{3m_1g}{4M+m_1+m_2} & -\frac{3m_2g}{4M+m_1+m_2} & 0 & 0 & 0\\ 0 & \frac{3(4m+4m_1+m_2)g}{4(4M+m_1+m_2)\ell_1} & \frac{9m_2g}{4(4M+m_1+m_2)\ell_1} & 0 & 0& 0\\ 0 & \frac{9gm_1}{4(4M+m_1+m_2)\ell_2} & \frac{3(4m+m_1+4m_2)g}{4(4M+m_1+m_2)\ell_2} & 0 & 0& 0\\ \end{array}\right]}_{A} \left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right]}\\ \displaystyle{+ \underbrace{ \left[\begin{array}{c} 0\\ 0\\ 0\\ \frac{4}{4M+m_1+m_2}\\ -\frac{3}{(4M+m_1+m_2)\ell_1}\\ -\frac{3}{(4M+m_1+m_2)\ell_2} \end{array}\right] }_{B} \underbrace{F(t)}_{u(t)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b146d12ebbd934f835113e9f5a66a050_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccccc} f_1 & f_2 & f_3 & f_4 & f_5 & f_6 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (r(t)-r_c)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a754530a145458dc98285892cb123a80_l3.png)
![Rendered by QuickLaTeX.com (6.1)\quad \begin{array}{l} \displaystyle{ \frac{d}{dt}\left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] =}\\ \displaystyle{ \left[\begin{array}{cccccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & -\frac{3m_1g}{Mm_1+m_1^2+(3M+m1)m_2} & -\frac{3m_2g}{Mm_1+m_1^2+(3M+m1)m_2} \\ 0 & \frac{3(4Mm_1+4m_1^2+3m_2^2+3(18M+13m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m1)m_2)\ell_1} & \frac{9(2M+m_1)m_2g}{(4Mm_1+m_1^2+(3M+m1)m_2)\ell_1} \\ 0 & \frac{9(2Mm_1+m_1^2+3(2M+m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} & \frac{3(4Mm_1+m_1^2+12(3M+m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} \\ \end{array}\right.}\\ \displaystyle{\left.\begin{array}{cccccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ \end{array}\right] \left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right]}\\ \displaystyle{+ \underbrace{\left[\begin{array}{c} 0\\ 0\\ 0\\ \frac{4m_1+3m_2}{4Mm_1+m_1^2+(3M+m1)m_2}\\ -\frac{3(2m_1+m2)}{2Mm_1+m_1^2+(3M+m1)m_2}\\ \frac{3m_1}{2(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} \end{array}\right] }_{B} \underbrace{F(t)}_{u(t)}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c0d8773e32ffbef0fd7275146dab4774_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccccc} f_1 & f_2 & f_3 & f_4 & f_5 & f_6 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (r(t)-r_c)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-39932c622bf561d62c488e285deca01f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \boxed{\left[\begin{array}{c} -w \\ r \end{array}\right] = \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] \left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5a63c22e2c20de8035fdefcbe9d60119_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \boxed{{\rm rank}\, \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S}=n+m} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b2fcb8d3d07f55b008eda2e6a5836e50_l3.png)
 図1 積分動作を加えた状態フィードバックによる閉ループ系
図1 積分動作を加えた状態フィードバックによる閉ループ系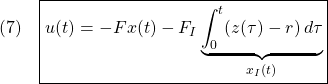
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \boxed{ %\underbrace{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] %}_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} A-BF & -BF_I \\ C & 0 \end{array}\right] }_{A_{EF}} %\underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] %}_{x_E(t)} + %\underbrace{ \left[\begin{array}{c} w \\ -r \end{array}\right] %}_{w_E} }}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a13e4e217df7e1cd4a8873612c945fbd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad A_{EF} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} - \left[\begin{array}{cc} B \\ 0 \end{array}\right] \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ae3e582f261444dac1f56aa447ce0eaa_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \begin{array}{ll} A_{EF}^{-1} =& S^{-1}+ S^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] \left(I_m- \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] S^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] \right)^{-1} \\[5mm] &\times \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] S^{-1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e0f009cac08e772a5836cd7f89991b53_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \boxed{A_{EF}^{-1} = \left[\begin{array}{cc} I_n & 0 \\ -F_I^{-1}F & -F_I^{-1} \end{array}\right] S^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0b2df9b56c6c85b1e3bfe245468fe652_l3.png)
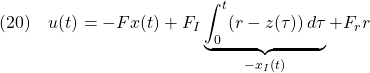
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \boxed{\frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] %}_{x_E(t)-x_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E1}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] %}_{x_E(t)-x_{E\infty}} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E1}} (u(t)-u_\infty)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2bcd3f36f880707fe8bc60b89fa6dbb6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(24)\quad \boxed{\frac{d}{dt} %\underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] %}_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} %\underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] %}_{\dot{x}_E(t)} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} {\dot u}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-acdd13f2ef2c1d92a0004a5f47cda17a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(25)\quad \left[\begin{array}{c} {\dot x}(t)-w \\ z(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-73ee9071a72e5208f32daf364e891bb9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(26)\quad \boxed{\left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-429e0ebfec7903d5dc5ce87f5046bed1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(27)\quad \boxed{\frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-69dd980e629d5d4d9cf34dc90dbc246d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(28)\quad \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cc8034db5edc1a000b2f2add912d9e66_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(29)\quad \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e7784673b16ee3dc6fc71b2e2e461a8c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(30)\quad u(t)-u_\infty=- \underbrace{\left[\begin{array}{cc} F & F_I \end{array}\right] }_{F_{E1}} \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-49e57cd33d9728f3bb2e32ce3cc5341c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad {\dot u}(t)=- \underbrace{\left[\begin{array}{cc} F & F_I \end{array}\right] }_{F_{E2}} \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-38d968135e7c7820854f8a99e80ed705_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(32)\quad {\dot u}(t)=- \underbrace{\left[\begin{array}{cc} K & K_I \end{array}\right] }_{K_{E3}} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a0dd224c0271441aad07fc15b5834f36_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(33)\quad {\dot u}(t)=- \underbrace{\left[\begin{array}{cc} K & K_I \end{array}\right] \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]^{-1} }_{K_{E3}S^{-1}} \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9efa6f3fc30539bde922fde97f38394c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(35)\quad \boxed{\left[\begin{array}{cc} F & F_I \end{array}\right] = \left[\begin{array}{cc} K & K_I \end{array}\right] \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-effa6673748e4582607e705f8cec8e0b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(36)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-09c7b450fba91ff4da2925235911deb2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(38)\quad \int_0^\infty \left( \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right]^T Q_E \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] +{\dot u}^T(t)R_E{\dot u}(t)\right)\,dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c670e9177dbb8cc950866876198e2e52_l3.png)
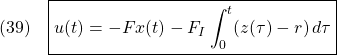
![Rendered by QuickLaTeX.com \displaystyle{(40)\quad \boxed{\left[\begin{array}{cc} F & F_I \end{array}\right] = \left[\begin{array}{cc} K & K_I \end{array}\right] \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bbcfc692f32dddd6063c223f23f96d7e_l3.png)
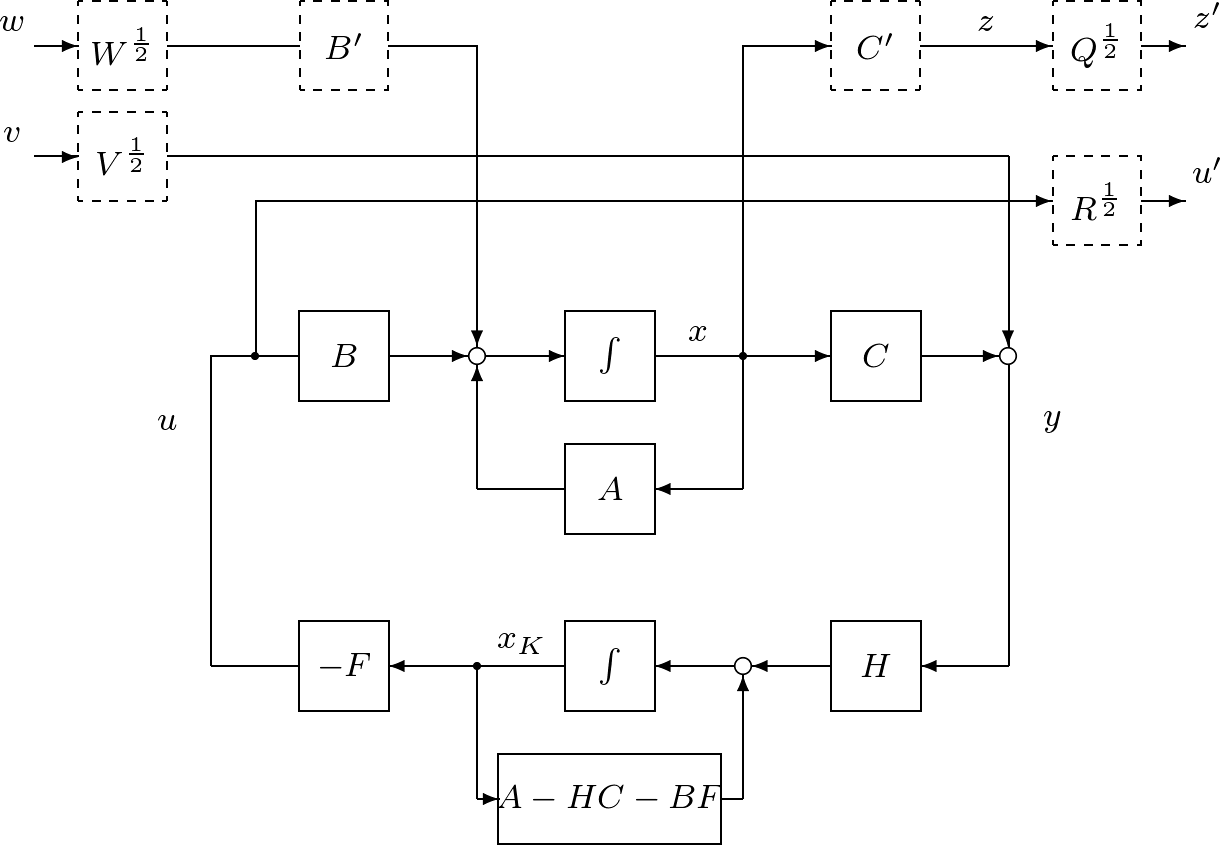 図1 LQG制御系設計の枠組み
図1 LQG制御系設計の枠組み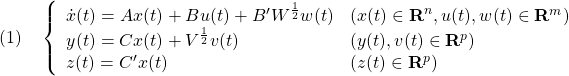
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \boxed{\begin{array}{l} \left[\begin{array}{cc} \dot{x}(t) \\ \dot{\hat{x}}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A & -BF \\ HC&A-HC-BF \end{array}\right] }_{A_{CL1}} \left[\begin{array}{cc} {x}(t) \\ \hat{x}(t) \end{array}\right] + \underbrace{ \left[\begin{array}{cc} B'W^{\frac{1}{2}} & 0 \\ 0 & HV^{\frac{1}{2}} \end{array}\right] }_{B_{CL1}} \left[\begin{array}{cc} {w}(t) \\ {v}(t) \end{array}\right]\\ \left[\begin{array}{cc} {y'}(t) \\ {u'}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} Q^{\frac{1}{2}}C' & 0 \\ 0 & -R^{\frac{1}{2}}F \end{array}\right] }_{C_{CL1}} \left[\begin{array}{cc} {x}(t) \\ \hat{x}(t) \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6e6de0ac1c24534b05d96168f970e1fc_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \boxed{\begin{array}{l} \left[\begin{array}{cc} \dot{x}(t) \\ \dot{e}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A-BF & -BF \\ 0 & A-HC \end{array}\right] }_{A_{CL2}} \left[\begin{array}{cc} {x}(t) \\ {e}(t) \end{array}\right] +\underbrace{ \left[\begin{array}{cc} B'W^{\frac{1}{2}} & 0 \\ -B'W^{\frac{1}{2}} & HV^{\frac{1}{2}} \end{array}\right] }_{B_{CL2}} \left[\begin{array}{cc} {w}(t) \\ {v}(t) \end{array}\right]\\ \left[\begin{array}{cc} {y'}(t) \\ {u'}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} Q^{\frac{1}{2}}C' & 0 \\ -R^{\frac{1}{2}}F & -R^{\frac{1}{2}}F \end{array}\right] }_{C_{CL2}} \left[\begin{array}{cc} {x}(t) \\ {e}(t) \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-81a989326d7d4a34c5752f6aecf84dec_l3.png)
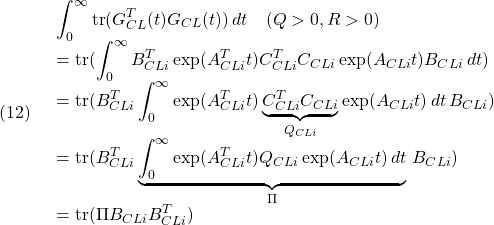
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \begin{array}{l} \Pi A_{CL1}= \left[\begin{array}{cc} \Pi_{1}&\Pi_{3} \\ \Pi_{3}^T&\Pi_{2} \end{array}\right] \left[\begin{array}{cc} A & -BF \\ HC&A-HC-BF \end{array}\right]\\ = \left[\begin{array}{cc} \Pi_{1}A+\Pi_{3}HC & -\Pi_{1}BF+\Pi_{3}(A-HC-BF)\\ \Pi_{3}^TA+\Pi_{2}HC & -\Pi_{3}^TBF+\Pi_{2}(A-HC-BF) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c429aa33a0e5684bc85b0263996ad5ef_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(19)\quad \begin{array}{l} A_{CL1}^T\Pi =(\Pi A_{CL1})^T\\ =\left[\begin{array}{cc} A^T\Pi_{1}+C^TH^T\Pi_{3}^T&\\ -F^TB^T\Pi_{1}+(A-HC-BF)^T\Pi_{3}^T & \end{array}\right.\\ \left.\begin{array}{cc} A^T\Pi_{3}+C^TH^T\Pi_{2}\\ -F^TB^T\Pi_{3}+(A-HC-BF)^T\Pi_{2} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c914ac5d6ae500873c120fe9e3c82eef_l3.png)
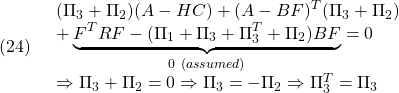
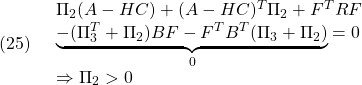
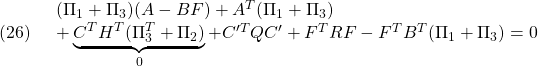
![Rendered by QuickLaTeX.com \displaystyle{(29)\quad \begin{array}{l} A_{CL1}\Gamma= \left[\begin{array}{cc} A & -BF \\ HC&A-HC-BF \end{array}\right] \left[\begin{array}{cc} \Gamma_{1}&\Gamma_{3} \\ \Gamma_{3}^T&\Gamma_{2} \end{array}\right]\\ =\left[\begin{array}{cc} A\Gamma_{1} -BF\Gamma_{3}^T &A\Gamma_{3} -BF\Gamma_{2}\\ HC\Gamma_{1}+(A-HC-BF)\Gamma_{3}^T &HC\Gamma_{3}+(A-HC-BF)\Gamma_{2} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b5efbe327872da02c0cdae613082e8a5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(30)\quad \begin{array}{l} \Gamma A_{CL1}^T =(A_{CL1}\Gamma)^T\\ =\left[\begin{array}{cc} \Gamma_{1}A^T -\Gamma_{3}F^TB^T & \Gamma_{1}C^TH^T+\Gamma_{3}(A-HC-BF)^T\\ \Gamma_{3}^TA^T -\Gamma_{2}F^TB^T & \Gamma_{3}^TC^TH^T+\Gamma_{2}(A-HC-BF)^T \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-166202eb44f8bebfc11fcdbb0cf09ab8_l3.png)
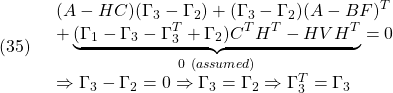
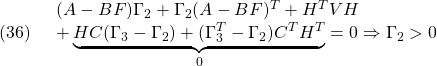
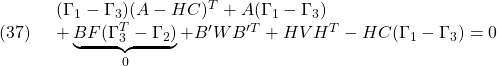
![Rendered by QuickLaTeX.com \displaystyle{(42)\quad \begin{array}{l} \Pi A_{CL1}\Gamma= \left[\begin{array}{cc} \Pi_{1}&\Pi_{3} \\ \Pi_{3}^T&\Pi_{2} \end{array}\right] \left[\begin{array}{cc} A & -BF \\ HC&A-HC-BF \end{array}\right] \Gamma\\ =\left[\begin{array}{cc} \Pi_{1}A+\Pi_{3}HC & -\Pi_{1}BF+\Pi_{3}(A-HC-BF)\\ \Pi_{3}^TA+\Pi_{2}HC & -\Pi_{3}^TBF+\Pi_{2}(A-HC-BF) \end{array}\right] \left[\begin{array}{cc} \Gamma_{1}&\Gamma_{3} \\ \Gamma_{3}^T&\Gamma_{2} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5cf2147ab153e0a23d8488f0452990da_l3.png)
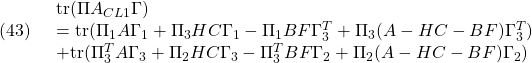
![Rendered by QuickLaTeX.com \displaystyle{(46)\quad \begin{array}{l} A_{CL1}^T\Pi\Gamma=(\Pi A_{CL1})^T\Gamma=\\ \left[\begin{array}{cc} A^T\Pi_{1}+C^TH^T\Pi_{3}^T&\\ -F^TB^T\Pi_{1}+(A-HC-BF)^T\Pi_{3}^T & \end{array}\right.\\ \left.\begin{array}{cc} A^T\Pi_{3}+C^TH^T\Pi_{2}\\ -F^TB^T\Pi_{3}+(A-HC-BF)^T\Pi_{2} \end{array}\right] \left[\begin{array}{cc} \Gamma_{1}&\Gamma_{3} \\ \Gamma_{3}^T&\Gamma_{2} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-98094a2e6a48cf9f59754bbc5f21fdef_l3.png)
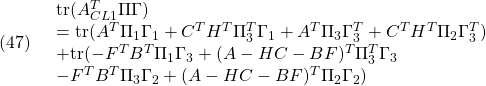
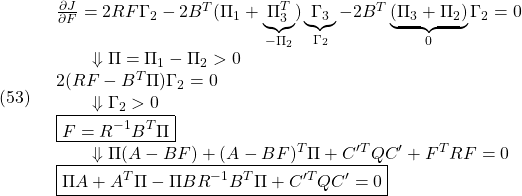
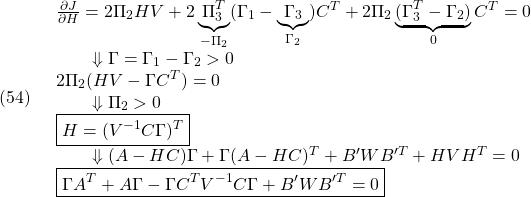
![Rendered by QuickLaTeX.com \displaystyle{(2.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccc} f_1 & f_2 & f_3 & f_4 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8d5882a8b8f1b74147cc2112bdbb8ae2_l3.png)
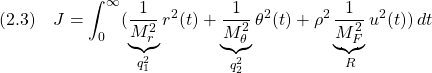
![Rendered by QuickLaTeX.com (3.1)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] = \underbrace{\left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & -\frac{6\cos\alpha mg}{8M+(5-3\cos2\alpha)m} & 0 & 0\\ 0 & \frac{6(M+m)g}{(8M+(5-3\cos2\alpha)m)\ell} & 0 & 0\\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)}}\\ \displaystyle{+ \underbrace{\left[\begin{array}{c} 0\\ 0\\ \frac{8}{8M+(5-3\cos2\alpha)m}\\ \frac{6\cos\alpha}{(8M+(5-3\cos2\alpha)m)\ell} \end{array}\right] }_{B} \underbrace{(F(t)-F^*)}_{u(t)}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1e8e92c6bb441706aa61fe16a4949d88_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccc} f_1 & f_2 & f_3 & f_4 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-274a0a5464ab474a19584e0c009000c0_l3.png)
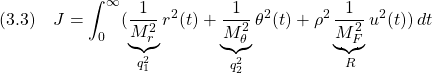
![Rendered by QuickLaTeX.com (4.1)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} \theta_1(t)-\theta_1^*\\ \theta_2(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] =}\\ \displaystyle{\underbrace{\left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \frac{3(m_1+2m_2)g}{(4m_1+3m_2)\ell_1} & -\frac{9m_2g}{2(4m_1+3m_2)\ell_1} & 0 & 0\\ -\frac{9(m_1+2m_2)g}{2(4m_1+3m_2)\ell_1} & \frac{9m_2g}{(4m_1+3m_2)\ell_2} & 0 & 0\\ \end{array}\right] }_{A} \left[\begin{array}{c} \theta_1(t)-\theta_1^*\\ \theta_2(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right]\\ \displaystyle{+ \underbrace{\left[\begin{array}{c} 0\\ 0\\ \frac{6}{2(4m_1+3m_2)\ell_1^2}\\ -\frac{9}{2(4m_1+3m_2)\ell_1\ell_2} \end{array}\right] }_{B} \underbrace{(\tau(t)-\tau^*)}_{u(t)}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3da30b65a938c38050e7c91085f9fd66_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccc} f_1 & f_2 & f_3 & f_4 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} \theta_1(t)-\theta_1^*\\ \theta_2(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9203232703f89cebce4d2815ea6198c8_l3.png)
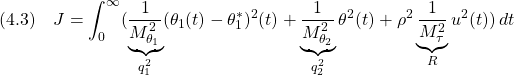
![Rendered by QuickLaTeX.com \displaystyle{(5.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccccc} f_1 & f_2 & f_3 & f_4 & f_5 & f_6 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b79eb1ba937c787a6245460a8ab2b42c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccccc} f_1 & f_2 & f_3 & f_4 & f_5 & f_6 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7d04a46a79f37a8e8c816d56bf20170d_l3.png)
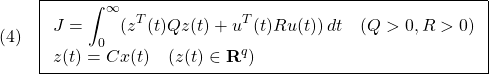
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \boxed{\left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] = \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] + \left[\begin{array}{c} 0 \\ 1 \end{array}\right] u(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4872e6ab89edfca755c552863cc2bd93_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right] + \left[\begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ - \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{c} 0 \\ 1 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] + \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right]\\ = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d28749ac5a43f35cf85d06d327748bb5_l3.png)
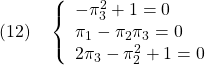
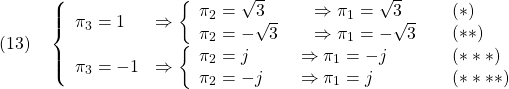
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \boxed{\left\{\begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] %}_{\dot{x}(t)} = %\underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -2\zeta\omega_n \end{array}\right] %}_{A} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] + %\underbrace{ \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] %}_{B} \\ y(t)= %\underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] %}_{C} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] \end{array}\right.} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4804d9477777bd149c8abe1925ce71fe_l3.png)
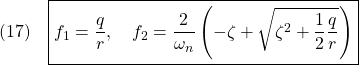
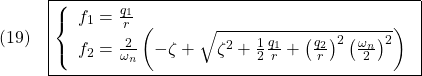
![Rendered by QuickLaTeX.com \displaystyle{(20)\quad \boxed{\left\{\begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] %}_{\dot x} = %\underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] %}_{A} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] %}_{x} + %\underbrace{ \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] %}_{B} u(t) \\ y(t)= %\underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] %}_{C} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] \end{array}\right.} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cff43f0c2dd25afe220d33c00beba1c3_l3.png)
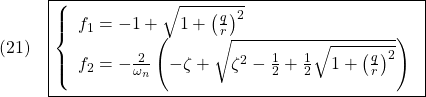
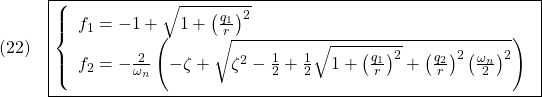
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \boxed{M=\left[\begin{array}{cc} A & -BR^{-1}B^T \\ C^TQC & -A^T \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7eb0ba79a865b0a2499ee0421c036a1b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(24)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} A & -BR^{-1}B^T \\ -C^TQC & -A^T \end{array}\right]}_{M(2n\times 2n)} \underbrace{ \left[\begin{array}{c} V_1 \\ V_2 \end{array}\right]}_{V^-(2n\times n)}\\ = \underbrace{ \left[\begin{array}{c} V_1 \\ V_2 \end{array}\right]}_{V^-(2n\times n)} \underbrace{ {\rm diag}\{\lambda_1,\cdots,\lambda_n\} }_{\Lambda^-(n\times n)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f8a2558fcebdca5d42752fab2101867b_l3.png)
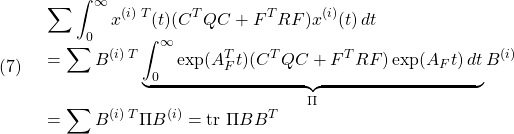
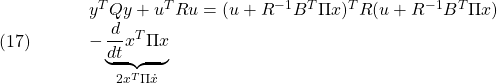
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ 0 & -2\zeta\omega_n \end{array}\right] + \left[\begin{array}{cc} 0 & 0 \\ 1 & -2\zeta\omega_n \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ - \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] r^{-2} \left[\begin{array}{cc} 0 & \omega_n^2 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ + \left[\begin{array}{c} 1 \\ 0 \end{array}\right] q^{2} \left[\begin{array}{cc} 1 & 0 \end{array}\right] % \left[\begin{array}{cc} % q_1^2 & 0 \\ % 0 & q_2^2 % \end{array}\right] = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e43567c4046c4807bb16901e4c9095c1_l3.png)
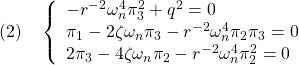
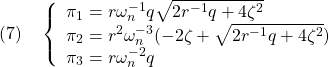
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \left[\begin{array}{cc} f_1 & f_2 \end{array}\right]=r^{-2} \left[\begin{array}{cc} 0 & \omega_n^2 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]=r^{-2}\omega_n^2 \left[\begin{array}{cc} \pi_3 & \pi_2 \end{array}\right]\\ = \left[\begin{array}{cc} \frac{q}{r} & \frac{2}{\omega_n}\left(-\zeta+\sqrt{\zeta^2+\frac{1}{2}\frac{q}{r}}\right) \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ac9df3a510b53e5194c148972b29d62f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ 0 & -2\zeta\omega_n \end{array}\right] + \left[\begin{array}{cc} 0 & 0 \\ 1 & -2\zeta\omega_n \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ - \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] r^{-2} \left[\begin{array}{cc} 0 & \omega_n^2 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ + \left[\begin{array}{cc} q_1^2 & 0 \\ 0 & q_2^2 \end{array}\right] = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ddd699d8aac23ef2a497f48ee1ecff2d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{ll} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] + \left[\begin{array}{cc} 0 & -\omega_n^2 \\ 1 & -2\zeta\omega_n \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ - \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] r^{-2} \left[\begin{array}{cc} 0 & \omega_n^2 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ + \left[\begin{array}{c} 1 \\ 0 \end{array}\right] q^2 \left[\begin{array}{cc} 1 & 0 \end{array}\right] = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2773454b3e211d96ee83363fb88da2a2_l3.png)
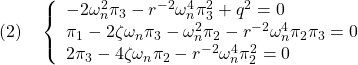
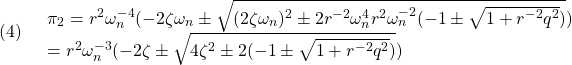
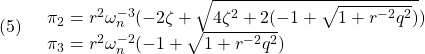
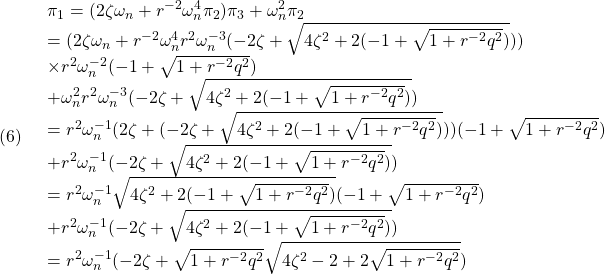
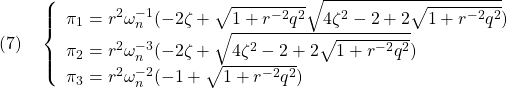
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \left[\begin{array}{cc} f_1 & f_2 \end{array}\right]=r^{-2} \left[\begin{array}{cc} 0 & \omega_n^2 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]=r^{-2}\omega_n^2 \left[\begin{array}{cc} \pi_3 & \pi_2 \end{array}\right]\\ = \left[\begin{array}{cc} -1+\sqrt{1+\left(\frac{q}{r}\right)^2} & -\frac{2}{\omega_n}\left(-\zeta+\sqrt{\zeta^2-\frac{1}{2}+\frac{1}{2}\sqrt{1+\left(\frac{q}{r}\right)^2}}\right) \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b52bac7cab88d375a41fa037afb2d31a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] + \left[\begin{array}{cc} 0 & -\omega_n^2 \\ 1 & -2\zeta\omega_n \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ - \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] r^{-2} \left[\begin{array}{cc} 0 & \omega_n^2 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ + \left[\begin{array}{cc} q_1^2 & 0 \\ 0 & q_2^2 \end{array}\right] = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e85a2fc5c10628fc6c41a4d64cd73e6c_l3.png)
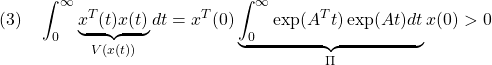
![Rendered by QuickLaTeX.com (4)\quad \begin{array}{l} \Pi A+A^T\Pi\\ \displaystyle{=\int_0^\infty\exp(A^Tt)\exp(At)dt A+A^T \int_0^\infty\exp(A^Tt)\exp(At)dt}\\ \displaystyle{=\int_0^\infty\frac{d}{dt}(\exp(A^Tt)\exp(At))dt=\left[\exp(A^Tt)\exp(At)\right]_0^\infty\\ =\exp(A^T\infty)\underbrace{\exp(A\infty)}_{0}-\exp(A^T0)\underbrace{\exp(A0)}_{I_n}=-I_n}\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-59a1e80997a4165ad1b001b5bb29d526_l3.png)
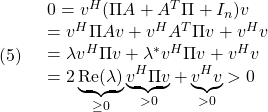
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \underbrace{ \left[\begin{array}{cc} p_1 & p_3 \\ p_3 & p_2 \end{array}\right] }_{P} \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -2 & -3 \end{array}\right] }_{A} + \underbrace{ \left[\begin{array}{cc} 0 & -2 \\ 1 & -3 \end{array}\right] }_{A^T} \underbrace{ \left[\begin{array}{cc} p_1 & p_3 \\ p_3 & p_2 \end{array}\right] }_{P} =- \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right] }_{I_2} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-85e9e5691877d6104d33dc0ab99c2307_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \left[\begin{array}{ccc} 0 & 0 & -4 \\ 1 & -2 & -3 \\ 0 & -6 & 2 \end{array}\right] \left[\begin{array}{c} p_1 \\ p_2 \\ p_3 \end{array}\right] = \left[\begin{array}{c} -1 \\ 0 \\ -1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-141e2af5be5bb2484bbf9f73b996b8f4_l3.png)
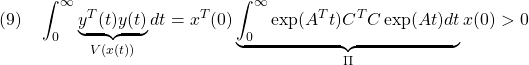
![Rendered by QuickLaTeX.com (10)\quad \begin{array}{l} \Pi A+A^T\Pi\\ \displaystyle{=\int_0^\infty\exp(A^Tt)C^TC\exp(At)dt A+A^T \int_0^\infty\exp(A^Tt)C^TC\exp(At)dt}\\ \displaystyle{=\int_0^\infty\frac{d}{dt}(\exp(A^Tt)C^TC\exp(At))dt=\left[\exp(A^Tt)C^TC\exp(At)\right]_0^\infty\\ =\exp(A^T\infty)C^TC\underbrace{\exp(A\infty)}_{0}-\exp(A^T0)C^TC\underbrace{\exp(A0)}_{I_n}=-C^TC}\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-19deb8818548c3e2e4134cf297e36e9a_l3.png)
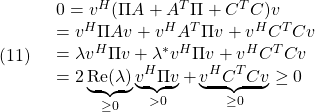
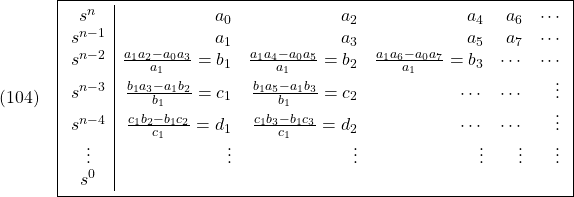
![Rendered by QuickLaTeX.com \displaystyle{(105)\quad \boxed{\begin{array}{l} D_1=a_1 \\ D_2={\rm det}< \left[\begin{array}{cc} a_1 & a_3 \\ a_0 & a_2 \end{array}\right] \\ D_3={\rm det} \left[\begin{array}{ccc} a_1 & a_3 & a_5 \\ a_0 & a_2 & a_4 \\ 0 & a_1 & a_3 \end{array}\right] \\ \vdots \\ D_{n-1}={\rm det} \left[\begin{array}{ccccc} a_1 & a_3 & a_5 & \cdots & a_{2n-3} \\ a_0 & a_2 & a_4 & \cdots & a_{2n-4} \\ 0 & a_1 & a_3 & \cdots & a_{2n-5} \\ 0 & a_0 & a_2 & \cdots & a_{2n-6} \\ 0 & 0 & a_1 & \cdots & a_{2n-7} \\ \vdots & \vdots & \ddots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & a_{n-1} \\ \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cc23ec66f0d8f9ecc82f04778b09aa0e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(108)\quad A=\left[\begin{array}{cccccc} 0 & 1 & 0 & \cdots & 0\\ 0 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \cdots & 1\\ -a_n & -a_{n-1} & -a_{n-2} & \cdots & -a_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c7d5fc3807d87258ca18739049a3c9c4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(109)\quad B=\left[\begin{array}{ccccccc} 0 & 1 & \cdots & 0 & 0 & 0 \\ -b_n & 0 & \cdots & 0 & 0 & 0 \\ 0 & -b_{n-1} & \cdots & 0 & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots& \vdots\\ 0 & 0 & \cdots & -b_3 & 0 & 1 \\ 0 & 0 & \cdots & 0 & -b_2 & -b_1 \end{array}\right]=TAT^{-1} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cdf74d6527d9a40e2edc50d31ea063c0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(111)\quad \Pi=\left[\begin{array}{ccccccc} b_1b_2\cdots b_n & 0 & \cdots & 0 \\ 0 & b_1b_2\cdots b_{n-1} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & b_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6699b7ac084d6a76d67a99ac23fa9a16_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(113)\quad \left[\begin{array}{ccccccc} b_1b_2\cdots b_n & 0 & \cdots & 0 \\ 0 & b_1b_2\cdots b_{n-1} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & b_1 \end{array}\right] \left[\begin{array}{ccccccc} 0 & 1 & \cdots & 0 & 0 & 0 \\ -b_n & 0 & \cdots & 0 & 0 & 0 \\ 0 & -b_{n-1} & \cdots & 0 & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots& \vdots\\ 0 & 0 & \cdots & -b_3 & 0 & 1 \\ 0 & 0 & \cdots & 0 & -b_2 & -b_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5000a96cd5039f37342bd31231f6bdc9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \left[\begin{array}{ccccccc} 0 & b_1b_2\cdots b_n & \cdots & 0 & 0 & 0 \\ -b_1b_2\cdots b_n & 0 & \cdots & 0 & 0 & 0 \\ 0 & -b_1b_2\cdots b_{n-1} & \cdots & 0 & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots& \vdots\\ 0 & 0 & \cdots & -b_1b_2b_3 & 0 & b_1b_2 \\ 0 & 0 & \cdots & 0 & -b_1b_2 & -b_1^2 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0d026755db647d96cd2f69b8819ea73f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(114)\quad &&\Pi B+B^T\Pi= \left[\begin{array}{ccccccc} 0 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & -2b_1^2 \end{array}\right] =- \underbrace{ \left[\begin{array}{cccc} 0 \\ \vdots \\ 0 \\ \sqrt{2}b_1 \end{array}\right] }_{H^T} \underbrace{ \left[\begin{array}{cccc} 0 & \cdots & 0 & \sqrt{2}b_1 \end{array}\right] }_{H} \nonumber }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f8ab89e9688d8e627f8beae5f665393c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(115)\quad {\rm rank} \left[\begin{array}{ccccccc} B-\lambda I_n \\ H \end{array}\right] = {\rm rank} \left[\begin{array}{ccccccc} -\lambda & 1 & \cdots & 0 & 0 & 0 \\ -b_n & -\lambda & \cdots & 0 & 0 & 0 \\ 0 & -b_{n-1} & \cdots & 0 & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots& \vdots\\ 0 & 0 & \cdots & -b_3 & -\lambda& 1 \\ 0 & 0 & \cdots & 0 & -b_2 & -b_1-\lambda \\ 0 & 0 & \cdots & 0 & 0 & \sqrt{2}b_1 \end{array}\right]=n }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3b8414a60038a059b11aa00019bc8ffc_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(117)\quad A=\left[\begin{array}{cccccc} 0 & 1 & 0 & \cdots & 0\\ 0 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \cdots & 1\\ -a_n & -a_{n-1} & -a_{n-2} & \cdots & -a_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e8e53c908512662a1ea7325469a8ff3f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(118)\quad B=\left[\begin{array}{ccccccc} 0 & 1 & \cdots & 0 & 0 & 0 \\ -b_n & 0 & \cdots & 0 & 0 & 0 \\ 0 & -b_{n-1} & \cdots & 0 & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots& \vdots\\ 0 & 0 & \cdots & -b_3 & 0 & 1 \\ 0 & 0 & \cdots & 0 & -b_2 & -b_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3dc206086d1292a18c0690d402c2c609_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(122)\quad \Lambda=\left[\begin{array}{ccccccc} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & \lambda_n \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-633928ba777d0e14931171b0cd98fc55_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(123)\quad V_A=\left[\begin{array}{ccccccc} 1 & 1 & \cdots & 1 \\ \lambda_1 & \lambda_2 & \cdots & \lambda_n \\ \vdots & \vdots & \ddots & \vdots \\ \lambda_1^{n-1} & \lambda_2^{n-1} & \cdots & \lambda_n^{n-1} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bea0f2e6122a57e8ed81f0c2e1207e84_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ A=\left[\begin{array}{cccccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ -a_3 & -a_2 & -a_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b78bd1f02bf94aeda3823f4c8a63a447_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ B=\left[\begin{array}{cccccc} 0 & 1 & 0 \\ -b_3 & 0 & 1 \\ 0 & -b_2 & -b_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-671723d030ae668b83b04db608c87a02_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{cccccc} 0 & 1 & 0 \\ -b_3 & 0 & 1 \\ 0 & -b_2 & -b_1 \end{array}\right] \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \end{array}\right]= \lambda \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e54f5e4b2f7794e495f792b5d85297e9_l3.png)
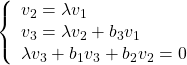
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \end{array}\right]= \left[\begin{array}{l} 1 \\ \lambda \\ \lambda^2+b_3 \end{array}\right] = \underbrace{ \left[\begin{array}{cccccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ b_3 & 0 & 1 \end{array}\right]}_{\Gamma} \left[\begin{array}{c} 1 \\ \lambda \\ \lambda^2 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d7b5153ea774cdb5e3261c19e75b6f9e_l3.png)
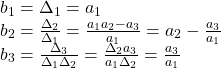
![Rendered by QuickLaTeX.com \displaystyle{ A=\left[\begin{array}{cccccc} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -a_4 & -a_3 & -a_2 & -a_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7ff706457d487dadae751b14f7d3acaa_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ B=\left[\begin{array}{cccccc} 0 & 1 & 0 & 0 \\ -b_4 & 0 & 1 & 0 \\ 0 & -b_3 & 0 & 1 \\ 0 & 0 & -b_2 & -b_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-da5df5023f6c35c4de93859da6ea9fde_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{cccccc} 0 & 1 & 0 & 0 \\ -b_4 & 0 & 1 & 0 \\ 0 & -b_3 & 0 & 1 \\ 0 & 0 & -b_2 & -b_1 \end{array}\right] \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 \end{array}\right]= \lambda \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-399fe6c79f1dd6f54f84d18c4054af42_l3.png)
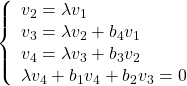
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 \end{array}\right]= \left[\begin{array}{l} 1 \\ \lambda \\ \lambda^2+b_4 \\ \lambda^3+(b_3+b_4)\lambda \end{array}\right] = \underbrace{ \left[\begin{array}{cccccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ b_4 & 0 & 1 & 0 \\ 0 & b_3+b_4 & 0 & 1 \end{array}\right]}_{\Gamma} \left[\begin{array}{c} 1 \\ \lambda \\ \lambda^2 \\ \lambda^3 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f33ce8a3dfbcf995152d8b4e5697ef53_l3.png)
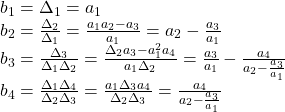
![Rendered by QuickLaTeX.com \displaystyle{ A=\left[\begin{array}{cccccc} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ -a_5 & -a_4 & -a_3 & -a_2 & -a_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f0a9e02ff4a508c3702747c6f22eeac1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ B=\left[\begin{array}{cccccc} 0 & 1 & 0 & 0 & 0 \\ -b_5 & 0 & 1 & 0 & 0 \\ 0 & -b_4 & 0 & 1 & 0 \\ 0 & 0 & -b_3 & 0 & 1 \\ 0 & 0 & 0 & -b_2 & -b_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3fd5a82630d2f98d35fb92d870129912_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{cccccc} 0 & 1 & 0 & 0 & 0 \\ -b_5 & 0 & 1 & 0 & 0 \\ 0 & -b_4 & 0 & 1 & 0 \\ 0 & 0 & -b_3 & 0 & 1 \\ 0 & 0 & 0 & -b_2 & -b_1 \end{array}\right] \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 \\ v_5 \end{array}\right]= \lambda \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 \\ v_5 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0c8ad97efe9f7c22114534ef6080b3f5_l3.png)
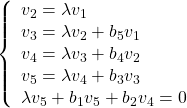
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 \\ v_5 \end{array}\right]= \left[\begin{array}{l} 1 \\ \lambda \\ \lambda^2+b_5 \\ \lambda^3+(b_4+b_5)\lambda \\ \lambda^4+(b_3+b_4+b_5)\lambda^2+b_3b_5 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cf3aab51d558601a7ac9dadd513c23e7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \underbrace{ \left[\begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ b_5 & 0 & 1 & 0 & 0 \\ 0 & b_4+b_5 & 0 & 1 & 0 \\ b_3b_5 & 0 & b_3+b_4+b_5 & 0 & 1 \end{array}\right]}_{\Gamma} \left[\begin{array}{c} 1 \\ \lambda \\ \lambda^2 \\ \lambda^3 \\ \lambda^4 \end{array}\right] \nonumber }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ac175e71aca1a6030212e539c67f8b9d_l3.png)
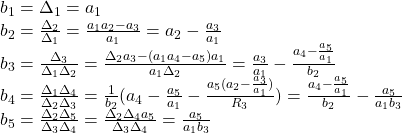
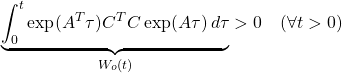
![Rendered by QuickLaTeX.com {\rm rank}\, \underbrace{ \left[\begin{array}{c} C \\ CA \\ \vdots\\ CA^{n-1} \end{array}\right] }_{observability\ matrix} =n](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6253173de124e69f731cff9f00238073_l3.png)