LQI制御の応用…Homework
[1] 倒立振子は制御なしには平衡状態を保てないので、制御技術の有効性を示すのに、よく研究されています。次図は様々な倒立振子を示しています。
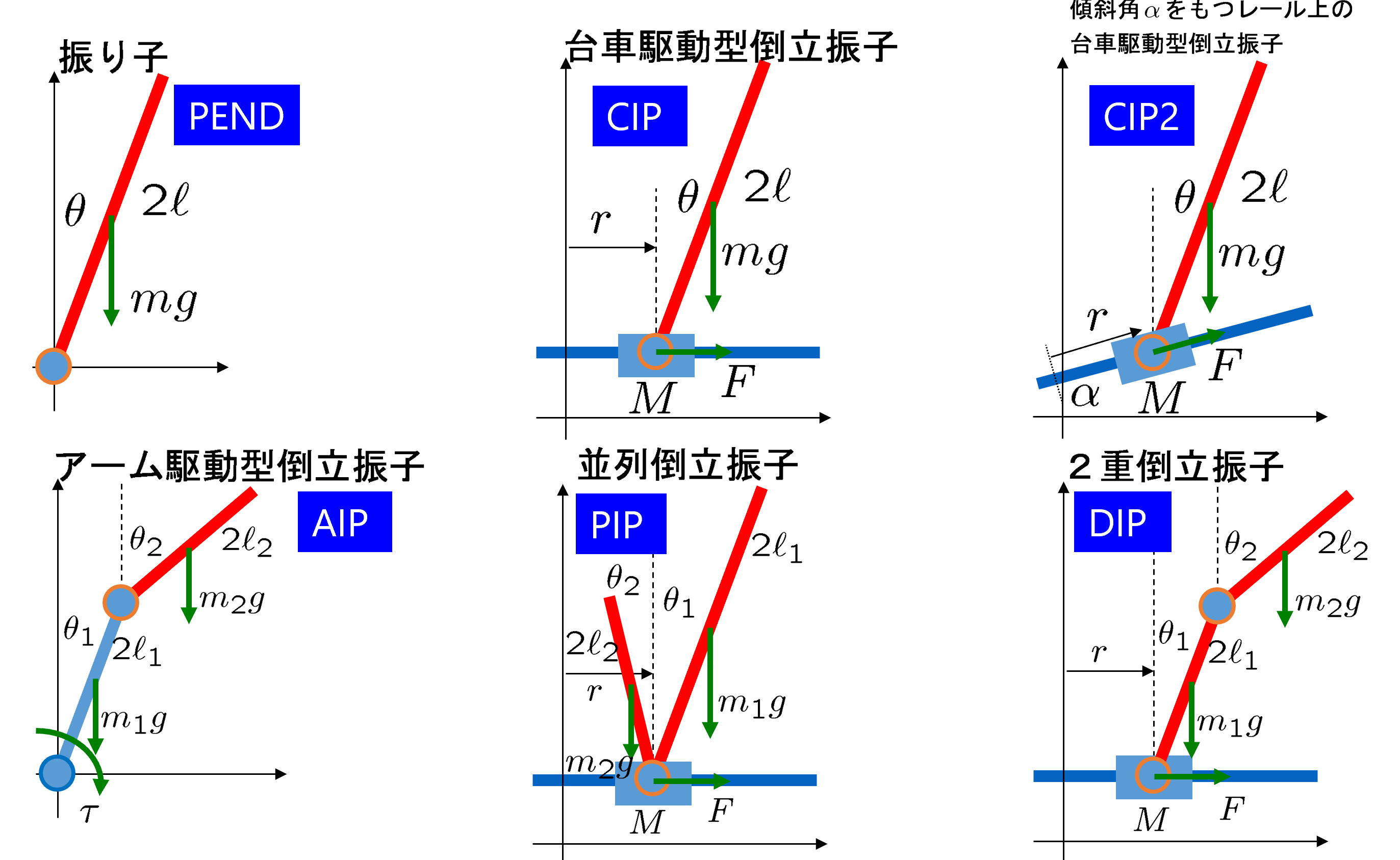 図1 様々な倒立振子
図1 様々な倒立振子
これらの倒立振子について、非線形シミュレータを開発し、平衡状態まわりの挙動を表す線形状態方程式を得ていました。これらに基づいて、以下では、LQ制御系を設計します。
[2] CIP
平衡状態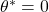 周りの挙動を表す線形状態方程式は次式で与えられます。
周りの挙動を表す線形状態方程式は次式で与えられます。
![Rendered by QuickLaTeX.com \displaystyle{(2.1)\quad \frac{d}{dt}\left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & -\frac{3gm}{4M+m} & 0 & 0\\ 0 & \frac{3(M+m)g}{(4M+m)\ell} & 0 & 0\\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ 0\\ \frac{4}{4M+m}\\ \frac{3}{(4M+m)\ell} \end{array}\right] }_{B} \underbrace{F(t)}_{u(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-84a6ca484c9323a3fd95f4660cfea7d9_l3.png)
これに対して、倒立位置を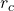 に変更可能とする、積分動作をもつ状態フィードバック
に変更可能とする、積分動作をもつ状態フィードバック
![Rendered by QuickLaTeX.com \displaystyle{(2.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccc} f_1 & f_2 & f_3 & f_4 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (r(t)-r_c)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c730ca98f152a46bbeb44247cb831a1a_l3.png)
を、LQI制御のアルゴリズムに沿って設計します。
ステップ1 被制御変数の決定
制御目的は倒立位置を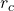 に変更し、安定化することですから
に変更し、安定化することですから
![Rendered by QuickLaTeX.com \displaystyle{(2.3)\quad \underbrace{r(t)}_{z(t)}= \underbrace{ \left[\begin{array}{cccc} 1 & 0 & 0 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b3d58870882b86ba47d53ab648e41923_l3.png)
のように選びます。このとき、明らかに次式が成り立ちます。
![Rendered by QuickLaTeX.com \displaystyle{(2.4)\quad \underbrace{\left[\begin{array}{c} 0\\ 0\\ 0\\ 0\\\hline r_c \end{array}\right] }_{\left[\begin{array}{c} -w \\ r_c \end{array}\right]} = \underbrace{\left[\begin{array}{cccc|c} 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & -\frac{3gm}{4M+m} & 0 & 0 & \frac{4}{4M+m}\\ 0 & \frac{3(M+m)g}{(4M+m)\ell} & 0 & 0 & \frac{3}{(4M+m)\ell}\\\hline 1 & 0 & 0 & 0 & 0 \end{array}\right] }_{S=\left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]} \underbrace{\left[\begin{array}{c} r_c\\ 0\\ 0\\ 0\\\hline 0 \end{array}\right] }_{\left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6e862f5ab4dc45e7e238f3e42b3b277a_l3.png)
ここで、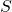 は正則であることから、倒立位置を変えたときの状態
は正則であることから、倒立位置を変えたときの状態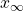 と入力
と入力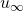 が一意に定まります。
が一意に定まります。
ステップ2 偏差系の安定化
偏差系
![Rendered by QuickLaTeX.com \displaystyle{(2.5)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_{E}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c7d0b3f0821d3f8401967d391989d5f3_l3.png)
を、状態フィードバック
![Rendered by QuickLaTeX.com \displaystyle{(2.6)\quad {\dot u}(t)=- \left[\begin{array}{cc} K & K_I \end{array}\right] \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-daf0a6680fa0cc9f98ffdb21a28cd95b_l3.png)
によるLQ制御で安定化します。その際、評価関数としてはたとえば
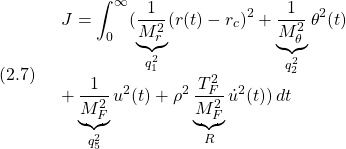
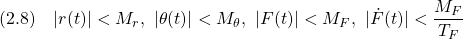
を選び、これを最小にするような(2.6)を設計します。
ステップ3 積分動作を加えた状態フィードバックの構成
次式から積分動作を加えた状態フィードバック(2.2)を構成します。
![Rendered by QuickLaTeX.com \displaystyle{(2.9)\quad \left[\begin{array}{cc} F & F_I \end{array}\right] = \left[\begin{array}{cc} K & K_I \end{array}\right] \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]^{-1} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-746d16bd7ab96ea7c7a07db38e294e6e_l3.png)
| MATLAB |
%cCIP_lqi.m
%-----
clear all, close all
global mc m ell g th0
mc=1; m=0.1; ell=0.2; g=9.8;
th0=0/180*pi %input('th(0) = <0,180> ')/180*pi;
%-----
A=[zeros(2,2) eye(2);zeros(2,4)];
A(3,1)=0;
A(3,2)=-3*m*g/(m+4*mc);
A(4,1)=0;
A(4,2)=3*(m+mc)*g/((m+4*mc)*ell);
B=zeros(4,1);
B(3)=4/(m+4*mc);
B(4)=-3/((m+4*mc)*ell);
%-----
Tcart=1; Mr=0.5;
Tpend=1/4*2*pi*sqrt(4/3*ell/g); Mth=3/180*pi;
Tamp=0.1; Mamp=1;
CM=eye(2,4); CS=[1 0]; C=CS*CM;
n=size(A,1); m=size(C,1); r=size(B,2);
%-----
AE=[A B;zeros(m,n+m)];
BE=[zeros(n,m);eye(m)];
CE=eye(n+m);
QE=diag([1/Mr 1/Mth Tcart/Mr*0 Tpend/Mth*0 1/Mamp].^2);
RE=(Tamp/Mamp)^2;
[KE,pcl]=opt(AE,BE,CE,QE,RE);
FE=KE/[A B;C zeros(m)];
pcl, F=FE(:,1:n), FI=FE(:,n+1:n+m)
%-----
CE=diag([100,180/pi])*eye(2,5);
sysE=ss(AE-BE*KE,[],[CE;-KE],[]);
t=0:0.05:5;
rc=0.5
xE0=[-rc;0;0;0;0];
initial(sysE,xE0,t), grid
%-----
xs=[0;0;0;0];
us=0;
sim("nCIP_lqi")
%-----
|
[3] CIP2
平衡状態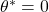 と平衡入力
と平衡入力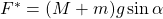 周りの挙動を表す線形状態方程式は次式で与えられます。
周りの挙動を表す線形状態方程式は次式で与えられます。
![Rendered by QuickLaTeX.com (3.1)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] = \underbrace{\left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & -\frac{6\cos\alpha mg}{8M+(5-3\cos2\alpha)m} & 0 & 0\\ 0 & \frac{6(M+m)g}{(8M+(5-3\cos2\alpha)m)\ell} & 0 & 0\\ \end{array}\right] }_{A(\alpha)} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)}}\\ \displaystyle{+ \underbrace{\left[\begin{array}{c} 0\\ 0\\ \frac{8}{8M+(5-3\cos2\alpha)m}\\ \frac{6\cos\alpha}{(8M+(5-3\cos2\alpha)m)\ell} \end{array}\right] }_{B(\alpha)} \underbrace{(F(t)-F^*)}_{u(t)}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e1dd7f9098a60203914c3ec06dcf5e98_l3.png)
これに対して、倒立位置を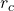 に変更可能とする、積分動作をもつ状態フィードバック
に変更可能とする、積分動作をもつ状態フィードバック
![Rendered by QuickLaTeX.com \displaystyle{(3.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccc} f_1 & f_2 & f_3 & f_4 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (r(t)-r_c)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3a4cfa12b94bd29a0a664260285d99b8_l3.png)
を、LQI制御のアルゴリズムに沿って設計します。
●レールの傾斜角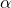 は未知とするのが実際的です。そこで
は未知とするのが実際的です。そこで
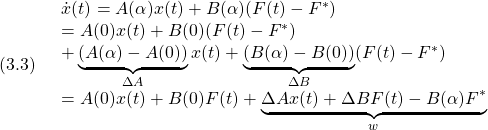
として、レールの傾斜がないときの(2.1)に外乱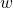 が加わっていると考えます。もちろん
が加わっていると考えます。もちろん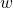 は定値ではないのですが、どれくらいの効果があるかシミュレーションで確かめてみます。
は定値ではないのですが、どれくらいの効果があるかシミュレーションで確かめてみます。
| MATLAB |
%cCIP2_lqi.m
%-----
clear all, close all
global mc m ell g alpha th0
mc=1; m=0.1; ell=0.2; g=9.8;
alpha=3/180*pi;
th0=3/180*pi %input('ths = <0,180> ')/180*pi;
%-----
A=[zeros(2,2) eye(2);zeros(2,4)];
A(3,1)=0;
A(3,2)=-6*cos(alpha)*m*g/(8*mc+(5-3*cos(2*alpha))*m);
A(4,1)=0;
A(4,2)=6*(m+mc)*g/((8*mc+(5-3*cos(2*alpha))*m)*ell);
B=zeros(4,1);
B(3)=8/(8*mc+(5-3*cos(2*alpha))*m);
B(4)=-6*cos(alpha)/((8*mc+(5-3*cos(2*alpha))*m)*ell);
%----- alpha=0の設計モデル
A=[zeros(2,2) eye(2);zeros(2,4)];
A(3,1)=0;
A(3,2)=-3*m*g/(m+4*mc);
A(4,1)=0;
A(4,2)=3*(m+mc)*g/((m+4*mc)*ell);
B=zeros(4,1);
B(3)=4/(m+4*mc);
B(4)=-3/((m+4*mc)*ell);
%-----
Tcart=1; Mr=0.5;
Tpend=1/4*2*pi*sqrt(4/3*ell/g); Mth=3/180*pi;
Tamp=0.1; Mamp=1;
CM=eye(2,4); CS=[1 0]; C=CS*CM;
n=size(A,1); m=size(C,1); r=size(B,2);
%-----
AE=[A B;zeros(m,n+m)];
BE=[zeros(n,m);eye(m)];
CE=eye(n+m);
QE=diag([1/Mr 1/Mth Tcart/Mr*0 Tpend/Mth*0 1/Mamp].^2);
RE=(Tamp/Mamp)^2;
[KE,pcl]=opt(AE,BE,CE,QE,RE);
FE=KE/[A B;C zeros(m)];
pcl, F=FE(:,1:n), FI=FE(:,n+1:n+m)
%-----
CE=diag([100,180/pi])*eye(2,5);
sysE=ss(AE-BE*KE,[],[CE;-KE],[]);
t=0:0.05:5;
rc=0.5
xE0=[-rc;0;0;0;0];
initial(sysE,xE0,t), grid
%-----
xs=[0;0;0;0];
us=(mc+m)*g*sin(alpha)*0;
sim("nCIP2_lqi")
%-----
%eof
|
[4] AIP
平衡状態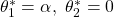 と平衡入力
と平衡入力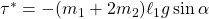 周りの挙動を表す線形状態方程式は次式で与えられます。
周りの挙動を表す線形状態方程式は次式で与えられます。
![Rendered by QuickLaTeX.com (4.1)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} \theta_1(t)\\ \theta_2(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] =}\\ \displaystyle{\underbrace{(\left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \frac{3(m_1+2m_2)g}{(4m_1+3m_2)\ell_1} & -\frac{9m_2g}{2(4m_1+3m_2)\ell_1} & 0 & 0\\ -\frac{9(m_1+2m_2)g}{2(4m_1+3m_2)\ell_1} & \frac{9m_2g}{(4m_1+3m_2)\ell_2} & 0 & 0\\ \end{array}\right]+\Delta A) }_{A(\alpha)=A+\Delta A} \underbrace{\left[\begin{array}{c} \theta_1(t)\\ \theta_2(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] }_{x(t)}\\ \displaystyle{+ \underbrace{(\left[\begin{array}{c} 0\\ 0\\ \frac{6}{2(4m_1+3m_2)\ell_1^2}\\ -\frac{9}{2(4m_1+3m_2)\ell_1\ell_2} \end{array}\right]+\Delta B) }_{B(\alpha)=B+\Delta B} \underbrace{(\tau(t)-\tau^*)}_{u(t)}}\\ =Ax(t)+B\tau(t)+\underbrace{\Delta Ax(t)+\Delta B\tau(t)-B(\alpha)\tau^*}_{w} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6e5d5f40649f7ccecd6e3e7aea53bb6f_l3.png)
これに対して、アームの角度を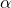 に変更可能とする、積分動作をもつ状態フィードバック
に変更可能とする、積分動作をもつ状態フィードバック
![Rendered by QuickLaTeX.com \displaystyle{(4.2)\quad \tau(t)= \underbrace{- \left[\begin{array}{cccc} f_1 & f_2 & f_3 & f_4 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} \theta_1(t)\\ \theta_2(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (\theta_1(t)-\alpha)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5a9d737b654d24c373c67149fdb430f1_l3.png)
を、LQI制御のアルゴリズムに沿って設計します。
| MATLAB |
%cAIP_lq.m
%-----
clear all, close all
global m1 m2 ell1 ell2 g th10 th20
m1=0.1; m2=0.2; ell1=0.1; ell2=0.2; g=9.8;
th10=0/180*pi %input('th1(0) = <0,180> ')/180*pi;
th20=0/180*pi %input('th2(0) = <0,180> ')/180*pi;
%----- th10=0 における線形モデル
A=[zeros(2,2) eye(2);zeros(2,4)];
A(3,1)=3*(2*m2+m1)*g/((3*m2+4*m1)*ell1);
A(3,2)=-9*m2*g/(2*(3*m2+4*m1)*ell1);
A(4,1)=-9*(2*m2+m1)*g/(2*(3*m2+4*m1)*ell2);
A(4,2)=3*(3*m2+m1)*g/((3*m2+4*m1)*ell2);
B=zeros(4,1);
B(3)=3/((3*m2+4*m1)*ell1^2);
B(4)=-9/(2*(3*m2+4*m1)*ell1*ell2);
%-----
Tpend1=1/4*2*pi*sqrt(4/3*ell1/g); Mth1=3/180*pi;
Tpend2=1/4*2*pi*sqrt(4/3*ell2/g); Mth2=3/180*pi;
Tamp=0.1; Mamp=1;
CM=eye(2,4); CS=[1 0]; C=CS*CM;
n=size(A,1); m=size(C,1); r=size(B,2);
%-----
AE=[A B;zeros(m,n+m)];
BE=[zeros(n,m);eye(m)];
CE=eye(n+m);
QE=diag([1/Mth1 1/Mth2 Tpend1/Mth1*0 Tpend2/Mth2*0 1/Mamp].^2);
RE=(Tamp/Mamp)^2;
[KE,pcl]=opt(AE,BE,CE,QE,RE);
FE=KE/[A B;C zeros(m)];
pcl, F=FE(:,1:n), FI=FE(:,n+1:n+m)
%-----
CE=diag([180/pi,180/pi])*eye(2,5);
sysE=ss(AE-BE*KE,[],[CE;-KE],[]);
t=0:0.01:1;
th1c=10/180*pi
xE0=[-th10;-th20;0;0;0];
initial(sysE,xE0,t), grid
%-----
xs=[0;0;0;0];
us=-(m1+2*m2)*ell1*g*sin(th1c)
sim("nAIP_lqi")
%-----
%eof
|
[5] PIP
平衡状態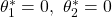 周りの挙動を表す線形状態方程式は次式で与えられます。
周りの挙動を表す線形状態方程式は次式で与えられます。
![Rendered by QuickLaTeX.com (5.1)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] =}\\ \displaystyle{\underbrace{\left[\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ 0 & -\frac{3m_1g}{4M+m_1+m_2} & -\frac{3m_2g}{4M+m_1+m_2} & 0 & 0 & 0\\ 0 & \frac{3(4m+4m_1+m_2)g}{4(4M+m_1+m_2)\ell_1} & \frac{9m_2g}{4(4M+m_1+m_2)\ell_1} & 0 & 0& 0\\ 0 & \frac{9gm_1}{4(4M+m_1+m_2)\ell_2} & \frac{3(4m+m_1+4m_2)g}{4(4M+m_1+m_2)\ell_2} & 0 & 0& 0\\ \end{array}\right]}_{A} \left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right]}\\ \displaystyle{+ \underbrace{ \left[\begin{array}{c} 0\\ 0\\ 0\\ \frac{4}{4M+m_1+m_2}\\ -\frac{3}{(4M+m_1+m_2)\ell_1}\\ -\frac{3}{(4M+m_1+m_2)\ell_2} \end{array}\right] }_{B} \underbrace{F(t)}_{u(t)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b146d12ebbd934f835113e9f5a66a050_l3.png)
これに対して、倒立位置を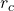 に変更可能とする、積分動作をもつ状態フィードバック
に変更可能とする、積分動作をもつ状態フィードバック
![Rendered by QuickLaTeX.com \displaystyle{(5.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccccc} f_1 & f_2 & f_3 & f_4 & f_5 & f_6 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (r(t)-r_c)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a754530a145458dc98285892cb123a80_l3.png)
を、LQI制御のアルゴリズムに沿って設計します。
| MATLAB |
%cPIP_lqi.m
%-----
clear all, close all
global mc m1 m2 ell1 ell2 g th10 th20
mc=1; m1=0.1; m2=0.2; ell1=0.15; ell2=0.2; g=9.8;
th10=0/180*pi %input('th1(0) = <0,180> ')/180*pi;
th20=-1/180*pi %input('th2(0) = <0,180> ')/180*pi;
%-----
A=[zeros(3,3) eye(3);zeros(3,6)];
A(4,1)=0;
A(4,2)=-3*m1*g/(m1+m2+4*mc);
A(4,3)=-3*m2*g/(m1+m2+4*mc);
A(5,1)=0;
A(5,2)=(12*m1+3*m2+12*mc)*g/((4*m1+4*m2+16*mc)*ell1);
A(5,3)=9*m2*g/((4*m1+4*m2+16*mc)*ell1);
A(6,1)=0;
A(6,2)=9*m1*g/((4*m1+4*m2+16*mc)*ell2);
A(6,3)=(3*m1+12*m2+12*mc)*g/((4*m1+4*m2+16*mc)*ell2);
B=zeros(6,1);
B(4)=4/(m1+m2+4*mc);
B(5)=-3/((m1+m2+4*mc)*ell1);
B(6)=-3/((m1+m2+4*mc)*ell2);
%-----
Tcart=1; Mr=0.5;
Tpend1=1/4*2*pi*sqrt(4/3*ell1/g); Mth1=3/180*pi;
Tpend2=1/4*2*pi*sqrt(4/3*ell2/g); Mth2=3/180*pi;
Tamp=0.1; Mamp=1;
CM=eye(3,6); CS=[1 0 0]; C=CS*CM;
n=size(A,1); m=size(C,1); r=size(B,2);
%-----
AE=[A B;zeros(m,n+m)];
BE=[zeros(n,m);eye(m)];
CE=eye(n+m);
QE=diag([1/Mr 1/Mth1 1/Mth2 Tcart/Mr*0 Tpend1/Mth1*0 Tpend2/Mth2*0 1/Mamp].^2);
RE=(Tamp/Mamp)^2;
[KE,pcl]=opt(AE,BE,CE,QE,RE);
FE=KE/[A B;C zeros(m)];
pcl, F=FE(:,1:n), FI=FE(:,n+1:n+m)
%-----
CE=diag([100,180/pi,180/pi])*eye(3,7);
sysE=ss(AE-BE*KE,[],[CE;-KE],[]);
t=0:0.05:5;
rc=0.5
xE0=[-rc;0;0;0;0;0;0];
initial(sysE,xE0,t), grid
%-----
xs=[0;0;0;0;0;0];
us=0;
sim("nPIP_lqi")
%-----
%eof
|
[6] DIP
平衡状態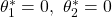 周りの挙動を表す線形状態方程式は次式で与えられます。
周りの挙動を表す線形状態方程式は次式で与えられます。
![Rendered by QuickLaTeX.com (6.1)\quad \begin{array}{l} \displaystyle{ \frac{d}{dt}\left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] =}\\ \displaystyle{ \left[\begin{array}{cccccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & -\frac{3m_1g}{Mm_1+m_1^2+(3M+m1)m_2} & -\frac{3m_2g}{Mm_1+m_1^2+(3M+m1)m_2} \\ 0 & \frac{3(4Mm_1+4m_1^2+3m_2^2+3(18M+13m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m1)m_2)\ell_1} & \frac{9(2M+m_1)m_2g}{(4Mm_1+m_1^2+(3M+m1)m_2)\ell_1} \\ 0 & \frac{9(2Mm_1+m_1^2+3(2M+m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} & \frac{3(4Mm_1+m_1^2+12(3M+m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} \\ \end{array}\right.}\\ \displaystyle{\left.\begin{array}{cccccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ \end{array}\right] \left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right]}\\ \displaystyle{+ \underbrace{\left[\begin{array}{c} 0\\ 0\\ 0\\ \frac{4m_1+3m_2}{4Mm_1+m_1^2+(3M+m1)m_2}\\ -\frac{3(2m_1+m2)}{2Mm_1+m_1^2+(3M+m1)m_2}\\ \frac{3m_1}{2(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} \end{array}\right] }_{B} \underbrace{F(t)}_{u(t)}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c0d8773e32ffbef0fd7275146dab4774_l3.png)
これに対して、倒立位置を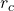 に変更可能とする、積分動作をもつ状態フィードバック
に変更可能とする、積分動作をもつ状態フィードバック
![Rendered by QuickLaTeX.com \displaystyle{(6.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccccc} f_1 & f_2 & f_3 & f_4 & f_5 & f_6 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (r(t)-r_c)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-39932c622bf561d62c488e285deca01f_l3.png)
を、LQI制御のアルゴリズムに沿って設計します。
| MATLAB |
%cDIP_lqi.m
%-----
clear all, close all
global mc m1 m2 ell1 ell2 g th10 th20
mc=1; m=0.1; m1=m; m2=m; ell=0.15; ell1=ell; ell2=ell; g=9.8;
th10=1/180*pi %input('th1(0) = <0,180> ')/180*pi;
th20=0 %input('th2(0) = <0,180> ')/180*pi;
%-----
A=[zeros(3,3) eye(3);zeros(3,6)];
A(4,1)=0;
A(4,2)=-18*m*g/(2*m+7*mc);
A(4,3)=3*m*g/(4*m+14*mc);
A(5,1)=0;
A(5,2)=(15*m+12*mc)*g/((2*m+7*mc)*ell);
A(5,3)=-(9*m+18*mc)*g/((8*m+28*mc)*ell);
A(6,1)=0;
A(6,2)=-(9*m+18*mc)*g/((2*m+7*mc)*ell);
A(6,3)=(15*m+48*mc)*g/((8*m+28*mc)*ell);
B=zeros(6,1);
B(4)=7/(2*m+7*mc);
B(5)=-9/((4*m+14*mc)*ell);
B(6)=3/((4*m+14*mc)*ell);
%------
Tcart=1; Mr=0.5;
Tpend1=1/4*2*pi*sqrt(4/3*ell1/g); Mth1=3/180*pi;
Tpend2=1/4*2*pi*sqrt(4/3*ell2/g); Mth2=3/180*pi;
Tamp=0.1; Mamp=1;
CM=eye(3,6); CS=[1 0 0]; C=CS*CM;
n=size(A,1); m=size(C,1); r=size(B,2);
%-----
AE=[A B;zeros(m,n+m)];
BE=[zeros(n,m);eye(m)];
CE=eye(n+m);
QE=diag([1/Mr 1/Mth1 1/Mth2 Tcart/Mr*0 Tpend1/Mth1*0 Tpend2/Mth2*0 1/Mamp].^2);
RE=(Tamp/Mamp)^2;
[KE,pcl]=opt(AE,BE,CE,QE,RE);
FE=KE/[A B;C zeros(m)];
pcl, F=FE(:,1:n), FI=FE(:,n+1:n+m)
%-----
CE=diag([100,180/pi,180/pi])*eye(3,7);
sysE=ss(AE-BE*KE,[],[CE;-KE],[]);
t=0:0.05:5;
rc=0.5
xE0=[-rc;0;0;0;0;0;0];
initial(sysE,xE0,t), grid
%-----
xs=[0;0;0;0;0;0];
us=0;
sim("nDIP_lqi")
%-----
%eof
|
 図1 様々な倒立振子
図1 様々な倒立振子![]() 周りの挙動を表す線形状態方程式は次式で与えられます。
周りの挙動を表す線形状態方程式は次式で与えられます。![Rendered by QuickLaTeX.com \displaystyle{(2.1)\quad \frac{d}{dt}\left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & -\frac{3gm}{4M+m} & 0 & 0\\ 0 & \frac{3(M+m)g}{(4M+m)\ell} & 0 & 0\\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ 0\\ \frac{4}{4M+m}\\ \frac{3}{(4M+m)\ell} \end{array}\right] }_{B} \underbrace{F(t)}_{u(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-84a6ca484c9323a3fd95f4660cfea7d9_l3.png)
![]() に変更可能とする、積分動作をもつ状態フィードバック
に変更可能とする、積分動作をもつ状態フィードバック![Rendered by QuickLaTeX.com \displaystyle{(2.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccc} f_1 & f_2 & f_3 & f_4 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (r(t)-r_c)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c730ca98f152a46bbeb44247cb831a1a_l3.png)
![]() に変更し、安定化することですから
に変更し、安定化することですから![Rendered by QuickLaTeX.com \displaystyle{(2.3)\quad \underbrace{r(t)}_{z(t)}= \underbrace{ \left[\begin{array}{cccc} 1 & 0 & 0 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b3d58870882b86ba47d53ab648e41923_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2.4)\quad \underbrace{\left[\begin{array}{c} 0\\ 0\\ 0\\ 0\\\hline r_c \end{array}\right] }_{\left[\begin{array}{c} -w \\ r_c \end{array}\right]} = \underbrace{\left[\begin{array}{cccc|c} 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & -\frac{3gm}{4M+m} & 0 & 0 & \frac{4}{4M+m}\\ 0 & \frac{3(M+m)g}{(4M+m)\ell} & 0 & 0 & \frac{3}{(4M+m)\ell}\\\hline 1 & 0 & 0 & 0 & 0 \end{array}\right] }_{S=\left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]} \underbrace{\left[\begin{array}{c} r_c\\ 0\\ 0\\ 0\\\hline 0 \end{array}\right] }_{\left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6e862f5ab4dc45e7e238f3e42b3b277a_l3.png)
![]() は正則であることから、倒立位置を変えたときの状態
は正則であることから、倒立位置を変えたときの状態![]() と入力
と入力![]() が一意に定まります。
が一意に定まります。![Rendered by QuickLaTeX.com \displaystyle{(2.5)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_{E}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c7d0b3f0821d3f8401967d391989d5f3_l3.png)
![]()
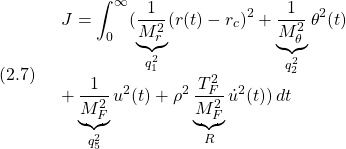
![]()
![]()
![]() と平衡入力
と平衡入力![]() 周りの挙動を表す線形状態方程式は次式で与えられます。
周りの挙動を表す線形状態方程式は次式で与えられます。![Rendered by QuickLaTeX.com (3.1)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] = \underbrace{\left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & -\frac{6\cos\alpha mg}{8M+(5-3\cos2\alpha)m} & 0 & 0\\ 0 & \frac{6(M+m)g}{(8M+(5-3\cos2\alpha)m)\ell} & 0 & 0\\ \end{array}\right] }_{A(\alpha)} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)}}\\ \displaystyle{+ \underbrace{\left[\begin{array}{c} 0\\ 0\\ \frac{8}{8M+(5-3\cos2\alpha)m}\\ \frac{6\cos\alpha}{(8M+(5-3\cos2\alpha)m)\ell} \end{array}\right] }_{B(\alpha)} \underbrace{(F(t)-F^*)}_{u(t)}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e1dd7f9098a60203914c3ec06dcf5e98_l3.png)
![]() に変更可能とする、積分動作をもつ状態フィードバック
に変更可能とする、積分動作をもつ状態フィードバック![Rendered by QuickLaTeX.com \displaystyle{(3.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccc} f_1 & f_2 & f_3 & f_4 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (r(t)-r_c)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3a4cfa12b94bd29a0a664260285d99b8_l3.png)
![]() は未知とするのが実際的です。そこで
は未知とするのが実際的です。そこで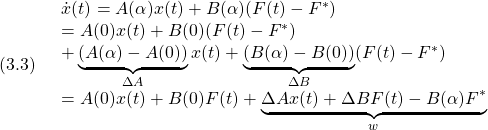
![]() が加わっていると考えます。もちろん
が加わっていると考えます。もちろん![]() は定値ではないのですが、どれくらいの効果があるかシミュレーションで確かめてみます。
は定値ではないのですが、どれくらいの効果があるかシミュレーションで確かめてみます。![]() と平衡入力
と平衡入力![]() 周りの挙動を表す線形状態方程式は次式で与えられます。
周りの挙動を表す線形状態方程式は次式で与えられます。![Rendered by QuickLaTeX.com (4.1)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} \theta_1(t)\\ \theta_2(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] =}\\ \displaystyle{\underbrace{(\left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \frac{3(m_1+2m_2)g}{(4m_1+3m_2)\ell_1} & -\frac{9m_2g}{2(4m_1+3m_2)\ell_1} & 0 & 0\\ -\frac{9(m_1+2m_2)g}{2(4m_1+3m_2)\ell_1} & \frac{9m_2g}{(4m_1+3m_2)\ell_2} & 0 & 0\\ \end{array}\right]+\Delta A) }_{A(\alpha)=A+\Delta A} \underbrace{\left[\begin{array}{c} \theta_1(t)\\ \theta_2(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] }_{x(t)}\\ \displaystyle{+ \underbrace{(\left[\begin{array}{c} 0\\ 0\\ \frac{6}{2(4m_1+3m_2)\ell_1^2}\\ -\frac{9}{2(4m_1+3m_2)\ell_1\ell_2} \end{array}\right]+\Delta B) }_{B(\alpha)=B+\Delta B} \underbrace{(\tau(t)-\tau^*)}_{u(t)}}\\ =Ax(t)+B\tau(t)+\underbrace{\Delta Ax(t)+\Delta B\tau(t)-B(\alpha)\tau^*}_{w} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6e5d5f40649f7ccecd6e3e7aea53bb6f_l3.png)
![]() に変更可能とする、積分動作をもつ状態フィードバック
に変更可能とする、積分動作をもつ状態フィードバック![Rendered by QuickLaTeX.com \displaystyle{(4.2)\quad \tau(t)= \underbrace{- \left[\begin{array}{cccc} f_1 & f_2 & f_3 & f_4 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} \theta_1(t)\\ \theta_2(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (\theta_1(t)-\alpha)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5a9d737b654d24c373c67149fdb430f1_l3.png)
![]() 周りの挙動を表す線形状態方程式は次式で与えられます。
周りの挙動を表す線形状態方程式は次式で与えられます。![Rendered by QuickLaTeX.com (5.1)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] =}\\ \displaystyle{\underbrace{\left[\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ 0 & -\frac{3m_1g}{4M+m_1+m_2} & -\frac{3m_2g}{4M+m_1+m_2} & 0 & 0 & 0\\ 0 & \frac{3(4m+4m_1+m_2)g}{4(4M+m_1+m_2)\ell_1} & \frac{9m_2g}{4(4M+m_1+m_2)\ell_1} & 0 & 0& 0\\ 0 & \frac{9gm_1}{4(4M+m_1+m_2)\ell_2} & \frac{3(4m+m_1+4m_2)g}{4(4M+m_1+m_2)\ell_2} & 0 & 0& 0\\ \end{array}\right]}_{A} \left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right]}\\ \displaystyle{+ \underbrace{ \left[\begin{array}{c} 0\\ 0\\ 0\\ \frac{4}{4M+m_1+m_2}\\ -\frac{3}{(4M+m_1+m_2)\ell_1}\\ -\frac{3}{(4M+m_1+m_2)\ell_2} \end{array}\right] }_{B} \underbrace{F(t)}_{u(t)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b146d12ebbd934f835113e9f5a66a050_l3.png)
![]() に変更可能とする、積分動作をもつ状態フィードバック
に変更可能とする、積分動作をもつ状態フィードバック![Rendered by QuickLaTeX.com \displaystyle{(5.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccccc} f_1 & f_2 & f_3 & f_4 & f_5 & f_6 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (r(t)-r_c)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a754530a145458dc98285892cb123a80_l3.png)
![]() 周りの挙動を表す線形状態方程式は次式で与えられます。
周りの挙動を表す線形状態方程式は次式で与えられます。![Rendered by QuickLaTeX.com (6.1)\quad \begin{array}{l} \displaystyle{ \frac{d}{dt}\left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] =}\\ \displaystyle{ \left[\begin{array}{cccccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & -\frac{3m_1g}{Mm_1+m_1^2+(3M+m1)m_2} & -\frac{3m_2g}{Mm_1+m_1^2+(3M+m1)m_2} \\ 0 & \frac{3(4Mm_1+4m_1^2+3m_2^2+3(18M+13m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m1)m_2)\ell_1} & \frac{9(2M+m_1)m_2g}{(4Mm_1+m_1^2+(3M+m1)m_2)\ell_1} \\ 0 & \frac{9(2Mm_1+m_1^2+3(2M+m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} & \frac{3(4Mm_1+m_1^2+12(3M+m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} \\ \end{array}\right.}\\ \displaystyle{\left.\begin{array}{cccccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ \end{array}\right] \left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right]}\\ \displaystyle{+ \underbrace{\left[\begin{array}{c} 0\\ 0\\ 0\\ \frac{4m_1+3m_2}{4Mm_1+m_1^2+(3M+m1)m_2}\\ -\frac{3(2m_1+m2)}{2Mm_1+m_1^2+(3M+m1)m_2}\\ \frac{3m_1}{2(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} \end{array}\right] }_{B} \underbrace{F(t)}_{u(t)}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c0d8773e32ffbef0fd7275146dab4774_l3.png)
![]() に変更可能とする、積分動作をもつ状態フィードバック
に変更可能とする、積分動作をもつ状態フィードバック![Rendered by QuickLaTeX.com \displaystyle{(6.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccccc} f_1 & f_2 & f_3 & f_4 & f_5 & f_6 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (r(t)-r_c)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-39932c622bf561d62c488e285deca01f_l3.png)