可検出性と可観測性…Homework
[1] 制御対象のモデルが
![]()
で与えられるとき、これに対する状態オブザーバは、微分方程式
![]()
で与えられました。ここで、オブザーバゲイン![]() を
を![]() が安定行列になるように選ぶ必要がありました。でもこれはいつでも可能であるわけではありません。すなわち
が安定行列になるように選ぶ必要がありました。でもこれはいつでも可能であるわけではありません。すなわち![]() を
を![]() が安定行列になるように選べる場合に状態オブザーバが構成可能となり、このとき可検出性(detectability)が成り立つと言います。
が安定行列になるように選べる場合に状態オブザーバが構成可能となり、このとき可検出性(detectability)が成り立つと言います。
![]() を安定行列とするためには、双対システム
を安定行列とするためには、双対システム
![]()
に対する状態フィードバック
![]()
による閉ループ系
![]()
を安定化して求めます。ということは、可検出性の条件は双対システムの可安定性と等価になります。すなわち可安定性の条件において
![]()
のように置き換えて、次が得られます。
|
【可検出性の定義とその等価な条件】
定義DD: 状態オブザーバを構成可能 条件D1: 条件D2: |
可検出性の判定は行列![]() と
と![]() を用いて行われるので、可検出性が成り立つとき、対
を用いて行われるので、可検出性が成り立つとき、対![]() は可検出対という言い方をします。
は可検出対という言い方をします。
可安定性よりも強い条件として可制御性がありましたが、これに対応する概念は可観測性(observability)と言われ、これと等価な条件は次のようにまとめられます。
|
【可観測性の定義とその等価な条件】
定義DO: 任意有限時間 条件O1: 条件O2: 条件O3: 条件O4: 条件O5: 条件O6: |
可観測性の判定も行列![]() と
と![]() を用いて行われるので、可観測性が成り立つとき、対
を用いて行われるので、可観測性が成り立つとき、対![]() は可観測対という言い方をします。条件O1の積分式を可観測性グラミアン行列、条件O2の行列を可観測性行列と呼びます。また条件O4を満足する
は可観測対という言い方をします。条件O1の積分式を可観測性グラミアン行列、条件O2の行列を可観測性行列と呼びます。また条件O4を満足する![]() の固有値を
の固有値を![]() は可観測固有値、満足しない固有値を不可観測固有値と呼びます。
は可観測固有値、満足しない固有値を不可観測固有値と呼びます。
上で述べたように、可観測性の議論は、可制御性の議論において、![]() を
を![]() に、
に、![]() を
を![]() に置き換えて行えばよいので、次が成り立ちます。
に置き換えて行えばよいので、次が成り立ちます。
条件O6![]() 条件O1
条件O1![]() 条件O2
条件O2![]() 条件O3
条件O3![]() 条件O4
条件O4![]() 条件O5
条件O5
●<定義DO![]() 条件O1>
条件O1>
適当な入力のもとでの出力は次式で表されます。
![]()
ここで、零状態応答は計算できますので、これを出力から引いた![]() を次のようにおきます。
を次のようにおきます。
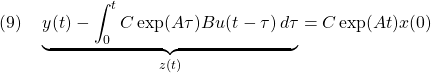
したがって、入出力データ![]() から,初期状態
から,初期状態![]() を一意に決定できるかが問題となります。
を一意に決定できるかが問題となります。
このとき、![]() を否定して、矛盾を導きます。
を否定して、矛盾を導きます。
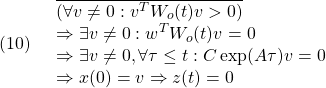
これは、入出力データ![]() から,初期状態
から,初期状態![]() を一意に決定できることにはならないことを示しています。
を一意に決定できることにはならないことを示しています。
●<条件O1![]() 定義DO>
定義DO>
上と同様に(9)を考えますと、入出力データ![]() から,初期状態
から,初期状態![]() は次式で計算できます。
は次式で計算できます。
![]()
実際、左辺は、次のように![]() となります。
となります。
![]()
以上で、可観測性![]() O1
O1![]() O2が示されました。
O2が示されました。
Note A43 可安定性と可制御性
●状態フィーバックにより安定化できることを可安定性と言います。
|
【可安定性の定義とその等価な条件】
定義DS: 状態フィードバックにより安定化可能 条件S1: 条件S2: |
可安定性の判定は行列![]() と
と![]() を用いて行われるので、可安定性が成り立つとき、対
を用いて行われるので、可安定性が成り立つとき、対![]() は可安定対という言い方をします。
は可安定対という言い方をします。
●可安定性の十分条件として次の可制御性が知られています。
|
【可制御性の定義とその等価な条件】
定義DC: 任意初期状態を,任意有限時間内に,任意状態に移動可能 条件C1: 条件C2: 条件C3: 条件C4: 条件C5: |
可制御性の判定も行列![]() と
と![]() を用いて行われるので、可制御性が成り立つとき、対
を用いて行われるので、可制御性が成り立つとき、対![]() は可制御対という言い方をします。条件C1の積分式を可制御性グラミアン行列、条件C2の行列を可制御性行列と呼びます。また条件C4を満足する
は可制御対という言い方をします。条件C1の積分式を可制御性グラミアン行列、条件C2の行列を可制御性行列と呼びます。また条件C4を満足する![]() の固有値を
の固有値を![]() は可制御固有値、満足しない固有値を不可制御固有値と呼びます。
は可制御固有値、満足しない固有値を不可制御固有値と呼びます。
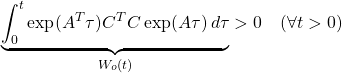
![Rendered by QuickLaTeX.com {\rm rank}\, \underbrace{ \left[\begin{array}{c} C \\ CA \\ \vdots\\ CA^{n-1} \end{array}\right] }_{observability\ matrix} =n](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6253173de124e69f731cff9f00238073_l3.png)