LQI制御…Homework
[1] 次の可制御かつ可観測な![]() 次系を考えます。
次系を考えます。
![]()
![]()
ここで、状態方程式には、操作入力![]() のほかに、定値外乱
のほかに、定値外乱![]() が加わっていること、出力方程式における行列
が加わっていること、出力方程式における行列![]() を
を![]() と書いたことに注意します。いま、出力変数の一部やそれらの組合せからなる新しい
と書いたことに注意します。いま、出力変数の一部やそれらの組合せからなる新しい![]() 個の被制御変数(controlled variables)を
個の被制御変数(controlled variables)を
![]()
のように選び(![]() は可観測対)、定値外乱があるにも拘わらず、制御目的
は可観測対)、定値外乱があるにも拘わらず、制御目的
![]()
を達成したいとします。ここで、定数ベクトル![]() は
は![]() 個の設定値からなる。もし制御目的(4)が物理的に可能とすると、ある状態
個の設定値からなる。もし制御目的(4)が物理的に可能とすると、ある状態![]() と入力
と入力![]() が確定し
が確定し
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \boxed{\left[\begin{array}{c} -w \\ r \end{array}\right] = \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] \left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5a63c22e2c20de8035fdefcbe9d60119_l3.png)
の関係を満足しているはずです。したがって、どのような![]() と
と![]() に対しても、
に対しても、![]() と
と![]() が定まるように、被制御変数(3)を
が定まるように、被制御変数(3)を
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \boxed{{\rm rank}\, \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S}=n+m} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b2fcb8d3d07f55b008eda2e6a5836e50_l3.png)
が成り立つように選ぶものとします。
 図1 積分動作を加えた状態フィードバックによる閉ループ系
図1 積分動作を加えた状態フィードバックによる閉ループ系
[2] さて、制御目的(4)を達成するために、図1に示すような、つぎの積分動作を加えた状態フィードバックを考えます。
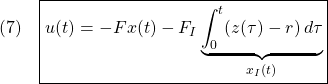
ここで、第2項は積分動作を表しています。このように![]() を定義すると
を定義すると
![]()
を得ます。(1)と(8)を合わせて
![]()
を得ます。(9)に、(7)すなわち
![]()
を代入すると、閉ループ系は、つぎのように表されます。
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \boxed{ %\underbrace{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] %}_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} A-BF & -BF_I \\ C & 0 \end{array}\right] }_{A_{EF}} %\underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] %}_{x_E(t)} + %\underbrace{ \left[\begin{array}{c} w \\ -r \end{array}\right] %}_{w_E} }}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a13e4e217df7e1cd4a8873612c945fbd_l3.png)
いま、![]() は安定行列であるとします。このとき、
は安定行列であるとします。このとき、![]() は正則であり、つぎのように書けます。
は正則であり、つぎのように書けます。
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad A_{EF} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} - \left[\begin{array}{cc} B \\ 0 \end{array}\right] \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ae3e582f261444dac1f56aa447ce0eaa_l3.png)
よって、![]() の逆行列は、公式
の逆行列は、公式
![]()
を用いて
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \begin{array}{ll} A_{EF}^{-1} =& S^{-1}+ S^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] \left(I_m- \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] S^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] \right)^{-1} \\[5mm] &\times \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] S^{-1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e0f009cac08e772a5836cd7f89991b53_l3.png)
ここで、
![]()
に注意して、整理すると
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \boxed{A_{EF}^{-1} = \left[\begin{array}{cc} I_n & 0 \\ -F_I^{-1}F & -F_I^{-1} \end{array}\right] S^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0b2df9b56c6c85b1e3bfe245468fe652_l3.png)
のように計算されます。ところで、(11)から
![]()
を得ます。この第1ブロック行は、(5)より
![]()
となって、(5)の第2ブロック行から制御目的(4)が成り立ちます。また、(17)の第2ブロック行から
![]()
を得ます。ここで、設定値![]() は既知だから、
は既知だから、![]() に関係した項
に関係した項![]() をフィードフォワードして、速応性を改善できます。すなわち、制御目的(4)を達成する制御方式は
をフィードフォワードして、速応性を改善できます。すなわち、制御目的(4)を達成する制御方式は
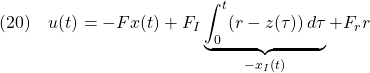
のように表され、ここで、![]() はつぎのように決定できます。
はつぎのように決定できます。
![]()
[3] これまで、閉ループ系(11)において、![]() は安定行列であるとしていました。ここでは、これを満足させるための具体的手段として、先に学んだLQ制御を使うことを考えます。LQ制御の議論における閉ループ系は自励系(入力をもたない系)を前提にしていましたが、本章における閉ループ系は入力をもつことに注意が必要です。この前提を満足させるために、定常状態との差をとって得られる偏差系(error system)が用いられます。
は安定行列であるとしていました。ここでは、これを満足させるための具体的手段として、先に学んだLQ制御を使うことを考えます。LQ制御の議論における閉ループ系は自励系(入力をもたない系)を前提にしていましたが、本章における閉ループ系は入力をもつことに注意が必要です。この前提を満足させるために、定常状態との差をとって得られる偏差系(error system)が用いられます。
制御目的(4)が達成されたとき成り立つ(5)より
![]()
を得ます(![]() は定数ベクトル)。まず、(9)から(22)を引いて、つぎの偏差系を得ます。
は定数ベクトル)。まず、(9)から(22)を引いて、つぎの偏差系を得ます。
偏差系E1:
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \boxed{\frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] %}_{x_E(t)-x_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E1}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] %}_{x_E(t)-x_{E\infty}} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E1}} (u(t)-u_\infty)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2bcd3f36f880707fe8bc60b89fa6dbb6_l3.png)
この両辺を微分すれば、状態変数の中の定数ベクトルを除くことができて
偏差系E2:
![Rendered by QuickLaTeX.com \displaystyle{(24)\quad \boxed{\frac{d}{dt} %\underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] %}_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} %\underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] %}_{\dot{x}_E(t)} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} {\dot u}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-acdd13f2ef2c1d92a0004a5f47cda17a_l3.png)
を得ます。さらに、(1)と(3)をまとめた
![Rendered by QuickLaTeX.com \displaystyle{(25)\quad \left[\begin{array}{c} {\dot x}(t)-w \\ z(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-73ee9071a72e5208f32daf364e891bb9_l3.png)
から(5)を引いて、つぎの関係式が成り立ちます。
![Rendered by QuickLaTeX.com \displaystyle{(26)\quad \boxed{\left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-429e0ebfec7903d5dc5ce87f5046bed1_l3.png)
これに基づいて、偏差系E2に座標変換を行えば
偏差系E3:
![Rendered by QuickLaTeX.com \displaystyle{(27)\quad \boxed{\frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-69dd980e629d5d4d9cf34dc90dbc246d_l3.png)
を得ます。ここで、つぎの関係式を用いました。
![Rendered by QuickLaTeX.com \displaystyle{(28)\quad \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cc8034db5edc1a000b2f2add912d9e66_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(29)\quad \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e7784673b16ee3dc6fc71b2e2e461a8c_l3.png)
●これら3つの偏差系E1,E2,E3はすべて可制御ですが、どれを用いるのがよいのでしょう?
偏差系E1に対する安定化状態フィードバックを
![Rendered by QuickLaTeX.com \displaystyle{(30)\quad u(t)-u_\infty=- \underbrace{\left[\begin{array}{cc} F & F_I \end{array}\right] }_{F_{E1}} \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-49e57cd33d9728f3bb2e32ce3cc5341c_l3.png)
とします。これにより![]() を安定行列とすることはできますが、(30)は実装上の難があります。
を安定行列とすることはできますが、(30)は実装上の難があります。
偏差系E2に対する安定化状態フィードバックを
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad {\dot u}(t)=- \underbrace{\left[\begin{array}{cc} F & F_I \end{array}\right] }_{F_{E2}} \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-38d968135e7c7820854f8a99e80ed705_l3.png)
とします。これにより![]() を安定行列とすることはできますが、LQ設計時の重み係数の決定に難があります。
を安定行列とすることはできますが、LQ設計時の重み係数の決定に難があります。
偏差系E3に対する安定化状態フィードバックを
![Rendered by QuickLaTeX.com \displaystyle{(32)\quad {\dot u}(t)=- \underbrace{\left[\begin{array}{cc} K & K_I \end{array}\right] }_{K_{E3}} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a0dd224c0271441aad07fc15b5834f36_l3.png)
とします。これにより![]() を安定行列とできます。一方、(32)は(26)を用いると
を安定行列とできます。一方、(32)は(26)を用いると
![Rendered by QuickLaTeX.com \displaystyle{(33)\quad {\dot u}(t)=- \underbrace{\left[\begin{array}{cc} K & K_I \end{array}\right] \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]^{-1} }_{K_{E3}S^{-1}} \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9efa6f3fc30539bde922fde97f38394c_l3.png)
と書けます。したがって
![]()
も安定行列となります。そして、
![Rendered by QuickLaTeX.com \displaystyle{(35)\quad \boxed{\left[\begin{array}{cc} F & F_I \end{array}\right] = \left[\begin{array}{cc} K & K_I \end{array}\right] \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-effa6673748e4582607e705f8cec8e0b_l3.png)
とおいて、(33)の両辺を積分すれば、制御測(7)が得られます。このことは偏差系E3の優位性を示唆しているといえます。
[4] 以下に、偏差系E3をLQ制御により安定化して、積分動作を加えた状態フィードバックを構成する手順を示します。
アルゴリズム <LQI制御>
ステップ1 被制御変数の決定
![]() が正則となるように(
が正則となるように(![]() )、セレクタ行列
)、セレクタ行列![]() を決めます(一般に、多入力多出力系の場合、どの操作変数でどの被制御変数を制御するのかについて、物理的に実現可能な1対1対応を考えることが重要です。その際、被制御変数はフィードバックされるので観測量の中から選ばれなけばなりません)。
を決めます(一般に、多入力多出力系の場合、どの操作変数でどの被制御変数を制御するのかについて、物理的に実現可能な1対1対応を考えることが重要です。その際、被制御変数はフィードバックされるので観測量の中から選ばれなけばなりません)。
ステップ2 偏差系の安定化
偏差系
![Rendered by QuickLaTeX.com \displaystyle{(36)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-09c7b450fba91ff4da2925235911deb2_l3.png)
を、状態フィードバック
![]()
によるLQ制御で安定化します。その際、評価関数としては
![Rendered by QuickLaTeX.com \displaystyle{(38)\quad \int_0^\infty \left( \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right]^T Q_E \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] +{\dot u}^T(t)R_E{\dot u}(t)\right)\,dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c670e9177dbb8cc950866876198e2e52_l3.png)
を用います。ただし、![]() は可観測対とします。
は可観測対とします。
ステップ3 積分動作を加えた状態フィードバックの構成
つぎの積分動作を加えた状態フィードバックを構成します。
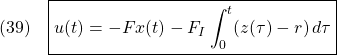
ただし
![Rendered by QuickLaTeX.com \displaystyle{(40)\quad \boxed{\left[\begin{array}{cc} F & F_I \end{array}\right] = \left[\begin{array}{cc} K & K_I \end{array}\right] \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bbcfc692f32dddd6063c223f23f96d7e_l3.png)
この手順で設計された積分動作を加えた状態フィードバックによる制御方式をLQI制御(LQ control with integral action)と呼びます。