最小次元状態オブザーバ…Homework
[1] 制御対象のモデルが
![]()
で与えられるとします。これに対する状態オブザーバは、微分方程式
![]()
で表され、解ベクトル![]() は、制御対象の状態ベクトル
は、制御対象の状態ベクトル![]() と同じ次元数
と同じ次元数![]() を持ちます。
を持ちます。
いま、出力方程式![]() (
(![]() のサイズは
のサイズは![]() 、行フルランク)を通して、状態に関する情報が部分的に得られていることに注目します。そこで、もう一つの補完的な出力方程式
、行フルランク)を通して、状態に関する情報が部分的に得られていることに注目します。そこで、もう一つの補完的な出力方程式![]() (
(![]() のサイズは
のサイズは![]() 、行フルランク)を
、行フルランク)を![]() が正則となるように適切に選んで
が正則となるように適切に選んで
![]()
とすれば、状態に関する全情報が得られそうです。もちろん
![]()
を達成する仕組みが必要です。いま、その仕組みを
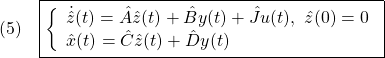
とします。(5)の第1式から、![]() を掛けた(1)の第1式を辺々引くと
を掛けた(1)の第1式を辺々引くと
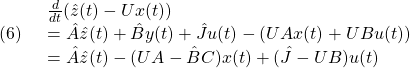
を得ます。ここで
![]()
を仮定し、![]() を
を
![]()
とおけば
![]()
を得ます。もし![]() が安定行列であれば、(4)を達成できます。また
が安定行列であれば、(4)を達成できます。また
![]()
を仮定すると
![]()
を得て、状態推定が行われていることがわかります。状態オブザーバ(2)と比べると、計算機内で解くべき微分方程式の解ベクトルの次元数が![]() から
から![]() に低次元化されていることになります。
に低次元化されていることになります。![]() が正則となるためには、
が正則となるためには、![]() の行数は
の行数は![]() 以下にすることはできませんから、最小次元状態オブザーバと呼ばれています。
以下にすることはできませんから、最小次元状態オブザーバと呼ばれています。
[2] 以上から、適当な![]() を選んで、(7)、(8)、(10)を満足し、安定行列
を選んで、(7)、(8)、(10)を満足し、安定行列![]() をもつ(3)を設計することを考えます。たとえば
をもつ(3)を設計することを考えます。たとえば![]() のときは
のときは![]() のように選びます(
のように選びます(![]() のサイズは
のサイズは![]() )。このとき、(7)と(10)をまとめた
)。このとき、(7)と(10)をまとめた
![]()
において、![]() (
(![]() のサイズは
のサイズは![]() )のように分割すると
)のように分割すると
![]()
![]()
より、![]() 、
、![]() 、
、![]() 、
、![]() は次式から求められます。
は次式から求められます。
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \boxed{\left\{\begin{array}{lll} \hat{A}=A_{22}-LA_{12}\\ \hat{B}=A_{21}-LA_{11}+\hat{A}L\\ \hat{C}= \left[\begin{array}{cc} 0\\ I_{n-p} \end{array}\right]\\ \hat{D}= \left[\begin{array}{cc} I_{p}\\ L \end{array}\right] \end{array}\right.} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ba9d6526eff83e7894d3ec54c6f96e0f_l3.png)
ここで、![]() は
は![]() が安定行列となるように選ぶ必要があります。そのためには
が安定行列となるように選ぶ必要があります。そのためには![]() が可観測対であればよいのですが、これについてはあとで触れます。また、
が可観測対であればよいのですが、これについてはあとで触れます。また、![]() は(10)から定めます。
は(10)から定めます。
● モータの状態方程式
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \left[\begin{array}{c} \dot{\theta}(t)\\ \dot{\omega}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -\frac{1}{T_m} \end{array}\right] }_{A} \left[\begin{array}{c} \theta(t)\\ \omega(t) \end{array}\right]+ \underbrace{ \left[\begin{array}{c} 0\\ \frac{1}{K_ET_m} \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e95207cda654ebaf7485fe467b4eff54_l3.png)
と出力方程式
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \left[\begin{array}{c} \theta(t)\\ \omega(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-181f79035e64702aea850bc818dfa728_l3.png)
に対する状態オブザーバの低次元化を行ってみます。ちょうど![]() となっているので、
となっているので、![]() とおきます。設計式(15)に
とおきます。設計式(15)に![]() 、
、![]() 、
、![]() 、
、![]() を代入して
を代入して
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \left\{\begin{array}{lll} \hat{A}=-\frac{1}{T_m}-L\\ \hat{B}=\hat{A}L\\ \hat{C}= \left[\begin{array}{cc} 0\\ 1 \end{array}\right]\\ \hat{D}= \left[\begin{array}{cc} 1\\ L \end{array}\right]\\ \hat{J}=\frac{1}{K_ET_m} \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5c9ef1b1a40ae6aeaab1a8d4e8bfc53c_l3.png)
ここで、![]() は
は![]() とするのであれば
とするのであれば![]() と決めます。以上から、次の低次元化された状態オブザーバが得られました。
と決めます。以上から、次の低次元化された状態オブザーバが得られました。
![Rendered by QuickLaTeX.com \displaystyle{(19)\quad \left\{\begin{array}{lll} \dot{\hat{z}}(t)=\underbrace{-\frac{\alpha}{T_m}}_{\hat{A}}\hat{z}(t) +\underbrace{\frac{\alpha(1-\alpha)}{T_m^2}}_{\hat{B}}y(t) +\underbrace{\frac{1}{K_ET_m}}_{\hat{J}}u(t),\ \hat{z}(0)=0\\ \hat{x}(t)= \underbrace{ \left[\begin{array}{cc} 0\\ 1 \end{array}\right]}_{\hat{C}}\hat{z}(t) + \underbrace{ \left[\begin{array}{cc} 1\\ L \end{array}\right] }_{\hat{D}}y(t) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9bfd472ab38f4e90833894fadfad6f9d_l3.png)
●次図は![]() 、
、![]() の下で、
の下で、![]() と変えたとき、状態オブザーバが真の状態を推定する様子をシミュレーションしています。
と変えたとき、状態オブザーバが真の状態を推定する様子をシミュレーションしています。
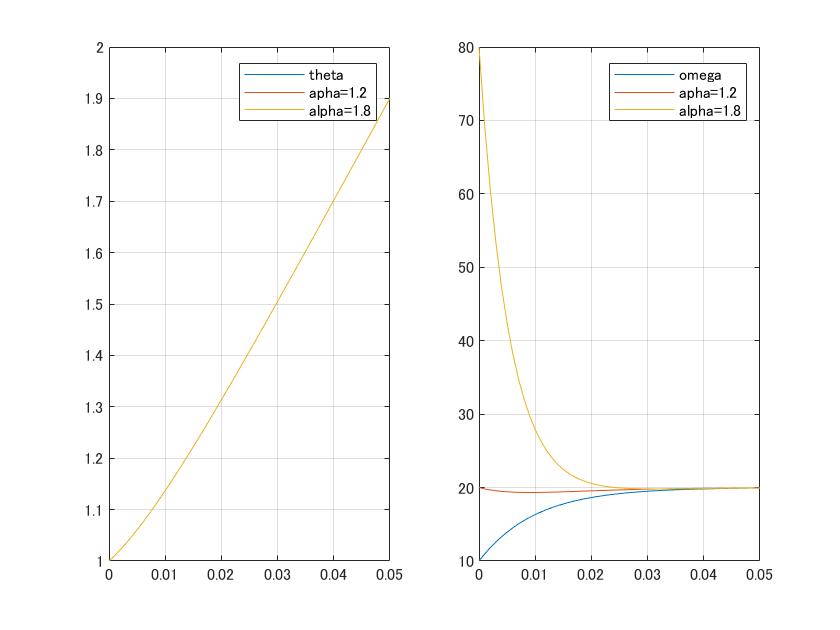 図1 状態推定の例
図1 状態推定の例
演習 A42…Flipped Classroom
次のコードを用いて図1のグラフを描け。
| MATLAB |
|
| SCILAB |
|
Note A42 線形関数オブザーバ
制御対象の状態空間表現
![]()
に対して、もう一つの状態空間表現
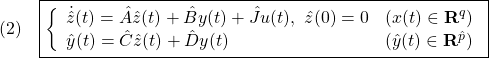
を考えます。ただし、サイズ![]() の行列
の行列![]() とサイズ
とサイズ![]() の行列
の行列![]() に対して
に対して
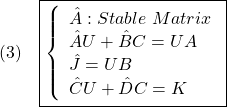
が満足されるものとします。このとき
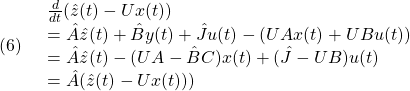
から
![]()
を得ます。また
![]()
を得て、状態の線形関数![]() の推定が行われていることがわかります。
の推定が行われていることがわかります。
したがって、条件(3)を満足する状態空間表現(2)は、線形関数オブザーバと呼ばれます。特に![]() のとき、は最小次元状態オブザーバとなります。
のとき、は最小次元状態オブザーバとなります。
●興味深いのは、状態フィードバック
![]()
を推定させる場合で、線形関数オブザーバの次元数![]() が最小次元状態オブザーバの次数
が最小次元状態オブザーバの次数![]() より小さくできる可能性があります。
より小さくできる可能性があります。
たとえば機械系でよく見られる、次の1入力![]() 出力
出力![]() 次系
次系
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \left\{\begin{array}{l} \left[\begin{array}{c} \dot{y}(t)\\ \ddot{y}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} 0 & I_p \\ A_{21} & A_{22} \end{array}\right] }_{A} \left[\begin{array}{c} y(t)\\ \dot{y}(t) \end{array}\right]+ \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t)\\ y(t)= \underbrace{ \left[\begin{array}{cc} I_n & 0 \end{array}\right] }_{C} \left[\begin{array}{c} y(t)\\ \dot{y}(t) \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-70c3410208fc14d4768b6a45442062a9_l3.png)
および、これに対する状態フィードバック
![]()
を考えます。この状態フィードバックを推定する線形関数オブザーバは、![]() 入力1出力1次系
入力1出力1次系
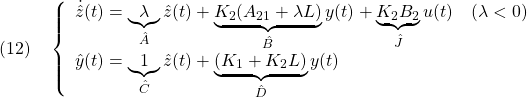
として得られます。実際、![]() と
と![]() を
を
![]()
と選べば、(3)の第2、3、4式を満足していることを次のように確かめることができます。
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \begin{array}{l} \underbrace{ \lambda K_2\left[\begin{array}{cc} -L & I_p \end{array}\right] + K_2(A_{21}+\lambda L) \left[\begin{array}{cc} I_n & 0 \end{array}\right] }_{\hat{A}U+\hat{B}C} = \underbrace{ K_2\left[\begin{array}{cc} -L & I_p \end{array}\right] \left[\begin{array}{cc} 0 & I_p \\ A_{21} & A_{22} \end{array}\right] }_{UA}\\ \underbrace{ K_2B_2 }_{\hat{J}} = \underbrace{ K_2\left[\begin{array}{cc} -L & I_p \end{array}\right] \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{UB}\\ \underbrace{ 1\cdot K_2\left[\begin{array}{cc} -L & I_p \end{array}\right] + (K_1+K_2L) \left[\begin{array}{cc} I_n & 0 \end{array}\right] }_{\hat{C}U+\hat{D}C} = \underbrace{ \left[\begin{array}{cc} K_1 & K_2 \end{array}\right] }_{K} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-92fe0b99d4f40416cb7cd4fdcf78d696_l3.png)
●状態フィードバックを推定する線形関数オブザーバ(したがって最小次元状態オブザーバ)に対しても分離定理を示すことができます。すなわち制御対象のモデル(1)に対して、![]() の場合の(3)を満たす線形関数オブザーバ(2)による閉ループ系は
の場合の(3)を満たす線形関数オブザーバ(2)による閉ループ系は
![]()
を定義すると、次式となります。
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \boxed{\left[\begin{array}{c} \dot{x}(t) \\ \dot{e}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A-BF & -B\hat{C} \\ 0 & \hat{A} \end{array}\right] }_{A_{CL}} \left[\begin{array}{c} x(t) \\ e(t) \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a941bbb0ba1845c0025a886fd7d9e55a_l3.png)
この第1式は(1)の状態方程式の![]() に、(2)の出力方程式の
に、(2)の出力方程式の![]() を代入して
を代入して
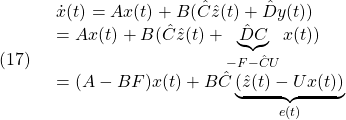
のように得られます。また、第2式は(6)そのものです。