リャプノフ方程式…Homework
[1] 対象が平衡状態にあることは線形状態方程式![]() において、
において、![]() を意味します。そこで平衡状態が乱されて
を意味します。そこで平衡状態が乱されて![]() となる時刻を
となる時刻を![]() にとると、線形状態方程式は次式となります。
にとると、線形状態方程式は次式となります。
![]()
これに出力方程式
![]()
を考慮する場合も含めると、漸近安定性の判定法は次のようにまとめられます。
——————————————————————————————————————–
【漸近安定性の定義とその等価な条件】
定義DA: ![]()
条件A0: ![]()
条件A1: ![]()
条件A2: ![]()
条件A3: ![]() ただし、
ただし、![]() は可観測対
は可観測対
——————————————————————————————————————–
ここで、条件A2、条件A3における行列方程式はリャプノフ方程式と呼ばれます。
<定義DA![]() 条件A0
条件A0![]() 条件A1>
条件A1>
はすでに示しています。以下では、
<定義DA![]() 条件A2
条件A2![]() 条件A1>および
条件A1>および
<定義DA![]() 条件A3
条件A3![]() 条件A1>
条件A1>
を示して全部の等価性を主張します。
●<定義DA![]() 条件A2
条件A2![]() 条件A1> 定義DAより、(1)の解
条件A1> 定義DAより、(1)の解![]() の二乗面積は有界となり、
の二乗面積は有界となり、
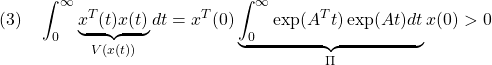
から、![]() が定まります。これは次のようにリャプノフ方程式を満足します。
が定まります。これは次のようにリャプノフ方程式を満足します。
![Rendered by QuickLaTeX.com (4)\quad \begin{array}{l} \Pi A+A^T\Pi\\ \displaystyle{=\int_0^\infty\exp(A^Tt)\exp(At)dt A+A^T \int_0^\infty\exp(A^Tt)\exp(At)dt}\\ \displaystyle{=\int_0^\infty\frac{d}{dt}(\exp(A^Tt)\exp(At))dt=\left[\exp(A^Tt)\exp(At)\right]_0^\infty\\ =\exp(A^T\infty)\underbrace{\exp(A\infty)}_{0}-\exp(A^T0)\underbrace{\exp(A0)}_{I_n}=-I_n}\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-59a1e80997a4165ad1b001b5bb29d526_l3.png)
次に、条件A2が成り立つとします。![]() が
が![]() を満たす固有値
を満たす固有値![]() をもつとし、これに対応する固有ベクトルを
をもつとし、これに対応する固有ベクトルを![]() とします。このとき
とします。このとき
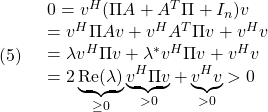
となって矛盾。したがって条件A1を得ます。
●安定行列![]() に対して条件A2を確かめます。リャプノフ方程式は
に対して条件A2を確かめます。リャプノフ方程式は
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \underbrace{ \left[\begin{array}{cc} p_1 & p_3 \\ p_3 & p_2 \end{array}\right] }_{P} \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -2 & -3 \end{array}\right] }_{A} + \underbrace{ \left[\begin{array}{cc} 0 & -2 \\ 1 & -3 \end{array}\right] }_{A^T} \underbrace{ \left[\begin{array}{cc} p_1 & p_3 \\ p_3 & p_2 \end{array}\right] }_{P} =- \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right] }_{I_2} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-85e9e5691877d6104d33dc0ab99c2307_l3.png)
となり、次の連立1次方程式に書き直すことができます。
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \left[\begin{array}{ccc} 0 & 0 & -4 \\ 1 & -2 & -3 \\ 0 & -6 & 2 \end{array}\right] \left[\begin{array}{c} p_1 \\ p_2 \\ p_3 \end{array}\right] = \left[\begin{array}{c} -1 \\ 0 \\ -1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-141e2af5be5bb2484bbf9f73b996b8f4_l3.png)
これより、次を得ます。
![]()
●<定義DA![]() 条件A3
条件A3![]() 条件A1> 定義DAより、(1),(2)の解
条件A1> 定義DAより、(1),(2)の解![]() の二乗面積は有界となり、
の二乗面積は有界となり、
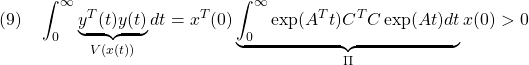
から、![]() が定まります。ここで、
が定まります。ここで、![]() は可観測対の条件が、可観測性グラミアン
は可観測対の条件が、可観測性グラミアン![]() を保証し、
を保証し、![]() が成り立ちます。これは次のようにリャプノフ方程式を満足します。
が成り立ちます。これは次のようにリャプノフ方程式を満足します。
![Rendered by QuickLaTeX.com (10)\quad \begin{array}{l} \Pi A+A^T\Pi\\ \displaystyle{=\int_0^\infty\exp(A^Tt)C^TC\exp(At)dt A+A^T \int_0^\infty\exp(A^Tt)C^TC\exp(At)dt}\\ \displaystyle{=\int_0^\infty\frac{d}{dt}(\exp(A^Tt)C^TC\exp(At))dt=\left[\exp(A^Tt)C^TC\exp(At)\right]_0^\infty\\ =\exp(A^T\infty)C^TC\underbrace{\exp(A\infty)}_{0}-\exp(A^T0)C^TC\underbrace{\exp(A0)}_{I_n}=-C^TC}\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-19deb8818548c3e2e4134cf297e36e9a_l3.png)
次に、条件A3が成り立つとします。![]() が
が![]() を満たす固有値
を満たす固有値![]() をもつとし、これに対応する固有ベクトルを
をもつとし、これに対応する固有ベクトルを![]() とします。このとき
とします。このとき
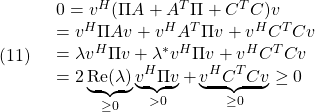
となって矛盾。したがって条件A1を得ます。
Note A51 ラウス・フルビッツの安定判別法
次式で表される![]() 次自由系を考えます。
次自由系を考えます。
![]()
この漸近安定性は
![]()
で定義され,![]() 行列のすべての固有値の実部が負であることが必要十分条件であることはよく知られています。
行列のすべての固有値の実部が負であることが必要十分条件であることはよく知られています。![]() 行列の中に不確かなパラメータを含む場合,漸近安定性を保証する範囲を求めるために,Routh-Hurwitzの安定判別法が有用です。これは,
行列の中に不確かなパラメータを含む場合,漸近安定性を保証する範囲を求めるために,Routh-Hurwitzの安定判別法が有用です。これは,![]() 行列の特性多項式
行列の特性多項式
![]()
の係数![]() から得られるRouth表
から得られるRouth表
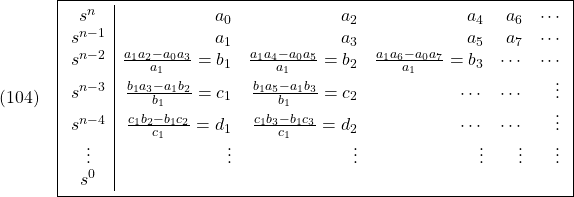
の第1列の要素![]() がすべて正(
がすべて正(![]() )であれば漸近安定,または係数
)であれば漸近安定,または係数![]() がすべて正(
がすべて正(![]() )かつHurwitz行列式
)かつHurwitz行列式
![Rendered by QuickLaTeX.com \displaystyle{(105)\quad \boxed{\begin{array}{l} D_1=a_1 \\ D_2={\rm det}< \left[\begin{array}{cc} a_1 & a_3 \\ a_0 & a_2 \end{array}\right] \\ D_3={\rm det} \left[\begin{array}{ccc} a_1 & a_3 & a_5 \\ a_0 & a_2 & a_4 \\ 0 & a_1 & a_3 \end{array}\right] \\ \vdots \\ D_{n-1}={\rm det} \left[\begin{array}{ccccc} a_1 & a_3 & a_5 & \cdots & a_{2n-3} \\ a_0 & a_2 & a_4 & \cdots & a_{2n-4} \\ 0 & a_1 & a_3 & \cdots & a_{2n-5} \\ 0 & a_0 & a_2 & \cdots & a_{2n-6} \\ 0 & 0 & a_1 & \cdots & a_{2n-7} \\ \vdots & \vdots & \ddots & \ddots & \vdots \\ 0 & 0 & 0 & \cdots & a_{n-1} \\ \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cc23ec66f0d8f9ecc82f04778b09aa0e_l3.png)
がすべて正であれば漸近安定と判定します。両者の間には,次が成り立ちます。
![]()
●たとえば、![]() の場合は、次の条件となります。
の場合は、次の条件となります。
![]() の場合は、
の場合は、![]()
![]() の場合は、
の場合は、![]()
証明
●Routh-Hurwitzの安定判別法の時間領域における証明については,P.C.Parksによって,自由系が漸近安定であるための必要十分条件
![]()
に基づくものが示されています(ただし,![]() は可観測対)。彼は
は可観測対)。彼は
![Rendered by QuickLaTeX.com \displaystyle{(108)\quad A=\left[\begin{array}{cccccc} 0 & 1 & 0 & \cdots & 0\\ 0 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \cdots & 1\\ -a_n & -a_{n-1} & -a_{n-2} & \cdots & -a_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c7d5fc3807d87258ca18739049a3c9c4_l3.png)
を,ある正則行列![]() で相似変換した行列
で相似変換した行列
![Rendered by QuickLaTeX.com \displaystyle{(109)\quad B=\left[\begin{array}{ccccccc} 0 & 1 & \cdots & 0 & 0 & 0 \\ -b_n & 0 & \cdots & 0 & 0 & 0 \\ 0 & -b_{n-1} & \cdots & 0 & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots& \vdots\\ 0 & 0 & \cdots & -b_3 & 0 & 1 \\ 0 & 0 & \cdots & 0 & -b_2 & -b_1 \end{array}\right]=TAT^{-1} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cdf74d6527d9a40e2edc50d31ea063c0_l3.png)
に対して
![]()
を満足する![]() と
と![]() を,次のように求めています。
を,次のように求めています。
![Rendered by QuickLaTeX.com \displaystyle{(111)\quad \Pi=\left[\begin{array}{ccccccc} b_1b_2\cdots b_n & 0 & \cdots & 0 \\ 0 & b_1b_2\cdots b_{n-1} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & b_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6699b7ac084d6a76d67a99ac23fa9a16_l3.png)
![]()
実際,![]() を計算してみると
を計算してみると
![Rendered by QuickLaTeX.com \displaystyle{(113)\quad \left[\begin{array}{ccccccc} b_1b_2\cdots b_n & 0 & \cdots & 0 \\ 0 & b_1b_2\cdots b_{n-1} & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & b_1 \end{array}\right] \left[\begin{array}{ccccccc} 0 & 1 & \cdots & 0 & 0 & 0 \\ -b_n & 0 & \cdots & 0 & 0 & 0 \\ 0 & -b_{n-1} & \cdots & 0 & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots& \vdots\\ 0 & 0 & \cdots & -b_3 & 0 & 1 \\ 0 & 0 & \cdots & 0 & -b_2 & -b_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5000a96cd5039f37342bd31231f6bdc9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \left[\begin{array}{ccccccc} 0 & b_1b_2\cdots b_n & \cdots & 0 & 0 & 0 \\ -b_1b_2\cdots b_n & 0 & \cdots & 0 & 0 & 0 \\ 0 & -b_1b_2\cdots b_{n-1} & \cdots & 0 & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots& \vdots\\ 0 & 0 & \cdots & -b_1b_2b_3 & 0 & b_1b_2 \\ 0 & 0 & \cdots & 0 & -b_1b_2 & -b_1^2 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0d026755db647d96cd2f69b8819ea73f_l3.png)
となります。したがって
![Rendered by QuickLaTeX.com \displaystyle{(114)\quad &&\Pi B+B^T\Pi= \left[\begin{array}{ccccccc} 0 & 0 & \cdots & 0 \\ 0 & 0 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & -2b_1^2 \end{array}\right] =- \underbrace{ \left[\begin{array}{cccc} 0 \\ \vdots \\ 0 \\ \sqrt{2}b_1 \end{array}\right] }_{H^T} \underbrace{ \left[\begin{array}{cccc} 0 & \cdots & 0 & \sqrt{2}b_1 \end{array}\right] }_{H} \nonumber }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f8ab89e9688d8e627f8beae5f665393c_l3.png)
が得られます。明らかに,![]() のとき
のとき
![Rendered by QuickLaTeX.com \displaystyle{(115)\quad {\rm rank} \left[\begin{array}{ccccccc} B-\lambda I_n \\ H \end{array}\right] = {\rm rank} \left[\begin{array}{ccccccc} -\lambda & 1 & \cdots & 0 & 0 & 0 \\ -b_n & -\lambda & \cdots & 0 & 0 & 0 \\ 0 & -b_{n-1} & \cdots & 0 & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots& \vdots\\ 0 & 0 & \cdots & -b_3 & -\lambda& 1 \\ 0 & 0 & \cdots & 0 & -b_2 & -b_1-\lambda \\ 0 & 0 & \cdots & 0 & 0 & \sqrt{2}b_1 \end{array}\right]=n }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3b8414a60038a059b11aa00019bc8ffc_l3.png)
となり,![]() は可観測対です。また,関係式
は可観測対です。また,関係式
![]()
が成り立つことが示されており,![]() の正定性からRouth-Hurwitzの安定判別法の妥当性が出ます。
の正定性からRouth-Hurwitzの安定判別法の妥当性が出ます。
●以下では、2つの行列
![Rendered by QuickLaTeX.com \displaystyle{(117)\quad A=\left[\begin{array}{cccccc} 0 & 1 & 0 & \cdots & 0\\ 0 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \cdots & 1\\ -a_n & -a_{n-1} & -a_{n-2} & \cdots & -a_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e8e53c908512662a1ea7325469a8ff3f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(118)\quad B=\left[\begin{array}{ccccccc} 0 & 1 & \cdots & 0 & 0 & 0 \\ -b_n & 0 & \cdots & 0 & 0 & 0 \\ 0 & -b_{n-1} & \cdots & 0 & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots& \vdots\\ 0 & 0 & \cdots & -b_3 & 0 & 1 \\ 0 & 0 & \cdots & 0 & -b_2 & -b_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3dc206086d1292a18c0690d402c2c609_l3.png)
に対して
![]()
を満足する座標変換行列![]() を導出します。ここで
を導出します。ここで
![]()
が成り立ちます。
さて、次の関係式はよく知られています。
![]()
ただし
![Rendered by QuickLaTeX.com \displaystyle{(122)\quad \Lambda=\left[\begin{array}{ccccccc} \lambda_1 & 0 & \cdots & 0 \\ 0 & \lambda_2 & \cdots & 0 \\ \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & \cdots & \lambda_n \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-633928ba777d0e14931171b0cd98fc55_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(123)\quad V_A=\left[\begin{array}{ccccccc} 1 & 1 & \cdots & 1 \\ \lambda_1 & \lambda_2 & \cdots & \lambda_n \\ \vdots & \vdots & \ddots & \vdots \\ \lambda_1^{n-1} & \lambda_2^{n-1} & \cdots & \lambda_n^{n-1} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bea0f2e6122a57e8ed81f0c2e1207e84_l3.png)
ここで,簡単のために,![]() の固有値
の固有値![]() は互いに相異なるものとします。このとき
は互いに相異なるものとします。このとき
![]()
を満足する![]() を求めれば,座標変換行列
を求めれば,座標変換行列![]() は
は
![]()
のように表されます。
(119)に関する補足
●![]() のとき
のとき
![]()
![]()
ですから,自明な場合
![]()
で,![]() ,すなわち
,すなわち![]() となります。
となります。
●![]() のとき
のとき
![Rendered by QuickLaTeX.com \displaystyle{ A=\left[\begin{array}{cccccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ -a_3 & -a_2 & -a_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b78bd1f02bf94aeda3823f4c8a63a447_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ B=\left[\begin{array}{cccccc} 0 & 1 & 0 \\ -b_3 & 0 & 1 \\ 0 & -b_2 & -b_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-671723d030ae668b83b04db608c87a02_l3.png)
となります。いま
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{cccccc} 0 & 1 & 0 \\ -b_3 & 0 & 1 \\ 0 & -b_2 & -b_1 \end{array}\right] \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \end{array}\right]= \lambda \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e54f5e4b2f7794e495f792b5d85297e9_l3.png)
すなわち
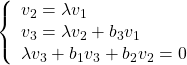
となる![]() を求めると
を求めると
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \end{array}\right]= \left[\begin{array}{l} 1 \\ \lambda \\ \lambda^2+b_3 \end{array}\right] = \underbrace{ \left[\begin{array}{cccccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ b_3 & 0 & 1 \end{array}\right]}_{\Gamma} \left[\begin{array}{c} 1 \\ \lambda \\ \lambda^2 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d7b5153ea774cdb5e3261c19e75b6f9e_l3.png)
ただし
![]()
これは
![]()
と一致しなければならないので
![]()
となります。また,Hurwitz行列式を用いて
![]()
と表されるます。実際
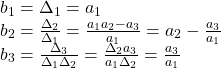
以上から,![]() ,すなわち
,すなわち![]() となります。
となります。
●![]() のとき
のとき
![Rendered by QuickLaTeX.com \displaystyle{ A=\left[\begin{array}{cccccc} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -a_4 & -a_3 & -a_2 & -a_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7ff706457d487dadae751b14f7d3acaa_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ B=\left[\begin{array}{cccccc} 0 & 1 & 0 & 0 \\ -b_4 & 0 & 1 & 0 \\ 0 & -b_3 & 0 & 1 \\ 0 & 0 & -b_2 & -b_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-da5df5023f6c35c4de93859da6ea9fde_l3.png)
となります。いま
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{cccccc} 0 & 1 & 0 & 0 \\ -b_4 & 0 & 1 & 0 \\ 0 & -b_3 & 0 & 1 \\ 0 & 0 & -b_2 & -b_1 \end{array}\right] \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 \end{array}\right]= \lambda \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-399fe6c79f1dd6f54f84d18c4054af42_l3.png)
すなわち
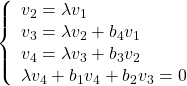
となる![]() を求めると
を求めると
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 \end{array}\right]= \left[\begin{array}{l} 1 \\ \lambda \\ \lambda^2+b_4 \\ \lambda^3+(b_3+b_4)\lambda \end{array}\right] = \underbrace{ \left[\begin{array}{cccccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ b_4 & 0 & 1 & 0 \\ 0 & b_3+b_4 & 0 & 1 \end{array}\right]}_{\Gamma} \left[\begin{array}{c} 1 \\ \lambda \\ \lambda^2 \\ \lambda^3 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f33ce8a3dfbcf995152d8b4e5697ef53_l3.png)
ただし
![]()
これは
![]()
と一致しなければならないので
![]()
となります。また,Hurwitz行列式を用いて
![]()
と表されます。実際
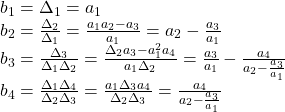
以上から,![]() ,すなわち
,すなわち![]() となります。
となります。
●![]() のとき
のとき
![Rendered by QuickLaTeX.com \displaystyle{ A=\left[\begin{array}{cccccc} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ -a_5 & -a_4 & -a_3 & -a_2 & -a_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f0a9e02ff4a508c3702747c6f22eeac1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ B=\left[\begin{array}{cccccc} 0 & 1 & 0 & 0 & 0 \\ -b_5 & 0 & 1 & 0 & 0 \\ 0 & -b_4 & 0 & 1 & 0 \\ 0 & 0 & -b_3 & 0 & 1 \\ 0 & 0 & 0 & -b_2 & -b_1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3fd5a82630d2f98d35fb92d870129912_l3.png)
となります。いま
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{cccccc} 0 & 1 & 0 & 0 & 0 \\ -b_5 & 0 & 1 & 0 & 0 \\ 0 & -b_4 & 0 & 1 & 0 \\ 0 & 0 & -b_3 & 0 & 1 \\ 0 & 0 & 0 & -b_2 & -b_1 \end{array}\right] \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 \\ v_5 \end{array}\right]= \lambda \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 \\ v_5 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0c8ad97efe9f7c22114534ef6080b3f5_l3.png)
すなわち
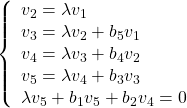
となる![]() を求めると
を求めると
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \\ v_4 \\ v_5 \end{array}\right]= \left[\begin{array}{l} 1 \\ \lambda \\ \lambda^2+b_5 \\ \lambda^3+(b_4+b_5)\lambda \\ \lambda^4+(b_3+b_4+b_5)\lambda^2+b_3b_5 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cf3aab51d558601a7ac9dadd513c23e7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \underbrace{ \left[\begin{array}{cccccc} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ b_5 & 0 & 1 & 0 & 0 \\ 0 & b_4+b_5 & 0 & 1 & 0 \\ b_3b_5 & 0 & b_3+b_4+b_5 & 0 & 1 \end{array}\right]}_{\Gamma} \left[\begin{array}{c} 1 \\ \lambda \\ \lambda^2 \\ \lambda^3 \\ \lambda^4 \end{array}\right] \nonumber }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ac175e71aca1a6030212e539c67f8b9d_l3.png)
ただし
![]()
これは
![]()
と一致しなければならないので
![]()
となります。また,Hurwitz行列式を用いて
![]()
と表される。実際
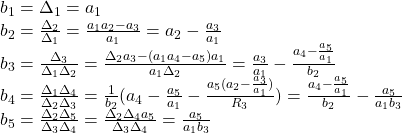
以上から,![]() ,すなわち
,すなわち![]() となる。
となる。
●ここまで調べれば、![]() の場合の(119)から
の場合の(119)から![]() の場合の(119)を示すことができる思います(あとでやってみます)。
の場合の(119)を示すことができる思います(あとでやってみます)。