LQG制御…Homework
[1] 次のようなオブザーバベース・コントローラによる閉ループ系を考えます。ここで,新しい入力![]() と
と![]() がそれぞれ
がそれぞれ![]() と
と![]() の平方根行列(
の平方根行列(![]() に対し
に対し![]() を満足する行列
を満足する行列![]() を
を![]() で表す)により重み付けられて,
で表す)により重み付けられて,![]() 次系の入力側(
次系の入力側(![]() を介して)と出力側に設置されています。また新しい出力
を介して)と出力側に設置されています。また新しい出力![]() と入力
と入力![]() が取り出されており,それぞれ
が取り出されており,それぞれ![]() と
と![]() の平方根行列により重み付けられています。
の平方根行列により重み付けられています。
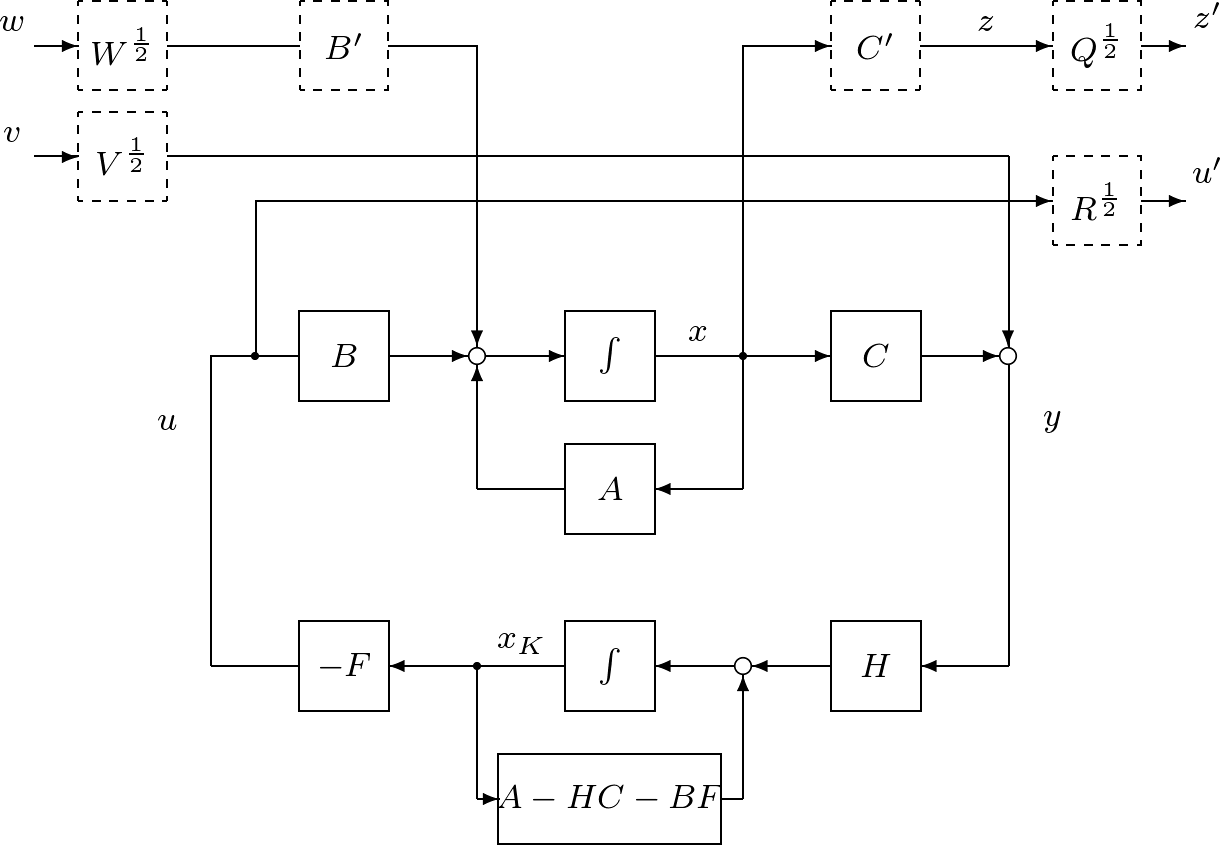 図1 LQG制御系設計の枠組み
図1 LQG制御系設計の枠組み
可制御かつ可観測な制御対象
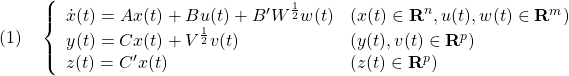
を安定化するオブザーバベース・コントローラ
![]()
を2次形式評価関数
![]()
を最小にするように、![]() と
と![]() を決定する問題を考えます。これらは
を決定する問題を考えます。これらは
![]()
![]()
を満足する![]() と
と![]() を用いて、次のように与えられます。
を用いて、次のように与えられます。
![]()
![]()
このような制御方式をLQG制御と呼びます。
[2] 上の安定な閉ループ系は次式で表されます。
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \boxed{\begin{array}{l} \left[\begin{array}{cc} \dot{x}(t) \\ \dot{\hat{x}}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A & -BF \\ HC&A-HC-BF \end{array}\right] }_{A_{CL1}} \left[\begin{array}{cc} {x}(t) \\ \hat{x}(t) \end{array}\right] + \underbrace{ \left[\begin{array}{cc} B'W^{\frac{1}{2}} & 0 \\ 0 & HV^{\frac{1}{2}} \end{array}\right] }_{B_{CL1}} \left[\begin{array}{cc} {w}(t) \\ {v}(t) \end{array}\right]\\ \left[\begin{array}{cc} {y'}(t) \\ {u'}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} Q^{\frac{1}{2}}C' & 0 \\ 0 & -R^{\frac{1}{2}}F \end{array}\right] }_{C_{CL1}} \left[\begin{array}{cc} {x}(t) \\ \hat{x}(t) \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6e6de0ac1c24534b05d96168f970e1fc_l3.png)
これに座標変換
![]()
を行うと
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \boxed{\begin{array}{l} \left[\begin{array}{cc} \dot{x}(t) \\ \dot{e}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A-BF & -BF \\ 0 & A-HC \end{array}\right] }_{A_{CL2}} \left[\begin{array}{cc} {x}(t) \\ {e}(t) \end{array}\right] +\underbrace{ \left[\begin{array}{cc} B'W^{\frac{1}{2}} & 0 \\ -B'W^{\frac{1}{2}} & HV^{\frac{1}{2}} \end{array}\right] }_{B_{CL2}} \left[\begin{array}{cc} {w}(t) \\ {v}(t) \end{array}\right]\\ \left[\begin{array}{cc} {y'}(t) \\ {u'}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} Q^{\frac{1}{2}}C' & 0 \\ -R^{\frac{1}{2}}F & -R^{\frac{1}{2}}F \end{array}\right] }_{C_{CL2}} \left[\begin{array}{cc} {x}(t) \\ {e}(t) \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-81a989326d7d4a34c5752f6aecf84dec_l3.png)
となります。このとき閉ループ系のインパルス応答は次式で与えられます。
![]()
●![]() に対して、評価関数
に対して、評価関数![]() の総和は次式で与えられます。
の総和は次式で与えられます。
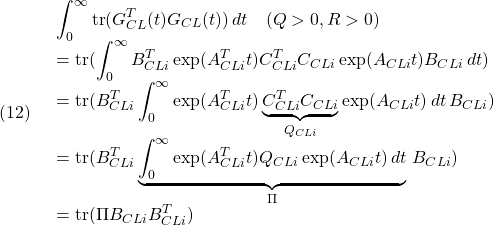
ここで![]() は次式を満足します。
は次式を満足します。
![]()
ラグランジュの未定定数法を適用するために、次の評価関数を考えます。
![]()
これを最小化する場合の必要条件は、次式となります。
![]()
以下では、次の分割を考えます。
![]()
[3] ![]() の場合について、必要条件を一つ一つ調べていきます。
の場合について、必要条件を一つ一つ調べていきます。
●![]()
![]()
において
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \begin{array}{l} \Pi A_{CL1}= \left[\begin{array}{cc} \Pi_{1}&\Pi_{3} \\ \Pi_{3}^T&\Pi_{2} \end{array}\right] \left[\begin{array}{cc} A & -BF \\ HC&A-HC-BF \end{array}\right]\\ = \left[\begin{array}{cc} \Pi_{1}A+\Pi_{3}HC & -\Pi_{1}BF+\Pi_{3}(A-HC-BF)\\ \Pi_{3}^TA+\Pi_{2}HC & -\Pi_{3}^TBF+\Pi_{2}(A-HC-BF) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c429aa33a0e5684bc85b0263996ad5ef_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(19)\quad \begin{array}{l} A_{CL1}^T\Pi =(\Pi A_{CL1})^T\\ =\left[\begin{array}{cc} A^T\Pi_{1}+C^TH^T\Pi_{3}^T&\\ -F^TB^T\Pi_{1}+(A-HC-BF)^T\Pi_{3}^T & \end{array}\right.\\ \left.\begin{array}{cc} A^T\Pi_{3}+C^TH^T\Pi_{2}\\ -F^TB^T\Pi_{3}+(A-HC-BF)^T\Pi_{2} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c914ac5d6ae500873c120fe9e3c82eef_l3.png)
![]()
を代入して、次を得ます。
![]()
![]()
![]()
(22)+(23)より
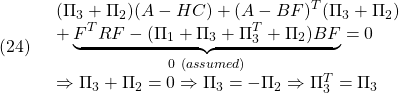
(23)より
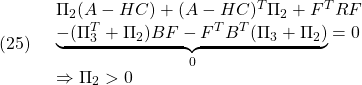
(21)+(22)より
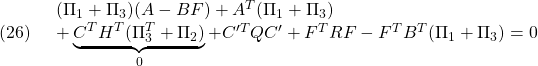
![]()
●![]()
![]()
において
![Rendered by QuickLaTeX.com \displaystyle{(29)\quad \begin{array}{l} A_{CL1}\Gamma= \left[\begin{array}{cc} A & -BF \\ HC&A-HC-BF \end{array}\right] \left[\begin{array}{cc} \Gamma_{1}&\Gamma_{3} \\ \Gamma_{3}^T&\Gamma_{2} \end{array}\right]\\ =\left[\begin{array}{cc} A\Gamma_{1} -BF\Gamma_{3}^T &A\Gamma_{3} -BF\Gamma_{2}\\ HC\Gamma_{1}+(A-HC-BF)\Gamma_{3}^T &HC\Gamma_{3}+(A-HC-BF)\Gamma_{2} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b5efbe327872da02c0cdae613082e8a5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(30)\quad \begin{array}{l} \Gamma A_{CL1}^T =(A_{CL1}\Gamma)^T\\ =\left[\begin{array}{cc} \Gamma_{1}A^T -\Gamma_{3}F^TB^T & \Gamma_{1}C^TH^T+\Gamma_{3}(A-HC-BF)^T\\ \Gamma_{3}^TA^T -\Gamma_{2}F^TB^T & \Gamma_{3}^TC^TH^T+\Gamma_{2}(A-HC-BF)^T \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-166202eb44f8bebfc11fcdbb0cf09ab8_l3.png)
![]()
を代入して、次を得ます。
![]()
![]()
![]()
(33)-(34)より
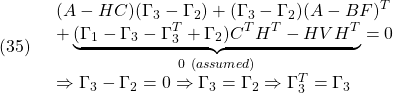
(34)より
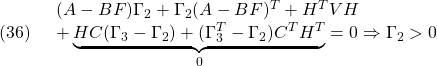
(32)-(33)より
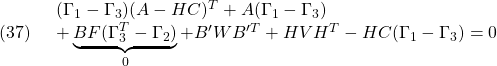
![]()
●準備1
![]()
(1) ![]()
![]()
![]()
●準備2
![Rendered by QuickLaTeX.com \displaystyle{(42)\quad \begin{array}{l} \Pi A_{CL1}\Gamma= \left[\begin{array}{cc} \Pi_{1}&\Pi_{3} \\ \Pi_{3}^T&\Pi_{2} \end{array}\right] \left[\begin{array}{cc} A & -BF \\ HC&A-HC-BF \end{array}\right] \Gamma\\ =\left[\begin{array}{cc} \Pi_{1}A+\Pi_{3}HC & -\Pi_{1}BF+\Pi_{3}(A-HC-BF)\\ \Pi_{3}^TA+\Pi_{2}HC & -\Pi_{3}^TBF+\Pi_{2}(A-HC-BF) \end{array}\right] \left[\begin{array}{cc} \Gamma_{1}&\Gamma_{3} \\ \Gamma_{3}^T&\Gamma_{2} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5cf2147ab153e0a23d8488f0452990da_l3.png)
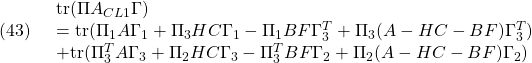
![]()
![]()
●準備3
![Rendered by QuickLaTeX.com \displaystyle{(46)\quad \begin{array}{l} A_{CL1}^T\Pi\Gamma=(\Pi A_{CL1})^T\Gamma=\\ \left[\begin{array}{cc} A^T\Pi_{1}+C^TH^T\Pi_{3}^T&\\ -F^TB^T\Pi_{1}+(A-HC-BF)^T\Pi_{3}^T & \end{array}\right.\\ \left.\begin{array}{cc} A^T\Pi_{3}+C^TH^T\Pi_{2}\\ -F^TB^T\Pi_{3}+(A-HC-BF)^T\Pi_{2} \end{array}\right] \left[\begin{array}{cc} \Gamma_{1}&\Gamma_{3} \\ \Gamma_{3}^T&\Gamma_{2} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-98094a2e6a48cf9f59754bbc5f21fdef_l3.png)
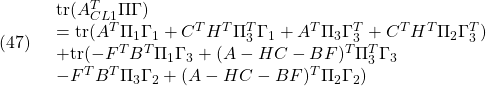
![]()
![]()
●準備4
![]()
![]()
![]()
●![]()
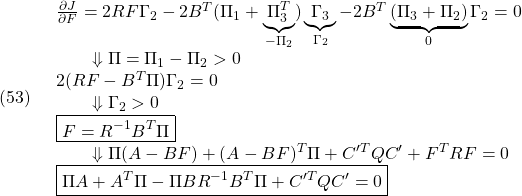
●![]()
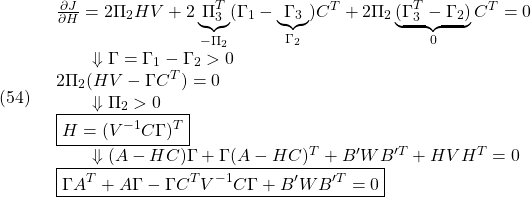
補遺 上述の議論では、次についての検討が必要です。
検討事項1 (13)の妥当性
検討事項2 (24),(35)における仮定の妥当性
検討事項3 ![]() の場合の導出
の場合の導出
検討事項4 十分性の証明