Home Work
[M] 数学的には、
![]()
において、行列![]() と
と![]() が対角ブロックに位置し、上三角ブロック行列になるので、2つの行列の固有値がそのまま分離することを言っているのかな。
が対角ブロックに位置し、上三角ブロック行列になるので、2つの行列の固有値がそのまま分離することを言っているのかな。
[C] 上式は、状態オブザーバの推定誤差の振舞いは、状態フィードバックによる制御動作に影響を及ぼさないことを意味しているよ。でも状態推定がもたもたしていると、望ましい状態フィードバックができなくなるので、行列![]() と
と![]() の固有値の相対的位置関係に注意が必要となるのかな。Flipped Classroomで考えるようだね。
の固有値の相対的位置関係に注意が必要となるのかな。Flipped Classroomで考えるようだね。
[P] 制御と観測の話が分離してしまうというのは、なんだか理論がよくできていると思うけど、偶然なのかな、それとも必然なのかな?
Flipped Classroom
[1] 1次系
![]()
に対するオブザーバベース・コントローラ
![]()
による閉ループ系の状態方程式は
![]()
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \left[\begin{array}{c} \dot{x}(t)\\ \dot{\hat x}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} a & -bf \\ hc & a-hc-bf \end{array}\right] }_{A_F} \left[\begin{array}{c} x(t)\\ \hat{x}(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ab12592f43f3b77f1c260b59b5ec43ce_l3.png)
[2] 次式が成り立ちます。
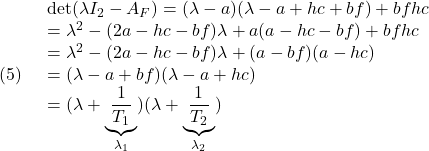
ここで、2通りの対応付けが考えられます。
![]()
一方、![]() の関係より、
の関係より、![]() 、
、![]() だから、上の対応付けでは、次が成り立ちます。
だから、上の対応付けでは、次が成り立ちます。
![]()
ここで、![]() は、状態推定の速さ(
は、状態推定の速さ(![]() )が制御動作(
)が制御動作(![]() )より遅いこと意味し、望ましくありません。しかし、
)より遅いこと意味し、望ましくありません。しかし、![]() は、状態推定の速さ(
は、状態推定の速さ(![]() )が制御動作(
)が制御動作(![]() )より速いこと意味し、こちらの方が望ましいと言えます。
)より速いこと意味し、こちらの方が望ましいと言えます。
[3] n次系
![]()
に対する状態オブザーバ
![]()
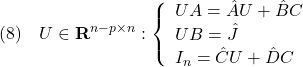
の出力![]() を用いて、制御則
を用いて、制御則
![]()
を実施するとします。このときの閉ループ系の状態方程式は
![]()
すなわち
![]()
ここで、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \left[\begin{array}{c} x(t)\\ z(t)-Ux(t) \end{array}\right]= \left[\begin{array}{cc} I_n & 0 \\ -U & I_{n-p} \end{array}\right] \left[\begin{array}{c} x(t)\\ z(t) \end{array}\right]\\ \Leftrightarrow \left[\begin{array}{c} x(t)\\ z(t) \end{array}\right]= \left[\begin{array}{cc} I_n & 0 \\ U & I_{n-p} \end{array}\right] \left[\begin{array}{c} x(t)\\ z(t)-Ux(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aebbca8364a7efdd8c75db19db35f3f3_l3.png)
を行うと
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \left[\begin{array}{cc} I_n & 0 \\ U & I_{n-p} \end{array}\right] \frac{d}{dt} \left[\begin{array}{c} x(t)\\ z(t)-Ux(t) \end{array}\right]\\ =\left[\begin{array}{cc} A-BF\hat{D}C & -BF\hat{C} \\ (\hat{B}-\hat{J}F\hat{D})C & \hat{A}-\hat{J}F\hat{C} \end{array}\right] \left[\begin{array}{cc} I_n & 0 \\ U & I_{n-p} \end{array}\right] \left[\begin{array}{c} x(t)\\ z(t)-Ux(t) \end{array}\right]\\ =\left[\begin{array}{cc} A-BF\hat{D}C-BF\hat{C}U & -BF\hat{C} \\ (\hat{B}-\hat{J}F\hat{D})C+(\hat{A}-\hat{J}F\hat{C})U & \hat{A}-\hat{J}F\hat{C} \end{array}\right] \left[\begin{array}{c} x(t)\\ z(t)-Ux(t) \end{array}\right]\\ =\left[\begin{array}{cc} A-BF & -BF\hat{C} \\ \hat{A}U+\hat{B}C-\hat{J}F & \hat{A}-\hat{J}F\hat{C} \end{array}\right] \left[\begin{array}{c} x(t)\\ z(t)-Ux(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6ca670e5cb79fa79d75fe45725d27eb3_l3.png)
したがって
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \frac{d}{dt} \left[\begin{array}{c} x(t)\\ z(t)-Ux(t) \end{array}\right]\\ =\left[\begin{array}{cc} I_n & 0 \\ -U & I_{n-p} \end{array}\right] \left[\begin{array}{cc} A-BF & -BF\hat{C} \\ \hat{A}U+\hat{B}C-\hat{J}F & \hat{A}-\hat{J}F\hat{C} \end{array}\right] \left[\begin{array}{c} x(t)\\ z(t)-Ux(t) \end{array}\right]\\ = \left[\begin{array}{cc} A-BF & -BF\hat{C} \\ 0 & \hat{A} \end{array}\right] \left[\begin{array}{c} x(t)\\ z(t)-Ux(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7edd4e4176516592df5785f7ac0562c2_l3.png)
Home Work [P] もし状態変数の一部が観測変数そのものであれば、状態オブザーバは既知の観測変数も推定しており、無駄なことをしているというのが、低次元化の動機かな? [M] 出力方程式 [C] 状態フィードバック Flipped Classroom 5.2 [2] (5.23)と(5.24)はそのままで、(5.26)が次式となります。
Home Work 5.1 [C] 状態オブザーバは、当時学生だったルーエンバーガーが企業研修相当の機会で発明したものだと聞いたことがあるよ。実際、wikipediaには、次の記述があるね。 In his dissertation Luenberger introduced new methods for construction of state observers. The celebrated Luenberger observer is named after him. [P] えー、すごいね。どうやって、見つけたのだろうか?やはり、推定誤差をネガティブ・フィードバックすれば、その誤差は小さくなるはずだと思ったのだろうね? [M] 状態フィードバックによる安定化問題は、行列 Flipped Classroom 5.1 だから これが右辺 に等しいので [2] (図5.3左図は縦軸の単位はradですが、Program 51ではdegに変換しています。配布するプログラムは、図5.3をそのまま出力します。)
[C] 状態フィードバックに関する条件として次を学んだことになるね。 定義DS: 状態フィードバックにより安定化可能 条件S1: 条件S2: 定義DC: 任意初期状態を,任意有限時間内に,任意状態に移動可能 条件C1: 条件C2: 条件C3: 条件C4: 条件C5: [P] 可制御性は、敢えて言えば、瞬間移動が可能であると言えるのかな?実際にはありえないから、線形理論の限界でもあるね。 [M] これらの証明については、次を参照するらしいよ。 (詳しい説明は、あとで行う予定です。)
Home Work 4.2 [P] 手のひらに2本の棒を倒立させる制御は考えたことがなかったけど、とても興味深いな。全く同じ長さではできなけど、長さが違えばできるらしいよ。 [M] 安定化できるかどうかのチェックを、行列 [C] いわゆる可安定性とか可制御性が成り立つかどうかをチェックすれば良いわけだ。これらがどう違うかを理解したり、様々な条件の等価性については、補遺で説明するらしいけど、まだかな? Flipped Classroom 4.2 [2] 可制御性を数値計算で調べる場合は、条件C4を用います。 [3] 条件S1や条件C4が成り立たないことを確認してください。 [4] 初期値をいろいろ変えて、シミュレーションしてみてください。
Home Work 4.1 [M] 数学的には、行列 [P] 物理的には、ばね定数や摩擦係数を変えることになって、デバイスを変えたわけではないのにダイナミックスが変わってしまい、ちょっと不思議な気がするね。 [C] ある高名な研究者の解説には「状態フィードバックは最強である」という表現があるらしいよ。これはすべての状態変数の動きを監視していて、変化があれば即座にアクチュエータにフィードバックできれば、これ以上の制御動作はないという意味らしいよ。 Flipped Classroom 4.1 [2] 多入力の場合は、閉ループ系の固有値を指定しただけでは、状態フォードバックは一意の定まらなことを、しっかり認識してください。たとえば、適当な初期値を与えて応答が異なることを確認してみてください。
安定判別 [C] 漸近安定性の等価な条件として次を学んだことになるね。 定義DA: 条件A0: 条件A1: [P] なぜ行列 [M] 2次系の場合は分かったからは、あとは一般の場合の証明ができるかどうかだ。そのためには、まず実Jordan標準形を理解する必要があり、次が参考になるらしいよ。 その上で、実Jordan標準形の行列指数関数を考えるのだそうだ。次が参考になるらしいよ。 (以上、とりあえず手がかりとなる材料を示しておきます。)
Home Work 3.3 [P] 日産の技術紹介でスカイフック制御のビデオを見たことがあるよ。油圧で減衰係数を200通りも変えられると説明されていたね。これにより、高速運転のときはしっかりした足回りにしたり、低速で段差を乗り越えるような場合は柔らかく受け止めるようにできるらしいよ。高度なアクティブ制御の一例かな。 [M] 状況に応じて制御則が変わるのはすごいと思うが、閉ループ系はいつも漸近安定と言えるのだろうか? [C] ゲインスケジューリング制御の授業では、減衰係数を可変にする制御系設計がレポート課題だったな。確か閉ループ系の安定性が議論されていたと思うけど。 Flipped Classroom 3.3 行列 となって、必ず複素左半平面にあることがわかります。 [2] 応答の評価は次の通りです。速応性と静粛性はトレードオフの関係にあります。妥協点は ●
Home Work 3.2 [C] 安定判別といえば、古典制御ではナイキストの安定定理、ラウス・フルビッツの判定法を思い出すね。それらの手続きについては習ったけど、特にラウス・フルビッツの判定法の証明は習ったかな? [M] 数学的には行列 [P] 固有値とか、固有ベクトルとか、線形代数で習ったけど、Jordan標準形の導出などちょっとついていけなかった。ましてや、これらの物理的な意味など説明できるのかな? Flipped Classroom 3.2 [6] 不安定な固有値には赤色をつけてみてください。
Home Work 3.1 [P] 漸近安定性の意味は、平衡状態が乱されたときに復帰できるかどうかなので、物理的には明らかだね。 [C] でも状態空間表現におけ3つの行列 [M] Flipped Classroom 3.1 [2] 平衡状態は
CT52 低次元化
![]() の他に、別の補完的かつ仮想的な観測方程式
の他に、別の補完的かつ仮想的な観測方程式![]() を考えて、これを推定する仕組みを導入したわけだよね。
を考えて、これを推定する仕組みを導入したわけだよね。![]() の実施のために、状態オブザーバの出力を用いるのであれば、一気に
の実施のために、状態オブザーバの出力を用いるのであれば、一気に![]() そのものを推定することも考えられているよ。
そのものを推定することも考えられているよ。
[1] 図5.4の左図は観測変数がそのままでており、右図は観測できない状態変数を推定する様子を示しています。ここで、低次元化されたオブザーバは観測出力からの直達項の影響を受けていることに注意してください。
訂正 図5.4を出力するProgram 52は、最新のものではありませんでした。最新のp52a.m、p52a.sceを入手してください。図5.4はOKです。
MATLAB
%MATLAB: p52a.m (2024/5/1修正)
Tm=0.01; KE=0.05;
x0=[1;10];
t=0:0.001:0.05;
[t1,x1]=ode45(@(t,x) [0 1; 0 -1/Tm]*x+[0;1/Tm/KE],t,x0);
%-----Part 1
alpha=1.2
L=-(1-alpha)/Tm;
%[t2,x2]=ode45(@(t,x) (-1/Tm-L)*x,t,-x0);
[t2,x2]=ode45(@(t,x) (-1/Tm-L)*x,t,-[-L 1]*x0);
%-----Part 2
alpha=1.8
L=-(1-alpha)/Tm;
%[t3,x3]=ode45(@(t,x) (-1/Tm-L)*x,t,-x0);
[t3,x3]=ode45(@(t,x) (-1/Tm-L)*x,t,-[-L 1]*x0);
%-----
subplot(121), plot(t,x1(:,1)), hold on
subplot(121), plot(t,x1(:,1),'-.')
subplot(121), plot(t,x1(:,1),'--')
grid, axis([0 0.05 0 2])
legend('theta','alpha=1.2','alpha=1.8');
xlabel('t'), ylabel('theta(t)')
subplot(122), plot(t,x1(:,2)), hold on
%subplot(122), plot(t,x1(:,2)+x2(:,2),'-.')
%subplot(122), plot(t,x1(:,2)+x3(:,2),'--')
subplot(122), plot(t,x1(:,2)+x2,'-.')
subplot(122), plot(t,x1(:,2)+x3,'--')
%grid, axis([0 0.05 0 30])
grid, axis([0 0.05 0 80])
legend('omega','alpha=1.2','alpha=1.8');
xlabel('t'), ylabel('omega(t)')
SCILAB
//SCILAB: p52a.sce (2024/5/1修正)
Tm=0.01; KE=0.05;
function dx=f1(t,x),dx=[0 1; 0 -1/Tm]*x+[0;1/Tm/KE], endfunction
x0=[1;10];
t0=0; t=0:0.001:0.05;
x1=ode(x0,t0,t,f1);
//-----Part 1
alpha=1.2
L=-(1-alpha)/Tm;
function dx=f2(t,x),dx=(-1/Tm-L)*x, endfunction
//x2=ode(-x0,t0,t,f2);
x2=ode(-[-L 1]*x0,t0,t,f2);
//-----Part 2
alpha=1.8
L=-(1-alpha)/Tm;
//x3=ode(-x0,t0,t,f2);
x3=ode(-[-L 1]*x0,t0,t,f2);
//-----
subplot(121),plot(t,x1(1,:))
subplot(121),plot(t,x1(1,:),'-.')
subplot(121),plot(t,x1(1,:),'--')
mtlb_grid, mtlb_axis([0 0.05 0 2])
legend(['theta';'alpha=1.2';'alpha=1.8']);
xlabel('t'), ylabel('theta(t)')
subplot(122),plot(t,x1(2,:))
//subplot(122),plot(t,x1(2,:)+x2(2,:),'-.')
//subplot(122),plot(t,x1(2,:)+x3(2,:),'--')
subplot(122),plot(t,x1(2,:)+x2,'-.')
subplot(122),plot(t,x1(2,:)+x3,'--')
//mtlb_grid, mtlb_axis([0 0.05 0 30])
mtlb_grid, mtlb_axis([0 0.05 0 80])
xlabel('t'), ylabel('omega(t)')
legend(['omega';'alpha=1.2';'alpha=1.8']);![]()
CT51 状態オブザーバ
![]() と
と![]() を用いて、可安定性や可制御性として論じられるけど、状態オブザーバの構成問題は、行列
を用いて、可安定性や可制御性として論じられるけど、状態オブザーバの構成問題は、行列![]() と
と![]() を用いて、可検出性や可観測性として論じられているね。何せセンサの不足を補えるのだから、とてつもなく便利だよね。
を用いて、可検出性や可観測性として論じられているね。何せセンサの不足を補えるのだから、とてつもなく便利だよね。
[1] (5.18)の左辺を計算すると![]()
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \begin{array}{ll} \det(\lambda I_n-A+HC)=\det\left[\begin{array}{cc}\lambda+h_1 & -1\\h_2 & \lambda+\frac{1}{T_m}\end{array}\right]\\ =(\lambda+h_1)(\lambda+\frac{1}{T_m})+h_2 =\lambda^2+(h_1+\frac{1}{T_m})\lambda+\frac{h_1}{T_m}+h_2 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-45bb6fc8e4ce84fa42476448fb19ae3e_l3.png)
![]()
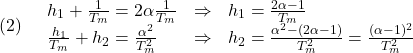
![]() の値によって状態推定の様子がどう違うを観察し、どちらの値が望ましいかをどう判定すればよいかを考えてみてください。
の値によって状態推定の様子がどう違うを観察し、どちらの値が望ましいかをどう判定すればよいかを考えてみてください。CT43 補遺4
【可安定性の定義とその等価な条件】
![]() (
(![]() は
は![]() のすべての不安定固有値)
のすべての不安定固有値)![]() (
(![]() は
は![]() のすべての不安定固有値)
のすべての不安定固有値)
【可制御性の定義とその等価な条件】
![]()
![]()
![]() を選んで,
を選んで,![]() の固有値を任意に設定可能
の固有値を任意に設定可能![]() (
(![]() は
は![]() のすべての固有値)
のすべての固有値)![]() (
(![]() は
は![]() のすべての固有値)
のすべての固有値)
CT42 いつ安定化できるか
![]() と
と![]() を用いてできるなんて、なんとすばらしい!
を用いてできるなんて、なんとすばらしい!
[1] 可安定性を数値計算で調べる場合は、条件S1を用います。CT41 状態フィードバック
![]() が行列
が行列![]() に変わるので、不安定固有値を安定固有値に移動させる可能性さえあるということかな。
に変わるので、不安定固有値を安定固有値に移動させる可能性さえあるということかな。
[1] プログラムを解析して、どのような固有値を設定しようとしているか、また正しい状態フィードバックが求まっているか調べてください。また、自分で指定した固有値に設定する状態フィードバックゲインを求めてみてください。CT34 補遺3
【漸近安定性の定義とその等価な条件】
![]()
![]()
![]()
![]() だけを用いるのか、その理由を物理的に説明できま~す。
だけを用いるのか、その理由を物理的に説明できま~す。CT33 パッシブ制御
[1] 行列![]() の特性方程式は
の特性方程式は![]()
![]() の固有値は
の固有値は![]()
![]() でしょうか?
でしょうか?![]() のとき、速応性は〇、静粛性は×
のとき、速応性は〇、静粛性は×
●![]() のとき、速応性は△、静粛性は△
のとき、速応性は△、静粛性は△
●![]() のとき、速応性はx、静粛性は〇
のとき、速応性はx、静粛性は〇CT32 安定判別
![]() の固有値がすべて複素左半平面にあるかどうかだけどね。
の固有値がすべて複素左半平面にあるかどうかだけどね。
[1],[2],[3],[4],[5] 次のサイトを参照してください。CT31 漸近安定性
![]() のうち、どうして行列
のうち、どうして行列![]() だけしか関係しないのかな?
だけしか関係しないのかな?![]() の場合は、状態方程式は微分方程式なので、その解は複雑なはずだよね。なぜ
の場合は、状態方程式は微分方程式なので、その解は複雑なはずだよね。なぜ![]() とするのかな?
とするのかな?
[1] 漸近安定性は、平衡入力のもとで平常状態の振舞い(状態方程式の解)に関係しています。線形状態方程式において平衡入力は![]() で表されるから、行列
で表されるから、行列![]() だけしか関係しません。この説明を行なえる人は少ないようです。
だけしか関係しません。この説明を行なえる人は少ないようです。![]() で表されるから、零に漸近しているのは
で表されるから、零に漸近しているのは![]() の場合だけです。テキストはモノクロ印刷なので、必ずプログラムを実行してください。
の場合だけです。テキストはモノクロ印刷なので、必ずプログラムを実行してください。