Home Work
[M] 数学的には、
![]()
において、行列![]() と
と![]() が対角ブロックに位置し、上三角ブロック行列になるので、2つの行列の固有値がそのまま分離することを言っているのかな。
が対角ブロックに位置し、上三角ブロック行列になるので、2つの行列の固有値がそのまま分離することを言っているのかな。
[C] 上式は、状態オブザーバの推定誤差の振舞いは、状態フィードバックによる制御動作に影響を及ぼさないことを意味しているよ。でも状態推定がもたもたしていると、望ましい状態フィードバックができなくなるので、行列![]() と
と![]() の固有値の相対的位置関係に注意が必要となるのかな。Flipped Classroomで考えるようだね。
の固有値の相対的位置関係に注意が必要となるのかな。Flipped Classroomで考えるようだね。
[P] 制御と観測の話が分離してしまうというのは、なんだか理論がよくできていると思うけど、偶然なのかな、それとも必然なのかな?
Flipped Classroom
[1] 1次系
![]()
に対するオブザーバベース・コントローラ
![]()
による閉ループ系の状態方程式は
![]()
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \left[\begin{array}{c} \dot{x}(t)\\ \dot{\hat x}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} a & -bf \\ hc & a-hc-bf \end{array}\right] }_{A_F} \left[\begin{array}{c} x(t)\\ \hat{x}(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ab12592f43f3b77f1c260b59b5ec43ce_l3.png)
[2] 次式が成り立ちます。
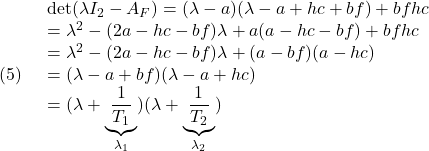
ここで、2通りの対応付けが考えられます。
![]()
一方、![]() の関係より、
の関係より、![]() 、
、![]() だから、上の対応付けでは、次が成り立ちます。
だから、上の対応付けでは、次が成り立ちます。
![]()
ここで、![]() は、状態推定の速さ(
は、状態推定の速さ(![]() )が制御動作(
)が制御動作(![]() )より遅いこと意味し、望ましくありません。しかし、
)より遅いこと意味し、望ましくありません。しかし、![]() は、状態推定の速さ(
は、状態推定の速さ(![]() )が制御動作(
)が制御動作(![]() )より速いこと意味し、こちらの方が望ましいと言えます。
)より速いこと意味し、こちらの方が望ましいと言えます。
[3] n次系
![]()
に対する状態オブザーバ
![]()
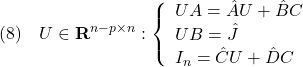
の出力![]() を用いて、制御則
を用いて、制御則
![]()
を実施するとします。このときの閉ループ系の状態方程式は
![]()
すなわち
![]()
ここで、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \left[\begin{array}{c} x(t)\\ z(t)-Ux(t) \end{array}\right]= \left[\begin{array}{cc} I_n & 0 \\ -U & I_{n-p} \end{array}\right] \left[\begin{array}{c} x(t)\\ z(t) \end{array}\right]\\ \Leftrightarrow \left[\begin{array}{c} x(t)\\ z(t) \end{array}\right]= \left[\begin{array}{cc} I_n & 0 \\ U & I_{n-p} \end{array}\right] \left[\begin{array}{c} x(t)\\ z(t)-Ux(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aebbca8364a7efdd8c75db19db35f3f3_l3.png)
を行うと
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \left[\begin{array}{cc} I_n & 0 \\ U & I_{n-p} \end{array}\right] \frac{d}{dt} \left[\begin{array}{c} x(t)\\ z(t)-Ux(t) \end{array}\right]\\ =\left[\begin{array}{cc} A-BF\hat{D}C & -BF\hat{C} \\ (\hat{B}-\hat{J}F\hat{D})C & \hat{A}-\hat{J}F\hat{C} \end{array}\right] \left[\begin{array}{cc} I_n & 0 \\ U & I_{n-p} \end{array}\right] \left[\begin{array}{c} x(t)\\ z(t)-Ux(t) \end{array}\right]\\ =\left[\begin{array}{cc} A-BF\hat{D}C-BF\hat{C}U & -BF\hat{C} \\ (\hat{B}-\hat{J}F\hat{D})C+(\hat{A}-\hat{J}F\hat{C})U & \hat{A}-\hat{J}F\hat{C} \end{array}\right] \left[\begin{array}{c} x(t)\\ z(t)-Ux(t) \end{array}\right]\\ =\left[\begin{array}{cc} A-BF & -BF\hat{C} \\ \hat{A}U+\hat{B}C-\hat{J}F & \hat{A}-\hat{J}F\hat{C} \end{array}\right] \left[\begin{array}{c} x(t)\\ z(t)-Ux(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6ca670e5cb79fa79d75fe45725d27eb3_l3.png)
したがって
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \frac{d}{dt} \left[\begin{array}{c} x(t)\\ z(t)-Ux(t) \end{array}\right]\\ =\left[\begin{array}{cc} I_n & 0 \\ -U & I_{n-p} \end{array}\right] \left[\begin{array}{cc} A-BF & -BF\hat{C} \\ \hat{A}U+\hat{B}C-\hat{J}F & \hat{A}-\hat{J}F\hat{C} \end{array}\right] \left[\begin{array}{c} x(t)\\ z(t)-Ux(t) \end{array}\right]\\ = \left[\begin{array}{cc} A-BF & -BF\hat{C} \\ 0 & \hat{A} \end{array}\right] \left[\begin{array}{c} x(t)\\ z(t)-Ux(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7edd4e4176516592df5785f7ac0562c2_l3.png)