Home Work 8.2
[C] ここでも、定常偏差を生じさせる定値外乱の除去に焦点を当てているようだ。
[P] 位置を目標値(定値)に合わせるときは、速度は0にしか合わせられないということだね。
[M] 3次の行列の逆行列の計算が、こんなところで出てきたね。
Flipped Classroom 8.2
[1] (8.15)ではなく、(8.17)から![]() は
は![]() に漸近するはず。図8.6の下段のシミュレーションはプログラムから
に漸近するはず。図8.6の下段のシミュレーションはプログラムから![]() ではなく
ではなく![]() だから、その値は-1に漸近しており、
だから、その値は-1に漸近しており、![]() は1に漸近することが確かめられます。(下段のシミュレーションが
は1に漸近することが確かめられます。(下段のシミュレーションが![]() となるように、プログラムを変更する予定です。)
となるように、プログラムを変更する予定です。)
[2] 偏差系の安定化を、閉ループ系の固有値を指定して求めています。
Home Work 8.1 [C] 積分器は目標値(定値)との定常偏差をなくすために必要となると思っていたけど、ここでの説明はちょっと違うね。定常偏差を生じさせる定値外乱の除去に焦点を当てているようだ。 [P] 積分器が未知の外乱を推定するとは、不思議な気がするね。 [M] でも数学的には、確かに標値との定常偏差をなくすことと、積分器が未知の外乱を推定することが証明されているよ。 Flipped Classroom 8.1 [2] 多い風の場合は、
[C] LQ制御の要点をまとめると、次のようになるかな。 を安定化する状態フィードバック の決定法を考えます。一つの方法は,閉ループ系 の時間応答に関する評価規範として,2次形式評価関数 を設定し,これを最小化する問題を解くことです。ただし、 の解 [P] LQ制御は、運動の自由度の連成を解きほぐすという意味の多変数制御を保証するわけではなさそうだ。やはり、運動の自由度の対応するアクチュエーションを工夫して、状態空間モデルを得ることが大切ということかな? [M] LQ制御に関する証明については、次を参照するらしいよ。 まず閉ループ系の安定性を表す制約条件について そして、一般の状態フィードバックについて さらには、オブザーバベースコントローラについて (詳しい説明は、あとで行う予定です。)
Home Work 7.2 [P] よく多変数制御というけど、制御対象の運動の複数の自由度を同時に操ることを意味しているのであれば、本当にできるのかなと思ってしまう。 [C] 制御対象の可制御性と可観測性を前提とし、2次形式評価関数を最小化する状態FBを求めるLQ制御は、多変数制御のための強力なツールとなっているらしいよ。 [M] その導出は、基本的には1入力系の場合と同じアプローチでできて、最終的にはリッカチ方程式という行列の2次方程式を解くことになるんだ。 Flipped Classroom 7.2
Home Work 7.1 [P] 平衡状態から外れたとき、これを戻すためには、いろいろな「軌道(時系列)」があると思うけど、何かリーズナブルな決め方はあるのかな? [C] 状態変数の振る舞い(2乗面積)と操作変数の振る舞い(2乗面積)のトレードオフを計ることがよく行われているよ。 [M] トレードオフの意味だけど、高校で、次の関数の最小値を求める問題があったね。 右辺第1項は増加関数、第2項は減少関数だから、グラフを描いてみると、最小値が生まれているよね。 Flipped Classroom 7.1 評価関数はスカラ値を取るので、定数倍してもOKだから、 これから を解くと すなわち したがって
n次系の周波数応答 次の漸近安定な1入力1出力 このとき、正弦波入力 に対する零状態応答を計算します。そのために を、零状態応答の式 に代入して ここで これから正弦波入力(3)に対する零状態応答は、 これは、入力が正弦波のときは、時間が十分立てば、出力も正弦波となることを示しています。その振幅と位相はそれぞれ
Home Work 6.3 [P] 物理の言葉ではないと思うけど、無定位系とよばれる制御対象があるよ。モータやビークルのように、復原項がない場合は、位置が定まらないという意味らしい。無定位系では、位置についてステップ応答の実験ができないよね。 [C] 単位フィードバックを行えば、ステップ応答の実験ができるのだけど、フィードバックの知識がないと気が付かないかな。 [M] 位置と速度を状態変数にもつ無定位系 に対して、単位フィードバック によって復原項を入れると、次のような2次系になるからだね。 Flipped Classroom 6.3 [2] を用いて、ステップ応答は次のように計算されます。 [3] ヒントより、 [4] [5]
Home Work 6.2 [P] 一般にインパルス応答を実験で求めようとすると大変そうだね。構造試験ではインパルス・ハンマーという道具が使用されるらしいけど、やはりインパルス応答が調べられているんだね。 [M] インパルス応答の定義式(6.24)をよく見てみると、 となっていて、これは [C] この考え方は、非線形シミュレータで適当な初期値を与えたいときに役に立ちそうだね。 Flipped Classroom 6.2 を解くと これは次のように場合分けされます。 [2] となることから、インパルス応答は次のように計算されます。 となることから、インパルス応答は次のように計算されます。 となることから、インパルス応答は次のように計算されます。
Home Work 6.1 [P] 1次系の実用例としては、心臓のペースメーカがあるね。これはRC電気回路で、コンデンサへの充放電を繰り返しているよ。 [M] コンデンサの放電はいわゆる零入力応答(初期値応答)だけど、一般の外部入力があるときは非斉次微分方程式となって、数学的には面倒だね。でもテキストの説明は比較的わかりやすいかな。 [C] 1次系と言えば時定数、その説明には2通り(初期値応答またはステップ応答を用いて)あるかな。船舶分野では、1次系を「野本モデル」とよび、世界的に通用するらしいよ。その時定数は船が真っすぐ進むかどうか(進路安定性)の判断に使われ、なんと時定数が負の場合もあるというから驚きだね。 Flipped Classroom 6.1 ちなみに、(6.8)を用いた場合 [2] これが [3] 図6.2の〇で示す点をクリックすればよいと言えます。
まず穴埋め問題の解答を示します。太字がキーワードなので、確認してください。 [1] 制御対象の状態空間表現が与えられているとする。これは「状態方程式」 [2] いま、何らかの外乱により平衡状態が乱され、 [3] いま、制御対象が安定ではないとき、これを「状態フィードバック」 [4] 状態フィードバックを実施するためには、全ての状態変数を、「センサ」を用いて計測する必要がある。しかし、これはいつも可能とは限らないので、状態変数の値を漸近的に推定する「状態オブザーバ」 [5] 状態フィードバックを状態オブザーバを用いて、 【選択肢】 (a) 発展方程式、(b) 状態方程式、(c) 次に、可検出性と可観測性の証明は、とりあえず次を参照してください。
CT81 定値外乱下の速度制御
[1] (8.10)から![]() は
は![]() に漸近するはず。図8.3の下段のシミュレーションはプログラムから
に漸近するはず。図8.3の下段のシミュレーションはプログラムから![]() ではなく
ではなく![]() だから、その値は-1に漸近しており、
だから、その値は-1に漸近しており、![]() は1に漸近することが確かめられます。(下段のシミュレーションが
は1に漸近することが確かめられます。(下段のシミュレーションが![]() となるように、プログラムを変更する予定です。)
となるように、プログラムを変更する予定です。)![]() とします。
とします。CT73 補遺7
【LQ制御】 可制御な制御対象
![]()
![]()
![]()
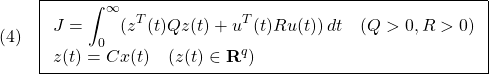
![]() は可観測対とします。これによる状態フィードバックのゲイン行列
は可観測対とします。これによる状態フィードバックのゲイン行列![]() は,リッカチ方程式
は,リッカチ方程式![]()
![]() を用いて,次式で与えられます。
を用いて,次式で与えられます。![]()
CT72 2次系のLQ制御
[1] 仮に![]() としても、閉ループ2次系の減衰係数は
としても、閉ループ2次系の減衰係数は![]() となっており、十分減衰がかかっていることを意味しています。
となっており、十分減衰がかかっていることを意味しています。
[2] 著者は、プログラムopt.mを用いて、多くの制御問題を解いてきました。世界一重要なツールと言っても過言ではないと思っています。CT71 1次系のLQ制御
![]()
[1] ![]() で割ると、
で割ると、![]()
![]() は操作のためのコストとみなせます。すなわちコスト
は操作のためのコストとみなせます。すなわちコスト![]() がより小さくなると、操作はより大きな振る舞いが許されます。
がより小さくなると、操作はより大きな振る舞いが許されます。![]() のときはcheap controlと呼ばれます。
のときはcheap controlと呼ばれます。
[2] ![]()
![]()
![]() の場合の固有ベクトルは
の場合の固有ベクトルは![]()
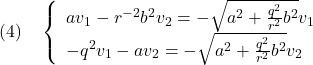
![]() の場合(と規格化する場合)は
の場合(と規格化する場合)は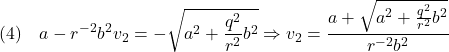
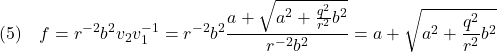
CT64 補遺6
![]() 次系の状態空間表現を考えます。
次系の状態空間表現を考えます。![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com (5)\quad \begin{array}{l} \displaystyle{y(t)=\int_0^tC\exp(A(t-\tau))Be^{j\omega\tau}d\tau}\\ \displaystyle{=C\exp(At)\int_0^te^{j\omega\tau}\exp(-A\tau)Bd\tau}\\ \displaystyle{=C\exp(At)\int_0^t\exp(j\omega\tau I_n)\exp(-A\tau)Bd\tau}\\ \displaystyle{=C\exp(At)\int_0^t\exp((j\omega I_n-A)\tau)Bd\tau}\\ \displaystyle{=C\exp(At) \left[\frac{}{}\exp((j\omega I_n-A)\tau)\right]_0^t(j\omega I_n-A)^{-1}B}\\ \displaystyle{=C\exp(At) (\exp((j\omega I_n-A)t)-I_n)(j\omega I_n-A)^{-1}B}\\ \displaystyle{=-C\exp(At)(j\omega I_n-A)^{-1}B+C\exp(At)\exp(j\omega t I_n)\exp(-At)(j\omega I_n-A)^{-1}B}\\ \displaystyle{=-C\exp(At)(j\omega I_n-A)^{-1}B+C(j\omega I_n-A)^{-1}Be^{j\omega t}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cf72e1d083b5093019ffc1a9ae42a3ca_l3.png)
![]() とすると
とすると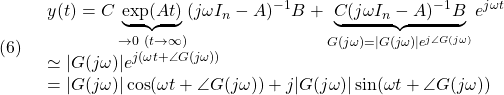
![]() のとき次式で与えられます。
のとき次式で与えられます。![]()
![]() の絶対値と偏角となっています。
の絶対値と偏角となっています。CT63 2次系のステップ応答
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] = \left[\begin{array}{cc} 0 & 1\\ 0 & -2\zeta\omega_n \end{array}\right] \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] + \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right] u(t)\\ y(t)= \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-661cd10c44d4ff35fee28f4948abb6d0_l3.png)
![]()
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] = \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] + \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right] u(t)\\ y(t)= \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6477ab865fc15a390483159f094f3237_l3.png)
[1] ![]()
![]() のとき、インパルス応答を積分して、ステップ応答は次のように計算されます。
のとき、インパルス応答を積分して、ステップ応答は次のように計算されます。![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \displaystyle{S(t)=\int_0^tG(\tau)d\tau=\int_0^t\frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}(e^{\lambda_2\tau}-e^{\lambda_1\tau})d\tau}\\ \displaystyle{= \frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}\left[\frac{e^{\lambda_2\tau}}{\lambda_2}-\frac{e^{\lambda_1\tau}}{\lambda_1}\right]_0^t}\\ \displaystyle{=\frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}(\frac{e^{\lambda_2t}}{\lambda_2}-\frac{e^{\lambda_1t}}{\lambda_1})-\frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}(\frac{1}{\lambda_2}-\frac{1}{\lambda_1})}\\ \displaystyle{=1+\frac{1}{\lambda_2-\lambda_1}(\lambda_1e^{\lambda_2t}-\lambda_2e^{\lambda_1t})} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d173fcf8b486b5642e9d12ff5b071c67_l3.png)
![]()
![]() のとき、インパルス応答を積分して、ステップ応答は次のように計算されます。
のとき、インパルス応答を積分して、ステップ応答は次のように計算されます。![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \displaystyle{S(t)=\int_0^tG(\tau)d\tau=\int_0^t\lambda^2\tau e^{\lambda\tau}d\tau}\\ \displaystyle{=\lambda^2\left[\tau \frac{1}{\lambda}e^{\lambda\tau}\right]_0^t -\lambda^2\int_0^t \frac{1}{\lambda}e^{\lambda\tau}d\tau}\\ \displaystyle{=\lambda te^{\lambda t}-\lambda\left[\frac{1}{\lambda}e^{\lambda\tau}\right]_0^t}\\ \displaystyle{=1+(\lambda t-1)e^{\lambda t}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a118c65350e9a4f5d018ff031436c980_l3.png)
![]()
![]() のとき、インパルス応答を積分して、公式
のとき、インパルス応答を積分して、公式![]()
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \displaystyle{S(t)=\int_0^tG(\tau)d\tau=\int_0^t\frac{\omega_n^2}{\lambda_I}e^{\lambda_R\tau}\sin\lambda_I \tau d\tau}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I}\left[ \frac{e^{\lambda_R\tau}}{\lambda_R^2+\lambda_I^2}(\lambda_R\sin\lambda_I\tau-\lambda_I\cos\lambda_I\tau)\right]_0^t}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I}\frac{1}{\omega_n^2} (e^{\lambda_Rt}(\lambda_R\sin\lambda_It-\lambda_I\cos\lambda_It)+\lambda_I)}\\ \displaystyle{=1-\frac{\omega_n}{\lambda_I}e^{\lambda_Rt} (\sin\lambda_It\times\frac{-\lambda_R}{\omega_n}+\cos\lambda_It\times\frac{\lambda_I}{\omega_n})}\\ \displaystyle{=1-\frac{\omega_n}{\lambda_I}e^{\lambda_Rt} (\sin\lambda_It\cos\phi+\cos\lambda_It\sin\phi)}\\ \displaystyle{=1-\frac{\omega_n}{\lambda_I}e^{\lambda_Rt}\sin(\lambda_It+\phi) \quad(\phi=\tan^{-1}\frac{\lambda_I}{-\lambda_R})} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3793ae4ad3dcc7b944a94325418dafe8_l3.png)
![]() だから
だから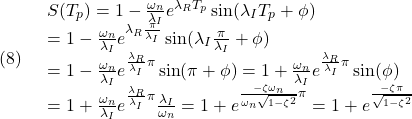
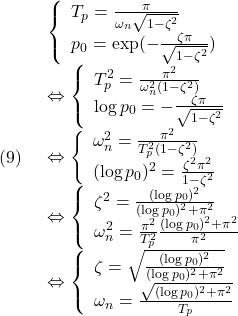
CT62 2次系のインパルス応答
![]()
![]() の場合の零入力応答を並べたものと言えるね。そうすると、数学的には、インパルス応答は初期値を
の場合の零入力応答を並べたものと言えるね。そうすると、数学的には、インパルス応答は初期値を![]() の各列ベクトルに設定したときの応答ということになるね。
の各列ベクトルに設定したときの応答ということになるね。
[1] ![]()
![]()
![]()
![]() のとき、
のとき、![]()
![]()
![]() のとき、
のとき、![]()
![]()
![]() のとき、
のとき、![]()
![]()
![]() のとき
のとき![Rendered by QuickLaTeX.com \displaystyle{(6.28.1)\quad \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} = \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda_1 & \lambda_2 \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda_1& 0\\ 0 & \lambda_2 \end{array}\right] }_{\Lambda} \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda_1 & \lambda_2 \end{array}\right]^{-1} }_{V^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-55420fa8d904daf4b15519c41cdf76d3_l3.png)
![]()
![Rendered by QuickLaTeX.com (3)\quad \begin{array}{l} \displaystyle{G(t)=C\exp(At)B=CV\exp(\Lambda t)V^{-1}B}\\ \displaystyle{ =\left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{cc} 1 & 1\\ \lambda_1 & \lambda_2 \end{array}\right] \left[\begin{array}{cc} e^{\lambda_1t}& 0\\ 0 & e^{\lambda_2t} \end{array}\right] \frac{1}{\lambda_2-\lambda_1} \left[\begin{array}{cc} \lambda_2 & -1\\ -\lambda_1 & 1 \end{array}\right] \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right]}\\ \displaystyle{ =\frac{\omega_n^2}{\lambda_2-\lambda_1} \left[\begin{array}{cc} e^{\lambda_1t}& e^{\lambda_2t} \end{array}\right] \left[\begin{array}{cc} -1\\ 1 \end{array}\right]}\\ \displaystyle{=\frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}(e^{\lambda_2t}-e^{\lambda_1t})} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ece0a94935b01bc18444d5eda16a8c81_l3.png)
![]()
![]() のとき、
のとき、![]() とおいて
とおいて![Rendered by QuickLaTeX.com \displaystyle{(6.28.2)\quad \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} = \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda & \lambda+1 \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda & 1\\ 0 & \lambda \end{array}\right] }_{\Lambda} \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda & \lambda+1 \end{array}\right]^{-1} }_{V^{-1}}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2aa64e76606a532fd70c083aeb8b841c_l3.png)
![]()
![Rendered by QuickLaTeX.com (4)\quad \begin{array}{l} \displaystyle{G(t)=C\exp(At)B=CV\exp(\Lambda t)V^{-1}B}\\ \displaystyle{= \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{cc} 1 & 1\\ \lambda & \lambda+1 \end{array}\right] e^{\lambda t} \left[\begin{array}{cc} 1 & t\\ 0 & 1 \end{array}\right] \frac{1}{\lambda+1-\lambda} \left[\begin{array}{cc} \lambda+1 & -1\\ -\lambda & 1 \end{array}\right] \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right]}\\ \displaystyle{= \omega_n^2 e^{\lambda t} \left[\begin{array}{cc} 1 & t+1 \end{array}\right] \left[\begin{array}{cc} -1\\ 1 \end{array}\right]}\\ \displaystyle{=\lambda^2te^{\lambda t}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bd0b2182726886d2d304b2d77efc4e50_l3.png)
![]()
![]() のとき、
のとき、![]() とおいて
とおいて![Rendered by QuickLaTeX.com \displaystyle{(6.28.3)\quad \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} = \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ \lambda_R & \lambda_I \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array}\right] }_{\Lambda} \underbrace{ \frac{1}{\lambda_I} \left[\begin{array}{cc} \lambda_I & 0 \\ -\lambda_R & 1 \end{array}\right] }_{V^{-1}}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3e35b572620304540cd24c080a37c5e6_l3.png)
![]()
![Rendered by QuickLaTeX.com (5)\quad \begin{array}{l} \displaystyle{G(t)=C\exp(At)B=CV\exp(\Lambda t)V^{-1}B}\\ \displaystyle{=\left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{cc} 1 & 0\\ \lambda_R & \lambda_I \end{array}\right] e^{\lambda_R t} \left[\begin{array}{cc} \cos\lambda_I t & \sin\lambda_I t\\ \sin\lambda_I t & \cos\lambda_I t \end{array}\right] \frac{1}{\lambda_I} \left[\begin{array}{cc} \lambda_I & 0\\ -\lambda_R & 1 \end{array}\right] \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right]}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I} e^{\lambda_R t} \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{cc} \cos\lambda_I t & \sin\lambda_I t\\ \sin\lambda_I t & \cos\lambda_I t \end{array}\right] \left[\begin{array}{cc} 0\\ 1 \end{array}\right]}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I} e^{\lambda_R t}\sin\lambda_I t} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a477b9d880d04fc189e4d07dd0af3a5e_l3.png)
CT61 1次系の応答
[1] (6.9)を用いた場合![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} y(t)=ce^{at}x(0)+\int_0^t ce^{a\tau}b\cdot u(t-\tau)d\tau\\ =1\cdot e^{-\frac{1}{T}t}\cdot 0+\int_0^t 1\cdot e^{-\frac{1}{T}(\tau)}\frac{K}{T}\cdot 1d\tau\\ =\frac{K}{T}\int_0^t e^{-\frac{1}{T}\tau}d\tau =\frac{K}{T}\frac{1}{-\frac{1}{T}}\left[e^{-\frac{1}{T}\tau}\right]_0^t\\ =-K(e^{-\frac{1}{T}t}-1) =K(1-e^{-\frac{1}{T}t}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-89824d3bceb275182df1b023c188934b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \begin{array}{l} y(t)=ce^{at}x(0)+\int_0^t ce^{a(t-\tau)}b\cdot u(\tau)d\tau\\ =1\cdot e^{-\frac{1}{T}t}\cdot 0+\int_0^t 1\cdot e^{-\frac{1}{T}(t-\tau)}\frac{K}{T}\cdot 1d\tau\\ =\frac{K}{T}e^{-\frac{1}{T}t} \int_0^t e^{\frac{1}{T}\tau}d\tau =\frac{K}{T}e^{-\frac{1}{T}t} \frac{1}{\frac{1}{T}}\left[e^{\frac{1}{T}\tau}\right]_0^t\\ =Ke^{-\frac{1}{T}t}(e^{\frac{1}{T}t}-1) =K(1-e^{-\frac{1}{T}t}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9cdfaa1363ddf24276d4161f070e2a9a_l3.png)
![]() における接線の式は、傾きが
における接線の式は、傾きが![]() 、切片が
、切片が![]() だから
だから![]()
![]() の値をとる時刻は
の値をとる時刻は![]() となります。また、
となります。また、![]() だから
だから![]()
CT54 補遺5
![]() と観測方程式
と観測方程式![]() からなる。ここで、
からなる。ここで、![]() はそれぞれ次数
はそれぞれ次数![]() をもつベクトル、
をもつベクトル、![]() はそれぞれサイズ
はそれぞれサイズ![]() をもつ行列である。また、初期状態「
をもつ行列である。また、初期状態「![]() 」は、平衡状態を表すように選ばれているものとする。
」は、平衡状態を表すように選ばれているものとする。![]() となったとする。このとき、次第に平衡状態に戻るとき、すなわち
となったとする。このとき、次第に平衡状態に戻るとき、すなわち![]() となるとき、制御対象は「漸近安定」であるという。そのための条件は、行列
となるとき、制御対象は「漸近安定」であるという。そのための条件は、行列![]() が安定行列、すなわち行列
が安定行列、すなわち行列![]() の「すべての固有値の実部が負」であることである。
の「すべての固有値の実部が負」であることである。![]() により安定化したい。すなわち、閉ループ系の行列「
により安定化したい。すなわち、閉ループ系の行列「![]() 」を安定行列としたい。それが可能かどうか調べるためには、「可制御」性の条件「
」を安定行列としたい。それが可能かどうか調べるためには、「可制御」性の条件「![]() 」が成立するかどうかをチェックすればよい。
」が成立するかどうかをチェックすればよい。![]() が用いられる。これは、
が用いられる。これは、![]() となるように、オフザーバゲイン
となるように、オフザーバゲイン![]() を選択することにより達成される。それが可能かどうか調べるためには、「可観測」性の条件「
を選択することにより達成される。それが可能かどうか調べるためには、「可観測」性の条件「![Rendered by QuickLaTeX.com {{\rm rank}\left[\begin{array}{c}C\\CA\\\vdots\\CA^{n-1}\end{array}\right]=n}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cd3a603d073f86a0f8958553cc9912a7_l3.png) 」が成立するかどうかをチェックすればよい。
」が成立するかどうかをチェックすればよい。![]() のように実施するとき、状態空間表現
のように実施するとき、状態空間表現![]() 、
、![]() を「オブザーバベース」コントローラと呼ぶ。これによる閉ループ系の固有値の集合は、行列「
を「オブザーバベース」コントローラと呼ぶ。これによる閉ループ系の固有値の集合は、行列「![]() 」の固有値の集合と行列「
」の固有値の集合と行列「![]() 」の固有値の集合の和集合となることが知られている。したがって、状態フィードバックと状態オブザーバの設計は独立に行うことができる。ただ、制御動作より状態推定が速く行われなければならないので、複素平面上で、行列「
」の固有値の集合の和集合となることが知られている。したがって、状態フィードバックと状態オブザーバの設計は独立に行うことができる。ただ、制御動作より状態推定が速く行われなければならないので、複素平面上で、行列「![]() 」の固有値は行列「
」の固有値は行列「![]() 」の固有値のより左寄りとすることが考えられる。
」の固有値のより左寄りとすることが考えられる。![]() 、(d)
、(d)![]() 、(e)安定、(f)漸近安定、(g)不安定、(h)すべての固有値の実部が負、(i)ある固有値の実部が負、(j)すべての固有値の実部が正、(k)ある固有値の実部が正、(l)状態フィードバック、(m)状態オブザーバ、(n)
、(e)安定、(f)漸近安定、(g)不安定、(h)すべての固有値の実部が負、(i)ある固有値の実部が負、(j)すべての固有値の実部が正、(k)ある固有値の実部が正、(l)状態フィードバック、(m)状態オブザーバ、(n)![]() 、(o)
、(o)![]() 、(p)
、(p)![]() 、(q)可制御、(r)可観測、(s)可安定、(t)可検出、(u)
、(q)可制御、(r)可観測、(s)可安定、(t)可検出、(u)![]() 、(v)
、(v)![Rendered by QuickLaTeX.com {{\rm rank}\left[\begin{array}{c}C\\CA\\\vdots\\CA^{n-1}\end{array}\right]=n}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cd3a603d073f86a0f8958553cc9912a7_l3.png) 、(w)アクチュエータ、(x)センサ、(y)PID、(z)オブザーバベース
、(w)アクチュエータ、(x)センサ、(y)PID、(z)オブザーバベース