最小次元状態オブザーバ…Homework
[1] 制御対象のモデルが
![]()
で与えられるとします。これに対する状態オブザーバは、微分方程式
![]()
で表され、解ベクトル![]() は、制御対象の状態ベクトル
は、制御対象の状態ベクトル![]() と同じ次元数
と同じ次元数![]() を持ちます。
を持ちます。
いま、出力方程式![]() (
(![]() のサイズは
のサイズは![]() 、行フルランク)を通して、状態に関する情報が部分的に得られていることに注目します。そこで、もう一つの補完的な出力方程式
、行フルランク)を通して、状態に関する情報が部分的に得られていることに注目します。そこで、もう一つの補完的な出力方程式![]() (
(![]() のサイズは
のサイズは![]() 、行フルランク)を
、行フルランク)を![]() が正則となるように適切に選んで
が正則となるように適切に選んで
![]()
とすれば、状態に関する全情報が得られそうです。もちろん
![]()
を達成する仕組みが必要です。いま、その仕組みを
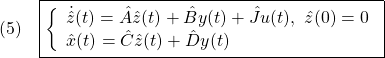
とします。(5)の第1式から、![]() を掛けた(1)の第1式を辺々引くと
を掛けた(1)の第1式を辺々引くと
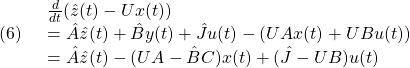
を得ます。ここで
![]()
を仮定し、![]() を
を
![]()
とおけば
![]()
を得ます。もし![]() が安定行列であれば、(4)を達成できます。また
が安定行列であれば、(4)を達成できます。また
![]()
を仮定すると
![]()
を得て、状態推定が行われていることがわかります。状態オブザーバ(2)と比べると、計算機内で解くべき微分方程式の解ベクトルの次元数が![]() から
から![]() に低次元化されていることになります。
に低次元化されていることになります。![]() が正則となるためには、
が正則となるためには、![]() の行数は
の行数は![]() 以下にすることはできませんから、最小次元状態オブザーバと呼ばれています。
以下にすることはできませんから、最小次元状態オブザーバと呼ばれています。
[2] 以上から、適当な![]() を選んで、(7)、(8)、(10)を満足し、安定行列
を選んで、(7)、(8)、(10)を満足し、安定行列![]() をもつ(3)を設計することを考えます。たとえば
をもつ(3)を設計することを考えます。たとえば![]() のときは
のときは![]() のように選びます(
のように選びます(![]() のサイズは
のサイズは![]() )。このとき、(7)と(10)をまとめた
)。このとき、(7)と(10)をまとめた
![]()
において、![]() (
(![]() のサイズは
のサイズは![]() )のように分割すると
)のように分割すると
![]()
![]()
より、![]() 、
、![]() 、
、![]() 、
、![]() は次式から求められます。
は次式から求められます。
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \boxed{\left\{\begin{array}{lll} \hat{A}=A_{22}-LA_{12}\\ \hat{B}=A_{21}-LA_{11}+\hat{A}L\\ \hat{C}= \left[\begin{array}{cc} 0\\ I_{n-p} \end{array}\right]\\ \hat{D}= \left[\begin{array}{cc} I_{p}\\ L \end{array}\right] \end{array}\right.} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ba9d6526eff83e7894d3ec54c6f96e0f_l3.png)
ここで、![]() は
は![]() が安定行列となるように選ぶ必要があります。そのためには
が安定行列となるように選ぶ必要があります。そのためには![]() が可観測対であればよいのですが、これについてはあとで触れます。また、
が可観測対であればよいのですが、これについてはあとで触れます。また、![]() は(10)から定めます。
は(10)から定めます。
● モータの状態方程式
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \left[\begin{array}{c} \dot{\theta}(t)\\ \dot{\omega}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -\frac{1}{T_m} \end{array}\right] }_{A} \left[\begin{array}{c} \theta(t)\\ \omega(t) \end{array}\right]+ \underbrace{ \left[\begin{array}{c} 0\\ \frac{1}{K_ET_m} \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e95207cda654ebaf7485fe467b4eff54_l3.png)
と出力方程式
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \left[\begin{array}{c} \theta(t)\\ \omega(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-181f79035e64702aea850bc818dfa728_l3.png)
に対する状態オブザーバの低次元化を行ってみます。ちょうど![]() となっているので、
となっているので、![]() とおきます。設計式(15)に
とおきます。設計式(15)に![]() 、
、![]() 、
、![]() 、
、![]() を代入して
を代入して
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \left\{\begin{array}{lll} \hat{A}=-\frac{1}{T_m}-L\\ \hat{B}=\hat{A}L\\ \hat{C}= \left[\begin{array}{cc} 0\\ 1 \end{array}\right]\\ \hat{D}= \left[\begin{array}{cc} 1\\ L \end{array}\right]\\ \hat{J}=\frac{1}{K_ET_m} \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5c9ef1b1a40ae6aeaab1a8d4e8bfc53c_l3.png)
ここで、![]() は
は![]() とするのであれば
とするのであれば![]() と決めます。以上から、次の低次元化された状態オブザーバが得られました。
と決めます。以上から、次の低次元化された状態オブザーバが得られました。
![Rendered by QuickLaTeX.com \displaystyle{(19)\quad \left\{\begin{array}{lll} \dot{\hat{z}}(t)=\underbrace{-\frac{\alpha}{T_m}}_{\hat{A}}\hat{z}(t) +\underbrace{\frac{\alpha(1-\alpha)}{T_m^2}}_{\hat{B}}y(t) +\underbrace{\frac{1}{K_ET_m}}_{\hat{J}}u(t),\ \hat{z}(0)=0\\ \hat{x}(t)= \underbrace{ \left[\begin{array}{cc} 0\\ 1 \end{array}\right]}_{\hat{C}}\hat{z}(t) + \underbrace{ \left[\begin{array}{cc} 1\\ L \end{array}\right] }_{\hat{D}}y(t) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9bfd472ab38f4e90833894fadfad6f9d_l3.png)
●次図は![]() 、
、![]() の下で、
の下で、![]() と変えたとき、状態オブザーバが真の状態を推定する様子をシミュレーションしています。
と変えたとき、状態オブザーバが真の状態を推定する様子をシミュレーションしています。
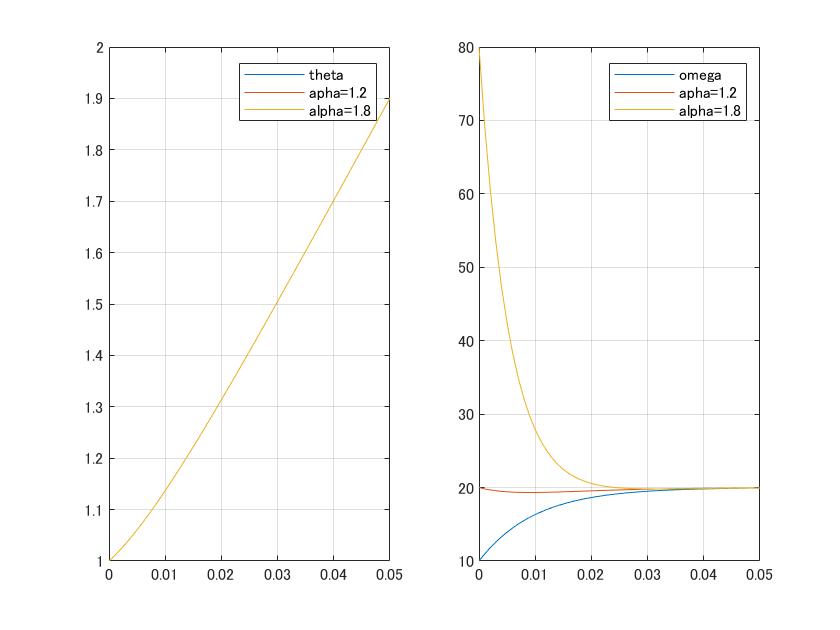 図1 状態推定の例
図1 状態推定の例
演習 A42…Flipped Classroom
次のコードを用いて図1のグラフを描け。
| MATLAB |
|
| SCILAB |
|
Note A42 線形関数オブザーバ
制御対象の状態空間表現
![]()
に対して、もう一つの状態空間表現
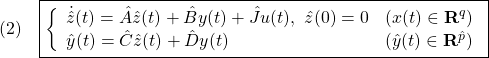
を考えます。ただし、サイズ![]() の行列
の行列![]() とサイズ
とサイズ![]() の行列
の行列![]() に対して
に対して
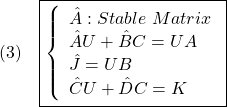
が満足されるものとします。このとき
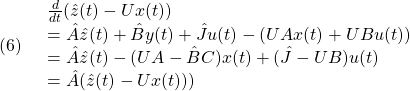
から
![]()
を得ます。また
![]()
を得て、状態の線形関数![]() の推定が行われていることがわかります。
の推定が行われていることがわかります。
したがって、条件(3)を満足する状態空間表現(2)は、線形関数オブザーバと呼ばれます。特に![]() のとき、は最小次元状態オブザーバとなります。
のとき、は最小次元状態オブザーバとなります。
●興味深いのは、状態フィードバック
![]()
を推定させる場合で、線形関数オブザーバの次元数![]() が最小次元状態オブザーバの次数
が最小次元状態オブザーバの次数![]() より小さくできる可能性があります。
より小さくできる可能性があります。
たとえば機械系でよく見られる、次の1入力![]() 出力
出力![]() 次系
次系
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \left\{\begin{array}{l} \left[\begin{array}{c} \dot{y}(t)\\ \ddot{y}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} 0 & I_p \\ A_{21} & A_{22} \end{array}\right] }_{A} \left[\begin{array}{c} y(t)\\ \dot{y}(t) \end{array}\right]+ \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t)\\ y(t)= \underbrace{ \left[\begin{array}{cc} I_n & 0 \end{array}\right] }_{C} \left[\begin{array}{c} y(t)\\ \dot{y}(t) \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-70c3410208fc14d4768b6a45442062a9_l3.png)
および、これに対する状態フィードバック
![]()
を考えます。この状態フィードバックを推定する線形関数オブザーバは、![]() 入力1出力1次系
入力1出力1次系
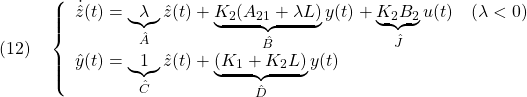
として得られます。実際、![]() と
と![]() を
を
![]()
と選べば、(3)の第2、3、4式を満足していることを次のように確かめることができます。
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \begin{array}{l} \underbrace{ \lambda K_2\left[\begin{array}{cc} -L & I_p \end{array}\right] + K_2(A_{21}+\lambda L) \left[\begin{array}{cc} I_n & 0 \end{array}\right] }_{\hat{A}U+\hat{B}C} = \underbrace{ K_2\left[\begin{array}{cc} -L & I_p \end{array}\right] \left[\begin{array}{cc} 0 & I_p \\ A_{21} & A_{22} \end{array}\right] }_{UA}\\ \underbrace{ K_2B_2 }_{\hat{J}} = \underbrace{ K_2\left[\begin{array}{cc} -L & I_p \end{array}\right] \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{UB}\\ \underbrace{ 1\cdot K_2\left[\begin{array}{cc} -L & I_p \end{array}\right] + (K_1+K_2L) \left[\begin{array}{cc} I_n & 0 \end{array}\right] }_{\hat{C}U+\hat{D}C} = \underbrace{ \left[\begin{array}{cc} K_1 & K_2 \end{array}\right] }_{K} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-92fe0b99d4f40416cb7cd4fdcf78d696_l3.png)
●状態フィードバックを推定する線形関数オブザーバ(したがって最小次元状態オブザーバ)に対しても分離定理を示すことができます。すなわち制御対象のモデル(1)に対して、![]() の場合の(3)を満たす線形関数オブザーバ(2)による閉ループ系は
の場合の(3)を満たす線形関数オブザーバ(2)による閉ループ系は
![]()
を定義すると、次式となります。
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \boxed{\left[\begin{array}{c} \dot{x}(t) \\ \dot{e}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A-BF & -B\hat{C} \\ 0 & \hat{A} \end{array}\right] }_{A_{CL}} \left[\begin{array}{c} x(t) \\ e(t) \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a941bbb0ba1845c0025a886fd7d9e55a_l3.png)
この第1式は(1)の状態方程式の![]() に、(2)の出力方程式の
に、(2)の出力方程式の![]() を代入して
を代入して
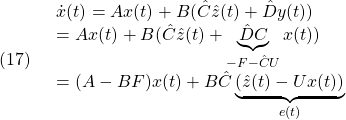
のように得られます。また、第2式は(6)そのものです。
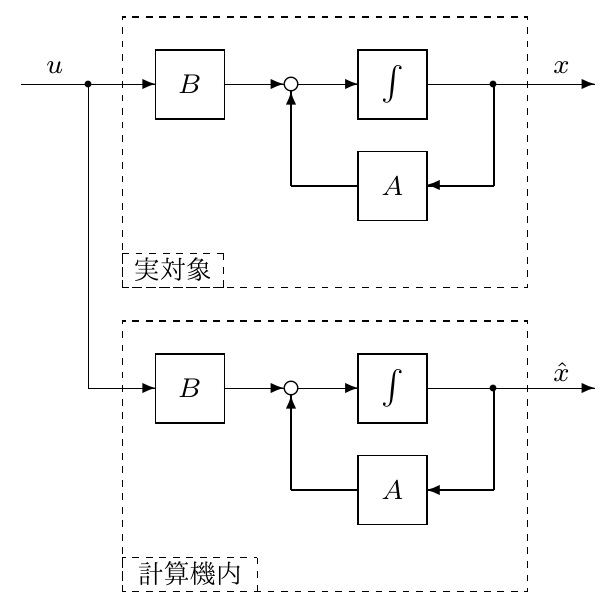 図1 状態オブザーバの考え方(1)
図1 状態オブザーバの考え方(1)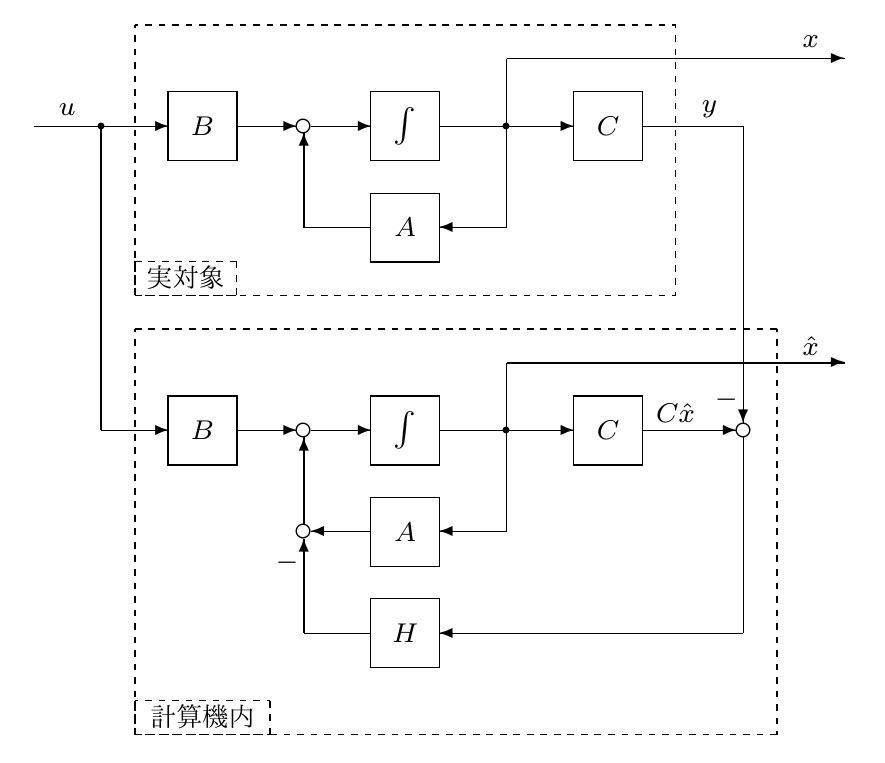 図2 状態オブザーバの考え方(2)
図2 状態オブザーバの考え方(2)![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \left[\begin{array}{c} \dot{\theta}(t)\\ \dot{\omega}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -\frac{1}{T_m} \end{array}\right] }_{A} \left[\begin{array}{c} \theta(t)\\ \omega(t) \end{array}\right]+ \underbrace{ \left[\begin{array}{c} 0\\ \frac{1}{K_ET_m} \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a95eaa65d14cb9fd7e4b2c26e0599949_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \left[\begin{array}{c} \theta(t)\\ \omega(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b3827f897e0c0c4d4bd29eb0213d28ef_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \left[\begin{array}{c} \dot{\hat{\theta}}(t)\\ \dot{\hat{\omega}}(t) \end{array}\right] =(A-HC) \left[\begin{array}{c} \hat{\theta}(t)\\ \hat{\omega}(t) \end{array}\right] +Bu(t)+Hy(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d8751c5f7f39274e29ad827c0d037478_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(19)\quad \begin{array}{l} \det \left[\begin{array}{cc} \lambda+h_1 & -1 \\ h_2 & \lambda+\frac{1}{T_m} \end{array}\right]\\ =(\lambda+h_1)(\lambda+\frac{1}{T_m})+h_2\\ =\lambda^2+(h_1+\frac{1}{T_m})\lambda+h_1\frac{1}{T_m}+h_2\\ =\lambda^2+2\alpha\frac{1}{T_m}\lambda+(\alpha\frac{1}{T_m})^2\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7385eb112c8af51a54d93f1ffabef5d1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(21)\quad \begin{array}{l} \left[\begin{array}{c} \dot{\hat{\theta}}(t)\\ \dot{\hat{\omega}}(t) \end{array}\right] =\underbrace{ \left[\begin{array}{cc} -\frac{2\alpha-1}{T_m} & 1 \\ -\frac{(\alpha-1)^2}{T_m^2} & -\frac{1}{T_m} \end{array}\right] }_{A-HC} \left[\begin{array}{c} \hat{\theta}(t)\\ \hat{\omega}(t) \end{array}\right] +\underbrace{ \left[\begin{array}{c} 0\\ \frac{1}{K_ET_m} \end{array}\right] }_{B}u(t)\\ + \underbrace{\left[\begin{array}{c} \frac{2\alpha-1}{T_m} \\ \frac{(\alpha-1)^2}{T_m^2} \end{array}\right] }_{H}y(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b514337c82c45e6315198b0db3388da8_l3.png)
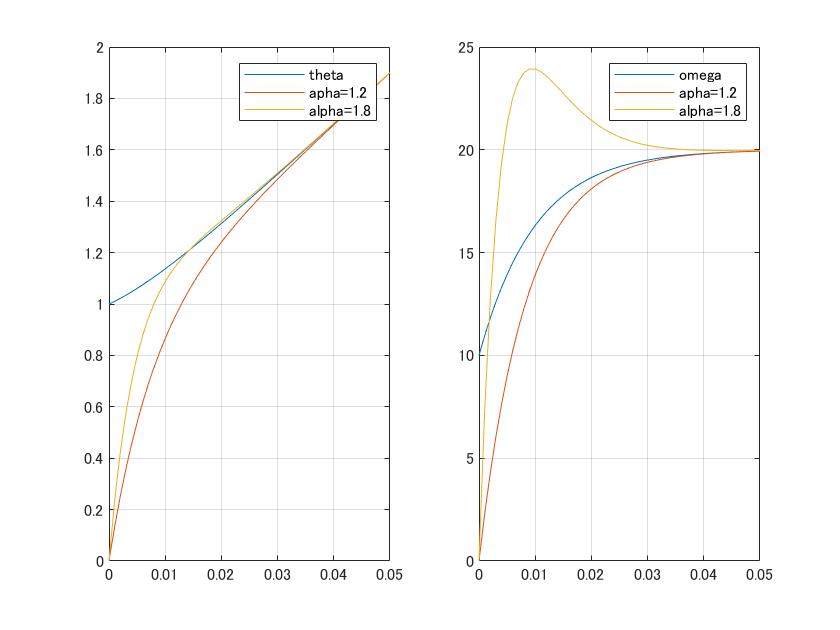 図3 状態推定の例
図3 状態推定の例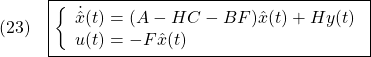
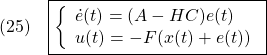
![Rendered by QuickLaTeX.com \displaystyle{(29)\quad \boxed{\left[\begin{array}{c} \dot{x}(t) \\ \dot{e}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A-BF & -BF \\ 0 & A-HC \end{array}\right] }_{A_{CL}} \left[\begin{array}{c} x(t) \\ e(t) \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8c6ec4764b02f704e5faf2444cdf4250_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} A \underbrace{ \left[\begin{array}{cccc} B & AB &\cdots & A^{n-1}B \end{array}\right] }_{T_1^{-1}}\\ = \underbrace{ \left[\begin{array}{cccc} B & AB &\cdots & A^{n-1}B \end{array}\right] }_{T_1^{-1}} \underbrace{ \left[\begin{array}{ccccc} 0 & \cdots & 0 & -a_n \\ 1 & \cdots & 0 & -a_{n-1} \\ \vdots & \ddots & \vdots &\vdots\\ 0 & \cdots & 1 & -a_1 \end{array}\right] }_{A_1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0db546a70235247b2e03b1bb4ba933e0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \boxed{ \begin{array}{l} A_1=T_1AT_1^{-1}= \left[\begin{array}{ccccc} 0 & \cdots & 0 & -a_n \\ 1 & \cdots & 0 & -a_{n-1} \\ \vdots & \ddots & \vdots &\vdots\\ 0 & \cdots & 1 & -a_1 \end{array}\right]\\ B_1=T_1B= \left[\begin{array}{cc} 1 \\ 0\\ \vdots\\ 0 \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c6cf45471e92537f21ce37771de23573_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{ccccc} 0 & \cdots & 0 & -a_n \\ 1 & \cdots & 0 & -a_{n-1} \\ \vdots & \ddots & \vdots &\vdots\\ 0 & \cdots & 1 & -a_1 \end{array}\right] }_{A_1} \underbrace{ \left[\begin{array}{ccccc} a_{n-1} & a_{n-2} & \cdots & a_1 & 1 \\ a_{n-2} & a_{n-3} & \cdots & 1 & 0 \\ \vdots & \vdots & \cdots & \vdots & \vdots \\ a_1 & 1 & \cdots & 0 & 0 \\ 1 & 0 & \cdots & 0 & 0 \end{array}\right] }_{T_2^{-1}}\\ =\underbrace{ \left[\begin{array}{ccccc} a_{n-1} & a_{n-2} & \cdots & a_1 & 1 \\ a_{n-2} & a_{n-3} & \cdots & 1 & 0 \\ \vdots & \vdots & \cdots & \vdots & \vdots \\ a_1 & 1 & \cdots & 0 & 0 \\ 1 & 0 & \cdots & 0 & 0 \end{array}\right] }_{T_2^{-1}} \underbrace{ \left[\begin{array}{ccccc} 0 & 1 & \cdots & 0\\ \vdots & \vdots & \cdots & \vdots \\ 0 & 0 & \cdots & 1\\ -a_n & -a_{n-1} & \cdots & -a_1 \end{array}\right] }_{A_2} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5f95461a20f296c7ece2c87fd871f594_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} {\rm LHS}=\\ \left[\begin{array}{cc} 0_{1\times n-1} & -a_n \\ I_{n-1\times n-1} & \left[\begin{array}{c} -a_{n-1} \\ \vdots\\ -a_1 \end{array}\right] \end{array}\right] \left[\begin{array}{cccc|c} a_{n-1} & a_{n-2} & \cdots & a_1 & 1 \\ a_{n-2} & a_{n-3} & \cdots & 1 & 0 \\ \vdots & \vdots & \cdots & \vdots & \vdots \\ a_1 & 1 & \cdots & 0 & 0 \\\hline 1 & 0 & \cdots & 0 & 0 \end{array}\right]\\ = \left[\begin{array}{cccc|c} -a_n & 0 & \cdots & 0 & 0 \\\hline 0 & a_{n-2} & \cdots & a_1 & 1 \\ 0 & a_{n-3} & \cdots & 1 & 0 \\ \vdots & \vdots & \cdots & \vdots & \vdots \\ 0 & 1 & \cdots & 0 & 0 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-19724dd9a4d938871edbfcd49d9674ac_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \begin{array}{l} {\rm RHS}=\\ \left[\begin{array}{cccc|c} a_{n-1} & a_{n-2} & \cdots & a_1 & 1 \\ a_{n-2} & a_{n-3} & \cdots & 1 & 0 \\ \vdots & \vdots & \cdots & \vdots & \vdots \\ a_1 & 1 & \cdots & 0 & 0 \\\hline 1 & 0 & \cdots & 0 & 0 \end{array}\right] \left[\begin{array}{cc} 0_{n-1\times 1} & I_{n-1\times n-1} \\ -a_n & \left[\begin{array}{ccc} -a_{n-1} & \cdots & -a_1 \end{array}\right] \end{array}\right]\\ = \left[\begin{array}{c|cccc} -a_n & 0 & \cdots & 0 & 0 \\ 0 & a_{n-2} & \cdots & a_1 & 1 \\ 0 & a_{n-3} & \cdots & 1 & 0 \\ \vdots & \vdots & \cdots & \vdots & \vdots \\\hline 0 & 1 & \cdots & 0 & 0 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ff97f31f2cbd01f24fdf56d95b63fc41_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \boxed{ \begin{array}{l} A_2=T_2A_1T_2^{-1}= \left[\begin{array}{ccccc} 0 & 1 & \cdots & 0\\ \vdots & \vdots & \cdots & \vdots \\ 0 & 0 & \cdots & 1\\ -a_n & -a_{n-1} & \cdots & -a_1 \end{array}\right]\\ B_2=T_2B_1= \left[\begin{array}{cc} 0 \\ \vdots\\ 0\\ 1 \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ce6be79123d0d41f08f5578f356f1fc8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \begin{array}{l} A= \left[\begin{array}{ccc} 0 & 7 & 4 \\ 1 & -1 & -2\\ 0 & 3 & 1 \end{array}\right],\ B= \left[\begin{array}{cc} 1 & 0 \\ 0 & 0 \\ 0 & 1 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eb613b4ad7959f598c2311a3efa6522d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \begin{array}{l} {\rm rank} \left[\begin{array}{ccc} B & AB & A^2B \end{array}\right]= {\rm rank}\ \left[\begin{array}{cc|cc|cc} 1 & 0 & 0 & 4 & 7 & -10\\ 0 & 0 & 1 & -2 & -1 & 4\\ 0 & 1 & 0 & 1 & 3 & 5 \end{array}\right]=3 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-778441ef0b082221824194bd7f62be96_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(22)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} 7 \\ -1 \\ 3 \end{array}\right] }_{A^2B_1} = \underbrace{7}_{\alpha_{110}} \underbrace{ \left[\begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right] }_{B_1} +\underbrace{(-1)}_{\alpha_{111}} \underbrace{ \left[\begin{array}{c} 0 \\ 1 \\ 0 \end{array}\right] }_{AB_1} +\underbrace{3}_{\alpha_{120}} \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right] }_{B_2} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a3ced55d0387a8aca744280338c5e6a1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} 4 \\ -2 \\ 1 \end{array}\right] }_{AB_2} = \underbrace{4}_{\alpha_{210}} \underbrace{ \left[\begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right] }_{B_1} +\underbrace{(-2)}_{\beta_{21}} \underbrace{ \left[\begin{array}{c} 0 \\ 1 \\ 0 \end{array}\right] }_{AB_1} +\underbrace{1}_{\alpha_{220}} \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right] }_{B_2} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c63e0b1e9096a4bd9c5fbf5321eee21e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(24)\quad \begin{array}{l} A \underbrace{ \left[\begin{array}{ccc} B_1 & AB_1 & B_2 \end{array}\right] }_{T_1^{-1}} =\underbrace{ \left[\begin{array}{ccc} B_1 & AB_1 & B_2 \end{array}\right] }_{T_1^{-1}} \underbrace{ \left[\begin{array}{ccc} 0 & \alpha_{110} & \alpha_{210} \\ 1 & \alpha_{111} & \beta_{21}\\ 0 & \alpha_{120} & \alpha_{220} \end{array}\right] }_{A_1}\\ &&B= \underbrace{ \left[\begin{array}{ccc} B_1 & AB_1 & B_2 \end{array}\right] }_{T_1^{-1}} \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ 0 & 0 \\ 0 & 1 \end{array}\right] }_{B_1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-23bf562ea179dfd172e768b601e987e8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(25)\quad \begin{array}{l} A_1=T_1AT_1^{-1}= \left[\begin{array}{ccc} 0 & \alpha_{110} & \alpha_{210} \\ 1 & \alpha_{111} & \beta_{21}\\ 0 & \alpha_{120} & \alpha_{220} \end{array}\right] =\left[\begin{array}{ccc} 0 & 7 & 4 \\ 1 & -1 & -2\\ 0 & 3 & 1 \end{array}\right]\\ & B_1=T_1B= \left[\begin{array}{cc} 1 & 0 \\ 0 & 0 \\ 0 & 1 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-88db77c1df02bff109ddfadff44909d0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(26)\quad \begin{array}{l} &&\underbrace{ \left[\begin{array}{cc|c} 0 & \alpha_{110} & \alpha_{210} \\ 1 & \alpha_{111} & \beta_{21}\\\hline 0 & \alpha_{120} & \alpha_{220} \end{array}\right] }_{A_1} \underbrace{ \left[\begin{array}{cc|c} -\alpha_{111} & 1 & -\beta_{21} \\ 1 & 0 & 0\\\hline 0 & 0 & 1 \end{array}\right] }_{T_2^{-1}}\\ &=\underbrace{ \left[\begin{array}{cc|c} -\alpha_{111} & 1 & -\beta_{21} \\ 1 & 0 & 0\\\hline 0 & 0 & 1 \end{array}\right] }_{T_2^{-1}} \underbrace{ \left[\begin{array}{cc|c} 0 & 1 & 0 \\ \alpha_{110}+\beta_{21}\alpha_{120} & \alpha_{111} & \alpha_{210}+\beta_{21}\alpha_{220}\\\hline \alpha_{120} & 0 & \alpha_{220} \end{array}\right] }_{A_2} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2373ee4453ef9f5ca62b357ea4f5af85_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(27)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc|c} 0 & 7 & 4 \\ 1 & -1 & -2\\\hline 0 & 3 & 1 \end{array}\right] }_{A_1} \underbrace{ \left[\begin{array}{cc|c} 1 & 1 & 2 \\ 1 & 0 & 0\\\hline 0 & 0 & 1 \end{array}\right] }_{T_2^{-1}} =\underbrace{ \left[\begin{array}{cc|c} 1 & 1 & 2 \\ 1 & 0 & 0\\\hline 0 & 0 & 1 \end{array}\right] }_{T_2^{-1}} \underbrace{ \left[\begin{array}{cc|c} 0 & 1 & 0 \\ 1 & -1 & 2\\\hline 3 & 0 & 1 \end{array}\right] }_{A_2} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-81ad23e553d3ac1f2251a084315e5637_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(28)\quad \begin{array}{l} {\rm LHS}= \left[\begin{array}{ccc} 0 & \alpha_{110} & \alpha_{210} \\ 1 & \alpha_{111} & \beta_{21}\\ 0 & \alpha_{120} & \alpha_{220} \end{array}\right] \left[\begin{array}{ccc} -\alpha_{111} & 1 & -\beta_{21} \\ 1 & 0 & 0\\ 0 & 0 & 1 \end{array}\right]\\ &= \left[\begin{array}{ccc} \alpha_{110} & 0 & \alpha_{210} \\ 0 & 1 & 0 \\ \alpha_{120} & 0 & \alpha_{220} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ff6b2af74632e3a4fd169e0966ea8151_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(29)\quad \begin{array}{l} {\rm RHS}=\\ & \left[\begin{array}{ccc} -\alpha_{111} & 1 & -\beta_{21} \\ 1 & 0 & 0\\ 0 & 0 & 1 \end{array}\right] \left[\begin{array}{ccc} 0 & 1 & 0 \\ \alpha_{110}+\beta_{21}\alpha_{120} & \alpha_{111} & \alpha_{210}+\beta_{21}\alpha_{220}\\ \alpha_{120} & 0 & \alpha_{220} \end{array}\right]\\ &= \left[\begin{array}{ccc} \alpha_{110} & 0 & \alpha_{210} \\ 0 & 1 & 0 \\ \alpha_{120} & 0 & \alpha_{220} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dc856f38b38aa12a6681d314436326e4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(30)\quad \begin{array}{l} &A_2=T_2A_1T_2^{-1}= \left[\begin{array}{ccc} 0 & 1 & 0 \\ 1 & -1 & 2\\ 3 & 0 & 1 \end{array}\right]\\ & B_2=T_2B_1= \left[\begin{array}{cc} 0 & 0 \\ 1 & -2 \\ 0 & 1 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d09264d70c8d356c3673229affb13c0e_l3.png)
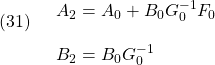
![Rendered by QuickLaTeX.com \displaystyle{(32)\quad \begin{array}{l} &A_0= \left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array}\right],\ B_0= \left[\begin{array}{cc} 0 & 0 \\ 1 & 0 \\ 0 & 1 \end{array}\right]\\ &F_0= \left[\begin{array}{cc|c} \alpha_{110} & \alpha_{111} & \alpha_{210}\\\hline \alpha_{120} & 0 & \alpha_{220} \end{array}\right] = \left[\begin{array}{cc|c} 7 & -1 & 4\\\hline 3 & 0 & 1 \end{array}\right]\\ &&G_0= \left[\begin{array}{cc} 1 & -\beta_{21} \\ 0 & 1 \end{array}\right] = \left[\begin{array}{cc} 1 & 2 \\ 0 & 1 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f7fac589e781be176791d6411cfa2b6f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(35)\quad \begin{array}{l} A_2-B_2F_2= \left[\begin{array}{ccc} 0 & 1 & 0 \\ -a_2' & -a_1' & 0\\ 0 & 0 & -a_3' \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b1fda1f343ed6a79a8ad37d75b7bcfa5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(40)\quad \begin{array}{l} \alpha_{ij}= \left\{\begin{array}{l} \left[\begin{array}{c} \alpha_{ij0} \\ \vdots \\ \alpha_{ij,n_j-1} \end{array}\right]\ (n_j\le n_i)\\ \left[\begin{array}{c} \alpha_{ij0} \\ \vdots \\ \alpha_{ij,n_i-1}\\ \beta_{ij} \\ 0_{n_j-n_i-1\times 1} \\ \end{array}\right]\ (j<i, n_j>n_i)\\ \left[\begin{array}{c} \alpha_{ij0} \\ \vdots \\ \alpha_{ij,n_i-1}\\ 0 \\ 0_{n_j-n_i-1\times 1} \\ \end{array}\right]\ (j>i, n_j>n_i) \end{array}\right. \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c23ae84821c038972864db04da0214c9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(41)\quad \begin{array}{l} A \underbrace{ \left[\begin{array}{c|c|c} B_1\ \cdots\ A^{n_1-1}B_1 & \cdots & B_m\ \cdots\ A^{n_m-1}B_m \end{array}\right] }_{T_1^{-1}}\\ =\underbrace{ \left[\begin{array}{c|c|c} B_1\ \cdots\ A^{n_1-1}B_1 & \cdots & B_m\ \cdots\ A^{n_m-1}B_m \end{array}\right] }_{T_1^{-1}}\\ \times \underbrace{ \left[\begin{array}{c|c|c} \begin{array}{c|c} \begin{array}{c} 0_{1\times n_1-1} \\ I_{n_1-1} \end{array} & \alpha_{11} \end{array} &\cdots & \begin{array}{c|c} 0_{n_1\times n_m-1} & \alpha_{m1} \end{array} \\\hline \vdots & \cdots & \vdots \\\hline \begin{array}{c|c} 0_{n_m\times n_1-1} & \alpha_{1m} \end{array} & \cdots & \begin{array}{c|c} \begin{array}{c} 0_{1\times n_m-1} \\ I_{n_m-1} \end{array} & \alpha_{mm} \end{array} \end{array}\right] }_{A_1}\\ B= \underbrace{ \left[\begin{array}{c|c|c} B_1\ \cdots\ A^{n_1-1}B_1 & \cdots & B_m\ \cdots\ A^{n_m-1}B_m \end{array}\right] }_{T_1^{-1}}\\ \times \underbrace{ \left[\begin{array}{c|c|c} \begin{array}{c} 1 \\ 0_{n_1-1\times1} \end{array} &\cdots & 0_{n_1\times1} \\\hline \vdots & \cdots & \vdots \\\hline 0_{n_m\times1} & \cdots & \begin{array}{c} 1 \\ 0_{n_m-1\times1} \end{array} \end{array}\right] }_{B_1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ba8411b7aefa63e3beacc9f736d8a5d3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(42)\quad \boxed{ \begin{array}{l} A_1=T_1AT_1^{-1}= \left[\begin{array}{c|c|c} \begin{array}{c|c} \begin{array}{c} 0_{1\times n_1-1} \\ I_{n_1-1} \end{array} & \alpha_{11} \end{array} &\cdots & \begin{array}{c|c} 0_{n_1\times n_m-1} & \alpha_{m1} \end{array} \\\hline \vdots & \cdots & \vdots \\\hline \begin{array}{c|c} 0_{n_m\times n_1-1} & \alpha_{1m} \end{array} & \cdots & \begin{array}{c|c} \begin{array}{c} 0_{1\times n_m-1} \\ I_{n_m-1} \end{array} & \alpha_{mm} \end{array} \end{array}\right]\\ B_1=T_1B= \left[\begin{array}{c|c|c} \begin{array}{c} 1 \\ 0_{n_1-1\times1} \end{array} &\cdots & 0_{n_1\times1} \\\hline \vdots & \ddots & \vdots \\\hline 0_{n_m\times1} & \cdots & \begin{array}{c} 1 \\ 0_{n_m-1\times1} \end{array} \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8e4adc89f2c6c1dc40584401f4d58d65_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(43)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c|c|c} \begin{array}{c|c} \begin{array}{c} 0_{1\times n_1-1} \\ I_{n_1-1} \end{array} & \alpha_{11} \end{array} &\cdots & \begin{array}{c|c} 0_{n_1\times n_m-1} & \alpha_{m1} \end{array} \\\hline \vdots & \cdots & \vdots \\\hline \begin{array}{c|c} 0_{n_m\times n_1-1} & \alpha_{1m} \end{array} & \cdots & \begin{array}{c|c} \begin{array}{c} 0_{1\times n_m-1} \\ I_{n_m-1} \end{array} & \alpha_{mm} \end{array} \end{array}\right] }_{A_1}\\ \times \underbrace{ \left[\begin{array}{ccc} L_{11} & \cdots & L_{m1} \\ \vdots & \cdots & \vdots \\ L_{1m} & \cdots & L_{mm} \end{array}\right] }_{T_2^{-1}} =\underbrace{ \left[\begin{array}{ccc} L_{11} & \cdots & L_{m1} \\ \vdots & \cdots & \vdots \\ L_{1m} & \cdots & L_{mm} \end{array}\right] }_{T_2^{-1}} \underbrace{ (A_0+B_0G_0^{-1}F_0) }_{A_2} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4fd1e3c6e397b538020d3db0dace632d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(44)\quad \begin{array}{l} L_{ii}=-\left[\begin{array}{ccc} S_{n_i}\alpha_{ii} & \cdots & S_{n_i}^{n_i}\alpha_{ii} \end{array}\right]+J_{n_1}\\ L_{ij}=-\left[\begin{array}{ccc} S_{n_j}\alpha_{ij} & \cdots & S_{n_j}^{n_i}\alpha_{ij} \end{array}\right]\\ S_\nu= \left[\begin{array}{cc} 0_{\nu-1\times 1} & I_{\nu-1}\\ 0 & 0_{1\times\nu-1} \end{array}\right] \\ J_\nu= \left[\begin{array}{ccc} 0 & \cdots & 1 \\ \vdots & \cdot & \vdots \\ 1 & \cdots & 0 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2e418066db7cccbf51e4cc7658f79c17_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(45)\quad \begin{array}{l} A_0= \left[\begin{array}{c|c|c} S_{n_1} & \cdots & 0_{n_1\times n_m} \\\hline \vdots & \ddots & \vdots \\\hline 0_{n_m\times n_1} & \cdots & S_{n_m} \end{array}\right]\\ B_0= \left[\begin{array}{c|c|c} \begin{array}{c} 0_{n_1-1\times 1} \\ 1 \end{array} & \cdots & 0_{n_1\times1} \\\hline \vdots & \ddots & \vdots \\\hline 0_{n_m\times1} & \cdots & \begin{array}{c} 0_{n_m-1\times 1} \\ 1 \end{array} \end{array}\right]\\ F_0= \left[\begin{array}{ccc|c|ccc} \bar\alpha_{110} & \cdots & \bar\alpha_{11,n_1-1} & \cdots & \bar\alpha_{m10} & \cdots & \bar\alpha_{m1,n_m-1}\\ \vdots & \cdots & \vdots & \cdots & \vdots & \cdots & \vdots \\ \bar\alpha_{1m0} & \cdots & \bar\alpha_{1m,n_1-1} & \cdots & \bar\alpha_{mm0} & \cdots & \bar\alpha_{mm,n_m-1}\\ \end{array}\right]\\ \bar\alpha_{ijk}= \left\{\begin{array}{ll} \alpha_{ijk} & (k\verb|<| n_j)\\ 0 & (k\ge n_j)\end{array}\right.\\ G_0=\left[\begin{array}{cccl} 1&\bar\beta_{21}&\cdots&\bar\beta_{m1}\\ 0&1&\ddots&\vdots\\ \vdots&\ddots&\ddots&\bar\beta_{m,m-1}\\ 0&0&\cdots&1\end{array}\right]\\ \bar\beta_{ij}=\left\{\begin{array}{ll} -\beta_{ij} &(n_j\ge n_i)\\ 0 &(n_j\verb|<|n_i) \end{array}\right. \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-32b1c40783488872664cb189555fb1d7_l3.png)
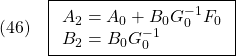
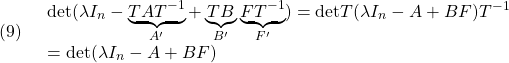
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{ll} {\rm rank}\, [\begin{array}{cccc} \underbrace{TB}_{B'} & \underbrace{TAT^{-1}}_{A'}\underbrace{TB}_{B'} & \cdots & \underbrace{(TAT^{-1})^{n-1}}_{A'^{n-1}}\underbrace{TB}_{B'} \end{array}] \\ ={\rm rank}\, T[\begin{array}{cccc} B & AB &\cdots & A^{n-1}B \end{array}]\\ ={\rm rank}\, [\begin{array}{cccc} B & AB &\cdots & A^{n-1}B \end{array}] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-608b923e2c31088baa89055db8bbcf5f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \boxed{ \left[\begin{array}{c} \dot{x}_1'(t) \\ \dot{x}_2'(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A_{\#} & X \\ 0 & A_k \end{array}\right] }_{TAT^{-1}} \left[\begin{array}{c} x_1'(t) \\ x_2'(t) \end{array}\right] + \underbrace{ \left[\begin{array}{c} B_{\#} \\ 0 \end{array}\right] }_{TB} u(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d045d7f6e58128cfb562afcad80f28e6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \left[\begin{array}{cc} T^TB & T^TAT \end{array}\right]= \left[\begin{array}{c|cccc|c} B_1 & A_1 & X & \cdots & X & X \\ 0 & B_2 & A_2 & \cdots & X & X \\ \vdots & & \ddots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & B_{k-1} & A_{k-1} & X \\ \hline 0 & 0 & \cdots & 0 & B_k & A_k \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2b8e62783604bcf64eef31f4d8a42b0b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \left[\begin{array}{c|cccc|c} B_1 & A_1-\lambda I_{m_1} & X & \cdots & X & X \\ 0 & B_2 & A_2-\lambda I_{m_2} & \cdots & X & X \\ \vdots & & \ddots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & B_{k-1} & A_{k-1}-\lambda I_{m_{k-1}} & X \\ \hline 0 & 0 & \cdots & 0 & B_k & A_k-\lambda I_{m_k} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-07d18a8741d94acb1d81ddaf19f9a337_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \Sigma^{(j)}= \left[\begin{array}{cc} \Sigma_1^{(j)} & 0 \\ 0 & 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a79928b336591d941023ec661933d6ad_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad A= \left[\begin{array}{ccc} 0 & 0 & 0 \\ 0 & -1 & 1 \\ 0 & 0 & 0 \end{array}\right] ,\ B= \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \\ 0 & 1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-474bab461a7a10da1d3931fc1fae01df_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad B^{(1)}= \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 1 \\ \frac{1}{\sqrt{2}} & 0 & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{array}\right] }_{U^{(1)}} \underbrace{ \left[\begin{array}{cc} \sqrt{2} & 0 \\ 0 & 1 \\ 0 & 0 \end{array}\right] }_{\Sigma^{(1)}} \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right]^T }_{V^{(1)T}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-46fba17a52676c6d9cace3cfbf263ce8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad A^{(2)}= \left[\begin{array}{cc|c} 0 & 0 & 1 \\ 0 & 0 & 0 \\ \hline 0 & 0 & -1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1562ebd0e8d3441e17c801dd71458311_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \begin{array}{l} \left[\begin{array}{cc} T^TB & T^TAT \end{array}\right]= \left[\begin{array}{ccc} B_1 & A_1 & X \\ 0 & B_2 & A_2 \end{array}\right]= \left[\begin{array}{cc|cc|c} 0 & \sqrt{2} & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 & -1 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f8026f4008095d9ddb2549a401bee577_l3.png)
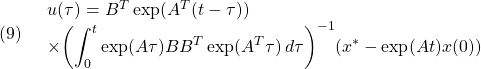
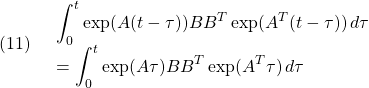
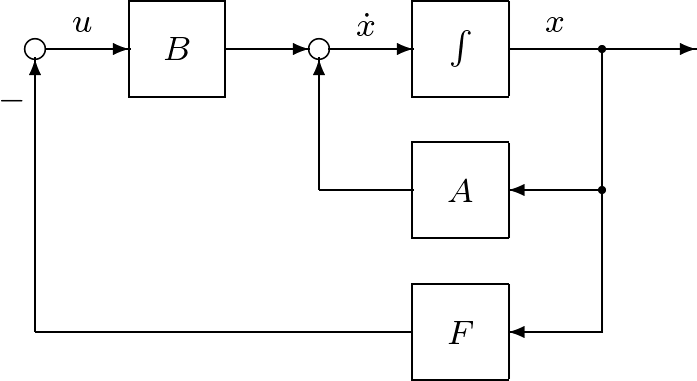 図1 状態フィードバックによる閉ループ系
図1 状態フィードバックによる閉ループ系![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} A_F^2+a_1'A_F+a_2'I_2=0\\ \quad\Downarrow\\ (A-BF)A_F+a_1'(A-BF)+a_2'I_2=0\\ \quad\Downarrow\\ AA_F-BFA_F+a_1'A-a_1'BF+a_2'I_2=0\\ \quad\Downarrow\\ A(A-BF)+a_1'A+a_2'I_2=BFA_F+a_1'BF\\ \quad\Downarrow\\ A^2+a_1'A+a_2'I_2=BF(A_F+a_1'I_2)+ABF\\ \quad\Downarrow\\ A^2+a_1'A+a_2'I_2=\left[\begin{array}{ccc} B &AB \end{array}\right] \left[\begin{array}{ccc} F(A_F+a_1'I_2)\\ F \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-58bb1c562247a773cc1edf865ae91cad_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} A_F^3+a_1'A_F^2+a_2'A_F+a_3'I_3=0\\ \quad\Downarrow\\ (A-BF)(A_F^2+a_1'A_F+a_2'I_3)+a_3'I_3=0\\ \quad\Downarrow\\ A(A_F^2+a_1'A_F+a_2'I_3)+a_3'I_3\\=BF(A_F^2+a_1'A_F+a_2'I_3)\\ \quad\Downarrow\\ A((A-BF)A_F+a_1'(A-BF)+a_2'I_3)+a_3'I_3\\=BF(A_F^2+a_1'A_F+a_2'I_3)\\ \quad\Downarrow\\ A^2(A-BF)+a_1'A^2+a_2'A+a_3'I_3\\ =BF(A_F^2+a_1'A_F+a_2'I_3)+ABF(A_F+a_1'I_3)\\ \quad\Downarrow\\ A^3+a_1'A^2+a_2'A+a_3'I_3\\ =BF(A_F^2+a_1'A_F+a_2'I_3)+ABF(A_F+a_1'I_3)+A^2BF\\ \quad\Downarrow\\ A^3+a_1'A^2+a_2'A+a_3'I_3\\ =\left[\begin{array}{ccc} B &AB&A^2B \end{array}\right] \left[\begin{array}{ccc} F(A_F^2+a_1'A_F+a_2'I_3)\\ F(A_F+a_1'I_3)\\ F \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2e1d5f3518704a7eb5ccf03446662208_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad %\begin{array}{l} A^n+a'_1A^{n-1}+\cdots+a'_nI_n =\left[\begin{array}{cccc} B & AB &\cdots & A^{n-1}B \end{array}\right] \left[\begin{array}{ccc} X_{n-1}\\ \vdots\\ X_1\\ F \end{array}\right] %\end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1a417bf647a9f2f3adebc7f2a80b6017_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \boxed{\begin{array}{l} F= \left[\begin{array}{cccc} 0 & \cdots & 0 & 1 \end{array}\right] \left[\begin{array}{cccc} B & AB &\cdots & A^{n-1}B \end{array}\right]^{-1}\\ \times (A^n+a'_1A^{n-1}+\cdots+a'_nI_n) \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fec91a15818dbf1db1e87f86c46972c1_l3.png)

![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \begin{equation} \frac{d}{dt} \left[\begin{array}{c} \theta_1\\ \theta_2\\ \dot\theta_1\\ \dot\theta_2\\ \end{array}\right]= \left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ a_1 & 0 & 0 & 0\\ 0 & a_2 & 0 & 0\\ \end{array}\right] \left[\begin{array}{c} \theta_1\\ \theta_2\\ \dot\theta_1\\ \dot\theta_2\\ \end{array}\right]+ \left[\begin{array}{c} 0\\ 0\\ b_1\\ b_2\\ \end{array}\right]\tau }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3a3fa72bbe74de9a255bf87116b40789_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{equation} \left[\begin{array}{cccc} B & AB & A^2B & A^3B \end{array}\right] = \left[\begin{array}{cccc} 0 &b_1 &0 &a_1b_1\\ 0 &b_2 &0 &a_2b_2\\ b_1&0 &a_1b_1 &0\\ b_2&0 &a_2b_2 &0\\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c96e667021ae4a5a4f1f35e8b5fc078e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1a)\quad \underbrace{ \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} 0 \\ K\omega_n^2 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2c38bce5a54dbe22b2c1cfbb9ac7882a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1b)\quad y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f5e291f6df4bf13c895efeb7714483d4_l3.png)
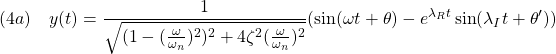
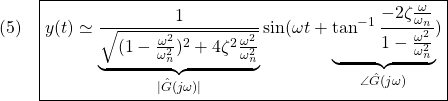
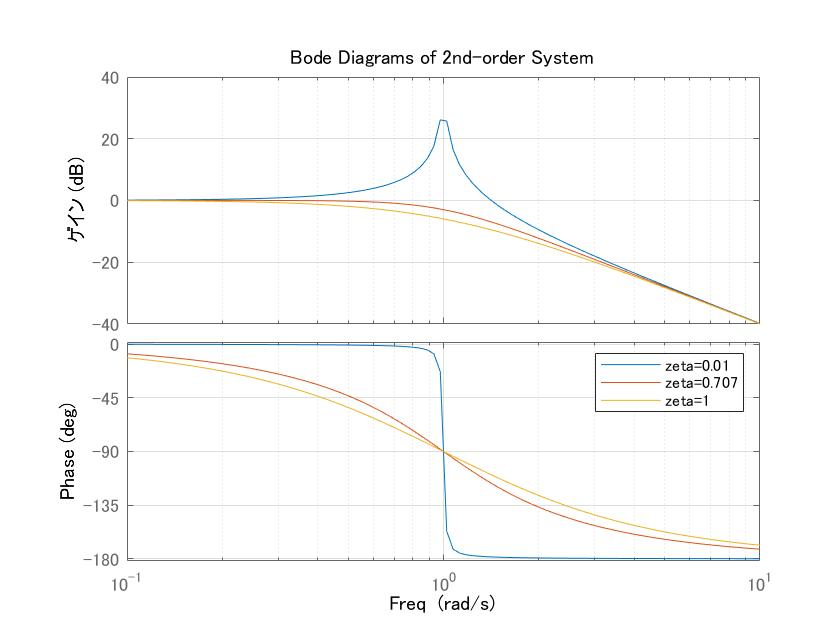 図1 2次系の周波数応答の比較
図1 2次系の周波数応答の比較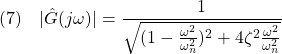
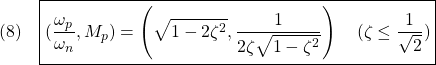
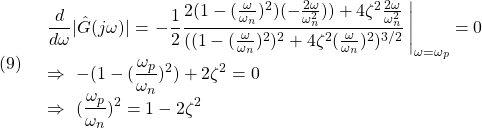
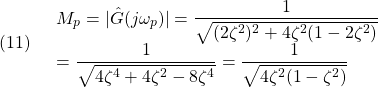
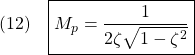
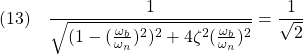
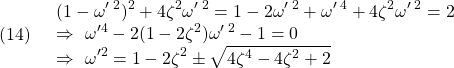
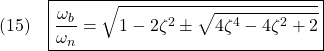
![Rendered by QuickLaTeX.com (5)\quad \begin{array}{l} \displaystyle{y(t)=\int_0^tC\exp(A(t-\tau))Be^{j\omega\tau}d\tau}\\ \displaystyle{=C\exp(At)\int_0^te^{j\omega\tau}\exp(-A\tau)Bd\tau}\\ \displaystyle{=C\exp(At)\int_0^t\exp(j\omega\tau I_n)\exp(-A\tau)Bd\tau}\\ \displaystyle{=C\exp(At)\int_0^t\exp((j\omega I_n-A)\tau)Bd\tau}\\ \displaystyle{=C\exp(At) \left[\frac{}{}\exp((j\omega I_n-A)\tau)\right]_0^t(j\omega I_n-A)^{-1}B}\\ \displaystyle{=C\exp(At) (\exp((j\omega I_n-A)t)-I_n)(j\omega I_n-A)^{-1}B}\\ \displaystyle{=-C\exp(At)(j\omega I_n-A)^{-1}B+C\exp(At)\exp(j\omega t I_n)\exp(-At)(j\omega I_n-A)^{-1}B}\\ \displaystyle{=-C\exp(At)(j\omega I_n-A)^{-1}B+C(j\omega I_n-A)^{-1}Be^{j\omega t}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cf72e1d083b5093019ffc1a9ae42a3ca_l3.png)
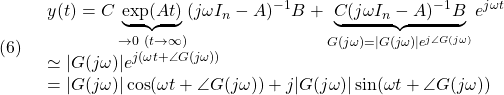
![Rendered by QuickLaTeX.com \displaystyle{(1a)\quad \underbrace{ \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b716bd0f77f40c082b3d8efd7314fe4f_l3.png)
![Rendered by QuickLaTeX.com (5)\quad \begin{array}{l} \displaystyle{y(t)=\int_0^t\frac{\omega_n^2}{\lambda_I}e^{\lambda_R(t-\tau)}\sin\lambda_I(t-\tau)\sin\omega\tau\,d\tau}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I}e^{\lambda_Rt}\sin\lambda_It\int_0^te^{-\lambda_R\tau}\sin\omega\tau\cos\lambda_I\tau\,d\tau}\\ \displaystyle{-\frac{\omega_n^2}{\lambda_I}e^{\lambda_Rt}\cos\lambda_It\int_0^te^{-\lambda_R\tau}\sin\omega\tau\sin\lambda_I\tau\,d\tau}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I}e^{\lambda_Rt}\sin\lambda_It\times}\\ \displaystyle{(\left[\frac{e^{-\lambda_R\tau}(-\lambda_R\sin(\omega+\lambda_I)\tau-(\omega+\lambda_I)\cos(\omega+\lambda_I)\tau)}{2(\lambda_R^2+(\omega+\lambda_I)^2)}\right.}\\ \displaystyle{+\left.\frac{e^{-\lambda_R\tau}(-\lambda_R\sin(\omega-\lambda_I)\tau-(\omega-\lambda_I)\cos(\omega-\lambda_I)\tau)}{2(\lambda_R^2+(\omega-\lambda_I)^2)}\right]_0^t)}\\ \displaystyle{-\frac{\omega_n^2}{\lambda_I}e^{\lambda_Rt}\cos\lambda_It\times}\\ \displaystyle{(\left[-\frac{e^{-\lambda_R\tau}(-\lambda_R\cos(\omega+\lambda_I)\tau+(\omega+\lambda_I)\sin(\omega+\lambda_I)\tau)}{2(\lambda_R^2+(\omega+\lambda_I)^2)}\right.}\\ \displaystyle{+\left.\frac{e^{-\lambda_R\tau}(-\lambda_R\cos(\omega-\lambda_I)\tau+(\omega-\lambda_I)\sin(\omega-\lambda_I)\tau)}{2(\lambda_R^2+(\omega-\lambda_I)^2)^2}\right]_0^t)}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I}e^{\lambda_Rt}\sin\lambda_It\times}\\ \displaystyle{(\frac{e^{-\lambda_Rt}(-\lambda_R\sin(\omega+\lambda_I)t-(\omega+\lambda_I)\cos(\omega+\lambda_I)t)+\omega+\lambda_I}{2(\lambda_R^2+(\omega+\lambda_I)^2)}}\\ \displaystyle{+\frac{e^{-\lambda_Rt}(-\lambda_R\sin(\omega-\lambda_I)t-(\omega-\lambda_I)\cos(\omega-\lambda_I)t)+\omega-\lambda_I}{2(\lambda_R^2+(\omega-\lambda_I)^2)})}\\ \displaystyle{-\frac{\omega_n^2}{\lambda_I}e^{\lambda_Rt}\cos\lambda_It\times}\\ \displaystyle{(\frac{-e^{-\lambda_Rt}(-\lambda_R\cos(\omega+\lambda_I)t+(\omega+\lambda_I)\sin(\omega+\lambda_I)t)-\lambda_R}{2(\lambda_R^2+(\omega+\lambda_I)^2)}}\\ \displaystyle{+\frac{e^{-\lambda_Rt}(-\lambda_R\cos(\omega-\lambda_I)t+(\omega-\lambda_I)\sin(\omega-\lambda_I)t)+\lambda_R}{2(\lambda_R^2+(\omega-\lambda_I)^2)})} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0862d7bcce2485ad411ad20ffd65abfd_l3.png)

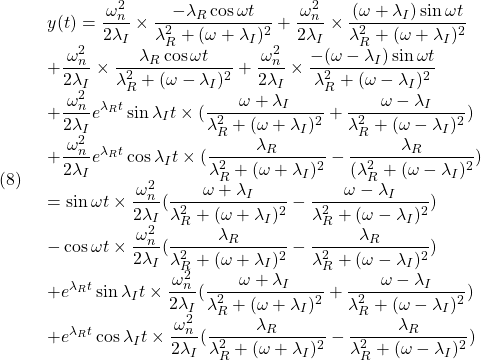
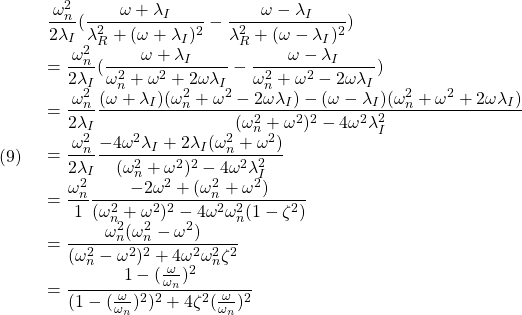
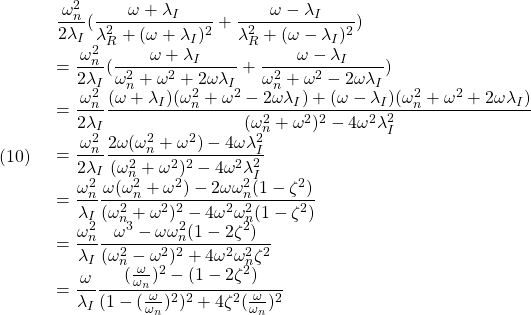
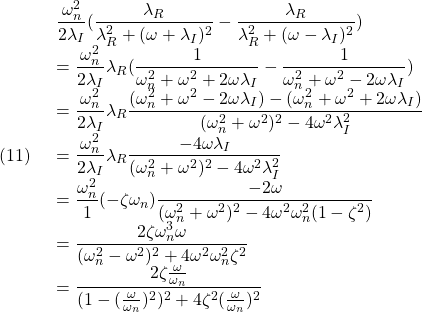
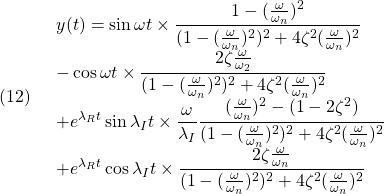
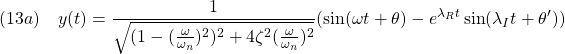
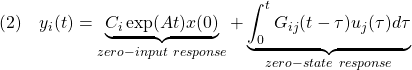
![Rendered by QuickLaTeX.com \displaystyle{(6a)\quad \underbrace{ \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} 0 \\ K\omega_n^2 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-163123fac605973ff5bb7e352fe8a4e4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6b)\quad y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c9800fcc5420d0c26c37f1aa628b4db9_l3.png)
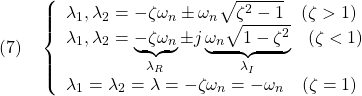
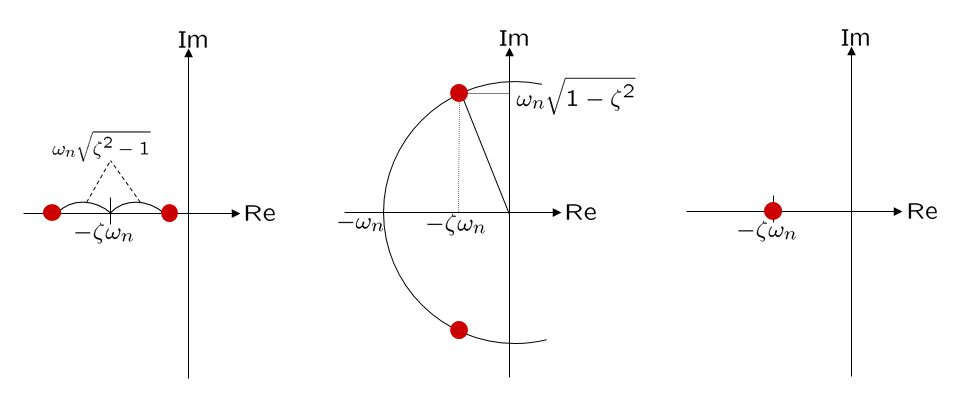 図1
図1 ![Rendered by QuickLaTeX.com (9)\quad \begin{array}{l} \displaystyle{S(t)=\int_0^tG(\tau)d\tau=\int_0^t\frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}(e^{\lambda_2\tau}-e^{\lambda_1\tau})d\tau}\\ \displaystyle{= \frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}\left[\frac{e^{\lambda_2\tau}}{\lambda_2}-\frac{e^{\lambda_1\tau}}{\lambda_1}\right]_0^t}\\ \displaystyle{=\frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}(\frac{e^{\lambda_2t}}{\lambda_2}-\frac{e^{\lambda_1t}}{\lambda_1})-\frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}(\frac{1}{\lambda_2}-\frac{1}{\lambda_1})}\\ \displaystyle{=1+\frac{1}{\lambda_2-\lambda_1}(\lambda_1e^{\lambda_2t}-\lambda_2e^{\lambda_1t})} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-71159c7ee47771d4db9ea63f64ac8347_l3.png)
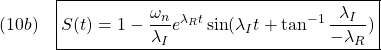
![Rendered by QuickLaTeX.com (12)\quad \begin{array}{l} \displaystyle{S(t)=\int_0^tG(\tau)d\tau=\int_0^t\frac{\omega_n^2}{\lambda_I}e^{\lambda_R\tau}\sin\lambda_I \tau d\tau}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I}\left[ \frac{e^{\lambda_R\tau}}{\lambda_R^2+\lambda_I^2}(\lambda_R\sin\lambda_I\tau-\lambda_I\cos\lambda_I\tau)\right]_0^t}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I}\frac{1}{\omega_n^2} (e^{\lambda_Rt}(\lambda_R\sin\lambda_It-\lambda_I\cos\lambda_It)+\lambda_I)}\\ \displaystyle{=1-\frac{\omega_n}{\lambda_I}e^{\lambda_Rt} (\sin\lambda_It\times\frac{-\lambda_R}{\omega_n}+\cos\lambda_It\times\frac{\lambda_I}{\omega_n})}\\ \displaystyle{=1-\frac{\omega_n}{\lambda_I}e^{\lambda_Rt} (\sin\lambda_It\cos\phi+\cos\lambda_It\sin\phi)}\\ \displaystyle{=1-\frac{\omega_n}{\lambda_I}e^{\lambda_Rt}\sin(\lambda_It+\phi) \quad(\phi=\tan^{-1}\frac{\lambda_I}{-\lambda_R})} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-70211d9c75bdadc0383d2b9c1b25fa64_l3.png)
![Rendered by QuickLaTeX.com (14)\quad \begin{array}{l} \displaystyle{S(t)=\int_0^tG(\tau)d\tau=\int_0^t\lambda^2\tau e^{\lambda\tau}d\tau}\\ \displaystyle{=\lambda^2\left[\tau \frac{1}{\lambda}e^{\lambda\tau}\right]_0^t -\lambda^2\int_0^t \frac{1}{\lambda}e^{\lambda\tau}d\tau}\\ \displaystyle{=\lambda te^{\lambda t}-\lambda\left[\frac{1}{\lambda}e^{\lambda\tau}\right]_0^t}\\ \displaystyle{=1+(\lambda t-1)e^{\lambda t}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f57dc1b1984646aeeeaafbb17bfcee60_l3.png)
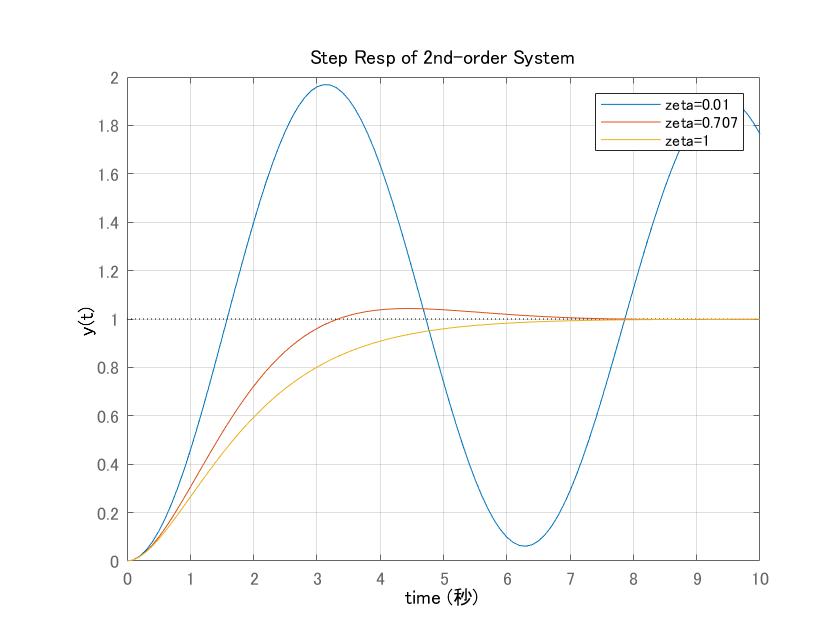 図2 2次系のステップ応答の比較
図2 2次系のステップ応答の比較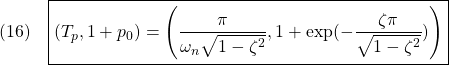
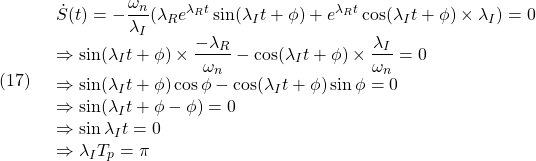
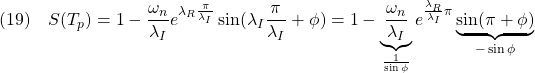
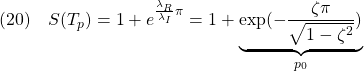
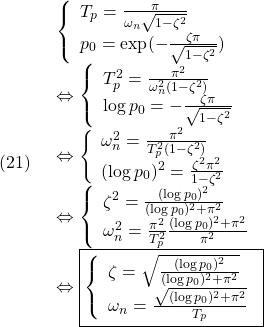
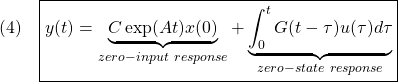
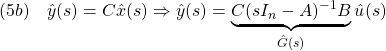
 図1 多変数系時間等応答の相互関係
図1 多変数系時間等応答の相互関係![Rendered by QuickLaTeX.com \displaystyle{(7a)\quad \boxed{\underbrace{ \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} 0 \\ K\omega_n^2 \end{array}\right] }_{B} u(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aa4b19afa6fbdeb818288fb5934edb63_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7b)\quad y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1ef77e878f73e539d8dc80f6688ac1a5_l3.png)
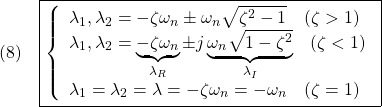
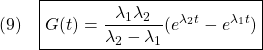
![Rendered by QuickLaTeX.com \displaystyle{(10a)\quad \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} = \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda_1 & \lambda_2 \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda_1& 0\\ 0 & \lambda_2 \end{array}\right] }_{\Lambda} \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda_1 & \lambda_2 \end{array}\right]^{-1} }_{V^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3cecd035fcbda6f346f77661cc428347_l3.png)
![Rendered by QuickLaTeX.com (11)\quad \begin{array}{l} \displaystyle{G(t)=C\exp(At)B=CV\exp(\Lambda t)V^{-1}B}\\ \displaystyle{ =\left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{cc} 1 & 1\\ \lambda_1 & \lambda_2 \end{array}\right] \left[\begin{array}{cc} e^{\lambda_1t}& 0\\ 0 & e^{\lambda_2t} \end{array}\right] \frac{1}{\lambda_2-\lambda_1} \left[\begin{array}{cc} \lambda_2 & -1\\ -\lambda_1 & 1 \end{array}\right] \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right]}\\ \displaystyle{ =\frac{\omega_n^2}{\lambda_2-\lambda_1} \left[\begin{array}{cc} e^{\lambda_1t}& e^{\lambda_2t} \end{array}\right] \left[\begin{array}{cc} -1\\ 1 \end{array}\right]}\\ \displaystyle{=\frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}(e^{\lambda_2t}-e^{\lambda_1t})} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1f10feaa91b2bb7d8913903cbd15b9c3_l3.png)
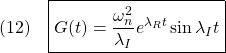
![Rendered by QuickLaTeX.com \displaystyle{(13a)\quad \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} = \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ \lambda_R & \lambda_I \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array}\right] }_{\Lambda} \underbrace{ \frac{1}{\lambda_I} \left[\begin{array}{cc} \lambda_I & 0 \\ -\lambda_R & 1 \end{array}\right] }_{V^{-1}}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-615266a9890c4e3022d07970c6f5f659_l3.png)
![Rendered by QuickLaTeX.com (14)\quad \begin{array}{l} \displaystyle{G(t)=C\exp(At)B=CV\exp(\Lambda t)V^{-1}B}\\ \displaystyle{=\left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{cc} 1 & 0\\ \lambda_R & \lambda_I \end{array}\right] e^{\lambda_R t} \left[\begin{array}{cc} \cos\lambda_I t & \sin\lambda_I t\\ \sin\lambda_I t & \cos\lambda_I t \end{array}\right] \frac{1}{\lambda_I} \left[\begin{array}{cc} \lambda_I & 0\\ -\lambda_R & 1 \end{array}\right] \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right]}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I} e^{\lambda_R t} \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{cc} \cos\lambda_I t & \sin\lambda_I t\\ \sin\lambda_I t & \cos\lambda_I t \end{array}\right] \left[\begin{array}{cc} 0\\ 1 \end{array}\right]}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I} e^{\lambda_R t}\sin\lambda_I t} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2f44bd53bbc94bd725169439890f6d6f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(16a)\quad \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} = \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda & \lambda+1 \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda & 1\\ 0 & \lambda \end{array}\right] }_{\Lambda} \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda & \lambda+1 \end{array}\right]^{-1} }_{V^{-1}}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8cd4b43f3e55efbc7942c5a68825fdd5_l3.png)
![Rendered by QuickLaTeX.com (17)\quad \begin{array}{l} \displaystyle{G(t)=C\exp(At)B=CV\exp(\Lambda t)V^{-1}B}\\ \displaystyle{= \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{cc} 1 & 1\\ \lambda & \lambda+1 \end{array}\right] e^{\lambda t} \left[\begin{array}{cc} 1 & t\\ 0 & 1 \end{array}\right] \frac{1}{\lambda+1-\lambda} \left[\begin{array}{cc} \lambda+1 & -1\\ -\lambda & 1 \end{array}\right] \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right]}\\ \displaystyle{= \omega_n^2 e^{\lambda t} \left[\begin{array}{cc} 1 & t+1 \end{array}\right] \left[\begin{array}{cc} -1\\ 1 \end{array}\right]}\\ \displaystyle{=\lambda^2te^{\lambda t}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-879b5bb9640f77dc6264c3509e6d3b66_l3.png)
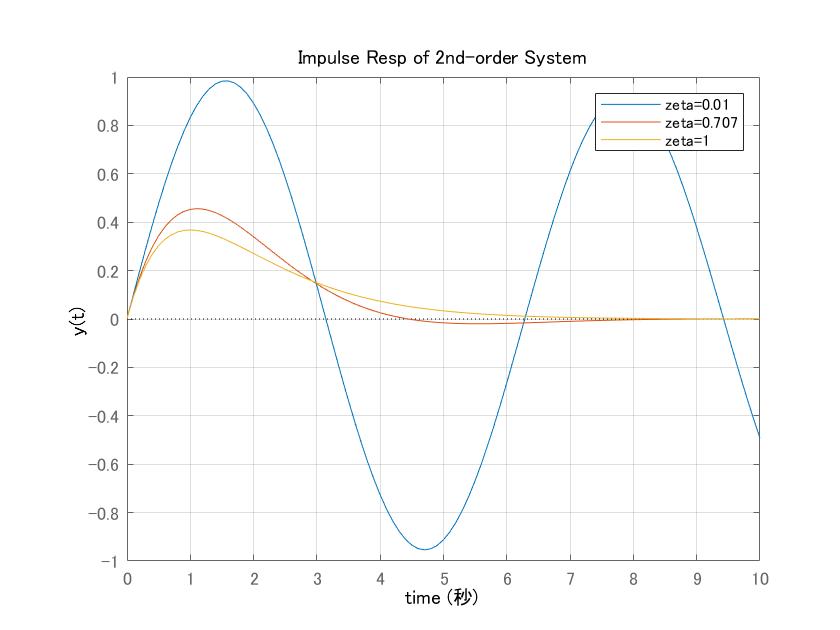 図3 2次系のインパルス応答の比較
図3 2次系のインパルス応答の比較
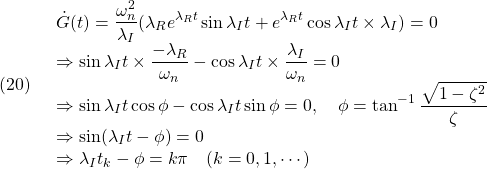
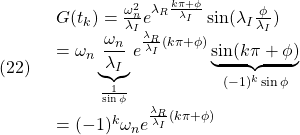
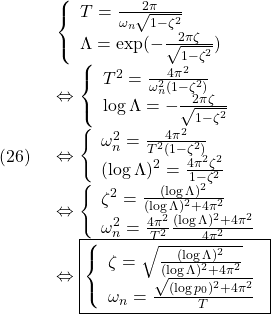
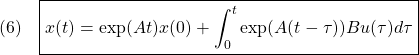
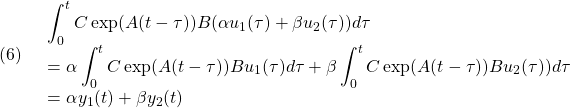

![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \underbrace{ \left[\begin{array}{l} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{3g}{4\ell}&-\frac{c}{J} \end{array}\right] }_{A=A_1} \underbrace{ \left[\begin{array}{l} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4b0ce9ec40944273a34f18d341b8adee_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{l} \theta(t)-\pi \\ \omega(t)-0 \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ \frac{3g}{4\ell}&-\frac{c}{J} \end{array}\right] }_{A=A_2} \underbrace{ \left[\begin{array}{l} \theta(t)-\pi \\ \omega(t)-0 \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-41c9758c694af6b502977f96707d2252_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \underbrace{ \left[\begin{array}{l} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{l} x_1(t) \\ x_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-046c4f6841329195eebc57253eb3c74e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \underbrace{ \left[\begin{array}{l} {x}_1(t) \\ {x}_2(t) \end{array}\right] }_{{x}(t)}= \underbrace{ \left[\begin{array}{cc} e^{a_{11}t} & 0 \\ 0 & e^{a_{22}t} \\ \end{array}\right] }_{\exp(At)} \underbrace{ \left[\begin{array}{l} x_1(0) \\ x_2(0) \end{array}\right] }_{x(0)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3fc962831e63a0a25061b8aa13a7e276_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \underbrace{ \left[\begin{array}{l} {y}_1(t) \\ {y}_2(t) \end{array}\right] }_{y(t)}= \underbrace{ \left[\begin{array}{cc} t_{11} & t_{12} \\ t_{21} & t_{22} \\ \end{array}\right] }_{T} \underbrace{ \left[\begin{array}{l} x_1(t) \\ x_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1f9192d4ccaf8b281f53ec8515bc7e4e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \underbrace{ \left[\begin{array}{l} {x}_1(t) \\ {x}_2(t) \end{array}\right] }_{x(t)}= \underbrace{ \left[\begin{array}{cc} v_{11} & v_{12} \\ v_{21} & v_{22} \\ \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{l} y_1(t) \\ y_2(t) \end{array}\right] }_{y(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c2d9dcfa810ad808ce73e74692c8a23e_l3.png)
![Rendered by QuickLaTeX.com (27)\quad \begin{array}{l} \displaystyle{{\rm det}(\lambda I_2-\left[\begin{array}{cc} 0 & 1 \\ -\frac{3g}{4\ell}&-\frac{c}{J} \end{array}\right]) =\lambda^2+\frac{c}{J}\lambda+\frac{3g}{4\ell}=0}\\ \displaystyle{\Rightarrow \lambda=\frac{1}{2}(-\frac{c}{J}\pm\sqrt{\frac{c^2}{J^2}-4\frac{3g}{4\ell}})} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-583dc0fe6afab483b2d75508fcda8317_l3.png)
![Rendered by QuickLaTeX.com (28)\quad \begin{array}{l} \displaystyle{{\rm det}(\lambda I_2-\left[\begin{array}{cc} 0 & 1 \\ \frac{3g}{4\ell}&-\frac{c}{J} \end{array}\right]) =\lambda^2+\frac{c}{J}\lambda-\frac{3g}{4\ell}=0}\\ \displaystyle{\Rightarrow \lambda=\frac{1}{2}(-\frac{c}{J}\pm\sqrt{\frac{c^2}{J^2}+4\frac{3g}{4\ell}})} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-99fa4cb16d7c26822049e462a9e29955_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(30)\quad \left[\begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array}\right]= \underbrace{\lambda_RI_2}_{X}+ \underbrace{\lambda_I \left[\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array}\right]}_{Y} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8472da3e29ace3b64c9ea7116ccbc33a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad \left[\begin{array}{cc} \lambda & 1 \\ 0 & \lambda \end{array}\right]= \underbrace{\lambda I_2}_{X}+ \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right]}_{Y} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dcdfdae4bb1e403c6e462b17b09f27aa_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4a)\quad A=\underbrace{\left[\begin{array}{cc} v_1 & v_2 \end{array}\right]}_{V} \underbrace{\left[\begin{array}{cc} \lambda_1 & 0 \\ 0 & \lambda_2 \end{array}\right]}_{\Lambda_1} \underbrace{\left[\begin{array}{cc} v_1 & v_2 \end{array}\right]^{-1}}_{V^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bb555c7741c2c5d90cef778c129e86b1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4b)\quad \begin{array}{l} A=\underbrace{\left[\begin{array}{cc} v_R+jv_I & v_R-jv_I \end{array}\right]}_{V} \left[\begin{array}{cc} \lambda_R+j\lambda_I & 0 \\ 0 & \lambda_R-j\lambda_I \end{array}\right]\\ \times\underbrace{\left[\begin{array}{cc} v_R+jv_I & v_R-jv_I \end{array}\right]^{-1}}_{V^{-1}}\\ =\underbrace{\left[\begin{array}{cc} v_R & v_I \end{array}\right]}_{V'} \underbrace{\left[\begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array}\right]}_{\Lambda_2} \underbrace{\left[\begin{array}{cc} v_R & v_I \end{array}\right]^{-1}}_{V'^{-1}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e0fbba71d2b00a6133e75ae5071cf18d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4c)\quad A=\underbrace{\left[\begin{array}{cc} v & v' \end{array}\right]}_{V} \underbrace{\left[\begin{array}{cc} \lambda & 1 \\ 0 & \lambda \end{array}\right]}_{\Lambda_3} \underbrace{\left[\begin{array}{cc} v & v' \end{array}\right]^{-1}}_{V^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-96f0aeda7d33e0892c1b3ae15b9c822f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5a)\quad \exp(A t)=\underbrace{\left[\begin{array}{cc} v_1 & v_2 \end{array}\right]}_{V} \underbrace{\left[\begin{array}{cc} e^{\lambda_1t} & 0 \\ 0 & e^{\lambda_2 t} \end{array}\right]}_{\exp(\Lambda_1 t)} \underbrace{\left[\begin{array}{cc} v_1 & v_2 \end{array}\right]^{-1}}_{V^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a2c20a571b582858c129f9525483fde7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5b)\quad \exp(A t)=\underbrace{\left[\begin{array}{cc} v_R & v_I \end{array}\right]}_{V'} \underbrace{e^{\lambda_R t} \left[\begin{array}{cc} \cos(\lambda_It) & \sin(\lambda_It) \\ -\sin(\lambda_It) & \cos(\lambda_It) \end{array}\right]}_{\exp(\Lambda_2 t)} \underbrace{\left[\begin{array}{cc} v_R & v_I \end{array}\right]^{-1}}_{V'^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e2598816f3c649ae154eb107c7bd9756_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5c)\quad \exp(A t)=\underbrace{\left[\begin{array}{cc} v & v' \end{array}\right]}_{V} \underbrace{e^{\lambda t} \left[\begin{array}{cc} 1 & t \\ 0 & 1 \end{array}\right]}_{\exp(\Lambda_3 t)} \underbrace{\left[\begin{array}{cc} v & v' \end{array}\right]^{-1}}_{V^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1ccd3c10da477fac06071a60073df28c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6a)\quad \begin{array}{l} x(t)=\underbrace{\left[\begin{array}{cc} v_1 & v_2 \end{array}\right]}_{V} \underbrace{\left[\begin{array}{cc} e^{\lambda_1t} & 0 \\ 0 & e^{\lambda_2 t} \end{array}\right]}_{\exp(\Lambda_1 t)} \underbrace{\left[\begin{array}{cc} v_1 & v_2 \end{array}\right]^{-1}x(0)}_{\left[\begin{array}{c} c_1\\c_2 \end{array}\right]}\\ =c_1e^{\lambda_1t}v_1+c_2e^{\lambda_2t}v_2 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b73bdf17802abab8139590333ce5ddc8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6b)\quad \begin{array}{l} x(t)=\underbrace{\left[\begin{array}{cc} v_R & v_I \end{array}\right]}_{V'} \underbrace{e^{\lambda_R t} \left[\begin{array}{cc} \cos(\lambda_It) & \sin(\lambda_It) \\ -\sin(\lambda_It) & \cos(\lambda_It) \end{array}\right]}_{\exp(\Lambda_2 t)} \underbrace{\left[\begin{array}{cc} v_R & v_I \end{array}\right]^{-1}x(0)}_{\left[\begin{array}{c} c_1\\c_2 \end{array}\right]}\\ =c_1e^{\lambda_Rt}(\cos(\lambda_It)v_R-\sin(\lambda_It)v_I)+c_2e^{\lambda_Rt}(\sin(\lambda_It)v_R+\cos(\lambda_It)v_I) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-68447de2b9180ed5ba5e49bac88f6ad3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6c)\quad \begin{array}{l} x(t)=\underbrace{\left[\begin{array}{cc} v & v' \end{array}\right]}_{V} \underbrace{e^{\lambda t} \left[\begin{array}{cc} 1 & t \\ 0 & 1 \end{array}\right]}_{\exp(\Lambda_3 t)} \underbrace{\left[\begin{array}{cc} v & v' \end{array}\right]^{-1}x(0)}_{\left[\begin{array}{c} c_1\\c_2 \end{array}\right]}\\ =c_1e^{\lambda t}v+c_2e^{\lambda t}(tv+v') \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a89702614e30351370d03c8a88ab2200_l3.png)