状態オブザーバ…Homework
[1] 状態フィードバックは、すべての状態変数の変化を捉えてフィードバックするので、この意味で最強の手段ですが、一般には絵に描いた餅ですと言ったら驚くでしょうか?これは実際にはすべての状態変数にセンサを配置できるわけではないからです。でもちょっと待ってください。状態方程式が分かっているのですから、これを計算機内で解いてやれば良いのではないでしょうか?そのアイデアを図1に示します。
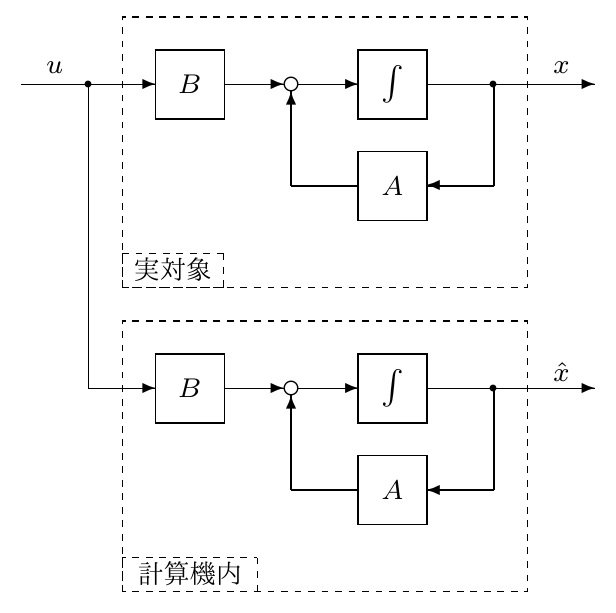 図1 状態オブザーバの考え方(1)
図1 状態オブザーバの考え方(1)
●いま制御対象の状態空間表現を
![]()
とします。これを計算機で解きますが、その状態と出力を区別して
![]()
で表します。(2)から(1)の第1式どうしを辺々引くと
![]()
を得ます。ここで![]() が安定行列でない限り
が安定行列でない限り
![]()
とはなりません。
●そこで、図2に示すような工夫が行われました。
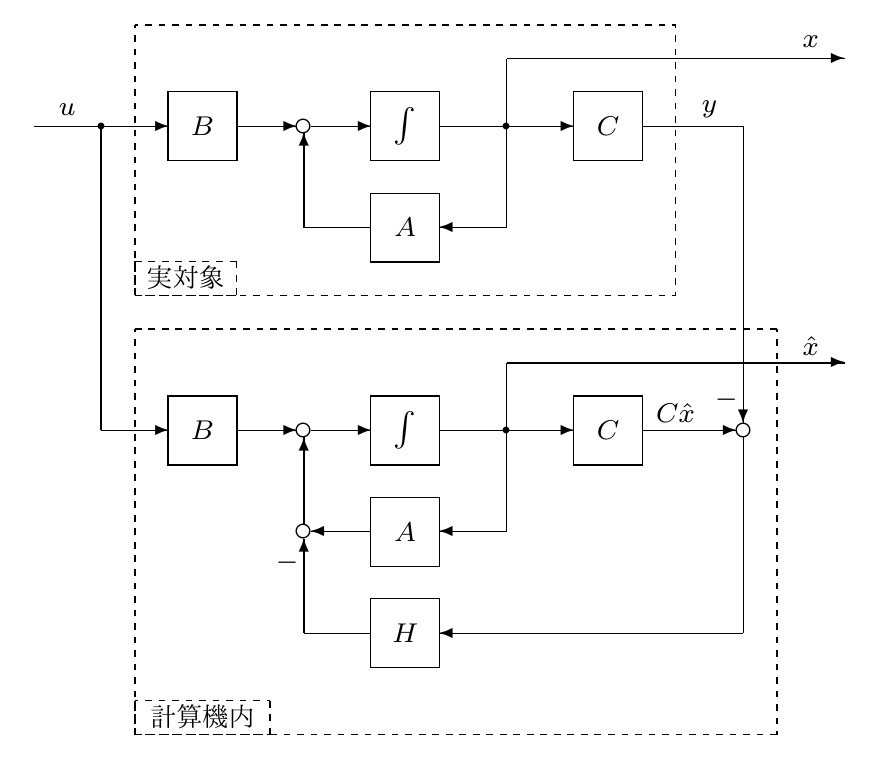 図2 状態オブザーバの考え方(2)
図2 状態オブザーバの考え方(2)
(2)の状態方程式に次のような補正項を加えます。
![]()
すなわち
![]()
ここで、![]() は適合するサイズを持つ行列です。(6)から(1)の第1式どうしを辺々引くと
は適合するサイズを持つ行列です。(6)から(1)の第1式どうしを辺々引くと
![]()
を得ます。ここで![]() が安定行列であるとすると
が安定行列であるとすると
![]()
が成り立ちます。すなわち(6)の状態![]() は、制御対象の状態
は、制御対象の状態![]() を漸近的に推定することができます。
を漸近的に推定することができます。![]() が安定行列である(6)を状態オブザーバ、行列
が安定行列である(6)を状態オブザーバ、行列![]() をオブザーバゲインと呼びます。
をオブザーバゲインと呼びます。
さて、任意の正方行列![]() に対して
に対して![]() であることに注意して
であることに注意して
![]()
が成り立ちます。これから![]() を安定行列とするためには、状態方程式
を安定行列とするためには、状態方程式
![]()
に対する状態フィードバック
![]()
による閉ループ系が
![]()
となるので、これを安定化する(12)を求めて、オブザーバゲイン![]() を決定すればよいことが分かります。
を決定すればよいことが分かります。
状態方程式(10)をもつ物理系は存在せず、双対システムと呼ばれる仮想的なシステムであり、このシステムに対する状態フィードバック(11)の設計を通して、状態オブザーバの設計ができることになります。
[2] モータの状態方程式
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \left[\begin{array}{c} \dot{\theta}(t)\\ \dot{\omega}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -\frac{1}{T_m} \end{array}\right] }_{A} \left[\begin{array}{c} \theta(t)\\ \omega(t) \end{array}\right]+ \underbrace{ \left[\begin{array}{c} 0\\ \frac{1}{K_ET_m} \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a95eaa65d14cb9fd7e4b2c26e0599949_l3.png)
と出力方程式
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \left[\begin{array}{c} \theta(t)\\ \omega(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b3827f897e0c0c4d4bd29eb0213d28ef_l3.png)
に対する状態オブザーバ
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \left[\begin{array}{c} \dot{\hat{\theta}}(t)\\ \dot{\hat{\omega}}(t) \end{array}\right] =(A-HC) \left[\begin{array}{c} \hat{\theta}(t)\\ \hat{\omega}(t) \end{array}\right] +Bu(t)+Hy(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d8751c5f7f39274e29ad827c0d037478_l3.png)
を、![]() の固有値が
の固有値が
![]()
となるようにオブザーバゲイン![]() を求めます。ここでは
を求めます。ここでは
![]()
における係数比較から直接求めてみます。
![]()
を(17)に代入して
![Rendered by QuickLaTeX.com \displaystyle{(19)\quad \begin{array}{l} \det \left[\begin{array}{cc} \lambda+h_1 & -1 \\ h_2 & \lambda+\frac{1}{T_m} \end{array}\right]\\ =(\lambda+h_1)(\lambda+\frac{1}{T_m})+h_2\\ =\lambda^2+(h_1+\frac{1}{T_m})\lambda+h_1\frac{1}{T_m}+h_2\\ =\lambda^2+2\alpha\frac{1}{T_m}\lambda+(\alpha\frac{1}{T_m})^2\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7385eb112c8af51a54d93f1ffabef5d1_l3.png)
ここで係数比較により次式を得ます。
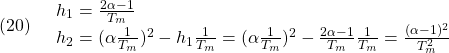
これらから定まるオブザーバゲイン![]() を用いて、状態オブザーバは次式のように構成されます。
を用いて、状態オブザーバは次式のように構成されます。
![Rendered by QuickLaTeX.com \displaystyle{(21)\quad \begin{array}{l} \left[\begin{array}{c} \dot{\hat{\theta}}(t)\\ \dot{\hat{\omega}}(t) \end{array}\right] =\underbrace{ \left[\begin{array}{cc} -\frac{2\alpha-1}{T_m} & 1 \\ -\frac{(\alpha-1)^2}{T_m^2} & -\frac{1}{T_m} \end{array}\right] }_{A-HC} \left[\begin{array}{c} \hat{\theta}(t)\\ \hat{\omega}(t) \end{array}\right] +\underbrace{ \left[\begin{array}{c} 0\\ \frac{1}{K_ET_m} \end{array}\right] }_{B}u(t)\\ + \underbrace{\left[\begin{array}{c} \frac{2\alpha-1}{T_m} \\ \frac{(\alpha-1)^2}{T_m^2} \end{array}\right] }_{H}y(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b514337c82c45e6315198b0db3388da8_l3.png)
●次図は![]() 、
、![]() の下で、
の下で、![]() と変えたとき、状態オブザーバが真の状態を推定する様子をシミュレーションしています。
と変えたとき、状態オブザーバが真の状態を推定する様子をシミュレーションしています。
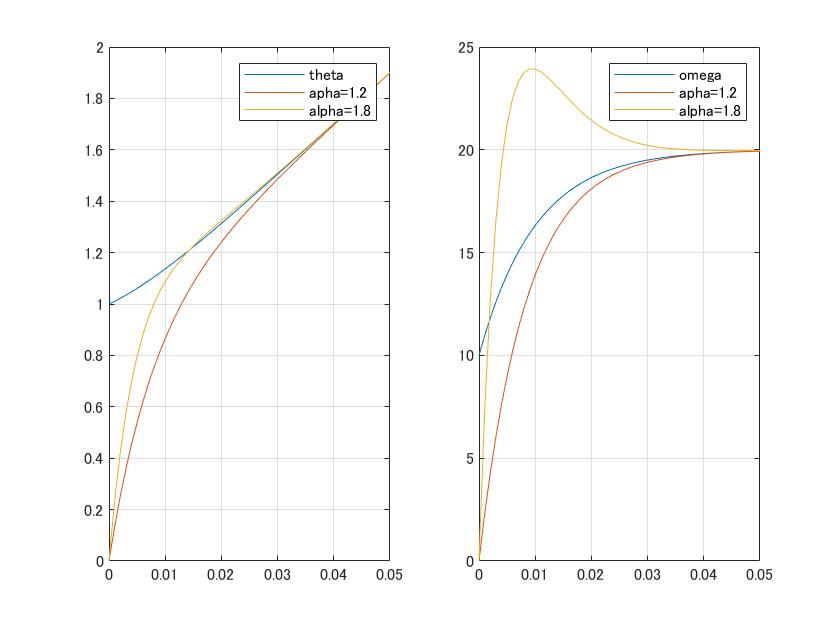 図3 状態推定の例
図3 状態推定の例
演習 A41…Flipped Classroom
次のコードを用いて図3のグラフを描け。
| MATLAB |
|
| SCILAB |
|
[3] ![]() 次系
次系
![]()
に対する状態フィードバック![]() は、状態オブザーバを用いて、次のように実施されます。
は、状態オブザーバを用いて、次のように実施されます。
![]()
すなわち
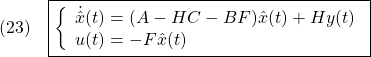
これをオブザーバベースコントローラと呼びます。ここで、![]() と
と![]() は安定行列ですが、
は安定行列ですが、![]() が安定行列と限らないことに注意してください。また、
が安定行列と限らないことに注意してください。また、
![]()
とおくとき、オブザーバベースコントローラは次式でも表せることに注意してください。
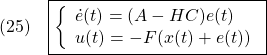
さて、オブザーバベースコントローラ(23)による閉ループ系は次式となります。
![]()
ここで、座標変換
![]()
を行うと、
![]()
に注意して、閉ループ系の状態方程式として、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(29)\quad \boxed{\left[\begin{array}{c} \dot{x}(t) \\ \dot{e}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A-BF & -BF \\ 0 & A-HC \end{array}\right] }_{A_{CL}} \left[\begin{array}{c} x(t) \\ e(t) \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8c6ec4764b02f704e5faf2444cdf4250_l3.png)
したがって、![]() の固有値は、
の固有値は、![]() と
と![]() の固有値からなり、オブザーバベースコントローラによる閉ループ系は漸近安定であることが分かります。このことは状態フィードバックゲイン
の固有値からなり、オブザーバベースコントローラによる閉ループ系は漸近安定であることが分かります。このことは状態フィードバックゲイン![]() の設計は状態オブザーバゲイン
の設計は状態オブザーバゲイン![]() の設計とは独立して行ってよいことを意味しており、大変重要な性質(分離定理)として知られています。
の設計とは独立して行ってよいことを意味しており、大変重要な性質(分離定理)として知られています。