漸近安定性…Homework
[0] 次図に示すように軸支された剛体振り子は2つの静止した平衡状態(![]() )と(
)と(![]() )を持ちます。
)を持ちます。

いまこの平衡状態から棒を少し傾けて手を離すと、明らかに違った振舞いをします。実際には軸回りの摩擦や空気抵抗による抗力があるので、平衡状態(![]() )の方は元に戻りますが、平衡状態(
)の方は元に戻りますが、平衡状態(![]() )の方は元に戻ることなく平衡状態(
)の方は元に戻ることなく平衡状態(![]() )に落ち着くでしょう。前者を漸近安定、後者を不安定とよびます。このような違いは平衡状態回りでの振舞いを表す線形状態方程式にどのように反映されているのか気になるところです。
)に落ち着くでしょう。前者を漸近安定、後者を不安定とよびます。このような違いは平衡状態回りでの振舞いを表す線形状態方程式にどのように反映されているのか気になるところです。
●この場合の運動方程式は次式となります。
![]()
ここで、右辺の第2項が角速度に比例する抗力を表しています(![]() は定数)。これから平衡状態(
は定数)。これから平衡状態(![]() )と(
)と(![]() )に応じて次の状態方程式を得ます。
)に応じて次の状態方程式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \underbrace{ \left[\begin{array}{l} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{3g}{4\ell}&-\frac{c}{J} \end{array}\right] }_{A=A_1} \underbrace{ \left[\begin{array}{l} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4b0ce9ec40944273a34f18d341b8adee_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{l} \theta(t)-\pi \\ \omega(t)-0 \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ \frac{3g}{4\ell}&-\frac{c}{J} \end{array}\right] }_{A=A_2} \underbrace{ \left[\begin{array}{l} \theta(t)-\pi \\ \omega(t)-0 \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-41c9758c694af6b502977f96707d2252_l3.png)
以下では、行列![]() の固有値を調べて、漸近安定かどうかを判定できることを説明します。
の固有値を調べて、漸近安定かどうかを判定できることを説明します。
[1] 制御対象が平衡状態にあることは線形状態方程式![]() において、
において、![]() を意味します。そこで平衡状態が乱されて
を意味します。そこで平衡状態が乱されて![]() となる時刻を
となる時刻を![]() にとると、線形状態方程式は次式となります。
にとると、線形状態方程式は次式となります。
![]()
漸近安定であることは平衡状態![]() に戻ることでしたから、次のように表すことができます。
に戻ることでしたから、次のように表すことができます。
![]()
そのための条件を検討するため、微分方程式![]() の解を求める必要があります。これは次式で表されます(Note A21-1参照)。
の解を求める必要があります。これは次式で表されます(Note A21-1参照)。
![]()
ここで、![]() は
は![]() 次元ベクトル、
次元ベクトル、![]() は
は![]() 次正方行列です。任意の
次正方行列です。任意の![]() 次正方行列
次正方行列![]() に対して、行列指数関数
に対して、行列指数関数![]() は
は
![]()
で定義されます。そこで、解の表現式(6)を![]() の場合について詳しく説明します。
の場合について詳しく説明します。
[2] いま2次系に限定して、微分方程式![]() を要素を明示して書くと
を要素を明示して書くと
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \underbrace{ \left[\begin{array}{l} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{l} x_1(t) \\ x_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-046c4f6841329195eebc57253eb3c74e_l3.png)
すなわち
![]()
となります。もし![]() が対角行列で、
が対角行列で、![]() であれば
であれば
![]()
となって、解は
![]()
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \underbrace{ \left[\begin{array}{l} {x}_1(t) \\ {x}_2(t) \end{array}\right] }_{{x}(t)}= \underbrace{ \left[\begin{array}{cc} e^{a_{11}t} & 0 \\ 0 & e^{a_{22}t} \\ \end{array}\right] }_{\exp(At)} \underbrace{ \left[\begin{array}{l} x_1(0) \\ x_2(0) \end{array}\right] }_{x(0)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3fc962831e63a0a25061b8aa13a7e276_l3.png)
ですから、解の表現式(6)は納得できると思います。
[3] それでは![]() が対角行列でない場合はどうするかですが、一対一対応の変数変換
が対角行列でない場合はどうするかですが、一対一対応の変数変換
![]()
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \underbrace{ \left[\begin{array}{l} {y}_1(t) \\ {y}_2(t) \end{array}\right] }_{y(t)}= \underbrace{ \left[\begin{array}{cc} t_{11} & t_{12} \\ t_{21} & t_{22} \\ \end{array}\right] }_{T} \underbrace{ \left[\begin{array}{l} x_1(t) \\ x_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1f9192d4ccaf8b281f53ec8515bc7e4e_l3.png)
を考えます。またこの逆変換を次式で表しておきます。
![]()
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \underbrace{ \left[\begin{array}{l} {x}_1(t) \\ {x}_2(t) \end{array}\right] }_{x(t)}= \underbrace{ \left[\begin{array}{cc} v_{11} & v_{12} \\ v_{21} & v_{22} \\ \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{l} y_1(t) \\ y_2(t) \end{array}\right] }_{y(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c2d9dcfa810ad808ce73e74692c8a23e_l3.png)
ここで、![]() が成り立つので、
が成り立つので、![]() は
は![]() の逆行列
の逆行列![]() (
(![]() )となっています。逆行列をもつ行列は正則行列と呼ばれます。
)となっています。逆行列をもつ行列は正則行列と呼ばれます。
すなわち、微分方程式![]() に対して、正則行列
に対して、正則行列![]() による変数変換
による変数変換![]() を行ないます。
を行ないます。![]() (
(![]() )と両辺を微分した
)と両辺を微分した![]() を代入して次を得ます。
を代入して次を得ます。
![]()
この変換された行列![]() をできるだけ対角化します。その議論は、線形代数において
をできるだけ対角化します。その議論は、線形代数において![]() を標準形とする方法として学びました。もし
を標準形とする方法として学びました。もし![]() を求めることができると
を求めることができると
![]()
となって、漸近安定性(5)の判定は、
![]()
の判定に帰着されます。ここで、収束先の![]() は
は![]() 次の零行列です。
次の零行列です。
[4] さて、2次行列の標準形は次の3つに分類されます。
![]()
![]()
![]()
ここで、![]() は虚数単位
は虚数単位![]() 、
、![]() 、
、![]() 、
、![]() はすべて実数です。また任意の
はすべて実数です。また任意の![]() 次正方行列
次正方行列![]() に対する行列式を
に対する行列式を![]() で表すと
で表すと
![]()
すなわち、![]() は行列
は行列![]() の固有値の集合です。
の固有値の集合です。![]() は特性多項式と呼ばれます。
は特性多項式と呼ばれます。
上の3種類の![]() について
について![]() を具体的に計算してみます。その結果は次式となります。
を具体的に計算してみます。その結果は次式となります。
![]()
![]()
![]()
したがって、漸近安定性(5)すなわち(19)が成り立つのは、(24)のとき![]() かつ
かつ![]() 、(25)のとき
、(25)のとき![]() 、(26)のとき
、(26)のとき![]() であることがわかると思います。したがって、
であることがわかると思います。したがって、
漸近安定性のための条件は行列![]() のすべての固有値の実部が負であること
のすべての固有値の実部が負であること
です。対偶をとれば、一つでも実部が負の固有値があれば不安定と判定します。実部が負の固有値を安定固有値、実部が非負の固有値を不安定固有値と呼びます。
●この漸近安定性の条件は、高次系についても同様に成り立ちます(Note A21-2を参照)。
●上の剛体振り子の場合の漸近安定性を判定するために行列![]() の固有値を調べてみます。まず、平衡状態(
の固有値を調べてみます。まず、平衡状態(![]() )の場合、次式を得ます。
)の場合、次式を得ます。
![Rendered by QuickLaTeX.com (27)\quad \begin{array}{l} \displaystyle{{\rm det}(\lambda I_2-\left[\begin{array}{cc} 0 & 1 \\ -\frac{3g}{4\ell}&-\frac{c}{J} \end{array}\right]) =\lambda^2+\frac{c}{J}\lambda+\frac{3g}{4\ell}=0}\\ \displaystyle{\Rightarrow \lambda=\frac{1}{2}(-\frac{c}{J}\pm\sqrt{\frac{c^2}{J^2}-4\frac{3g}{4\ell}})} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-583dc0fe6afab483b2d75508fcda8317_l3.png)
これから行列![]() の固有値の実部は必ず負となります(根号内が負の場合は明らか、正の場合は根号を開いても
の固有値の実部は必ず負となります(根号内が負の場合は明らか、正の場合は根号を開いても![]() より小)。したがって、平衡状態(
より小)。したがって、平衡状態(![]() )は漸近安定と判定できます。
)は漸近安定と判定できます。
次に、平衡状態(![]() )の場合、次式を得ます。
)の場合、次式を得ます。
![Rendered by QuickLaTeX.com (28)\quad \begin{array}{l} \displaystyle{{\rm det}(\lambda I_2-\left[\begin{array}{cc} 0 & 1 \\ \frac{3g}{4\ell}&-\frac{c}{J} \end{array}\right]) =\lambda^2+\frac{c}{J}\lambda-\frac{3g}{4\ell}=0}\\ \displaystyle{\Rightarrow \lambda=\frac{1}{2}(-\frac{c}{J}\pm\sqrt{\frac{c^2}{J^2}+4\frac{3g}{4\ell}})} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-99fa4cb16d7c26822049e462a9e29955_l3.png)
これから行列![]() の固有値は実数となり、一つは正、他は負となります。したがって、平衡状態(
の固有値は実数となり、一つは正、他は負となります。したがって、平衡状態(![]() )は漸近安定ではないと判定できます。
)は漸近安定ではないと判定できます。
実は2次系の場合特性多項式の係数がすべて正であることが、漸近安定であるための条件であることがラウスフルビッツの判定法として知られています。
演習A21-1…Flipped Classroom
![]() 行列指数関数について次の指数法則が成り立つことを示せ。
行列指数関数について次の指数法則が成り立つことを示せ。
![]()
![]() 行列指数関数の定義から、(24)を示せ。
行列指数関数の定義から、(24)を示せ。
![]() 行列指数関数の定義から、次式を用いて、(25)を示せ。
行列指数関数の定義から、次式を用いて、(25)を示せ。
![Rendered by QuickLaTeX.com \displaystyle{(30)\quad \left[\begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array}\right]= \underbrace{\lambda_RI_2}_{X}+ \underbrace{\lambda_I \left[\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array}\right]}_{Y} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8472da3e29ace3b64c9ea7116ccbc33a_l3.png)
![]() 行列指数関数の定義から、次式を用いて、(26)を示せ。
行列指数関数の定義から、次式を用いて、(26)を示せ。
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad \left[\begin{array}{cc} \lambda & 1 \\ 0 & \lambda \end{array}\right]= \underbrace{\lambda I_2}_{X}+ \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right]}_{Y} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dcdfdae4bb1e403c6e462b17b09f27aa_l3.png)
演習A21-2…Flipped Classroom
与えられた行列![]() に基づいて漸近安定性を調べるプログラムを次に示す。行列
に基づいて漸近安定性を調べるプログラムを次に示す。行列![]() を実部が大きな順に表示されるように改良せよ。
を実部が大きな順に表示されるように改良せよ。
| MATLAB |
|
| SCILAB |
|
Note A21-1 自由系の時間応答
![]() 次自由系を表す微分方程式
次自由系を表す微分方程式
![]()
の解は
![]()
と表されます。これが解であることは元の微分方程式に代入すればすぐに確かめられ、また次のようにして導くことができます。
元の微分方程式を
![]()
と書いて、左から積分因数と呼ばれる![]() をかけると
をかけると
![]()
すなわち
![]()
したがって、![]() を定数ベクトルとして
を定数ベクトルとして
![]()
ここで、![]() とおくと
とおくと![]() は初期値
は初期値![]() に等しいので
に等しいので
![]()
と表されます。
Note A21-2 高次系の漸近安定性
●行列指数関数を用いると、微分方程式
![]()
の解は次のように表されます。
![]()
ここで
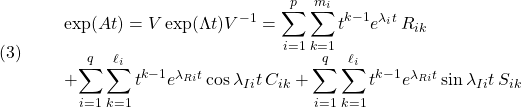
と書けることに注意します(![]() は適当な
は適当な![]() 次実正方行列)。
次実正方行列)。
したがって、任意の![]() に対して、
に対して、![]() のとき
のとき![]() となるための条件は
となるための条件は
![]()
となります。これは![]() のすべての固有値の実部が負を意味します。
のすべての固有値の実部が負を意味します。
●![]() (
(![]() )の解のグラフを見ると、
)の解のグラフを見ると、![]() の場合は、漸近安定ではないが、発散はしないので、不安定とまではいえないのではないかと思うかもしれません。したがって零の固有値を不安定とみなすのか、安定とみなすか迷うところです。しかし、
の場合は、漸近安定ではないが、発散はしないので、不安定とまではいえないのではないかと思うかもしれません。したがって零の固有値を不安定とみなすのか、安定とみなすか迷うところです。しかし、![]() において、
において、![]() の場合、解は
の場合、解は![]() となって、
となって、![]() の第2要素が零でない場合は発散します。
の第2要素が零でない場合は発散します。
いま、![]() において、
において、![]() のすべての固有値の実部は負または零の場合を考え、実部が零の固有値
のすべての固有値の実部は負または零の場合を考え、実部が零の固有値![]() の重複度を
の重複度を![]() とし、次が成り立つとします。
とし、次が成り立つとします。
![]()
左辺は幾何学的重複度、左辺は代数学的重複度と呼ばれています。すべての実部が零の固有値について、幾何学的重複度と代数学的重複度が等しいことが、解が発散しないために追加的に要請される条件であることが知られています。上の例の場合、幾何学的重複度は2-1=1、代数学的重複度は2ですから、この条件は成立していないことがわかります。
Note A21-3 自由系の時間応答は固有値と固有ベクトルからどのように構成されるか
●2次自由系
![]()
の解は次のように表されます。
![]()
2次行列![]() の標準形は次の3つに分類されます。
の標準形は次の3つに分類されます。
![]()
![]()
![]()
ここで、![]() は虚数単位
は虚数単位![]() 、
、![]() 、
、![]() 、
、![]() はすべて実数です。
はすべて実数です。
このとき2次行列は、対応する固有ベクトルを用いて、次のように表されます。
![Rendered by QuickLaTeX.com \displaystyle{(4a)\quad A=\underbrace{\left[\begin{array}{cc} v_1 & v_2 \end{array}\right]}_{V} \underbrace{\left[\begin{array}{cc} \lambda_1 & 0 \\ 0 & \lambda_2 \end{array}\right]}_{\Lambda_1} \underbrace{\left[\begin{array}{cc} v_1 & v_2 \end{array}\right]^{-1}}_{V^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bb555c7741c2c5d90cef778c129e86b1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4b)\quad \begin{array}{l} A=\underbrace{\left[\begin{array}{cc} v_R+jv_I & v_R-jv_I \end{array}\right]}_{V} \left[\begin{array}{cc} \lambda_R+j\lambda_I & 0 \\ 0 & \lambda_R-j\lambda_I \end{array}\right]\\ \times\underbrace{\left[\begin{array}{cc} v_R+jv_I & v_R-jv_I \end{array}\right]^{-1}}_{V^{-1}}\\ =\underbrace{\left[\begin{array}{cc} v_R & v_I \end{array}\right]}_{V'} \underbrace{\left[\begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array}\right]}_{\Lambda_2} \underbrace{\left[\begin{array}{cc} v_R & v_I \end{array}\right]^{-1}}_{V'^{-1}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e0fbba71d2b00a6133e75ae5071cf18d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4c)\quad A=\underbrace{\left[\begin{array}{cc} v & v' \end{array}\right]}_{V} \underbrace{\left[\begin{array}{cc} \lambda & 1 \\ 0 & \lambda \end{array}\right]}_{\Lambda_3} \underbrace{\left[\begin{array}{cc} v & v' \end{array}\right]^{-1}}_{V^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-96f0aeda7d33e0892c1b3ae15b9c822f_l3.png)
ここで、![]() 、
、![]() 、
、![]() 、
、![]() はすべて2次元の実ベクトルです(
はすべて2次元の実ベクトルです(![]() は一般化固有ベクトル)。
は一般化固有ベクトル)。
これらの行列指数関数は次式となります。
![Rendered by QuickLaTeX.com \displaystyle{(5a)\quad \exp(A t)=\underbrace{\left[\begin{array}{cc} v_1 & v_2 \end{array}\right]}_{V} \underbrace{\left[\begin{array}{cc} e^{\lambda_1t} & 0 \\ 0 & e^{\lambda_2 t} \end{array}\right]}_{\exp(\Lambda_1 t)} \underbrace{\left[\begin{array}{cc} v_1 & v_2 \end{array}\right]^{-1}}_{V^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a2c20a571b582858c129f9525483fde7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5b)\quad \exp(A t)=\underbrace{\left[\begin{array}{cc} v_R & v_I \end{array}\right]}_{V'} \underbrace{e^{\lambda_R t} \left[\begin{array}{cc} \cos(\lambda_It) & \sin(\lambda_It) \\ -\sin(\lambda_It) & \cos(\lambda_It) \end{array}\right]}_{\exp(\Lambda_2 t)} \underbrace{\left[\begin{array}{cc} v_R & v_I \end{array}\right]^{-1}}_{V'^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e2598816f3c649ae154eb107c7bd9756_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5c)\quad \exp(A t)=\underbrace{\left[\begin{array}{cc} v & v' \end{array}\right]}_{V} \underbrace{e^{\lambda t} \left[\begin{array}{cc} 1 & t \\ 0 & 1 \end{array}\right]}_{\exp(\Lambda_3 t)} \underbrace{\left[\begin{array}{cc} v & v' \end{array}\right]^{-1}}_{V^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1ccd3c10da477fac06071a60073df28c_l3.png)
これらを(2)に代入して
![Rendered by QuickLaTeX.com \displaystyle{(6a)\quad \begin{array}{l} x(t)=\underbrace{\left[\begin{array}{cc} v_1 & v_2 \end{array}\right]}_{V} \underbrace{\left[\begin{array}{cc} e^{\lambda_1t} & 0 \\ 0 & e^{\lambda_2 t} \end{array}\right]}_{\exp(\Lambda_1 t)} \underbrace{\left[\begin{array}{cc} v_1 & v_2 \end{array}\right]^{-1}x(0)}_{\left[\begin{array}{c} c_1\\c_2 \end{array}\right]}\\ =c_1e^{\lambda_1t}v_1+c_2e^{\lambda_2t}v_2 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b73bdf17802abab8139590333ce5ddc8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6b)\quad \begin{array}{l} x(t)=\underbrace{\left[\begin{array}{cc} v_R & v_I \end{array}\right]}_{V'} \underbrace{e^{\lambda_R t} \left[\begin{array}{cc} \cos(\lambda_It) & \sin(\lambda_It) \\ -\sin(\lambda_It) & \cos(\lambda_It) \end{array}\right]}_{\exp(\Lambda_2 t)} \underbrace{\left[\begin{array}{cc} v_R & v_I \end{array}\right]^{-1}x(0)}_{\left[\begin{array}{c} c_1\\c_2 \end{array}\right]}\\ =c_1e^{\lambda_Rt}(\cos(\lambda_It)v_R-\sin(\lambda_It)v_I)+c_2e^{\lambda_Rt}(\sin(\lambda_It)v_R+\cos(\lambda_It)v_I) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-68447de2b9180ed5ba5e49bac88f6ad3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6c)\quad \begin{array}{l} x(t)=\underbrace{\left[\begin{array}{cc} v & v' \end{array}\right]}_{V} \underbrace{e^{\lambda t} \left[\begin{array}{cc} 1 & t \\ 0 & 1 \end{array}\right]}_{\exp(\Lambda_3 t)} \underbrace{\left[\begin{array}{cc} v & v' \end{array}\right]^{-1}x(0)}_{\left[\begin{array}{c} c_1\\c_2 \end{array}\right]}\\ =c_1e^{\lambda t}v+c_2e^{\lambda t}(tv+v') \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a89702614e30351370d03c8a88ab2200_l3.png)
●一般の自由系についても、同様の式が成り立ち、![]() の固有値と固有ベクトルがどのように時間応答に寄与しているかの分析ができ、モード間の連成について考察することができます。
の固有値と固有ベクトルがどのように時間応答に寄与しているかの分析ができ、モード間の連成について考察することができます。