n次系の時間応答…Homework
[1] 次の![]() 入力
入力![]() 出力
出力![]() 次系の状態空間表現を考えます。
次系の状態空間表現を考えます。
![]()
これから、![]() 次系の時間応答の表現式
次系の時間応答の表現式
![]()
を得ます。ここで、インパルス応答行列
![]()
を定義しますと(![]() )、上式は
)、上式は
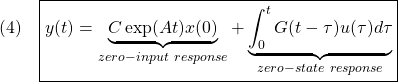
すなわち、![]() 次系の時間応答は、零入力応答(第1項)と零状態応答(第2項)の和となります。
次系の時間応答は、零入力応答(第1項)と零状態応答(第2項)の和となります。
いま、(1)をラプラス変換して、![]() とすると(零状態応答だけを考えます)
とすると(零状態応答だけを考えます)
![]()
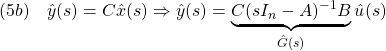
ここで現れた
![]()
を伝達関数行列と呼びます。
●![]() 次系の時間応答についての相互関係は次図のように表されます。多変数系の場合、
次系の時間応答についての相互関係は次図のように表されます。多変数系の場合、![]() 番目の入力から
番目の入力から![]() 番目の出力までのステップ応答と周波数応答を考えます。
番目の出力までのステップ応答と周波数応答を考えます。
 図1 多変数系時間等応答の相互関係
図1 多変数系時間等応答の相互関係
2次系の時間応答…Homework
[2] さて、次のようにパラメタライズされた漸近安定な1入力1出力2次系の状態空間表現を考えます。![]() 、
、![]() 、
、![]() はそれぞれ減衰係数、固有角周波数、定常ケインと呼ばれます。
はそれぞれ減衰係数、固有角周波数、定常ケインと呼ばれます。
![Rendered by QuickLaTeX.com \displaystyle{(7a)\quad \boxed{\underbrace{ \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} 0 \\ K\omega_n^2 \end{array}\right] }_{B} u(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aa4b19afa6fbdeb818288fb5934edb63_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7b)\quad y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1ef77e878f73e539d8dc80f6688ac1a5_l3.png)
以下では、簡単のため![]() とした2次系に対するインパルス応答(3)を求めます。そのために、行列
とした2次系に対するインパルス応答(3)を求めます。そのために、行列![]() の固有値
の固有値![]() を計算すると、
を計算すると、![]() 、
、![]() 、
、![]() に応じて、それぞれ次に示すようになります。
に応じて、それぞれ次に示すようになります。
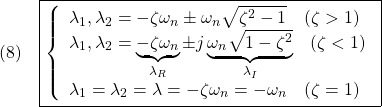
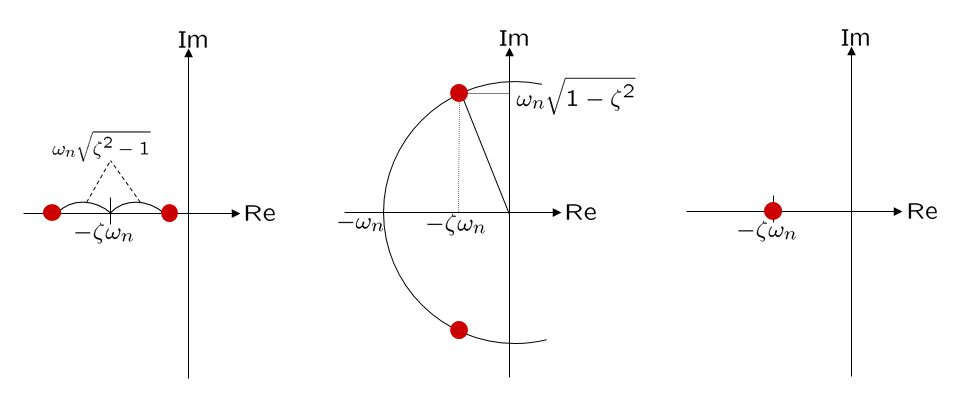 図2
図2 ![]() の固有値分布
の固有値分布
[3] 2次系のインパルス応答(1)
![]() のとき、
のとき、![]() とおくと、インパルス応答は次式で与えられます。
とおくと、インパルス応答は次式で与えられます。
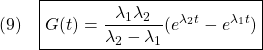
実際
![Rendered by QuickLaTeX.com \displaystyle{(10a)\quad \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} = \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda_1 & \lambda_2 \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda_1& 0\\ 0 & \lambda_2 \end{array}\right] }_{\Lambda} \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda_1 & \lambda_2 \end{array}\right]^{-1} }_{V^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3cecd035fcbda6f346f77661cc428347_l3.png)
![]()
となることから、インパルス応答は次のように計算されます。
![Rendered by QuickLaTeX.com (11)\quad \begin{array}{l} \displaystyle{G(t)=C\exp(At)B=CV\exp(\Lambda t)V^{-1}B}\\ \displaystyle{ =\left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{cc} 1 & 1\\ \lambda_1 & \lambda_2 \end{array}\right] \left[\begin{array}{cc} e^{\lambda_1t}& 0\\ 0 & e^{\lambda_2t} \end{array}\right] \frac{1}{\lambda_2-\lambda_1} \left[\begin{array}{cc} \lambda_2 & -1\\ -\lambda_1 & 1 \end{array}\right] \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right]}\\ \displaystyle{ =\frac{\omega_n^2}{\lambda_2-\lambda_1} \left[\begin{array}{cc} e^{\lambda_1t}& e^{\lambda_2t} \end{array}\right] \left[\begin{array}{cc} -1\\ 1 \end{array}\right]}\\ \displaystyle{=\frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}(e^{\lambda_2t}-e^{\lambda_1t})} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1f10feaa91b2bb7d8913903cbd15b9c3_l3.png)
[4] 2次系のインパルス応答(2)
![]() のとき、
のとき、![]() とおくと、インパルス応答とステップ応答はそれぞれそれぞれ次式で与えられます。
とおくと、インパルス応答とステップ応答はそれぞれそれぞれ次式で与えられます。
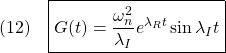
実際
![Rendered by QuickLaTeX.com \displaystyle{(13a)\quad \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} = \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ \lambda_R & \lambda_I \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array}\right] }_{\Lambda} \underbrace{ \frac{1}{\lambda_I} \left[\begin{array}{cc} \lambda_I & 0 \\ -\lambda_R & 1 \end{array}\right] }_{V^{-1}}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-615266a9890c4e3022d07970c6f5f659_l3.png)
![]()
となることから、インパルス応答は次のように計算されます。
![Rendered by QuickLaTeX.com (14)\quad \begin{array}{l} \displaystyle{G(t)=C\exp(At)B=CV\exp(\Lambda t)V^{-1}B}\\ \displaystyle{=\left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{cc} 1 & 0\\ \lambda_R & \lambda_I \end{array}\right] e^{\lambda_R t} \left[\begin{array}{cc} \cos\lambda_I t & \sin\lambda_I t\\ \sin\lambda_I t & \cos\lambda_I t \end{array}\right] \frac{1}{\lambda_I} \left[\begin{array}{cc} \lambda_I & 0\\ -\lambda_R & 1 \end{array}\right] \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right]}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I} e^{\lambda_R t} \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{cc} \cos\lambda_I t & \sin\lambda_I t\\ \sin\lambda_I t & \cos\lambda_I t \end{array}\right] \left[\begin{array}{cc} 0\\ 1 \end{array}\right]}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I} e^{\lambda_R t}\sin\lambda_I t} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2f44bd53bbc94bd725169439890f6d6f_l3.png)
[5] 2次系のインパルス応答(3)
![]() のとき、
のとき、![]() とおくと、インパルス応答とステップ応答はそれぞれそれぞれ次式で与えられます。
とおくと、インパルス応答とステップ応答はそれぞれそれぞれ次式で与えられます。
![]()
実際
![Rendered by QuickLaTeX.com \displaystyle{(16a)\quad \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} = \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda & \lambda+1 \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda & 1\\ 0 & \lambda \end{array}\right] }_{\Lambda} \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda & \lambda+1 \end{array}\right]^{-1} }_{V^{-1}}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8cd4b43f3e55efbc7942c5a68825fdd5_l3.png)
![]()
となることから、インパルス応答は次のように計算されます。
![Rendered by QuickLaTeX.com (17)\quad \begin{array}{l} \displaystyle{G(t)=C\exp(At)B=CV\exp(\Lambda t)V^{-1}B}\\ \displaystyle{= \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{cc} 1 & 1\\ \lambda & \lambda+1 \end{array}\right] e^{\lambda t} \left[\begin{array}{cc} 1 & t\\ 0 & 1 \end{array}\right] \frac{1}{\lambda+1-\lambda} \left[\begin{array}{cc} \lambda+1 & -1\\ -\lambda & 1 \end{array}\right] \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right]}\\ \displaystyle{= \omega_n^2 e^{\lambda t} \left[\begin{array}{cc} 1 & t+1 \end{array}\right] \left[\begin{array}{cc} -1\\ 1 \end{array}\right]}\\ \displaystyle{=\lambda^2te^{\lambda t}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-879b5bb9640f77dc6264c3509e6d3b66_l3.png)
2次振動系の同定…Homework
[7] 2次系(7)において、![]() 、
、![]() 、
、![]() の場合、インパルス応答のシミュレーション例を示します。
の場合、インパルス応答のシミュレーション例を示します。
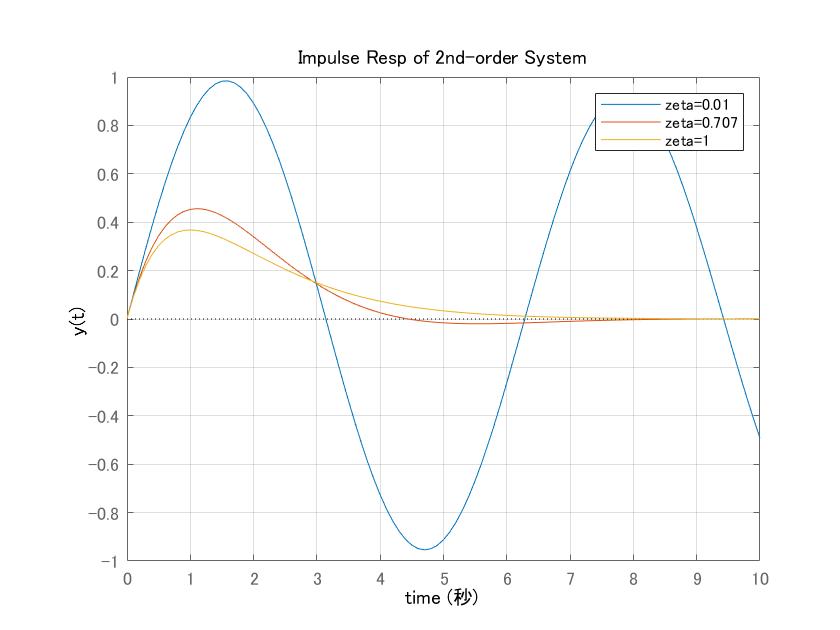 図3 2次系のインパルス応答の比較
図3 2次系のインパルス応答の比較
![]() の場合の(7)で表される2次系を2次振動系と呼びます。そのインパルス応答
の場合の(7)で表される2次系を2次振動系と呼びます。そのインパルス応答
![]()
の第k+1番目![]() の頂点の座標について、次が成り立ちます。
の頂点の座標について、次が成り立ちます。
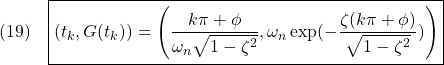
実際、![]() を計算すると
を計算すると
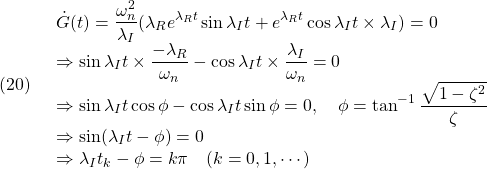
となって、次式を得ます。
![]()
この時刻![]() における
における![]() の値は
の値は
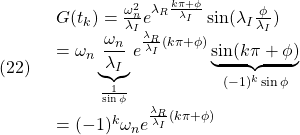
となって、次式を得ます。
![]()
●さて、(19)からそれぞれ次の関係式を得ます。
![]()
![]()
(24)はインパルス応答の隣合う山と山の時間間隔(または谷と谷の時間間隔)![]() は一定であることを示しています。(25)はインパルス応答の隣合う山と山の振幅比(または谷と谷の振幅比)
は一定であることを示しています。(25)はインパルス応答の隣合う山と山の振幅比(または谷と谷の振幅比)![]() は一定であることを示しています。
は一定であることを示しています。
したがって、次のように、![]() から
から![]() を得ることができます。
を得ることができます。
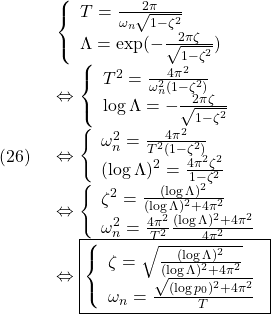
演習A22…Flipped Classroom
図2の応答#1を描き、2つの山の頂点の座標をマウスをクリックして取得し、減衰係数と固有角周波数を求めるプログラムを作成せよ。
| MATLAB |
|
| SCILAB |
|
Note A22-1 状態方程式の解
![]() 次系の状態方程式
次系の状態方程式
![]()
の解を求めてみます。Note A21と同様にして
![]()
までは問題ないと思います。これを![]() から
から![]() まで積分して
まで積分して
![]()
すなわち
![]()
したがって
![]()
ここで、![]() を
を![]() に、
に、![]() を
を![]() と置き換えれば
と置き換えれば
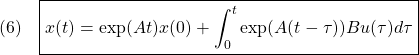
が得られます。
Note A22-2 重ね合わせの原理
次の![]() 入力
入力![]() 出力
出力![]() 次系の状態空間表現を考えます。
次系の状態空間表現を考えます。
![]()
2つの入力![]() と
と![]() に対するそれぞれの零状態応答は
に対するそれぞれの零状態応答は
![]()
![]()
となります。このとき入力
![]()
に対する零状態応答は
![]()
となります。実際、
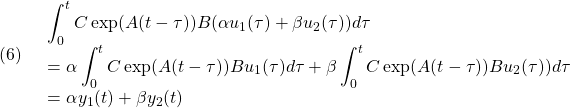
このとき、重ね合わせの原理が成り立つ、![]() 次系(1)は線形系(Linear System)であると言います。重ね合わせの原理が成り立たないときは非線形系(Nonlinear System)であると言います。たとえば入力を2倍したときの時間応答が元の時間応答の2倍にならなければ非線形系であると判断できます。
次系(1)は線形系(Linear System)であると言います。重ね合わせの原理が成り立たないときは非線形系(Nonlinear System)であると言います。たとえば入力を2倍したときの時間応答が元の時間応答の2倍にならなければ非線形系であると判断できます。