可制御標準形 | 制御系CAD

可制御標準形…Homework

[1] ある平衡状態周りの挙動が線形状態方程式

$\displaystyle{(1)\quad \dot{x}(t)=Ax(t)+Bu(t)\quad(x(t)\in{\rm\bf R}^n,u(t)\in{\rm\bf R}^m) }$

で表される制御対象に対して、座標変換

$\displaystyle{(2)\quad x'(t)=Tx(t)\Leftrightarrow x(t)=T^{-1}x'(t) }$

を行うと（ $T$ は正則行列）、状態方程式は次式となります。

$\displaystyle{(3)\quad \dot{x}'(t)=\underbrace{TAT^{-1}}_{A'}x'(t)+\underbrace{TB}_{B'}u(t) }$

このとき、漸近安定性、可安定性、可制御性は、座標変換によって不変であることを確かめることができます。実際、漸近安定性については

$\displaystyle{(4)\quad {\rm det}(\lambda I_n-\underbrace{TAT^{-1}}_{A'}) ={\rm det}T(\lambda I_n-A)T^{-1} ={\rm det}(\lambda I_n-A) }$

から明らかです。また、(1)に対する状態フィードバック

$\displaystyle{(5)\quad u(t)=-Fx(t) }$

による閉ループ系

$\displaystyle{(6)\quad \dot{x}(t)=(A-BF)x(t) }$

は座標変換後は

$\displaystyle{(7)\quad u(t)=-\underbrace{FT^{-1}}_{F'}x'(t) }$

を(3)に代入して

$\displaystyle{(8)\quad \dot{x}'(t)=(TAT^{-1}-TBFT^{-1})x'(t) }$

となることに注意します。このとき、可安定性については

$\displaystyle{(9)\quad \begin{array}{l} {\rm det}(\lambda I_n-\underbrace{TAT^{-1}}_{A'}+\underbrace{TB}_{B'}\underbrace{FT^{-1}}_{F'}) ={\rm det}T(\lambda I_n-A+BF)T^{-1}\\ ={\rm det}(\lambda I_n-A+BF) \end{array} }$

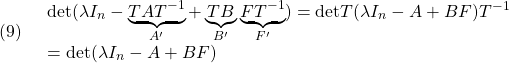
から明らかです。また、可制御性については

$\displaystyle{(10)\quad \begin{array}{ll} {\rm rank}\, [\begin{array}{cccc} \underbrace{TB}_{B'} & \underbrace{TAT^{-1}}_{A'}\underbrace{TB}_{B'} & \cdots & \underbrace{(TAT^{-1})^{n-1}}_{A'^{n-1}}\underbrace{TB}_{B'} \end{array}] \\ ={\rm rank}\, T[\begin{array}{cccc} B & AB &\cdots & A^{n-1}B \end{array}]\\ ={\rm rank}\, [\begin{array}{cccc} B & AB &\cdots & A^{n-1}B \end{array}] \end{array} }$

から明らかです。

●可安定性と可制御性は座標変換によって不変であることに基づいて，可安定性や可制御性の判別をしやすいように座標変換行列 $T$ を選ぶことを考えます。すなわち， $n$ 次系(1)に対して，次の可制御標準形に座標変換できるかどうかを調べます。

$\displaystyle{(11)\quad \boxed{ \left[\begin{array}{c} \dot{x}_1'(t) \\ \dot{x}_2'(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A_{\#} & X \\ 0 & A_k \end{array}\right] }_{TAT^{-1}} \left[\begin{array}{c} x_1'(t) \\ x_2'(t) \end{array}\right] + \underbrace{ \left[\begin{array}{c} B_{\#} \\ 0 \end{array}\right] }_{TB} u(t)} }$

ただし， $(A_{\#},B_{\#})$ は可制御対とします。このブロック線図を描いてみればわかるように，状態 $x_2'$ は入力 $u$ の影響を受けることはありません。したがって，可制御性は成立しないこと，そして $A_k$ が安定行列かどうかが可安定性と関係していることは想像がつくと思います。以下では，次の判定法が導かれること示します。

「可制御標準形に座標変換したとき， $A_k$ が安定行列のとき可安定性が成り立ち，そうでないときは可安定性は成り立たない。また，可制御標準形において $A_k$ が存在しなければ，可制御性が成り立っている。」

[2]　(11)を得るような座標変換行列 $T$ の候補は，階段化アルゴリズム（Note A33参照）を用いて、次のように得られます。

定理　サイズ $n\times n$ の行列 $A$ とサイズ $n\times m$ の行列 $B$ に対して，つぎのように変換する直交行列 $T$ が存在する。

$\displaystyle{(12)\quad \left[\begin{array}{cc} T^TB & T^TAT \end{array}\right]= \left[\begin{array}{c|cccc|c} B_1 & A_1 & X & \cdots & X & X \\ 0 & B_2 & A_2 & \cdots & X & X \\ \vdots & & \ddots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & B_{k-1} & A_{k-1} & X \\ \hline 0 & 0 & \cdots & 0 & B_k & A_k \end{array}\right] }$

ここで， $k$ は正整数，また $B_j$ のサイズを $m_j\times m_{j-1}$ とするとき( $m_0=m,\ m_1+\cdots+m_k=n$ )，つぎが成り立つ（ $B_1,\cdots,B_{k-1}$ は横長の形状となり，行フルランクをもつ。また， $B_k$ は横長で，行フルランクをもつ行列または零行列のどちらかである。）。

$\displaystyle{(13)\quad {\rm rank}\,B_j=m_j\quad (j=1,\cdots,k-1) }$
$\displaystyle{(14)\quad {\rm rank}\,B_k=m_k\ または\ 0 }$
$\displaystyle{(15)\quad m\ge m_1 \ge \cdots \ge m_{k-1} \ge m_k }$

このとき， $(A,B)$ が可制御対であるための必要十分条件は

条件C0:　(12)において， $B_k\ne 0$

が成り立つことである。また， $(A,B)$ が可安定対であるための必要十分条件は、つぎが成り立つことである。

条件S0:　(12)において， $B_k=0$ のとき， $A_k$ は安定行列

$B_k=0$ のとき，(11)のような形式が得られていることは，(12)の $T$ を上の $T^{-1}=T^T$ と読み替えれば明らかであろう。

●可制御性の定義とその等価な条件は次のようにまとめられます。

【可制御性の定義とその等価な条件】

定義DC:　任意初期状態を，任意有限時間内に，任意状態に移動可能

条件C1:　 $\displaystyle{\int_0^t \exp(A\tau)BB^T\exp(A^T\tau)\,d\tau>0 \quad (\forall t>0)}$

条件C2:　 ${\rm rank}\, \left[\begin{array}{cccc} B & AB & \cdots & A^{n-1}B \end{array}\right]=n$

条件C3:　 $F$ を選んで， $A-BF$ の固有値を任意に設定可能

条件C0:　(12)において， $B_k\ne 0$

条件C4:　 ${\rm rank}\, \left[\begin{array}{cc} B & A-\lambda I_n \end{array}\right] =n$ 　( $\lambda$ は $A$ のすべての固有値)

条件C5:　 $B^Tw=0,\ A^Tw=\lambda w \Rightarrow w=0$ 　( $\lambda$ は $A$ のすべての固有値)

すでに定義DC $\Leftrightarrow$ 条件C1 $\Leftrightarrow$ 条件C2を示していますので、以下では条件C3 $\Rightarrow$ 条件C0 $\Rightarrow$ 条件C4 $\Leftrightarrow$ 条件C5 $\Rightarrow$ 条件C2を示します。

＜条件C3 $\Rightarrow$ 条件C0＞ $B_k=0$ とすると，(12)を用いて

$\displaystyle{(16)\quad {\rm det}(\lambda I_n-T^TAT+T^TB\cdot FT) ={\rm det}\left(\lambda I_n- \left[\begin{array}{cc} X & X \\ 0 & A_k \end{array}\right] \right) }$

となり，閉ループ系において $A_k$ の固有値はそのまま残るが，C3に矛盾しています。

＜条件C0 $\Rightarrow$ 条件C4＞　 $\lambda$ を任意の複素数とする。 $[\begin{array}{cc} T^TB & T^TAT-\lambda I_n \end{array}]$ に，(12)を適用すると

$\displaystyle{(17)\quad \left[\begin{array}{c|cccc|c} B_1 & A_1-\lambda I_{m_1} & X & \cdots & X & X \\ 0 & B_2 & A_2-\lambda I_{m_2} & \cdots & X & X \\ \vdots & & \ddots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & B_{k-1} & A_{k-1}-\lambda I_{m_{k-1}} & X \\ \hline 0 & 0 & \cdots & 0 & B_k & A_k-\lambda I_{m_k} \end{array}\right] }$

を得ます。ここで， $B_1,\cdots,B_k$ は横長の形状となり，行フルランク(行数に等しい階数)をもつので

$\displaystyle{(18)\quad \left[\begin{array}{cc} T^TB & T^TAT-\lambda I_n \end{array}\right] = T^T \left[\begin{array}{cc} B & A-\lambda I_n \end{array}\right] \left[\begin{array}{cc} I_n & 0 \\ 0 & T \end{array}\right] }$

に，シルベスターの公式を適用して

$\displaystyle{(19)\quad {\rm rank}\, [\begin{array}{cc} T^TB & T^TAT-\lambda I_n \end{array}] = {\rm rank}\, [\begin{array}{cc} B & A-\lambda I_n \end{array}] =n }$

を得ます。この階数が $n$ より小さくなるのは，(17)から明らかなように， $\lambda$ が $A_k$ の固有値に等しい場合です。したがって， $\lambda$ は $A$ の固有値について調べれば十分である。すなわち，条件C4を得たことになります。

＜条件C4 $\Leftrightarrow$ 条件C5＞　条件C4は， $w$ を $n$ 次元ベクトルとして

$\displaystyle{(20)\quad w^T\, [\begin{array}{cc} B & A-\lambda I_n \end{array}] =0 \Rightarrow w =0 }$

すなわち

$\displaystyle{(21)\quad B^Tw=0,\ A^Tw=\lambda w \Rightarrow w=0 }$

と等価です。

＜条件C5 $\Rightarrow$ 条件C2＞　条件C5より

$\displaystyle{(22)\quad w^TA^{i-1}B=0\quad (i=0,1,2,\cdots) }$

を得て

$\displaystyle{(23)\quad w^T\, [\begin{array}{ccccc} B & AB & \cdots & A^{n-1}B \end{array}] =0 \Rightarrow w =0 }$

が成り立つ。これは条件C2を意味します。

[3]　可安定性の定義とその等価な条件は次のようにまとめられます。

【可安定性の定義とその等価な条件】

定義DS:　状態フィードバックにより安定化可能

条件S0:　(12)において， $B_k=0$ のとき， $A_k$ は安定行列

条件S1:　 ${\rm rank}\, \left[\begin{array}{cc} B & A-\lambda I_n \end{array}\right] =n$ 　( $\lambda$ は $A$ のすべての不安定固有値)

条件S2:　 $B^Tw=0,\ A^Tw=\lambda w \Rightarrow w=0$ 　( $\lambda$ は $A$ のすべての不安定固有値)

＜定義DS $\Leftrightarrow$ 条件S0＞　可制御であれば可安定であるので，不可制御で可安定の場合をどのように特徴付けるかを考えます。不可制御であれば条件C0が不成立なので， $B_k=0$ となり， $A_k$ の固有値だけは状態フィードバックによってどうすることもできません。このとき可安定であるためには， $A_k$ が安定行列であることを前提とするしかありません。これは条件S0そのものです。また，可安定性と可制御性と相違は，前者が $B_k\ne0$ ばかりでなく $B_k=0$ を許すところにあることに注意します。

＜条件S0 $\Leftrightarrow$ 条件S1 $\Leftrightarrow$ 条件S2＞　条件S1 $\Leftrightarrow$ 条件S2は，条件C4 $\Leftrightarrow$ 条件C5の場合と同様にして明らかです。そこで、条件S0との等価性を調べます。 $B_k=0$ のとき，(17)の行列のランクが落ちるのは

$\displaystyle{(24)\quad {\rm rank}\, \left. [\begin{array}{cc} B_k & A_k-\lambda I_{m_k} \end{array}] \right|_{B_k=0} = {\rm rank}\, [\begin{array}{cc} 0 & A_k-\lambda I_{m_k} \end{array}] \le m_k }$

の部分で， $\lambda$ が $A_k$ の固有値に一致した場合になります。したがって，条件S0を保証するためには， $\lambda$ に $A_k$ のすべての不安定固有値を入れて，(17)を調べ，行フルランクとなればよいことになります。

Note A33　階段化アルゴリズム　

アルゴリズム＜階段化アルゴリズム(staircase algorithm)＞
入力パラメータ $m,\,n,\,A(n\times n),\,B(n\times m)$
出力パラメータ $k,\,m_1,\cdots,m_k,\,T(n\times n)$
ステップ1 初期化

$j=0,\,s=0,\,m_0=m,\,T^{(1)}=I_n,\,B^{(1)}=B,\,A^{(1)}=A$ とおく。

ステップ2 $B^{(j)}$ の階数決定

$j$ を $j+1$ に更新し， $B^{(j)}(n-s\times m_{j-1})$ に対して，つぎの特異値分解を行い， $B^{(j)}$ の階数 $m_j$ と $U^{(j)}(n-s\times n-s)$ を求める。

$\displaystyle{(1)\quad B^{(j)}=U^{(j)}\Sigma^{(j)}V^{(j)}\,^T }$

$\displaystyle{(2)\quad \Sigma^{(j)}= \left[\begin{array}{cc} \Sigma_1^{(j)} & 0 \\ 0 & 0 \end{array}\right] }$

もし $m_j=n-s$ または $m_j=0$ ならば， $k=j,\,T=T^{(j)}$ と設定して終了する。そうでないときは，ステップ3へ行く。

ステップ3 座標変換

$W^{(j)}(n\times n)$ を， $U^{(j)}(n-s\times n-s)$ を用いて

$\displaystyle{(3)\quad W^{(j)}= \left[\begin{array}{cc} I_s & 0 \\ 0 & U^{(j)} \end{array}\right] }$

と設定し， $A^{(j+1)}(n\times n)$ と $T^{(j+1)}(n\times n)$ を，次式から求める。

$\displaystyle{(4)\quad A^{(j+1)}=W^{(j)}\,^TA^{(j)}W^{(j)},\ T^{(j+1)}=T^{(j)}W^{(j)} }$

ステップ4 $B^{(j)}$ の切り出し

$s$ を $s+m_j$ に更新し， $A^{(j+1)}(n\times n)$ に対してつぎの分割を行い， $B^{(j+1)}(n-s\times m_j)$ を得て,ステップ2へ戻る。

$\displaystyle{(5)\quad A^{(j+1)}= \left[\begin{array}{ccc} X(s\times s-m_j) & X(s\times m_j) & X(s\times n-s) \\ 0 & B^{(j+1)} & X \end{array}\right] }$

●階段化アルゴリズムを適用した数値例を示します。

$\displaystyle{(6)\quad A= \left[\begin{array}{ccc} 0 & 0 & 0 \\ 0 & -1 & 1 \\ 0 & 0 & 0 \end{array}\right] ,\ B= \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \\ 0 & 1 \end{array}\right] }$

に対して、階段化アルゴリズムの各ステップは，つぎのように計算されます。

ステップ1： $j=0,\,s=0,\,m_0=2,\,T^{(1)}=I_3,\,B^{(1)}=B,\,A^{(1)}=A$ とおく。
ステップ2： $j=1$ とし， $B^{(1)}$ に対する特異値分解

$\displaystyle{(7)\quad B^{(1)}= \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 1 \\ \frac{1}{\sqrt{2}} & 0 & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{array}\right] }_{U^{(1)}} \underbrace{ \left[\begin{array}{cc} \sqrt{2} & 0 \\ 0 & 1 \\ 0 & 0 \end{array}\right] }_{\Sigma^{(1)}} \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right]^T }_{V^{(1)T}} }$

から， $B^{(1)}$ の階数 $m_1=2$ と $U^{(1)}$ が求まる。
ステップ3： $m_1\ne3$ かつ $m_1\ne0$ なので，ステップ4へ行く。
ステップ4： $W^{(1)}=U^{(1)}$ とし， $A^{(2)}=W^{(1)}\,^TA^{(1)}W^{(1)}$ を求めると

$\displaystyle{(8)\quad A^{(2)}= \left[\begin{array}{cc|c} 0 & 0 & 1 \\ 0 & 0 & 0 \\ \hline 0 & 0 & -1 \end{array}\right] }$

となり， $T^{(2)}=W^{(1)}$ とする。
ステップ5： $s=2$ とする。 $A^{(2)}$ に対する分割から， $B^{(2)}= [\begin{array}{cc} 0 & 0 \end{array}]$ を得る。
ステップ2′： $j=2$ とする。 $B^{(2)}$ は零行列なので，その階数は $m_2=0$ である。
ステップ3′： $m_2=0$ なので， $k=2,\,T=T^{(2)}$ のように設定する。

以上から，(12)は，つぎのように得られた。

$\displaystyle{(9)\quad \begin{array}{l} \left[\begin{array}{cc} T^TB & T^TAT \end{array}\right]= \left[\begin{array}{ccc} B_1 & A_1 & X \\ 0 & B_2 & A_2 \end{array}\right]= \left[\begin{array}{cc|cc|c} 0 & \sqrt{2} & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 & -1 \end{array}\right] \end{array} }$

ここで， $B_2$ は零行列で， $A_2=-1<0$ より，条件S0が成り立つ。よって， $(A,B)$ は可安定である。

演習 A33…Flipped Classroom

$1^\circ$ 階段化アルゴリズムのコードは次のように書ける。上の数値例で確かめよ。

MATLAB

%staircase.m
%----- 
 function [T,m]=staircase(A,B,tol)
   [n,r]=size(B);
   j=0; s=0; T=eye(n); B1=B; A1=A;
   while j＜n
     j=j+1; [U1,S1,V1]=svd(B1);
     m(j)=rank(B1,tol);
     if (m(j)==n-s)|(m(j)==0),k=j; break, end
     W=[eye(s)       zeros(s,n-s) ;
        zeros(n-s,s) U1          ];
     T=T*W; A1=W'*A1*W;
     s=s+m(j); B1=A1(s+1:n,s-m(j)+1:s);
 end
%-----
%eof