| SCILAB |
//ship9.sce
//-----
function [LME,LMI,OBJ]=synlmi(YLIST)
[gam,R,S,AK1,BK1,CK1,DK1,AK2,BK2,CK2,DK2,AK3,BK3,CK3,DK3]=YLIST(:);
LME1=R-R';
LME2=S-S';
LME=list(LME1,LME2);
LMI0=[R eye(A1);eye(A1) S];
AW1=[A1*R+B2*CK1 A1+B2*DK1*C2;
AK1 S*A1+BK1*C2];
LMI11=-(AW1+AW1'+2*alpha*LMI0);
LMI21=-[-r*LMI0 AW1;AW1 -r*LMI0];
LMI31=-[sin(th)*AW1 cos(th)*AW1;-cos(th)*AW1 sin(th)*AW1];
LMI31=LMI31+LMI31';
BW=[B1+B2*DK1*D21;
S*B1+BK1*D21];
CW1=[C11*R+D121*CK1 C11+D121*DK1*C2];
[p,m]=size(D11);
LMI41=-[AW1+AW1' BW CW1'
BW' -gam*eye(m,m) (D11+D121*DK1*D21)'
CW1 D11+D121*DK1*D21 -gam*eye(p,p)];
[p,m]=size(DK1);
LMI51=-[-1e2*eye(m,m) DK1';DK1 -1e2*eye(p,p)];
//
AW2=[A2*R+B2*CK2 A2+B2*DK2*C2;
AK2 S*A2+BK2*C2];
LMI12=-(AW2+AW2'+2*alpha*LMI0);
LMI22=-[-r*LMI0 AW2;AW2 -r*LMI0];
LMI32=-[sin(th)*AW2 cos(th)*AW2;-cos(th)*AW2 sin(th)*AW2];
LMI32=LMI32+LMI32';
BW=[B1+B2*DK2*D21;
S*B1+BK2*D21];
CW2=[C12*R+D122*CK2 C12+D122*DK2*C2];
[p,m]=size(D11);
LMI42=-[AW2+AW2' BW CW2'
BW' -gam*eye(m,m) (D11+D122*DK2*D21)'
CW2 D11+D122*DK2*D21 -gam*eye(p,p)];
[p,m]=size(DK2);
LMI52=-[-1e2*eye(m,m) DK2';DK2 -1e2*eye(p,p)];
//
AW3=[A3*R+B2*CK3 A3+B2*DK3*C2;
AK3 S*A3+BK3*C2];
LMI13=-(AW3+AW3'+2*alpha*LMI0);
LMI23=-[-r*LMI0 AW3;AW3 -r*LMI0];
LMI33=-[sin(th)*AW3 cos(th)*AW3;-cos(th)*AW3 sin(th)*AW3];
LMI33=LMI33+LMI33';
BW=[B1+B2*DK3*D21;
S*B1+BK3*D21];
CW3=[C13*R+D123*CK3 C13+D123*DK3*C2];
[p,m]=size(D11);
LMI43=-[AW3+AW3' BW CW3'
BW' -gam*eye(m,m) (D11+D123*DK3*D21)'
CW3 D11+D123*DK3*D21 -gam*eye(p,p)];
[p,m]=size(DK3);
LMI53=-[-1e2*eye(m,m) DK3';DK3 -1e2*eye(p,p)];
LMI=list(LMI0,LMI11,LMI21,LMI31,LMI41,LMI51,LMI12,LMI22,LMI32,LMI42,LMI52,LMI13,LMI23,LMI33,LMI43,LMI53);
OBJ=gam;
endfunction
//-----
function [AK,BK,CK,DK]=syncont(R,S,ak,bk,ck,dk)
[u,sd,v]=svd(eye()-S*R); Ni=sqrt(sd)\u'; Mti=v/sqrt(sd);
AK=Ni*(ak-S*(A-B2*dk*C2)*R-bk*C2*R-S*B2*ck)*Mti;
BK=Ni*(bk-S*B2*dk);
CK=(ck-dk*C2*R)*Mti;
DK=dk;
endfunction
//=====
T1=118; T2=7.8; T3=18.5; Tship=T1+T2-T3; Kship=0.185;
Tdelta=10; Kdelta=1; tL=9;
wD1=tL; wD2=tL; wD3=tL; wI1=0.01; wI2=0.01; wI3=0.01;
//
A0=[0 1 0;0 -1/Tship Kship/Tship;0 0 -1/Tdelta]; B0=[0;0;Kdelta/Tdelta];
C0=[1 0 0];
//-----
Us=7.7; U1=Us*0.5; U2=Us*1.5; U3=(U1+U2)/2; U32=U1*U2;
a0=[ 0 1 0 0;
0 0 0 0;
0 0 -1/Tdelta 0;
-1 0 0 0];
a1=[ 0 0 0 0;
0 -1/Us/Tship 0 0;
0 0 0 0;
0 0 0 0];
a2=[ 0 0 0 0;
0 0 1/Us^2*Kship/Tship 0;
0 0 0 0;
0 0 0 0];
A1=a0+U1*a1+U1^2*a2;
A2=a0+U2*a1+U2^2*a2;
A3=a0+U3*a1+U32*a2;
B1=[zeros(3,1);1];
B2=[B0;0];
C11=[zeros(1,3) wI1;wD1*C0*A0 0;zeros(1,4)];
C12=[zeros(1,3) wI2;wD2*C0*A0 0;zeros(1,4)];
C13=[zeros(1,3) wI3;wD3*C0*A0 0;zeros(1,4)];
D11=zeros(3,1);
D121=[0;wD1*C0*B0;1];
D122=[0;wD2*C0*B0;1];
D123=[0;wD3*C0*B0;1];
C2=[C0 0;zeros(1,3) 1];
D21=[0;0];
D22=[0;0];
//-----
alpha=0.01; r=15; th=%pi/4;
gam0=100; R0=eye(4,4); S0=eye(4,4);
AK0=-eye(4,4); BK0=ones(4,2); CK0=ones(1,4); DK0=ones(1,2);
YLIST0=list(gam0,R0,S0,AK0,BK0,CK0,DK0,AK0,BK0,CK0,DK0,AK0,BK0,CK0,DK0);
YLIST=lmisolver(YLIST0,synlmi);
[gam,R,S,ak1,bk1,ck1,dk1,ak2,bk2,ck2,dk2,ak3,bk3,ck3,dk3]=YLIST(:);
//
A=A1; [AK1,BK1,CK1,DK1]=syncont(R,S,ak1,bk1,ck1,dk1);
plK1=spec(AK1),
ACL1=[A1+B2*DK1*C2 B2*CK1;BK1*C2 AK1];
BCL1=[B1+B2*DK1*D21;BK1*D21];
CCL1=[C2(1,:) zeros(1,4)];
plCL1=spec(ACL1)
//
A=A2; [AK2,BK2,CK2,DK2]=syncont(R,S,ak2,bk2,ck2,dk2);
plK2=spec(AK2),
ACL2=[A2+B2*DK2*C2 B2*CK2;BK2*C2 AK2];
BCL2=[B2+B2*DK2*D21;BK2*D21];
CCL2=[C2(1,:) zeros(1,4)];
plCL2=spec(ACL2)
//
A=A3; [AK3,BK3,CK3,DK3]=syncont(R,S,ak3,bk3,ck3,dk3);
plK3=spec(AK3),
ACL3=[A3+B2*DK3*C2 B2*CK3;BK3*C2 AK3];
BCL3=[B1+B2*DK3*D21;BK3*D21];
CCL3=[C2(1,:) zeros(1,4)];
plCL3=spec(ACL3)
//-----
AK1=[AK1 BK1(:,2);zeros(1,5)];
BK1=[BK1(:,1) zeros(4,1); -1 1];
CK1=[CK1 DK1(:,2)];
DK1=[DK1(:,1) 0];
AL1=[A1 B2*CK1;zeros(5,4) AK1];
BL1=[B2*DK1; BK1];
CL1=[C2 D22*CK1];
DL1=D22*DK1;
clf(0),clf(1)
w=logspace(-3,0,100); nw=length(w);
g=freq(A0,B0,C0,%i*w);
for i=1:nw, ga(i)=20*log10(norm(g(:,i))); end
scf(0);plot2d(w,ga,logflag='ln')
gws=20*log10(abs(wI1./(%i*w))); gwt=20*log10(abs(wD1^(-1)./(%i*w)));
scf(0);plot2d(w,gws,logflag='ln')
scf(0);plot2d(w,gwt,logflag='ln')
g=freq(AL1,BL1(:,1),CL1(1,:),DL1(1,1),%i*w);
for i=1:nw, ga(i)=20*log10(abs(g(:,i))); end
scf(0);plot2d(w,ga,logflag='ln'),mtlb_grid,mtlb_axis([10^(-3) 10^0 -80 60])
g=freq(ACL1,BCL1,CCL1,%i*w);
for i=1:nw, ga(i)=20*log10(abs(g(:,i))); end
scf(1);plot2d(w,ga,logflag='ln')
for i=1:nw, ga(i)=20*log10(abs(1-g(:,i))); end
scf(1);plot2d(w,ga,logflag='ln'),mtlb_grid,mtlb_axis([10^(-3) 10^0 -80 60])
scf(1);plot2d(w,-gws,logflag='ln')
scf(1);plot2d(w,gwt,logflag='ln')
//
clf(2),clf(3)
AK2=[AK2 BK2(:,2);zeros(1,5)];
BK2=[BK2(:,1) zeros(4,1); -1 1];
CK2=[CK2 DK2(:,2)];
DK2=[DK2(:,1) 0];
AL2=[A2 B2*CK1;zeros(5,4) AK1];
BL2=[B2*DK1; BK1];
CL2=[C2 D22*CK1];
DL2=D22*DK1;
w=logspace(-3,0,100); nw=length(w);
g=freq(A0,B0,C0,%i*w);
for i=1:nw, ga(i)=20*log10(norm(g(:,i))); end
scf(2);plot2d(w,ga,logflag='ln')
gws=20*log10(abs(wI2./(%i*w))); gwt=20*log10(abs(wD2^(-1)./(%i*w)));
scf(2);plot2d(w,gws,logflag='ln')
scf(2);plot2d(w,gwt,logflag='ln')
g=freq(AL2,BL2(:,1),CL2(1,:),DL2(1,1),%i*w);
for i=1:nw, ga(i)=20*log10(abs(g(:,i))); end
scf(2);plot2d(w,ga,logflag='ln'),mtlb_grid,mtlb_axis([10^(-3) 10^0 -80 60])
g=freq(ACL2,BCL2,CCL2,%i*w);
for i=1:nw, ga(i)=20*log10(abs(g(:,i))); end
scf(3);plot2d(w,ga,logflag='ln')
for i=1:nw, ga(i)=20*log10(abs(1-g(:,i))); end
scf(3);plot2d(w,ga,logflag='ln'),mtlb_grid,mtlb_axis([10^(-3) 10^0 -80 60])
scf(3);plot2d(w,-gws,logflag='ln')
scf(3);plot2d(w,gwt,logflag='ln')
//
clf(4),clf(5)
AK3=[AK3 BK3(:,2);zeros(1,5)];
BK3=[BK3(:,1) zeros(4,1); -1 1];
CK3=[CK3 DK3(:,2)];
DK3=[DK3(:,1) 0];
AL3=[A3 B2*CK1;zeros(5,4) AK1];
BL3=[B2*DK1; BK1];
CL3=[C2 D22*CK1];
DL3=D22*DK1;
w=logspace(-3,0,100); nw=length(w);
g=freq(A0,B0,C0,%i*w);
for i=1:nw, ga(i)=20*log10(norm(g(:,i))); end
scf(4);plot2d(w,ga,logflag='ln')
gws=20*log10(abs(wI3./(%i*w))); gwt=20*log10(abs(wD3^(-1)./(%i*w)));
scf(4);plot2d(w,gws,logflag='ln')
scf(4);plot2d(w,gwt,logflag='ln')
g=freq(AL3,BL3(:,1),CL3(1,:),DL3(1,1),%i*w);
for i=1:nw, ga(i)=20*log10(abs(g(:,i))); end
scf(4);plot2d(w,ga,logflag='ln'),mtlb_grid,mtlb_axis([10^(-3) 10^0 -80 60])
g=freq(ACL3,BCL3,CCL3,%i*w);
for i=1:nw, ga(i)=20*log10(abs(g(:,i))); end
scf(5);plot2d(w,ga,logflag='ln')
for i=1:nw, ga(i)=20*log10(abs(1-g(:,i))); end
scf(5);plot2d(w,ga,logflag='ln'),mtlb_grid,mtlb_axis([10^(-3) 10^0 -80 60])
scf(5);plot2d(w,-gws,logflag='ln')
scf(5);plot2d(w,gwt,logflag='ln')
//return
//=====
a0=[ 0 1 0 ;
0 0 0 ;
0 0 -1/Tdelta ];
a1=[ 0 0 0 ;
0 -1/Us/Tship 0 ;
0 0 0 ];
a2=[ 0 0 0 ;
0 0 1/Us^2*Kship/Tship;
0 0 0 ];
A1=a0+U1*a1+U1^2*a2;
A2=a0+U2*a1+U2^2*a2;
A3=a0+U3*a1+U32*a2;
//-----
function Q=interp3(P1,P2,P3,P)
x1=P1(1); x2=P2(1); x3=P3(1); x=P(1);
y1=P1(2); y2=P2(2); y3=P3(2); y=P(2);
alpha=((x1-x2)*(y2-y3)-(x2-x3)*(y1-y2));
Q(1) =((x -x2)*(y2-y3)-(x2-x3)*(y -y2))/alpha;
Q(2) =((x1-x3)*(y -y3)-(x -x3)*(y1-y3))/alpha;
Q(3) =((x1-x2)*(y2-y )-(x2-x )*(y1-y2))/alpha;
endfunction
//
function Ut=U(t,ID)
if ID==0, Ut=Us,
else
if t<=ID*100, Ut=Us-(Us-U1)/(ID*100)*t, else Ut=U1, end
end
endfunction
//
function dxG=fG(t,xG), dxG=AG(t)*xG+B0*ut, endfunction
//
function AGt=AG(t),
P1=[U1;U1^2]; P2=[U2;U2^2]; P3=[U3;U3^2]; Ut=U(t,ID); P=[Ut;Ut^2];
Q=interp3(P1,P2,P3,P); p1=Q(1); p2=Q(2); p3=Q(3);
AGt=p1*A1+p2*A2+p3*A3;
endfunction
//
function dxK=fK(t,xK),
dxK=AK(t)*xK+BK(t)*yt,
endfunction
//
function AKt=AK(t),
P1=[U1;U1^2]; P2=[U2;U2^2]; P3=[U3;U3^2]; Ut=U(t,ID); P=[Ut;Ut^2];
Q=interp3(P1,P2,P3,P); p1=Q(1); p2=Q(2); p3=Q(3);
AKt=p1*AK1+p2*AK2+p3*AK3;
endfunction
//
function BKt=BK(t),
P1=[U1;U1^2]; P2=[U2;U2^2]; P3=[U3;U3^2]; Ut=U(t,ID); P=[Ut;Ut^2];
Q=interp3(P1,P2,P3,P); p1=Q(1); p2=Q(2); p3=Q(3);
BKt=p1*BK1+p2*BK2+p3*BK3;
endfunction
//
function CKt=CK(t),
P1=[U1;U1^2]; P2=[U2;U2^2]; P3=[U3;U3^2]; Ut=U(t,ID); P=[Ut;Ut^2];
Q=interp3(P1,P2,P3,P); p1=Q(1); p2=Q(2); p3=Q(3);
CKt=p1*CK1+p2*CK2+p3*CK3;
endfunction
//
function DKt=DK(t),
P1=[U1;U1^2]; P2=[U2;U2^2]; P3=[U3;U3^2]; Ut=U(t,ID); P=[Ut;Ut^2];
Q=interp3(P1,P2,P3,P); p1=Q(1); p2=Q(2); p3=Q(3);
DKt=p1*DK1+p2*DK2+p3*DK3;
endfunction
//-----
clf(6)
t0=0; t1=300; nt=1500; td=(t1-t0)/nt; t=t0:td:t1; iL=tL/td;
xG=zeros(3,1); y=0; xK=zeros(5,1); u=0; ID=0;
for i=1:nt
if i<=iL, yt=[0;1]; ut=0;
else yt=[y(:,i-iL);1]; ut=CK(t(i))*xK(:,i)+DK(t(i))*yt; end
xG=[xG ode(xG(:,i),t(i),t(i+1),fG)];
xK=[xK ode(xK(:,i),t(i),t(i+1),fK)];
y=[y xG(1,i+1)]; u=[u ut];
end
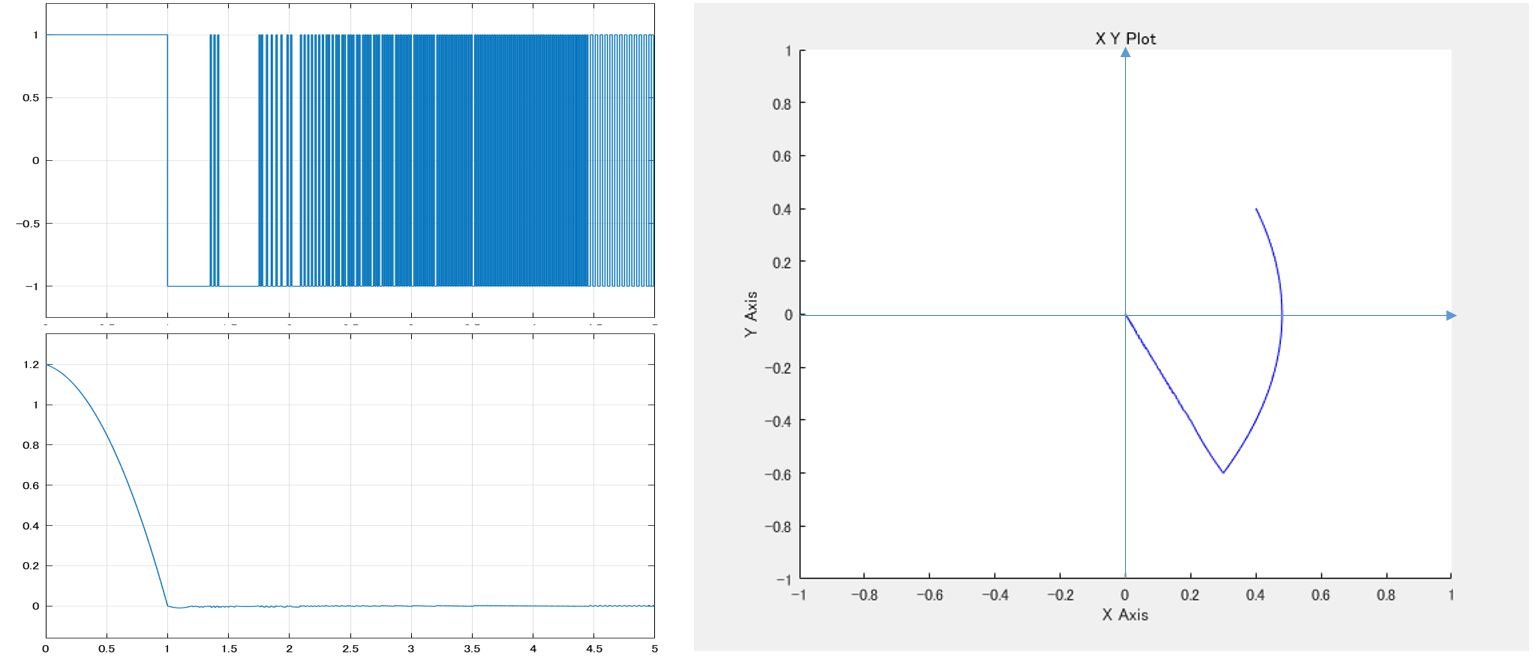
scf(6);subplot(211),plot(t,y,'b');
scf(6);subplot(212),plot(t,u,'b');
//
xG=zeros(3,1); y=0; xK=zeros(5,1); u=0; ID=1;
for i=1:nt
if i<=iL, yt=[0;1]; ut=0;
else yt=[y(:,i-iL);1]; ut=CK(t(i))*xK(:,i)+DK(t(i))*yt; end
xG=[xG ode(xG(:,i),t(i),t(i+1),fG)];
xK=[xK ode(xK(:,i),t(i),t(i+1),fK)];
y=[y xG(1,i+1)]; u=[u ut];
end
scf(6);subplot(211),plot(t,y,'r');
scf(6);subplot(212),plot(t,u,'r');
//
xG=zeros(3,1); y=0; xK=zeros(5,1); u=0; ID=2;
for i=1:nt
if i<=iL, yt=[0;1]; ut=0;
else yt=[y(:,i-iL);1]; ut=CK(t(i))*xK(:,i)+DK(t(i))*yt; end
xG=[xG ode(xG(:,i),t(i),t(i+1),fG)];
xK=[xK ode(xK(:,i),t(i),t(i+1),fK)];
y=[y xG(1,i+1)]; u=[u ut];
end
scf(6);subplot(211),plot(t,y,'m');
scf(6);subplot(212),plot(t,u,'m');
//
xG=zeros(3,1); y=0; xK=zeros(5,1); u=0; ID=3;
for i=1:nt
if i<=iL, yt=[0;1]; ut=0;
else yt=[y(:,i-iL);1]; ut=CK(t(i))*xK(:,i)+DK(t(i))*yt; end
xG=[xG ode(xG(:,i),t(i),t(i+1),fG)];
xK=[xK ode(xK(:,i),t(i),t(i+1),fK)];
y=[y xG(1,i+1)]; u=[u ut];
end
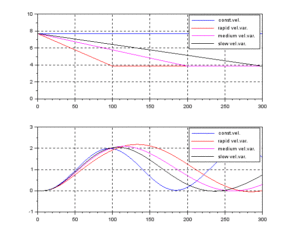
scf(6);subplot(211),plot(t,y,'k'),mtlb_grid,mtlb_axis([t0 t1 -0.5 1.5]);
//legend(['const.vel.';'rapid vel.var.';'medium vel.var.';'slow vel.var.'])
scf(6);subplot(212),plot(t,u,'k'),mtlb_grid,mtlb_axis([t0 t1 -1 1]);
legend(['const.vel.';'rapid vel.var.';'medium vel.var.';'slow vel.var.'])
//-----
//eof
|
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot x(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a4c8217b8c641b28c9d2c724fc2462cb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0639c7053096db5f35e066d8fec1086a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d6ab22ac2ca3b874b7f25f131d7dadba_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{\bar{x}}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22}\\ \end{array}\right] }_{\bar{A}=T_s A T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \bar{B}_2 \end{array}\right] }_{\bar{B}=T_sB} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c151e790bb46588ffe833fc57ad6301b_l3.png)
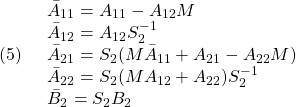
![]() 、すなわち、状態が超平面内に拘束されているとすると
、すなわち、状態が超平面内に拘束されているとすると![]()
![]() の振る舞いは
の振る舞いは![]() によって決まります。一方、
によって決まります。一方、![]() の振る舞いは
の振る舞いは![]()
![]()
![]()
![]() が安定行列となるようにスイッチング関数を選ぶためには、(8)に対する状態フィードバックによる安定化問題を解けばよいことが分かります。
が安定行列となるようにスイッチング関数を選ぶためには、(8)に対する状態フィードバックによる安定化問題を解けばよいことが分かります。![]() を決定する方法が提案されています。
を決定する方法が提案されています。![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \boxed{J=\int_0^\infty \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right]^T }_{x^T(t)} \underbrace{ \left[\begin{array}{cc} Q_{11} & Q_{12} \\ Q_{21} & Q_{22} \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} dt} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-720950a912af5f2005feadc55eef2316_l3.png)
![]()
![]()
![]()
![]()
![]()
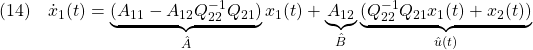
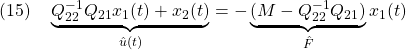
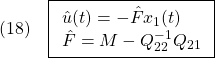
![]()
![]()
![]() を決めればよいことがわかります。
を決めればよいことがわかります。![]()
![]() スイッチング関数決定プログラムswflqrを用いて、図1の台車駆動型倒立振子を安定化する次のSMC則を求めよ。
スイッチング関数決定プログラムswflqrを用いて、図1の台車駆動型倒立振子を安定化する次のSMC則を求めよ。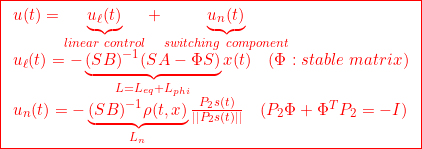
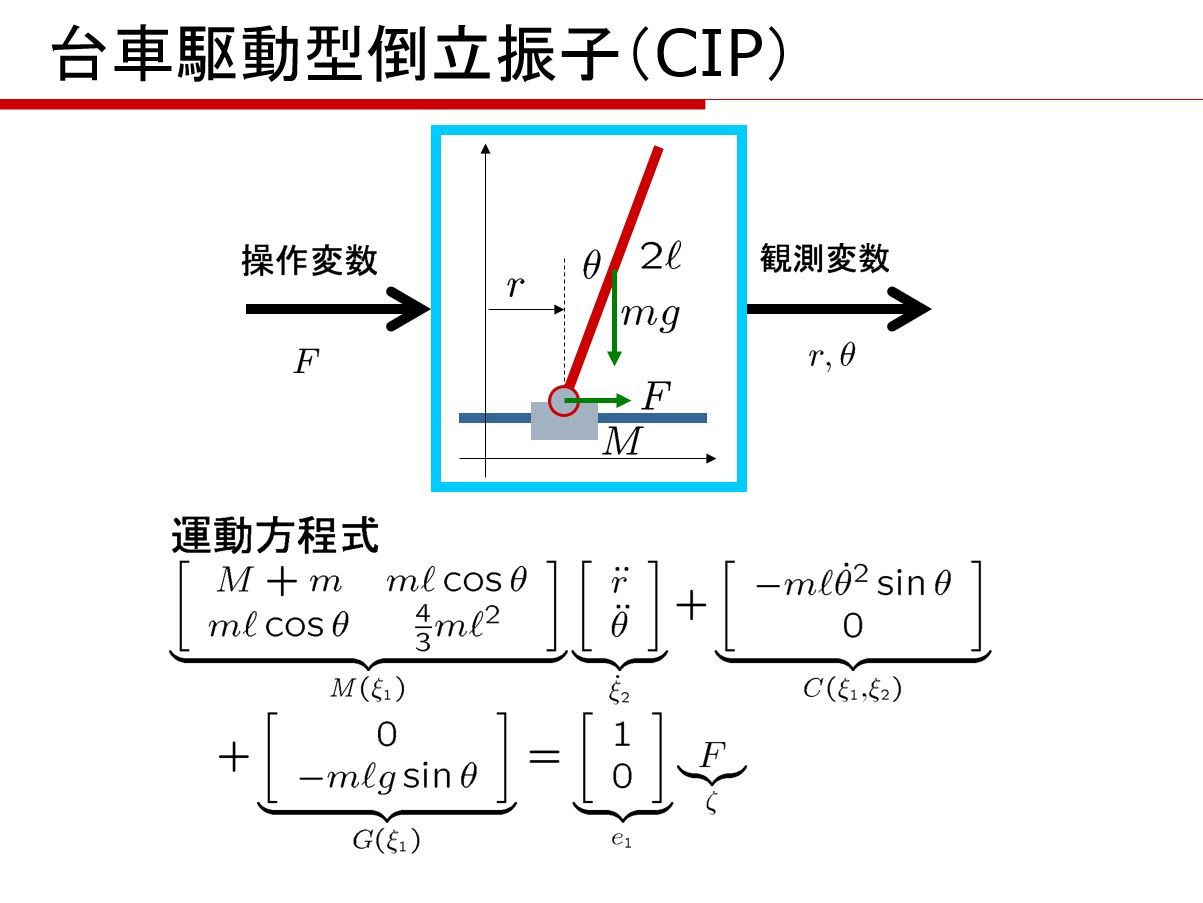

![]() を求めるプログラムswflqrが開発されています。
を求めるプログラムswflqrが開発されています。![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \boxed{\underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t) + \underbrace{ \left[\begin{array}{l} f_u(t,x)\\ f_m(t,x,u) \end{array}\right] }_{f(t,x,u)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7d9915e30ab5eebb009f8eba1931c74b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \boxed{s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I_m \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} \ (M=S_2^{-1}S_1)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fd9d30f50f0b1a358dd111e982cf142d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9b7409c24983e2cf677cd893ab39c8b1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} I & 0 \\ -M & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{\bar{x}}(t)}\\ = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{cc} I & 0 \\ -M & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t)\\ + \underbrace{ \left[\begin{array}{l} f_u(t,x)\\ f_m(t,x,u) \end{array}\right] }_{f(t,x,u)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2603c79f9420895b735d182a315f4d6a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{\bar{x}}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{cc} A_{11}-A_{12}M & A_{12}S_2^{-1} \\ A_{21}-A_{22}M & A_{22}S_2^{-1} \\ \end{array}\right] }_{AT_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}\\ + \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t) + \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{l} f_u(t,x)\\ f_m(t,x,u) \end{array}\right] }_{f(t,x,u)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-97d89cd7503cc935f956b67dce447b04_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \boxed{ \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{\bar{x}}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22}\\ \end{array}\right] }_{\bar{A}=T_s A T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \bar{B}_2 \end{array}\right] }_{\bar{B}=T_sB} u(t)\\ + \underbrace{ \left[\begin{array}{c} f_u(t,x)\\ S_1f_u(t,x)+S_2f_m(t,x,u) \end{array}\right] }_{T_sf(t,x,u)} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-00ef0c4a7e2512e1cdc58d5395f78586_l3.png)
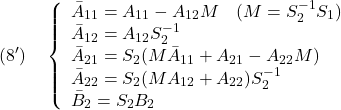
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \boxed{ \begin{array}{lll} V(\bar{x})= \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} P_1 & 0\\ 0 & P_2 \end{array}\right] }_{P} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}\\ \Rightarrow \dot{V}(\bar{x})\le - \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} Q_1 & 0\\ 0 & I \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} \end{array}}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b728547541ea693965c4fb59721e61ea_l3.png)
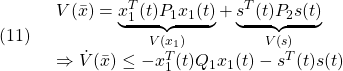
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{cl} (12.1) & s(t)=0\\ \Downarrow &\\ (12.2) & \dot{s}(t)=0\\ \Downarrow &\\ (12.3) & \bar{A}_{21}x_1(t)+\bar{A}_{22}s(t)+\bar{B}_{2}u(t)=0\\ \Downarrow &\\ (12.4) & u_{eq}(t)=-\underbrace{\bar{B}_{2}^{-1}}_{([0\ I]T_sB)^{-1}} \underbrace{\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right]}_{[0\ I]T_sAT_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}\\ \Downarrow & by\ S=[0\ I]T_s, x=T_s^{-1}\bar{x}\\ (12.5) & u_{eq}(t)=-(SB)^{-1}SAx(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aa7375ffaeacc584b4d99f678aa447a2_l3.png)
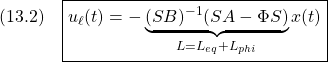
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{s}(t) \end{array}\right] = \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ 0 & \Phi \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ + \left[\begin{array}{c} f_u(t,x)\\ \bar{B}_{2}u_n(t)+S_2(Mf_u(t,x)+f_m(t,x,u)) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1b7f283e78147327758f740eb0f3d38a_l3.png)
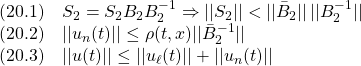
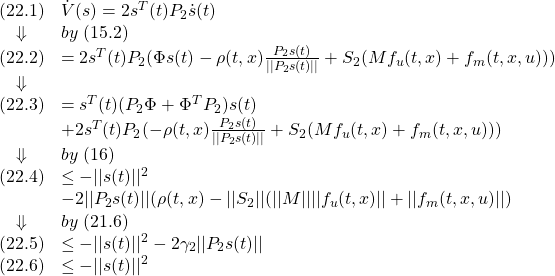
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{x}_{r1}(t)\\ \dot{x}_{r2}(t) \end{array}\right] }_{\dot{x}_r(t)} = \underbrace{ \left[\begin{array}{cc} A_{r11} & A_{r12} \\ A_{r21} & A_{r22} \\ \end{array}\right] }_{A_r=T_rAT_r^T} \underbrace{ \left[\begin{array}{c} x_{r1}(t)\\ x_{r2}(t) \end{array}\right] }_{x_r(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \Sigma_1V^T \end{array}\right] }_{B_r=T_rB} u(t)\\ + \underbrace{ \left[\begin{array}{l} f_{ru}(t,x)\\ f_{rm}(t,x,u) \end{array}\right] }_{f_r(t,x,u)=T_rf(t,x,u)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-37c0842a8446b8a7abc1cbf016179aba_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_{r1} & S_{r2} \\ \end{array}\right] }_{S_r=ST_r^T} \underbrace{ \left[\begin{array}{c} x_{r1}(t)\\ x_{r2}(t) \end{array}\right] }_{x_r(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-988fe8c3933d54a6b2a2343fa71b6828_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \underbrace{ \left[\begin{array}{c} \dot{\theta}\\ \dot{\omega}\\ \dot{i}_a \end{array}\right] }_{\dot{x}} = \underbrace{ \left[\begin{array}{cc|c} 0 & 1 & 0\\ 0 & 0 & \frac{K_t}{J_0}\\\hline 0 & -\frac{K_e}{L_0} & -\frac{R}{L_0} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \theta\\ \omega\\ i_a \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{c} 0\\ 0\\\hline \frac{1}{L_0} \end{array}\right] }_{B} \underbrace{ v_a }_{u} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f34e214e8999446dc4f74a57bf7ab251_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad s= \underbrace{ \left[\begin{array}{ccc} \frac{J_0}{K_t}\omega_n^2 & 2\frac{J_0}{K_t}\zeta\omega_n & 1 \end{array}\right] }_{S}x \quad(M= \left[\begin{array}{ccc} \frac{J_0}{K_t}\omega_n^2 & 2\frac{J_0}{K_t}\zeta\omega_n \end{array}\right]) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-37b3f655680fcf1663a507a6815010ae_l3.png)
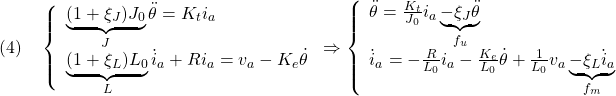
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \dot{x}=Ax+Bu+ \left[\begin{array}{c} 0\\ f_{u}\\ f_{m} \end{array}\right]%} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-403044bf0348dcd88eba34f879facf92_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} {\rm rank}\left[\begin{array}{cc} B & \lambda I_n-A \end{array}\right]\\ = {\rm rank}\left[\begin{array}{ccc} 0 & A_{11}-\lambda I_m & A_{12}\\ B_{2} & A_{21} & A_{22}-\lambda I_m \end{array}\right]\\ = {\rm rank}\left[\begin{array}{ccc} A_{11}-\lambda I_m & A_{12} \end{array}\right]+m \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-585e01601ba9a848826ac5abbfdf9019_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} {\rm det}\left[\begin{array}{cc} \lambda I_n-A & -B\\ -S & 0 \end{array}\right]\\ = {\rm det}\left[\begin{array}{ccc} \lambda I_{n-m}-A_{11} & -A_{12} & 0\\ -A_{21} & \lambda I_m-A_{22} & -B_{2}\\ -S_1 & -S_2 & 0 \end{array}\right]=0\\ \Leftrightarrow {\rm det}\left[\begin{array}{ccc} \lambda I_{n-m}-A_{11} & -A_{12} \\ -S_1 & -S_2 \end{array}\right]=0\\ \Leftrightarrow{\rm det} \left[\begin{array}{cc} I_{n-m} & -A_{12}S_2^{-1} \\ 0 & I_m \end{array}\right]\left[\begin{array}{cc} \lambda I_{n-m}-\bar{A}_{11} & 0 \\ 0 & -S_2 \end{array}\right] \left[\begin{array}{cc} I_{n-m} & 0 \\ M & I_m \end{array}\right]\\ ={\rm det}(\lambda I_{n-m}-\bar{A}_{11}){\rm det}(-S_2)=0\\ \Leftrightarrow {\rm det}(\lambda I_{n-m}-\bar{A}_{11})=0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-571e2b9312a22e1a6842d8c5bcbcb33f_l3.png)
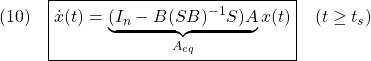
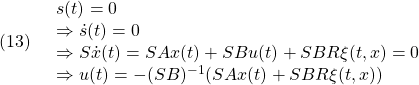
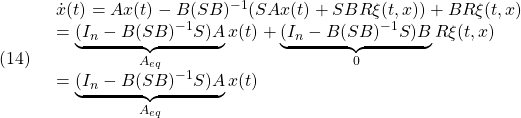
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} 0 & 1\\ 0 & 0 \end{array}\right] }_{A} \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right]+ \underbrace{ \left[\begin{array}{c} 0\\ 1 \end{array}\right] }_{B} u(t)+ \underbrace{ \left[\begin{array}{c} 0\\ -a\sin x_1(t) \end{array}\right] }_{f} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5f207f5d4fc2ee68a8e5cbb3983a83af_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ s(t)= \underbrace{ \left[\begin{array}{cc} m & 1 \end{array}\right] }_{S} \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3a1328c53082e4bc421dbdb031541ce8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad A= \left[\begin{array}{cccc|c} 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & 0 & \vdots \\ \vdots & & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & 0 & 1 \\\hline -a_1 & -a_2 & \cdots & \cdots & -a_n \end{array}\right],\quad B=\left[\begin{array}{c} 0 \\ 0 \\ \vdots \\ 0 \\\hline 1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ef11f7c43ce31771dd5871c77048689e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \begin{array}{r} \Delta A(t)= \left[\begin{array}{cccc|c} 0 & 0 & 0 & \cdots & 0 \\ 0 & 0 & 0 & 0 & \vdots \\ \vdots & & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & 0 & 0 \\\hline -\delta_1(t) & -\delta_2(t) & \cdots & \cdots & -\delta_n(t) \end{array}\right]\\ k_i^-\le\delta_i(t)\le k_i^+\quad(i=1,\cdots,n) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-34525207b48d6d25b7f649dbf4d8bc0a_l3.png)
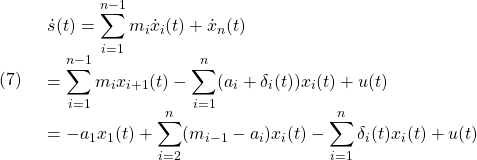
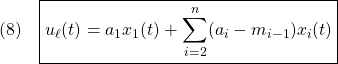
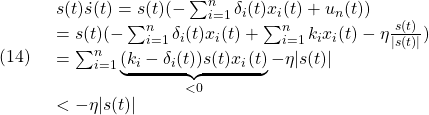
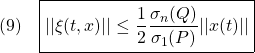
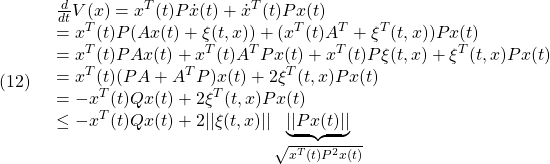
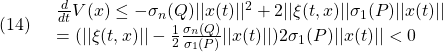
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \left[\begin{array}{c} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -4 & -1 \end{array}\right] }_{A} \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right] + \underbrace{\left[\begin{array}{c} 0 \\ 1 \end{array}\right]}_{D}\underbrace{\sin(2t)}_{\xi(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-686b73217e57bd77cd759540d3fae61f_l3.png)
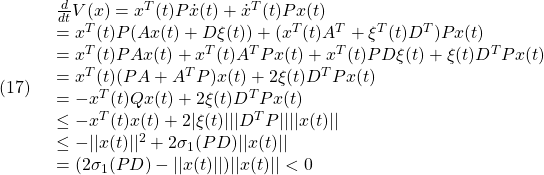
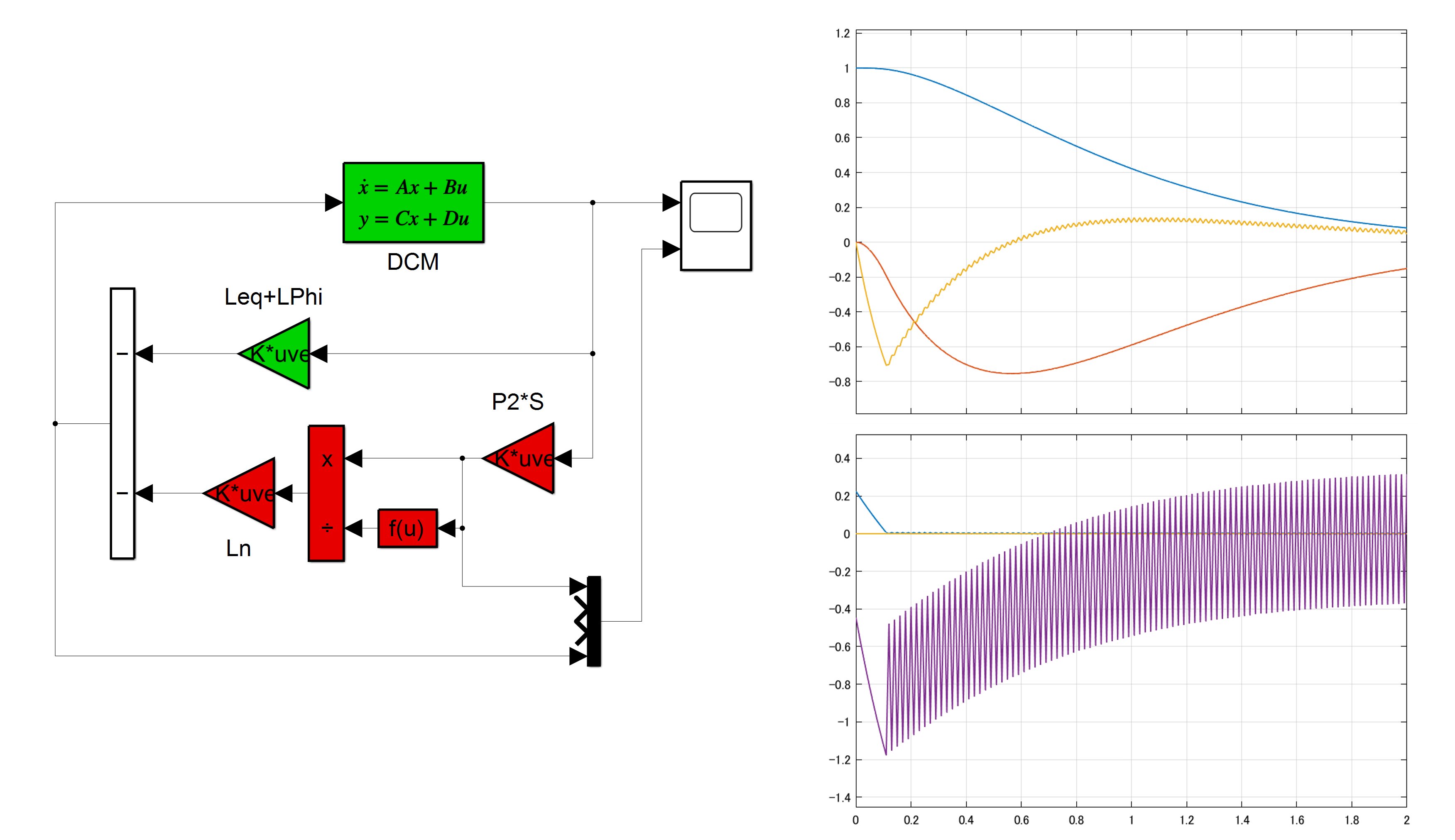
 図1 モデルの不確かさがある場合の解軌道
図1 モデルの不確かさがある場合の解軌道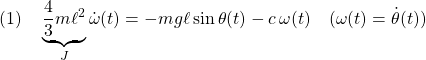
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \frac{d}{dt} \underbrace{\left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right]}_{x} = \underbrace{ \left[\begin{array}{c} \omega(t) \\ -\frac{mg\ell}{J}\sin\theta(t)-\frac{c}{J}\omega(t) \end{array}\right] }_{f(x)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3b7ba41f7598be72c8ae81339591673c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad V=\frac{1}{2} \underbrace{ \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right]^T \left[\begin{array}{cc} \frac{1}{2}\frac{c^2}{J} & \frac{1}{2}c \\ \frac{1}{2}c & J \end{array}\right] \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right] }_{x^T(t)Px(t)} +mg\ell(1-\cos\theta(t))>0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-98c8ff12c9923ef1a298272fc344e4e4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \dot{V}(t)=\frac{1}{2}(x^TP\dot{x}+\dot{x}^TPx)+mg\ell\omega\sin\theta =x^TP\dot{x}+mg\ell\omega\sin\theta\\ =\left[\begin{array}{c} \theta \\ \omega \end{array}\right]^T \left[\begin{array}{cc} p_1 & p_3 \\ p_3 & p_2 \end{array}\right] \left[\begin{array}{c} \omega \\ -\frac{mg\ell}{J}\sin\theta-\frac{c}{J}\omega \end{array}\right]+mg\ell\omega\sin\theta\\ =\left[\begin{array}{cc} \theta &\omega \end{array}\right] \left[\begin{array}{cc} p_1\omega -p_3(\frac{mg\ell}{J}\sin\theta+\frac{c}{J}\omega) \\ p_3\omega -p_2(\frac{mg\ell}{J}\sin\theta+\frac{c}{J}\omega) \end{array}\right]+mg\ell\omega\sin\theta\\ =p_1\theta\omega -p_3(\frac{mg\ell}{J}\theta\sin\theta+\frac{c}{J}\theta\omega)+ p_3\omega^2 -p_2(\frac{mg\ell}{J}\omega\sin\theta+\frac{c}{J}\omega^2)+mg\ell\omega\sin\theta\\ =-\frac{mg\ell}{J}\sin\theta(p_3\theta+p_2\omega-J\omega) +(p_3-p_2\frac{c}{J})\omega^2+(p_1-p_3\frac{c}{J})\theta\omega \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6c783b4a46a73e78fb425f69bfa45499_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \left[\begin{array}{c} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{mg\ell}{J} & -\frac{c}{J} \end{array}\right] }_{A} \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ \frac{mg\ell}{J} \end{array}\right] }_{D} \underbrace{ (\theta(t)-\sin\theta(t)) }_{\xi(x)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0c7be17a5704d87667dc74b647c5f7da_l3.png)
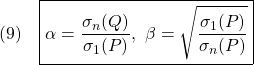
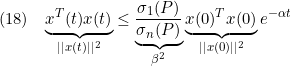
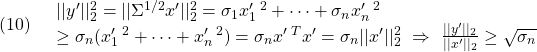
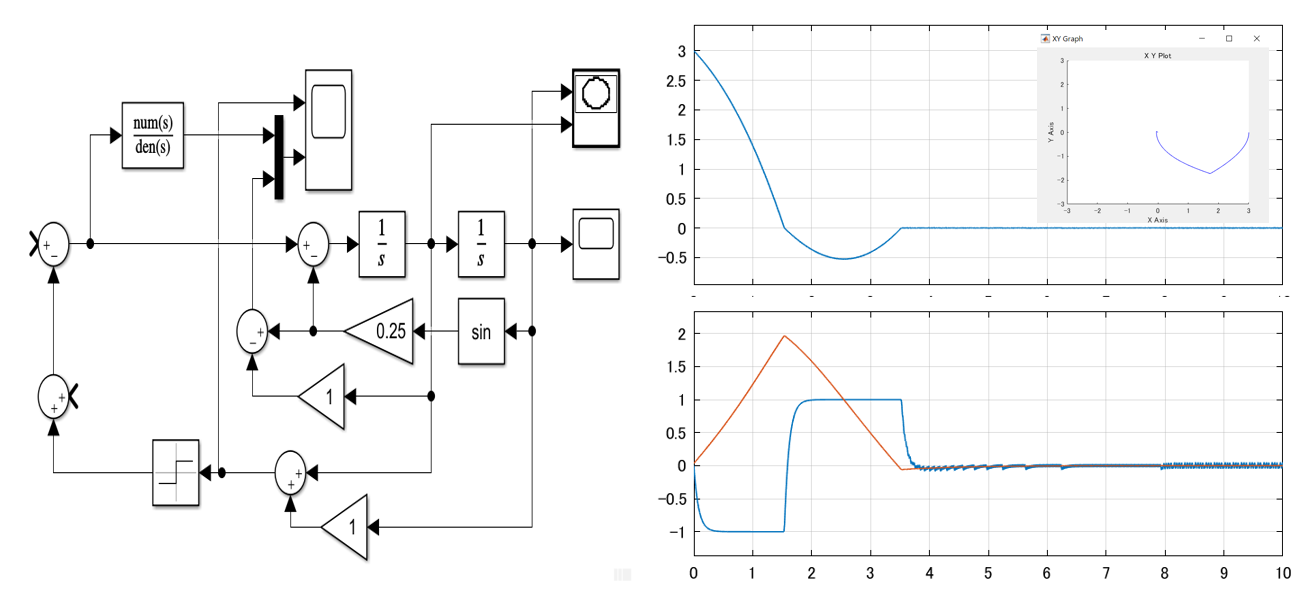
 図2
図2 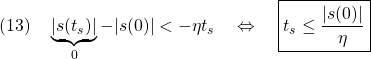
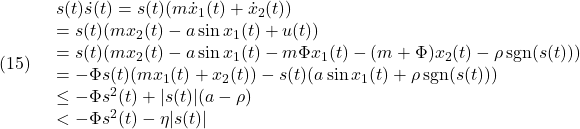
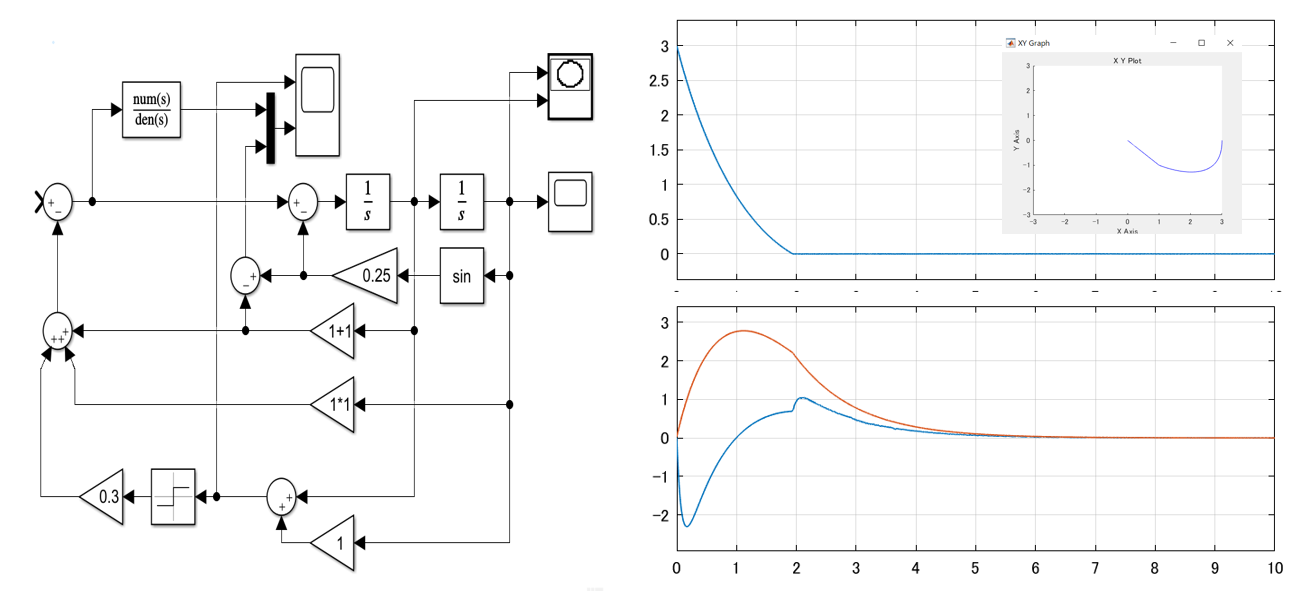
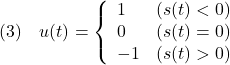
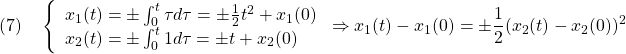

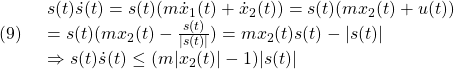

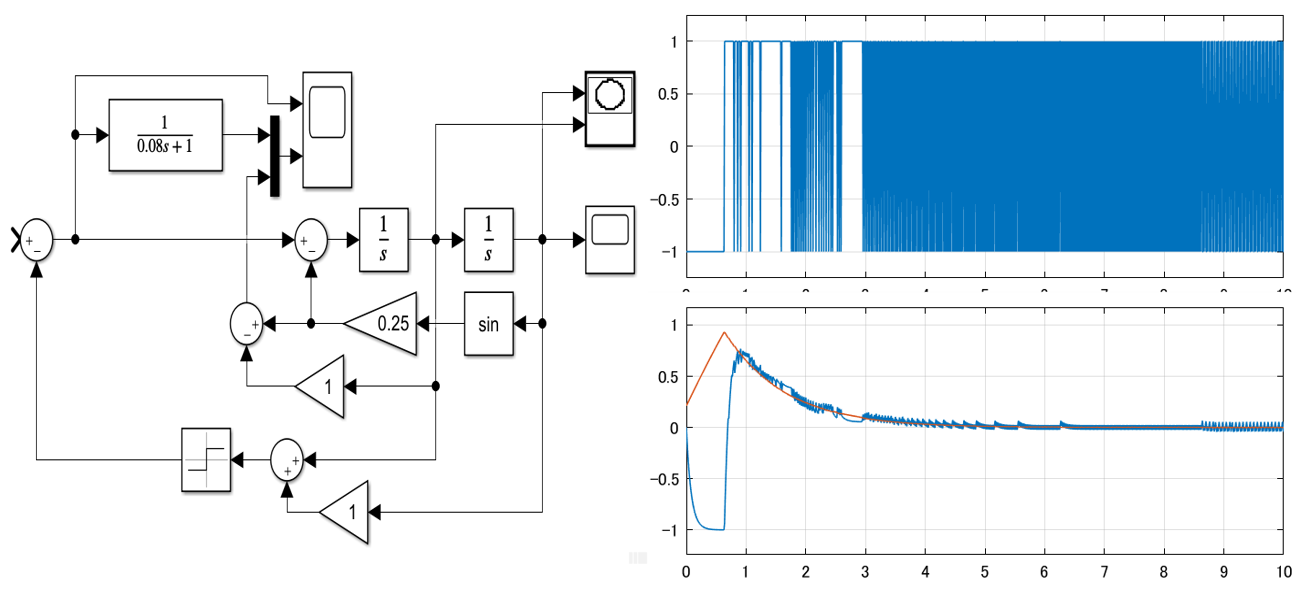

![Rendered by QuickLaTeX.com \displaystyle{(1a)\quad \underbrace{ \left[\begin{array}{c|ccc} \alpha & m_1 & \dots &m_N \\ \hline m_1 & 1 & & 0 \\ \vdots & & \ddots & \\ m_N & 0 & & 1 \\ \end{array}\right] }_{M=\left[\begin{array}{cc} M_{11} & M_{12} \\ M_{21} & M_{22} \end{array}\right]} \underbrace{ \left[\begin{array}{c} \ddot{\theta} \\ \hline \ddot{r}_1 \\ \vdots \\ \ddot{r}_N \end{array}\right] }_{\ddot{\xi}} + \underbrace{ \left[\begin{array}{c|ccc} 0 & 0 & \dots &0 \\ \hline 0 & \Omega_1^2 & & 0 \\ \vdots & & \ddots & \\ 0 & 0 & & \Omega_N^2 \\ \end{array}\right] }_{K=\left[\begin{array}{cc} K_{11} & K_{12} \\ K_{21} & K_{22} \end{array}\right]} \underbrace{ \left[\begin{array}{c} \theta \\ \hline r_1 \\ \vdots \\ r_N \end{array}\right] }_{\xi} = \underbrace{ \left[\begin{array}{c} 1 \\ \hline 0 \\ \vdots \\ 0 \end{array}\right] }_{B_2} u' }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-346490e79fcc2267740093f5fde47d5f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1b)\quad \eta(\xi)= \underbrace{ \left[\begin{array}{c|ccc} 0 & \phi_1(\xi) & \dots &\phi_N(\xi) \end{array}\right] }_{C_1} \underbrace{ \left[\begin{array}{c} \theta \\ \hline r_1 \\ \vdots \\ r_N \end{array}\right] }_{\xi} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8a564535f5712a1756e4d97b569ada10_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2a)\quad \underbrace{ \left[\begin{array}{c} \dot{\xi} \\ \ddot{\xi} \end{array}\right] }_{\dot{x}} = \underbrace{ \left[\begin{array}{cc} 0_{N+1\times N+1} & I_{N+1} \\ M^{-1}K & 0_{N+1\times N+1} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \xi \\ \dot{\xi} \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{cc} 0_{N+1\times 1} \\ M^{-1}B_2 \end{array}\right] }_{B} u'}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-524df64b74898d10a9e6574263d3ca12_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2b)\quad \eta(\xi)= \underbrace{ \left[\begin{array}{cc} C_1 & 0_{1\times N} \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \xi \\ \dot{\xi} \end{array}\right] }_{x} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6e8294598be55b2b237fc74f95338ce8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{ \left[\begin{array}{c} m_1 \\ \vdots \\ m_N \\ \end{array}\right] }_{M_{21}} \ddot{\theta} + \underbrace{ \left[\begin{array}{c} \ddot{r}_1 \\ \vdots \\ \ddot{r}_N \end{array}\right] }_{\ddot{r}} + \underbrace{ \left[\begin{array}{ccc} \Omega_1^2 & & 0 \\ & \ddots & \\ 0 & & \Omega_N^2 \\ \end{array}\right] }_{K_{22}} \underbrace{ \left[\begin{array}{c} r_1 \\ \vdots \\ r_N \end{array}\right] }_{r} = \left[\begin{array}{c} 0 \\ \vdots \\ 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-83e03635bb43c77e2201d7335edf4248_l3.png)
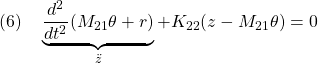
![Rendered by QuickLaTeX.com \displaystyle{(7a)\quad \underbrace{ \left[\begin{array}{c} \dot{z} \\ \dot{\theta} \\\hline \ddot{z} \\ \ddot{\theta} \end{array}\right] }_{\dot{x}} = \underbrace{ \left[\begin{array}{cc|cc} 0_{N\times N} & 0_{N\times 1} & I_N & 0_{N\times 1} \\ 0_{1\times N} & 0 & 0_{1\times N} & 1 \\\hline -K_{22} & K_{22}M_{21} & 0_{N\times N} & 0_{N\times 1} \\ 0_{1\times N} & 0 & 0_{1\times N} & -\frac{1}{T_a} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} {z} \\ {\theta} \\\hline \dot{z} \\ \dot{\theta} \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{cc} 0_{N\times 1} \\ 0 \\\hline 0_{N\times 1} \\ \frac{1}{T_a} \end{array}\right] }_{B} \dot{\theta}_c}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4e568bda7882b131b5b24ac100e86af6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7b)\quad \eta(\xi)= \underbrace{ \left[\begin{array}{ccc} \phi_1(\xi) & \cdots & \phi_N(\xi) \end{array}\right] \left[\begin{array}{cc|cc} I_N & -M_{21} & 0_{N\times N} & 0_{N\times 1} \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} {z} \\ {\theta} \\\hline \dot{z} \\ \dot{\theta} \end{array}\right] }_{x} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4598350d67871b8cea2146c9120e81d4_l3.png)

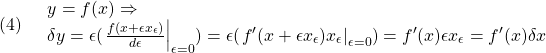
![Rendered by QuickLaTeX.com \displaystyle{ +\left[\rho A \int_0^{L} (x^2+{y}^2)\dot{\theta}+x\dot{y})\delta{\theta}dx\right]_{t_0}^{t_1}-\int_{t_0}^{t_1}\rho A \int_0^{L} \frac{d}{dt}((x^2+{y}^2)\dot{\theta}+x\dot{y})\delta{\theta}dxdt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f2118385d5eb945d389e6974e74e24cb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ +\left[\rho A \int_0^{L} (x\dot{\theta}+\dot{y}) \delta{y}dx\right]_{t_0}^{t_1}-\int_{t_0}^{t_1}\rho A \int_0^{L}\frac{d}{dt}(x\dot{\theta}+\dot{y})\delta{y}dxdt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cc6f74dcfcb568ed2b50d8e94189dc56_l3.png)
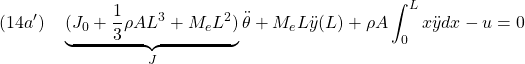
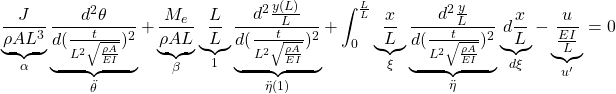
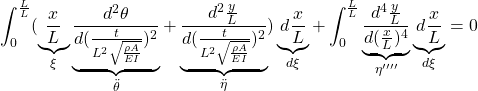
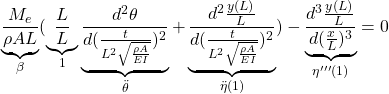
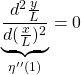
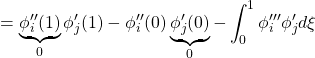
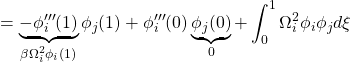
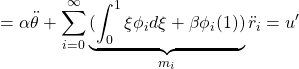
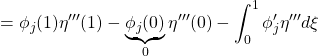
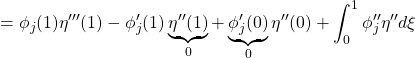
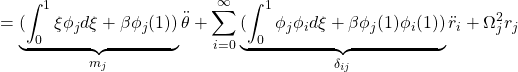
![Rendered by QuickLaTeX.com \displaystyle{(31a)\quad \underbrace{ \left[\begin{array}{c|ccc} \alpha & m_1 & \dots &m_N \\ \hline m_1 & 1 & & 0 \\ \vdots & & \ddots & \\ m_N & 0 & & 1 \\ \end{array}\right] }_{M=\left[\begin{array}{cc} M_{11} & M_{12} \\ M_{21} & M_{22} \end{array}\right]} \underbrace{ \left[\begin{array}{c} \ddot{\theta} \\ \hline \ddot{r}_1 \\ \vdots \\ \ddot{r}_N \end{array}\right] }_{\ddot{\xi}} + \underbrace{ \left[\begin{array}{c|ccc} 0 & 0 & \dots &0 \\ \hline 0 & \Omega_1^2 & & 0 \\ \vdots & & \ddots & \\ 0 & 0 & & \Omega_N^2 \\ \end{array}\right] }_{K=\left[\begin{array}{cc} K_{11} & K_{12} \\ K_{21} & M_{22} \end{array}\right]} \underbrace{ \left[\begin{array}{c} \theta \\ \hline r_1 \\ \vdots \\ r_N \end{array}\right] }_{\xi} = \underbrace{ \left[\begin{array}{c} 1 \\ \hline 0 \\ \vdots \\ 0 \end{array}\right] }_{B_2} u' }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-406d85fd430e037da5f5fde6fb0cad78_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(31b)\quad \eta(\xi)= \underbrace{ \left[\begin{array}{c|ccc} 0 & \phi_1(\xi) & \dots &\phi_N(\xi) \end{array}\right] }_{C_1} \underbrace{ \left[\begin{array}{c} \theta \\ \hline r_1 \\ \vdots \\ r_N \end{array}\right] }_{\xi} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ffc9ed02df3822a5d966a2c9ff2b13e0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(33a)\quad \underbrace{ \left[\begin{array}{c} \dot{\xi} \\ \ddot{\xi} \end{array}\right] }_{\dot{x}} = \underbrace{ \left[\begin{array}{cc} 0_{N+1\times N+1} & I_{N+1} \\ M^{-1}K & 0_{N+1\times N+1} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \xi \\ \dot{\xi} \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{cc} 0_{N+1\times 1} \\ M^{-1}B_2 \end{array}\right] }_{B} u'}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d04b4ccfb3bb84e6759113fd60916749_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(33b)\quad \eta(\xi)= \underbrace{ \left[\begin{array}{cc} C_1 & 0_{1\times N} \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \xi \\ \dot{\xi} \end{array}\right] }_{x} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3fe155c9c292f0b7a39bf25b09174740_l3.png)
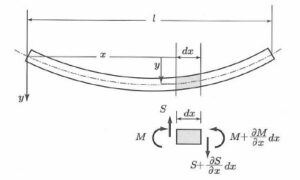
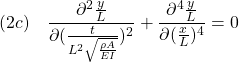 ,
, 
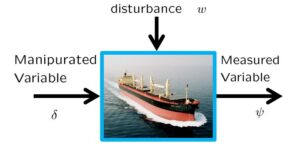
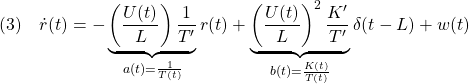
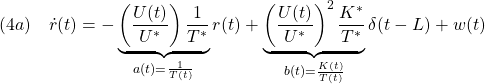
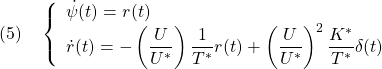
![Rendered by QuickLaTeX.com \displaystyle{(7a)\quad \underbrace{ \left[\begin{array}{c} \dot{\psi}(t) \\ \dot{r}(t) \\ \dot{\delta}(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0\\ 0 & -\left(\frac{U}{U^*}\right)\frac{1}{T^*} & \left(\frac{U}{U^*}\right)^2\frac{K^*}{T^*} \\ 0 & 0 & -\frac{1}{T_a} \end{array}\right] }_{A(U,U^2)} \underbrace{ \left[\begin{array}{c} \psi(t) \\ r(t) \\ \delta(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ \frac{K_a}{T_a} \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c40bbf2a01c1e41bb4cb2a38046541e9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7b)\quad \underbrace{ \psi(t) }_{y(t)} = \underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \psi(t) \\ r(t) \\ \delta(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-faf87c1ef2f82cfeaf915946a02f861a_l3.png)
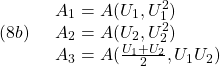
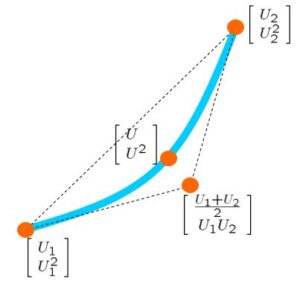
![Rendered by QuickLaTeX.com \displaystyle{(8c)\quad \begin{array}{l} p_1(U,U^2)=\frac{1}{p_0}\det \left[\begin{array}{cc} U-U_3 & U_2-U_3 \\ U^2-U_1U_2 & U_2^2-U_1U_2 \\ \end{array}\right]\\ p_2(U,U^2)=\frac{1}{p_0}\det \left[\begin{array}{cc} U_1-U_3 & U-U_3 \\ U_1^2-U_1U_2 & U^2-U_1U_2 \\ \end{array}\right]\\ p_3(U,U^2)=\frac{1}{p_0}\det \left[\begin{array}{cc} U_1-U_2 & U_2-U \\ U_1^2-U_2^2 & U_2^2-U^2 \\ \end{array}\right]\\ p_0=\det \left[\begin{array}{cc} U_1-U_2 & U_2-U_3 \\ U_1^2-U_2^2 & U_2^2-U_1U_2 \\ \end{array}\right]\\ p_1(U,U^2)+p_2(U,U^2)+p_3(U,U^2)=1 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7b82416721e9f2c01e1e17b0b24b075c_l3.png)
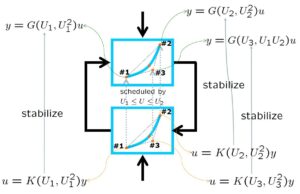
![Rendered by QuickLaTeX.com \displaystyle{(9a)\quad P: \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x} \\ \dot{x}_I \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A(U,U^2)& 0 \\ -C & 0 \end{array}\right] }_{A(U,U^2)} \left[\begin{array}{c} x \\ x_I \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_1} r + \underbrace{\left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_2} u\\ \underbrace{ \left[\begin{array}{c} y_{11} \\ y_{12} \end{array}\right] }_{y_1} = \underbrace{ \left[\begin{array}{cc} 0 &\omega_I\\ \omega_DCA(U,U^2) & 0 \end{array}\right] }_{C_1} \left[\begin{array}{c} x \\ x_I \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \end{array}\right] }_{D_{11}} r + \underbrace{ \left[\begin{array}{c} 0 \\ \omega_DCB \end{array}\right] }_{D_{12}} u\\ \underbrace{ \left[\begin{array}{c} y \\ x_I \end{array}\right] }_{y_2} = \underbrace{ \left[\begin{array}{cc} C & 0\\ 0 & 1 \end{array}\right] }_{C_2} \left[\begin{array}{c} x \\ x_I \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \end{array}\right] }_{D_{21}} r \end{array}\right.}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-34bf0da930252e74bd42cb1640969702_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10a)\quad K_0: \left\{\begin{array}{l} \dot{x}_K=A_K(U,U^2)x_K+ \underbrace{ \left[\begin{array}{cc} B_K^{(1)}(U,U^2) & B_K^{(2)}(U,U^2) \end{array}\right] }_{B_K(U,U^2)} \left[\begin{array}{c} y \\ x_I \end{array}\right] \\ u=C_K(U,U^2)x_K + \underbrace{ \left[\begin{array}{cc} D_K^{(1)}(U,U^2) & D_K^{(2)}(U,U^2) \end{array}\right] }_{D_K(U,U^2)} \left[\begin{array}{c} y \\ x_I \end{array}\right] \end{array}\right.}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a9bc3ecd695bd182e8c63d29351d1924_l3.png)
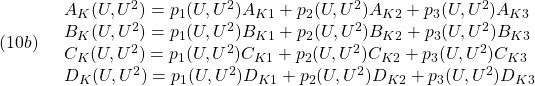
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad K: \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_K \\ \dot{x}_I \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A_K(U,U^2) & B_K^{(2)}(U,U^2) \\ 0 & 0 \end{array}\right] }_{A_K(U,U^2)} \left[\begin{array}{c} x_K \\ x_I \end{array}\right]\\ + \underbrace{ \left[\begin{array}{cc} B_K^{(1)}(U,U^2) & 0\\ -1& 1 \end{array}\right] }_{B_K(U,U^2)} \left[\begin{array}{c} y \\ r \end{array}\right] \\ u= \underbrace{ \left[\begin{array}{cc} C_K(U,U^2) & D_K^{(2)}(U,U^2) \end{array}\right] }_{C_K(U,U^2)} \left[\begin{array}{c} x_K \\ x_I \end{array}\right]\\ + \underbrace{ \left[\begin{array}{cc} D_K^{(1)}(U,U^2) & 0 \end{array}\right] }_{D_K(U,U^2)} \left[\begin{array}{c} y \\ r \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b11949446b4d75aac55c83f1105e175c_l3.png)




