[1] 柔軟構造物の制振問題をどう取り扱うかを考えて行きます。

この写真は米国の某大学で製作された制御実験装置です。柔軟ビームの一端をロボットアームで把持し、振動を抑制しながら回転させることが制御目的です。この柔軟ビームは水平方向ばかりでなく、垂直方向にも振動するのですが、ここでは水平方向だけの振動抑制問題を考えます。参考にしたのは次の文献です。
阿部・児島著:「無駄時間・分布定数系の制御」、コロナ社、2007
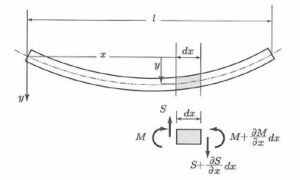
この本の6章「振動系」では、次のような制御対象「柔軟ビーム」を扱っています。

ここで、ビームの長さを![]() [m]、断面積を
[m]、断面積を![]() [m
[m![]() ]、密度を
]、密度を![]() [kg/m
[kg/m![]() ]、縦弾性係数を
]、縦弾性係数を![]() [N/m
[N/m![]() ]、断面2次モーメントを
]、断面2次モーメントを![]() [m
[m![]() ]、ハブの回転慣性モーメントを
]、ハブの回転慣性モーメントを![]() [kgm
[kgm![]() ]、ペイロードを
]、ペイロードを![]() [kg]とします。また、時刻
[kg]とします。また、時刻![]() [sec]における、ハブの回転角を
[sec]における、ハブの回転角を![]() [rad]、ハブの支持点から距離
[rad]、ハブの支持点から距離![]() [m]のビーム上の点の弾性変位を
[m]のビーム上の点の弾性変位を![]() [m]、その点の座標を
[m]、その点の座標を![]() とします。
とします。
このときハブの支持点![]() において次が成り立ちます。
において次が成り立ちます。
![]()
いま、![]() 、
、![]() をそれぞれ
をそれぞれ![]() 、
、![]() と略記すると、次式が成り立ちます。
と略記すると、次式が成り立ちます。
![]()
![]()
![]()
![]()
![]()
以下では、双曲線関数![]() 、
、![]() をそれぞれ
をそれぞれ![]() 、
、![]() と略記し、次の基本式を多用します。
と略記し、次の基本式を多用します。
![]() ,
,
![]()
![]() ,
, ![]()
![]() ,
, ![]()
また、次のような変分を取ることを頻繁に行います。
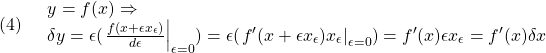
●柔軟ビームの運動方程式を、Hamilton Principleに基づいて導出します。
![]()
![]()
●![]()
![]()
![]()
![]()
![]()
●![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{ +\left[\rho A \int_0^{L} (x^2+{y}^2)\dot{\theta}+x\dot{y})\delta{\theta}dx\right]_{t_0}^{t_1}-\int_{t_0}^{t_1}\rho A \int_0^{L} \frac{d}{dt}((x^2+{y}^2)\dot{\theta}+x\dot{y})\delta{\theta}dxdt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f2118385d5eb945d389e6974e74e24cb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ +\left[\rho A \int_0^{L} (x\dot{\theta}+\dot{y}) \delta{y}dx\right]_{t_0}^{t_1}-\int_{t_0}^{t_1}\rho A \int_0^{L}\frac{d}{dt}(x\dot{\theta}+\dot{y})\delta{y}dxdt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cc6f74dcfcb568ed2b50d8e94189dc56_l3.png)
![]()
●![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
●![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
●![]()
![]()
![]()
![]()
![]()
●以上から、ハミルトン原理を表す上式の各項を
![]()
![]()
![]()
![]()
![]()
![]()
![]()
のように得たので、次式が成り立ちます。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
これから各変分の係数(下線部)を0と置いて、柔軟ビームの運動方程式として次式を得ます。
![]()
![]()
![]()
![]()
●高次項や高階微分項は微小であるとして、これらの近似を行います。まず第1式(13a)は
![]()
![]()
において![]() が微小であるとして、次のように近似します。
が微小であるとして、次のように近似します。
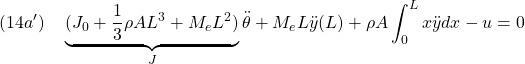
また、第2式(13b)と第3式(13c)は、![]() が微小であるとして、次のように近似します。
が微小であるとして、次のように近似します。
![]()
![]()
これらを次のように無次元化します。
![]() 第1式(14a’):
第1式(14a’):
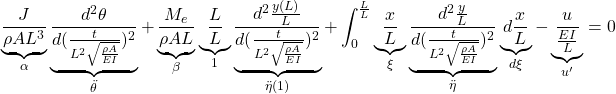
![]() 第2式(14b):
第2式(14b):
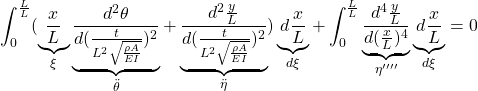
![]() 第3式(14c):
第3式(14c):
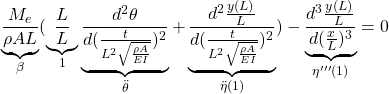
![]() 第4式(13d):
第4式(13d):
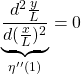
すなわち、代表長さ![]() 、代表時間
、代表時間![]() 、代表トルク
、代表トルク![]() として、無次元化した柔軟ビームの運動方程式は次式となります。
として、無次元化した柔軟ビームの運動方程式は次式となります。
![]()
![]()
![]()
![]()
ただし
![]()
![]()
![]()
![]()
[2] 以下では、モード法による求解方法を考えていきます。
そのために、![]() を仮定すると
を仮定すると
![]()
![]()
![]()
を得ます。ここで、変数分離![]() を行います。
を行います。
![]()
![]()
![]()
さらに、![]() ,
, ![]() を仮定しますと
を仮定しますと
![]()
![]()
![]()
を得ます。これから
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
を得ます。さらに![]() が満足すべき制約式を次のように得ます。
が満足すべき制約式を次のように得ます。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
●これを満足する![]() を、
を、![]() としますと、次のモード関数群を得たことになります。
としますと、次のモード関数群を得たことになります。
![]()
ただし
![]()
これらのモード関数はお互いに直交することが次のようにして示されます(![]() )。
)。
![]()
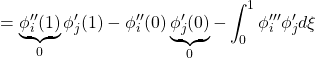
![]()
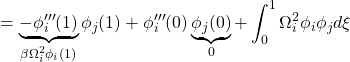
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
●結局、弾性変位![]() を、モード関数
を、モード関数![]() を時間関数
を時間関数![]() で重み付けて
で重み付けて
![]()
のように表します。この時間関数![]() の支配方程式は
の支配方程式は
![]()
![]()
から得られます。まず、第1式(26a)から
![]()
![]()
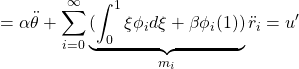
を得ます。次に
![]()
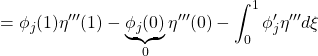
![]()
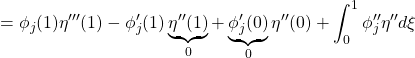
![]()
![]()
を考慮して、第2式(26b)から
![]()
![]()
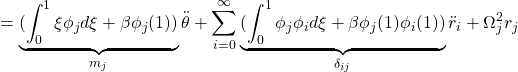
![]()
を得ます。すなわち時間関数![]() は次式を満足すべきことがわかります。
は次式を満足すべきことがわかります。
![]()
![]()
●これから、柔軟ビームに関するもう一つの運動方程式として、次を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(31a)\quad \underbrace{ \left[\begin{array}{c|ccc} \alpha & m_1 & \dots &m_N \\ \hline m_1 & 1 & & 0 \\ \vdots & & \ddots & \\ m_N & 0 & & 1 \\ \end{array}\right] }_{M=\left[\begin{array}{cc} M_{11} & M_{12} \\ M_{21} & M_{22} \end{array}\right]} \underbrace{ \left[\begin{array}{c} \ddot{\theta} \\ \hline \ddot{r}_1 \\ \vdots \\ \ddot{r}_N \end{array}\right] }_{\ddot{\xi}} + \underbrace{ \left[\begin{array}{c|ccc} 0 & 0 & \dots &0 \\ \hline 0 & \Omega_1^2 & & 0 \\ \vdots & & \ddots & \\ 0 & 0 & & \Omega_N^2 \\ \end{array}\right] }_{K=\left[\begin{array}{cc} K_{11} & K_{12} \\ K_{21} & M_{22} \end{array}\right]} \underbrace{ \left[\begin{array}{c} \theta \\ \hline r_1 \\ \vdots \\ r_N \end{array}\right] }_{\xi} = \underbrace{ \left[\begin{array}{c} 1 \\ \hline 0 \\ \vdots \\ 0 \end{array}\right] }_{B_2} u' }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-406d85fd430e037da5f5fde6fb0cad78_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(31b)\quad \eta(\xi)= \underbrace{ \left[\begin{array}{c|ccc} 0 & \phi_1(\xi) & \dots &\phi_N(\xi) \end{array}\right] }_{C_1} \underbrace{ \left[\begin{array}{c} \theta \\ \hline r_1 \\ \vdots \\ r_N \end{array}\right] }_{\xi} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ffc9ed02df3822a5d966a2c9ff2b13e0_l3.png)
ただし
![]()
![]()
![]()
![]()
![]()
![]()
![]()
これから次の状態空間表現を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(33a)\quad \underbrace{ \left[\begin{array}{c} \dot{\xi} \\ \ddot{\xi} \end{array}\right] }_{\dot{x}} = \underbrace{ \left[\begin{array}{cc} 0_{N+1\times N+1} & I_{N+1} \\ M^{-1}K & 0_{N+1\times N+1} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \xi \\ \dot{\xi} \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{cc} 0_{N+1\times 1} \\ M^{-1}B_2 \end{array}\right] }_{B} u'}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d04b4ccfb3bb84e6759113fd60916749_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(33b)\quad \eta(\xi)= \underbrace{ \left[\begin{array}{cc} C_1 & 0_{1\times N} \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \xi \\ \dot{\xi} \end{array}\right] }_{x} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3fe155c9c292f0b7a39bf25b09174740_l3.png)
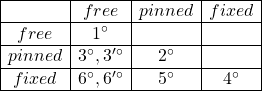
Note B64 モード関数
●ビーム(梁)の境界条件を、自由支持・ピン支持・固定支持と変えた場合のモード関数と振動数方程式を示します。ここで、![]() が解
が解 ![]() を持つための条件
を持つための条件 ![]() が使われていることに注意してください。
が使われていることに注意してください。
(藤田勝久:振動工学、森北出版より)
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
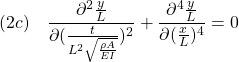 ,
, 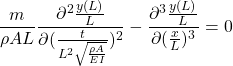
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]()
![]()
![]()
![]() 自由・自由支持の場合 (
自由・自由支持の場合 (![]() )
)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ピン・ピン支持の場合
ピン・ピン支持の場合
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ピン・自由支持の場合 (
ピン・自由支持の場合 (![]() )
)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ピン・質点付自由支持の場合
ピン・質点付自由支持の場合
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 固定・固定支持の場合
固定・固定支持の場合
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 固定・ピン支持の場合
固定・ピン支持の場合
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 固定・自由支持の場合 (
固定・自由支持の場合 (![]() )
)
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 固定・質点付自由支持の場合
固定・質点付自由支持の場合
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()