SM制御…Homework
[1] 次の無定位系(2重積分器)を考えます。
![]()
これに対して、スイッチング関数と呼ばれる
![]()
を用いて、制御則
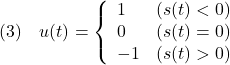
すなわち
![]()
を考えます。![]() の解は(
の解は(![]() に注意して)
に注意して)
![]()
また
![]()
となることから
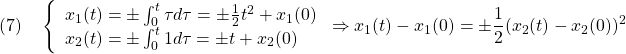
と計算できます。ここで、状態軌道は放物線となっていることに注意します。
●![]() 、
、![]() のときの状態軌道を図1に示します。
のときの状態軌道を図1に示します。

図1 ![]() のときの状態軌道
のときの状態軌道
これから直線![]() の上側と下側にある(横に寝た)放物線を切り替えて状態軌道が構成されていることが分かります。ところが、原点に近くなると奇妙な現象が生じます。
の上側と下側にある(横に寝た)放物線を切り替えて状態軌道が構成されていることが分かります。ところが、原点に近くなると奇妙な現象が生じます。
●![]() 、
、![]() のときの状態軌道を図2に示します。
のときの状態軌道を図2に示します。
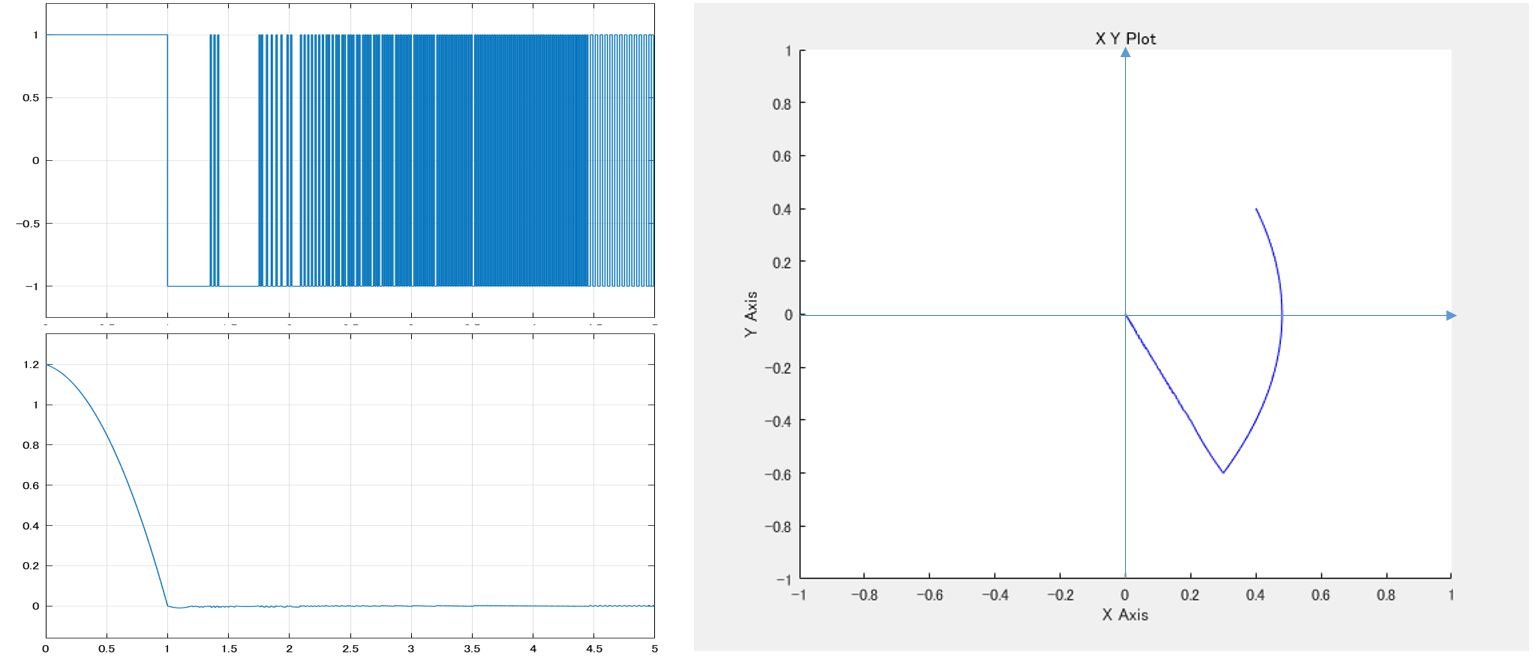
図2 ![]() のときの状態軌道
のときの状態軌道
これから状態軌道が直線![]() に到達すると、この直線上に拘束されて原点まで滑っていることが分かります。一体、何が起こっているのでしょう?
に到達すると、この直線上に拘束されて原点まで滑っていることが分かります。一体、何が起こっているのでしょう?
●これを調べるために
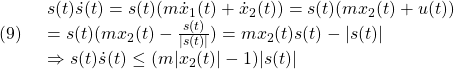
から、次が成り立つことがわかります。
![]()
いま(2)で定義した![]() は
は![]() 平面における
平面における![]() 軸の切片であることに注意します。(10)より、
軸の切片であることに注意します。(10)より、![]() のとき
のとき![]() なので切片
なので切片![]() は
は![]() 軸正の方から0に漸近します。一方、
軸正の方から0に漸近します。一方、![]() のとき
のとき![]() なので切片
なので切片![]() は
は![]() 軸負の方から0に漸近します。このことは状態は直線
軸負の方から0に漸近します。このことは状態は直線
![]()
の上に拘束されてしまうことを意味します。これから
![]()
となるので、つぎを得ます。
![]()
これは直線(2)を滑るように原点に向かうことを意味します。
●以上のように、適当なスイッチング関数![]() に対して、可到達条件
に対して、可到達条件
![]()
を満足させ、スライディング直線に乗せたあと、原点に向かって滑らせる制御方式をスライディングモード制御と呼びます。
[2] いまスライディング直線に乗る時刻を![]() とすると、次が成り立ちます。
とすると、次が成り立ちます。
![]()
また(9)では次式を用いました。
![]()
そうすると(15)と(16)を合わせて、スライディング直線を滑らせる制御則は
![]()
のように考えられ、等価制御と呼ばれています。
●等価制御はスライディングモード制御そのものではないのですが、どのように違うか、次のシミュレーション例を見てください。これからスライディングモード制御則を1次システム![]() を通したものが等価制御とよく合っていることがわかります。この1次システムはアクチュエータのダイナミックス(による帯域制限)を表しているとみなすことができます。
を通したものが等価制御とよく合っていることがわかります。この1次システムはアクチュエータのダイナミックス(による帯域制限)を表しているとみなすことができます。

図3 SMCとその等価制御(![]() )
)
そうであれば最初から等価制御を用いればよいではないかと思うかもしれませんが、等価制御はあくまでスライディングモードに突入後の制御則です。したがって、まずは可到達条件(14)を満足させて、スライディングモードを実現する必要があることに注意してください。
[3] 剛体振子の運動方程式は次式で与えられました。
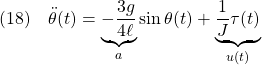
![]() ,
, ![]() とおいて、次の非線形状態方程式を得ます。
とおいて、次の非線形状態方程式を得ます。
![]()
これは、次式のように、無定位系(2重積分器)に非線形項が加えられたものとみなすことができます。
![]()
そこで、これまでのスライディングモード制御(4)をそのまま用いたときの様子を調べてみます。
次は仮に![]() とした場合のシミュレーション結果です。一見、図3と変わらないように見えます。
とした場合のシミュレーション結果です。一見、図3と変わらないように見えます。
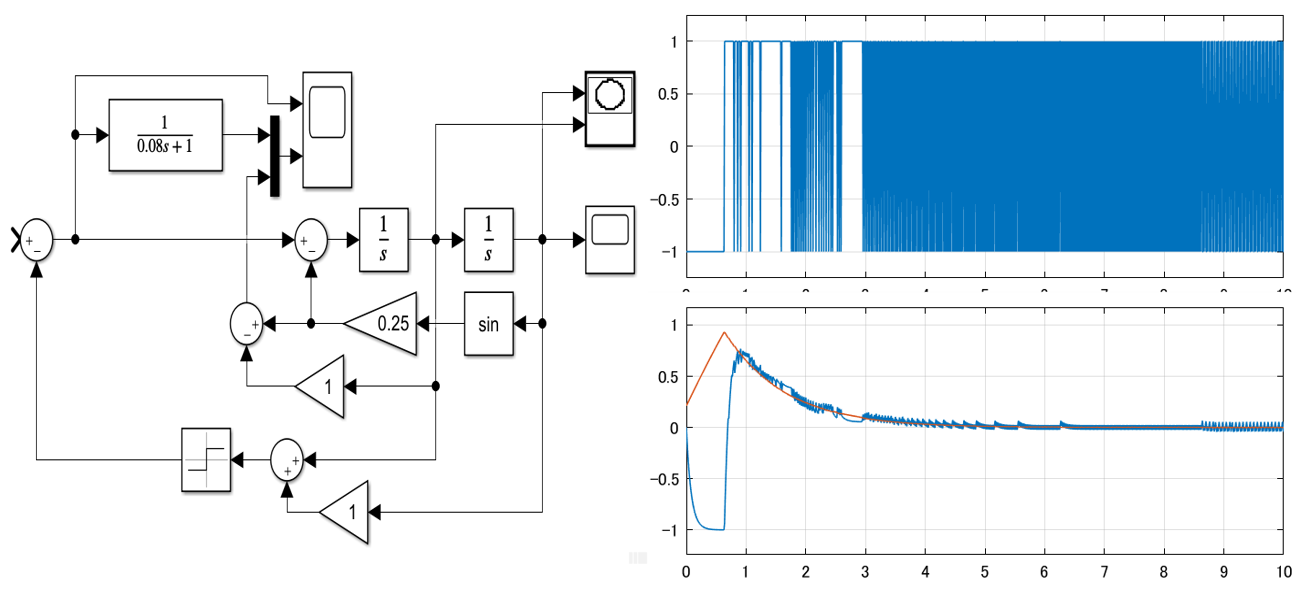
図4 振り子のSMCとその等価制御(![]() )
)
ここには、次の等価制御もシミュレーションされています。
![]()
実は、無定位系そのものは非線形項を考慮していないのに、これに非線形項が加わった場合の影響を抑制していることが分かります。この事実がスライディングモード制御を大変魅力的なものとしています。
演習C01…Flipped Classroom
![]() smc11.slxとsmc12.slxを用いて、図1、図2のシミュレーションを行え。
smc11.slxとsmc12.slxを用いて、図1、図2のシミュレーションを行え。
![]() smc13.slxとsmc14.slxを用いて、図3、図4のシミュレーションを行え。
smc13.slxとsmc14.slxを用いて、図3、図4のシミュレーションを行え。