| MATLAB |
%of_syn_lmi6.m
%-----
A=[0 1;-1 -2*0.01]; B1=[0;1]; B2=B1;
C1=[1 0;0 0]; D11=[0;0]; D12=[0;1];
C2=[1 0]; D21=0; D22=0;
%-----
setlmis([]);
gam=lmivar(1,[1 0]);
R=lmivar(1,[2 1]);
S=lmivar(1,[2 1]);
Ak=lmivar(2,[2 2]);
Bk=lmivar(2,[2 1]);
Ck=lmivar(2,[1 2]);
Dk=lmivar(2,[1 1]);
%-----
lmiRS=newlmi;
lmiterm([lmiRS 1 1 R],A,1,'s'); %#1:R*A'+AR
lmiterm([lmiRS 1 1 Ck],B2,1,'s'); %#1:Ck'*B2'+B2*Ck
lmiterm([lmiRS 2 1 0],A'); %#1:A'
lmiterm([lmiRS 2 1 Ak],1,1); %#1:Ak
lmiterm([lmiRS 2 1 -Dk],C2',B2'); %#1:C2'*Dk'*B2'
lmiterm([lmiRS 2 2 S],1,A,'s'); %#1:A'*S+S*A
lmiterm([lmiRS 2 2 Bk],1,C2,'s'); %#1:C2'*Bk'+Bk*C2
lmiterm([lmiRS 1 3 0],B1); %#1:B1
lmiterm([lmiRS 1 3 Dk],B2,D21); %#1:B2*Dk*D21
lmiterm([lmiRS 2 3 S],1,B1); %#1:S*B1
lmiterm([lmiRS 2 3 Bk],1,D21); %#1:Bk*D21
lmiterm([lmiRS 3 3 gam],-1,1); %#1:-gam
lmiterm([lmiRS 4 1 R],C1,1); %#1:C1*R
lmiterm([lmiRS 4 1 Ck],D12,1); %#1:D12*Ck
lmiterm([lmiRS 4 2 0],C1); %#1:C1
lmiterm([lmiRS 4 2 Dk],D12,C2); %#1:D12*Dk*C2
lmiterm([lmiRS 4 3 0],D11); %#1:D11
lmiterm([lmiRS 4 3 Dk],D12,D21); %#1:D12*Dk*D21
lmiterm([lmiRS 4 4 gam],-1,1); %#1:-gam
%-----
alpha=0.1;
lmiPL1=newlmi;
lmiterm([lmiPL1 1 1 R],A,1,'s'); %#2:R*A'+A*R
lmiterm([lmiPL1 1 1 Ck],B2,1,'s'); %#2:Ck'*B2'+B2*Ck
lmiterm([lmiPL1 2 1 Ak],1,1); %#2:Ak
lmiterm([lmiPL1 1 2 0],A); %#2:A
lmiterm([lmiPL1 1 2 Dk],B2,C2); %#2:B2*Dk*C2
lmiterm([lmiPL1 2 2 S],1,A,'s'); %#2:A'*S+S*A
lmiterm([lmiPL1 2 2 Bk],1,C2,'s'); %#2:C2'*Bk'+Bk*C2
%
lmiterm([lmiPL1 1 1 R],2*alpha,1); %#2:2*alpha*R
lmiterm([lmiPL1 2 1 0],2*alpha); %#2:2*alpha*I
lmiterm([lmiPL1 2 2 S],2*alpha,1); %#2:2*alpha*S
%-----
r=2;
lmiPL2=newlmi;
lmiterm([lmiPL2 1 1 R],-r,1); %#3:-r*R
lmiterm([lmiPL2 2 1 0],-r); %#3:-r*I
lmiterm([lmiPL2 2 2 S],-r,1); %#3:-r*S
%
lmiterm([lmiPL2 1 3 R],A,1); %#3:A*R
lmiterm([lmiPL2 1 3 Ck],B2,1); %#3:B2*Ck
lmiterm([lmiPL2 2 3 Ak],1,1); %#3:Ak
lmiterm([lmiPL2 1 4 0],A); %#3:A
lmiterm([lmiPL2 1 4 Dk],B2,C2); %#3:B2*Dk*C2
lmiterm([lmiPL2 2 4 S],1,A); %#3:S*A
lmiterm([lmiPL2 2 4 Bk],1,C2); %#3:Bk*C2
%
lmiterm([lmiPL2 3 3 R],-r,1); %#3:-r*R
lmiterm([lmiPL2 4 3 0],-r); %#3:-r*I
lmiterm([lmiPL2 4 4 S],-r,1); %#3:-r*S
%-----
th=0.4*pi; sth=sin(th); cth=cos(th);
lmiPL3=newlmi;
lmiterm([lmiPL3 1 1 R],sth*A,1,'s'); %#4:sth*(R*A'+A*R)
lmiterm([lmiPL3 1 1 Ck],sth*B2,1,'s');%#4:sth*(Ck'*B2'+B2*Ck)
lmiterm([lmiPL3 2 1 Ak],sth,1); %#4:sth*(Ak)
lmiterm([lmiPL3 1 2 0],sth*A); %#4:sth*(A)
lmiterm([lmiPL3 1 2 Dk],sth*B2,C2); %#4:sth*(B2*Dk*C2)
lmiterm([lmiPL3 2 2 S],1,sth*A,'s'); %#4:sth*(A'*S+S*A)
lmiterm([lmiPL3 2 2 Bk],1,sth*C2,'s');%#4:sth*(C2'*Bk'+Bk*C2)
%
% lmiterm([lmiPL3 1 3 R],1,cth*A'); %#4:cth*(R*A')
% lmiterm([lmiPL3 1 3 R],-cth*A,1); %#4:cth*(-A*R)
% lmiterm([lmiPL3 1 3 -Ck],cth*B2',1);%#4:cth*(Ck'*B2')
% lmiterm([lmiPL3 1 3 Ck],-cth*B2,1); %#4:cth*(-B2*Ck)
lmiterm([lmiPL3 1 3 R],cth*A,1); %#1:cth*(A*R)
lmiterm([lmiPL3 1 3 R],1,-cth*A'); %#1:cth*(-R*A')
lmiterm([lmiPL3 1 3 Ck],cth*B2,1); %#1:cth*(B*Ck)
lmiterm([lmiPL3 1 3 -Ck],-cth*B2',1); %#1:cth*(-Ck'*B')
lmiterm([lmiPL3 2 3 Ak],cth,1); %#4:cth*(Ak)
lmiterm([lmiPL3 1 4 -Ak],-cth,1); %#4:cth*(-Ak')
lmiterm([lmiPL3 1 4 0],A); %#4:cth*(A)
lmiterm([lmiPL3 2 3 0],-A'); %#4:cth*(-A')
lmiterm([lmiPL3 1 4 Dk],cth*B2,C2); %#4:cth*(B2*Dk*C2)
lmiterm([lmiPL3 2 3 -Dk],-cth*C2',B2');%#4:cth*(-C2'*Dk'*B2')
lmiterm([lmiPL3 2 4 S],1,cth*A); %#4:cth*(S*A)
lmiterm([lmiPL3 2 4 S],-cth*A',1); %#4:cth*(-A'*S)
lmiterm([lmiPL3 2 4 Bk],1,cth*C2); %#4:cth*(Bk*C2)
lmiterm([lmiPL3 2 4 -Bk],-cth*C2',1); %#4:cth*(-C2'*Bk')
%
lmiterm([lmiPL3 3 3 R],sth*A,1,'s'); %#4:sth*(R*A'+A*R)
lmiterm([lmiPL3 3 3 Ck],sth*B2,1,'s');%#4:sth*(Ck'*B2'+B2*Ck)
lmiterm([lmiPL3 4 3 Ak],sth,1); %#4:sth*(Ak)
lmiterm([lmiPL3 3 4 0],sth*A); %#4:sth*(A)
lmiterm([lmiPL3 3 4 Dk],sth*B2,C2); %#4:sth*(B2*Dk*C2)
lmiterm([lmiPL3 4 4 S],1,sth*A,'s'); %#4:sth*(A'*S+S*A)
lmiterm([lmiPL3 4 4 Bk],1,sth*C2,'s');%#4:sth*(C2'*Bk'+Bk*C2)
%-----
posX=-newlmi;
lmiterm([posX 1 1 R],1,1); %#5:R
lmiterm([posX 2 1 0],1); %#5:I
lmiterm([posX 2 2 S],1,1); %#5:S
%-----
lmiDk=-newlmi;
lmiterm([lmiDk 1 1 0],1e2); %#6:1e2
lmiterm([lmiDk 2 2 0],1e2); %#6:1e2
lmiterm([lmiDk 2 1 Dk],1,1); %#6:Dk
%-----
lmig=newlmi;
lmiterm([lmig,1,1,gam],1,1); %#7:gam
lmiterm([lmig,1,1,0],-1e3); %#7:1e3
%-----
LMIs=getlmis;
cobj=zeros(1,decnbr(LMIs));
cobj(1)=1;
[cost,xopt]=mincx(LMIs,cobj);
%-----
gopt=dec2mat(LMIs,xopt,gam)
R=dec2mat(LMIs,xopt,R);
S=dec2mat(LMIs,xopt,S);
ak=dec2mat(LMIs,xopt,Ak);
bk=dec2mat(LMIs,xopt,Bk);
ck=dec2mat(LMIs,xopt,Ck);
dk=dec2mat(LMIs,xopt,Dk);
[u,sd,v]=svd(eye(size(A,1)-S*R);
sd=diag(sqrt(1./diag(sd)));
Ni=sd*u'; Mti=v*sd;
AK=Ni*(ak-S*(A-B2*dk*C2)*R-bk*C2*R-S*B2*ck)*Mti;
BK=Ni*(bk-S*B2*dk);
CK=(ck-dk*C2*R)*Mti;
DK=dk;
%-----
pl=eig(A)
ACL=[A+B2*DK*C2 B2*CK;
BK*C2 AK];
plCL=eig(ACL)
close all,figure(1)
dregion(alpha,0,r,th,r*[-1,1,-1,1])
plot(real(pl),imag(pl),'x',real(plCL),imag(plCL),'*')
BCL=[B1+B2*DK*D21;
BK*D21];
CCL=[C1+D12*DK*C2 D12*CK];
DCL=D11+D12*DK*D21;
figure(2)
ol=ltisys(A,B1,C1,D11);
cl=ltisys(ACL,BCL,CCL,DCL);
om=logspace(-1,1,100);
splot(cl,'sv',om),hold on
splot(ol,'sv',om),grid
%-----
%eof
|
![]() 次系
次系![]() の
の![]() ノルムが
ノルムが![]() より小となるためのLMI条件は、次の通りでした。
より小となるためのLMI条件は、次の通りでした。![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \displaystyle{{\rm tr} (CW_cC^T)<\gamma^2\quad(W_c=\int_0^\infty \exp(At)BB^T\exp(A^Tt)dt)}\\\\ \displaystyle{\Leftrightarrow \exists X_c>0,\ Q_c>0:\\ \left[\begin{array}{cc} A^TX_c+X_cA & X_cB \\ B^TX_c & -I \end{array}\right]<0,\ \left[\begin{array}{cc} X_c & C^T \\ C & Q_c \end{array}\right]>0,\ {\rm tr}(Q_c)<\gamma^2}\\\\ \displaystyle{\Leftrightarrow \exists Y_c>0,\ Q_c>0:\\ \left[\begin{array}{cc} Y_cA^T+AY_c & B \\ B^T & -I \end{array}\right]<0,\ \left[\begin{array}{cc} Y_c & Y_cC^T \\ CY_c & Q_c \end{array}\right]>0,\ {\rm tr}(Q_c)<\gamma^2} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4740750e1fdf8093b1f6322284a78a12_l3.png)

![]() 次系を考えます。
次系を考えます。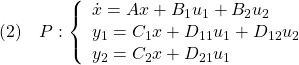
![]()
![Rendered by QuickLaTeX.com \displaystyle{(4) \begin{array}{l} P_{CL}: \\ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x} \\ \dot{x}_K \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} A+B_2D_KC_2 & B_2C_K \\ B_KC_2 & A_K \end{array}\right] }_{A_{CL}} \left[\begin{array}{c} x \\ x_K \end{array}\right] + \underbrace{ \left[\begin{array}{ccc} B_1+B_2D_KD_{21} \\ B_KD_{21} \end{array}\right] }_{B_{CL}} u_1\\ y_1 = \underbrace{ \left[\begin{array}{ccc} C_1+D_{12}D_KC_2 & D_{12}C_K \end{array}\right] }_{C_{CL}} \left[\begin{array}{c} x \\ x_K \end{array}\right] + \underbrace{ (D_{11}+D_{12}D_KD_{21}) }_{D_{CL}} u_1 \end{array}\right. \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f53ae5ac3451ed7d23911ed463c5c53a_l3.png)
![]() ノルムを考えますが、直達項
ノルムを考えますが、直達項![]() が0となるように、
が0となるように、![]() 、
、![]() とします。すなわち閉ループ系
とします。すなわち閉ループ系![Rendered by QuickLaTeX.com \displaystyle{(5) \begin{array}{l} P_{CL}: \\ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x} \\ \dot{x}_K \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} A & B_2C_K \\ B_KC_2 & A_K \end{array}\right] }_{A_{CL}} \left[\begin{array}{c} x \\ x_K \end{array}\right] + \underbrace{ \left[\begin{array}{ccc} B_1 \\ B_KD_{21} \end{array}\right] }_{B_{CL}} u_1\\ y_1 = \underbrace{ \left[\begin{array}{ccc} C_1 & D_{12}C_K \end{array}\right] }_{C_{CL}} \left[\begin{array}{c} x \\ x_K \end{array}\right] \end{array}\right. \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d9ee0d76c4323fd2167e246115a0ba75_l3.png)
![]() ノルムが
ノルムが![]() より小、すなわち
より小、すなわち![]()
![]() を求める問題を考えます。
を求める問題を考えます。![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \exists Y_{CL}>0,\ Q>0:\\ \left[\begin{array}{cc} Y_{CL}A_{CL}^T+A_{CL}Y_{CL} & B_{CL} \\ B_{CL}^T & -I \end{array}\right]<0,\\ \left[\begin{array}{cc} Y_{CL} & Y_{CL}C_{CL}^T \\ C_{CL}Y_{CL} & Q \end{array}\right]>0,\\ {\rm tr}(Q)<\gamma^2 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4b9dc7d5c8ae7d5f7820077476af8b06_l3.png)
![]() を代入して
を代入して![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \exists \Pi_1\Pi_2^{-1}>0,\ Q>0:\\ \left[\begin{array}{cc} \Pi_2^{-T}\Pi_1^TA_{CL}^T+A_{CL}\Pi_1\Pi_2^{-1} & B_{CL} \\ B_{CL}^T & -I \end{array}\right]<0,\\ \left[\begin{array}{cc} \Pi_2^{-T}\Pi_1^T & \Pi_2^{-T}\Pi_1^TC_{CL}^T \\ C_{CL}\Pi_1\Pi_2^{-1} & Q \end{array}\right]>0,\\ {\rm tr}(Q)<\gamma^2 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9e104f2b0398c383a30ed6b905cd3e8d_l3.png)
![]() 、右から
、右から![]() をかけると、次のようなLMIとなります。
をかけると、次のようなLMIとなります。![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \begin{array}{l} \exists \Pi_2^T\Pi_1>0,\ Q>0:\\ \left[\begin{array}{cc} \Pi_1^TA_{CL}^T\Pi_2+\Pi_2^TA_{CL}\Pi_1 & \Pi_2^TB_{CL} \\ B_{CL}^T\Pi_2 & -I \end{array}\right]<0,\\ \left[\begin{array}{cc} \Pi_1^T\Pi_2 & \Pi_1^TC_{CL}^T \\ C_{CL}\Pi_1 & Q \end{array}\right]>0,\\ {\rm tr}(Q)<\gamma^2 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bc5d943db7eceee17783ff93d1b5b6b4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} \Pi_2^TA_{CL}\Pi_1= \left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] \left[\begin{array}{ccc} A & B_2C_K \\ B_KC_2 & A_K \end{array}\right] \left[\begin{array}{cc} R & I \\ M^T & 0 \end{array}\right] \\ =\left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] \left[\begin{array}{ccc} AR+B_2C_KM^T & A \\ B_KC_2R+A_KM^T & B_KC_2 \end{array}\right] \\ =\left[\begin{array}{ccc} AR+B_2C_KM^T & A\\ SAR+SB_2C_KM^T+NB_KCR+NA_KM^T & SA+NB_KC_2 \end{array}\right] \\ =\left[\begin{array}{cc} AR+B_2{\cal C}_K & A \\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3d2317dcd404dd712b36e3efd136ce5a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \Pi_2^TB_{CL}= \left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] \left[\begin{array}{ccc} B_1 \\ B_KD_{21} \end{array}\right] \\ =\left[\begin{array}{ccc} B_1 \\ SB_1+NB_KD_{21} \end{array}\right] =\left[\begin{array}{ccc} B_1 \\ SB_1+{\cal B}_KD_{21} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d753b7e0b856f8e28ca5d5f8804803ab_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} C_{CL}\Pi_1= \left[\begin{array}{ccc} C_1 & D_{12}C_K \end{array}\right] \left[\begin{array}{cc} R & I \\ M^T & 0 \end{array}\right] \\ =\left[\begin{array}{ccc} C_1R+D_{12}C_KM^T & C_1 \end{array}\right] \\ =\left[\begin{array}{ccc} C_1R+D_{12}{\cal C}_K & C_1 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-923ae56b395be17601883366623ec0c1_l3.png)
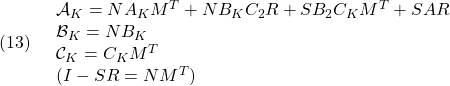
![]() を最小化し、
を最小化し、 ![]() を求め、次式によって出力フィードバックのゲインを決定します。
を求め、次式によって出力フィードバックのゲインを決定します。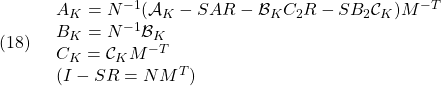
![]() 次のコードを参考にして、
次のコードを参考にして、![]() 制御(出力FB)を求める関数を作成せよ。
制御(出力FB)を求める関数を作成せよ。![Rendered by QuickLaTeX.com \displaystyle{(15) \left[\begin{array}{ccc} \left[\begin{array}{cc} AR+B_2{\cal C}_K & A\\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right]+(*)^T & \left[\begin{array}{c} B_1 \\ SB_1+{\cal B}_KD_{21} \end{array}\right]\\ (*)^T & -I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eb7747d66fa3d59761d94a015b17d9c1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(16) \left[\begin{array}{cc} \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] & (*)^T \\ \left[\begin{array}{cc} C_1R+D_{12}{\cal C}_K & C_1 \end{array}\right] & Q \end{array}\right]>0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7b27bab2fc29a6081c3f57198e95f0b8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1) \begin{array}{lll} && \sup_{\omega\in{\rm\bf R}}||\hat{G}(j\omega)||_2<\gamma \nonumber\\ &\Leftrightarrow& \exists X>0:\ \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma I & D^T \\ C & D & -\gamma I \end{array}\right]<0 \nonumber\\ &\Leftrightarrow& \exists Y>0:\ \left[\begin{array}{ccc} YA^T+AY & B & YC^T \\ B^T & -\gamma I & D^T \\ CY & D & -\gamma I \end{array}\right]<0\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eb1de97e8a1b06912197472c90ad05e5_l3.png)
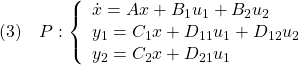
![Rendered by QuickLaTeX.com \displaystyle{(5) \begin{array}{l} P_{CL}: \\ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x} \\ \dot{x}_K \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} A+B_2D_KC_2 & B_2C_K \\ B_KC_2 & A_K \end{array}\right] }_{A_{CL}} \left[\begin{array}{c} x \\ x_K \end{array}\right] + \underbrace{ \left[\begin{array}{ccc} B_1+B_2D_KD_{21} \\ B_KD_{21} \end{array}\right] }_{B_{CL}} u_1\\ y_1 = \underbrace{ \left[\begin{array}{ccc} C_1+D_{12}D_KC_2 & D_{12}C_K \end{array}\right] }_{C_{CL}} \left[\begin{array}{c} x \\ x_K \end{array}\right] + \underbrace{ (D_{11}+D_{12}D_KD_{21}) }_{D_{CL}} u_1 \end{array}\right. \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2dd70838946d03d3ab984179f3b7d3f4_l3.png)
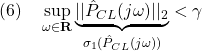
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \exists Y_{CL}>0:\ \left[\begin{array}{ccc} Y_{CL}A_{CL}^T+A_{CL}Y_{CL} & B_{CL} & Y_{CL}C_{CL}^T \\ B_{CL}^T & -\gamma I & D_{CL}^T \\ C_{CL}Y_{CL} & D_{CL} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ccc6bd8e5c1593548f942810686e27e0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \exists \Pi_1\Pi_2^{-1}>0:\ \left[\begin{array}{ccc} \Pi_2^{-T}\Pi_1^TA_{CL}^T+A_{CL}\Pi_1\Pi_2^{-1} & B_{CL} & \Pi_2^{-T}\Pi_1^TC_{CL}^T \\ B_{CL}^T & -\gamma I & D_{CL}^T \\ C_{CL}\Pi_1\Pi_2^{-1} & D_{CL} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d63a7b09fc6927497933c2d9ac659f7e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \exists \Pi_2^T\Pi_1>0:\ \left[\begin{array}{ccc} \Pi_1^TA_{CL}^T\Pi_2+\Pi_2^TA_{CL}\Pi_1 & \Pi_2^TB_{CL} & \Pi_1^TC_{CL}^T \\ B_{CL}^T\Pi_2 & -\gamma I & D_{CL}^T \\ C_{CL}\Pi_1 & D_{CL} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7976677da89389b0f79fb5b4a9aac527_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \Pi_2^TA_{CL}\Pi_1= \left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] \left[\begin{array}{ccc} A+B_2D_KC_2 & B_2C_K \\ B_KC_2 & A_K \end{array}\right] \left[\begin{array}{cc} R & I \\ M^T & 0 \end{array}\right] \\ =\left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] \left[\begin{array}{ccc} (A+B_2D_KC_2)R+B_2C_KM^T & A+B_2D_KC_2 \\ B_KC_2R+A_KM^T & B_KC_2 \end{array}\right] \\ =\left[\begin{array}{ccc} (A+B_2D_KC_2)R+B_2C_KM^T & \\ S(A+B_2D_KC_2)R+SB_2C_KM^T+NB_KCR+NA_KM^T & \end{array}\right. \\ \left.\begin{array}{ccc} & A+B_2D_KC_2 \\ & S(A+B_2D_KC_2)+NB_KC_2 \end{array}\right] \\ =\left[\begin{array}{cc} AR+B_2{\cal C}_K & A+B_2D_KC_2 \\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d79e51c89c40ae80b0c6446a23daa362_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \Pi_2^TB_{CL}= \left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] \left[\begin{array}{ccc} B_1+B_2D_KD_{21} \\ B_KD_{21} \end{array}\right] \\ =\left[\begin{array}{ccc} B_1+B_2D_KD_{21} \\ S(B_1+B_2D_KD_{21})+NB_KD_{21} \end{array}\right] =\left[\begin{array}{ccc} B_1+B_2D_KD_{21} \\ SB_1+{\cal B}_KD_{21} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a426811990f69d6297aaad7f2544eb65_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \begin{array}{l} C_{CL}\Pi_1= \left[\begin{array}{ccc} C_1+D_{12}D_KC_2 & D_{12}C_K \end{array}\right] \left[\begin{array}{cc} R & I \\ M^T & 0 \end{array}\right] \\ =\left[\begin{array}{ccc} (C_1+D_{12}D_KC_2)R+D_{12}C_KM^T & C_1+D_{12}D_KC_2 \end{array}\right] \\ =\left[\begin{array}{ccc} C_1R+D_{12}{\cal C}_K & C_1+D_{12}D_KC_2 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-913e7b88945a8ea6aee40b1542674159_l3.png)
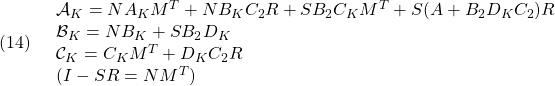
![Rendered by QuickLaTeX.com \displaystyle{(16) \left[\begin{array}{ccc} \left[\begin{array}{cc} AR+B_2{\cal C}_K & A+B_2D_KC_2\\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right]+(*)^T & \left[\begin{array}{c} B_1+B_2D_KD_{21} \\ SB_1+{\cal B}_KD_{21} \end{array}\right] & (*)^T \\ (*)^T & -\gamma I & (*)^T \\ \left[\begin{array}{cc} C_1R+D_{12}{\cal C}_K & C_1+D_{12}D_KC_2 \end{array}\right] & D_{11} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3070fcd4f3d258cf999951fbb4f9fbe5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17) \begin{array}{l} \left[\begin{array}{cc} AR+B_2{\cal C}_K & A+B_2D_KC_2\\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right] +(*)^T %\nonumber\\&& +\alpha \left[\begin{array}{cc} R & I \\ I & S \end{array}\right]<0} \\ \left[\begin{array}{cc} -r \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] & \left[\begin{array}{cc} AR+B_2{\cal C}_K & A+B_2D_KC_2\\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right] \\ (*)^T & -r \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] \end{array}\right] <0 \\ \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]\otimes \left[\begin{array}{cc} AR+B_2{\cal C}_K & A+B_2D_KC_2\\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right]+ (*)^T <0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7d7cb3c0df233a8a04c1e6b3e9b25962_l3.png)
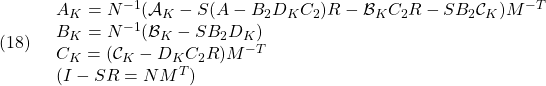
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \left[\begin{array}{c} \dot{x} \\ \dot{x}_K \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} A+BD_KC & BC_K \\ B_KC & A_K \end{array}\right] }_{A_{CL}} \left[\begin{array}{c} x \\ x_K \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b4fa3fc3acef0120663cbc7929c84396_l3.png)
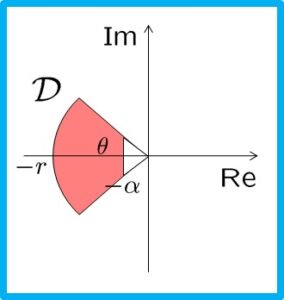
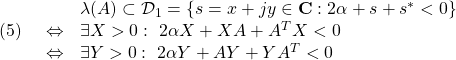
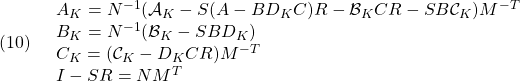
![Rendered by QuickLaTeX.com \displaystyle{(11) \begin{array}{lll} &&\lambda(A)\subset {\cal D}_2=\{s=x+jy\in{\rm\bf C}: \left[\begin{array}{cc} -r & s \\ s^* & -r \end{array}\right] <0 \}\nonumber\\ &\Leftrightarrow& \exists X>0:\ \left[\begin{array}{cc} -rX & XA \\ A^TX & -rX \end{array}\right]<0 \nonumber\\ &\Leftrightarrow& \exists Y>0:\ \left[\begin{array}{cc} -rY & AY \\ YA^T & -rY \end{array}\right]<0\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cef2a962a3396f8afb1b770218baf02b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{cc} -r \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] & \left[\begin{array}{cc} AR+B{\cal C}_K & A+BD_KC \\ {\cal A}_K & SA+{\cal B}_KC \end{array}\right] \\ \left[\begin{array}{cc} AR+B{\cal C}_K & A+BD_KC \\ {\cal A}_K & SA+{\cal B}_KC \end{array}\right]^T & -r \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] \end{array}\right] <0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8ee8a916fb01e341b6b05b9dec8adee2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(16) \begin{array}{lll} &&\lambda(A)\subset {\cal D}_3=\{s=x+jy\in{\rm\bf C}:\\ && \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]s + \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]^Ts^* <0 \}\nonumber\\ &&\Leftrightarrow \exists X>0:\ \left[\begin{array}{cc} \sin\theta(XA+A^TX) & \cos\theta(XA-A^TX) \\ -\cos\theta(XA-A^TX) & \sin\theta(XA+A^TX) \end{array}\right] <0 \nonumber\\ &&\Leftrightarrow \exists Y>0:\ \left[\begin{array}{cc} \sin\theta(AY+YA^T) & \cos\theta(AY-YA^T) \\ -\cos\theta(AY-YA^T) & \sin\theta(AY+YA^T) \end{array}\right] <0\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bfd97f662a8d6ff7c86a2dec2b62b921_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(20)\quad \begin{array}{l} \exists \left[\begin{array}{cc} R & I \\ I & S \end{array}\right]>0:\ \\ \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right] \otimes \left[\begin{array}{cc} AR+B{\cal C}_K & A+BD_KC \\ {\cal A}_K & SA+{\cal B}_KC \end{array}\right]+ \\ (\left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right] \otimes \left[\begin{array}{cc} AR+B{\cal C}_K & A+BD_KC \\ {\cal A}_K & SA+{\cal B}_KC \end{array}\right])^T <0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-405aa571dd83441fa45f2e21e96b3c03_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} S & N \\ N^T & S' \end{array}\right] }_{X_{CL}} \underbrace{ \left[\begin{array}{cc} R & M \\ M^T & R' \end{array}\right] }_{Y_{CL}=X^{-1}_{CL}} = \left[\begin{array}{cc} I & 0 \\ 0 & I \end{array}\right] \quad(SR+NM^T=I)\\ \underbrace{ \left[\begin{array}{cc} R & M \\ M^T & R' \end{array}\right] }_{Y_{CL}} \underbrace{ \left[\begin{array}{cc} S & N \\ N^T & S' \end{array}\right] }_{X_{CL}=Y^{-1}_{CL}} = \left[\begin{array}{cc} I & 0 \\ 0 & I \end{array}\right] \quad(RS+MN^T=I) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fd01714fd5e49b60bc3e606ac49694bb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad X_{CL}= \underbrace{ \left[\begin{array}{cc} I & S \\ 0 & N^T \end{array}\right] }_{\Pi_2} \underbrace{ \left[\begin{array}{cc} R & I \\ M^T & 0 \end{array}\right]^{-1} }_{\Pi_1^{-1}} = \underbrace{ \left[\begin{array}{cc} R & M \\ I & 0 \end{array}\right]^{-1} }_{\Pi_1^{-T}} \underbrace{ \left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] }_{\Pi_2^T} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c03ff30c1097edc6cffd80c6cbec396d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad Y_{CL}= \underbrace{ \left[\begin{array}{cc} R & I \\ M^T & 0 \end{array}\right] }_{\Pi_1} \underbrace{ \left[\begin{array}{cc} I & S \\ 0 & N^T \end{array}\right]^{-1} }_{\Pi_2^{-1}} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right]^{-1} }_{\Pi_2^{-T}} \underbrace{ \left[\begin{array}{cc} R & M \\ I & 0 \end{array}\right] }_{\Pi_1^T} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6f5ea3d73a1aa4cea557b17a0bec6ba5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] = \underbrace{ \left[\begin{array}{cc} R & M \\ I & 0 \end{array}\right] }_{\Pi_1^T} \underbrace{ \left[\begin{array}{cc} I & S \\ 0 & N^T \end{array}\right] }_{\Pi_2} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] }_{\Pi_2^T} \underbrace{ \left[\begin{array}{cc} R & I \\ M^T & 0 \end{array}\right] }_{\Pi_1} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-01f14a656f5f1a28a0df2c534bc39542_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \begin{array}{l} \Pi_2^TA_{CL}\Pi_1= \left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] \left[\begin{array}{ccc} A+BD_KC & BC_K \\ B_KC & A_K \end{array}\right] \left[\begin{array}{cc} R & I \\ M^T & 0 \end{array}\right] \\ =\left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] \left[\begin{array}{ccc} (A+BD_KC)R+BC_KM^T & A+BD_KC \\ B_KCR+A_KM^T & B_KC \end{array}\right] \\ =\left[\begin{array}{ccc} (A+BD_KC)R+BC_KM^T & \\ S(A+BD_KC)R+SBC_KM^T+NB_KCR+NA_KM^T & \end{array}\right. \\ \left.\begin{array}{ccc} & A+BD_KC \\ & S(A+BD_KC)+NB_KC \end{array}\right] \\ =\left[\begin{array}{cc} AR+B{\cal C}_K & A+BD_KC \\ {\cal A}_K & SA+{\cal B}_KC \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7768573f62703ece20c21171c0e69882_l3.png)
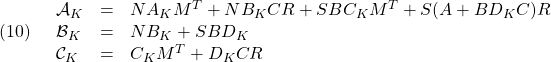
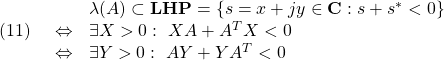
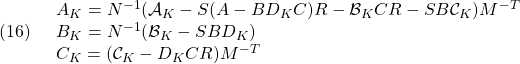
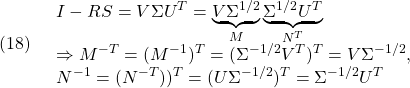
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \exists U_{PQ}:\ \left[\begin{array}{c} P \\ Q \end{array}\right]U_{PQ}=0 \quad\Rightarrow\quad \left\{\begin{array}{l} \exists U_{P}:\ P\underbrace{ \left[\begin{array}{cc} U_{PQ} & U_P \end{array}\right] }_{W_P}=0\\ \exists U_{Q}:\ Q\underbrace{ \left[\begin{array}{cc} U_{PQ} & U_Q \end{array}\right] }_{W_Q}=0\\ \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-732e424cb0a0b6856203c2887f795534_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \Leftrightarrow \left[\begin{array}{cccc} \Psi_{11} & \Psi_{12} & \Psi_{13} & \Psi_{14} \\ \Psi_{12}^T & \Psi_{22} & \Psi_{23}& \Psi_{24}\\ \Psi_{13}^T & \Psi_{23}^T & \Psi_{33} & \Psi_{34}\\ \Psi_{14}^T & \Psi_{24}^T & \Psi_{34}^T & \Psi_{44} \end{array}\right] +\left[\begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & \Theta_{11}^T & 0 & \Theta_{12}^T \\ 0 & \Theta_{21}^T & 0 & \Theta_{22}^T \end{array}\right] +\left[\begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & \Theta_{11} & \Theta_{21} \\ 0 & 0 & 0 & 0 \\ 0 & 0 & \Theta_{12} & \Theta_{22} \end{array}\right] < 0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8df35b0d0eded8e0048a0d63693847dc_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \Leftrightarrow \left[\begin{array}{ccc|c} \Psi_{11} & \Psi_{12} & \Psi_{13} & \Psi_{14} \\ \Psi_{12}^T & \Psi_{22} & \Psi_{23}+\Theta_{11} & \Psi_{24}+\Theta_{21} \\ \Psi_{13}^T & \Psi_{23}^T+\Theta_{11}^T & \Psi_{33} & \Psi_{34}+\Theta_{12} \\ \hline \Psi_{14}^T & \Psi_{24}^T+\Theta_{21}^T & \Psi_{34}^T+\Theta_{12}^T & \Psi_{44}+\Theta_{22}+\Theta_{22}^T \end{array}\right]<0}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c38812ba3c2440e987782ee4c75177a3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{\Leftrightarrow \left\{\begin{array}{l} \left[\begin{array}{cccc} \Psi_{11} & \Psi_{12} & \Psi_{13} \\ \Psi_{12}^T & \Psi_{22} & \Psi_{23}+\Theta_{11} \\ \Psi_{13}^T & \Psi_{23}^T+\Theta_{11}^T & \Psi_{33} \end{array}\right] < 0 \\ \quad\\ \Psi_{44}+\Theta_{22}+\Theta_{22}^T-\\ \left[\begin{array}{c} \Psi_{14} \\ \Psi_{24}+\Theta_{21} \\ \Psi_{34}+\Theta_{12} \end{array}\right]^T \left[\begin{array}{cccc} \Psi_{11} & \Psi_{12} & \Psi_{13} \\ \Psi_{12}^T & \Psi_{22} & \Psi_{23}+\Theta_{11} \\ \Psi_{13}^T & \Psi_{23}^T+\Theta_{11}^T & \Psi_{33} \end{array}\right]^{-1} \left[\begin{array}{c} \Psi_{14} \\ \Psi_{24}+\Theta_{21}^T \\ \Psi_{34}+\Theta_{12}^T \end{array}\right] < 0 \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0b09c3219c54b4e57f477f9e1f9a5cfa_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \left[\begin{array}{ccc} I & 0 & 0 \\ -\Psi_{12}^T\Psi_{11}^{-1} & I & 0 \\ -\Psi_{13}^T\Psi_{11}^{-1} & 0 & I \end{array}\right] \left[\begin{array}{cccc} \Psi_{11} & \Psi_{12} & \Psi_{13} \\ \Psi_{12}^T & \Psi_{22} & \Psi_{23}+\Theta_{11} \\ \Psi_{13}^T & \Psi_{23}^T+\Theta_{11}^T & \Psi_{33} \end{array}\right]\\ \times \left[\begin{array}{ccc} I & -\Psi_{11}^{-1}\Psi_{12} & -\Psi_{11}^{-1}\Psi_{13} \\ 0 & I & 0 \\ 0 & 0 & I \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1e76c8b05c4fec546ea5dcaeb7bc0880_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \Leftrightarrow \left[\begin{array}{ccc} \Psi_{11} & 0 & 0 \\ 0 & \Psi_{22}-\Psi_{12}^T\Psi_{11}^{-1}\Psi_{12} & \Theta_{11}+\Psi_{23}-\Psi_{12}^T\Psi_{11}^{-1}\Psi_{13} \\ 0 & \Theta_{11}^T+\Psi_{23}^T-\Psi_{13}^T\Psi_{11}^{-1}\Psi_{12} & \Psi_{33}-\Psi_{13}^T\Psi_{11}^{-1}\Psi_{13} \end{array}\right] < 0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ae8fb6d275c9abbf9f70e0b28fd49f9d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \underbrace{ \left[\begin{array}{cc} \Psi_{11} & \Psi_{12} \\ \Psi_{12}^T & \Psi_{22} \end{array}\right] }_{W_P^T\Psi W_P} < 0,\ \underbrace{ \left[\begin{array}{cc} \Psi_{11} & \Psi_{13} \\ \Psi_{13}^T & \Psi_{33} \end{array}\right] }_{W_Q^T\Psi W_Q}< 0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-19e320b41b055e34b3fc56bc65f0f8a1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} S & N \\ X & S' \end{array}\right] }_{W} \underbrace{ \left[\begin{array}{cc} R & M \\ Y & R' \end{array}\right] }_{V=W^{-1}} = \left[\begin{array}{cc} I & 0 \\ 0 & I \end{array}\right] \quad(I=SR+NY=SR-NS'^{-1}XR)\\ \underbrace{ \left[\begin{array}{cc} R & M \\ Y & R' \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} S & N \\ X & S' \end{array}\right] }_{W=V^{-1}} = \left[\begin{array}{cc} I & 0 \\ 0 & I \end{array}\right] \quad(I=RS+MX=RS-MR'^{-1}YS) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3448bb3b806d0ccacda7242882b9895e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad 0< \underbrace{ \left[\begin{array}{cc} S & L_{\ell}S' \\ L_r & S' \end{array}\right] }_W + \underbrace{ \left[\begin{array}{cc} S^T & L_r^T \\ S'\,^TL_{\ell}^T & S'\,^T \end{array}\right] }_{W^T} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-de6dadd7dd24bb41f9f007525cb9b86a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \underbrace{ \left[\begin{array}{cc} S+S^T & L_r^T \\ L_r & 0 \end{array}\right] }_{\Psi} + \underbrace{ \left[\begin{array}{c} 0 \\ I \end{array}\right] }_{P^T} \underbrace{ S'\,^T }_{\Theta^T} \underbrace{ \left[\begin{array}{cc} L_\ell^T & I \end{array}\right] }_{Q} + \underbrace{ \left[\begin{array}{c} L_{\ell} \\ I \end{array}\right] }_{Q^T} \underbrace{ S' }_{\Theta} \underbrace{ \left[\begin{array}{cc} 0 & I \end{array}\right] }_{P}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e1f30f8f2b570b7c38a37a83dd1e92fa_l3.png)
![Rendered by QuickLaTeX.com \Leftrightarrow \left\{\begin{array}{l} \underbrace{ \left[\begin{array}{cc} I & 0 \end{array}\right] }_{W_P^T} \underbrace{ \left[\begin{array}{cc} S+S^T & L_r^T \\ L_r & 0 \end{array}\right] }_{\Psi} \underbrace{ \left[\begin{array}{c} I \\ 0 \end{array}\right] }_{W_P}<0 \quad (\underbrace{ \left[\begin{array}{cc} 0 & I \end{array}\right] }_{P} \underbrace{ \left[\begin{array}{c} I \\ 0 \end{array}\right] }_{W_P}=0)\\ \underbrace{ \left[\begin{array}{cc} I & -L_\ell \end{array}\right] }_{W_Q^T} \underbrace{ \left[\begin{array}{cc} S+S^T & L_r^T \\ L_r & 0 \end{array}\right] }_{\Psi} \underbrace{ \left[\begin{array}{c} I \\ -L_\ell^T \end{array}\right] }_{W_Q}<0 \quad (\underbrace{ \left[\begin{array}{cc} L_\ell^T & I \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} I \\ -L_\ell^T \end{array}\right] }_{W_Q}=0)\\ \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f2b8bbeeeaa60f811e8eae65ea966250_l3.png)
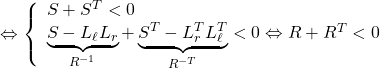
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad 0< \underbrace{ \left[\begin{array}{cc} R & L_{\ell}R' \\ L_r & R' \end{array}\right] }_V + \underbrace{ \left[\begin{array}{cc} R^T & L_r^T \\ R'\,^TL_{\ell}^T & R'\,^T \end{array}\right] }_{V^T} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f99b468e094a204216d80c309b78f582_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \underbrace{ \left[\begin{array}{cc} R+R^T & L_r^T \\ L_r & 0 \end{array}\right] }_{\Psi} + \underbrace{ \left[\begin{array}{c} 0 \\ I \end{array}\right] }_{P^T} \underbrace{ R'\,^T }_{\Theta^T} \underbrace{ \left[\begin{array}{cc} L_\ell^T & I \end{array}\right] }_{Q} + \underbrace{ \left[\begin{array}{c} L_{\ell} \\ I \end{array}\right] }_{Q^T} \underbrace{ R' }_{\Theta} \underbrace{ \left[\begin{array}{cc} 0 & I \end{array}\right] }_{P}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-77ba77917ab5a14d39db909ea189fa99_l3.png)
![Rendered by QuickLaTeX.com \Leftrightarrow \left\{\begin{array}{l} \underbrace{ \left[\begin{array}{cc} I & 0 \end{array}\right] }_{W_P^T} \underbrace{ \left[\begin{array}{cc} R+R^T & L_r^T \\ L_r & 0 \end{array}\right] }_{\Psi} \underbrace{ \left[\begin{array}{c} I \\ 0 \end{array}\right] }_{W_P}<0 \quad (\underbrace{ \left[\begin{array}{cc} 0 & I \end{array}\right] }_{P} \underbrace{ \left[\begin{array}{c} I \\ 0 \end{array}\right] }_{W_P}=0)\\ \underbrace{ \left[\begin{array}{cc} I & -L_\ell \end{array}\right] }_{W_Q^T} \underbrace{ \left[\begin{array}{cc} R+R^T & L_r^T \\ L_r & 0 \end{array}\right] }_{\Psi} \underbrace{ \left[\begin{array}{c} I \\ -L_\ell^T \end{array}\right] }_{W_Q}<0 \quad (\underbrace{ \left[\begin{array}{cc} L_\ell^T & I \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} I \\ -L_\ell^T \end{array}\right] }_{W_Q}=0)\\ \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9c87357de622e87966262b65b5d6b291_l3.png)
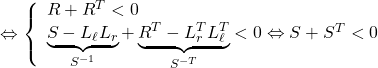
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} S & N \\ N^T & S' \end{array}\right] }_W \underbrace{ \left[\begin{array}{cc} R & M \\ M^T & R' \end{array}\right] }_{V=W^{-1}} = \left[\begin{array}{cc} I & 0 \\ 0 & I \end{array}\right] \quad(SR+NM^T=I) \\ \underbrace{ \left[\begin{array}{cc} R & M \\ M^T & R' \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} S & N \\ N^T & S' \end{array}\right] }_{W=V^{-1}} = \left[\begin{array}{cc} I & 0 \\ 0 & I \end{array}\right] \quad(RS+MN^T=I) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b5af46c0250be9099f8d39a21a2c9d18_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{\boxed{ \begin{array}{lll} && \left[\begin{array}{cc} P & M \\ M^T & Q \end{array}\right]<0\\ &\Leftrightarrow& P-MQ^{-1}M^T<0,\ Q<0\\ &\Leftrightarrow& P<0,\ Q-M^TP^{-1}M<0 \end{array} }}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4efd2df144b4ea2e4b5c0dd6970ed0ac_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{\boxed{ \begin{array}{lll} && \left[\begin{array}{cc} P & M \\ M^T & Q \end{array}\right]>0\\ &\Leftrightarrow& MQ^{-1}M^T-P>0,\ Q>0\\ &\Leftrightarrow& P>0,\ M^TP^{-1}M-Q>0 \end{array} }}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ff8466bc18b10c46d2a1973fde841fb2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad P: \left\{\begin{array}{l} \dot{x}=Ax+B_1u_1+B_2u_2 \\ \underbrace{ \left[\begin{array}{c} y\\ u \end{array}\right] }_{y_1} = \underbrace{ \left[\begin{array}{c} C\\ 0 \end{array}\right] }_{C_1} x+ \underbrace{ \left[\begin{array}{c} 0\\ 0 \end{array}\right] }_{D_{11}}u_1+ \underbrace{ \left[\begin{array}{c} 0\\ I \end{array}\right] }_{D_{12}} u_2 \\ y_2=x \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-233587c7d6ac6840b26399b32d7f5ae2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad P_{CL}: \left\{\begin{array}{l} \dot{x}=\underbrace{(A-B_2F)}_{A_{CL}}x+\underbrace{B_1}_{B_{CL}}u_1 \\ y_1= \underbrace{ \left[\begin{array}{c} C\\ -F \end{array}\right] }_{C_{CL}=C_1-D_{12}F} x \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1cff650bf6e54c686a46b654002f41e1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \begin{array}{l} \exists Y_{CL}>0,\ Q>0:\\ \left[\begin{array}{cc} Y_{CL}A_{CL}^T+A_{CL}Y_{CL} & B_{CL} \\ B_{CL}^T & -I \end{array}\right]<0,\\ \left[\begin{array}{cc} Y_{CL} & Y_{CL}C_{CL}^T \\ C_{CL}Y_{CL} & Q \end{array}\right]>0,\\ {\rm tr}(Q)<\gamma^2 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1f42fdc63af549cb6cd701aa40eac0f7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \displaystyle{\exists Y>0,\ Q>0:\\ \left[\begin{array}{cc} Y(A-B_2F)^T+(A-B_2F)Y & B_1 \\ B_1^T & -I \end{array}\right]<0,\\ \left[\begin{array}{cc} Y & Y(C_1-D_{12}F)^T \\ (C_1-D_{12}F)Y & Q \end{array}\right]>0,\\ {\rm tr}(Q)<\gamma^2} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-90a3259c718f1035238e2463a6c5aa42_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \displaystyle{\exists Y>0,\ Q>0:\\ \left[\begin{array}{cc} (AY-B_2Z)^T+AY-B_2Z & B_1 \\ B_1^T & -I \end{array}\right]<0,\\ \left[\begin{array}{cc} Y & (C_1Y-D_{12}Z)^T \\ C_1Y-D_{12}Z & Q \end{array}\right]>0,\\ {\rm tr}(Q)<\gamma^2} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6b9dad597d2aabf8ef8c277abdacbf55_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \begin{array}{lll} && \sup_{\omega\in{\rm\bf R}}||\hat{G}(j\omega)||_2<\gamma \nonumber\\ &\Leftrightarrow& \exists X>0:\ \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma I & D^T \\ C & D & -\gamma I \end{array}\right]<0 \nonumber\\ &\Leftrightarrow& \exists Y>0:\ \left[\begin{array}{ccc} YA^T+AY & B & YC^T \\ B^T & -\gamma I & D^T \\ CY & D & -\gamma I \end{array}\right]<0\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fabe9aa11942205106ce125d21aa0bd2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad P: \left\{\begin{array}{l} \dot{x}=Ax+B_1u_1+B_2u_2 \\ \underbrace{ \left[\begin{array}{c} y\\ u \end{array}\right] }_{y_1} = \underbrace{ \left[\begin{array}{c} C\\ 0 \end{array}\right] }_{C_1} x+ \underbrace{ \left[\begin{array}{c} 0\\ 0 \end{array}\right] }_{D_{11}}u_1+ \underbrace{ \left[\begin{array}{c} 0\\ I \end{array}\right] }_{D_{12}} u_2 \\ y_2=x \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-27beeceac3c340d1c4c8c1eccb769f14_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{()\quad P_{CL}: \left\{\begin{array}{l} \dot{x}=(A-B_2F)x+B_1u_1 \\ y_1= \underbrace{ \left[\begin{array}{c} C\\ -F \end{array}\right] }_{C_1-D_{12}F} x \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9e9c5bf547f30fa45ba83bf020767e9d_l3.png)
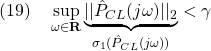
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{ccc} Y(A-B_2F)^T+(A-B_2F)Y & B_1 & Y(C_1-D_{12}F)^T \\ B_1^T & -\gamma I & D_{11}^T \\ (C_1-D_{12}F)Y & D_{11} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d53dc9e62d6af5b4cfc839c93b6d9673_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{ccc} (AY-B_2Z)^T+AY-B_2Z & B_1 & (C_1Y-D_{12}Z)^T \\ B_1^T & -\gamma I & D_{11}^T \\ C_1Y-D_{12}Z & D_{11} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f6a8dc294019aa496f62b9b21da1f984_l3.png)
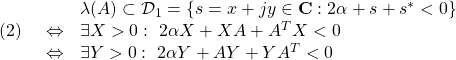
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \begin{array}{lll} &&\lambda(A)\subset {\cal D}_2=\{s=x+jy\in{\rm\bf C}: \left[\begin{array}{cc} -r & s \\ s^* & -r \end{array}\right] <0 \}\nonumber\\ &\Leftrightarrow& \exists X>0:\ \left[\begin{array}{cc} -rX & XA \\ A^TX & -rX \end{array}\right]<0 \nonumber\\ &\Leftrightarrow& \exists Y>0:\ \left[\begin{array}{cc} -rY & AY \\ YA^T & -rY \end{array}\right]<0\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9cde02783168cc87d584fcf28eb7011a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10) \begin{array}{lll} &&\lambda(A)\subset {\cal D}_3=\{s=x+jy\in{\rm\bf C}:\\ && \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]s + \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]^Ts^* <0 \}\nonumber\\ &&\Leftrightarrow \exists X>0:\ \left[\begin{array}{cc} \sin\theta(XA+A^TX) & \cos\theta(XA-A^TX) \\ -\cos\theta(XA-A^TX) & \sin\theta(XA+A^TX) \end{array}\right] <0 \nonumber\\ &&\Leftrightarrow \exists Y>0:\ \left[\begin{array}{cc} \sin\theta(AY+YA^T) & \cos\theta(AY-YA^T) \\ -\cos\theta(AY-YA^T) & \sin\theta(AY+YA^T) \end{array}\right] <0\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8ec7176d7e1ba9918e55f2d0c7c092ce_l3.png)

![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{l} \displaystyle{{\rm tr} (CW_cC^T)<\gamma^2}\\\\ \displaystyle{\Leftrightarrow \exists X_c>0,\ Q_c>0:\\ (1a)\quad\left[\begin{array}{cc} A^TX_c+X_cA & X_cB \\ B^TX_c & -I \end{array}\right]<0,\ \left[\begin{array}{cc} X_c & C^T \\ C & Q_c \end{array}\right]>0,\ {\rm tr}(Q_c)<\gamma^2}\\\\ \displaystyle{\Leftrightarrow \exists Y_c>0,\ Q_c>0:\\ (1b)\quad \left[\begin{array}{cc} Y_cA^T+AY_c & Y_cB \\ B^TY_c & -I \end{array}\right]<0,\ \left[\begin{array}{cc} Y_c & Y_cC^T \\ CY_c & Q_c \end{array}\right]>0,\ {\rm tr}(Q_c)<\gamma^2} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0e5eb15733d3b5cec658dab7afe757d6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{l} \displaystyle{{\rm tr} (B^TW_oB)<\gamma^2}\\\\ \displaystyle{\Leftrightarrow \exists X_o>0,\ Q_o>0:\\ (2a)\quad\left[\begin{array}{cc} AX_o+X_oA^T & X_oC^T \\ CX_o & -I \end{array}\right]<0,\ \left[\begin{array}{cc} X_o & B \\ B^T & Q_o \end{array}\right]>0,\ {\rm tr}(Q_o)<\gamma^2}\\\\ \displaystyle{\Leftrightarrow \exists Y_o>0,\ Q_o>0:\\ (2b)\quad\left[\begin{array}{cc} Y_oA+A^TY_o & Y_oC^T \\ CY_o & -I \end{array}\right]<0,\ \left[\begin{array}{cc} Y_o & Y_oB \\ B^TY_o & Q_o \end{array}\right]>0,\ {\rm tr}(Q_o)<\gamma^2} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0103a79b019093fcbd4360479821e521_l3.png)
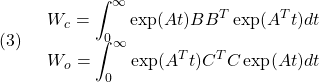
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} A^TX_c+X_cA+X_cBB^TX_c<0 \Leftrightarrow\ \left[\begin{array}{cc} A^TX_c+X_cA & X_cB \\ B^TX_c & -I \end{array}\right]<0 \\ AX_o+X_oA^T+X_oC^TCX_o<0 \Leftrightarrow\ \left[\begin{array}{cc} AX_o+X_oA^T & X_oC^T \\ CX_o & -I \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1eab031b7ca8535cebc0a481a954f426_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} {\rm tr} (CW_cC^T)<\gamma^2 \Leftrightarrow\ \left[\begin{array}{cc} X_c & C^T \\ C & Q_c \end{array}\right]>0,\ {\rm tr} (Q_c)<\gamma^2\\ {\rm tr} (B^TW_oB)<\gamma^2 \Leftrightarrow\ \left[\begin{array}{cc} X_o & B \\ B^T & Q_o \end{array}\right]>0,\ {\rm tr} (Q_o)<\gamma^2 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-94628f5f4d3a01a84d931ae427db5b3c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} CX_c^{-1}C^T-(CW_cC^T+\epsilon I)>0 \Leftrightarrow\ \left[\begin{array}{cc} X_c & C^T \\ C & CW_cC^T+\epsilon I \end{array}\right]>0\\ B^TX_o^{-1}B-(B^TW_oB+\epsilon I)>0 \Leftrightarrow\ \left[\begin{array}{cc} X_o & B \\ B^T & B^TW_oB+\epsilon I \end{array}\right]>0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a8a8eeaf32331b7bc67b6cdb89a3f7cc_l3.png)

![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \displaystyle{\sup_{u\in{\cal L}_2}\frac{||y(t)||_2}{||u(t)||_2} =\sup_{\omega\in{\rm\bf R}}||\hat{G}(j\omega)||_2<\gamma} \\ \displaystyle{\Leftrightarrow \exists X>0:\ \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D & -I \end{array}\right]<0} \\ \displaystyle{\Leftrightarrow \exists Y>0:\ \left[\begin{array}{ccc} YA^T+AY & B & YC^T \\ B^T & -\gamma^2 I & D^T \\ CY & D & -I \end{array}\right]<0} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cb76514d96e7c4115d9ea88e02ad0651_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \begin{array}{l} \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D &-I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{cc} A^TX+XA & XB \\ B^TX & -\gamma^2 I \end{array}\right] - \left[\begin{array}{cc} C^T\\ D^T \end{array}\right] (-I) %(-\gamma^{-1} I) \left[\begin{array}{cc} C & D \end{array}\right] <0 \\ \Leftrightarrow \left[\begin{array}{cc} A^TX+XA & XB \\ B^TX & 0 \end{array}\right] < \left[\begin{array}{cc} C^T & 0 \\ D^T & I \end{array}\right] \left[\begin{array}{cc} -I & 0 \\ 0 & \gamma^2 I \end{array}\right] \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5c2560cc668d6d0690878b8eedd8885c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \begin{array}{l} \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D & - I \end{array}\right]<0 \\ &\Leftrightarrow \forall \left[\begin{array}{c} x \\ u \end{array}\right]\ne0: \underbrace{ \left[\begin{array}{c} x \\ u \end{array}\right]^T \left[\begin{array}{cc} A^TX+XA & XB \\ B^TX & 0 \end{array}\right] \left[\begin{array}{c} x \\ u \end{array}\right] }_{\dot{V}(x)=\frac{d}{dt}(x^TXx)} \\ < \underbrace{ \left[\begin{array}{c} x \\ u \end{array}\right]^T \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right]^T \left[\begin{array}{cc} - I & 0 \\ 0 & \gamma^2 I \end{array}\right] \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right] \left[\begin{array}{c} x \\ u \end{array}\right] }_{s(u,y)=\gamma^2 u^Tu-y^Ty} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-474ab9036f2ca5939a3c709f1500ddf6_l3.png)
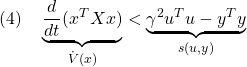
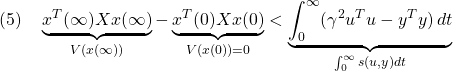
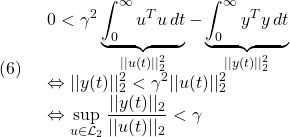
![Rendered by QuickLaTeX.com \displaystyle{(7) \begin{array}{l} \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D & -I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{ccc} A^TX+XA & X(B\sqrt{\gamma}) & (\frac{1}{\sqrt{\gamma}}C)^T \\ (B\sqrt{\gamma})^TX & - \gamma^2 I & D^T \\ (\frac{1}{\sqrt{\gamma}}C) & D & -I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{ccc} I & 0 & 0 \\ 0 & \sqrt{\gamma} I & 0 \\ 0 & 0 & \frac{1}{\sqrt{\gamma}} I \end{array}\right] \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma I & D^T \\ C & D &-\gamma I \end{array}\right] \left[\begin{array}{ccc} I & 0 & 0 \\ 0 & \sqrt{\gamma} I & 0 \\ 0 & 0 & \frac{1}{\sqrt{\gamma}} I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma I & D^T \\ C & D &-\gamma I \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9f78ef9deeaf1d5eba2e99bef8581c5e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \displaystyle{\sup_{u\in{\cal L}_2}\frac{||y(t)||_2}{||u(t)||_2} =\sup_{\omega\in{\rm\bf R}}||\hat{G}(j\omega)||_2<\gamma} \\ \displaystyle{\Leftrightarrow \exists X>0:\ \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma I & D^T \\ C & D & -\gamma I \end{array}\right]<0} \\ \displaystyle{\Leftrightarrow \exists Y>0:\ \left[\begin{array}{ccc} YA^T+AY & B & YC^T \\ B^T & -\gamma I & D^T \\ CY & D & -\gamma I \end{array}\right]<0} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0e630e89fa5b93c2df2468b74a26d002_l3.png)