| MATLAB |
%of_syn_lmi7.m
%-----
A=[0 1;-1 -2*0.01]; B1=[0;1]; B2=B1;
C1=[1 0;0 0]; D11=[0;0]; D12=[0;1];
C2=[1 0]; D21=0; D22=0;
[n,m]=size(B1); p=1;
%=====
setlmis([]);
gam=lmivar(1,[1 0]);
Q=lmivar(1,[p 1]);
R=lmivar(1,[n 1]);
S=lmivar(1,[n 1]);
Ak=lmivar(2,[n n]);
Bk=lmivar(2,[n p]);
Ck=lmivar(2,[m n]);
Dk=lmivar(2,[m p]);
%----- (15)
lmi1=newlmi;
lmiterm([lmi1 1 1 R],A,1,'s'); %#1:R*A'+AR
lmiterm([lmi1 1 1 Ck],B2,1,'s'); %#1:Ck'*B2'+B2*Ck
lmiterm([lmi1 2 1 0],A'); %#1:A'
lmiterm([lmi1 2 1 Ak],1,1); %#1:Ak
lmiterm([lmi1 2 2 S],1,A,'s'); %#1:A'*S+S*A
lmiterm([lmi1 2 2 Bk],1,C2,'s'); %#1:C2'*Bk'+Bk*C2
lmiterm([lmi1 1 3 0],B1); %#1:B1
lmiterm([lmi1 2 3 S],1,B1); %#1:S*B1
lmiterm([lmi1 2 3 Bk],1,D21); %#1:Bk*D21
lmiterm([lmi1 3 3 0],-1); %#1:-I
%----- (16)
lmi2=newlmi
lmiterm([-lmi2 1 1 R],1,1); %#2:R
lmiterm([-lmi2 2 1 0],1); %#2:I
lmiterm([-lmi2 2 2 S],1,1); %#2:S
lmiterm([-lmi2,3,1,R],C1,1); %#2:C1*R
lmiterm([-lmi2,3,1,Ck],D12,1); %#2:D12*Ck
lmiterm([-lmi2 3 3 Q],1,1); %#2:Q
%----- (17) gam-tr(Q)>0
CT=zeros(1,p*(p+1)/2);
for i=1:p, j=(i+1)*i/2; CT(j)=1; end
lmi3=newlmi;
lmiterm([-lmi3 1 1 gam],1,1); %#3:gam
lmiterm([-lmi3 1 1 Q],-CT,1); %#3:-tr(Q)
%======
LMIs=getlmis;
cobj=zeros(1,decnbr(LMIs));
cobj(1)=1;
[cost,xopt]=mincx(LMIs,cobj);
%-----
gopt=dec2mat(LMIs,xopt,gam)
R=dec2mat(LMIs,xopt,R);
S=dec2mat(LMIs,xopt,S);
ak=dec2mat(LMIs,xopt,Ak);
bk=dec2mat(LMIs,xopt,Bk);
ck=dec2mat(LMIs,xopt,Ck);
dk=dec2mat(LMIs,xopt,Dk);
[u,sd,v]=svd(eye(size(A,1)-S*R);
sd=diag(sqrt(1./diag(sd)));
Ni=sd*u'; Mti=v*sd;
AK=Ni*(ak-S*A*R-bk*C2*R-S*B2*ck)*Mti;
BK=Ni*bk;
CK=ck*Mti;
%-----
pl=eig(A)
ACL=[A B2*CK;
BK*C2 AK];
plCL=eig(ACL)
close all,figure(1)
dregion(0,0,2000,pi/2,2000*[-1,1,-1,1])
plot(real(pl),imag(pl),'x',real(plCL),imag(plCL),'*')
BCL=[B1;
BK*D21];
CCL=[C1 D12*CK];
DCL=zeros(2,1);
figure(2)
ol=ltisys(A,B1,C1,D11);
cl=ltisys(ACL,BCL,CCL,DCL);
om=logspace(-1,1,100);
splot(cl,'sv',om),hold on
splot(ol,'sv',om),grid
%-----
%eof
|
![]() 次系
次系![]() の
の![]() ノルムが
ノルムが![]() より小となるためのLMI条件は、次の通りでした。
より小となるためのLMI条件は、次の通りでした。![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \displaystyle{{\rm tr} (CW_cC^T)<\gamma^2\quad(W_c=\int_0^\infty \exp(At)BB^T\exp(A^Tt)dt)}\\\\ \displaystyle{\Leftrightarrow \exists X_c>0,\ Q_c>0:\\ \left[\begin{array}{cc} A^TX_c+X_cA & X_cB \\ B^TX_c & -I \end{array}\right]<0,\ \left[\begin{array}{cc} X_c & C^T \\ C & Q_c \end{array}\right]>0,\ {\rm tr}(Q_c)<\gamma^2}\\\\ \displaystyle{\Leftrightarrow \exists Y_c>0,\ Q_c>0:\\ \left[\begin{array}{cc} Y_cA^T+AY_c & B \\ B^T & -I \end{array}\right]<0,\ \left[\begin{array}{cc} Y_c & Y_cC^T \\ CY_c & Q_c \end{array}\right]>0,\ {\rm tr}(Q_c)<\gamma^2} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4740750e1fdf8093b1f6322284a78a12_l3.png)

![]() 次系を考えます。
次系を考えます。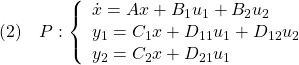
![]()
![Rendered by QuickLaTeX.com \displaystyle{(4) \begin{array}{l} P_{CL}: \\ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x} \\ \dot{x}_K \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} A+B_2D_KC_2 & B_2C_K \\ B_KC_2 & A_K \end{array}\right] }_{A_{CL}} \left[\begin{array}{c} x \\ x_K \end{array}\right] + \underbrace{ \left[\begin{array}{ccc} B_1+B_2D_KD_{21} \\ B_KD_{21} \end{array}\right] }_{B_{CL}} u_1\\ y_1 = \underbrace{ \left[\begin{array}{ccc} C_1+D_{12}D_KC_2 & D_{12}C_K \end{array}\right] }_{C_{CL}} \left[\begin{array}{c} x \\ x_K \end{array}\right] + \underbrace{ (D_{11}+D_{12}D_KD_{21}) }_{D_{CL}} u_1 \end{array}\right. \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f53ae5ac3451ed7d23911ed463c5c53a_l3.png)
![]() ノルムを考えますが、直達項
ノルムを考えますが、直達項![]() が0となるように、
が0となるように、![]() 、
、![]() とします。すなわち閉ループ系
とします。すなわち閉ループ系![Rendered by QuickLaTeX.com \displaystyle{(5) \begin{array}{l} P_{CL}: \\ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x} \\ \dot{x}_K \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} A & B_2C_K \\ B_KC_2 & A_K \end{array}\right] }_{A_{CL}} \left[\begin{array}{c} x \\ x_K \end{array}\right] + \underbrace{ \left[\begin{array}{ccc} B_1 \\ B_KD_{21} \end{array}\right] }_{B_{CL}} u_1\\ y_1 = \underbrace{ \left[\begin{array}{ccc} C_1 & D_{12}C_K \end{array}\right] }_{C_{CL}} \left[\begin{array}{c} x \\ x_K \end{array}\right] \end{array}\right. \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d9ee0d76c4323fd2167e246115a0ba75_l3.png)
![]() ノルムが
ノルムが![]() より小、すなわち
より小、すなわち![]()
![]() を求める問題を考えます。
を求める問題を考えます。![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \exists Y_{CL}>0,\ Q>0:\\ \left[\begin{array}{cc} Y_{CL}A_{CL}^T+A_{CL}Y_{CL} & B_{CL} \\ B_{CL}^T & -I \end{array}\right]<0,\\ \left[\begin{array}{cc} Y_{CL} & Y_{CL}C_{CL}^T \\ C_{CL}Y_{CL} & Q \end{array}\right]>0,\\ {\rm tr}(Q)<\gamma^2 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4b9dc7d5c8ae7d5f7820077476af8b06_l3.png)
![]() を代入して
を代入して![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \exists \Pi_1\Pi_2^{-1}>0,\ Q>0:\\ \left[\begin{array}{cc} \Pi_2^{-T}\Pi_1^TA_{CL}^T+A_{CL}\Pi_1\Pi_2^{-1} & B_{CL} \\ B_{CL}^T & -I \end{array}\right]<0,\\ \left[\begin{array}{cc} \Pi_2^{-T}\Pi_1^T & \Pi_2^{-T}\Pi_1^TC_{CL}^T \\ C_{CL}\Pi_1\Pi_2^{-1} & Q \end{array}\right]>0,\\ {\rm tr}(Q)<\gamma^2 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9e104f2b0398c383a30ed6b905cd3e8d_l3.png)
![]() 、右から
、右から![]() をかけると、次のようなLMIとなります。
をかけると、次のようなLMIとなります。![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \begin{array}{l} \exists \Pi_2^T\Pi_1>0,\ Q>0:\\ \left[\begin{array}{cc} \Pi_1^TA_{CL}^T\Pi_2+\Pi_2^TA_{CL}\Pi_1 & \Pi_2^TB_{CL} \\ B_{CL}^T\Pi_2 & -I \end{array}\right]<0,\\ \left[\begin{array}{cc} \Pi_1^T\Pi_2 & \Pi_1^TC_{CL}^T \\ C_{CL}\Pi_1 & Q \end{array}\right]>0,\\ {\rm tr}(Q)<\gamma^2 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bc5d943db7eceee17783ff93d1b5b6b4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} \Pi_2^TA_{CL}\Pi_1= \left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] \left[\begin{array}{ccc} A & B_2C_K \\ B_KC_2 & A_K \end{array}\right] \left[\begin{array}{cc} R & I \\ M^T & 0 \end{array}\right] \\ =\left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] \left[\begin{array}{ccc} AR+B_2C_KM^T & A \\ B_KC_2R+A_KM^T & B_KC_2 \end{array}\right] \\ =\left[\begin{array}{ccc} AR+B_2C_KM^T & A\\ SAR+SB_2C_KM^T+NB_KCR+NA_KM^T & SA+NB_KC_2 \end{array}\right] \\ =\left[\begin{array}{cc} AR+B_2{\cal C}_K & A \\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3d2317dcd404dd712b36e3efd136ce5a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \Pi_2^TB_{CL}= \left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] \left[\begin{array}{ccc} B_1 \\ B_KD_{21} \end{array}\right] \\ =\left[\begin{array}{ccc} B_1 \\ SB_1+NB_KD_{21} \end{array}\right] =\left[\begin{array}{ccc} B_1 \\ SB_1+{\cal B}_KD_{21} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d753b7e0b856f8e28ca5d5f8804803ab_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} C_{CL}\Pi_1= \left[\begin{array}{ccc} C_1 & D_{12}C_K \end{array}\right] \left[\begin{array}{cc} R & I \\ M^T & 0 \end{array}\right] \\ =\left[\begin{array}{ccc} C_1R+D_{12}C_KM^T & C_1 \end{array}\right] \\ =\left[\begin{array}{ccc} C_1R+D_{12}{\cal C}_K & C_1 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-923ae56b395be17601883366623ec0c1_l3.png)
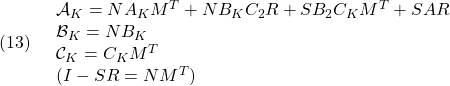
![]() を最小化し、
を最小化し、 ![]() を求め、次式によって出力フィードバックのゲインを決定します。
を求め、次式によって出力フィードバックのゲインを決定します。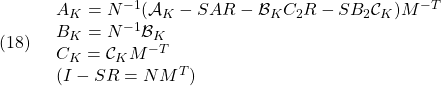
![]() 次のコードを参考にして、
次のコードを参考にして、![]() 制御(出力FB)を求める関数を作成せよ。
制御(出力FB)を求める関数を作成せよ。![Rendered by QuickLaTeX.com \displaystyle{(15) \left[\begin{array}{ccc} \left[\begin{array}{cc} AR+B_2{\cal C}_K & A\\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right]+(*)^T & \left[\begin{array}{c} B_1 \\ SB_1+{\cal B}_KD_{21} \end{array}\right]\\ (*)^T & -I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eb7747d66fa3d59761d94a015b17d9c1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(16) \left[\begin{array}{cc} \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] & (*)^T \\ \left[\begin{array}{cc} C_1R+D_{12}{\cal C}_K & C_1 \end{array}\right] & Q \end{array}\right]>0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7b27bab2fc29a6081c3f57198e95f0b8_l3.png)