状態FB用LMI(固有値制約)…Homework
[0] ![]() 次系
次系![]() に対する状態フィードバック
に対する状態フィードバック![]() による閉ループ系
による閉ループ系![]() において、
において、
![]()
となるように状態フィードバックゲイン![]() を求める問題を考えます。
を求める問題を考えます。
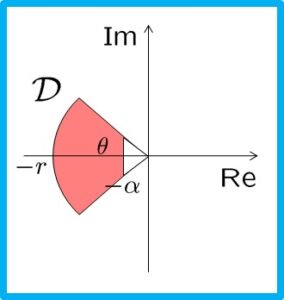
図1 領域![]()
[1] ![]() となるLMI条件は、次の通りでした。
となるLMI条件は、次の通りでした。
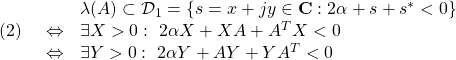
したがって、![]() となるLMI条件は、次のようになります。
となるLMI条件は、次のようになります。
![]()
これは、未知行列![]() と
と![]() の積
の積![]() をもつので、LMIではなく、lmisolverを用いて解くことができません。しかしながら、変数変換
をもつので、LMIではなく、lmisolverを用いて解くことができません。しかしながら、変数変換![]() を行うと、次のような
を行うと、次のような![]() と
と![]() に関するLMIとなります。
に関するLMIとなります。
|
|
これを解いて![]() と
と![]() を求め、次式によって状態フィードバックゲインを決定します。
を求め、次式によって状態フィードバックゲインを決定します。
![]()
[2] ![]() となるLMI条件は、次の通りでした。
となるLMI条件は、次の通りでした。
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \begin{array}{lll} &&\lambda(A)\subset {\cal D}_2=\{s=x+jy\in{\rm\bf C}: \left[\begin{array}{cc} -r & s \\ s^* & -r \end{array}\right] <0 \}\nonumber\\ &\Leftrightarrow& \exists X>0:\ \left[\begin{array}{cc} -rX & XA \\ A^TX & -rX \end{array}\right]<0 \nonumber\\ &\Leftrightarrow& \exists Y>0:\ \left[\begin{array}{cc} -rY & AY \\ YA^T & -rY \end{array}\right]<0\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9cde02783168cc87d584fcf28eb7011a_l3.png)
したがって、![]() となるLMI条件は、次のようになります。
となるLMI条件は、次のようになります。
![]()
ここで、変数変換![]() を行うと、次のような
を行うと、次のような![]() と
と![]() に関するLMIとなります。
に関するLMIとなります。
|
|
これを解いて![]() と
と![]() を求め、次式によって状態フィードバックゲインを決定します。
を求め、次式によって状態フィードバックゲインを決定します。
![]()
[3] ![]() となるLMI条件は、次の通りでした。
となるLMI条件は、次の通りでした。
![Rendered by QuickLaTeX.com \displaystyle{(10) \begin{array}{lll} &&\lambda(A)\subset {\cal D}_3=\{s=x+jy\in{\rm\bf C}:\\ && \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]s + \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]^Ts^* <0 \}\nonumber\\ &&\Leftrightarrow \exists X>0:\ \left[\begin{array}{cc} \sin\theta(XA+A^TX) & \cos\theta(XA-A^TX) \\ -\cos\theta(XA-A^TX) & \sin\theta(XA+A^TX) \end{array}\right] <0 \nonumber\\ &&\Leftrightarrow \exists Y>0:\ \left[\begin{array}{cc} \sin\theta(AY+YA^T) & \cos\theta(AY-YA^T) \\ -\cos\theta(AY-YA^T) & \sin\theta(AY+YA^T) \end{array}\right] <0\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8ec7176d7e1ba9918e55f2d0c7c092ce_l3.png)
したがって、![]() となるLMI条件は、次のようになります。
となるLMI条件は、次のようになります。
![]()
![]()
ここで、変数変換![]() を行うと、次のような
を行うと、次のような![]() と
と![]() に関するLMIとなります。
に関するLMIとなります。
|
|
これを解いて![]() と
と![]() を求め、次式によって状態フィードバックゲインを決定します。
を求め、次式によって状態フィードバックゲインを決定します。
![]()
演習B32…Flipped Classroom
![]() 次のコードを参考にして、
次のコードを参考にして、![]() を達成する状態FBを求める関数を作成せよ。
を達成する状態FBを求める関数を作成せよ。
| MATLAB |
|