YMCPBの線形モデル
●制御対象YMCPBの運動方程式として次式を考えます。
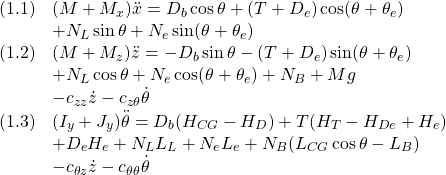
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(1')\quad \begin{array}{l} \left[\begin{array}{ccc} M+M_x & 0 & 0 \\ 0 & M+M_z & 0\\ 0 & 0 & I_y+J_y \end{array}\right] \left[\begin{array}{c} \ddot{x}\\ \ddot{z}\\ \ddot{\theta} \end{array}\right]= \left[\begin{array}{ccc} 0 & 0 & 0 \\ 0 & c_{zz} & c_{z\theta}\\ 0 & c_{\theta z} & c_{\theta\theta} \end{array}\right] \left[\begin{array}{c} \dot{x}\\ \dot{z}\\ \dot{\theta} \end{array}\right]\\ +\left[\begin{array}{c} D_b\cos\theta+(T+D_e)\cos(\theta+\theta_e)\\ -D_b\sin\theta-(T+D_e)\sin(\theta+\theta_e)\\ D_b(H_{CG}-H_D)+T(H_T-H_{De}+H_e)+D_eH_e \end{array}\right]\\ +\left[\begin{array}{c} N_L\sin\theta+N_e\sin(\theta+\theta_e)\\ N_L\cos\theta+N_e\cos(\theta+\theta_e)\\ N_LL_L+N_eL_e \end{array}\right] + \left[\begin{array}{c} 0 \\ N_B+Mg\\ N_B(L_{CG}\cos\theta-L_B) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5fcbf114446e6f6006a4add51667c0b6_l3.png)
ここで、![]() はそれぞれサージ、ヒーブ、ピッチを、
はそれぞれサージ、ヒーブ、ピッチを、![]() はそれぞれスラスト、船外機取付角を表しています。その他の物理パラメータの説明はここでは省略します。
はそれぞれスラスト、船外機取付角を表しています。その他の物理パラメータの説明はここでは省略します。
●いま状態変数ベクトルと操作変数ベクトルをそれぞれ
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \xi=\left[\begin{array}{c} x\\ z\\ \theta\\\hline \dot{x}\\ \dot{z}\\ \dot{\theta} \end{array}\right],\ \zeta=\left[\begin{array}{c} T\\ \theta_e \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-289b718cdf08a7268cfcc44b2dd308bb_l3.png)
ととると、次の非線形状態方程式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(3.1)\quad \underbrace{\frac{d}{dt}\left[\begin{array}{c} x\\ z\\ \theta\\\hline \dot{x}\\ \dot{z}\\ \dot{\theta} \end{array}\right]}_{\dot{\xi}}= \underbrace{ \left[\begin{array}{c} f_1(x,z,\theta,\dot{x},\dot{z},\dot{\theta},T,\theta_e)\\ f_2(x,z,\theta,\dot{x},\dot{z},\dot{\theta},T,\theta_e)\\ f_3(x,z,\theta,\dot{x},\dot{z},\dot{\theta},T,\theta_e)\\\hline f_4(x,z,\theta,\dot{x},\dot{z},\dot{\theta},T,\theta_e)\\ f_5(x,z,\theta,\dot{x},\dot{z},\dot{\theta},T,\theta_e)\\ f_6(x,z,\theta,\dot{x},\dot{z},\dot{\theta},T,\theta_e) \end{array}\right]}_{f(\xi,\zeta)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-986df1fe9bf874b3902a899fdb7379ed_l3.png)
ただし
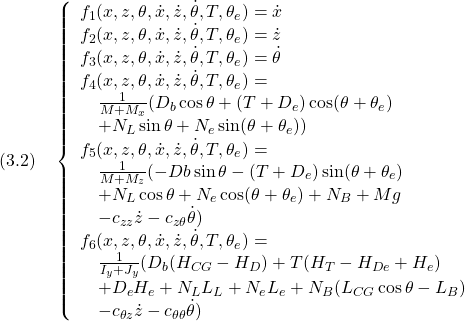
●制御対象YMCPBに対する制御目的は、あるスラスト![]() と取付角
と取付角![]() の下で、巡航速度
の下で、巡航速度![]() で走行するとき、一定の姿勢
で走行するとき、一定の姿勢![]() を保つこととします。これは、次の平衡状態
を保つこととします。これは、次の平衡状態![]() を、次の平衡入力
を、次の平衡入力![]() によって保持することとみなすことができます。
によって保持することとみなすことができます。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \xi^*=\left[\begin{array}{c} V^*t\\ z^*\\ \theta^*\\\hline V^*\\ 0\\ 0 \end{array}\right],\ \zeta^*=\left[\begin{array}{c} T^*\\ \theta_e^* \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5f6437de0791e355b2bdc371e694f78d_l3.png)
この平衡状態と平衡入力を定めるためには、![]() と
と![]() を所与として、残りの
を所与として、残りの![]() を次の非線形連立方程式を解いて求めます。
を次の非線形連立方程式を解いて求めます。
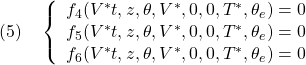
したがって、次式が成り立つことに注意します。
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad f(\xi^*,\zeta^*)= \left[\begin{array}{c} V^*\\ 0\\ 0\\\hline 0\\ 0\\ 0 \end{array}\right]=\frac{d}{dt}\xi^* }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7f31cdd4dd69a9639cb450150aaf8339_l3.png)
●この平衡状態![]() と平衡入力
と平衡入力![]() の回りで、非線形状態方程式
の回りで、非線形状態方程式![]() を線形近似します。
を線形近似します。
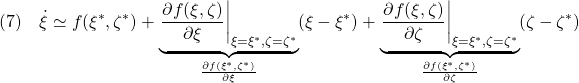
ここで(6)に注意して、線形状態方程式
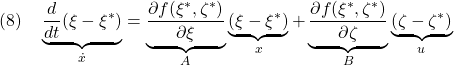
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \begin{array}{c} \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-V^*t\\ z(t)-z^*\\ \theta(t)-\theta^*\\\hline \dot{x}(t)-V^*\\ \dot{z}(t)\\ \dot{\theta}(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{ccc|ccc} 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\\hline 0 & a_{42} & a_{43} & a_{44} & a_{45} & a_{46} \\ 0 & a_{52} & a_{53} & a_{54} & a_{55} & a_{56} \\ 0 & a_{62} & a_{63} & a_{64} & a_{65} & a_{66} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x(t)-V^*t\\ z(t)-z^*\\ \theta(t)-\theta^*\\\hline \dot{x}(t)-V^*\\ \dot{z}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)}\\ + \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\\hline b_{41} & b_{42} \\ b_{51} & b_{52} \\ b_{61} & b_{62} \end{array}\right] }_{B} \underbrace{ \left[\begin{array}{c} T(t)-T^*\\ \theta_e(t)-\theta_e^*\\ \end{array}\right] }_{u(t)} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9015be8df754f0e7d33ca667c6ed948c_l3.png)
を得ます。
●次の5組のデータセットが与えられています。
| 艇 | 艇質量[kg] | 長手方向重心位置[m] | 備考 | |
| No1 | SPTM247 | 2709 | 1.9756 | INM抵抗試験レポートC2620-07CT18-RAP01による |
| No2 | SPTM247 | 2813 | 1.925 | 2021/8/2重量重心測定結果より |
| No3 | SPTM247 | 2845 | 1.937 | 2022/1/19重量重心測定結果より |
| No4 | SPTM247 | 2945 | 1.937 | No3重量に+100kg |
| No5 | SPTM247 | 2745 | 1.937 | No3重量に-100kg |
各データセットは、133個(![]() )の平衡状態と平衡入力と
)の平衡状態と平衡入力と![]() 行列を含みます(
行列を含みます(![]() 行列と
行列と![]() 行列は固定)。これらは、たとえば、データセットNo1に対しては図1のようにグラフ化されます。
行列は固定)。これらは、たとえば、データセットNo1に対しては図1のようにグラフ化されます。
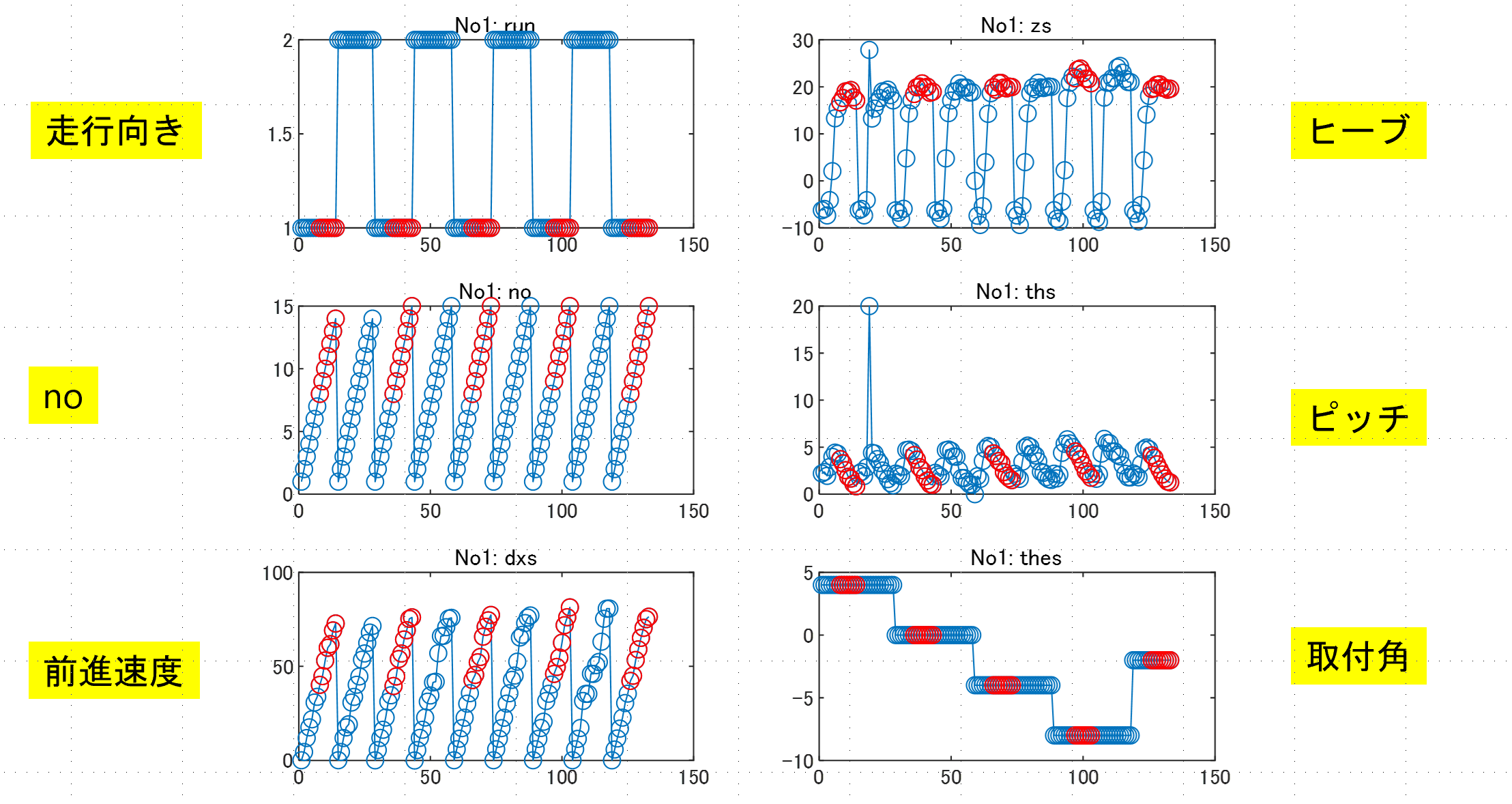
図1 データセットNo1における平衡状態
ここで、赤い〇の平衡状態は、制御系の設計および評価のために選ばれた、次表に示す39点です。![]() の場合の平衡状態回りの線形モデルについてコントローラを設計します。
の場合の平衡状態回りの線形モデルについてコントローラを設計します。
| run | k | ||
| -4 deg | run1 | 8,9,10,11,12,13,14 | |
| 0 deg | run1 | 36,37,38,39,40,41,42,43 | |
| 4 deg | run1 | 66,67,68,69,70,71,72,73 | |
| 8 deg | run1 | 96,97,98,99,100,101,102,103 | |
| 2 deg | run1 | 126,127,128,129,130,131,132,133 |
またデータセットNo1に対する行列![]() の固有値は図2のようにグラフ化されます。
の固有値は図2のようにグラフ化されます。
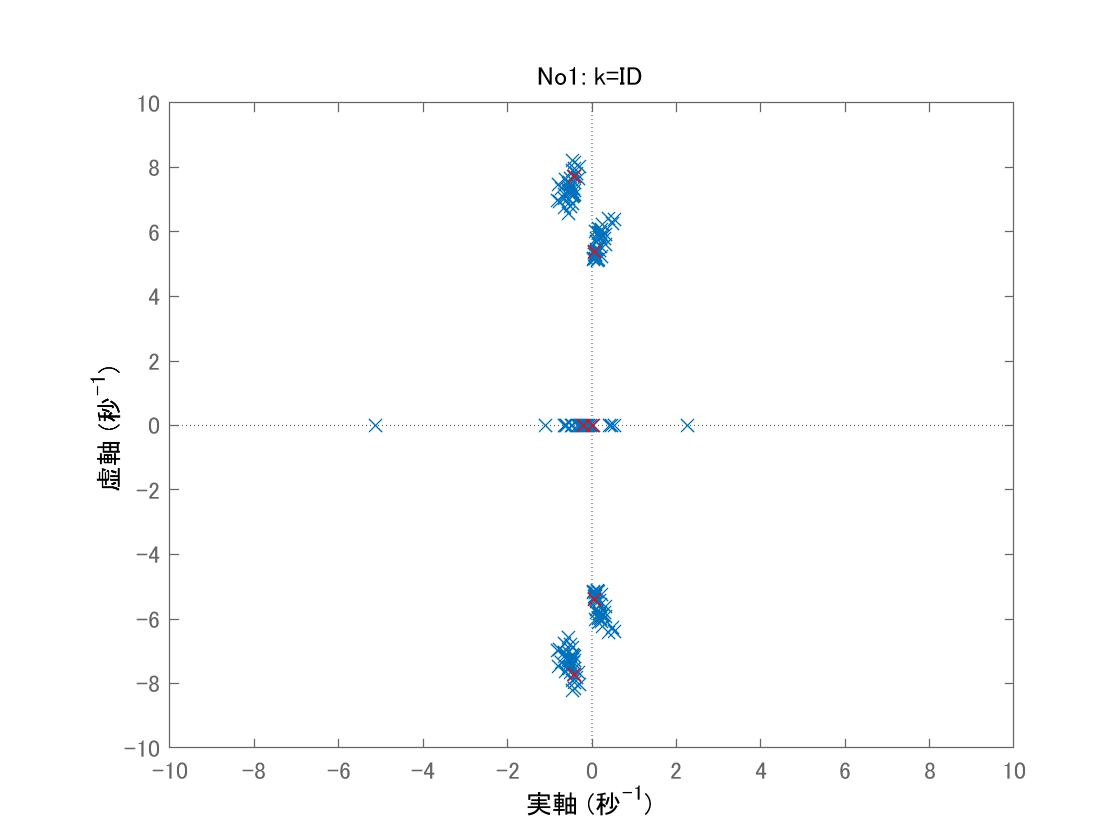
図2 データセットNo1における行列![]() の固有値
の固有値
各線形モデルに対して複素固有値が2対、実固有値が2個(うち1個は零)あることがわかります。不安定な複素固有値はピッチの振舞いに、安定な複素固有値はヒーブの振舞いに、非零実固有値は速度変動に関係しています。速度変動が発散する場合があることが気になるところです。
制御系設計用線形モデル
●制御系設計用線形モデルを得るために、まずアクチュエータについては、船外機の取付角を操作するためにレバーを引いた期間だけ一定の角速度![]() で回転するものとします。これを次式で表します。
で回転するものとします。これを次式で表します。
![]()
ここで、![]() は操作入力
は操作入力![]() が正のとき
が正のとき![]() 、負のとき
、負のとき![]() の値をとるものとします。すなわち
の値をとるものとします。すなわち
![]()
したがって、制御対象の状態方程式(9)とアクチュエータ(10)を合わせて、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{c} \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-V^*t\\ z(t)-z^*\\ \theta(t)-\theta^*\\\hline \dot{x}(t)-V^*\\ \dot{z}(t)\\ \dot{\theta}(t)\\\hline \theta_e(t)-\theta_e^* \end{array}\right] }_{\dot{x}_a(t)} = \underbrace{ \left[\begin{array}{ccc|ccc|c} 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0\\\hline 0 & a_{42} & a_{43} & a_{44} & a_{45} & a_{46} & b_{42}\\ 0 & a_{52} & a_{53} & a_{54} & a_{55} & a_{56} & b_{52}\\ 0 & a_{62} & a_{63} & a_{64} & a_{65} & a_{66} & b_{62}\\\hline 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right] }_{A_a} \underbrace{ \left[\begin{array}{c} x(t)-V^*t\\ z(t)-z^*\\ \theta(t)-\theta^*\\\hline \dot{x}(t)-V^*\\ \dot{z}(t)\\ \dot{\theta}(t)\\\hline \theta_e(t)-\theta_e^* \end{array}\right] }_{x_a(t)}\\ + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 0 \\\hline 0 \\ 0 \\ 0 \\\hline \omega_e \end{array}\right] }_{B_a}u_e(t) + \left[\begin{array}{c} 0 \\ 0 \\ 0 \\\hline b_{41} \\ b_{51} \\ b_{61} \\\hline 0 \end{array}\right]\underbrace{(T(t)-T^*)}_{0} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d60d11235671d929a5e705c533a692dc_l3.png)
また状態変数のうち、![]() 、
、![]() 、
、![]() が計測できるものとします。このとき、状態方程式(12)に対する観測方程式は次式で表されます。
が計測できるものとします。このとき、状態方程式(12)に対する観測方程式は次式で表されます。
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{y(t)} = \underbrace{ \left[\begin{array}{ccc|ccc|c} 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x(t)-V^*t\\ z(t)-z^*\\ \theta(t)-\theta^*\\\hline \dot{x}(t)-V^*\\ \dot{z}(t)\\ \dot{\theta}(t)\\\hline \theta_e(t)-\theta_e^* \end{array}\right] }_{x(t)} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-19a5fd67356f5063740009700e8d5cd0_l3.png)
●制御対象YMCPBに対する制御目的は、あるスラスト![]() と取付角
と取付角![]() の下で、巡航速度
の下で、巡航速度![]() で走行するとき、一定の姿勢
で走行するとき、一定の姿勢![]() を保つこととします。この制御目的に照らして、サージ方向の状態変数は省いてよく、また操作変数も船外機取付角に限定することができます。ヒーブ方向の状態変数を残すか省くかによって、次の2種類の線形モデルが考えられます。
を保つこととします。この制御目的に照らして、サージ方向の状態変数は省いてよく、また操作変数も船外機取付角に限定することができます。ヒーブ方向の状態変数を残すか省くかによって、次の2種類の線形モデルが考えられます。
5次元モデル
![Rendered by QuickLaTeX.com \displaystyle{(14.1)\quad \begin{array}{l} \underbrace{ \frac{d}{dt} \left[\begin{array}{c} z(t)-z^*\\ \theta(t)-\theta^*\\ \dot{z}(t)\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{ccccc} 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ a_{52} & a_{53} & a_{55} & a_{56} & b_{52}\\ a_{62} & a_{63} & a_{65} & a_{66} & b_{62}\\ 0 & 0 & 0 & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} z(t)-z^*\\ \theta(t)-\theta^*\\ \dot{z}(t)\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{x(t)}\\ + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \\ \omega_e \end{array}\right] }_{B} u_e(t) + \left[\begin{array}{c} 0 \\ 0 \\ a_{54} \\ a_{64} \\ 0 \end{array}\right] \underbrace{(\dot{x}(t)-V^*)}_{0} + \left[\begin{array}{c} 0 \\ 0 \\ b_{51} \\ b_{61} \\ 0 \end{array}\right]\underbrace{(T(t)-T^*)}_{0} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b66229e291e6a7c831c272149ccfd762_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14.2)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{y(t)} = \underbrace{ \left[\begin{array}{ccccc} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} z(t)-z^*\\ \theta(t)-\theta^*\\ \dot{z}(t)\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{x(t)} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-64265721f5befad0ff0fa09174416663_l3.png)
データセットNo1に対する行列![]() の固有値は図3のようにグラフ化されます。ここで、安定な固有値はヒーブの振舞いに、不安定な固有値はピッチの振舞いに関係しています。
の固有値は図3のようにグラフ化されます。ここで、安定な固有値はヒーブの振舞いに、不安定な固有値はピッチの振舞いに関係しています。
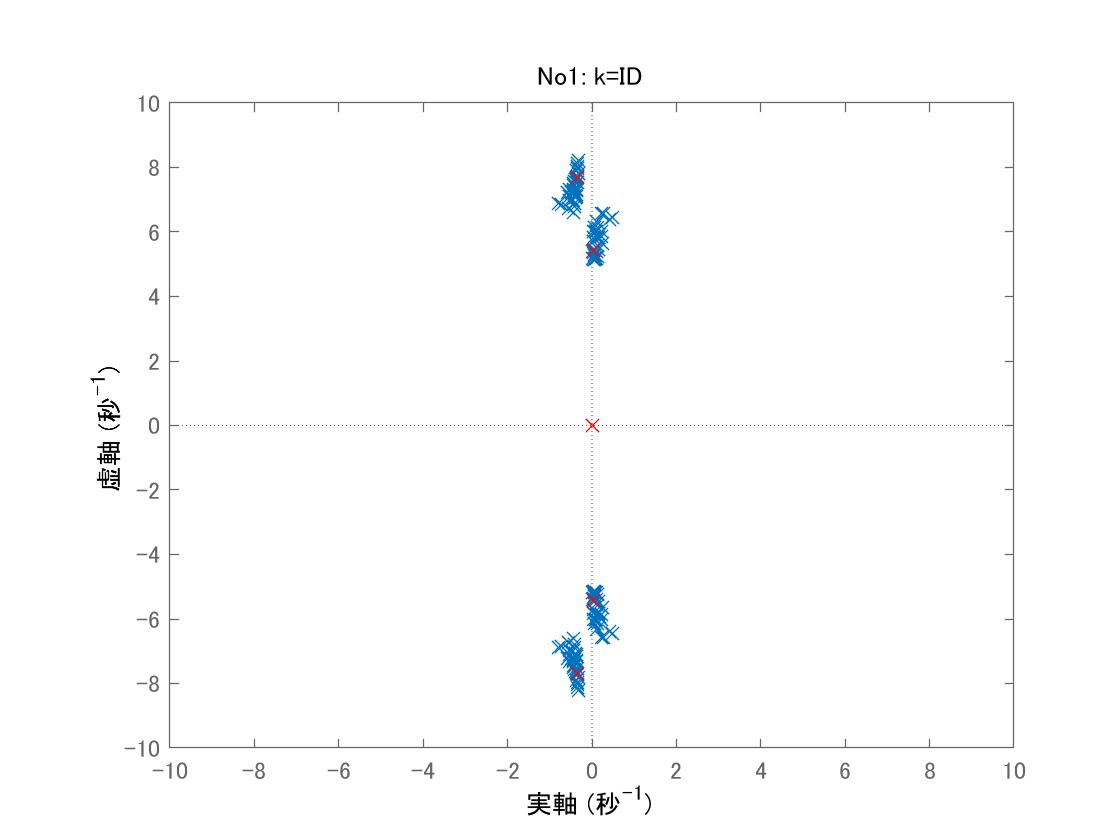
図3 データセットNo1を用いた5次元モデルの行列![]() の固有値
の固有値
3次元モデル
![Rendered by QuickLaTeX.com \displaystyle{(15.1)\quad \begin{array}{l} \underbrace{ \frac{d}{dt} \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0\\ a_{63} & a_{66} & b_{62}\\ 0 & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ \omega_e \end{array}\right] }_{B} u_e(t)\\ + \underbrace{\left[\begin{array}{cc} 0 & 0 \\ a_{62} & a_{65} \\ 0 & 0 \end{array}\right] \left[\begin{array}{c} z(t)-z^*\\ \dot{z}(t) \end{array}\right]}_{w(t)} + \left[\begin{array}{cc} 0 & 0 \\ a_{64} & b_{61} \\ 0 & 0 \end{array}\right] \underbrace{\left[\begin{array}{c} \dot{x}(t)-V^* \\ T(t)-T^* \end{array}\right]}_{0} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bf87259f32e1c8fdd86639d65f233881_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(15.2)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{y(t)} = \underbrace{ \left[\begin{array}{ccccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{x(t)} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2a21e890f7313ffc080ff529f06666fc_l3.png)
データセットNo1に対する行列![]() の固有値は図4のようにグラフ化されます。これからピッチに対応する固有値は不安定であることが分かります。
の固有値は図4のようにグラフ化されます。これからピッチに対応する固有値は不安定であることが分かります。
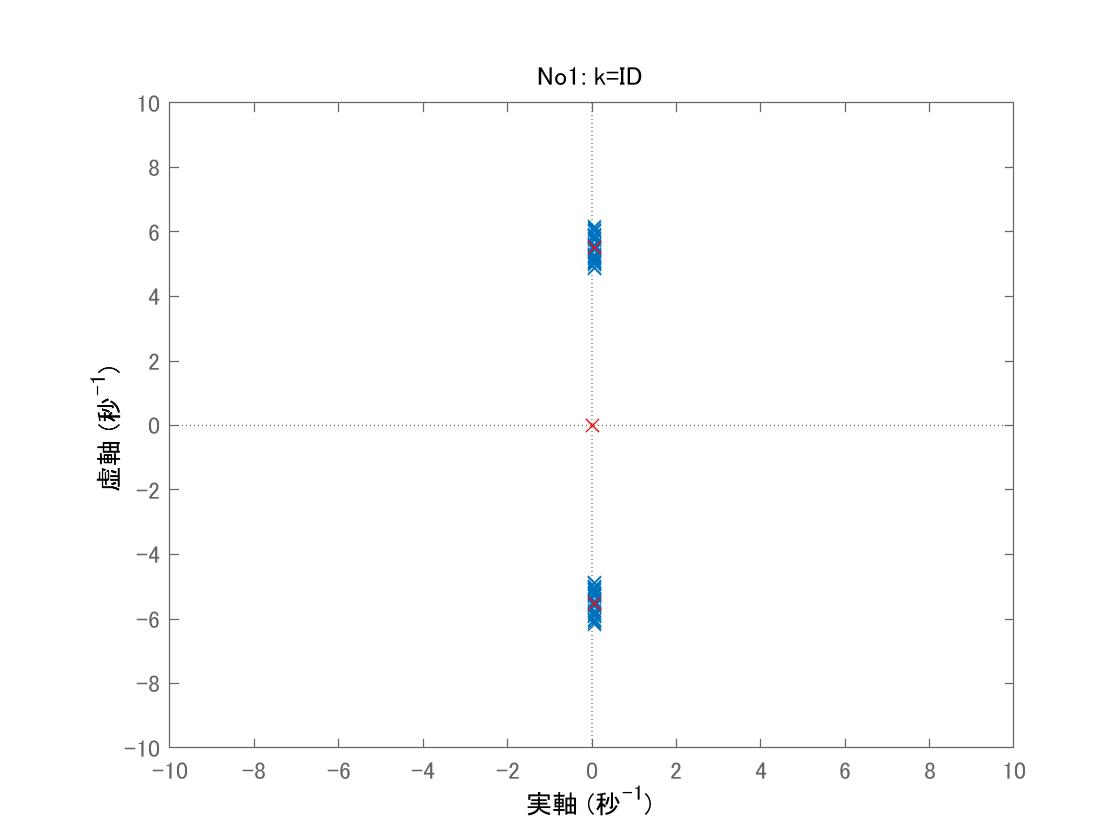
図4 データセットNo1を用いた3次元モデルの行列![]() の固有値
の固有値
●制御目的を達成する制御系を設計する立場から、2つのモデルを比較してみます。まず制御則として次式を考えます。
![]()
ここで、右辺第1項は状態フィードバック、第2項は船外機取付角をある収納状態![]() から所定の平衡入力値
から所定の平衡入力値![]() に設定するための積分動作です。
に設定するための積分動作です。
5次元モデル(14.1)の場合は、ヒーブに関する状態変数を計測できないので、状態オブザーバを用いてこれらを推定して、状態フィードバックを実施することになります。
一方3次元モデル(15.1)の場合は、状態フィードバックは実施できますが、ヒーブの振舞いの影響が外乱![]() として現れますので、これを抑制する必要があります。そのヒーブの振舞いは次式で表されます。
として現れますので、これを抑制する必要があります。そのヒーブの振舞いは次式で表されます。
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \begin{array}{l} \underbrace{ \frac{d}{dt} \left[\begin{array}{c} z(t)-z^*\\ \dot{z}(t) \end{array}\right] }_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{ccccc} 0 & 1 \\ a_{52} & a_{55} \end{array}\right] }_{A'} \underbrace{ \left[\begin{array}{c} z(t)-z^*\\ \dot{z}(t)\\ \end{array}\right] }_{x'(t)}\\ + \underbrace{ \left[\begin{array}{ccccc} 0 & 1 & 0\\ a_{53} & a_{56} & b_{52} \end{array}\right] }_{B'} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{y(t)}\\ + \left[\begin{array}{c} 0 \\ a_{54} \end{array}\right] \underbrace{(\dot{x}(t)-V^*)}_{0} + \left[\begin{array}{c} 0 \\ b_{51} \end{array}\right]\underbrace{(T(t)-T^*)}_{0} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d470e645c52cb94809030f2a1033637f_l3.png)
これからヒーブの振舞いには操作入力![]() は直接影響を及ぼさず、ピッチを通して間接的に影響すること分かります。ただ、これは漸近安定(
は直接影響を及ぼさず、ピッチを通して間接的に影響すること分かります。ただ、これは漸近安定(![]() は安定行列)なので、ピッチの安定化を速やかにできれば(
は安定行列)なので、ピッチの安定化を速やかにできれば(![]() が零に収束すれば)、(17)は考慮しなくともよいことになります。しかしながら、3次元モデルに対する状態フィードバックを5次元モデルに適用して、閉ループ系が漸近安定かどうかを調べておくことが考えられます。
が零に収束すれば)、(17)は考慮しなくともよいことになります。しかしながら、3次元モデルに対する状態フィードバックを5次元モデルに適用して、閉ループ系が漸近安定かどうかを調べておくことが考えられます。
制御系設計に3次元モデルを用いる場合は、状態オブザーバが不要となる利点がありますが、ヒーブの振舞いの影響が抑制されていることを確かめるために、5次元モデルに対する閉ループシミュレ-ションを行うことが重要になります。
●以上の結果を、![]() の場合の平衡状態回りの線形モデルについて数値で確認しておきます。
の場合の平衡状態回りの線形モデルについて数値で確認しておきます。
まず元の線形モデル(12)の行列![]() とその固有値は次のようになります。
とその固有値は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle{(18.1)\quad A= \left[\begin{array}{cccccc} 0 & 0 & 0 & 1.0000 & 0 & 0\\ 0 & 0 & 0 & 0 & 1.0000 & 0\\ 0 & 0 & 0 & 0 & 0 & 1.0000\\ 0 & 8.3458 & -6.9684 & -0.2549 & 0 & 0\\ 0 & -58.4515 & 67.9416 & 0.4686 & -0.7383 & -0.0369\\ 0 & 0.4559 & -30.3422 & -0.1922 & -0.0117 & 0.1175 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4b36eb6e0cb7156f03d9bf7681c55879_l3.png)
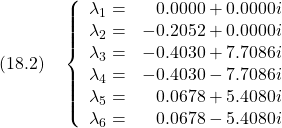
5次元モデル(14.1)における行列![]() とその固有値は次のようになります。
とその固有値は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle{(19.1)\quad A= \left[\begin{array}{ccccc} 0 & 0 & 1.0000 & 0 & 0\\ 0 & 0 & 0 & 1.0000 & 0\\ -58.4515 & 67.9416 & -0.7383 & -0.0369 & -0.0797\\ 0.4559 & -30.3422 & -0.0117 & 0.1175 & -2.7873\\ 0 & 0 & 0 & 0 & 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-385eb5461b75f3eab0188fc4a0c28dcf_l3.png)
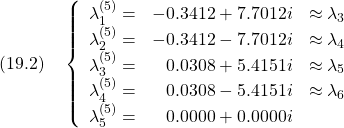
これからサージに関わる状態変数を除いた場合、ヒーブとピッチに関わる固有値![]() がほぼ引き継がれることが分かります。
がほぼ引き継がれることが分かります。
一方3次元モデル(15.1)における行列![]() とその固有値は次のようになります。
とその固有値は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle{(20.1)\quad A= \left[\begin{array}{ccc} 0 & 1.0000 & 0\\ -30.3422 & 0.1175 & -2.7873\\ 0 & 0 & 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-df1140cc4fabe39af15eb5dede652c01_l3.png)

これからさらにヒーブに関わる状態変数を除いた場合、ピッチに関わる固有値![]() がほぼ引き継がれることが分かります。
がほぼ引き継がれることが分かります。
●ヒーブとピッチに関わる固有値![]() の可制御性と可観測性を、5次元モデルを用いて調べてみます。
の可制御性と可観測性を、5次元モデルを用いて調べてみます。
![Rendered by QuickLaTeX.com \displaystyle{(21)\quad \left\{\begin{array}{l} \underline{\sigma}(\left[\begin{array}{cc} B & A-\lambda_1^{(5)} I_5 \end{array}\right])=0.0048^{*}\\ \underline{\sigma}(\left[\begin{array}{cc} B & A-\lambda_2^{(5)} I_5 \end{array}\right])=0.0048^{*}\\ \underline{\sigma}(\left[\begin{array}{cc} B & A-\lambda_3^{(5)} I_5 \end{array}\right])=0.0106\\ \underline{\sigma}(\left[\begin{array}{cc} B & A-\lambda_4^{(5)} I_5 \end{array}\right])=0.0106\\ \underline{\sigma}(\left[\begin{array}{cc} B & A-\lambda_5^{(5)} I_5 \end{array}\right])=0.1140\\ \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a7e4cf96c547aedfac2c36a38d07ed50_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(22)\quad \left\{\begin{array}{l} \underline{\sigma}(\left[\begin{array}{cc} C^T & A^T-\lambda_1^{(5)} I_5 \end{array}\right])=0.0146^{*}\\ \underline{\sigma}(\left[\begin{array}{cc} C^T & A^T-\lambda_2^{(5)} I_5 \end{array}\right])=0.0146^{*}\\ \underline{\sigma}(\left[\begin{array}{cc} C^T & A^T-\lambda_3^{(5)} I_5 \end{array}\right])=0.3129\\ \underline{\sigma}(\left[\begin{array}{cc} C^T & A^T-\lambda_4^{(5)} I_5 \end{array}\right])=0.3129\\ \underline{\sigma}(\left[\begin{array}{cc} C^T & A^T-\lambda_5^{(5)} I_5 \end{array}\right])=0.9940\\ \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9da4f1036a5ce1b33a3e76163bc55f97_l3.png)
(21)から、すべての固有値について行列![]() の最小特異値は正ですから、形式的には可制御性は成り立つと判定できます。ただ、*印の値が示すように、ヒーブはピッチに比べて相対的に可制御性の程度が弱く、状態フィードバックによる固有値の変更が難しいと言えます。したがって、制御対象は可制御でなく、むしろ可安定と判定することが考えられます。
の最小特異値は正ですから、形式的には可制御性は成り立つと判定できます。ただ、*印の値が示すように、ヒーブはピッチに比べて相対的に可制御性の程度が弱く、状態フィードバックによる固有値の変更が難しいと言えます。したがって、制御対象は可制御でなく、むしろ可安定と判定することが考えられます。
一方、(22)から、形式的には可観測性は成り立つと判定できます。ただ、*印の値が示すように、ヒーブはピッチに比べて相対的に可観測性の程度が弱く、状態オブザーバによる推定が難しいと言えます。
●操作入力(取付角)により、まずピッチが制御され、それがヒーブに影響を与えるという連成の仕組みを調べるために、(15.1)と(17)を数値で確かめてみます。
まず(15.1)は
![Rendered by QuickLaTeX.com \displaystyle{(15.1')\quad \begin{array}{l} \underbrace{ \frac{d}{dt} \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0\\ %a_{63} & a_{66} & b_{62}\\ -30.3422 & 0.1175 & -2.7873\\ 0 & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{x(t)}\\ + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ \omega_e \end{array}\right] }_{B} u_e(t) + \underbrace{\left[\begin{array}{cc} 0 & 0 \\ %a_{62} & a_{65} \\ 0.4559 & -0.0117 \\ 0 & 0 \end{array}\right] \left[\begin{array}{c} z(t)-z^*\\ \dot{z}(t) \end{array}\right]}_{w(t)} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6f7ec1b0d02eac3e57d854255ed386a7_l3.png)
となり、ヒーブのピッチへの影響を表す![]() に関わる係数
に関わる係数![]() の値がそれほど大きくなく、3次元モデルにおいても固有値が継承されることに注意します。
の値がそれほど大きくなく、3次元モデルにおいても固有値が継承されることに注意します。
一方(17)は
![Rendered by QuickLaTeX.com \displaystyle{(17')\quad \begin{array}{l} \underbrace{ \frac{d}{dt} \left[\begin{array}{c} z(t)-z^*\\ \dot{z}(t) \end{array}\right] }_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{ccccc} 0 & 1 \\ %a_{52} & a_{55} -58.4515 & -0.7383 \end{array}\right] }_{A'} \underbrace{ \left[\begin{array}{c} z(t)-z^*\\ \dot{z}(t)\\ \end{array}\right] }_{x'(t)}\\ + \underbrace{ \left[\begin{array}{ccccc} 0 & 1 & 0\\ %a_{53} & a_{56} & b_{52} 67.9416 & -0.0369 & -0.0797 \end{array}\right] }_{B'} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{y(t)} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dd41b1e619c39ebfa6602dc14ea3d00c_l3.png)
となります。これは漸近安定なので、ピッチの安定化が速やかに行えれば問題ないとと言えます。
●最後に、取付角からの伝達特性を調べておきます。
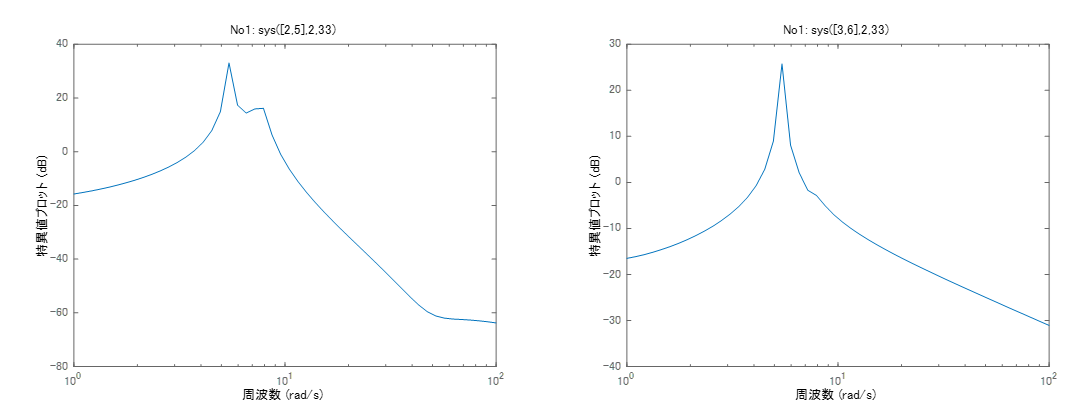
図5 取付角からヒーブまで(左図)とピッチまで(右図)の伝達特性
左図は2つの共振特性をもちますが、右図は(2つ目がほとんど消えていて)1つだけの共振特性をもちます。これから、ヒーブのピッチへの連成影響はほとんどないことがわかります。
●以上の数値例の結果を得るためのプログラムを以下に示します。
| MATLAB |
|
参考:漸近安定性
|
【漸近安定性の定義とその等価な条件】 定義DA: 条件A1: |
漸近安定性とは、定義DAより、平衡状態が乱されたとき復帰できるかどうかにかかわる概念で、条件A1より、![]() 行列の固有値がすべて複素左半面にあることを調べて判定されます。
行列の固有値がすべて複素左半面にあることを調べて判定されます。
参考:可制御性・可安定性
|
【可安定性の定義とその等価な条件】 定義DS: 状態フィードバックにより安定化可能 条件S1: 【可制御性の定義とその等価な条件】 |
可安定性は、定義DSより、状態フィードバックにより安定化可能であることを意味し、条件S1が判定条件として知られています。一方、可制御性については、条件C4が判定条件として知られています。両者の相違は、すでに左半平面にある安定な固有値について関与(再配置)するかどうかにあります。可安定性の判定では不安定な固有値のみで条件S1を判定しますが、可制御性の判定ではすべて固有値について条件C4を判定します。
それでは、![]() に対して、条件S1と条件C4に出てくる行列
に対して、条件S1と条件C4に出てくる行列
![]()
の階数をどのようにして計算するかですが、これは![]() の非零特異値の数で決定します。したがって、条件S1と条件C4は、最小特異値が正かどうかで判定します。
の非零特異値の数で決定します。したがって、条件S1と条件C4は、最小特異値が正かどうかで判定します。
参考:可観測性・可検出性
|
【可検出性の定義とその等価な条件】 定義DD: 状態オブザーバを構成可能 条件D1: 【可観測性の定義とその等価な条件】 |
可検出性は、定義DDより、状態オブザーバを構成可能であることを意味し、条件D1が判定条件として知られています。状態オブザーバの![]() 行列は
行列は![]() と表され、オブザーバゲイン
と表され、オブザーバゲイン![]() は、仮想システム
は、仮想システム![]() に対する状態FB
に対する状態FB![]() による閉ループ系
による閉ループ系![]() を安定化して決定します。したがって、可検出性は
を安定化して決定します。したがって、可検出性は![]() の可安定性を意味します。一方、可観測性については、条件O4が判定条件として知られています。可検出性との相違は、すでに左半平面にある安定な
の可安定性を意味します。一方、可観測性については、条件O4が判定条件として知られています。可検出性との相違は、すでに左半平面にある安定な![]() の固有値について
の固有値について![]() で再配置するかどうかにあります。可検出性の判定では不安定な固有値のみで条件D1を判定しますが、可観測性の判定ではすべて固有値について条件O4を判定します。
で再配置するかどうかにあります。可検出性の判定では不安定な固有値のみで条件D1を判定しますが、可観測性の判定ではすべて固有値について条件O4を判定します。
それでは、![]() に対して、条件D1と条件O4に出てくる行列
に対して、条件D1と条件O4に出てくる行列
![]()
の階数をどのようにして計算するかですが、これは![]() の非零特異値の数で決定します。したがって、条件D1と条件O4は、最小特異値が正かどうかで判定します。
の非零特異値の数で決定します。したがって、条件D1と条件O4は、最小特異値が正かどうかで判定します。
参考:状態オブザーバ
●通常の状態オブザーバは
![]()
で表され
![]()
のように漸近的に元の状態を推定するものです。行列![]() はオブザーバゲインと呼ばれ、
はオブザーバゲインと呼ばれ、![]() は安定行列とするように選ばれます。
は安定行列とするように選ばれます。
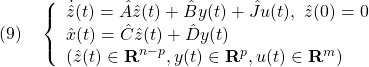
によって表される漸近安定なシステムで、この出力が![]() に漸近するように構成するものです。そのためには、あるサイズ
に漸近するように構成するものです。そのためには、あるサイズ![]() の行列
の行列![]() に対して次式を満足させることが必要十分となります。
に対して次式を満足させることが必要十分となります。
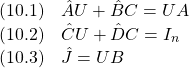
参考:最小実現
一般に,不可制御かつ不可観測な状態空間表現は適当な座標変換により,つぎの正準構造をもつように変換できることが知られています。
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \left[\begin{array}{c|c} TAT^{-1} & TB \\\hline CT^{-1} & D \end{array}\right] = \left[\begin{array}{cccc|c} A_1 & 0 & X_{13} & 0 & B_1 \\ X_{21} & A_2 & X_{23} & X_{24} & B_2 \\ 0 & 0 & A_3 & 0 & 0 \\ 0 & 0 & X_{43} & A_4 & 0 \\\hline C_1 & 0 & C_3 & 0 & 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4b2e92c732c0f76c1c7685becd70b05c_l3.png)
ここで,正方行列![]() ,
,![]() ,
,![]() ,
,![]() の次数は一意に定まり,
の次数は一意に定まり,![]() は可制御対,
は可制御対,![]() は可観測対です。この正準構造のブロック線図を図1に示します。
は可観測対です。この正準構造のブロック線図を図1に示します。

図1 正準構造のブロック線図
さて,つぎが成り立ちます。
![]()
すなわち,可制御かつ可観測な部分系が入力から出力までの伝達特性を表しています。
![Rendered by QuickLaTeX.com {\rm rank}\, \left[\begin{array}{c} C \\ CA \\ \vdots\\ CA^{n-1} \end{array}\right] =n](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c018f5737238e4ac298d377adf711de0_l3.png)
![Rendered by QuickLaTeX.com \boxed{{\rm rank} \left[\begin{array}{c} C \\ A-\lambda I_n \end{array}\right]=n}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-16e4ae46fa331c1889ac8dbffdb8b61a_l3.png) (
(