
上図のようなドローンについて、次の文献をフォローしていきます。
Randal Beard: Quadrotor Dynamics and Control, Rev0.1, Brigham Young University, 2008
以下では、![]() 、
、![]() をそれぞれ
をそれぞれ![]() 、
、![]() と略記します。
と略記します。
準備

●上図のように、ベクトル![]() を、ベクトル
を、ベクトル![]() のまわりに
のまわりに![]() だけ回転して得られるベクトル
だけ回転して得られるベクトル![]() の表現式を求めます。
の表現式を求めます。
![]()
ただし
![]()
![]()
![]()
から、次式を得ます。
![]()
ここで
![]()
![]()
![]()
とおくと
![]()
![Rendered by QuickLaTeX.com \displaystyle{\hat{n}\times{\bf p}= {\rm det} \left[\begin{array}{ccc} \hat{i}^0 & \hat{j}^0 & \hat{k}^0\\ \hat{n}_x & \hat{n}_y & \hat{n}_z\\ p_x^0 & p_y^0 & p_z^0 \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-987b3b87c684eb8f160259eccaed8b8c_l3.png)
![]()
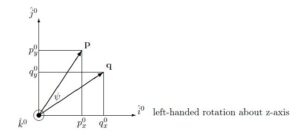
●![]() の場合(left-handed rotation about z-axis)
の場合(left-handed rotation about z-axis)
![]()
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} q_x^0 \\ q_y^0 \\ q_z^0 \end{array}\right] }_{{\bf q}} =(1-C_\psi) p_z^0 \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right] }_{\hat{i}} \hat{n}+C_\psi \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] -S_\psi \left[\begin{array}{c} -p_y^0 \\ p_x^0 \\ 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-12d5ca14cbcc4c55826c7d6d8f899987_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \underbrace{ \left[\begin{array}{ccc} C_\psi & S_\psi & 0 \\ -S_\psi & C_\psi & 0 \\ 0 & 0 & 1 \end{array}\right] }_{R(\phi)} \underbrace{ \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] }_{{\bf p}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-034528a2aacb8e95ad6d97e767cee015_l3.png)
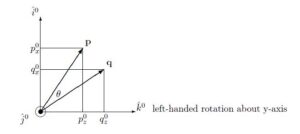
●![]() の場合(left-handed rotation about y-axis)
の場合(left-handed rotation about y-axis)
![]()
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} q_x^0 \\ q_y^0 \\ q_z^0 \end{array}\right] }_{{\bf q}} =(1-C_\theta) p_y^0 \underbrace{ \left[\begin{array}{c} 0 \\ 1 \\ 0 \end{array}\right] }_{\hat{j}} \hat{n}+C_\theta \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] -S_\theta \left[\begin{array}{c} p_z^0 \\ 0\\ -p_x^0 \\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a989718664a4f406a703678aa7bce25c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ =\underbrace{ \left[\begin{array}{ccc} C_\theta & 0 & -S_\theta \\ 0 & 1 & 0 \\ S_\theta & 0 & C_\theta \end{array}\right] }_{R(\theta)} \underbrace{ \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] }_{{\bf p}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-77d80bf487c6766d1c677f8791183be6_l3.png)
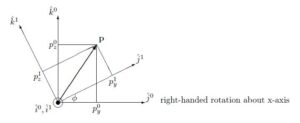
●![]() の場合(left-handed rotation about x-axis)
の場合(left-handed rotation about x-axis)
![]()
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} q_x^0 \\ q_y^0 \\ q_z^0 \end{array}\right] }_{{\bf q}} =(1-C_\phi) p_x^0 \underbrace{ \left[\begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right] }_{\hat{k}} \hat{n}+C_\phi \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] -S_\phi \left[\begin{array}{c} 0\\ -p_z^0 \\ p_y^0 \\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-59bae1ad5756ab21b2c3dfbfa893e055_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ =\underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & C_\phi & S_\phi \\ 0 & -S_\phi & C_\phi \end{array}\right] }_{R(\psi)} \underbrace{ \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] }_{{\bf p}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d1ab1c6a193d60691e385bcb0e30cfb3_l3.png)

以上のようなベクトルの回転は、相対的に座標軸を回転させても、把握できます。
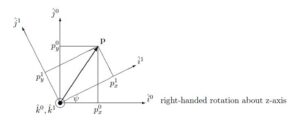
●right-handed rotation about z-axis
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} p_x^1 \\ p_y^1 \\ p_z^1 \end{array}\right] }_{{\bf p}^1} = \underbrace{ \left[\begin{array}{ccc} \hat{i}^1\cdot\hat{i}^0&\hat{i}^1\cdot\hat{j}^0&\hat{i}^1\cdot\hat{k}^0\\ \hat{j}^1\cdot\hat{i}^0&\hat{j}^1\cdot\hat{j}^0&\hat{j}^1\cdot\hat{k}^0\\ \hat{k}^1\cdot\hat{i}^0&\hat{k}^1\cdot\hat{j}^0&\hat{k}^1\cdot\hat{k}^0 \end{array}\right] }_{R_0^1(\psi)} \underbrace{ \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] }_{{\bf p}^0} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9e097cfdaee9cbb694b4d1748693d3c6_l3.png)
![]()
![Rendered by QuickLaTeX.com \displaystyle{ R_0^1(\psi)= \left[\begin{array}{ccc} C_\psi & S_\psi & 0 \\ -S_\psi & C_\psi & 0 \\ 0 & 0 & 1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-58ac6cd544f764f340163f5d9e7d61aa_l3.png)
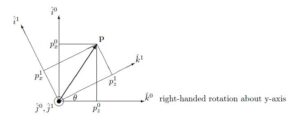
●right-handed rotation about y-axis
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} p_x^1 \\ p_y^1 \\ p_z^1 \end{array}\right] }_{{\bf p}^1} = \underbrace{ \left[\begin{array}{ccc} \hat{i}^1\cdot\hat{i}^0&\hat{i}^1\cdot\hat{j}^0&\hat{i}^1\cdot\hat{k}^0\\ \hat{j}^1\cdot\hat{i}^0&\hat{j}^1\cdot\hat{j}^0&\hat{j}^1\cdot\hat{k}^0\\ \hat{k}^1\cdot\hat{i}^0&\hat{k}^1\cdot\hat{j}^0&\hat{k}^1\cdot\hat{k}^0 \end{array}\right] }_{R_0^1(\theta)} \underbrace{ \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] }_{{\bf p}^0} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aceb055a39624b49b00c52ba93b2fafc_l3.png)
![]()
![Rendered by QuickLaTeX.com \displaystyle{ R_0^1(\theta)= \left[\begin{array}{ccc} C_\theta & 0 & -S_\theta \\ 0 & 1 & 0 \\ S_\theta & 0 & C_\theta \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bc434799df6aa0435586745ed76ca371_l3.png)
●right-handed rotation about x-axis
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} p_x^1 \\ p_y^1 \\ p_z^1 \end{array}\right] }_{{\bf p}^1} = \underbrace{ \left[\begin{array}{ccc} \hat{i}^1\cdot\hat{i}^0&\hat{i}^1\cdot\hat{j}^0&\hat{i}^1\cdot\hat{k}^0\\ \hat{j}^1\cdot\hat{i}^0&\hat{j}^1\cdot\hat{j}^0&\hat{j}^1\cdot\hat{k}^0\\ \hat{k}^1\cdot\hat{i}^0&\hat{k}^1\cdot\hat{j}^0&\hat{k}^1\cdot\hat{k}^0 \end{array}\right] }_{R_0^1(\phi)} \underbrace{ \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] }_{{\bf p}^0} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-be939844208f01e80bd96a4578eb7d9c_l3.png)
![]()
![Rendered by QuickLaTeX.com \displaystyle{ R_0^1(\phi)= \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & C_\phi & S_\phi \\ 0 & -S_\phi & C_\phi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9e26ef5f7bc02c2f2f19b14327fc67f6_l3.png)
座標系
●ドローンの運動の記述にあたっては、次のような地上座標系![]() と機体固定座標系
と機体固定座標系![]() を用います。
を用います。

![]() における機体の位置は次の変数で表します。
における機体の位置は次の変数で表します。
![]() : the inertial (north) position of the aircraft along
: the inertial (north) position of the aircraft along ![]() in
in ![]()
![]() : the inertial (east) position of the aircraft along
: the inertial (east) position of the aircraft along ![]() in
in ![]()
![]() : the altitude of the aircraft measured along
: the altitude of the aircraft measured along ![]() in
in ![]()
また、![]() は、
は、![]() から、次のオイラー角
から、次のオイラー角
![]() : the roll angle defined with respect to
: the roll angle defined with respect to ![]()
![]() : the pitch angle defined with respect to
: the pitch angle defined with respect to ![]()
![]() : the yaw angle defined with respect to
: the yaw angle defined with respect to ![]()
を用いて、次のように逐次回転して得られます。
![]()
ここで、![]() は原点を機体重心にもつ回転前の座標系(
は原点を機体重心にもつ回転前の座標系(![]() に平行)を表しています。
に平行)を表しています。
●![]() における任意ベクトル
における任意ベクトル![]() (後出の位置ベクトル、速度ベクトルなど)は、
(後出の位置ベクトル、速度ベクトルなど)は、![]() から、次のような変換を行って得られます。
から、次のような変換を行って得られます。
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{= \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & C_\phi & S_\phi \\ 0 & -S_\phi & C_\phi \end{array}\right] \left[\begin{array}{ccc} C_\theta & 0 & -S_\theta \\ 0 & 1 & 0 \\ S_\theta & 0 & C_\theta \end{array}\right] \left[\begin{array}{ccc} C_\psi & S_\psi & 0 \\ -S_\psi & C_\psi & 0 \\ 0 & 0 & 1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cbcf941c508f91c6e056f42732084bf5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \left[\begin{array}{ccc} C_\theta C_\psi & C_\theta S_\psi & -S_\theta \\ S_\phi S_\theta C_\psi - C_\phi S_\psi & S_\phi S_\theta S_\psi + C_\phi C_\psi & S_\phi C_\theta \\ C_\phi S_\theta C_\psi + C_\phi S_\psi & C_\phi S_\theta S_\psi - S_\phi C_\psi & C_\phi C_\theta \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bb9eeb9b54c7ae5be019eb255e6bdbd8_l3.png)
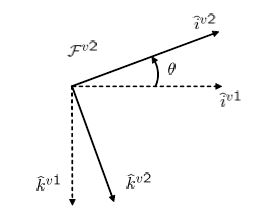
●![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{ R_v^{v1}(\psi)= \left[\begin{array}{ccc} C_\psi & S_\psi & 0 \\ -S_\psi & C_\psi & 0 \\ 0 & 0 & 1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-62a0d9a3674b84f4cc7fd9463923b711_l3.png)

●![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{ R_{v1}^{v2}(\theta)= \left[\begin{array}{ccc} C_\theta & 0 & -S_\theta \\ 0 & 1 & 0 \\ S_\theta & 0 & C_\theta \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-882fd5b2077da6bcc03598d35349e31f_l3.png)
●![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{ R_{v2}^b(\phi)= \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & C_\phi & S_\phi \\ 0 & -S_\phi & C_\phi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-65b7f87e8d6ceac41cc3eed6be19136b_l3.png)

●![]() における任意ベクトル
における任意ベクトル![]() (後出の位置ベクトル、速度ベクトルなど)の時間変化がどのように表されるかを調べます。
(後出の位置ベクトル、速度ベクトルなど)の時間変化がどのように表されるかを調べます。
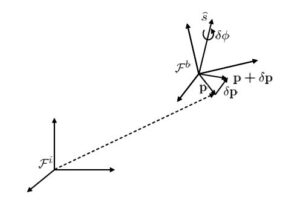
これは、次式で表されます。
![]()
実際
![]()
![]()
![]()
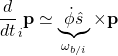
運動方程式
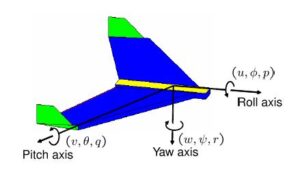
![]() における運動は次の変数を用いて表されます。
における運動は次の変数を用いて表されます。
![]() : the body frame velocity measured along
: the body frame velocity measured along ![]() in
in ![]()
![]() : the body frame velocity measured along
: the body frame velocity measured along ![]() in
in ![]()
![]() : the body frame velocity measured along
: the body frame velocity measured along ![]() in
in ![]()
![]() : the roll rate measured along
: the roll rate measured along ![]() in
in ![]()
![]() : the pitch rate measured along
: the pitch rate measured along ![]() in
in ![]()
![]() : the yaw rate measured along
: the yaw rate measured along ![]() in
in ![]()
これらが![]() からどう表されるか、すなわち次の変数の微分とどう関係するか(キネマティックス)を調べます。
からどう表されるか、すなわち次の変数の微分とどう関係するか(キネマティックス)を調べます。
![]() : the inertial (north) position of the quadrotor along
: the inertial (north) position of the quadrotor along ![]() in
in ![]()
![]() : the inertial (east) position of the quadrotor along
: the inertial (east) position of the quadrotor along ![]() in
in ![]()
![]() : the altitude of the aircraft measured along
: the altitude of the aircraft measured along ![]() in
in ![]()
![]() : the roll angle defined with respect to
: the roll angle defined with respect to ![]()
![]() : the pitch angle defined with respect to
: the pitch angle defined with respect to ![]()
![]() : the yaw angle defined with respect to
: the yaw angle defined with respect to ![]()
●![]() と
と![]() における速度ベクトルについては
における速度ベクトルについては
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} u \\ v \\ w \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} C_\theta C_\psi & C_\theta S_\psi & -S_\theta \\ S_\phi S_\theta C_\psi - C_\phi S_\psi & S_\phi S_\theta S_\psi + C_\phi C_\psi & S_\phi C_\theta \\ C_\phi S_\theta C_\psi + C_\phi S_\psi & C_\phi S_\theta S_\psi - S_\phi C_\psi & C_\phi C_\theta \end{array}\right] }_{R_v^b} \left[\begin{array}{c} \dot{p}_n \\ \dot{p}_e \\ -\dot{h} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-de39a8b9bd05d0eb4e506e36a8e0fa0a_l3.png)
の関係が成り立ちます。したがって、
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{p}_n \\ \dot{p}_e \\ -\dot{h} \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} C_\theta C_\psi &S_\phi S_\theta C_\psi - C_\phi S_\psi &C_\phi S_\theta C_\psi + C_\phi S_\psi \\ C_\theta S_\psi &S_\phi S_\theta S_\psi + C_\phi C_\psi &C_\phi S_\theta S_\psi - S_\phi C_\psi \\ -S_\theta &S_\phi C_\theta &C_\phi C_\theta \end{array}\right] }_{R_b^v=(R_v^b)^T} \left[\begin{array}{c} u \\ v \\ w \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d363a281bdd4e8b2b988be4d3069aa11_l3.png)
●![]() と
と![]() における角速度ベクトルについては
における角速度ベクトルについては
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} p \\ q \\ r \end{array}\right] = \underbrace{R_{v2}^b(\dot{\phi})}_{I} \left[\begin{array}{c} \dot{\phi} \\ 0 \\ 0 \end{array}\right] + R_{v2}^b(\phi)\underbrace{R_{v1}^{v2}(\dot{\theta})}_{I} \left[\begin{array}{c} 0 \\ \dot{\theta} \\ 0 \end{array}\right] + R_{v2}^b(\phi)R_{v1}^{v2}(\theta)\underbrace{R_{v}^{v1}(\dot{\psi})}_{I} \left[\begin{array}{c} 0 \\ 0 \\ \dot{\psi} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a04c24d997a7e6874afdd3b415001501_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \left[\begin{array}{c} \dot{\phi} \\ 0 \\ 0 \end{array}\right] + \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & C_\phi & S_\phi \\ 0 & -S_\phi & C_\phi \end{array}\right] \left[\begin{array}{c} 0 \\ \dot{\theta} \\ 0 \end{array}\right] + \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & C_\phi & S_\phi \\ 0 & -S_\phi & C_\phi \end{array}\right] \left[\begin{array}{ccc} C_\theta & 0 & -S_\theta \\ 0 & 1 & 0 \\ S_\theta & 0 & C_\theta \end{array}\right] \left[\begin{array}{c} 0 \\ 0 \\ \dot{\psi} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-97c20a9db7f00180754feff31ee807c8_l3.png)
の関係が成り立ちます。したがって、
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} p \\ q \\ r \end{array}\right]= \left[\begin{array}{ccc} 1 & 0 & -S_\theta \\ 0 & C_\phi & S_\phi C_\theta \\ 0 & -S_\phi & C_\phi C_\theta \end{array}\right] \left[\begin{array}{c} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-061d5edae9ebd68d687e9549b5a5a40b_l3.png)
すなわち、次の関係式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{array}\right] = \left[\begin{array}{ccc} 1 & S_\phi T_\theta & C_\phi T_\theta \\ 0 & C_\phi & -S_\phi \\ 0 & \frac{S_\phi}{C_\theta} & \frac{C_\phi}{C_\theta} \end{array}\right] \left[\begin{array}{c} p \\ q \\ r \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-10b9bc4111bd976ca0649bb42dfacd55_l3.png)
●次に並進運動(ダイナミックス)は次式で表されます。
![]()
![Rendered by QuickLaTeX.com \displaystyle{ \frac{d}{dt}_b \left[\begin{array}{c} u\\ v\\ w \end{array}\right] + \left[\begin{array}{c} p\\ q\\ r \end{array}\right] \times \left[\begin{array}{c} u\\ v\\ w \end{array}\right] =\frac{1}{m} \left[\begin{array}{c} f_x\\ f_y\\ f_z \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f49c0967c1c1583628163273d1cc944f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{u}\\ \dot{v}\\ \dot{w} \end{array}\right] =- \underbrace{ \left[\begin{array}{ccc} 0 & -r & q\\ r & 0 &-p\\ -q & p & 0 \end{array}\right] \left[\begin{array}{c} u\\ v\\ w \end{array}\right] }_{\left[\begin{array}{c} qw-rv \\ ru-pw\\ pv-qu \end{array}\right]} +\frac{1}{m} \left[\begin{array}{c} f_x\\ f_y\\ f_z \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6e5e479c4745afec971e8a449e1d7113_l3.png)
●また回転運動(ダイナミックス)は次式で表されます。
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{J= \left[\begin{array}{ccc} \int(y^2+z^2)dm & -\int xydm & -\int xzdm \\ -\int yxdm & \int(x^2+z^2)dm & -\int yzdm \\ -\int zxdm & -\int zydm & \int(x^2+y^2)dm \end{array}\right] =\left[\begin{array}{ccc} J_x & 0 & 0 \\ 0 & J_y & 0 \\ 0 & 0 & J_z \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-16d24597f8387fec8c1eb565263ad684_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \frac{d}{dt}_bJ \left[\begin{array}{c} p\\ q\\ r \end{array}\right] + \left[\begin{array}{c} p\\ q\\ r \end{array}\right] \times J \left[\begin{array}{c} p\\ q\\ r \end{array}\right] = \left[\begin{array}{c} \tau_\phi\\ \tau_\theta\\ \tau_\psi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3a28be1d9f68276f11ece9ae89a59304_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} J_x\dot{p}\\ J_y\dot{q}\\ J_z\dot{r} \end{array}\right] + \underbrace{ \left[\begin{array}{ccc} 0 & -r & q\\ r & 0 &-p\\ -q & p & 0 \end{array}\right] \left[\begin{array}{c} J_xp\\ J_yq\\ J_zr \end{array}\right] }_{\left[\begin{array}{c} (J_z-J_y)qr \\ (J_x-J_z)pr\\ (J_y-J_x)pq \end{array}\right]} = \left[\begin{array}{c} \tau_\phi\\ \tau_\theta\\ \tau_\psi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-11a81fab1a1c7f81823c26120d6d2b21_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{p}\\ \dot{q}\\ \dot{r} \end{array}\right] =- \underbrace{ \left[\begin{array}{ccc} 0 & 0 & \frac{J_z-J_y}{J_x}q\\ \frac{J_x-J_z}{J_y} r & 0 & 0\\ 0 & \frac{J_y-J_x}{J_z}p & 0 \end{array}\right] \left[\begin{array}{c} p\\ q\\ r \end{array}\right] }_{ \left[\begin{array}{c} \frac{J_z-J_y}{J_x}qr \\ \frac{J_x-J_z}{J_y}pr \\ \frac{J_y-J_x}{J_z}pq \end{array}\right] } + \left[\begin{array}{c} \frac{1}{J_x}\tau_\phi\\ \frac{1}{J_y}\tau_\theta\\ \frac{1}{J_z}\tau_\psi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3eb533fddc2cdc3acb2986b508ba0373_l3.png)
外力
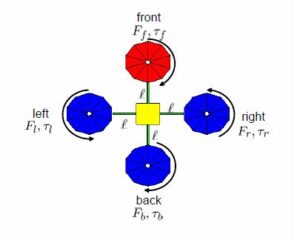
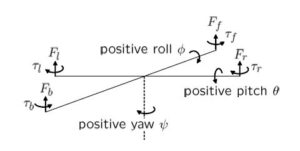
4つのモータへの回転指令を![]() とします。このとき、各モータによる推力とトルクは次式で表されます。
とします。このとき、各モータによる推力とトルクは次式で表されます。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
また、4つのモータの合推力と各軸回りのトルクは次式で表されます。
![]()
![]()
![]()
![]()
すなわち
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} F\\ \tau_\phi\\ \tau_\theta\\ \tau_\psi \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} k_1 & k_1 & k_1 & k_1 \\ 0 & -\ell k_1 & 0 & \ell k_1 \\ \ell k_1 & 0 & -\ell k_1 & 0 \\ -k_2 & k_2 & -k_2 & k_2 \end{array}\right] }_{{\cal M}} \left[\begin{array}{c} \delta_f\\ \delta_r\\ \delta_b\\ \delta_\ell \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2189a79e26837861510a7bb0f99f2a55_l3.png)
また、並進運動方程式の外力項は次式となります。
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} f_x\\ f_y\\ f_z \end{array}\right] = R_v^b \left[\begin{array}{c} 0\\ 0\\ mg \end{array}\right] + \left[\begin{array}{c} 0\\ 0\\ -F \end{array}\right] =mg \left[\begin{array}{ccc} -S_\theta \\ S_\phi C_\theta \\ C_\phi C_\theta \end{array}\right] + \left[\begin{array}{c} 0\\ 0\\ -F \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-46b8705ff1f44fac694d366bf9bfc130_l3.png)
このときドローンの運動方程式に基づく状態方程式は次式となります。
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{p}_n \\ \dot{p}_e \\ -\dot{h} \\ \hline \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \\ \hline \dot{u}\\ \dot{v}\\ \dot{w} \\ \hline \dot{p}\\ \dot{q}\\ \dot{r} \end{array}\right] = \left[\begin{array}{ccc|ccc} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array}\right.}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c057cf51cb84ad35be913e5f72b6b095_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left.\begin{array}{ccc|ccc} C_\theta C_\psi &S_\phi S_\theta C_\psi - C_\phi S_\psi &C_\phi S_\theta C_\psi + C_\phi S_\psi & 0 & 0 & 0\\ C_\theta S_\psi &S_\phi S_\theta S_\psi + C_\phi C_\psi &C_\phi S_\theta S_\psi - S_\phi C_\psi & 0 & 0 & 0\\ -S_\theta &S_\phi C_\theta &C_\phi C_\theta & 0 & 0 & 0\\ \hline 0 & 0 & 0 & 1 & S_\phi T_\theta & C_\phi T_\theta \\ 0 & 0 & 0 & 0 & C_\phi & -S_\phi \\ 0 & 0 & 0 & 0 & \frac{S_\phi}{C_\theta} & \frac{C_\phi}{C_\theta}\\ \hline 0 & r &- q & 0 & 0 & 0\\ r- & 0 &p & 0 & 0 & 0\\ q & -p & 0 & 0 & 0 & 0\\ \hline 0 & 0 & 0 & 0 & 0 & -\frac{J_z-J_y}{J_x}q\\ 0 & 0 & 0 & -\frac{J_x-J_z}{J_y} r & 0 & 0\\ 0 & 0 & 0 & 0 & -\frac{J_y-J_x}{J_z}p & 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ac9a7943b0d77c3ef3dcaeb6016011e8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \times \left[\begin{array}{c} p_n \\ p_e \\ -h \\ \hline \phi \\ \theta \\ \psi \\ \hline u\\ v\\ w \\ \hline p\\ q\\ r \end{array}\right] + \left[\begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \frac{1}{m} & 0 & 0 & 0 \\ \hline 0 & \frac{1}{J_x} & 0 & 0 \\ 0 & 0 & \frac{1}{J_y} & 0 \\ 0 & 0 & 0 & \frac{1}{J_z} \\ \end{array}\right] \left[\begin{array}{cccc} k_1 & k_1 & k_1 & k_1 \\ 0 & -\ell k_1 & 0 & \ell k_1 \\ \ell k_1 & 0 & -\ell k_1 & 0 \\ -k_2 & k_2 & -k_2 & k_2 \end{array}\right]^{-1} \left[\begin{array}{c} \delta_f\\ \delta_r\\ \delta_b\\ \delta_\ell \end{array}\right] + \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ \hline 0 \\ 0 \\ 0 \\ \hline -gS_\theta \\ gS_\phi C_\theta \\ gC_\phi C_\theta \\ \hline 0 \\ 0 \\ 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dfbd76199ec24769a2fab7d91200e5dc_l3.png)
これを見ると、![]() 行列に状態変数が絡んでおり、複雑なダイナミクスをもっていることが分かります。
行列に状態変数が絡んでおり、複雑なダイナミクスをもっていることが分かります。
運動方程式の簡単化
次の仮定のもとで、運動方程式の簡単化を行ないます。
仮定1: ![]() 、
、![]() 、
、![]() は小さく無視できる
は小さく無視できる
仮定2: ![]() 、
、![]() は小さく無視できる
は小さく無視できる
まず、仮定1のもとで、次の近似が可能です。
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{p}\\ \dot{q}\\ \dot{r} \end{array}\right] =- \left[\begin{array}{c} \frac{J_z-J_y}{J_x}qr \\ \frac{J_x-J_z}{J_y}pr \\ \frac{J_y-J_x}{J_z}pq \end{array}\right] + \left[\begin{array}{c} \frac{1}{J_x}\tau_\phi\\ \frac{1}{J_y}\tau_\theta\\ \frac{1}{J_z}\tau_\psi \end{array}\right] \simeq \left[\begin{array}{c} \frac{1}{J_x}\tau_\phi\\ \frac{1}{J_y}\tau_\theta\\ \frac{1}{J_z}\tau_\psi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f6a1e8b9f0e32ed0de052e40acd5d9e8_l3.png)
このとき、仮定2をおけば次の近似が可能です。
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{array}\right] = \left[\begin{array}{ccc} 1 & S_\phi T_\theta & C_\phi T_\theta \\ 0 & C_\phi & -S_\phi \\ 0 & \frac{S_\phi}{C_\theta} & \frac{C_\phi}{C_\theta} \end{array}\right] \left[\begin{array}{c} p \\ q \\ r \end{array}\right] \simeq \left[\begin{array}{c} p \\ q \\ r \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7588cb998bf45f4453bd790068da25cd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \ddot{\phi} \\ \ddot{\theta} \\ \ddot{\psi} \end{array}\right] \simeq \left[\begin{array}{c} \dot{p}\\ \dot{q}\\ \dot{r} \end{array}\right] \simeq \left[\begin{array}{c} \frac{1}{J_x}\tau_\phi\\ \frac{1}{J_y}\tau_\theta\\ \frac{1}{J_z}\tau_\psi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c00140559d247b19ba35379d4f2fc7d2_l3.png)
これは、機体の傾きを独立して制御できることを示しています。
さらに次のような近似が可能です。
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{p}_x \\ \dot{p}_y \\ \dot{p}_z \end{array}\right] = {R}_{v1}^b \left[\begin{array}{c} u \\ v \\ w \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-07b55ee0eb520a01571a66c82273a1b1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \ddot{p}_x \\ \ddot{p}_y \\ \ddot{p}_z \end{array}\right] = \underbrace{\dot{R}_{v1}^b}_{\simeq0} \left[\begin{array}{c} {u}\\ {v}\\ {w} \end{array}\right] + {R}_{v1}^b \left[\begin{array}{c} \dot{u}\\ \dot{v}\\ \dot{w} \end{array}\right] \simeq {R}_{v1}^b \left[\begin{array}{c} \dot{u}\\ \dot{v}\\ \dot{w} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b6a4f91764dbe1ccc821cb66b6c128a3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \ddot{p}_x \\ \ddot{p}_y \\ \ddot{p}_z \end{array}\right] \simeq \left[\begin{array}{ccc} C_\theta & S_\phi S_\theta & C_\phi S_\theta \\ 0 & C_\phi & -S_\phi \\ -S_\theta &S_\phi C_\theta &C_\phi C_\theta \end{array}\right] (g \left[\begin{array}{c} -S_\theta \\ S_\phi C_\theta \\ C_\phi C_\theta \end{array}\right] +\frac{1}{m} \left[\begin{array}{c} 0\\ 0\\ -F \end{array}\right]) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-806c2333ecc5b9e2f2176af3d06ac631_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \left[\begin{array}{c} 0 \\ 0 \\ g \end{array}\right] -\frac{1}{m}F \left[\begin{array}{ccc} C_\phi S_\theta \\ -S_\phi \\ C_\phi C_\theta \end{array}\right] \simeq \left[\begin{array}{c} 0 \\ 0 \\ g-\frac{1}{m}F \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a012c160125fa47849e9b54d7a6be80e_l3.png)
結局、ドローンの運動方程式は、次式のように簡単化されます。
![]()
![]()
![]()
![]()
いま,重力補償のために![]() から決まる
から決まる![]() を各操作入力に前もって加えておくことにすると、次式が成り立ちます。
を各操作入力に前もって加えておくことにすると、次式が成り立ちます。
![]()
![]()
![]()
![]()
![]()
![]()
このときドローンの線形状態方程式は次式となります。
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} \dot{p}_z \\ \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \\\hline \ddot{z} \\ \ddot{\phi} \\ \ddot{\theta} \\ \ddot{\psi} \\ \end{array}\right] }_{\dot{x}} = \underbrace{ \left[\begin{array}{cccc|cccc} 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\\hline 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array}\right] }_{A} % \left[\begin{array}{c|c} % 0_{4\times4} & I_4 \\\hline % 0_{4\times4} & 0_{4\times4} % \end{array}\right] \underbrace{ \left[\begin{array}{c} {p_z} \\ {\phi} \\ {\theta} \\ {\psi} \\\hline \dot{z} \\ \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \\ \end{array}\right] }_{x} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c2d526861def4102dd037941437ebbd2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{+ \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\\hline -\frac{k_f}{m} & -\frac{k_f}{m} & -\frac{k_f}{m} & -\frac{k_f}{m} \\ 0 & -\frac{\ell k_f}{J_x} & 0 & \frac{\ell k_f}{J_x} \\ \frac{\ell k_f}{J_y} & 0 & -\frac{\ell k_f}{J_y} & 0 \\ -\frac{k_\tau}{J_z} & \frac{k_\tau}{J_z} & -\frac{k_\tau}{J_z} & \frac{k_\tau}{J_z} \\ \end{array}\right] }_{B} % \left[\begin{array}{c} % 0_{4\times4} \\ % B_2 \\ % \end{array}\right] \underbrace{ \left[\begin{array}{c} \delta_f-\delta^* \\ \delta_r-\delta^* \\ \delta_b-\delta^* \\ \delta_\ell-\delta^* \\ \end{array}\right] }_{u} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b01d89585d73ec5fff8e27c5c03036e2_l3.png)
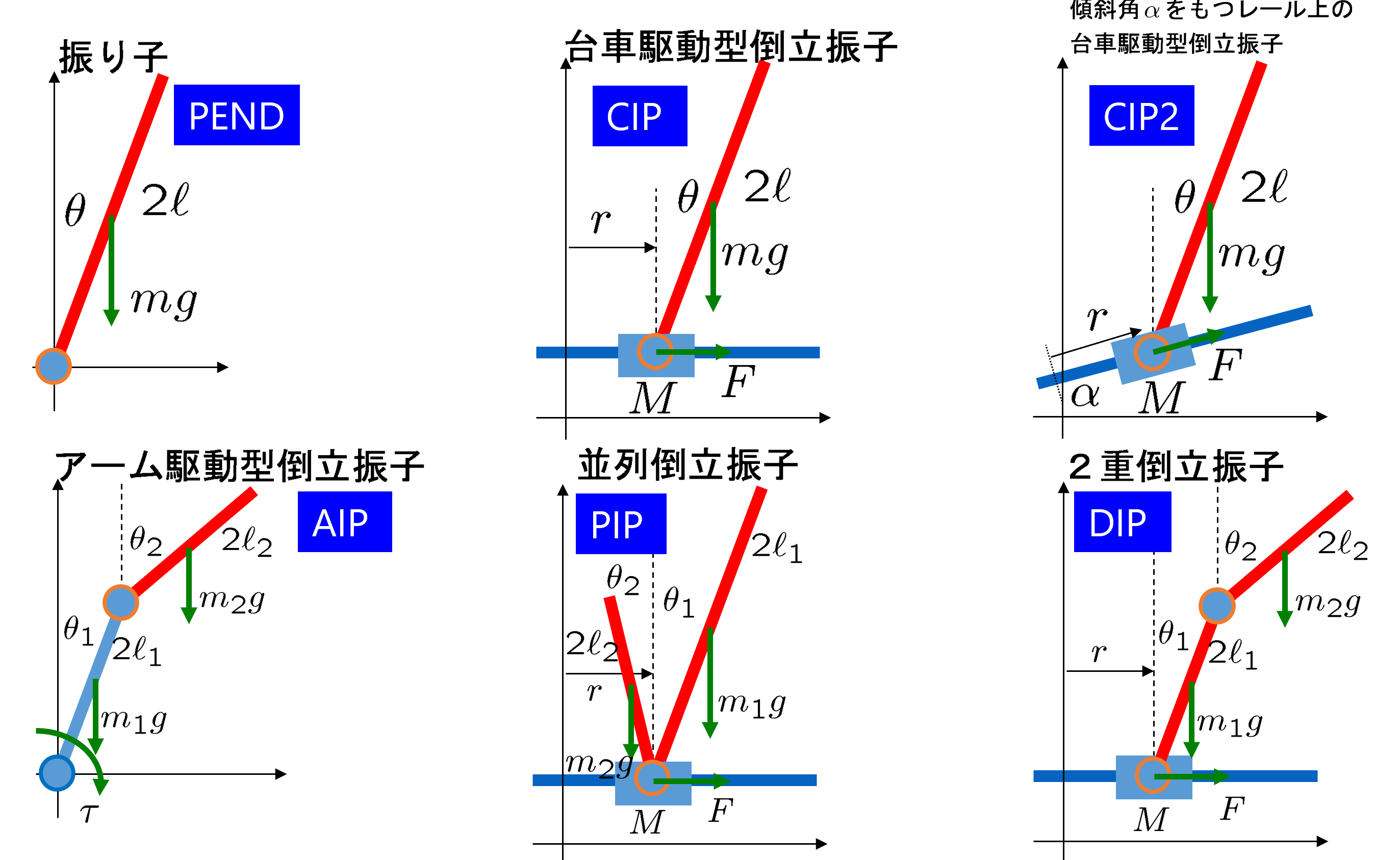 図1 様々な倒立振子
図1 様々な倒立振子![Rendered by QuickLaTeX.com (2.1)\quad \begin{array}{l} \displaystyle{\underbrace{ \left[\begin{array}{ccc} M+m & m\ell\cos\theta \\ m\ell\cos\theta & \frac{4}{3}m\ell^2 \end{array}\right] }_{M(\xi_1)} \underbrace{ \left[\begin{array}{c} \ddot{r} \\ \ddot{\theta} \end{array}\right] }_{\dot{\xi}_2}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 & -m\ell\sin\theta\dot{\theta} \\ 0 & 0 \end{array}\right] }_{C(\xi_1,\xi_2)} \underbrace{ \left[\begin{array}{c} \dot{r} \\ \dot{\theta} \end{array}\right] }_{\dot{\xi}_1}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0\\ -m\ell g\sin\theta \end{array}\right] }_{G(\xi_1)} = \underbrace{ \left[\begin{array}{c} 1 \\ 0 \end{array}\right] F}_{\tilde{F}}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b6b8157fad48af615f079cdbabc05028_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2.5)\quad \frac{d}{dt}\left[\begin{array}{c} r\\ \theta-\theta^*\\ \dot{r}\\ \dot{\theta} \end{array}\right] = \left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & -\frac{3gm}{4M+m} & 0 & 0\\ 0 & \frac{3(M+m)g}{(4M+m)\ell} & 0 & 0\\ \end{array}\right] \left[\begin{array}{c} r\\ \theta-\theta^*\\ \dot{r}\\ \dot{\theta} \end{array}\right] + \left[\begin{array}{c} 0\\ 0\\ \frac{4}{4M+m}\\ \frac{3}{(4M+m)\ell} \end{array}\right] F }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fae8887f4f90143f54cd71d63289bc0f_l3.png)
![Rendered by QuickLaTeX.com (3.1)\quad \begin{array}{l} \displaystyle{\underbrace{ \left[\begin{array}{ccc} M+m & m\ell\cos(\theta+\alpha) \\ m\ell\cos(\theta+\alpha) & \frac{4}{3}m\ell^2 \end{array}\right] }_{M(\xi_1)} \underbrace{ \left[\begin{array}{c} \ddot{r} \\ \ddot{\theta} \end{array}\right] }_{\dot{\xi}_2}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 & -m\ell\sin(\theta+\alpha)\dot{\theta} \\ 0 & 0 \end{array}\right] }_{C(\xi_1,\xi_2)} \underbrace{ \left[\begin{array}{c} \dot{r} \\ \dot{\theta} \end{array}\right] }_{\dot{\xi}_1}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} (M+m)g\sin\alpha\\ -m\ell g\sin\theta \end{array}\right] }_{G(\xi_1)} = \left[\begin{array}{c} 1 \\ 0 \end{array}\right] F} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9e90c77e32ef0131c7f6472d28283498_l3.png)
![Rendered by QuickLaTeX.com (3.5)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} r\\ \theta-\theta^*\\ \dot{r}\\ \dot{\theta} \end{array}\right] = \left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & -\frac{6\cos\alpha mg}{8M+(5-3\cos2\alpha)m} & 0 & 0\\ 0 & \frac{6(M+m)g}{(8M+(5-3\cos2\alpha)m)\ell} & 0 & 0\\ \end{array}\right] \left[\begin{array}{c} r\\ \theta-\theta^*\\ \dot{r}\\ \dot{\theta} \end{array}\right]}\\ \displaystyle{+ \left[\begin{array}{c} 0\\ 0\\ \frac{8}{8M+(5-3\cos2\alpha)m}\\ \frac{6\cos\alpha}{(8M+(5-3\cos2\alpha)m)\ell} \end{array}\right] (F-F^*)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-93deb9744dd26e8ee2880e1528f961ab_l3.png)
![Rendered by QuickLaTeX.com (4.1)\quad \begin{array}{l} \displaystyle{\underbrace{ \left[\begin{array}{ccc} (\frac{4}{3}m_1+4m_2)\ell_1^2 & 2m_2\ell_1\ell_2\cos(\theta_2-\theta_1)\\ 2m_2\ell_1\ell_2\cos(\theta_2-\theta_1) & \frac{4}{3}m_2\ell_2^2 \end{array}\right] }_{M(\xi_1)} \underbrace{ \left[\begin{array}{c} \ddot{\theta}_1 \\ \ddot{\theta}_2 \end{array}\right] }_{\dot{\xi}_2}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 & -2m_2\ell_1\ell_2\sin(\theta_2-\theta_1) \dot{\theta}_2\\ 2m_2\ell_1\ell_2\sin(\theta_2-\theta_1) \dot{\theta}_1 & 0\\ \end{array}\right] }_{C(\xi_1,\xi_2)} \underbrace{ \left[\begin{array}{c} \dot{\theta}_1 \\ \dot{\theta}_2 \end{array}\right] }_{\dot{\xi}_1}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} -(m_1+2m_2)\ell_1g\sin\theta_1\\ -m_2\ell_2g\sin\theta_2 \end{array}\right] }_{G(\xi_1)} = \underbrace{ \left[\begin{array}{c} 1 \\ 0 \end{array}\right] \tau}_{\tilde{\tau}}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-76a26f1d085c39daa570b8cee71ac8eb_l3.png)
![Rendered by QuickLaTeX.com (4.5a)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right] =}\\ \displaystyle{\left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \frac{3(m_1+2m_2)g}{(4m_1+3m_2)\ell_1} & -\frac{9m_2g}{2(4m_1+3m_2)\ell_1} & 0 & 0\\ -\frac{9(m_1+2m_2)g}{2(4m_1+3m_2)\ell_1} & \frac{9m_2g}{(4m_1+3m_2)\ell_2} & 0 & 0\\ \end{array}\right] \left[\begin{array}{c} \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right]}\\ \displaystyle{+ \left[\begin{array}{c} 0\\ 0\\ \frac{6}{2(4m_1+3m_2)\ell_1^2}\\ -\frac{9}{2(4m_1+3m_2)\ell_1\ell_2} \end{array}\right] (\tau-\tau^*)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a11a4d24890d0850335707e48115c732_l3.png)
![Rendered by QuickLaTeX.com (4.5b)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right] =}\\ \displaystyle{\left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ a_{31}(\alpha) & a_{32}(\alpha) & 0 & 0\\ a_{41}(\alpha) & a_{42}(\alpha) & 0 & 0 \end{array}\right] \left[\begin{array}{c} \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right]}\\ \displaystyle{+ \left[\begin{array}{c} 0\\ 0\\ \frac{6}{2(4m_1+3(4-3\cos^2\alpha)m_2)\ell_1^2}\\ -\frac{6}{2(4m_1+3(4-3\cos^2\alpha)m_2)\ell_1\ell_2} \end{array}\right] (\tau-\tau^*)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bbff369ea90195fe12e62e338448cbcd_l3.png)

![Rendered by QuickLaTeX.com (5.1)\quad \begin{array}{l} \displaystyle{\underbrace{ \left[\begin{array}{ccc} M+m_1+m_2 & (m_1+2m_2)\ell_1\cos\theta_1 & m_2\ell_2\cos\theta_2\\ (m_1+2m_2)\ell_1\cos\theta_1 & (\frac{4}{3}m_1+4m_2)\ell_1^2 & 2m_2\ell_1\ell_2\cos(\theta_2-\theta_1)\\ m_2\ell_2\cos\theta_2 & 2m_2\ell_1\ell_2\cos(\theta_2-\theta_1) & \frac{4}{3}m_2\ell_2^2 \end{array}\right] }_{M(\xi_1)} \underbrace{ \left[\begin{array}{c} \ddot{r} \\ \ddot{\theta}_1 \\ \ddot{\theta}_2 \end{array}\right] }_{\dot{\xi}_2}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 & -(m_1+2m_2)\ell_2\sin\theta_2 \dot{\theta}_1 & -m_2\ell_2\sin\theta_2 \dot{\theta}_2\\ 0 & 0 & 2m_2\ell_1\ell_2\sin(\theta_2-\theta_1) \dot{\theta}_2\\ 0 & 2m_2\ell_1\ell_2\sin(\theta_2-\theta_1) \dot{\theta}_1 & 0\\ \end{array}\right] }_{C(\xi_1,\xi_2)} \underbrace{ \left[\begin{array}{c} \dot{r} \\ \dot{\theta}_1 \\ \dot{\theta}_2 \end{array}\right] }_{\dot{\xi}_1}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 \\ (m_1+3m_2)\ell_1g\sin\theta_1\\ -m_2\ell_2g\sin\theta_2 \end{array}\right] }_{G(\xi_1)} = \underbrace{ \left[\begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right] F}_{\tilde{F}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-31c39d9c40fa5f71f3c50512937de667_l3.png)
![Rendered by QuickLaTeX.com (5.5)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} r\\ \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{r}\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right] =}\\ \displaystyle{\left[\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ 0 & -\frac{3m_1g}{4M+m_1+m_2} & -\frac{3m_2g}{4M+m_1+m_2} & 0 & 0 & 0\\ 0 & \frac{3(4m+4m_1+m_2)g}{4(4M+m_1+m_2)\ell_1} & \frac{9m_2g}{4(4M+m_1+m_2)\ell_1} & 0 & 0& 0\\ 0 & \frac{9gm_1}{4(4M+m_1+m_2)\ell_2} & \frac{3(4m+m_1+4m_2)g}{4(4M+m_1+m_2)\ell_2} & 0 & 0& 0\\ \end{array}\right] \left[\begin{array}{c} r\\ \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{r}\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right]}\\ \displaystyle{+ \left[\begin{array}{c} 0\\ 0\\ 0\\ \frac{4}{4M+m_1+m_2}\\ -\frac{3}{(4M+m_1+m_2)\ell_1}\\ -\frac{3}{(4M+m_1+m_2)\ell_2} \end{array}\right] F \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8554645545e9bed2d603331493dd90b7_l3.png)
![Rendered by QuickLaTeX.com (6.1)\quad \begin{array}{l} \displaystyle{\underbrace{ \left[\begin{array}{ccc} M+m_1+m_2 & m_1\ell_1\cos\theta_1 & -m_2\ell_2\cos\theta_2\\ m_1\ell_1\cos\theta_1 & \frac{4}{3}m_1\ell_1^2 & 0\\ -m_2\ell_2\cos\theta_2 & 0 & \frac{4}{3}m_2\ell_2^2 \end{array}\right] }_{M(\xi_1)} \underbrace{ \left[\begin{array}{c} \ddot{r} \\ \ddot{\theta}_1 \\ \ddot{\theta}_2 \end{array}\right] }_{\dot{\xi}_2}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 & -m_1\ell_2\sin\theta_2 \dot{\theta}_1 & -m_2\ell_2\sin\theta_2 \dot{\theta}_2\\ 0 & 0 & 0\\ 0 & 0 & 0\\ \end{array}\right] }_{C(\xi_1,\xi_2)} \underbrace{ \left[\begin{array}{c} \dot{r} \\ \dot{\theta}_1 \\ \dot{\theta}_2 \end{array}\right] }_{\dot{\xi}_1}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 \\ -m_1\ell_1g\sin\theta_1\\ -m_2\ell_2g\sin\theta_2 \end{array}\right] }_{G(\xi_1)} = \underbrace{ \left[\begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right] F}_{\tilde{F}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-93481c5d4d113644bf7b152b46e9779f_l3.png)
![Rendered by QuickLaTeX.com (6.5)\quad \begin{array}{l} \displaystyle{ \frac{d}{dt}\left[\begin{array}{c} r\\ \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{r}\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right] =}\\ \displaystyle{ \left[\begin{array}{cccccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & -\frac{3m_1g}{Mm_1+m_1^2+(3M+m1)m_2} & -\frac{3m_2g}{Mm_1+m_1^2+(3M+m1)m_2} \\ 0 & \frac{3(4Mm_1+4m_1^2+3m_2^2+3(18M+13m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m1)m_2)\ell_1} & \frac{9(2M+m_1)m_2g}{(4Mm_1+m_1^2+(3M+m1)m_2)\ell_1} \\ 0 & \frac{9(2Mm_1+m_1^2+3(2M+m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} & \frac{3(4Mm_1+m_1^2+12(3M+m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} \\ \end{array}\right.}\\ \displaystyle{\left.\begin{array}{cccccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ \end{array}\right] \left[\begin{array}{c} r\\ \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{r}\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right]}\\ \displaystyle{+ \left[\begin{array}{c} 0\\ 0\\ 0\\ \frac{4m_1+3m_2}{4Mm_1+m_1^2+(3M+m1)m_2}\\ -\frac{3(2m_1+m2)}{2Mm_1+m_1^2+(3M+m1)m_2}\\ \frac{3m_1}{2(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} \end{array}\right] F} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0ded80f948ddab3f936f91c1c7ea13d2_l3.png)
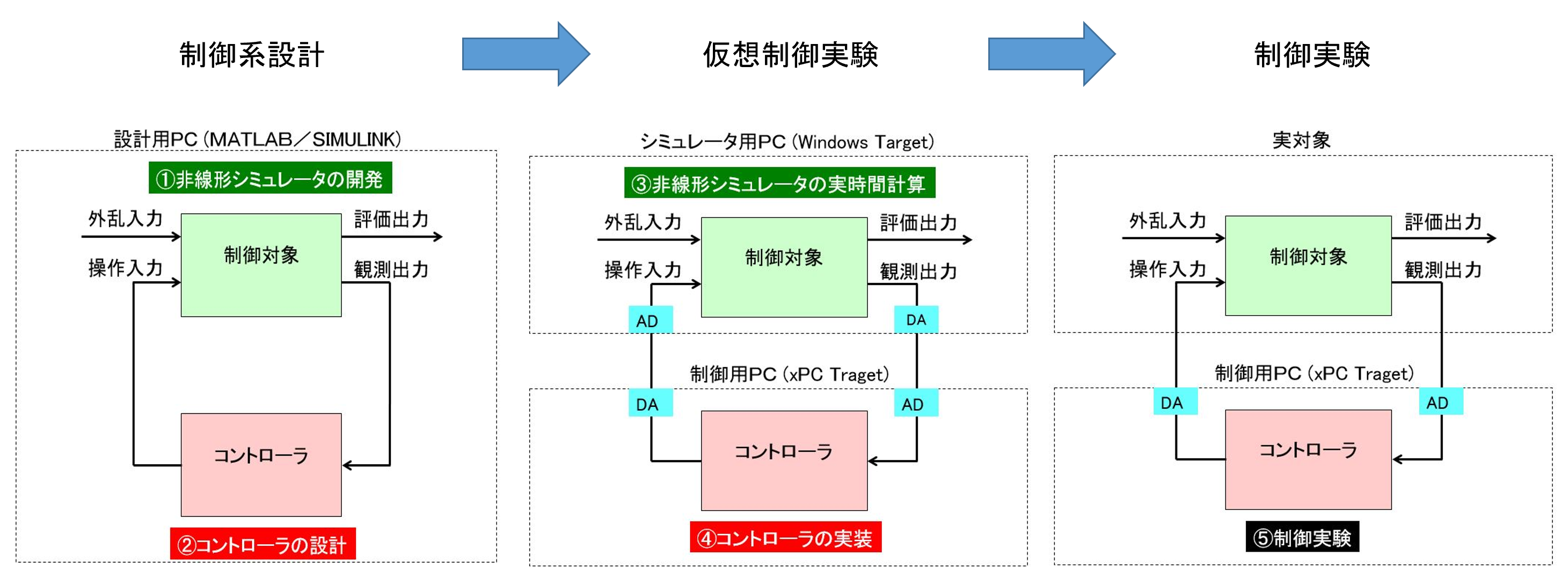 図1 HILS アプローチ
図1 HILS アプローチ 図2 単振り子
図2 単振り子 図3 単振り子の振動シミュレーション(モデルが線形か非線形か、初期状態を平衡状態周辺にとるかによる相違)
図3 単振り子の振動シミュレーション(モデルが線形か非線形か、初期状態を平衡状態周辺にとるかによる相違)![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \underbrace{ \left[\begin{array}{l} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{l} \omega(t) \\ -\frac{g}{L}\sin\theta(t) \end{array}\right] }_{f(x(t))} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ded67215525ba40fa5155a4367ed7405_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \underbrace{ \left[\begin{array}{l} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{g}{L}&0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{l} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ed5a0aa97035fe65dba8b64944a4a569_l3.png)
 図4 水タンクTANK
図4 水タンクTANK 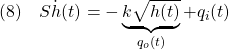
 図5 TANKの非線形シミュレータ
図5 TANKの非線形シミュレータ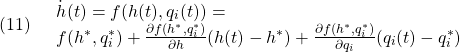
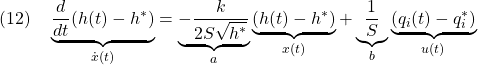
 図6 TANKの線形シミュレータ
図6 TANKの線形シミュレータ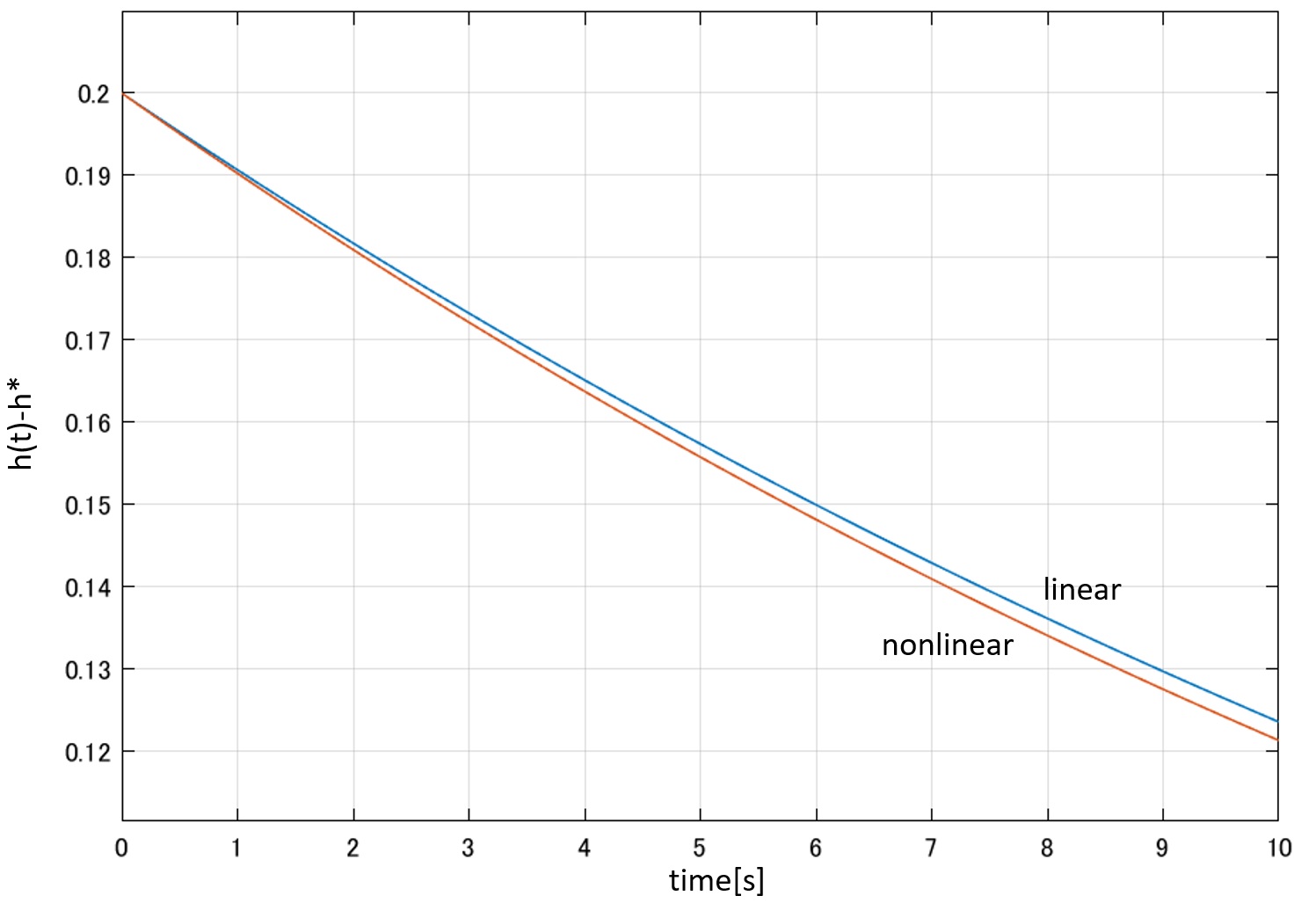 図7 TANKの非線形応答と線形応答の比較
図7 TANKの非線形応答と線形応答の比較 図8 TANKの非線形シミュレータと線形シミュレータ
図8 TANKの非線形シミュレータと線形シミュレータ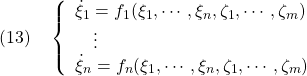
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \boxed{\dot{\xi}=f(\xi,\zeta)}\ \Leftrightarrow\ \underbrace{ \left[\begin{array}{l} \dot{\xi}_1 \\ \vdots \\ \dot{\xi}_n \end{array}\right] }_{\dot{\xi}} = \underbrace{ \left[\begin{array}{l} f_1(\xi,\zeta) \\ \quad\vdots \\ f_n(\xi,\zeta) \end{array}\right] }_{f(\xi,\zeta)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-92634287f13e8775d2c2a6ec25c7567c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad A=\frac{\partial\,f(\xi^*,\zeta^*)}{\partial\,\xi}= \left[\begin{array}{ccc} \frac{\partial f_1(\xi^*,\zeta^*)}{\partial \xi_1}&\cdots& \frac{\partial f_1(\xi^*,\zeta^*)}{\partial \xi_n}\\ \vdots&\ddots&\vdots\\ \frac{\partial f_n(\xi^*,\zeta^*)}{\partial \xi_1}&\cdots& \frac{\partial f_n(\xi^*,\zeta^*)}{\partial \xi_n} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9cbb1299b9fef4d94b388578973f2dd3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad B=\frac{\partial\,f(\xi^*,\zeta^*)}{\partial\,\zeta}= \left[\begin{array}{ccc} \frac{\partial f_1(\xi^*,\zeta^*)}{\partial \zeta_1}&\cdots& \frac{\partial f_1(\xi^*,\zeta^*)}{\partial \zeta_m}\\ \vdots&\ddots&\vdots\\ \frac{\partial f_n(\xi^*,\zeta^*)}{\partial \zeta_1}&\cdots& \frac{\partial f_n(\xi^*,\zeta^*)}{\partial \zeta_m} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-02d8fb9441471b4730389431ccc6f27c_l3.png)

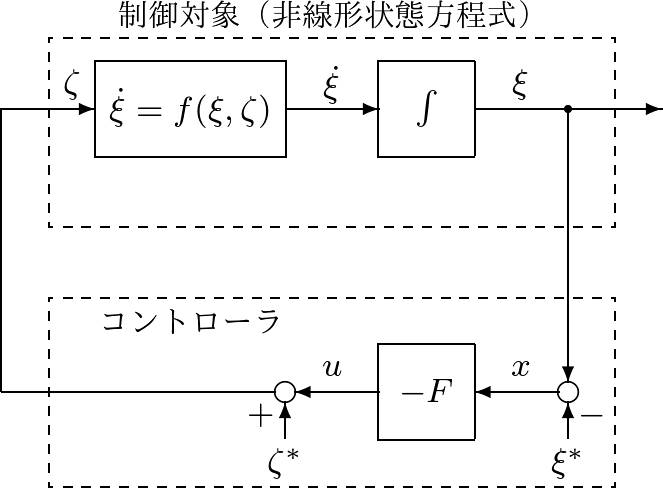
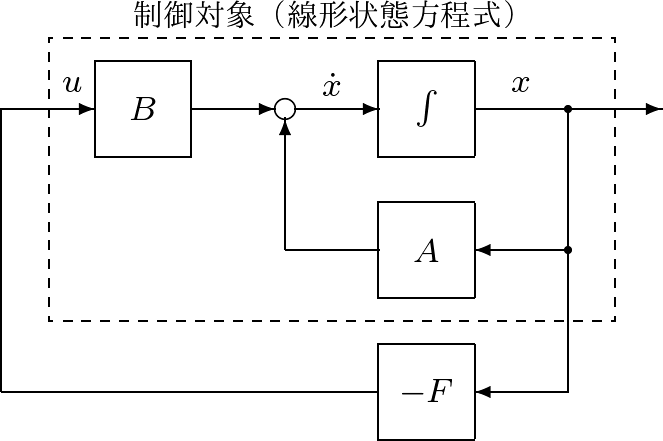
![Rendered by QuickLaTeX.com \displaystyle{(20)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{cc} \xi_1-\xi_1^* \\ \xi_2-\xi_2^* \end{array}\right] }_{\dot{x}=\dot{\xi}-\dot{\xi}^*}= \underbrace{ \left[\begin{array}{cc} \frac{\partial f_1(\xi^*,\tau^*)}{\partial \xi_1} & \frac{\partial f_1(\xi^*,\tau^*)}{\partial \xi_2} \\ \frac{\partial f_2(\xi^*,\tau^*)}{\partial \xi_1} & \frac{\partial f_2(\xi^*,\tau^*)}{\partial \xi_2} \end{array}\right] }_{A=\frac{\partial f(\xi^*,\tau^*)}{\partial \xi}} \underbrace{ \left[\begin{array}{l} \xi_1-\xi_1^* \\ \xi_2-\xi_2^* \end{array}\right] }_{x=\xi-\xi^*} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f2c5af558fdbb6c9d48962d44eed85a8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(22)\quad \underbrace{\frac{d}{dt} \left[\begin{array}{l} \xi_1 \\ \xi_2 \end{array}\right]}_{\dot{\xi}} =\underbrace{ \left[\begin{array}{l} \xi_2 \\ M^{-1}(\xi_1)(\zeta-C(\xi_1,\xi_2)\xi_2-G(\xi_1)) \end{array}\right]}_{f(\xi,\zeta)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5135df93ea761445ca840c16e381cc07_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(24)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{cc} \xi_1-\xi_1^* \\ \xi_2-\xi_2^* \end{array}\right] }_{\dot{x}}= \underbrace{ \left[\begin{array}{cc} 0 & I_n \\ A_{21} & A_{22} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{l} \xi_1-\xi_1^* \\ \xi_2-\xi_2^* \end{array}\right] }_{x}+ \underbrace{ \left[\begin{array}{cc} 0 \\ B_2 \end{array}\right] }_{B} \underbrace{ (\zeta-\zeta^*) }_{u} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-367b63505bbc335acbc7077f5650a169_l3.png)
 図1 剛体振り子
図1 剛体振り子![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \underbrace{ \left[\begin{array}{l} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{3g}{4\ell}&0 \end{array}\right] }_{A_\alpha} \underbrace{ \left[\begin{array}{l} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aab7f16339e56d265534f36b3b8a9366_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{l} \theta(t)-\pi \\ \omega(t)-0 \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ \frac{3g}{4\ell}&0 \end{array}\right] }_{A_\beta} \underbrace{ \left[\begin{array}{l} \theta(t)-\pi \\ \omega(t)-0 \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-89b5ecb0d715edc56311f92b25c00853_l3.png)
 図2 剛体振り子と同じ周期をもつ単振り子の長さは?
図2 剛体振り子と同じ周期をもつ単振り子の長さは?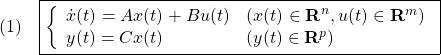
 図1 状態空間表現(1)のブロック線図
図1 状態空間表現(1)のブロック線図 図2 マス・バネ・ダンパからなる機械系
図2 マス・バネ・ダンパからなる機械系![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \underbrace{ \left[\begin{array}{c} \dot{r}(t) \\ \dot{v}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{K}{M} & -\frac{D}{M} \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} r(t) \\ v(t) \end{array}\right] }_{x(t)}+ \underbrace{ \left[\begin{array}{c} 0 \\ \frac{1}{M} \end{array}\right] }_B u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0f9eee4a83cd00ce26d47f602e1c5d9a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \underbrace{r(t)}_{y(t)}= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} r(t) \\ v(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e6aa71a57291ccf1f09944a3b8846465_l3.png)
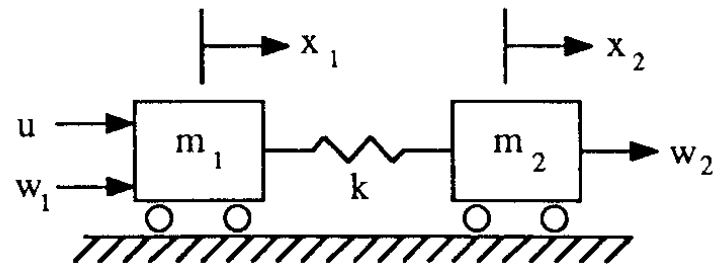
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \frac{d}{dt}\left[\begin{array}{c} x_1\\ x_2\\ \dot{x}_1\\ \dot{x}_2 \end{array}\right] = \left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{array}\right] \left[\begin{array}{c} x_1\\ x_2\\ \dot{x}_1\\ \dot{x}_2 \end{array}\right] + \left[\begin{array}{ccc} 0 & 0 & 0\\ 0 & 0 & 0\\ b_{31} & b_{32} & b_{33}\\ b_{41} & b_{42} & b_{43} \end{array}\right] \left[\begin{array}{c} u\\ w_1\\ w_2 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-797fe9e960cb81c588217b74e17d70fb_l3.png)
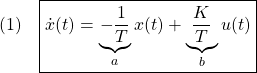
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \boxed{ \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] }_{\dot x} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{c} 0 \\ K\omega_n^2 \end{array}\right] }_{B} u(t) }}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-04009ed3d0edf5fa5a2060e9508b3422_l3.png)
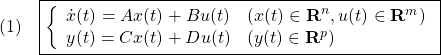
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \boxed{\left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right]= \left[\begin{array}{cc} A_1 & B_1C_2 \\ 0 & A_2 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] + \left[\begin{array}{cc} B_1D_2 \\ B_2 \end{array}\right] u_2(t) \\ y_1(t)= \left[\begin{array}{cc} C_1 & D_1C_2 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] +D_1D_2u_2(t) \end{array}\right.} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-36963521878ef7dd0808b96bae3bfff3_l3.png)
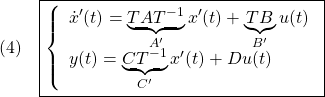
![Rendered by QuickLaTeX.com (4)\quad \begin{array}{l} \displaystyle{x(t)=e^{(a-bf)t}x(0)+\int_0^t e^{(a-bf)(t-\tau)}w\,d\tau}\\ \displaystyle{=e^{(a-bf)t}x(0)+\left[\frac{1}{-(a-bf)}e^{(a-bf)(t-\tau)}w\right]_0^t}\\ \displaystyle{=e^{(a-bf)t}x(0)+\frac{w}{-(a-bf)}(1-e^{(a-bf)t})}\\ \displaystyle{\rightarrow \frac{w}{-(a-bf)}\ne 0 \quad (t\rightarrow\infty)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-87ff2adf2a1f8bd25d390b2196807faa_l3.png)
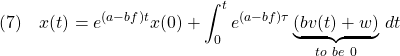
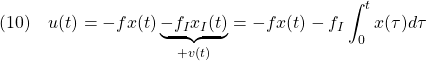
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad {\underbrace{ \left[\begin{array}{cc} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] }_{\dot{x}_E} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf_I \\ 1 & 0 \end{array}\right] }_{A_{EF}} \underbrace{ \left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] }_{x_E} + \underbrace{ \left[\begin{array}{cc} w \\ 0 \end{array}\right] }_{w_E}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-31b2a3c2e865a17fd4319135d80cb684_l3.png)
![Rendered by QuickLaTeX.com (14)\quad \begin{array}{l} \displaystyle{x_E(t)=\exp(A_{EF}t)x_E(0)+\int_0^t\exp(A_{EF}(t-\tau))w_E\,d\tau}\\ \displaystyle{=\exp(A_{EF}t)x_E(0)+\left[-\exp(A_{EF}(t-\tau))A_{EF}^{-1}w_E\right]_0^t}\\ \displaystyle{=\exp(A_{EF}t)x_E(0)-(I_2-\exp(A_{EF}t))A_{EF}^{-1}w_E}\\ \displaystyle{=\exp(A_{EF}t)(x_E(0)+A_{EF}^{-1}w_E)-A_{EF}^{-1}w_E}\\ \displaystyle{\rightarrow -A_{EF}^{-1}w_E \quad (t\rightarrow\infty)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3bca83642ec9ba9f633fe5e502d53148_l3.png)
![Rendered by QuickLaTeX.com (15)\quad \begin{array}{l} \displaystyle{\left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] \rightarrow - \left[\begin{array}{cc} a-bf & -bf_I \\ 1 & 0 \end{array}\right]^{-1} \left[\begin{array}{cc} w \\ 0 \end{array}\right]}\\ \displaystyle{ = -\frac{1}{bf_I} \left[\begin{array}{cc} 0 & bf_I \\ -1 & a-bf \end{array}\right] \left[\begin{array}{cc} w \\ 0 \end{array}\right] = \left[\begin{array}{cc} 0 \\ \frac{1}{bf_I}w \end{array}\right]} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b2e96500c3db9199db1fbc40cbaa0029_l3.png)
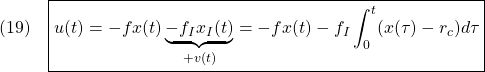
![Rendered by QuickLaTeX.com \displaystyle{(20)\quad \boxed{\underbrace{ \left[\begin{array}{cc} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] }_{\dot{x}_E} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf_I \\ 1 & 0 \end{array}\right] }_{A_{EF}} \underbrace{ \left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] }_{x_E} + \underbrace{ \left[\begin{array}{cc} w \\ -r_c \end{array}\right] }_{w_E}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ddef16b35db1273870bc586e72b3bb5a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(21)\quad \begin{array}{l} \displaystyle{\left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] \rightarrow - \left[\begin{array}{cc} a-bf & -bf_I \\ 1 & 0 \end{array}\right]^{-1} \left[\begin{array}{cc} w \\ -r_c \end{array}\right]}\\ \displaystyle{= -\frac{1}{bf_I} \left[\begin{array}{cc} 0 & bf_I \\ -1 & a-bf \end{array}\right] \left[\begin{array}{cc} w \\ -r_c \end{array}\right] = \left[\begin{array}{cc} r_c \\ \frac{1}{bf_I}w+\frac{a-bf}{bf_I}r_c \end{array}\right]} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f812ff0b7b34a62587cc56d0da3ad5fd_l3.png)
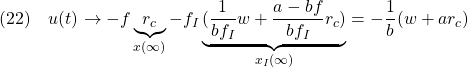
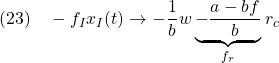
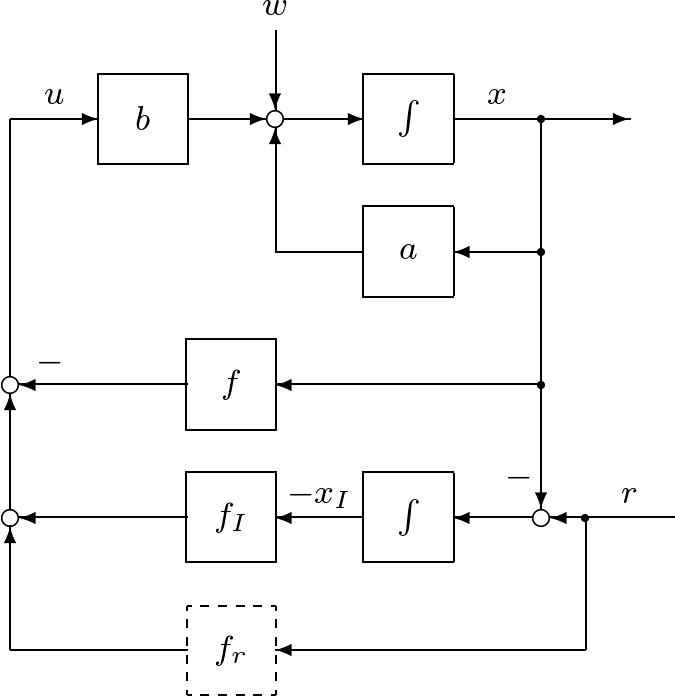
 図2 図1のシミュレーション例
図2 図1のシミュレーション例![Rendered by QuickLaTeX.com \displaystyle{(31)\quad \boxed{ \begin{array}{l} \left[\begin{array}{c} \dot{\hat{x}}(t) \\ \dot{x}_I(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} a-hc-bf & -bf_I \\ 0 & 0 \end{array}\right] }_{A_K} \left[\begin{array}{c} \hat{x}(t) \\ x_I(t) \end{array}\right] + \underbrace{ \left[\begin{array}{cc} h & 0\\ 1 & -1 \end{array}\right] }_{B_K} \left[\begin{array}{c} y(t) \\ r_c \end{array}\right]\\ u(t)= \underbrace{- \left[\begin{array}{cc} f & f_I \end{array}\right] }_{C_K} \left[\begin{array}{c} \hat{x}(t) \\ x_I(t) \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c9a64fdc6b3c7ee88c4b4ccbe8c58b7b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(33)\quad \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \\ \dot{\hat{x}}(t) \end{array}\right] = \left[\begin{array}{ccc} a & -bf_I & -bf \\ c & 0 & 0 \\ hc & -bf_I & a-hc-bf \end{array}\right] \left[\begin{array}{c} x(t) \\ x_I(t) \\ \hat{x}(t) \end{array}\right] + \left[\begin{array}{c} w \\ -r_c \\ 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ec175798327a5fc11b68b91a22172f0d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(34)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \\ e(t) \end{array}\right] = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -1 & 0 & 1 \end{array}\right] \left[\begin{array}{c} x(t) \\ x_I(t) \\ \hat{x}(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7ca97b463935b7f71dea225ffcb573f2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(35)\quad \boxed{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \\\hline \dot{e}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc|c} a-bf & -bf_I & -bf \\ c & 0 & 0 \\\hline 0 & 0 & a-hc \end{array}\right] }_{ A_{EF}'= \left[\begin{array}{c|c} A_{EF} & - \left[\begin{array}{cc} bf \\ 0 \end{array}\right] \\[5mm] \hline 0 & \widehat{a} \end{array}\right] } \left[\begin{array}{c} x(t) \\ x_I(t) \\\hline e(t) \end{array}\right] + \left[\begin{array}{c} w \\ -r_c \\\hline -w \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3a0c12a07d48d608c414bfef747b7ae3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(36)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \\\hline e(t) \end{array}\right] \ \rightarrow\ \underbrace{ \left[\begin{array}{c|c} A_{EF}^{-1} & -A_{EF}^{-1} \left[\begin{array}{cc} bf \\ 0 \end{array}\right] \widehat{a}^{-1} \\[5mm]\hline 0 & \widehat{a}^{-1} \end{array}\right] }_{A_{EF}'\,^{-1}} \left[\begin{array}{c} -w \\ r_c \\\hline w \end{array}\right] \quad (t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c8709893951656a10a2cf0aec18bef8b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(37)\quad \begin{array}{l} \displaystyle{\left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] \rightarrow \left[\begin{array}{cc} a-bf & -bf_I \\ c & 0 \end{array}\right]^{-1} \left[\begin{array}{cc} -w-bf\widehat{a}^{-1}w\\ r_c \end{array}\right]}\\ \displaystyle{= \frac{1}{cbf_I} \left[\begin{array}{cc} 0 & bf_I \\ -c & a-bf \end{array}\right] \left[\begin{array}{cc} -w-bf\widehat{a}^{-1}w\\ r_c \end{array}\right]}\\ \displaystyle{= \left[\begin{array}{cc} \frac{1}{c}r_c \\ \frac{1}{bf_I}w+\frac{1}{f_I}f\widehat{a}^{-1}w+\frac{a-bf}{cbf_I}r_c \end{array}\right]} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a0408f31040df6a4e4b055bc9c88bc05_l3.png)
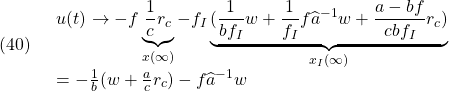
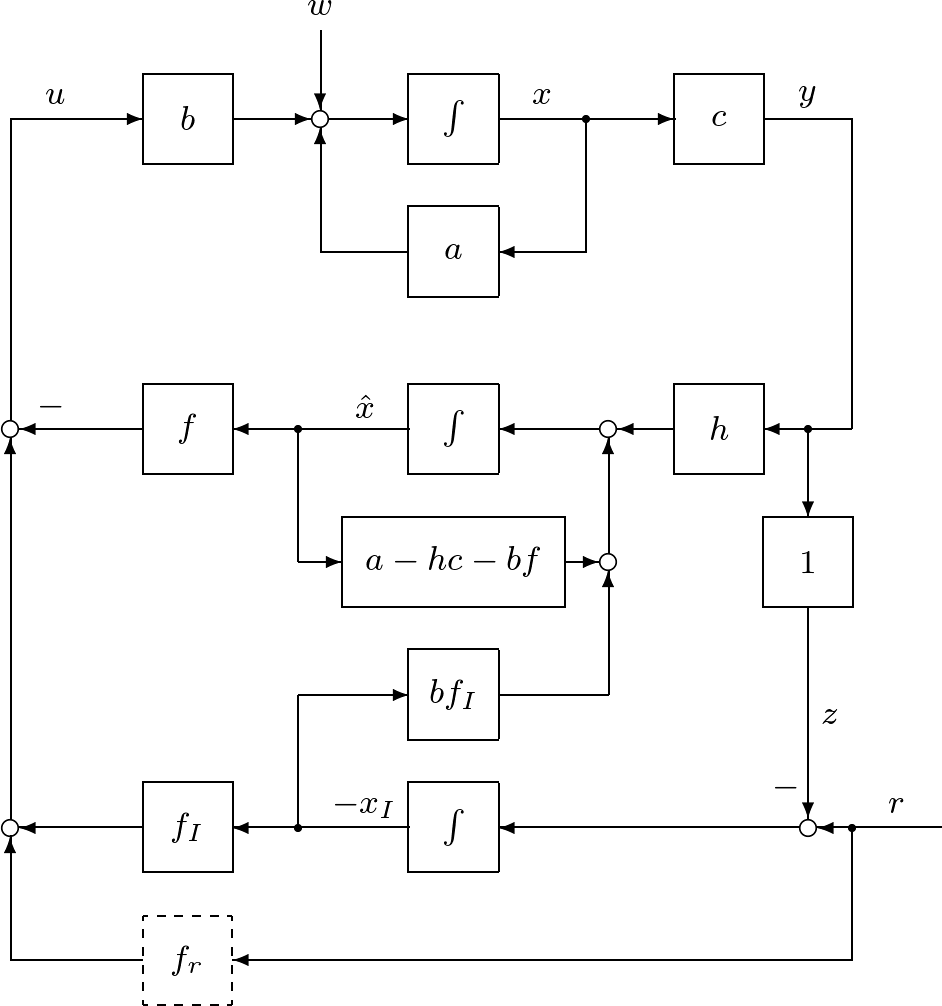 図3 積分動作を加えたオブザーバベースコントローラによる閉ループ系
図3 積分動作を加えたオブザーバベースコントローラによる閉ループ系![Rendered by QuickLaTeX.com \displaystyle{(41)\quad \underbrace{ \left[\begin{array}{cc} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] }_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf_I \\ c & 0 \end{array}\right] }_{A_{EF}} \underbrace{ \left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] }_{x_E(t)} + \underbrace{ \left[\begin{array}{cc} w \\ -r_c \end{array}\right] }_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f729fc6c953923d57572c53768579876_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(43)\quad \underbrace{ \left[\begin{array}{cc} qx(t)\\ ru(t) \end{array}\right] }_{y_{E}(t)} = \underbrace{ \left[\begin{array}{cc} q & 0 \\ -rf & -rf_I \end{array}\right] }_{C_{E}} \underbrace{ \left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] }_{x_{E}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0d18a388e7b6c8f9fa04453e84d71145_l3.png)
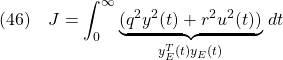
![Rendered by QuickLaTeX.com \displaystyle{(47)\quad \underbrace{\frac{d}{dt} \left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] }_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} a & 0 \\ c & 0 \end{array}\right] }_{A_E} \underbrace{ \left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] }_{x_E(t)} + \underbrace{ \left[\begin{array}{cc} b \\ 0 \end{array}\right] }_{B_E} u(t) + \underbrace{ \left[\begin{array}{cc} w \\ -r_c \end{array}\right] }_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4e152ba9118c145fdc3aa9097ad1291f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(48)\quad \underbrace{\frac{d}{dt} \left[\begin{array}{cc} x_\infty \\ x_{I\infty} \end{array}\right] }_{\dot{x}_{E\infty}=0} = \underbrace{ \left[\begin{array}{cc} a & 0 \\ c & 0 \end{array}\right] }_{A_E} \underbrace{ \left[\begin{array}{cc} x_\infty \\ x_{I\infty} \end{array}\right] }_{x_{E\infty}} + \underbrace{ \left[\begin{array}{cc} b \\ 0 \end{array}\right] }_{B_E} u_\infty + \underbrace{ \left[\begin{array}{cc} w \\ -r_c \end{array}\right] }_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-388e3b63a548f6ae3de1bca82350d6b8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(49)\quad \boxed{ \underbrace{\frac{d}{dt} \left[\begin{array}{cc} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{\dot{x}_{E1}(t)} = \underbrace{ \left[\begin{array}{cc} a & 0 \\ c & 0 \end{array}\right] }_{A_{E1}} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{x_{E1}(t)} + \underbrace{ \left[\begin{array}{cc} b \\ 0 \end{array}\right] }_{B_{E1}} \underbrace{(u(t)-u_\infty)}_{u_{E1}(t)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ef61060eeffd371eb2eb609612504541_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(50)\quad \underbrace{u(t)-u_\infty}_{u_{E1}(t)} =- \underbrace{ \left[\begin{array}{cc} f & f_I \end{array}\right] }_{F_E} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{x_{E1}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2de715ba671f8a4ff5fe87b581f7486f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(51)\quad \underbrace{\frac{d}{dt} \left[\begin{array}{cc} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{\dot{x}_{E1}(t)} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf_I \\ c & 0 \end{array}\right] }_{A_{EF}} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{x_{E1}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0ac4b58fae5895656374987e2e2dfb53_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(52)\quad \underbrace{ \left[\begin{array}{cc} q(x(t)-x_\infty) \\ r(u(t)-u_\infty) \end{array}\right] }_{y_{E1}(t)} = \underbrace{ \left[\begin{array}{cc} q & 0 \\ -rf & -rf_I \end{array}\right] }_{C_{E1}} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{x_{E1}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f6ff94e985ffd90ab5da603d6e28d94f_l3.png)
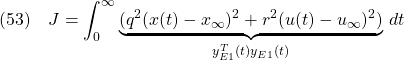
![Rendered by QuickLaTeX.com \displaystyle{(54)\quad \boxed{ \underbrace{\frac{d}{dt} \left[\begin{array}{cc} \dot{x}(t) \\ x(t)-r_c \end{array}\right] }_{\dot{x}_{E2}(t)} = \underbrace{ \left[\begin{array}{cc} a & 0 \\ c & 0 \end{array}\right] }_{A_{E2}} \underbrace{ \left[\begin{array}{cc} \dot{x}(t) \\ x(t)-r_c \end{array}\right] }_{x_{E2}(t)} + \underbrace{ \left[\begin{array}{cc} b \\ 0 \end{array}\right] }_{B_{E2}} \underbrace{\dot{u}(t)}_{u_{E2}(t)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d55bc528b4211e44104d9a016f1efe77_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(55)\quad \left[\begin{array}{cc} \dot{x}(t) \\ x(t)-r_c \end{array}\right] = \underbrace{ \left[\begin{array}{cc} a & b \\ c & 0 \end{array}\right] }_{S} \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b36ebc36ec3a8aa2b181e54a374490a4_l3.png)
![Rendered by QuickLaTeX.com (56)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} a & b \\ c & 0 \end{array}\right] }_{S} \frac{d}{dt} \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right]=\\ \underbrace{ \left[\begin{array}{cc} a & 0 \\ 1 & 0 \end{array}\right] }_{A_{E2}} \underbrace{ \left[\begin{array}{cc} a & b \\ c & 0 \end{array}\right] }_{S} \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] + \underbrace{ \left[\begin{array}{cc} b \\ 0 \end{array}\right] }_{B_{E2}} \underbrace{\dot{u}(t)}_{u_{E2}(t)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3fe9bb9955ebd8e2c8e93bbd706c8fe9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(57)\quad \boxed{\underbrace{ \frac{d}{dt} \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{\dot{x}_{E3}} = \underbrace{ \left[\begin{array}{cc} a & b \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}} + \underbrace{ \left[\begin{array}{cc} 0 \\ 1 \end{array}\right] }_{B_{E3}} \underbrace{\dot{u}(t)}_{u_{E3}(t)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c85ae085cc84c481ab12fad21f3f8ae0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(58)\quad \underbrace{\dot{u}(t)}_{u_{E3}(t)} =- \underbrace{ \left[\begin{array}{cc} k & k_I \end{array}\right] }_{K_E} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b8ffb28df7a25dd49c60692720881d34_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(59)\quad \underbrace{\frac{d}{dt} \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} a & b \\ -k & -k_I \end{array}\right] }_{A_{EK}} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-150f484db41dfcfd7bc2713f40cf1398_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(60)\quad \underbrace{ \left[\begin{array}{cc} q(x(t)-x_\infty) \\ r\dot{u}(t) \end{array}\right] }_{y_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} q & 0 \\ 0 & r\frac{d}{dt} \end{array}\right] }_{C_{E3}} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-36376901e37df555679c68adbb340194_l3.png)
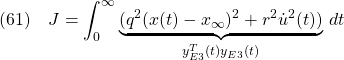
![Rendered by QuickLaTeX.com \displaystyle{(62)\quad \dot{u}(t) =- \underbrace{ \left[\begin{array}{cc} k & k_I \end{array}\right] }_{K_E} \underbrace{ \left[\begin{array}{cc} a & b \\ 1 & 0 \end{array}\right]^{-1} }_{S^{-1}} \left[\begin{array}{cc} \dot{x}(t) \\ x(t)-r_c \end{array}\right] =- \underbrace{ \left[\begin{array}{cc} f & f_I \end{array}\right] }_{F_E=K_ES^{-1}} \left[\begin{array}{cc} \dot{x}(t) \\ x(t)-r_c \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-84e71c3cc59f8a7feeedd162fdda01c6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(64)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} a & b \\ 0 & 0 \end{array}\right] }_{A_{E}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_{E}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0c41509ad03419a701e8ac16d5e5fdd9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(70)\quad \begin{array}{l} \dot{x}_K(t)=A_Kx_K(t)+B_K \left[\begin{array}{c} y(t) \\ r_c \end{array}\right]\\ u(t)=C_Kx_K(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a49a6c693b0b6603def7809f250eda5e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(71)\quad \begin{array}{l} A_K= \left[\begin{array}{cc} a-hc-bf & -bf_I \\ 0 & 0 \end{array}\right]\\ B_K= \left[\begin{array}{cc} h & 0\\ 1 & -1 \end{array}\right]\\ C_K=- \left[\begin{array}{cc} f & f_I \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-78a0c63e2aa625650bb1f5593550221b_l3.png)
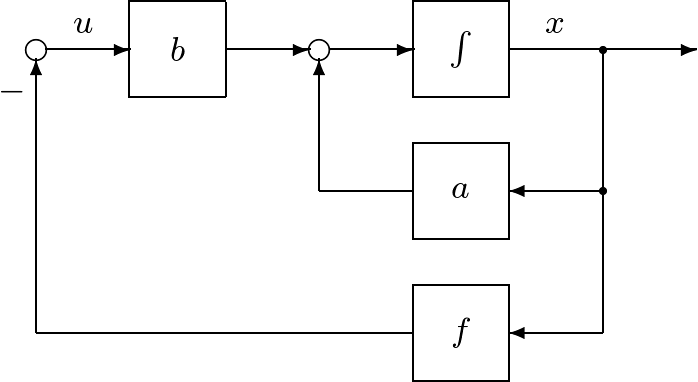 図1 状態フィードバックによる閉ループ系
図1 状態フィードバックによる閉ループ系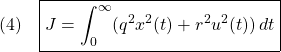
![Rendered by QuickLaTeX.com (6)\quad \begin{array}{lll} \displaystyle{J_x=\int_0^\infty q^2x^2(t)\,dt}\\ \displaystyle{=\int_0^\infty q^2e^{2(a-bf)t}x^2(0)\,dt}\\ \displaystyle{=q^2x^2(0)\left[\frac{1}{2(a-bf)}e^{2(a-bf)t}\right]_0^\infty}\\ \displaystyle{=\frac{q^2x^2(0)}{2(a-bf)}\left[\underbrace{e^{2(a-bf)\infty}}_{0}-\underbrace{e^{2(a-bf)0}}_{1}\right]}\\ \displaystyle{=-\frac{q^2}{2(a-bf)}x^2(0)>0\quad (a-bf<0)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ccbd56eae6c871c4d509a66bb0b1d13c_l3.png)
![Rendered by QuickLaTeX.com (8)\quad \begin{array}{lll} \displaystyle{J_u=\int_0^\infty r^2u^2(t)\,dt}\\ \displaystyle{=\int_0^\infty r^2f^2e^{2(a-bf)t}x^2(0)\,dt}\\ \displaystyle{=r^2f^2x^2(0)\left[\frac{1}{2(a-bf)}e^{2(a-bf)t}\right]_0^\infty}\\ \displaystyle{=-\frac{r^2f^2}{2(a-bf)}x^2(0)>0\quad (a-bf<0)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9f5dcb6b69a84056f569669f6625e961_l3.png)
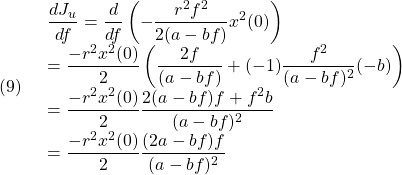
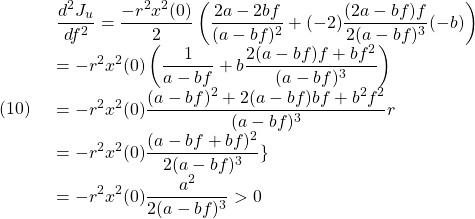
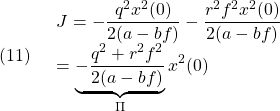
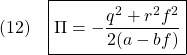
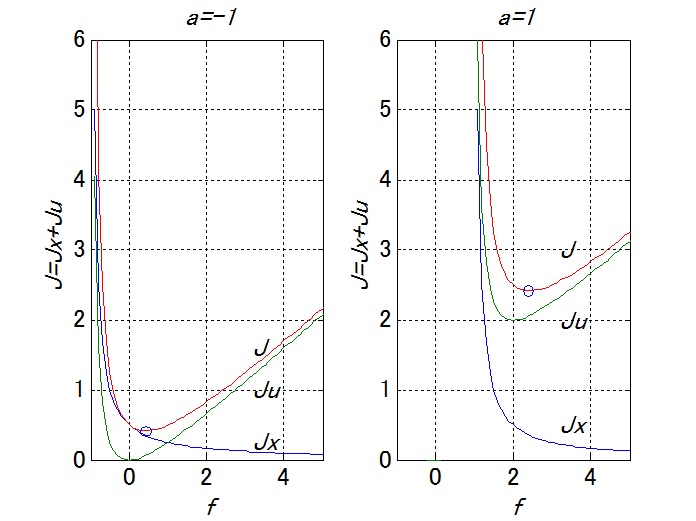 図2 評価関数の概形
図2 評価関数の概形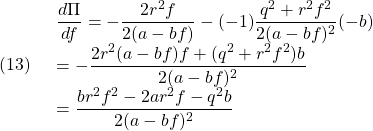
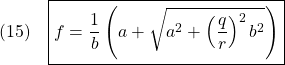
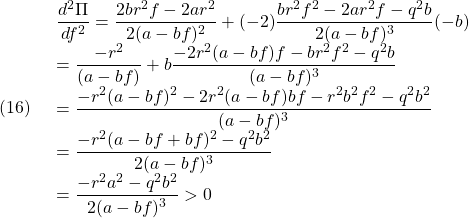
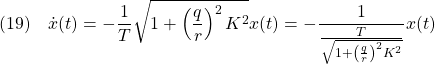
 図3 重み係数の比
図3 重み係数の比![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \left[\begin{array}{cc} v_1 \\ v_2 \end{array}\right] =\left[\begin{array}{cc} 1 \\ \frac{-a-\sqrt{a^2+r^{-2}b^2q^2}}{-r^{-2}b^2} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-818b80fae6a9d75606e700bc7229ad17_l3.png)
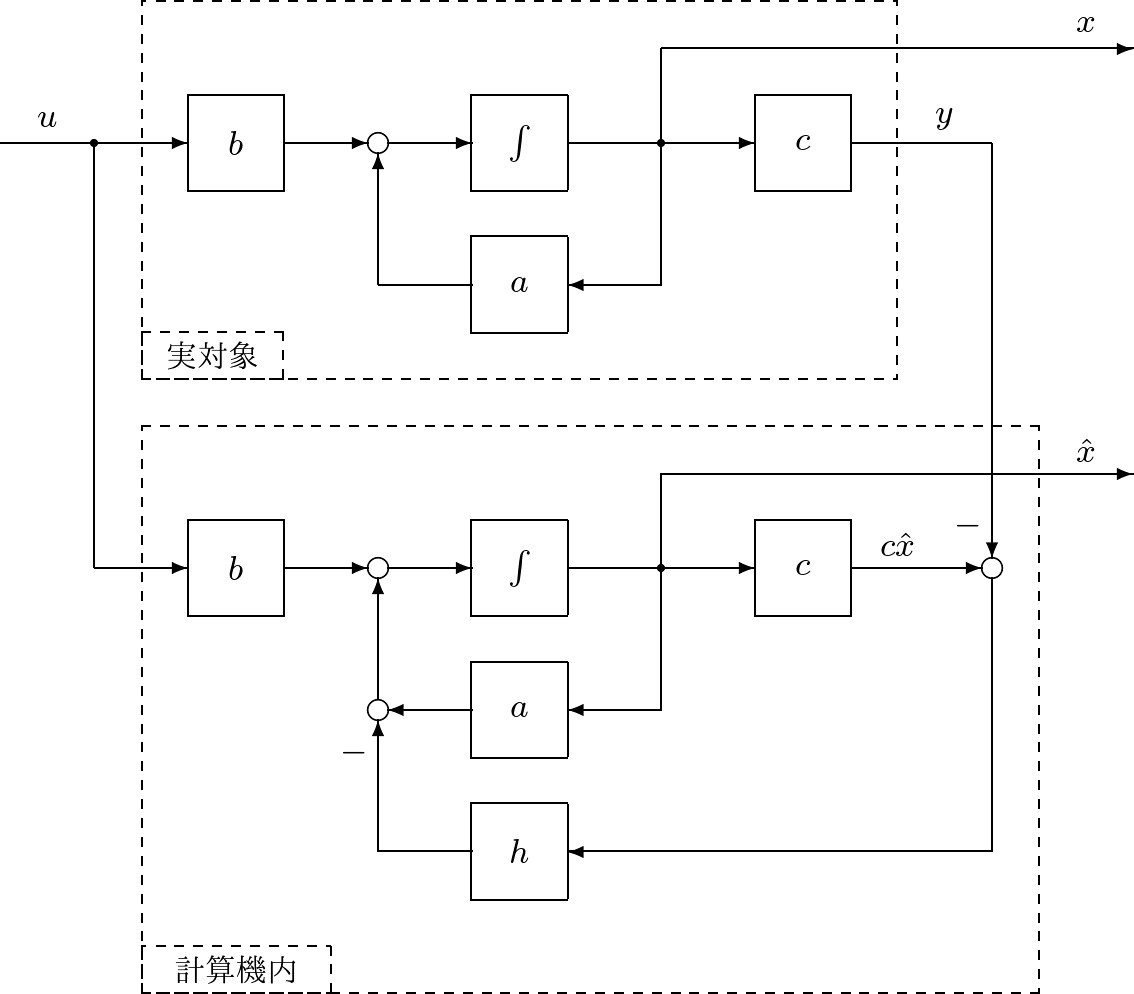 図4 状態オブザーバの考え方
図4 状態オブザーバの考え方![Rendered by QuickLaTeX.com \displaystyle{(36)\quad \left[\begin{array}{cc} \dot{x}(t)\\ \dot{\hat{x}}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} a& -bf\\ hc& a-hc-bf \end{array}\right] }_{A_F} \left[\begin{array}{cc} x(t)\\ \hat{x}(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bd0bda91887ef926493669aa7866308d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(37)\quad \boxed{ \left[\begin{array}{cc} \dot{x}(t)\\ \dot{e}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} a-bf & -bf\\ 0 & a-hc \end{array}\right] }_{A_F'} \left[\begin{array}{cc} x(t)\\ e(t) \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-36b6d2d539455492f72a79c84bbd9dfe_l3.png)
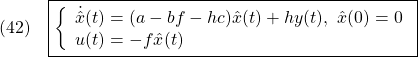
![Rendered by QuickLaTeX.com \displaystyle{(44)\quad \underbrace{ \left[\begin{array}{cc} \dot{x}(t)\\ \dot{e}(t) \end{array}\right] }_{\dot{x}_{CL}(t)} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf\\ 0 & a-hc \end{array}\right] }_{A_{CL}} \underbrace{ \left[\begin{array}{cc} x(t) \\ e(t) \end{array}\right] }_{x_{CL}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-18643919f74aadae99e3d8cd8e1b5bdb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(45)\quad \underbrace{ \left[\begin{array}{cc} qx(t)\\ ru(t) \end{array}\right] }_{y_{CL}(t)} = \underbrace{ \left[\begin{array}{cc} q & 0 \\ -rf & -rf \end{array}\right] }_{C_{CL}} \underbrace{ \left[\begin{array}{cc} x(t) \\ e(t) \end{array}\right] }_{x_{CL}(t)} \label{eq7.2.5}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-684ce689df1ece17dac2a773360c137d_l3.png)
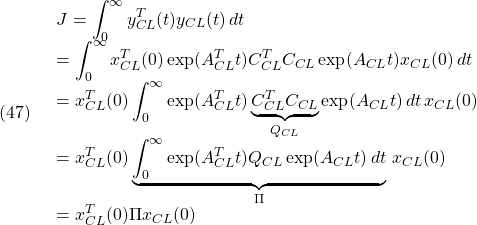

![Rendered by QuickLaTeX.com \displaystyle{(50)\quad &&\left[\begin{array}{cc} \dot{x}(t)\\ \dot{e}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} a-bf & -bf \\ 0 & a-hc \end{array}\right] }_{A_{CL}} \left[\begin{array}{cc} x(t)\\ e(t) \end{array}\right]\nonumber\\ &&+ \underbrace{ \left[\begin{array}{cc} \sigma & 0\\ -\sigma & h\rho \end{array}\right] }_{B_{CL}} \left[\begin{array}{cc} n_x(t)\\ n_y(t) \end{array}\right] \label{eq7.2.11}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3dae61b87dbc3a1048d873c29e860e77_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(51)\quad y^{(1)}_{CL}(t) = C_{CL}\exp(A_{CL}t) \underbrace{ \left[\begin{array}{cc} \sigma \\ -\sigma \end{array}\right] }_{x_{CL}(0)=B^{(1)}_{CL}} \label{eq7.2.12}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6d85ddaaacfba1399baf629b17e45713_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(52)\quad y^{(2)}_{CL}(t) = C_{CL}\exp(A_{CL}t) \underbrace{ \left[\begin{array}{cc} 0 \\ h\rho \end{array}\right] }_{x_{CL}(0)=B^{(2)}_{CL}} \label{eq7.2.13}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d2090f3554280d4f6ace06c772a5f0c6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(55)\quad \begin{array}{lll} && \underbrace{ \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] }_{\Pi} \underbrace{ \left[\begin{array}{cc} a-bf & -bf \\ 0 & a-hc \end{array}\right] }_{A_{CL}}\nonumber\\ &&+ \underbrace{ \left[\begin{array}{cc} a-bf & 0 \\ -bf & a-hc \end{array}\right] }_{A_{CL}^T} \underbrace{ \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] }_{\Pi}\nonumber\\ &&+ \underbrace{ \left[\begin{array}{cc} q^2+r^2f^2 & r^2f^2 \\ r^2f^2 & r^2f^2 \end{array}\right] }_{C_{CL}^TC_{CL}>0} = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array} \label{eq7.2.16}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-79305e587239433bbc038b894b5d433c_l3.png)
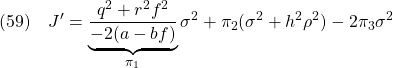
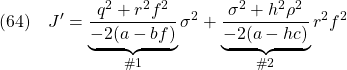
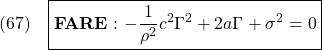
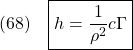
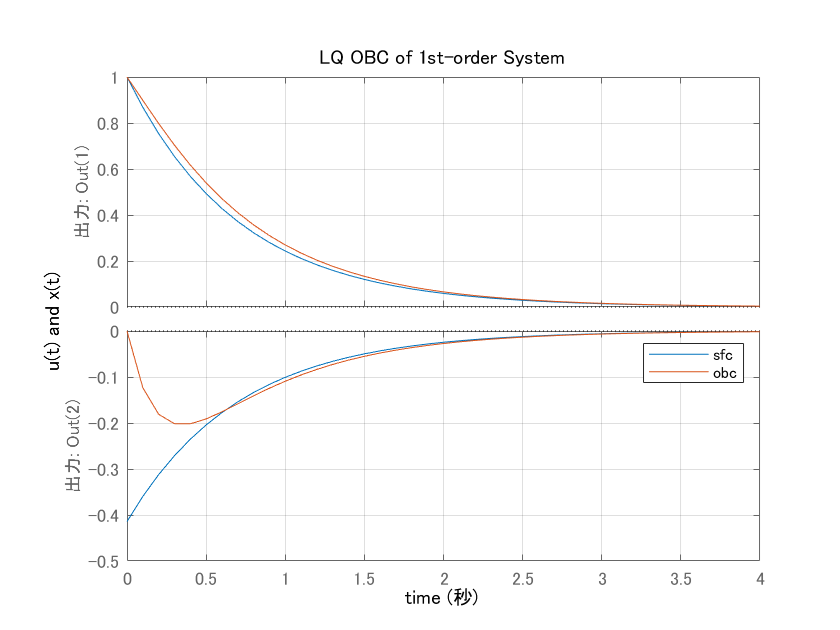 図6 状態フィードバックとオブザーバベース コントローラを用いた場合の応答の変化
図6 状態フィードバックとオブザーバベース コントローラを用いた場合の応答の変化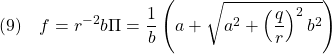
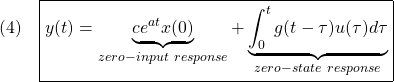
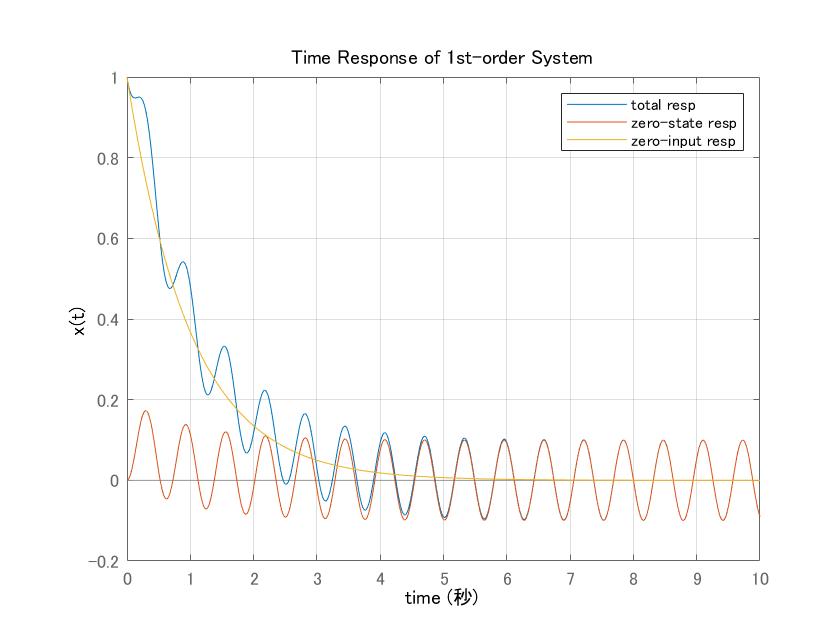
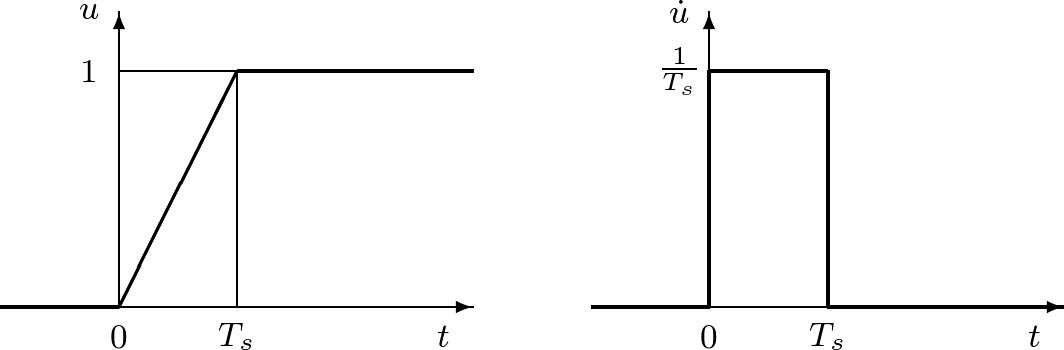

![Rendered by QuickLaTeX.com \displaystyle{(11)\quad y(t)=\frac{K}{T}\int_0^te^{-\frac{1}{T}\tau}d\tau=\frac{K}{T}\left[\frac{e^{-\frac{1}{T}\tau}}{-\frac{1}{T}}\right]_0^t =-K(e^{-\frac{1}{T}t}-1)=K(1-e^{-\frac{1}{T}t}) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7bfde10f7b48435b229585a7aded9380_l3.png)
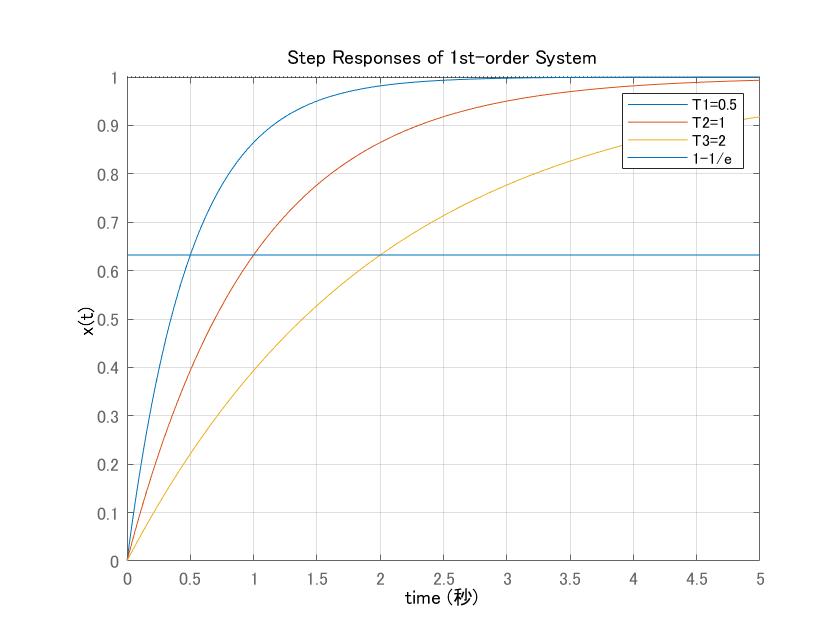
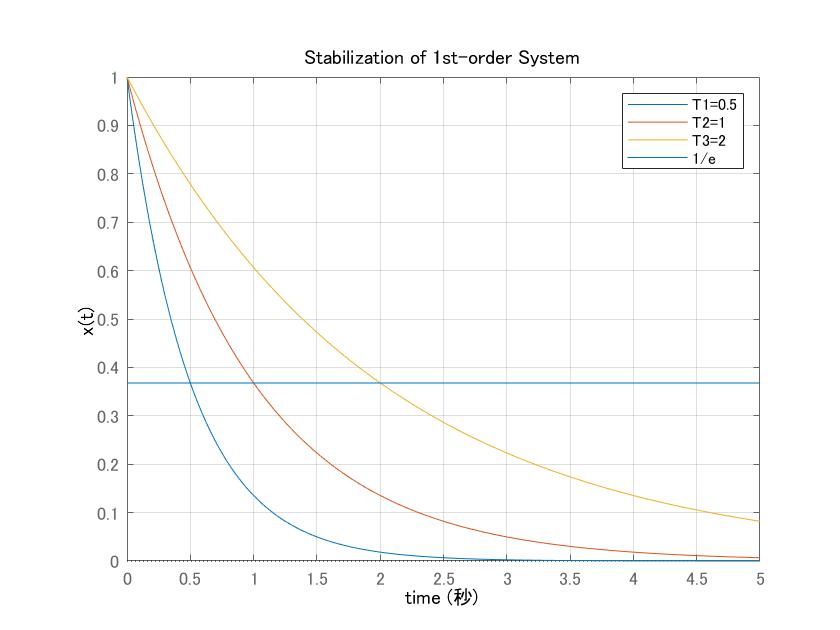
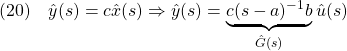
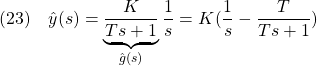
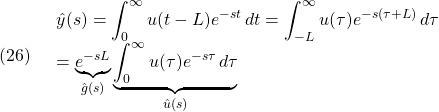
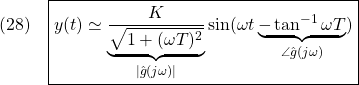

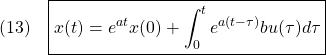
![Rendered by QuickLaTeX.com (4)\quad \begin{array}{l} \displaystyle{x(t)=\int_0^te^{a(t-\tau)}b \sin\omega\tau\,d\tau=e^{at}b\int_0^te^{-a\tau} \sin\omega\tau\,d\tau}\\ \displaystyle{=e^{at}b\left[\frac{e^{-a\tau}}{a^2+\omega^2}(-a\sin\omega\tau-\omega\cos\omega\tau)\right]_0^t}\\ \displaystyle{=\frac{e^{at}b}{a^2+\omega^2}(e^{-at}(-a\sin\omega t-\omega\cos\omega t)+\omega)}\\ \displaystyle{=\frac{b}{\sqrt{a^2+\omega^2}}(\sin\omega t\frac{-a}{\sqrt{a^2+\omega^2}}-\cos\omega t\frac{\omega}{\sqrt{a^2+\omega^2}}+e^{+at}\frac{\omega}{\sqrt{a^2+\omega^2}})}\\ \displaystyle{=\frac{b}{\sqrt{a^2+\omega^2}}(\sin\omega t\cos\theta-\cos\omega t\sin\theta+e^{+at}\sin\theta)}\\ \displaystyle{=\frac{b}{\sqrt{a^2+\omega^2}}(\sin(\omega t-\theta)+e^{+at}\sin\theta)\quad (\theta=\tan^{-1}\frac{\omega}{-a})}\\ \displaystyle{=\frac{b}{\sqrt{a^2+\omega^2}}(\sin(\omega t+\phi)-e^{+at}\sin\phi)\quad (\phi=-\theta)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ed887e5a02609da72f9c770b930e0a48_l3.png)
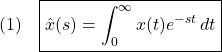
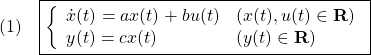
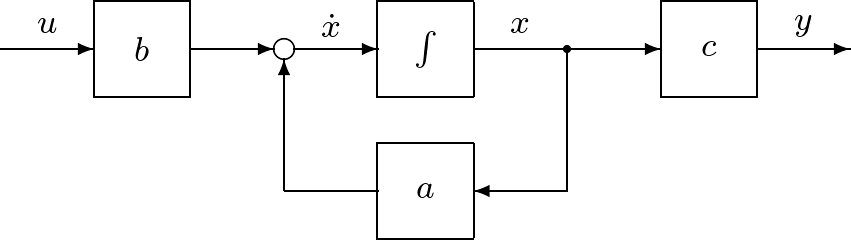

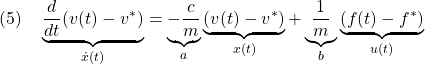
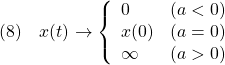
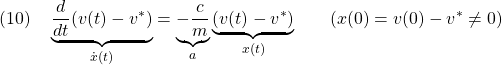
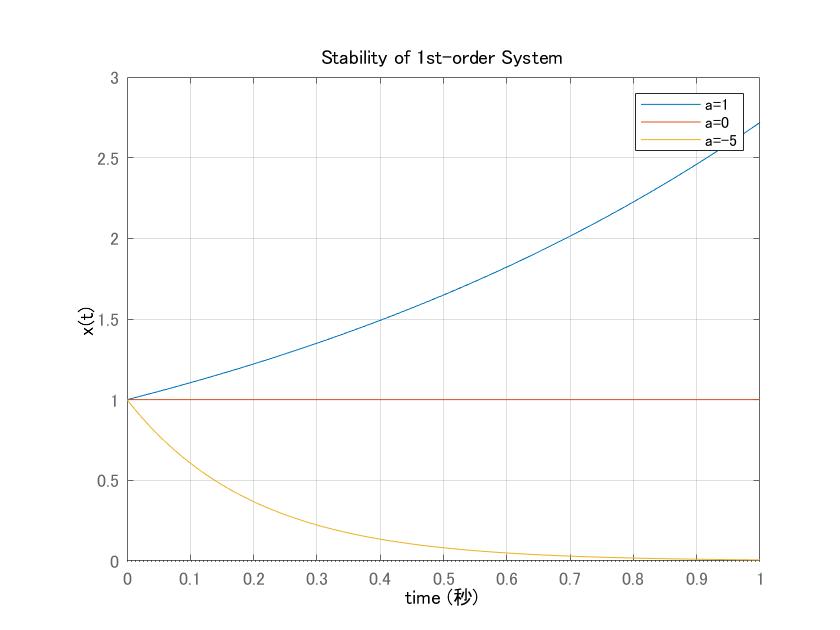 図3 どのグラフが漸近安定であるか?
図3 どのグラフが漸近安定であるか?![Rendered by QuickLaTeX.com \displaystyle{ q(\tau)= \left[\begin{array}{c} q_1(\tau) \\ \vdots\\ q_N(\tau) \\ \end{array}\right],\ \phi(\xi)= \left[\begin{array}{c} \phi_1(\xi) \\ \vdots\\ \phi_N(\xi) \\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eb7bf57075a262c97b517d94def84c2e_l3.png)
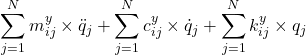
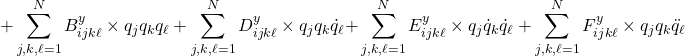
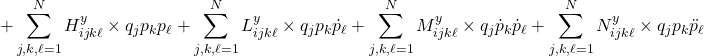
![Rendered by QuickLaTeX.com \displaystyle{ p(\tau)= \left[\begin{array}{c} p_1(\tau) \\ \vdots\\ p_N(\tau) \\ \end{array}\right],\ \psi(\xi)= \left[\begin{array}{c} \psi_1(\xi) \\ \vdots\\ \psi_N(\xi) \\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fd0c4d2c5fa9639928a6bead5eea84f4_l3.png)
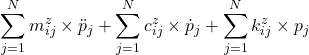
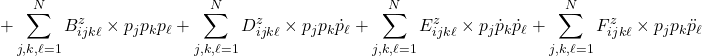
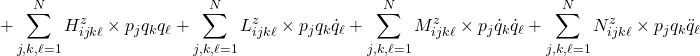
![Rendered by QuickLaTeX.com \displaystyle{ +\left[\begin{array}{cc} K_{qq} & K_{qp} \\ K_{pq} & K_{pp} \\ \end{array}\right] \left[ \begin{array}{c} q \\ p \end{array} \right] = \left[\begin{array}{c} \int_0^1\phi(\xi)\frac{L^3}{EI} f_yd\xi \\ \int_0^1\psi(\xi)\frac{L^3}{EI} f_zd\xi \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e290e382c54e788b99323cf80a06ac06_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{M_{qq}=[m^y_{ij} + \sum_{l,k=1}^NF^y_{ilkj}q_lq_k]_{i,j=1,\cdots,N}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-64b9cea8f35b506b42b4a39f23969063_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{M_{qp}=[\sum_{l,k=1}^N N^y_{ilkj} q_l p_k]_{i,j=1,\cdots,N}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f994a23e0e7bd4dd1208c9824da4c048_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{M_{pq}=[\sum_{l,k=1}^N N^z_{ilkj} p_l q_k]_{i,j=1,\cdots,N}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4804f4210c89799711a737b50ec9b496_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{M_{pp}=[m^z_{ij} + \sum_{l,k=1}^N F^z_{ilkj}p_l p_k]_{i,j=1,\cdots,N}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bf7c14a7d29adb632b291bede34ffaff_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{D_{qq}=[c^y_{ij} + \sum_{l,k=1}^ND^y_{ilkj}q_lq_k+ \sum_{l,k=1}^NE^y_{ilkj}q_l\dot{q}_k]_{i,j=1,\cdots,N}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-63c07599e604e03960db7edf1826a3e9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{D_{qp}=[\sum_{l,k=1}^NL^y_{ilkj}q_lp_k+\sum_{l,k=1}^NM^y_{ilkj}q_l\dot{p}_k]_{i,j=1,\cdots,N}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a47703d3ab98482bab2ab02647edf0e5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{D_{pq}=[\displaystyle\sum_{l,k=1}^NL^z_{ilkj}p_lq_k+\displaystyle\sum_{l,k=1}^NM^z_{ilkj}p_l\dot{q}_k]_{i,j=1,\cdots,N} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8ba846dda9b4e1a20fd16e8372ee42dc_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{D_{pp}=[c^z_{ij} + \displaystyle\sum_{l,k=1}^ND^z_{ilkj}p_lp_k+ \displaystyle\sum_{l,k=1}^NE^z_{ilkj}p_l\dot{p}_k]_{i,j=1,\cdots,N} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4854e88835c91a0efcbc614ad5179dff_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{K_{qq}=[k^y_{ij} + \displaystyle\sum_{l,k=1}^NB^y_{ilkj}q_kq_l+ \displaystyle\sum_{l,k=1}^NH^y_{ilkj}p_kp_l]_{i,j=1,\cdots,N}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-040d1c3fd7a13639a6bdd6969cb3e672_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{K_{pp}=[k^z_{ij} + \displaystyle\sum_{l,k=1}^NB^z_{ilkj}p_kp_l+ \displaystyle\sum_{l,k=1}^NH^z_{ilkj}q_kq_l]_{i,j=1,\cdots,N}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ef8cb395af4a7622a53810a8bebb9a74_l3.png)