1次系の時間応答…Homework
[1] 次の1入力1出力1次系の状態空間表現を考えます。
![]()
これから、1次系の時間応答の表現式
![]()
を得ます(Note A02-1参照)。ここで、インパルス応答と呼ばれる
![]()
を定義しますと、上式は
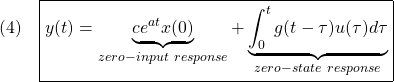
すなわち、1次系の時間応答は、零入力応答(第1項)と零状態応答(第2項)の和でとなります。
●実際、![]() 、
、![]() 、
、![]() について
について![]() を求めてみると次のグラフが得られます。
を求めてみると次のグラフが得られます。
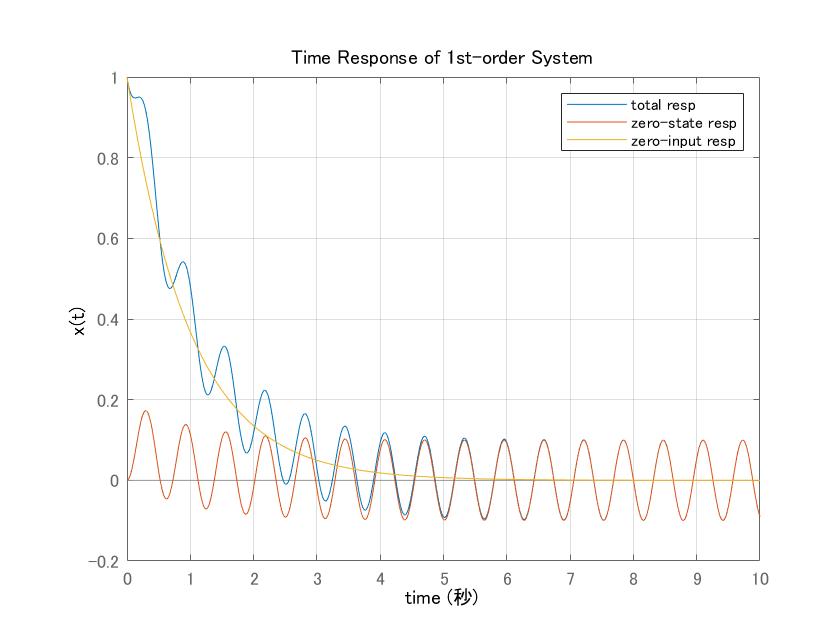
図1 どれが零状態応答か?
[2] (1)への入力![]() として次図の時間関数を考えます。
として次図の時間関数を考えます。
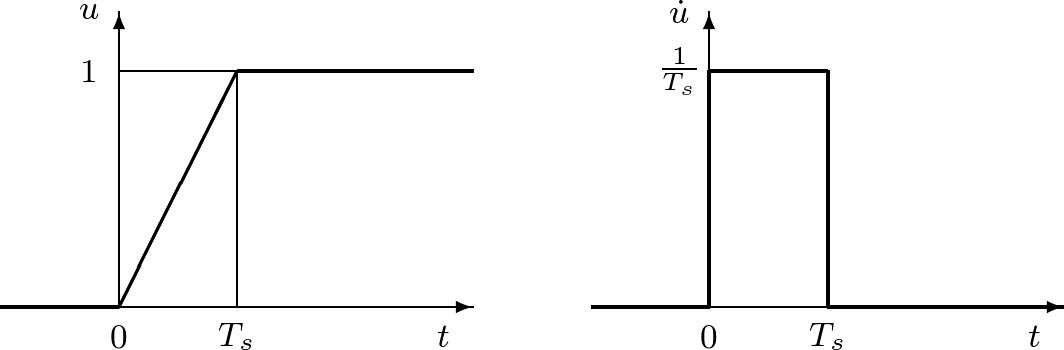
図2 ステップ入力とインパルス入力(![]() )
)
左図において![]() としたものがステップ入力、
としたものがステップ入力、
![]()
です。これを(2)に代入すると、
![]()
より、ステップ応答が次のように表されます。
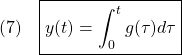
すなわち、インパルス応答を積分してステップ応答が得られます。逆に、ステップ応答を微分してインパルス応答が得られることも分かります。
図2の右図は左図の微分![]() を表していますが、
を表していますが、![]() としたものがインパルス入力(デルタ関数)です。実は(3)で定義したインパルス応答はこのインパルス入力に対する応答です。このことを理解するために、いま1次系の状態方程式を微分して
としたものがインパルス入力(デルタ関数)です。実は(3)で定義したインパルス応答はこのインパルス入力に対する応答です。このことを理解するために、いま1次系の状態方程式を微分して
![]()
を得ます。これは1次系に入力![]() を与えた場合の応答は
を与えた場合の応答は![]() であることを示しています。図2の左図で
であることを示しています。図2の左図で![]() としたステップ入力に対する応答がステップ応答です。図2の右図で
としたステップ入力に対する応答がステップ応答です。図2の右図で![]() としたインパルス入力はステップ入力の微分ですから、その応答はステップ応答の微分として得られ、インパルス応答となります。すなわち、ステップ応答を微分するとインパルス応答が得られることが分かります。
としたインパルス入力はステップ入力の微分ですから、その応答はステップ応答の微分として得られ、インパルス応答となります。すなわち、ステップ応答を微分するとインパルス応答が得られることが分かります。
[3] 特別な3種類の入力(ステップ入力、インパルス入力、正弦波入力)に対する零状態応答(ステップ応答、インパルス応答、正弦波応答)を考え、これらの相互関係を調べます。

図3 1次系の時間応答の相互関係
一般に、「システムを知る」ということは「どんな入力を与えられても出力を推測できる」ことを意味します。したがって、平衡状態(![]() )にある場合、インパルス応答さえ分かれば、畳み込み積分を行って出力(零状態応答)が計算できます。この意味で、インパルス応答は重要なのです。また、インパルス応答自体の計算は、
)にある場合、インパルス応答さえ分かれば、畳み込み積分を行って出力(零状態応答)が計算できます。この意味で、インパルス応答は重要なのです。また、インパルス応答自体の計算は、![]() としたときの零入力応答を求めて行います。ステップ応答が分かれば、これを微分してインパルス応答が分かります。また、インパルス応答をラプラス変換したものが、正弦波応答と密接に関係しています。このことはあとで詳しく述べます。
としたときの零入力応答を求めて行います。ステップ応答が分かれば、これを微分してインパルス応答が分かります。また、インパルス応答をラプラス変換したものが、正弦波応答と密接に関係しています。このことはあとで詳しく述べます。
[4] 次のようにパラメータライズされた漸近安定な1次系を考えます。![]() 、
、![]() はそれぞれ時定数、定常ゲインと呼ばれます。
はそれぞれ時定数、定常ゲインと呼ばれます。
![]()
このインパルス応答は次式で与えられます。
![]()
これを積分して
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad y(t)=\frac{K}{T}\int_0^te^{-\frac{1}{T}\tau}d\tau=\frac{K}{T}\left[\frac{e^{-\frac{1}{T}\tau}}{-\frac{1}{T}}\right]_0^t =-K(e^{-\frac{1}{T}t}-1)=K(1-e^{-\frac{1}{T}t}) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7bfde10f7b48435b229585a7aded9380_l3.png)
すなわちステップ応答は次式で表されます。
![]()
ここで、![]() のときは
のときは
![]()
となります。また、![]() での接線は
での接線は
![]()
ですから、![]() となります。この時定数
となります。この時定数![]() は、最終値
は、最終値![]() の63.2%まで到達する時間、または初期速度で到達した場合の時間(初期時刻における接線が
の63.2%まで到達する時間、または初期速度で到達した場合の時間(初期時刻における接線が![]() と交わる時刻)として特徴付けられます。
と交わる時刻)として特徴付けられます。
●実際、![]() 、
、![]() について、ステップ応答
について、ステップ応答![]() を求めてみると次のグラフが得られます。最終値
を求めてみると次のグラフが得られます。最終値![]() に到達する時間は大体
に到達する時間は大体![]() であることが分かります。
であることが分かります。
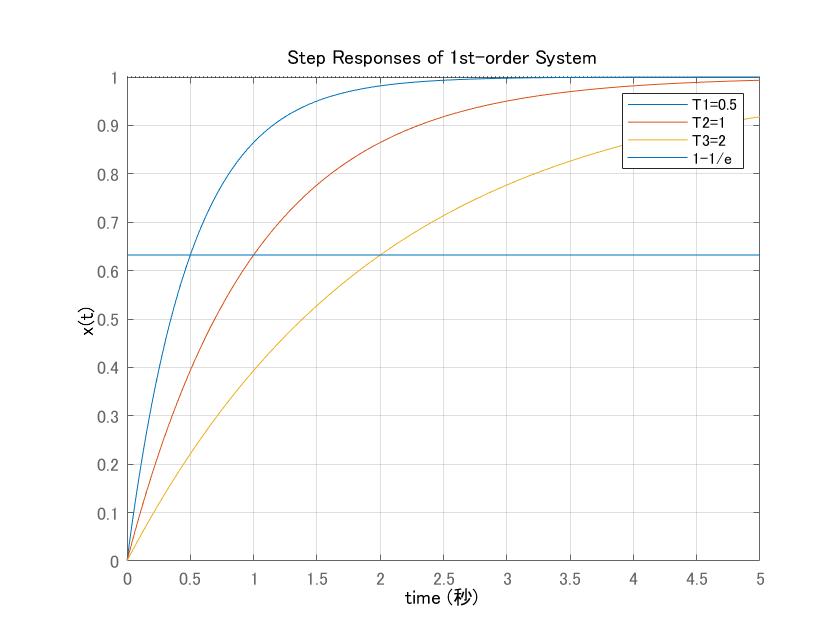
図4 1次系のステップ応答から時定数を求める補助線とは?
[5] 時定数は平衡状態に復帰する時間の目安にもなります。漸近安定な1次自由系を次のようにパラメータライズします。
![]()
この解は
![]()
ですから、![]() のときは
のときは
![]()
となります。また、![]() での接線は
での接線は
![]()
ですから、![]() となります。この時定数
となります。この時定数![]() は、初期値の36.7%まで復帰する時間、または初期速度で復帰した場合の時間(初期時刻における接線が0と交わる時刻)として特徴付けられます。
は、初期値の36.7%まで復帰する時間、または初期速度で復帰した場合の時間(初期時刻における接線が0と交わる時刻)として特徴付けられます。
●実際、時刻![]() において平衡状態
において平衡状態![]() が乱され
が乱され![]() になったとし、
になったとし、![]() について
について![]() を求めてみると次のグラフが得られます。平衡状態に復帰する時間は大体
を求めてみると次のグラフが得られます。平衡状態に復帰する時間は大体![]() であることを表します。
であることを表します。
<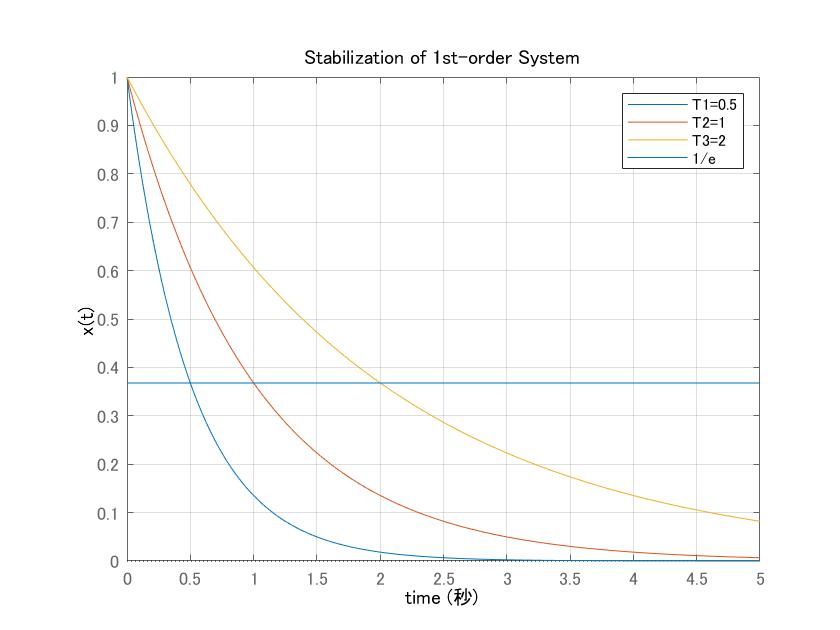
図5 1次自由系において平衡状態に復帰する時間(時定数)を定める補助線とは?
演習A02-1…Flipped Classroom
![]() 図1の時間応答を描くプログラムを作成せよ。
図1の時間応答を描くプログラムを作成せよ。
| MATLAB |
|
| SCILAB |
|
![]() 図4のステップ応答#1を描き、適当な補助線を引いて、交点の座標から時定数を求めるプログラムを作成せよ。
図4のステップ応答#1を描き、適当な補助線を引いて、交点の座標から時定数を求めるプログラムを作成せよ。
| MATLAB |
|
| SCILAB |
|
[6] 1次系(1)をラプラス変換(Note A02-3参照)して、![]() とすると(零状態応答を考えているので)
とすると(零状態応答を考えているので)
![]()
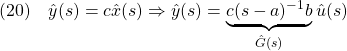
ここで現れた
![]()
を伝達関数と呼びます。伝達関数![]() に
に![]() を代入した
を代入した![]() を周波数伝達関数と呼び、正弦波入力に対する時間応答、すなわち周波数応答を特徴づけることができます。
を周波数伝達関数と呼び、正弦波入力に対する時間応答、すなわち周波数応答を特徴づけることができます。
●漸近安定な1次系(9)の伝達関数は次式で与えられます。
![]()
演習A02-2...Flipped Classroom
![]() 1次系のステップ応答を次式を逆ラプラス変換して求めなさい。
1次系のステップ応答を次式を逆ラプラス変換して求めなさい。
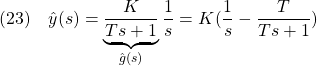
![]() 次のような無駄時間と呼ばれる特殊な入出力関係を考えます。
次のような無駄時間と呼ばれる特殊な入出力関係を考えます。
![]()
これをラプラス変換して無駄時間の伝達関数は次式をとなることを示しなさい。
![]()
ヒント:
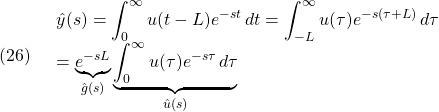
[7] 漸近安定な1次系(9)を考えます。正弦波入力に対する零状態応答すなわち周波数応答は、Note A02-2を参照して
![]()
ここで、![]() とすると
とすると
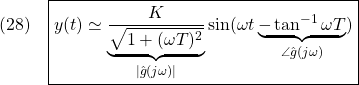
ただし
![]()
これは、入力が正弦波のときは、時間が十分立てば、出力も正弦波となることを示しています。その振幅と位相はそれぞれ![]() の絶対値と偏角となっています。
の絶対値と偏角となっています。
![]() をゲイン、
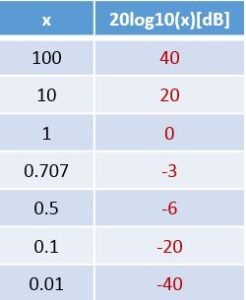
をゲイン、![]() を位相と呼びます。このゲイン線図と位相線図をペアにして片対数グラフにプロットしたものをボード線図と呼びます。ゲインはdb値(
を位相と呼びます。このゲイン線図と位相線図をペアにして片対数グラフにプロットしたものをボード線図と呼びます。ゲインはdb値(![]() )、位相はdeg値(
)、位相はdeg値(![]() )です。
)です。
●実際、![]() について、ボード線図を描いてみると次のグラフが得られます
について、ボード線図を描いてみると次のグラフが得られます

図6 1次系のボード線図から時定数を求める補助線とは?
ちなみに
![]()
を満足する![]() は
は
![]()
となり、帯域幅と呼びます。実際、上図で-3dBの水平線との交点が![]() であることが確かめられます。
であることが確かめられます。
演習A02-3...Flipped Classroom
![]() 図1のゲイン曲線#1を描き、3dB下がる点の座をマウスをクリックして取得し、時定数を求めるプログラムを作成せよ。
図1のゲイン曲線#1を描き、3dB下がる点の座をマウスをクリックして取得し、時定数を求めるプログラムを作成せよ。
| MATLAB |
|
| SCILAB |
|
Note A02-1 状態方程式の解
●(1次自由系を表す)微分方程式
![]()
の解は
![]()
と表されます。これが解であることは元の微分方程式に代入すればすぐに確かめられ、また次のようにして導くことができます。
元の微分方程式を
![]()
と書いて、左から積分因数と呼ばれる![]() をかけると
をかけると
![]()
すなわち
![]()
したがって、![]() を定数として
を定数として
![]()
ここで、![]() とおくと
とおくと![]() は初期値
は初期値![]() に等しいので
に等しいので
![]()
と表されます。
●(1次系の状態方程式を表す)微分方程式
![]()
の解を求めてみます。上と同様にして
![]()
までは問題ないと思います。これを![]() から
から![]() まで積分して
まで積分して
![]()
すなわち
![]()
したがって
![]()
ここで、![]() を
を![]() に、
に、![]() を
を![]() と置き換えれば
と置き換えれば
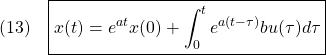
が得られます。
Note A02-2 正弦波応答
(1次系の状態方程式を表す)微分方程式
![]()
に対して、正弦波入力
![]()
に対する解を求めます。これは公式
![]()
を用いて、次のように得られます。
![Rendered by QuickLaTeX.com (4)\quad \begin{array}{l} \displaystyle{x(t)=\int_0^te^{a(t-\tau)}b \sin\omega\tau\,d\tau=e^{at}b\int_0^te^{-a\tau} \sin\omega\tau\,d\tau}\\ \displaystyle{=e^{at}b\left[\frac{e^{-a\tau}}{a^2+\omega^2}(-a\sin\omega\tau-\omega\cos\omega\tau)\right]_0^t}\\ \displaystyle{=\frac{e^{at}b}{a^2+\omega^2}(e^{-at}(-a\sin\omega t-\omega\cos\omega t)+\omega)}\\ \displaystyle{=\frac{b}{\sqrt{a^2+\omega^2}}(\sin\omega t\frac{-a}{\sqrt{a^2+\omega^2}}-\cos\omega t\frac{\omega}{\sqrt{a^2+\omega^2}}+e^{+at}\frac{\omega}{\sqrt{a^2+\omega^2}})}\\ \displaystyle{=\frac{b}{\sqrt{a^2+\omega^2}}(\sin\omega t\cos\theta-\cos\omega t\sin\theta+e^{+at}\sin\theta)}\\ \displaystyle{=\frac{b}{\sqrt{a^2+\omega^2}}(\sin(\omega t-\theta)+e^{+at}\sin\theta)\quad (\theta=\tan^{-1}\frac{\omega}{-a})}\\ \displaystyle{=\frac{b}{\sqrt{a^2+\omega^2}}(\sin(\omega t+\phi)-e^{+at}\sin\phi)\quad (\phi=-\theta)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ed887e5a02609da72f9c770b930e0a48_l3.png)
Note A02-3 ラプラス変換
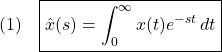
時間関数![]() のラプラス変換は次式によって定義されます。
のラプラス変換は次式によって定義されます。
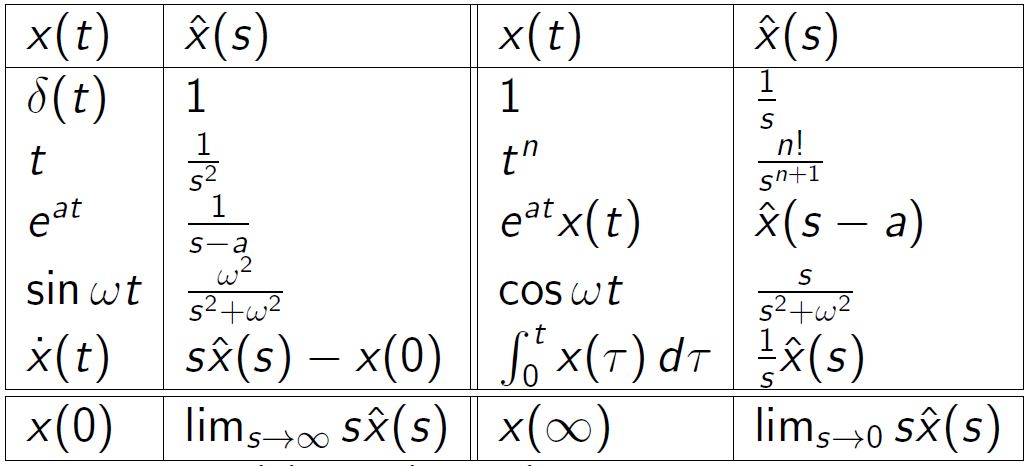
Note A02-4 dB値 ![]()