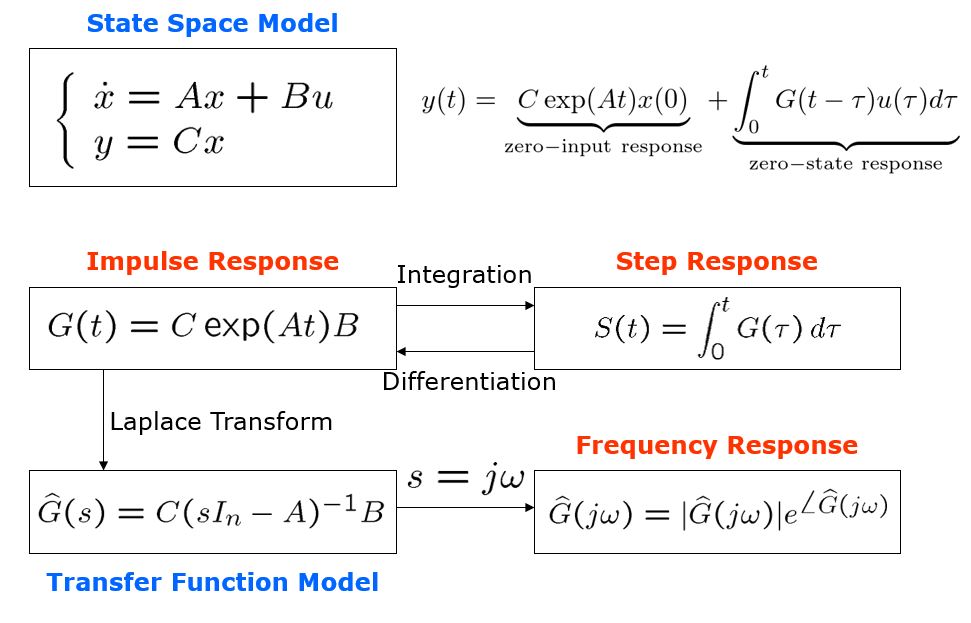
| MATLAB |
%sf_syn_lmi6.m
%-----
clear all, close all
A=[0 1;-1 -2*0.01]; B1=[0;1]; B2=B1;
C1=[1 0;0 0]; D11=[0;0]; D12=[0;1];
[n,m]=size(B2);
%-----
setlmis([]);
gam=lmivar(1,[1 0]);
Y=lmivar(1,[n 1]);
Z=lmivar(2,[m n]);
%-----
lmi1=newlmi;
lmiterm([lmi1,1,1,Y],A,1,'s'); %#1:A*Y+Y*A'
lmiterm([lmi1,1,1,Z],-B2,1,'s'); %#1:-(B2*Z+Z*B2')
lmiterm([lmi1,1,2,0],B1); %#1:B1
lmiterm([lmi1,2,2,gam],-1,1); %#1:-gam
lmiterm([lmi1,3,1,Y],C1,1); %#1:C1*Y
lmiterm([lmi1,3,1,Z],-D12,1); %#1:D12*Z
lmiterm([lmi1,3,2,0],D11); %#1:D11
lmiterm([lmi1,3,3,gam],-1,1); %#1:-gam
%-----
alpha=0.1;
lmi2=newlmi;
lmiterm([lmi2,1,1,Y],A,1,'s'); %#2:A*Y+Y*A'
lmiterm([lmi2,1,1,Z],-B2,1,'s'); %#2:-(B2*Z+Z'*B2')
lmiterm([lmi2,1,1,Y],2*alpha,1); %#2:2*alpha*Y
%-----
r=2;
lmi3=newlmi;
lmiterm([lmi3,1,1,Y],-r,1); %#3:-r*Y
lmiterm([lmi3,1,2,Y],A,1); %#3:A*Y
lmiterm([lmi3,1,2,Z],-B2,1); %#3:-B2*Z
lmiterm([lmi3,2,2,Y],-r,1); %#3:-r*Y
%-----
theta=pi/4; sth=sin(theta); cth=cos(theta);
lmi4=newlmi;
lmiterm([lmi4,1,1,Y],sth*A,1,'s'); %#4:sth*(A*Y+Y*A')
lmiterm([lmi4,1,1,Z],-sth*B2,1,'s');%#4:-sth*(B2*Z+Z'*B2')
lmiterm([lmi4,1,2,Y],cth*A,1); %#4:cth*A*Y
lmiterm([lmi4,1,2,Y],1,-cth*A'); %#4:-cth*Y*A'
lmiterm([lmi4,1,2,Z],-cth*B2,1); %#4:-cth*B2*Z
lmiterm([lmi4,1,2,-Z],1,cth*B2'); %#4:cth*Z'*B2'
lmiterm([lmi4,2,2,Y],sth*A,1,'s'); %#4:sth*(A*Y+Y*A')
lmiterm([lmi4,2,2,Z],-sth*B2,1,'s');%#4:-sth*(B2*Z+Z'*B2')
%-----
lmi5=newlmi;
lmiterm([-lmi5,1,1,Y],1,1); %#5:Y
%-----
lmi6=newlmi;
lmiterm([lmi6,1,1,gam],1,1); %#6:gam
lmiterm([-lmi6,1,1,0],1e3); %#6:1000
%-----
LMIs=getlmis;
cobj=zeros(1,decnbr(LMIs));
cobj(1)=1;
[cost,xopt]=mincx(LMIs,cobj);
gopt=dec2mat(LMIs,xopt,gam);
Y=dec2mat(LMIs,xopt,Y);
Z=dec2mat(LMIs,xopt,Z);
F=Z/Y;
%-----
pl=eig(A-B2*F)
close all,figure(1)
dregion(alpha,0,r,theta,r*[-1,1,-1,1])
plot(real(pl),imag(pl),'*')
figure(2)
ol=ltisys(A,B1,C1,D11);
cl=ltisys(A-B2*F,B1,C1-D12*F,D11);
om=logspace(-2,2,200);
splot(ssub(cl,1,1),'sv',om),hold on
splot(ssub(ol,1,1),'sv',om),grid
%-----
%eof
|
![]() 次系
次系![]() の
の![]() ノルムが
ノルムが![]() より小となるためのLMI条件は、次の通りでした。
より小となるためのLMI条件は、次の通りでした。![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \displaystyle{{\rm tr} (CW_cC^T)<\gamma^2\quad(W_c=\int_0^\infty \exp(At)BB^T\exp(A^Tt)dt)}\\\\ \displaystyle{\Leftrightarrow \exists X_c>0,\ Q_c>0:\\ \left[\begin{array}{cc} A^TX_c+X_cA & X_cB \\ B^TX_c & -I \end{array}\right]<0,\ \left[\begin{array}{cc} X_c & C^T \\ C & Q_c \end{array}\right]>0,\ {\rm tr}(Q_c)<\gamma^2}\\\\ \displaystyle{\Leftrightarrow \exists Y_c>0,\ Q_c>0:\\ \left[\begin{array}{cc} Y_cA^T+AY_c & B \\ B^T & -I \end{array}\right]<0,\ \left[\begin{array}{cc} Y_c & Y_cC^T \\ CY_c & Q_c \end{array}\right]>0,\ {\rm tr}(Q_c)<\gamma^2} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4740750e1fdf8093b1f6322284a78a12_l3.png)
![]() 次系を考えます。
次系を考えます。![Rendered by QuickLaTeX.com \displaystyle{(2)\quad P: \left\{\begin{array}{l} \dot{x}=Ax+B_1u_1+B_2u_2 \\ \underbrace{ \left[\begin{array}{c} y\\ u \end{array}\right] }_{y_1} = \underbrace{ \left[\begin{array}{c} C\\ 0 \end{array}\right] }_{C_1} x+ \underbrace{ \left[\begin{array}{c} 0\\ 0 \end{array}\right] }_{D_{11}}u_1+ \underbrace{ \left[\begin{array}{c} 0\\ I \end{array}\right] }_{D_{12}} u_2 \\ y_2=x \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-233587c7d6ac6840b26399b32d7f5ae2_l3.png)
![]()
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad P_{CL}: \left\{\begin{array}{l} \dot{x}=\underbrace{(A-B_2F)}_{A_{CL}}x+\underbrace{B_1}_{B_{CL}}u_1 \\ y_1= \underbrace{ \left[\begin{array}{c} C\\ -F \end{array}\right] }_{C_{CL}=C_1-D_{12}F} x \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1cff650bf6e54c686a46b654002f41e1_l3.png)
![]() ノルムが
ノルムが![]() より小、すなわち
より小、すなわち![]()
![]() を求める問題を考えます。
を求める問題を考えます。![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \begin{array}{l} \exists Y_{CL}>0,\ Q>0:\\ \left[\begin{array}{cc} Y_{CL}A_{CL}^T+A_{CL}Y_{CL} & B_{CL} \\ B_{CL}^T & -I \end{array}\right]<0,\\ \left[\begin{array}{cc} Y_{CL} & Y_{CL}C_{CL}^T \\ C_{CL}Y_{CL} & Q \end{array}\right]>0,\\ {\rm tr}(Q)<\gamma^2 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1f42fdc63af549cb6cd701aa40eac0f7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \displaystyle{\exists Y>0,\ Q>0:\\ \left[\begin{array}{cc} Y(A-B_2F)^T+(A-B_2F)Y & B_1 \\ B_1^T & -I \end{array}\right]<0,\\ \left[\begin{array}{cc} Y & Y(C_1-D_{12}F)^T \\ (C_1-D_{12}F)Y & Q \end{array}\right]>0,\\ {\rm tr}(Q)<\gamma^2} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-90a3259c718f1035238e2463a6c5aa42_l3.png)
![]() を行うと、次のような
を行うと、次のような![]() と
と![]() に関するLMIとなります。
に関するLMIとなります。![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \displaystyle{\exists Y>0,\ Q>0:\\ \left[\begin{array}{cc} (AY-B_2Z)^T+AY-B_2Z & B_1 \\ B_1^T & -I \end{array}\right]<0,\\ \left[\begin{array}{cc} Y & (C_1Y-D_{12}Z)^T \\ C_1Y-D_{12}Z & Q \end{array}\right]>0,\\ {\rm tr}(Q)<\gamma^2} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6b9dad597d2aabf8ef8c277abdacbf55_l3.png)
![]() と
と![]() を求め、次式によって状態フィードバックゲインを決定します。
を求め、次式によって状態フィードバックゲインを決定します。![]()
![]() 次のコードを参考にして、
次のコードを参考にして、![]() 制御(状態FB)を求める関数を作成せよ。
制御(状態FB)を求める関数を作成せよ。![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \begin{array}{lll} && \sup_{\omega\in{\rm\bf R}}||\hat{G}(j\omega)||_2<\gamma \nonumber\\ &\Leftrightarrow& \exists X>0:\ \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma I & D^T \\ C & D & -\gamma I \end{array}\right]<0 \nonumber\\ &\Leftrightarrow& \exists Y>0:\ \left[\begin{array}{ccc} YA^T+AY & B & YC^T \\ B^T & -\gamma I & D^T \\ CY & D & -\gamma I \end{array}\right]<0\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fabe9aa11942205106ce125d21aa0bd2_l3.png)

![Rendered by QuickLaTeX.com \displaystyle{(17)\quad P: \left\{\begin{array}{l} \dot{x}=Ax+B_1u_1+B_2u_2 \\ \underbrace{ \left[\begin{array}{c} y\\ u \end{array}\right] }_{y_1} = \underbrace{ \left[\begin{array}{c} C\\ 0 \end{array}\right] }_{C_1} x+ \underbrace{ \left[\begin{array}{c} 0\\ 0 \end{array}\right] }_{D_{11}}u_1+ \underbrace{ \left[\begin{array}{c} 0\\ I \end{array}\right] }_{D_{12}} u_2 \\ y_2=x \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-27beeceac3c340d1c4c8c1eccb769f14_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{()\quad P_{CL}: \left\{\begin{array}{l} \dot{x}=(A-B_2F)x+B_1u_1 \\ y_1= \underbrace{ \left[\begin{array}{c} C\\ -F \end{array}\right] }_{C_1-D_{12}F} x \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9e9c5bf547f30fa45ba83bf020767e9d_l3.png)
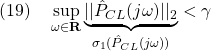
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{ccc} Y(A-B_2F)^T+(A-B_2F)Y & B_1 & Y(C_1-D_{12}F)^T \\ B_1^T & -\gamma I & D_{11}^T \\ (C_1-D_{12}F)Y & D_{11} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d53dc9e62d6af5b4cfc839c93b6d9673_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{ccc} (AY-B_2Z)^T+AY-B_2Z & B_1 & (C_1Y-D_{12}Z)^T \\ B_1^T & -\gamma I & D_{11}^T \\ C_1Y-D_{12}Z & D_{11} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f6a8dc294019aa496f62b9b21da1f984_l3.png)
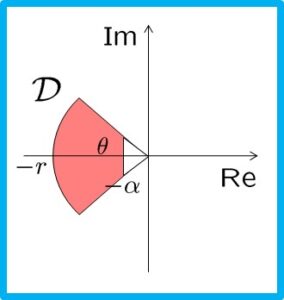
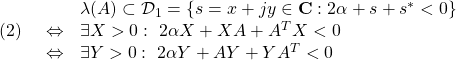
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \begin{array}{lll} &&\lambda(A)\subset {\cal D}_2=\{s=x+jy\in{\rm\bf C}: \left[\begin{array}{cc} -r & s \\ s^* & -r \end{array}\right] <0 \}\nonumber\\ &\Leftrightarrow& \exists X>0:\ \left[\begin{array}{cc} -rX & XA \\ A^TX & -rX \end{array}\right]<0 \nonumber\\ &\Leftrightarrow& \exists Y>0:\ \left[\begin{array}{cc} -rY & AY \\ YA^T & -rY \end{array}\right]<0\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9cde02783168cc87d584fcf28eb7011a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10) \begin{array}{lll} &&\lambda(A)\subset {\cal D}_3=\{s=x+jy\in{\rm\bf C}:\\ && \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]s + \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]^Ts^* <0 \}\nonumber\\ &&\Leftrightarrow \exists X>0:\ \left[\begin{array}{cc} \sin\theta(XA+A^TX) & \cos\theta(XA-A^TX) \\ -\cos\theta(XA-A^TX) & \sin\theta(XA+A^TX) \end{array}\right] <0 \nonumber\\ &&\Leftrightarrow \exists Y>0:\ \left[\begin{array}{cc} \sin\theta(AY+YA^T) & \cos\theta(AY-YA^T) \\ -\cos\theta(AY-YA^T) & \sin\theta(AY+YA^T) \end{array}\right] <0\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8ec7176d7e1ba9918e55f2d0c7c092ce_l3.png)

![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{l} \displaystyle{{\rm tr} (CW_cC^T)<\gamma^2}\\\\ \displaystyle{\Leftrightarrow \exists X_c>0,\ Q_c>0:\\ (1a)\quad\left[\begin{array}{cc} A^TX_c+X_cA & X_cB \\ B^TX_c & -I \end{array}\right]<0,\ \left[\begin{array}{cc} X_c & C^T \\ C & Q_c \end{array}\right]>0,\ {\rm tr}(Q_c)<\gamma^2}\\\\ \displaystyle{\Leftrightarrow \exists Y_c>0,\ Q_c>0:\\ (1b)\quad \left[\begin{array}{cc} Y_cA^T+AY_c & Y_cB \\ B^TY_c & -I \end{array}\right]<0,\ \left[\begin{array}{cc} Y_c & Y_cC^T \\ CY_c & Q_c \end{array}\right]>0,\ {\rm tr}(Q_c)<\gamma^2} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0e5eb15733d3b5cec658dab7afe757d6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{l} \displaystyle{{\rm tr} (B^TW_oB)<\gamma^2}\\\\ \displaystyle{\Leftrightarrow \exists X_o>0,\ Q_o>0:\\ (2a)\quad\left[\begin{array}{cc} AX_o+X_oA^T & X_oC^T \\ CX_o & -I \end{array}\right]<0,\ \left[\begin{array}{cc} X_o & B \\ B^T & Q_o \end{array}\right]>0,\ {\rm tr}(Q_o)<\gamma^2}\\\\ \displaystyle{\Leftrightarrow \exists Y_o>0,\ Q_o>0:\\ (2b)\quad\left[\begin{array}{cc} Y_oA+A^TY_o & Y_oC^T \\ CY_o & -I \end{array}\right]<0,\ \left[\begin{array}{cc} Y_o & Y_oB \\ B^TY_o & Q_o \end{array}\right]>0,\ {\rm tr}(Q_o)<\gamma^2} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0103a79b019093fcbd4360479821e521_l3.png)
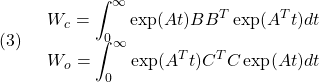
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} A^TX_c+X_cA+X_cBB^TX_c<0 \Leftrightarrow\ \left[\begin{array}{cc} A^TX_c+X_cA & X_cB \\ B^TX_c & -I \end{array}\right]<0 \\ AX_o+X_oA^T+X_oC^TCX_o<0 \Leftrightarrow\ \left[\begin{array}{cc} AX_o+X_oA^T & X_oC^T \\ CX_o & -I \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1eab031b7ca8535cebc0a481a954f426_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} {\rm tr} (CW_cC^T)<\gamma^2 \Leftrightarrow\ \left[\begin{array}{cc} X_c & C^T \\ C & Q_c \end{array}\right]>0,\ {\rm tr} (Q_c)<\gamma^2\\ {\rm tr} (B^TW_oB)<\gamma^2 \Leftrightarrow\ \left[\begin{array}{cc} X_o & B \\ B^T & Q_o \end{array}\right]>0,\ {\rm tr} (Q_o)<\gamma^2 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-94628f5f4d3a01a84d931ae427db5b3c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} CX_c^{-1}C^T-(CW_cC^T+\epsilon I)>0 \Leftrightarrow\ \left[\begin{array}{cc} X_c & C^T \\ C & CW_cC^T+\epsilon I \end{array}\right]>0\\ B^TX_o^{-1}B-(B^TW_oB+\epsilon I)>0 \Leftrightarrow\ \left[\begin{array}{cc} X_o & B \\ B^T & B^TW_oB+\epsilon I \end{array}\right]>0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a8a8eeaf32331b7bc67b6cdb89a3f7cc_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{\boxed{ \begin{array}{lll} && \left[\begin{array}{cc} P & M \\ M^T & Q \end{array}\right]<0\\ &\Leftrightarrow& P-MQ^{-1}M^T<0,\ Q<0\\ &\Leftrightarrow& P<0,\ Q-M^TP^{-1}M<0 \end{array} }}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4efd2df144b4ea2e4b5c0dd6970ed0ac_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{\boxed{ \begin{array}{lll} && \left[\begin{array}{cc} P & M \\ M^T & Q \end{array}\right]>0\\ &\Leftrightarrow& MQ^{-1}M^T-P>0,\ Q>0\\ &\Leftrightarrow& P>0,\ M^TP^{-1}M-Q>0 \end{array} }}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ff8466bc18b10c46d2a1973fde841fb2_l3.png)

![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \displaystyle{\sup_{u\in{\cal L}_2}\frac{||y(t)||_2}{||u(t)||_2} =\sup_{\omega\in{\rm\bf R}}||\hat{G}(j\omega)||_2<\gamma} \\ \displaystyle{\Leftrightarrow \exists X>0:\ \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D & -I \end{array}\right]<0} \\ \displaystyle{\Leftrightarrow \exists Y>0:\ \left[\begin{array}{ccc} YA^T+AY & B & YC^T \\ B^T & -\gamma^2 I & D^T \\ CY & D & -I \end{array}\right]<0} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cb76514d96e7c4115d9ea88e02ad0651_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \begin{array}{l} \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D &-I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{cc} A^TX+XA & XB \\ B^TX & -\gamma^2 I \end{array}\right] - \left[\begin{array}{cc} C^T\\ D^T \end{array}\right] (-I) %(-\gamma^{-1} I) \left[\begin{array}{cc} C & D \end{array}\right] <0 \\ \Leftrightarrow \left[\begin{array}{cc} A^TX+XA & XB \\ B^TX & 0 \end{array}\right] < \left[\begin{array}{cc} C^T & 0 \\ D^T & I \end{array}\right] \left[\begin{array}{cc} -I & 0 \\ 0 & \gamma^2 I \end{array}\right] \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5c2560cc668d6d0690878b8eedd8885c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \begin{array}{l} \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D & - I \end{array}\right]<0 \\ &\Leftrightarrow \forall \left[\begin{array}{c} x \\ u \end{array}\right]\ne0: \underbrace{ \left[\begin{array}{c} x \\ u \end{array}\right]^T \left[\begin{array}{cc} A^TX+XA & XB \\ B^TX & 0 \end{array}\right] \left[\begin{array}{c} x \\ u \end{array}\right] }_{\dot{V}(x)=\frac{d}{dt}(x^TXx)} \\ < \underbrace{ \left[\begin{array}{c} x \\ u \end{array}\right]^T \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right]^T \left[\begin{array}{cc} - I & 0 \\ 0 & \gamma^2 I \end{array}\right] \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right] \left[\begin{array}{c} x \\ u \end{array}\right] }_{s(u,y)=\gamma^2 u^Tu-y^Ty} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-474ab9036f2ca5939a3c709f1500ddf6_l3.png)
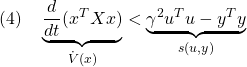
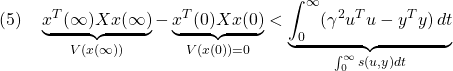
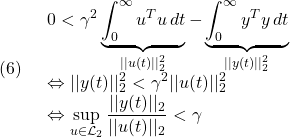
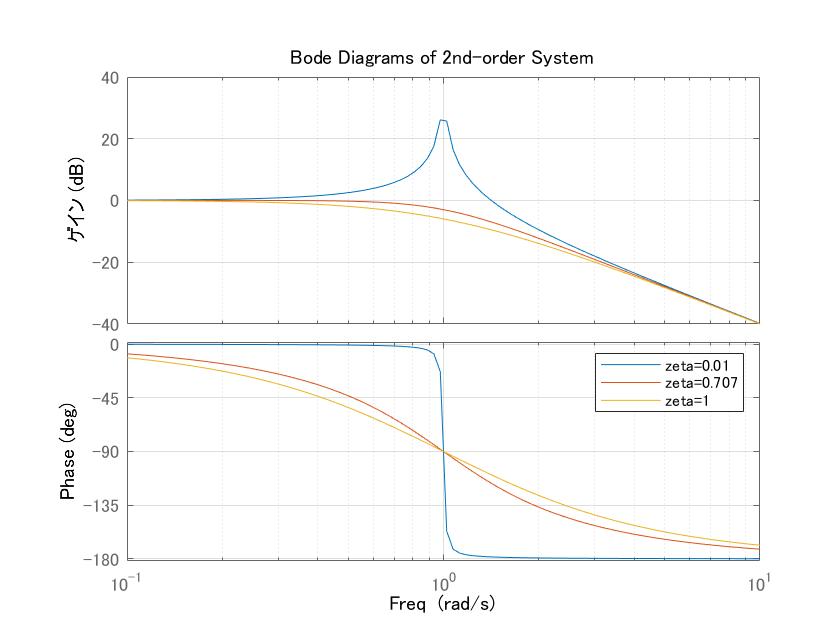
![Rendered by QuickLaTeX.com \displaystyle{(7) \begin{array}{l} \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D & -I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{ccc} A^TX+XA & X(B\sqrt{\gamma}) & (\frac{1}{\sqrt{\gamma}}C)^T \\ (B\sqrt{\gamma})^TX & - \gamma^2 I & D^T \\ (\frac{1}{\sqrt{\gamma}}C) & D & -I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{ccc} I & 0 & 0 \\ 0 & \sqrt{\gamma} I & 0 \\ 0 & 0 & \frac{1}{\sqrt{\gamma}} I \end{array}\right] \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma I & D^T \\ C & D &-\gamma I \end{array}\right] \left[\begin{array}{ccc} I & 0 & 0 \\ 0 & \sqrt{\gamma} I & 0 \\ 0 & 0 & \frac{1}{\sqrt{\gamma}} I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma I & D^T \\ C & D &-\gamma I \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9f78ef9deeaf1d5eba2e99bef8581c5e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \displaystyle{\sup_{u\in{\cal L}_2}\frac{||y(t)||_2}{||u(t)||_2} =\sup_{\omega\in{\rm\bf R}}||\hat{G}(j\omega)||_2<\gamma} \\ \displaystyle{\Leftrightarrow \exists X>0:\ \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma I & D^T \\ C & D & -\gamma I \end{array}\right]<0} \\ \displaystyle{\Leftrightarrow \exists Y>0:\ \left[\begin{array}{ccc} YA^T+AY & B & YC^T \\ B^T & -\gamma I & D^T \\ CY & D & -\gamma I \end{array}\right]<0} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0e630e89fa5b93c2df2468b74a26d002_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \boxed{\begin{array}{l} A= \underbrace{ \left[\begin{array}{cc} U_1 & U_2 \end{array}\right] }_{U(m\times m)} \underbrace{ \left[\begin{array}{cc} {\rm diag}\{\sigma_1,\cdots,\sigma_k\} & 0_{k\times (n-k)} \\ 0_{(m-k)\times k} & 0_{(m-k)\times (n-k)} \end{array}\right] }_{\Sigma= \left[\begin{array}{cc} \Sigma_1 & 0 \\ 0 & 0 \end{array}\right] \quad(\sigma_1\ge\cdots\ge\sigma_k) } \underbrace{ \left[\begin{array}{cc} V_1^T \\ V_2^T \end{array}\right] }_{V(n\times n)^T}\\ =U_1(m\times k)\Sigma_1(k\times k)V_1(n\times k)^T \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1a8bdd72019cbda663e2a40b3a70d3b6_l3.png)
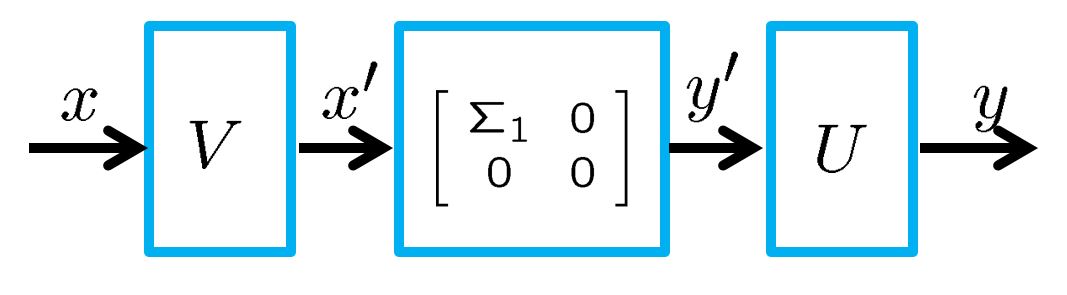 図3 特異値分解
図3 特異値分解
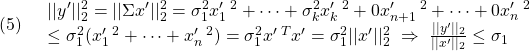
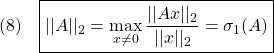
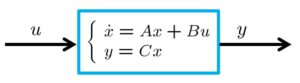
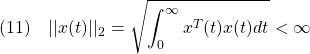
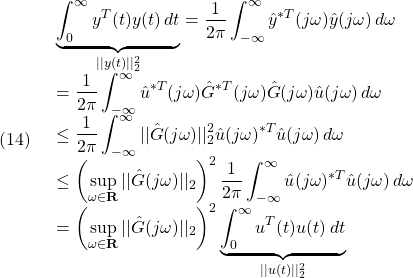
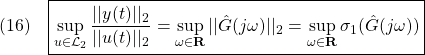

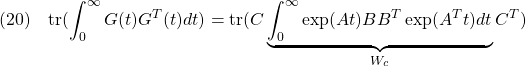
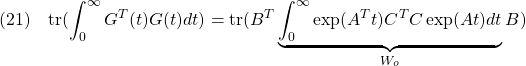
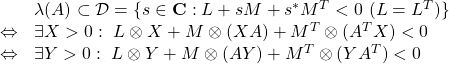
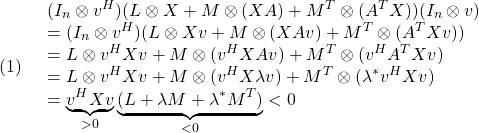
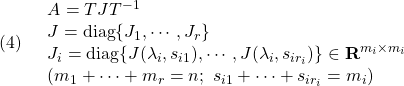
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad J(\lambda,k)=\left[\begin{array}{cccc} \lambda & 1 & & 0\\ 0 & \lambda & \ddots & \\ \vdots & \ddots & \ddots & 1 \\ 0 & \cdots & 0 & \lambda \end{array}\right]\in{\rm\bf R}^{k\times k} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ab96841e90e0d9dd55c8e1fbe6d37b58_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad T_\epsilon=\left[\begin{array}{cccc} 1 & 0 & \cdots & 0\\ 0 & \frac{1}{\epsilon} & \ddots & \vdots\\ \vdots & \ddots & \ddots & 0\\ 0 & \cdots & 0 & \frac{1}{\epsilon^{k-1}} \end{array}\right],\ T_\epsilon^{-1}=\left[\begin{array}{cccc} 1 & 0 & \cdots & 0\\ 0 & {\epsilon} & \ddots & \vdots\\ \vdots & \ddots & \ddots & 0\\ 0 & \cdots & 0 & {\epsilon^{k-1}} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-105301a3a42f7ab0eb9750acac26e2ce_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} T_\epsilon J(\lambda,k)T_\epsilon^{-1}\\ =T_\epsilon \left[\begin{array}{cccc} \lambda & 1 & & 0\\ 0 & \lambda & \ddots & \\ \vdots & \ddots & \ddots & 1 \\ 0 & \cdots & 0 & \lambda \end{array}\right] \left[\begin{array}{cccc} 1 & 0 & \cdots & 0\\ 0 & {\epsilon} & \ddots & \vdots\\ \vdots & \ddots & \ddots & 0\\ 0 & \cdots & 0 & {\epsilon^{k-1}} \end{array}\right]\\ =\left[\begin{array}{cccc} 1 & 0 & \cdots & 0\\ 0 & \frac{1}{\epsilon} & \ddots & \vdots\\ \vdots & \ddots & \ddots & 0\\ 0 & \cdots & 0 & \frac{1}{\epsilon^{k-1}} \end{array}\right] \left[\begin{array}{cccc} \lambda & \epsilon & & 0\\ 0 & \lambda\epsilon & \ddots & \\ \vdots & \ddots & \ddots & \epsilon^{k-1} \\ 0 & \cdots & 0 & \lambda\epsilon^{k-1} \end{array}\right]\\ =\left[\begin{array}{cccc} \lambda & \epsilon & & 0\\ 0 & \lambda & \ddots & \\ \vdots & \ddots & \ddots & \epsilon \\ 0 & \cdots & 0 & \lambda \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-517f70ee4d5a06e559e5f4be6fd4bd76_l3.png)
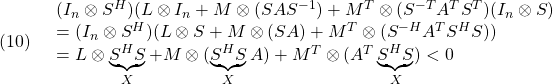

![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{lll} &&\lambda(A)\subset {\cal D}_3=\{s=x+jy\in{\rm\bf C}:\\ && \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]s + \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]^Ts^* <0 \}\nonumber\\ &&\Leftrightarrow \exists X>0:\ \left[\begin{array}{cc} \sin\theta(XA+A^TX) & \cos\theta(XA-A^TX) \\ -\cos\theta(XA-A^TX) & \sin\theta(XA+A^TX) \end{array}\right] <0 \nonumber\\ &&\Leftrightarrow \exists Y>0:\ \left[\begin{array}{cc} \sin\theta(AY+YA^T) & \cos\theta(AY-YA^T) \\ -\cos\theta(AY-YA^T) & \sin\theta(AY+YA^T) \end{array}\right] <0\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3b534e97017d8856b3ce56b56e0c3ab5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \begin{array}{lll} && \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]s + \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]^Ts^* <0 \nonumber\\ &\Leftrightarrow& \left[\begin{array}{cc} (s+s^*)\sin\theta & (s-s^*)\cos\theta \\ -(s-s^*)\cos\theta & (s+s^*)\sin\theta \end{array}\right] <0 \nonumber\\ &\Leftrightarrow& \left[\begin{array}{cc} 2x\sin\theta & 2jy\cos\theta \\ -2jy\cos\theta & 2x\sin\theta \end{array}\right] <0 \nonumber\\ &\Leftrightarrow& x\sin\theta-jy\cos\theta\frac{1}{x\sin\theta}(-j)y\cos\theta<0,\ x\sin\theta<0 \nonumber\\ &\Leftrightarrow& x^2\sin^2\theta-y^2\cos^2\theta>0,\ x<0 \nonumber\\ &\Leftrightarrow& \tan\theta>\frac{|y|}{-x},\ x<0 \nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0e18cdb9a2d398da5bbf4a4c180b6b22_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14) \begin{array}{lll} &&\left[\begin{array}{cc} v^{*T} & 0^{T}\\ 0^{T} & v^{*T} \end{array}\right] \left[\begin{array}{cc} \sin\theta(XA+A^TX) & \cos\theta(XA-A^TX) \\ -\cos\theta(XA-A^TX) & \sin\theta(XA+A^TX) \end{array}\right] \left[\begin{array}{cc} v & 0\\ 0 & v \end{array}\right] \nonumber\\ &=& \left[\begin{array}{cc} \sin\theta(v^{*T}X(\lambda v)+(\lambda^*v^{*T})Xv) & \cos\theta(v^{*T}X(\lambda v)-(\lambda^*v^{*T})Xv) \\ -\cos\theta(v^{*T}X(\lambda v)-(\lambda^*v^{*T})Xv) & \sin\theta(v^{*T}X(\lambda v)+(\lambda^*v^{*T})Xv) \end{array}\right] \nonumber\\ &=& \underbrace{ \left[\begin{array}{cc} (\lambda+\lambda^*)\sin\theta & (\lambda-\lambda^*)\cos\theta \\ -(\lambda-\lambda^*)\cos\theta & (\lambda+\lambda^*)\sin\theta \end{array}\right] }_{<0} \underbrace{v^{*T}Xv}_{>0}<0 \nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-285477ad44caf135647233332c329df5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(15) \begin{array}{lll} && \left[\begin{array}{cc} x_1^T & x_2^T \end{array}\right] \left[\begin{array}{cc} \sin\theta(XA+A^TX) & \cos\theta(XA-A^TX) \\ -\cos\theta(XA-A^TX) & \sin\theta(XA+A^TX) \end{array}\right] \left[\begin{array}{c} x_1\\ x_2 \end{array}\right] <0 \nonumber\\ &&\quad (\forall x_1,x_2\ne0)\nonumber\\ &\Leftrightarrow& \left[\begin{array}{cc} x_1^TX & x_2^TX \end{array}\right]\\ && \left[\begin{array}{cc} \sin\theta(AX^{-1}+X^{-1}A^T) & \cos\theta(AX^{-1}-X^{-1}A^T) \\ -\cos\theta(AX^{-1}-X^{-1}A^T) & \sin\theta(AX^{-1}+X^{-1}A^T) \end{array}\right] \left[\begin{array}{c} Xx_1\\ Xx_2 \end{array}\right] <0 \nonumber\\ &\Leftrightarrow& \left[\begin{array}{cc} y_1^T & y_2^T \end{array}\right] \left[\begin{array}{cc} \sin\theta(AY+YA^T) & \cos\theta(AY-YA^T) \\ -\cos\theta(AY-YA^T) & \sin\theta(AY+YA^T) \end{array}\right] \left[\begin{array}{c} y_1\\ y_2 \end{array}\right] <0 \nonumber\\ &&\quad (\forall y_1,y_2\ne0)\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-316c19f9344b2195c495883a36293683_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \begin{array}{lll} && \lambda(A)\subset {\cal D}={\cal D}_1\cap{\cal D}_2\cap{\cal D}_3\nonumber\\ &&\Leftrightarrow \exists X>0:\nonumber\\ & & \left\{\begin{array}{l} 2\alpha X+XA+A^TX<0 \\ \left[\begin{array}{cc} -rX & XA \\ A^TX & -rX \end{array}\right]<0 \\ \left[\begin{array}{cc} \sin\theta(XA+A^TX) & \cos\theta(XA-A^TX) \\ -\cos\theta(XA-A^TX) & \sin\theta(XA+A^TX) \end{array}\right] <0 \end{array}\right.\nonumber\\ &&\Leftrightarrow \exists Y>0:\nonumber\\ & & \left\{\begin{array}{l} 2\alpha Y+AY+YA^T<0 \\ \left[\begin{array}{cc} -rY & AY \\ YA^T & -rY \end{array}\right]<0 \\ \left[\begin{array}{cc} \sin\theta(AY+YA^T) & \cos\theta(AY-YA^T) \\ -\cos\theta(AY-YA^T) & \sin\theta(AY+YA^T) \end{array}\right] <0 \end{array}\right.\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a5629f5f3a111b24527162f90eb8cad4_l3.png)
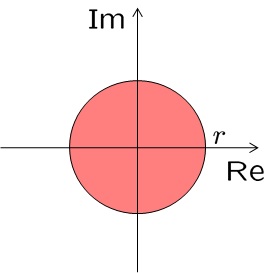
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{lll} &&\lambda(A)\subset {\cal D}_2=\{s=x+jy\in{\rm\bf C}: \left[\begin{array}{cc} -r & s \\ s^* & -r \end{array}\right] <0 \}\nonumber\\ &\Leftrightarrow& \exists X>0:\ \left[\begin{array}{cc} -rX & XA \\ A^TX & -rX \end{array}\right]<0 \nonumber\\ &\Leftrightarrow& \exists Y>0:\ \left[\begin{array}{cc} -rY & AY \\ YA^T & -rY \end{array}\right]<0\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5662d8b7c69301806b9c41c9e567c679_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \begin{array}{lll} && \left[\begin{array}{cc} -r & s \\ s^* & -r \end{array}\right]<0\\ &\Leftrightarrow& (-r)-s\frac{1}{(-r)}s^*<0,\ -r<0 \nonumber\\ &\Leftrightarrow& r^2-(x+jy)(x-jy)>0 \nonumber\\ &\Leftrightarrow& x^2+y^2<r^2 \nonumber\end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2a615e481d49cd65c7af58606dce9ebb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{lll} &&\left[\begin{array}{cc}v^{*T}&0^{T}\\0^{T}&v^{*T}\end{array}\right] \left[\begin{array}{cc}-rX&XA\\A^TX&-rX\end{array}\right] \left[\begin{array}{cc}v&0\\0&v\end{array}\right]\nonumber\\ &=& \left[\begin{array}{cc} -rv^{*T}Xv&v^{*T}X(\lambda v)\\ (\lambda^*v^{*T})Xv&-rv^{*T}Xv& \end{array}\right]\nonumber\\ &=& \underbrace{ \left[\begin{array}{cc} -r&\lambda\\\lambda^*&-r \end{array}\right] }_{<0} \underbrace{v^{*T}xv}_{>0}<0 \nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ee725f421be58c27c34f90905b890229_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{lll} && \left[\begin{array}{cc} x_1^T & x_2^T \end{array}\right] \left[\begin{array}{cc} -rX & XA \\ A^TX & -rX \end{array}\right] \left[\begin{array}{c} x_1\\ x_2 \end{array}\right] <0 \quad (\forall x_1,x_2\ne0)\nonumber\\ &\Leftrightarrow& \left[\begin{array}{cc} x_1^TX & x_2^TX \end{array}\right] \left[\begin{array}{cc} -rX^{-1} & AX^{-1} \\ X^{-1}A^T & -rX^{-1} \end{array}\right] \left[\begin{array}{c} Xx_1\\ Xx_2 \end{array}\right] <0 \nonumber\\ &\Leftrightarrow& \left[\begin{array}{cc} y_1^T & y_2^T \end{array}\right] \left[\begin{array}{cc} -rY & AY \\ YA^T & -rY \end{array}\right] \left[\begin{array}{c} y_1\\ y_2 \end{array}\right] <0 \quad (\forall y_1,y_2\ne0)\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c0fd523c8514218c28986c8a38f4dec1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \begin{array}{lll} &&\frac{x^2}{a^2}+\frac{y^2}{b^2}<1\Leftrightarrow\frac{(\frac{s+s^*}{2})^2}{a^2}+\frac{(\frac{s-s^*}{2j})^2}{b^2}<1 \\ &&\Leftrightarrow\ b^2(s+s^*)^2-a^2(s-s^*)^2<4a^2b^2\\ &&\Leftrightarrow\ (b(s+s^*)+a(s-s^*))(b(s+s^*)-a(s-s^*))<4a^2b^2 \\ &&\Leftrightarrow\ -4a^2b^2+((b+a)s+(b-a)s^*))((b-a)s+(b+a)s^*))<0 \\ &&\Leftrightarrow\ \left[\begin{array}{cc} -4a^2b^2 & (b+a)s+(b-a)s^* \\ (b-a)s+(b+a)s^* & -1 \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b25e3009225c1f9a4590486d7ac6c43d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(20)\quad \begin{array}{lll} &&\frac{x^2}{a^2}-\frac{y^2}{b^2}>1,\ x<-a\ \Leftrightarrow\ \frac{(\frac{s+s^*}{2})^2}{a^2}-\frac{(\frac{s-s^*}{2j})^2}{b^2}>1,\ \frac{s+s^*}{2}<-a}\\ &&\Leftrightarrow\ b^2(s+s^*)^2+a^2(s-s^*)^2>4a^2b^2,\ s+s^*+2a<0\\ &&\Leftrightarrow\ b^2(s+s^*+2a)(s+s^*-2a)+a^2(s-s^*)^2>0,\ s+s^*+2a<0\\ &&\Leftrightarrow\ b(s+s^*-2a)-\frac{-a^2(s-s^*)^2}{b(s+s^*+2a)}<0,b(s+s^*+2a)<0\\ &&\Leftrightarrow\ \left[\begin{array}{cc} b(s+s^*+2a) & a(s-s^*) \\ -a(s-s^*) & b(s+s^*-2a) \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-00ed2494a2b6bd5158edea1ece4fc648_l3.png)