状態フィードバック…Homework
[1] ある平衡状態周りの挙動が線形状態方程式
![]()
で表される制御対象に対して、状態フィードバック
![]()
を考えます。ここで、![]() を入力変数の個数、
を入力変数の個数、![]() を状態変数の個数とするとき、
を状態変数の個数とするとき、![]() はサイズ
はサイズ![]() のゲイン行列です。(2)を(1)に代入して、次式を得ます。
のゲイン行列です。(2)を(1)に代入して、次式を得ます。
![]()
以上の状況は次図のように図示されます。
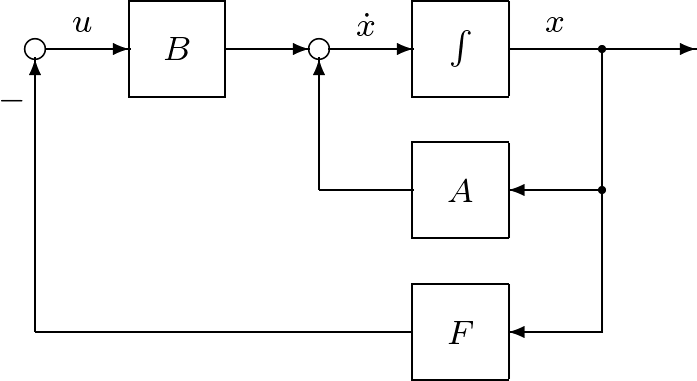 図1 状態フィードバックによる閉ループ系
図1 状態フィードバックによる閉ループ系
これは、制御対象とコントローラ(状態フィードバック)が閉路を構成することから、閉ループ系と呼ばれます。ここで、興味深いのは、制御対象が不安定であっても(行列![]() の固有値の一部が複素左半平面にあっても)、状態フィードバックを行って閉ループ系を構成すると、行列
の固有値の一部が複素左半平面にあっても)、状態フィードバックを行って閉ループ系を構成すると、行列![]() の固有値をすべて複素左半平面に移動させる可能性があることです。どのような条件の下で、どのようにゲイン行列
の固有値をすべて複素左半平面に移動させる可能性があることです。どのような条件の下で、どのようにゲイン行列![]() を決定できるかを検討する問題を状態フィードバックによる安定化問題と言います。
を決定できるかを検討する問題を状態フィードバックによる安定化問題と言います。
●状態フィードバックゲイン行列![]() を求めることは、適当な安定行列
を求めることは、適当な安定行列![]() を与えて、行列方程式
を与えて、行列方程式
![]()
を解くことに他なりません。よく学生さんは次のように解きます。
![]()
でも一般には![]() は正方行列ではないので、そもそも逆行列を考えることができません。
は正方行列ではないので、そもそも逆行列を考えることができません。![]() を安定行列とする状態フィードバックが求まる条件の説明は次節で行いますが、ここではその準備として、状態フィードバックゲイン行列
を安定行列とする状態フィードバックが求まる条件の説明は次節で行いますが、ここではその準備として、状態フィードバックゲイン行列![]() を求める公式を示します。
を求める公式を示します。
[2] いま行列![]() の特性多項式を次式で表します。
の特性多項式を次式で表します。
![]()
ケーリーハミルトンの定理から次式が成り立ちます。
![]()
これは![]() のとき、次のように書けます。
のとき、次のように書けます。
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} A_F^2+a_1'A_F+a_2'I_2=0\\ \quad\Downarrow\\ (A-BF)A_F+a_1'(A-BF)+a_2'I_2=0\\ \quad\Downarrow\\ AA_F-BFA_F+a_1'A-a_1'BF+a_2'I_2=0\\ \quad\Downarrow\\ A(A-BF)+a_1'A+a_2'I_2=BFA_F+a_1'BF\\ \quad\Downarrow\\ A^2+a_1'A+a_2'I_2=BF(A_F+a_1'I_2)+ABF\\ \quad\Downarrow\\ A^2+a_1'A+a_2'I_2=\left[\begin{array}{ccc} B &AB \end{array}\right] \left[\begin{array}{ccc} F(A_F+a_1'I_2)\\ F \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-58bb1c562247a773cc1edf865ae91cad_l3.png)
したがって、1入力系で![]() が正則ならば、次の公式を得ます。
が正則ならば、次の公式を得ます。
![]()
同様に、![]() のとき、次のように書けます。
のとき、次のように書けます。
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} A_F^3+a_1'A_F^2+a_2'A_F+a_3'I_3=0\\ \quad\Downarrow\\ (A-BF)(A_F^2+a_1'A_F+a_2'I_3)+a_3'I_3=0\\ \quad\Downarrow\\ A(A_F^2+a_1'A_F+a_2'I_3)+a_3'I_3\\=BF(A_F^2+a_1'A_F+a_2'I_3)\\ \quad\Downarrow\\ A((A-BF)A_F+a_1'(A-BF)+a_2'I_3)+a_3'I_3\\=BF(A_F^2+a_1'A_F+a_2'I_3)\\ \quad\Downarrow\\ A^2(A-BF)+a_1'A^2+a_2'A+a_3'I_3\\ =BF(A_F^2+a_1'A_F+a_2'I_3)+ABF(A_F+a_1'I_3)\\ \quad\Downarrow\\ A^3+a_1'A^2+a_2'A+a_3'I_3\\ =BF(A_F^2+a_1'A_F+a_2'I_3)+ABF(A_F+a_1'I_3)+A^2BF\\ \quad\Downarrow\\ A^3+a_1'A^2+a_2'A+a_3'I_3\\ =\left[\begin{array}{ccc} B &AB&A^2B \end{array}\right] \left[\begin{array}{ccc} F(A_F^2+a_1'A_F+a_2'I_3)\\ F(A_F+a_1'I_3)\\ F \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2e1d5f3518704a7eb5ccf03446662208_l3.png)
したがって、1入力系で![]() が正則ならば、次の公式を得ます。
が正則ならば、次の公式を得ます。
![]()
![]() の場合も同様にして、
の場合も同様にして、![]() の特性多項式(7)を
の特性多項式(7)を
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad %\begin{array}{l} A^n+a'_1A^{n-1}+\cdots+a'_nI_n =\left[\begin{array}{cccc} B & AB &\cdots & A^{n-1}B \end{array}\right] \left[\begin{array}{ccc} X_{n-1}\\ \vdots\\ X_1\\ F \end{array}\right] %\end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1a417bf647a9f2f3adebc7f2a80b6017_l3.png)
のように書き換えることができます。ここで、![]() はサイズ
はサイズ![]() の適当な行列です。したがって、1入力系で
の適当な行列です。したがって、1入力系で![]() が正則ならば、(12)の右辺の第2番目の行列の最下段にある
が正則ならば、(12)の右辺の第2番目の行列の最下段にある![]() を取りだすことにより、次の公式が得られます。
を取りだすことにより、次の公式が得られます。
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \boxed{\begin{array}{l} F= \left[\begin{array}{cccc} 0 & \cdots & 0 & 1 \end{array}\right] \left[\begin{array}{cccc} B & AB &\cdots & A^{n-1}B \end{array}\right]^{-1}\\ \times (A^n+a'_1A^{n-1}+\cdots+a'_nI_n) \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fec91a15818dbf1db1e87f86c46972c1_l3.png)
このように、1入力![]() 次系の場合は、
次系の場合は、![]() の
の![]() 個の要素が、
個の要素が、![]() の特性多項式の
の特性多項式の![]() 個の係数(すなわち
個の係数(すなわち![]() 個の固有値)を指定することにより決定されます。ところが
個の固有値)を指定することにより決定されます。ところが![]() 入力系の場合、
入力系の場合、![]() の固有値だけでは決まらず、対応する固有ベクトルまで指定する必要があります。このことを以下で調べてみます。
の固有値だけでは決まらず、対応する固有ベクトルまで指定する必要があります。このことを以下で調べてみます。
[3] いま、ジョルダン分解![]() を仮定して
を仮定して
![]()
ここで、![]() が対角行列の場合、
が対角行列の場合、![]() の固有値
の固有値![]() に対応する固有ベクトルを
に対応する固有ベクトルを![]() として
として
![]()
![]()
これより、もし![]() が
が![]() の固有値と一致しないならば、固有ベクトルの表現式として次式を得ます。
の固有値と一致しないならば、固有ベクトルの表現式として次式を得ます。
![]()
したがって、状態フィードバックゲイン行列![]() を求める次の手順が考えられます。
を求める次の手順が考えられます。
|
1) 2) 3) 次式で
|
この手順は簡潔ですが、1)の制約があること、2)の具体的な手法が不明であることなどの難点があります。状態フィードバックを定める手続きは、ある最適化問題の解として得ることが多く、これについてはあと説明します。
演習 A31…Flipped Classroom
![]() 次のコードを実行し、
次のコードを実行し、![]() の固有値を計算し、指定されているものになっていることを確かめよ。
の固有値を計算し、指定されているものになっていることを確かめよ。
| MATLAB |
|
![]() 次のコードを実行し、
次のコードを実行し、![]() の固有値と固有ベクトルを計算し、指定されているものになっていることを確かめよ。
の固有値と固有ベクトルを計算し、指定されているものになっていることを確かめよ。
| MATLAB |
|
Note A31 不可制御の例
どのような制御対象に対しても,閉ループ系を安定化する状態フィードバックが求まるわけではありません。たとえば、皆さんは小さいころ棒立て遊びをやった記憶があると思います。不安定なモノを安定化できた楽しい思い出だったと思います。それでは、2本の棒を同時に立てることはできたと思いますか?この状況を次図のように表します。

図 2本の棒立て制御
ここで、2本の棒の長さと質量をそれぞれ![]() と
と![]() とします。また鉛直線からの傾きを
とします。また鉛直線からの傾きを![]() とします。2本の棒は1つの軸に取り付けられており、自由に回転できるとします。この軸を左右に動かして回転トルクを与えるのですが、その結果として働くトルクをここでは
とします。2本の棒は1つの軸に取り付けられており、自由に回転できるとします。この軸を左右に動かして回転トルクを与えるのですが、その結果として働くトルクをここでは![]() で表します。このとき運動方程式は次式となります。ただし、
で表します。このとき運動方程式は次式となります。ただし、![]() 。
。
![]()
これから次の状態方程式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \begin{equation} \frac{d}{dt} \left[\begin{array}{c} \theta_1\\ \theta_2\\ \dot\theta_1\\ \dot\theta_2\\ \end{array}\right]= \left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ a_1 & 0 & 0 & 0\\ 0 & a_2 & 0 & 0\\ \end{array}\right] \left[\begin{array}{c} \theta_1\\ \theta_2\\ \dot\theta_1\\ \dot\theta_2\\ \end{array}\right]+ \left[\begin{array}{c} 0\\ 0\\ b_1\\ b_2\\ \end{array}\right]\tau }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3a3fa72bbe74de9a255bf87116b40789_l3.png)
ただし、![]() 、
、![]() 。
。
それでは、これを安定化する状態フィードバックゲインを求めてみます。上述の公式
![]()
を参照すれば、次の行列が正則である必要があります。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{equation} \left[\begin{array}{cccc} B & AB & A^2B & A^3B \end{array}\right] = \left[\begin{array}{cccc} 0 &b_1 &0 &a_1b_1\\ 0 &b_2 &0 &a_2b_2\\ b_1&0 &a_1b_1 &0\\ b_2&0 &a_2b_2 &0\\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c96e667021ae4a5a4f1f35e8b5fc078e_l3.png)
これは2つの棒の長さ違うときは正則となり、閉ループ系を安定化する状態フィードバックが求まります。ところが2つの棒が同じで、![]() となる場合は、第1行と第2行が同じとなり、第3行と第4行も同じとなり、正則性は失われます。これから全く同じ2本の棒の棒立ては成功しないと考えられます。これは「二兎を追うものは一兎も得ず」のことわざ通りですね。
となる場合は、第1行と第2行が同じとなり、第3行と第4行も同じとなり、正則性は失われます。これから全く同じ2本の棒の棒立ては成功しないと考えられます。これは「二兎を追うものは一兎も得ず」のことわざ通りですね。
![Rendered by QuickLaTeX.com \displaystyle{(1a)\quad \underbrace{ \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} 0 \\ K\omega_n^2 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2c38bce5a54dbe22b2c1cfbb9ac7882a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1b)\quad y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f5e291f6df4bf13c895efeb7714483d4_l3.png)
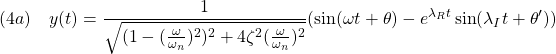
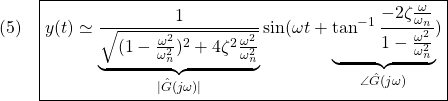
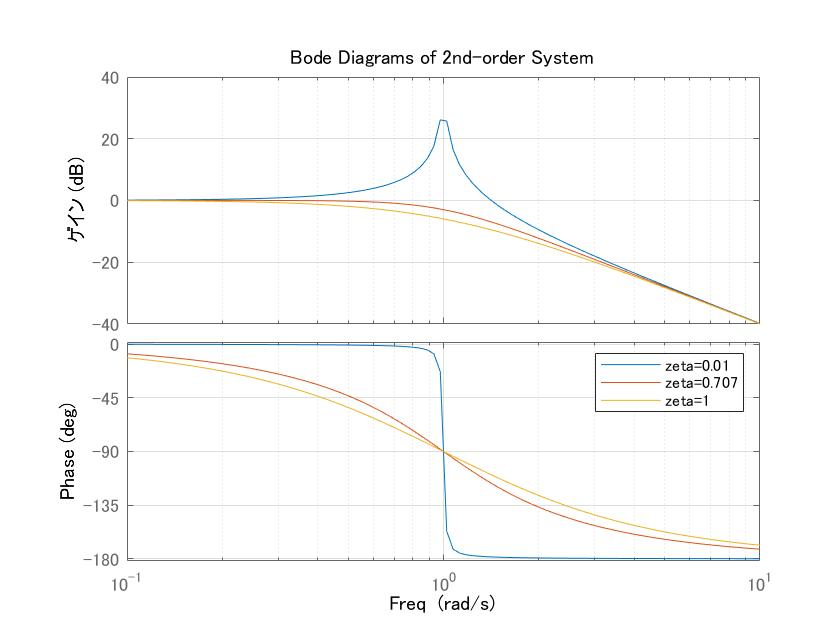 図1 2次系の周波数応答の比較
図1 2次系の周波数応答の比較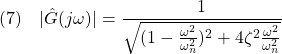
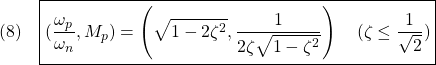
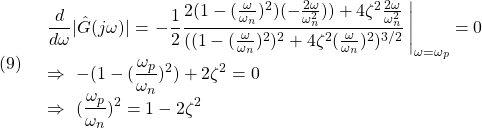
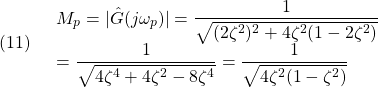
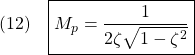
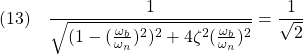
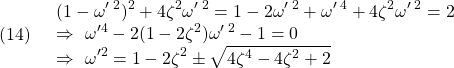
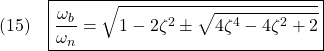
![Rendered by QuickLaTeX.com (5)\quad \begin{array}{l} \displaystyle{y(t)=\int_0^tC\exp(A(t-\tau))Be^{j\omega\tau}d\tau}\\ \displaystyle{=C\exp(At)\int_0^te^{j\omega\tau}\exp(-A\tau)Bd\tau}\\ \displaystyle{=C\exp(At)\int_0^t\exp(j\omega\tau I_n)\exp(-A\tau)Bd\tau}\\ \displaystyle{=C\exp(At)\int_0^t\exp((j\omega I_n-A)\tau)Bd\tau}\\ \displaystyle{=C\exp(At) \left[\frac{}{}\exp((j\omega I_n-A)\tau)\right]_0^t(j\omega I_n-A)^{-1}B}\\ \displaystyle{=C\exp(At) (\exp((j\omega I_n-A)t)-I_n)(j\omega I_n-A)^{-1}B}\\ \displaystyle{=-C\exp(At)(j\omega I_n-A)^{-1}B+C\exp(At)\exp(j\omega t I_n)\exp(-At)(j\omega I_n-A)^{-1}B}\\ \displaystyle{=-C\exp(At)(j\omega I_n-A)^{-1}B+C(j\omega I_n-A)^{-1}Be^{j\omega t}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cf72e1d083b5093019ffc1a9ae42a3ca_l3.png)
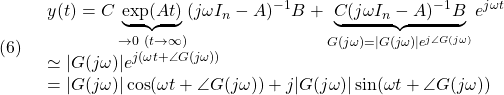
![Rendered by QuickLaTeX.com \displaystyle{(1a)\quad \underbrace{ \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b716bd0f77f40c082b3d8efd7314fe4f_l3.png)
![Rendered by QuickLaTeX.com (5)\quad \begin{array}{l} \displaystyle{y(t)=\int_0^t\frac{\omega_n^2}{\lambda_I}e^{\lambda_R(t-\tau)}\sin\lambda_I(t-\tau)\sin\omega\tau\,d\tau}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I}e^{\lambda_Rt}\sin\lambda_It\int_0^te^{-\lambda_R\tau}\sin\omega\tau\cos\lambda_I\tau\,d\tau}\\ \displaystyle{-\frac{\omega_n^2}{\lambda_I}e^{\lambda_Rt}\cos\lambda_It\int_0^te^{-\lambda_R\tau}\sin\omega\tau\sin\lambda_I\tau\,d\tau}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I}e^{\lambda_Rt}\sin\lambda_It\times}\\ \displaystyle{(\left[\frac{e^{-\lambda_R\tau}(-\lambda_R\sin(\omega+\lambda_I)\tau-(\omega+\lambda_I)\cos(\omega+\lambda_I)\tau)}{2(\lambda_R^2+(\omega+\lambda_I)^2)}\right.}\\ \displaystyle{+\left.\frac{e^{-\lambda_R\tau}(-\lambda_R\sin(\omega-\lambda_I)\tau-(\omega-\lambda_I)\cos(\omega-\lambda_I)\tau)}{2(\lambda_R^2+(\omega-\lambda_I)^2)}\right]_0^t)}\\ \displaystyle{-\frac{\omega_n^2}{\lambda_I}e^{\lambda_Rt}\cos\lambda_It\times}\\ \displaystyle{(\left[-\frac{e^{-\lambda_R\tau}(-\lambda_R\cos(\omega+\lambda_I)\tau+(\omega+\lambda_I)\sin(\omega+\lambda_I)\tau)}{2(\lambda_R^2+(\omega+\lambda_I)^2)}\right.}\\ \displaystyle{+\left.\frac{e^{-\lambda_R\tau}(-\lambda_R\cos(\omega-\lambda_I)\tau+(\omega-\lambda_I)\sin(\omega-\lambda_I)\tau)}{2(\lambda_R^2+(\omega-\lambda_I)^2)^2}\right]_0^t)}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I}e^{\lambda_Rt}\sin\lambda_It\times}\\ \displaystyle{(\frac{e^{-\lambda_Rt}(-\lambda_R\sin(\omega+\lambda_I)t-(\omega+\lambda_I)\cos(\omega+\lambda_I)t)+\omega+\lambda_I}{2(\lambda_R^2+(\omega+\lambda_I)^2)}}\\ \displaystyle{+\frac{e^{-\lambda_Rt}(-\lambda_R\sin(\omega-\lambda_I)t-(\omega-\lambda_I)\cos(\omega-\lambda_I)t)+\omega-\lambda_I}{2(\lambda_R^2+(\omega-\lambda_I)^2)})}\\ \displaystyle{-\frac{\omega_n^2}{\lambda_I}e^{\lambda_Rt}\cos\lambda_It\times}\\ \displaystyle{(\frac{-e^{-\lambda_Rt}(-\lambda_R\cos(\omega+\lambda_I)t+(\omega+\lambda_I)\sin(\omega+\lambda_I)t)-\lambda_R}{2(\lambda_R^2+(\omega+\lambda_I)^2)}}\\ \displaystyle{+\frac{e^{-\lambda_Rt}(-\lambda_R\cos(\omega-\lambda_I)t+(\omega-\lambda_I)\sin(\omega-\lambda_I)t)+\lambda_R}{2(\lambda_R^2+(\omega-\lambda_I)^2)})} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0862d7bcce2485ad411ad20ffd65abfd_l3.png)

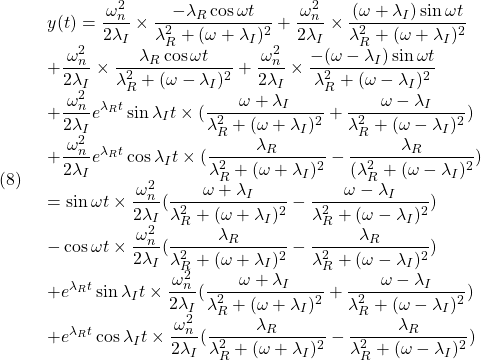
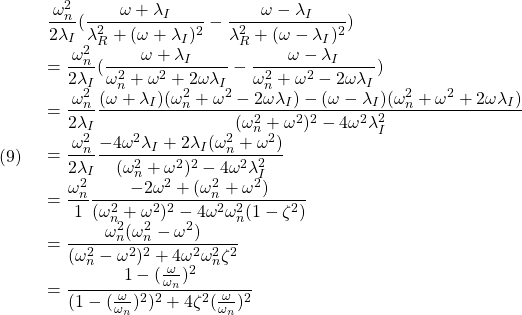
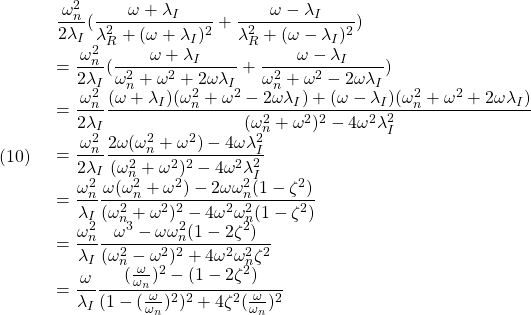
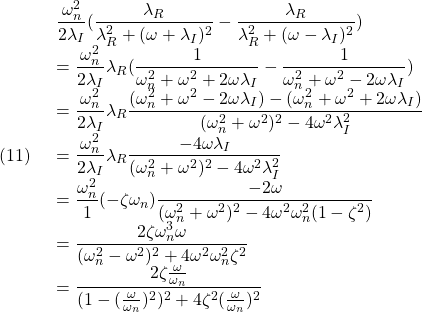
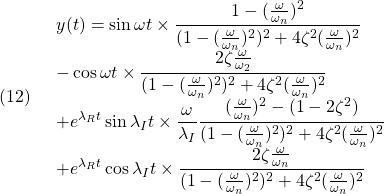
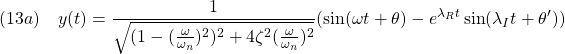
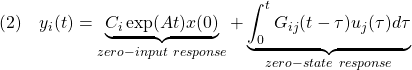
![Rendered by QuickLaTeX.com \displaystyle{(6a)\quad \underbrace{ \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} 0 \\ K\omega_n^2 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-163123fac605973ff5bb7e352fe8a4e4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6b)\quad y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c9800fcc5420d0c26c37f1aa628b4db9_l3.png)
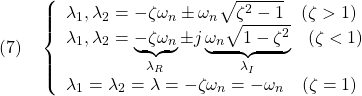
 図1
図1 ![Rendered by QuickLaTeX.com (9)\quad \begin{array}{l} \displaystyle{S(t)=\int_0^tG(\tau)d\tau=\int_0^t\frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}(e^{\lambda_2\tau}-e^{\lambda_1\tau})d\tau}\\ \displaystyle{= \frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}\left[\frac{e^{\lambda_2\tau}}{\lambda_2}-\frac{e^{\lambda_1\tau}}{\lambda_1}\right]_0^t}\\ \displaystyle{=\frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}(\frac{e^{\lambda_2t}}{\lambda_2}-\frac{e^{\lambda_1t}}{\lambda_1})-\frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}(\frac{1}{\lambda_2}-\frac{1}{\lambda_1})}\\ \displaystyle{=1+\frac{1}{\lambda_2-\lambda_1}(\lambda_1e^{\lambda_2t}-\lambda_2e^{\lambda_1t})} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-71159c7ee47771d4db9ea63f64ac8347_l3.png)
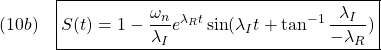
![Rendered by QuickLaTeX.com (12)\quad \begin{array}{l} \displaystyle{S(t)=\int_0^tG(\tau)d\tau=\int_0^t\frac{\omega_n^2}{\lambda_I}e^{\lambda_R\tau}\sin\lambda_I \tau d\tau}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I}\left[ \frac{e^{\lambda_R\tau}}{\lambda_R^2+\lambda_I^2}(\lambda_R\sin\lambda_I\tau-\lambda_I\cos\lambda_I\tau)\right]_0^t}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I}\frac{1}{\omega_n^2} (e^{\lambda_Rt}(\lambda_R\sin\lambda_It-\lambda_I\cos\lambda_It)+\lambda_I)}\\ \displaystyle{=1-\frac{\omega_n}{\lambda_I}e^{\lambda_Rt} (\sin\lambda_It\times\frac{-\lambda_R}{\omega_n}+\cos\lambda_It\times\frac{\lambda_I}{\omega_n})}\\ \displaystyle{=1-\frac{\omega_n}{\lambda_I}e^{\lambda_Rt} (\sin\lambda_It\cos\phi+\cos\lambda_It\sin\phi)}\\ \displaystyle{=1-\frac{\omega_n}{\lambda_I}e^{\lambda_Rt}\sin(\lambda_It+\phi) \quad(\phi=\tan^{-1}\frac{\lambda_I}{-\lambda_R})} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-70211d9c75bdadc0383d2b9c1b25fa64_l3.png)
![Rendered by QuickLaTeX.com (14)\quad \begin{array}{l} \displaystyle{S(t)=\int_0^tG(\tau)d\tau=\int_0^t\lambda^2\tau e^{\lambda\tau}d\tau}\\ \displaystyle{=\lambda^2\left[\tau \frac{1}{\lambda}e^{\lambda\tau}\right]_0^t -\lambda^2\int_0^t \frac{1}{\lambda}e^{\lambda\tau}d\tau}\\ \displaystyle{=\lambda te^{\lambda t}-\lambda\left[\frac{1}{\lambda}e^{\lambda\tau}\right]_0^t}\\ \displaystyle{=1+(\lambda t-1)e^{\lambda t}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f57dc1b1984646aeeeaafbb17bfcee60_l3.png)
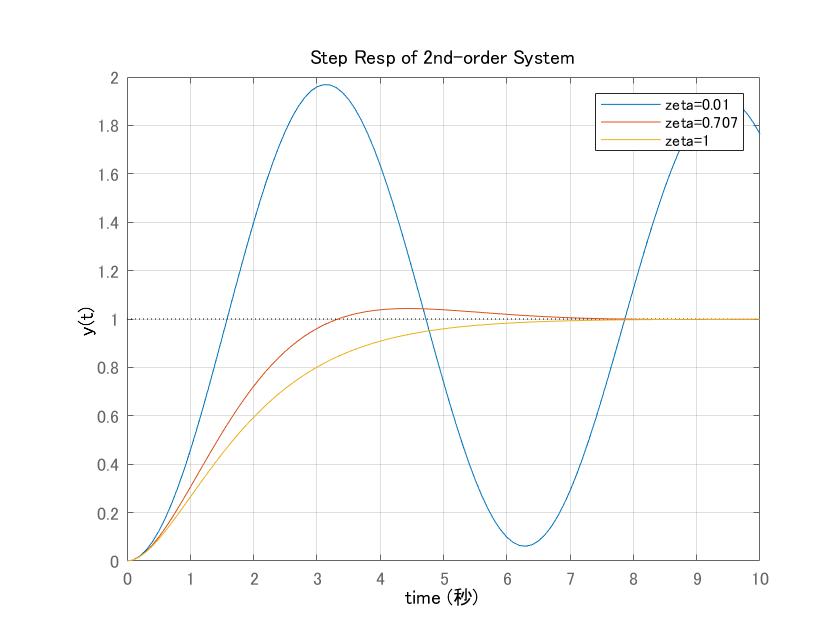 図2 2次系のステップ応答の比較
図2 2次系のステップ応答の比較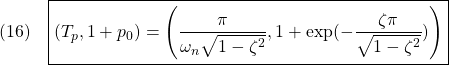
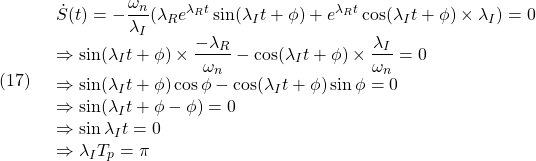
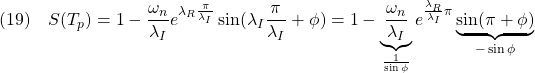
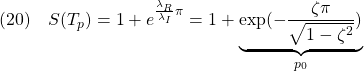
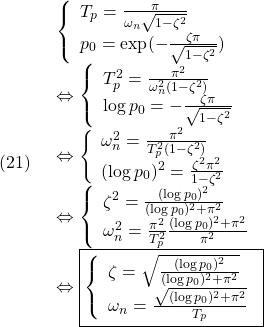
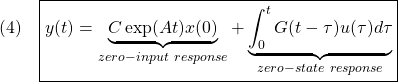
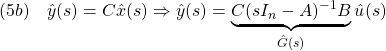
 図1 多変数系時間等応答の相互関係
図1 多変数系時間等応答の相互関係![Rendered by QuickLaTeX.com \displaystyle{(7a)\quad \boxed{\underbrace{ \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} 0 \\ K\omega_n^2 \end{array}\right] }_{B} u(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aa4b19afa6fbdeb818288fb5934edb63_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7b)\quad y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1ef77e878f73e539d8dc80f6688ac1a5_l3.png)
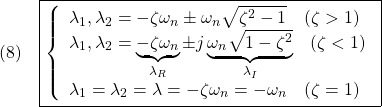
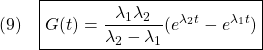
![Rendered by QuickLaTeX.com \displaystyle{(10a)\quad \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} = \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda_1 & \lambda_2 \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda_1& 0\\ 0 & \lambda_2 \end{array}\right] }_{\Lambda} \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda_1 & \lambda_2 \end{array}\right]^{-1} }_{V^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3cecd035fcbda6f346f77661cc428347_l3.png)
![Rendered by QuickLaTeX.com (11)\quad \begin{array}{l} \displaystyle{G(t)=C\exp(At)B=CV\exp(\Lambda t)V^{-1}B}\\ \displaystyle{ =\left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{cc} 1 & 1\\ \lambda_1 & \lambda_2 \end{array}\right] \left[\begin{array}{cc} e^{\lambda_1t}& 0\\ 0 & e^{\lambda_2t} \end{array}\right] \frac{1}{\lambda_2-\lambda_1} \left[\begin{array}{cc} \lambda_2 & -1\\ -\lambda_1 & 1 \end{array}\right] \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right]}\\ \displaystyle{ =\frac{\omega_n^2}{\lambda_2-\lambda_1} \left[\begin{array}{cc} e^{\lambda_1t}& e^{\lambda_2t} \end{array}\right] \left[\begin{array}{cc} -1\\ 1 \end{array}\right]}\\ \displaystyle{=\frac{\lambda_1 \lambda_2}{\lambda_2-\lambda_1}(e^{\lambda_2t}-e^{\lambda_1t})} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1f10feaa91b2bb7d8913903cbd15b9c3_l3.png)
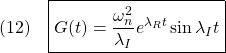
![Rendered by QuickLaTeX.com \displaystyle{(13a)\quad \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} = \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ \lambda_R & \lambda_I \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array}\right] }_{\Lambda} \underbrace{ \frac{1}{\lambda_I} \left[\begin{array}{cc} \lambda_I & 0 \\ -\lambda_R & 1 \end{array}\right] }_{V^{-1}}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-615266a9890c4e3022d07970c6f5f659_l3.png)
![Rendered by QuickLaTeX.com (14)\quad \begin{array}{l} \displaystyle{G(t)=C\exp(At)B=CV\exp(\Lambda t)V^{-1}B}\\ \displaystyle{=\left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{cc} 1 & 0\\ \lambda_R & \lambda_I \end{array}\right] e^{\lambda_R t} \left[\begin{array}{cc} \cos\lambda_I t & \sin\lambda_I t\\ \sin\lambda_I t & \cos\lambda_I t \end{array}\right] \frac{1}{\lambda_I} \left[\begin{array}{cc} \lambda_I & 0\\ -\lambda_R & 1 \end{array}\right] \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right]}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I} e^{\lambda_R t} \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{cc} \cos\lambda_I t & \sin\lambda_I t\\ \sin\lambda_I t & \cos\lambda_I t \end{array}\right] \left[\begin{array}{cc} 0\\ 1 \end{array}\right]}\\ \displaystyle{=\frac{\omega_n^2}{\lambda_I} e^{\lambda_R t}\sin\lambda_I t} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2f44bd53bbc94bd725169439890f6d6f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(16a)\quad \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} = \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda & \lambda+1 \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda & 1\\ 0 & \lambda \end{array}\right] }_{\Lambda} \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda & \lambda+1 \end{array}\right]^{-1} }_{V^{-1}}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8cd4b43f3e55efbc7942c5a68825fdd5_l3.png)
![Rendered by QuickLaTeX.com (17)\quad \begin{array}{l} \displaystyle{G(t)=C\exp(At)B=CV\exp(\Lambda t)V^{-1}B}\\ \displaystyle{= \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{cc} 1 & 1\\ \lambda & \lambda+1 \end{array}\right] e^{\lambda t} \left[\begin{array}{cc} 1 & t\\ 0 & 1 \end{array}\right] \frac{1}{\lambda+1-\lambda} \left[\begin{array}{cc} \lambda+1 & -1\\ -\lambda & 1 \end{array}\right] \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right]}\\ \displaystyle{= \omega_n^2 e^{\lambda t} \left[\begin{array}{cc} 1 & t+1 \end{array}\right] \left[\begin{array}{cc} -1\\ 1 \end{array}\right]}\\ \displaystyle{=\lambda^2te^{\lambda t}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-879b5bb9640f77dc6264c3509e6d3b66_l3.png)
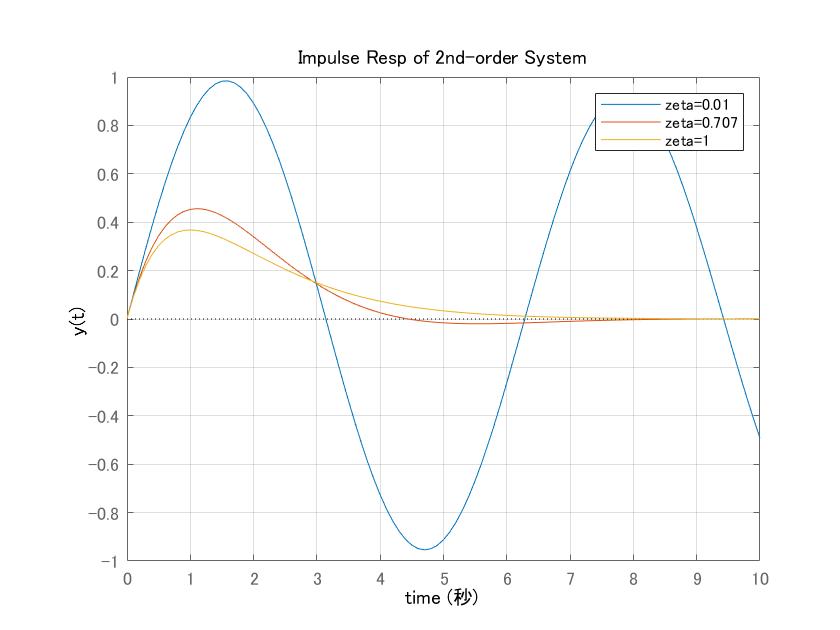 図3 2次系のインパルス応答の比較
図3 2次系のインパルス応答の比較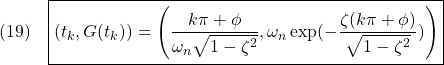
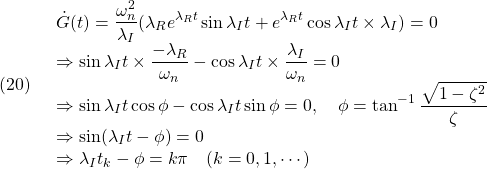
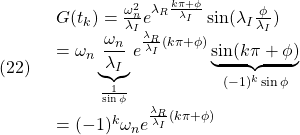
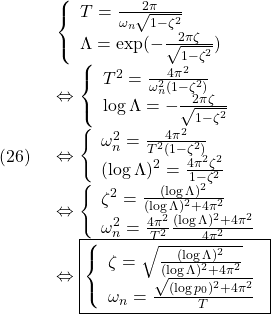
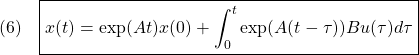
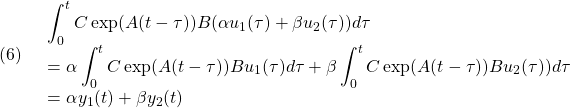

![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \underbrace{ \left[\begin{array}{l} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{3g}{4\ell}&-\frac{c}{J} \end{array}\right] }_{A=A_1} \underbrace{ \left[\begin{array}{l} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4b0ce9ec40944273a34f18d341b8adee_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{l} \theta(t)-\pi \\ \omega(t)-0 \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ \frac{3g}{4\ell}&-\frac{c}{J} \end{array}\right] }_{A=A_2} \underbrace{ \left[\begin{array}{l} \theta(t)-\pi \\ \omega(t)-0 \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-41c9758c694af6b502977f96707d2252_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \underbrace{ \left[\begin{array}{l} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{l} x_1(t) \\ x_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-046c4f6841329195eebc57253eb3c74e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \underbrace{ \left[\begin{array}{l} {x}_1(t) \\ {x}_2(t) \end{array}\right] }_{{x}(t)}= \underbrace{ \left[\begin{array}{cc} e^{a_{11}t} & 0 \\ 0 & e^{a_{22}t} \\ \end{array}\right] }_{\exp(At)} \underbrace{ \left[\begin{array}{l} x_1(0) \\ x_2(0) \end{array}\right] }_{x(0)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3fc962831e63a0a25061b8aa13a7e276_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \underbrace{ \left[\begin{array}{l} {y}_1(t) \\ {y}_2(t) \end{array}\right] }_{y(t)}= \underbrace{ \left[\begin{array}{cc} t_{11} & t_{12} \\ t_{21} & t_{22} \\ \end{array}\right] }_{T} \underbrace{ \left[\begin{array}{l} x_1(t) \\ x_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1f9192d4ccaf8b281f53ec8515bc7e4e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \underbrace{ \left[\begin{array}{l} {x}_1(t) \\ {x}_2(t) \end{array}\right] }_{x(t)}= \underbrace{ \left[\begin{array}{cc} v_{11} & v_{12} \\ v_{21} & v_{22} \\ \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{l} y_1(t) \\ y_2(t) \end{array}\right] }_{y(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c2d9dcfa810ad808ce73e74692c8a23e_l3.png)
![Rendered by QuickLaTeX.com (27)\quad \begin{array}{l} \displaystyle{{\rm det}(\lambda I_2-\left[\begin{array}{cc} 0 & 1 \\ -\frac{3g}{4\ell}&-\frac{c}{J} \end{array}\right]) =\lambda^2+\frac{c}{J}\lambda+\frac{3g}{4\ell}=0}\\ \displaystyle{\Rightarrow \lambda=\frac{1}{2}(-\frac{c}{J}\pm\sqrt{\frac{c^2}{J^2}-4\frac{3g}{4\ell}})} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-583dc0fe6afab483b2d75508fcda8317_l3.png)
![Rendered by QuickLaTeX.com (28)\quad \begin{array}{l} \displaystyle{{\rm det}(\lambda I_2-\left[\begin{array}{cc} 0 & 1 \\ \frac{3g}{4\ell}&-\frac{c}{J} \end{array}\right]) =\lambda^2+\frac{c}{J}\lambda-\frac{3g}{4\ell}=0}\\ \displaystyle{\Rightarrow \lambda=\frac{1}{2}(-\frac{c}{J}\pm\sqrt{\frac{c^2}{J^2}+4\frac{3g}{4\ell}})} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-99fa4cb16d7c26822049e462a9e29955_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(30)\quad \left[\begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array}\right]= \underbrace{\lambda_RI_2}_{X}+ \underbrace{\lambda_I \left[\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array}\right]}_{Y} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8472da3e29ace3b64c9ea7116ccbc33a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad \left[\begin{array}{cc} \lambda & 1 \\ 0 & \lambda \end{array}\right]= \underbrace{\lambda I_2}_{X}+ \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right]}_{Y} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dcdfdae4bb1e403c6e462b17b09f27aa_l3.png)
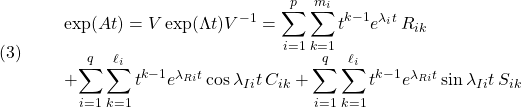
![Rendered by QuickLaTeX.com \displaystyle{(4a)\quad A=\underbrace{\left[\begin{array}{cc} v_1 & v_2 \end{array}\right]}_{V} \underbrace{\left[\begin{array}{cc} \lambda_1 & 0 \\ 0 & \lambda_2 \end{array}\right]}_{\Lambda_1} \underbrace{\left[\begin{array}{cc} v_1 & v_2 \end{array}\right]^{-1}}_{V^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bb555c7741c2c5d90cef778c129e86b1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4b)\quad \begin{array}{l} A=\underbrace{\left[\begin{array}{cc} v_R+jv_I & v_R-jv_I \end{array}\right]}_{V} \left[\begin{array}{cc} \lambda_R+j\lambda_I & 0 \\ 0 & \lambda_R-j\lambda_I \end{array}\right]\\ \times\underbrace{\left[\begin{array}{cc} v_R+jv_I & v_R-jv_I \end{array}\right]^{-1}}_{V^{-1}}\\ =\underbrace{\left[\begin{array}{cc} v_R & v_I \end{array}\right]}_{V'} \underbrace{\left[\begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array}\right]}_{\Lambda_2} \underbrace{\left[\begin{array}{cc} v_R & v_I \end{array}\right]^{-1}}_{V'^{-1}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e0fbba71d2b00a6133e75ae5071cf18d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4c)\quad A=\underbrace{\left[\begin{array}{cc} v & v' \end{array}\right]}_{V} \underbrace{\left[\begin{array}{cc} \lambda & 1 \\ 0 & \lambda \end{array}\right]}_{\Lambda_3} \underbrace{\left[\begin{array}{cc} v & v' \end{array}\right]^{-1}}_{V^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-96f0aeda7d33e0892c1b3ae15b9c822f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5a)\quad \exp(A t)=\underbrace{\left[\begin{array}{cc} v_1 & v_2 \end{array}\right]}_{V} \underbrace{\left[\begin{array}{cc} e^{\lambda_1t} & 0 \\ 0 & e^{\lambda_2 t} \end{array}\right]}_{\exp(\Lambda_1 t)} \underbrace{\left[\begin{array}{cc} v_1 & v_2 \end{array}\right]^{-1}}_{V^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a2c20a571b582858c129f9525483fde7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5b)\quad \exp(A t)=\underbrace{\left[\begin{array}{cc} v_R & v_I \end{array}\right]}_{V'} \underbrace{e^{\lambda_R t} \left[\begin{array}{cc} \cos(\lambda_It) & \sin(\lambda_It) \\ -\sin(\lambda_It) & \cos(\lambda_It) \end{array}\right]}_{\exp(\Lambda_2 t)} \underbrace{\left[\begin{array}{cc} v_R & v_I \end{array}\right]^{-1}}_{V'^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e2598816f3c649ae154eb107c7bd9756_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5c)\quad \exp(A t)=\underbrace{\left[\begin{array}{cc} v & v' \end{array}\right]}_{V} \underbrace{e^{\lambda t} \left[\begin{array}{cc} 1 & t \\ 0 & 1 \end{array}\right]}_{\exp(\Lambda_3 t)} \underbrace{\left[\begin{array}{cc} v & v' \end{array}\right]^{-1}}_{V^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1ccd3c10da477fac06071a60073df28c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6a)\quad \begin{array}{l} x(t)=\underbrace{\left[\begin{array}{cc} v_1 & v_2 \end{array}\right]}_{V} \underbrace{\left[\begin{array}{cc} e^{\lambda_1t} & 0 \\ 0 & e^{\lambda_2 t} \end{array}\right]}_{\exp(\Lambda_1 t)} \underbrace{\left[\begin{array}{cc} v_1 & v_2 \end{array}\right]^{-1}x(0)}_{\left[\begin{array}{c} c_1\\c_2 \end{array}\right]}\\ =c_1e^{\lambda_1t}v_1+c_2e^{\lambda_2t}v_2 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b73bdf17802abab8139590333ce5ddc8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6b)\quad \begin{array}{l} x(t)=\underbrace{\left[\begin{array}{cc} v_R & v_I \end{array}\right]}_{V'} \underbrace{e^{\lambda_R t} \left[\begin{array}{cc} \cos(\lambda_It) & \sin(\lambda_It) \\ -\sin(\lambda_It) & \cos(\lambda_It) \end{array}\right]}_{\exp(\Lambda_2 t)} \underbrace{\left[\begin{array}{cc} v_R & v_I \end{array}\right]^{-1}x(0)}_{\left[\begin{array}{c} c_1\\c_2 \end{array}\right]}\\ =c_1e^{\lambda_Rt}(\cos(\lambda_It)v_R-\sin(\lambda_It)v_I)+c_2e^{\lambda_Rt}(\sin(\lambda_It)v_R+\cos(\lambda_It)v_I) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-68447de2b9180ed5ba5e49bac88f6ad3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6c)\quad \begin{array}{l} x(t)=\underbrace{\left[\begin{array}{cc} v & v' \end{array}\right]}_{V} \underbrace{e^{\lambda t} \left[\begin{array}{cc} 1 & t \\ 0 & 1 \end{array}\right]}_{\exp(\Lambda_3 t)} \underbrace{\left[\begin{array}{cc} v & v' \end{array}\right]^{-1}x(0)}_{\left[\begin{array}{c} c_1\\c_2 \end{array}\right]}\\ =c_1e^{\lambda t}v+c_2e^{\lambda t}(tv+v') \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a89702614e30351370d03c8a88ab2200_l3.png)


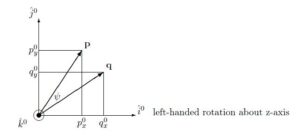
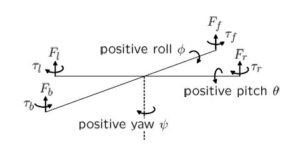
![Rendered by QuickLaTeX.com \displaystyle{\hat{n}\times{\bf p}= {\rm det} \left[\begin{array}{ccc} \hat{i}^0 & \hat{j}^0 & \hat{k}^0\\ \hat{n}_x & \hat{n}_y & \hat{n}_z\\ p_x^0 & p_y^0 & p_z^0 \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-987b3b87c684eb8f160259eccaed8b8c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} q_x^0 \\ q_y^0 \\ q_z^0 \end{array}\right] }_{{\bf q}} =(1-C_\psi) p_z^0 \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right] }_{\hat{i}} \hat{n}+C_\psi \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] -S_\psi \left[\begin{array}{c} -p_y^0 \\ p_x^0 \\ 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-12d5ca14cbcc4c55826c7d6d8f899987_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \underbrace{ \left[\begin{array}{ccc} C_\psi & S_\psi & 0 \\ -S_\psi & C_\psi & 0 \\ 0 & 0 & 1 \end{array}\right] }_{R(\phi)} \underbrace{ \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] }_{{\bf p}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-034528a2aacb8e95ad6d97e767cee015_l3.png)
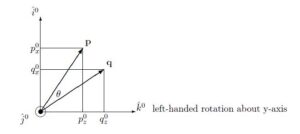
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} q_x^0 \\ q_y^0 \\ q_z^0 \end{array}\right] }_{{\bf q}} =(1-C_\theta) p_y^0 \underbrace{ \left[\begin{array}{c} 0 \\ 1 \\ 0 \end{array}\right] }_{\hat{j}} \hat{n}+C_\theta \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] -S_\theta \left[\begin{array}{c} p_z^0 \\ 0\\ -p_x^0 \\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a989718664a4f406a703678aa7bce25c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ =\underbrace{ \left[\begin{array}{ccc} C_\theta & 0 & -S_\theta \\ 0 & 1 & 0 \\ S_\theta & 0 & C_\theta \end{array}\right] }_{R(\theta)} \underbrace{ \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] }_{{\bf p}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-77d80bf487c6766d1c677f8791183be6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} q_x^0 \\ q_y^0 \\ q_z^0 \end{array}\right] }_{{\bf q}} =(1-C_\phi) p_x^0 \underbrace{ \left[\begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right] }_{\hat{k}} \hat{n}+C_\phi \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] -S_\phi \left[\begin{array}{c} 0\\ -p_z^0 \\ p_y^0 \\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-59bae1ad5756ab21b2c3dfbfa893e055_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ =\underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & C_\phi & S_\phi \\ 0 & -S_\phi & C_\phi \end{array}\right] }_{R(\psi)} \underbrace{ \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] }_{{\bf p}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d1ab1c6a193d60691e385bcb0e30cfb3_l3.png)

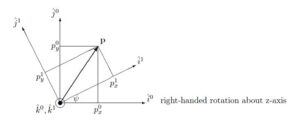
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} p_x^1 \\ p_y^1 \\ p_z^1 \end{array}\right] }_{{\bf p}^1} = \underbrace{ \left[\begin{array}{ccc} \hat{i}^1\cdot\hat{i}^0&\hat{i}^1\cdot\hat{j}^0&\hat{i}^1\cdot\hat{k}^0\\ \hat{j}^1\cdot\hat{i}^0&\hat{j}^1\cdot\hat{j}^0&\hat{j}^1\cdot\hat{k}^0\\ \hat{k}^1\cdot\hat{i}^0&\hat{k}^1\cdot\hat{j}^0&\hat{k}^1\cdot\hat{k}^0 \end{array}\right] }_{R_0^1(\psi)} \underbrace{ \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] }_{{\bf p}^0} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9e097cfdaee9cbb694b4d1748693d3c6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ R_0^1(\psi)= \left[\begin{array}{ccc} C_\psi & S_\psi & 0 \\ -S_\psi & C_\psi & 0 \\ 0 & 0 & 1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-58ac6cd544f764f340163f5d9e7d61aa_l3.png)
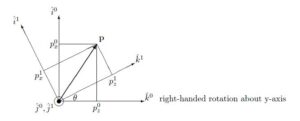
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} p_x^1 \\ p_y^1 \\ p_z^1 \end{array}\right] }_{{\bf p}^1} = \underbrace{ \left[\begin{array}{ccc} \hat{i}^1\cdot\hat{i}^0&\hat{i}^1\cdot\hat{j}^0&\hat{i}^1\cdot\hat{k}^0\\ \hat{j}^1\cdot\hat{i}^0&\hat{j}^1\cdot\hat{j}^0&\hat{j}^1\cdot\hat{k}^0\\ \hat{k}^1\cdot\hat{i}^0&\hat{k}^1\cdot\hat{j}^0&\hat{k}^1\cdot\hat{k}^0 \end{array}\right] }_{R_0^1(\theta)} \underbrace{ \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] }_{{\bf p}^0} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aceb055a39624b49b00c52ba93b2fafc_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ R_0^1(\theta)= \left[\begin{array}{ccc} C_\theta & 0 & -S_\theta \\ 0 & 1 & 0 \\ S_\theta & 0 & C_\theta \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bc434799df6aa0435586745ed76ca371_l3.png)
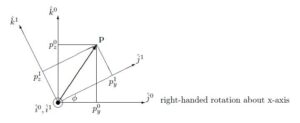
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} p_x^1 \\ p_y^1 \\ p_z^1 \end{array}\right] }_{{\bf p}^1} = \underbrace{ \left[\begin{array}{ccc} \hat{i}^1\cdot\hat{i}^0&\hat{i}^1\cdot\hat{j}^0&\hat{i}^1\cdot\hat{k}^0\\ \hat{j}^1\cdot\hat{i}^0&\hat{j}^1\cdot\hat{j}^0&\hat{j}^1\cdot\hat{k}^0\\ \hat{k}^1\cdot\hat{i}^0&\hat{k}^1\cdot\hat{j}^0&\hat{k}^1\cdot\hat{k}^0 \end{array}\right] }_{R_0^1(\phi)} \underbrace{ \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] }_{{\bf p}^0} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-be939844208f01e80bd96a4578eb7d9c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ R_0^1(\phi)= \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & C_\phi & S_\phi \\ 0 & -S_\phi & C_\phi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9e26ef5f7bc02c2f2f19b14327fc67f6_l3.png)

![Rendered by QuickLaTeX.com \displaystyle{= \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & C_\phi & S_\phi \\ 0 & -S_\phi & C_\phi \end{array}\right] \left[\begin{array}{ccc} C_\theta & 0 & -S_\theta \\ 0 & 1 & 0 \\ S_\theta & 0 & C_\theta \end{array}\right] \left[\begin{array}{ccc} C_\psi & S_\psi & 0 \\ -S_\psi & C_\psi & 0 \\ 0 & 0 & 1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cbcf941c508f91c6e056f42732084bf5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \left[\begin{array}{ccc} C_\theta C_\psi & C_\theta S_\psi & -S_\theta \\ S_\phi S_\theta C_\psi - C_\phi S_\psi & S_\phi S_\theta S_\psi + C_\phi C_\psi & S_\phi C_\theta \\ C_\phi S_\theta C_\psi + C_\phi S_\psi & C_\phi S_\theta S_\psi - S_\phi C_\psi & C_\phi C_\theta \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bb9eeb9b54c7ae5be019eb255e6bdbd8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ R_v^{v1}(\psi)= \left[\begin{array}{ccc} C_\psi & S_\psi & 0 \\ -S_\psi & C_\psi & 0 \\ 0 & 0 & 1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-62a0d9a3674b84f4cc7fd9463923b711_l3.png)

![Rendered by QuickLaTeX.com \displaystyle{ R_{v1}^{v2}(\theta)= \left[\begin{array}{ccc} C_\theta & 0 & -S_\theta \\ 0 & 1 & 0 \\ S_\theta & 0 & C_\theta \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-882fd5b2077da6bcc03598d35349e31f_l3.png)
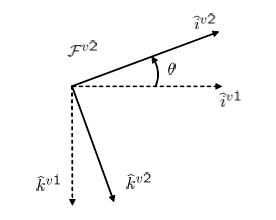
![Rendered by QuickLaTeX.com \displaystyle{ R_{v2}^b(\phi)= \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & C_\phi & S_\phi \\ 0 & -S_\phi & C_\phi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-65b7f87e8d6ceac41cc3eed6be19136b_l3.png)

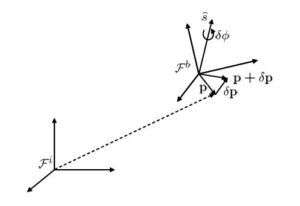
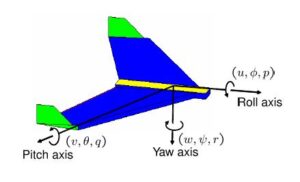
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} u \\ v \\ w \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} C_\theta C_\psi & C_\theta S_\psi & -S_\theta \\ S_\phi S_\theta C_\psi - C_\phi S_\psi & S_\phi S_\theta S_\psi + C_\phi C_\psi & S_\phi C_\theta \\ C_\phi S_\theta C_\psi + C_\phi S_\psi & C_\phi S_\theta S_\psi - S_\phi C_\psi & C_\phi C_\theta \end{array}\right] }_{R_v^b} \left[\begin{array}{c} \dot{p}_n \\ \dot{p}_e \\ -\dot{h} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-de39a8b9bd05d0eb4e506e36a8e0fa0a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{p}_n \\ \dot{p}_e \\ -\dot{h} \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} C_\theta C_\psi &S_\phi S_\theta C_\psi - C_\phi S_\psi &C_\phi S_\theta C_\psi + C_\phi S_\psi \\ C_\theta S_\psi &S_\phi S_\theta S_\psi + C_\phi C_\psi &C_\phi S_\theta S_\psi - S_\phi C_\psi \\ -S_\theta &S_\phi C_\theta &C_\phi C_\theta \end{array}\right] }_{R_b^v=(R_v^b)^T} \left[\begin{array}{c} u \\ v \\ w \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d363a281bdd4e8b2b988be4d3069aa11_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} p \\ q \\ r \end{array}\right] = \underbrace{R_{v2}^b(\dot{\phi})}_{I} \left[\begin{array}{c} \dot{\phi} \\ 0 \\ 0 \end{array}\right] + R_{v2}^b(\phi)\underbrace{R_{v1}^{v2}(\dot{\theta})}_{I} \left[\begin{array}{c} 0 \\ \dot{\theta} \\ 0 \end{array}\right] + R_{v2}^b(\phi)R_{v1}^{v2}(\theta)\underbrace{R_{v}^{v1}(\dot{\psi})}_{I} \left[\begin{array}{c} 0 \\ 0 \\ \dot{\psi} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a04c24d997a7e6874afdd3b415001501_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \left[\begin{array}{c} \dot{\phi} \\ 0 \\ 0 \end{array}\right] + \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & C_\phi & S_\phi \\ 0 & -S_\phi & C_\phi \end{array}\right] \left[\begin{array}{c} 0 \\ \dot{\theta} \\ 0 \end{array}\right] + \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & C_\phi & S_\phi \\ 0 & -S_\phi & C_\phi \end{array}\right] \left[\begin{array}{ccc} C_\theta & 0 & -S_\theta \\ 0 & 1 & 0 \\ S_\theta & 0 & C_\theta \end{array}\right] \left[\begin{array}{c} 0 \\ 0 \\ \dot{\psi} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-97c20a9db7f00180754feff31ee807c8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} p \\ q \\ r \end{array}\right]= \left[\begin{array}{ccc} 1 & 0 & -S_\theta \\ 0 & C_\phi & S_\phi C_\theta \\ 0 & -S_\phi & C_\phi C_\theta \end{array}\right] \left[\begin{array}{c} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-061d5edae9ebd68d687e9549b5a5a40b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{array}\right] = \left[\begin{array}{ccc} 1 & S_\phi T_\theta & C_\phi T_\theta \\ 0 & C_\phi & -S_\phi \\ 0 & \frac{S_\phi}{C_\theta} & \frac{C_\phi}{C_\theta} \end{array}\right] \left[\begin{array}{c} p \\ q \\ r \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-10b9bc4111bd976ca0649bb42dfacd55_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \frac{d}{dt}_b \left[\begin{array}{c} u\\ v\\ w \end{array}\right] + \left[\begin{array}{c} p\\ q\\ r \end{array}\right] \times \left[\begin{array}{c} u\\ v\\ w \end{array}\right] =\frac{1}{m} \left[\begin{array}{c} f_x\\ f_y\\ f_z \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f49c0967c1c1583628163273d1cc944f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{u}\\ \dot{v}\\ \dot{w} \end{array}\right] =- \underbrace{ \left[\begin{array}{ccc} 0 & -r & q\\ r & 0 &-p\\ -q & p & 0 \end{array}\right] \left[\begin{array}{c} u\\ v\\ w \end{array}\right] }_{\left[\begin{array}{c} qw-rv \\ ru-pw\\ pv-qu \end{array}\right]} +\frac{1}{m} \left[\begin{array}{c} f_x\\ f_y\\ f_z \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6e5e479c4745afec971e8a449e1d7113_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{J= \left[\begin{array}{ccc} \int(y^2+z^2)dm & -\int xydm & -\int xzdm \\ -\int yxdm & \int(x^2+z^2)dm & -\int yzdm \\ -\int zxdm & -\int zydm & \int(x^2+y^2)dm \end{array}\right] =\left[\begin{array}{ccc} J_x & 0 & 0 \\ 0 & J_y & 0 \\ 0 & 0 & J_z \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-16d24597f8387fec8c1eb565263ad684_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \frac{d}{dt}_bJ \left[\begin{array}{c} p\\ q\\ r \end{array}\right] + \left[\begin{array}{c} p\\ q\\ r \end{array}\right] \times J \left[\begin{array}{c} p\\ q\\ r \end{array}\right] = \left[\begin{array}{c} \tau_\phi\\ \tau_\theta\\ \tau_\psi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3a28be1d9f68276f11ece9ae89a59304_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} J_x\dot{p}\\ J_y\dot{q}\\ J_z\dot{r} \end{array}\right] + \underbrace{ \left[\begin{array}{ccc} 0 & -r & q\\ r & 0 &-p\\ -q & p & 0 \end{array}\right] \left[\begin{array}{c} J_xp\\ J_yq\\ J_zr \end{array}\right] }_{\left[\begin{array}{c} (J_z-J_y)qr \\ (J_x-J_z)pr\\ (J_y-J_x)pq \end{array}\right]} = \left[\begin{array}{c} \tau_\phi\\ \tau_\theta\\ \tau_\psi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-11a81fab1a1c7f81823c26120d6d2b21_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{p}\\ \dot{q}\\ \dot{r} \end{array}\right] =- \underbrace{ \left[\begin{array}{ccc} 0 & 0 & \frac{J_z-J_y}{J_x}q\\ \frac{J_x-J_z}{J_y} r & 0 & 0\\ 0 & \frac{J_y-J_x}{J_z}p & 0 \end{array}\right] \left[\begin{array}{c} p\\ q\\ r \end{array}\right] }_{ \left[\begin{array}{c} \frac{J_z-J_y}{J_x}qr \\ \frac{J_x-J_z}{J_y}pr \\ \frac{J_y-J_x}{J_z}pq \end{array}\right] } + \left[\begin{array}{c} \frac{1}{J_x}\tau_\phi\\ \frac{1}{J_y}\tau_\theta\\ \frac{1}{J_z}\tau_\psi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3eb533fddc2cdc3acb2986b508ba0373_l3.png)
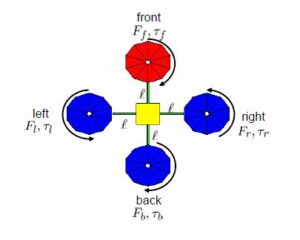
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} F\\ \tau_\phi\\ \tau_\theta\\ \tau_\psi \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} k_1 & k_1 & k_1 & k_1 \\ 0 & -\ell k_1 & 0 & \ell k_1 \\ \ell k_1 & 0 & -\ell k_1 & 0 \\ -k_2 & k_2 & -k_2 & k_2 \end{array}\right] }_{{\cal M}} \left[\begin{array}{c} \delta_f\\ \delta_r\\ \delta_b\\ \delta_\ell \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2189a79e26837861510a7bb0f99f2a55_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} f_x\\ f_y\\ f_z \end{array}\right] = R_v^b \left[\begin{array}{c} 0\\ 0\\ mg \end{array}\right] + \left[\begin{array}{c} 0\\ 0\\ -F \end{array}\right] =mg \left[\begin{array}{ccc} -S_\theta \\ S_\phi C_\theta \\ C_\phi C_\theta \end{array}\right] + \left[\begin{array}{c} 0\\ 0\\ -F \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-46b8705ff1f44fac694d366bf9bfc130_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{p}_n \\ \dot{p}_e \\ -\dot{h} \\ \hline \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \\ \hline \dot{u}\\ \dot{v}\\ \dot{w} \\ \hline \dot{p}\\ \dot{q}\\ \dot{r} \end{array}\right] = \left[\begin{array}{ccc|ccc} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array}\right.}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c057cf51cb84ad35be913e5f72b6b095_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left.\begin{array}{ccc|ccc} C_\theta C_\psi &S_\phi S_\theta C_\psi - C_\phi S_\psi &C_\phi S_\theta C_\psi + C_\phi S_\psi & 0 & 0 & 0\\ C_\theta S_\psi &S_\phi S_\theta S_\psi + C_\phi C_\psi &C_\phi S_\theta S_\psi - S_\phi C_\psi & 0 & 0 & 0\\ -S_\theta &S_\phi C_\theta &C_\phi C_\theta & 0 & 0 & 0\\ \hline 0 & 0 & 0 & 1 & S_\phi T_\theta & C_\phi T_\theta \\ 0 & 0 & 0 & 0 & C_\phi & -S_\phi \\ 0 & 0 & 0 & 0 & \frac{S_\phi}{C_\theta} & \frac{C_\phi}{C_\theta}\\ \hline 0 & r &- q & 0 & 0 & 0\\ r- & 0 &p & 0 & 0 & 0\\ q & -p & 0 & 0 & 0 & 0\\ \hline 0 & 0 & 0 & 0 & 0 & -\frac{J_z-J_y}{J_x}q\\ 0 & 0 & 0 & -\frac{J_x-J_z}{J_y} r & 0 & 0\\ 0 & 0 & 0 & 0 & -\frac{J_y-J_x}{J_z}p & 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ac9a7943b0d77c3ef3dcaeb6016011e8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \times \left[\begin{array}{c} p_n \\ p_e \\ -h \\ \hline \phi \\ \theta \\ \psi \\ \hline u\\ v\\ w \\ \hline p\\ q\\ r \end{array}\right] + \left[\begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \frac{1}{m} & 0 & 0 & 0 \\ \hline 0 & \frac{1}{J_x} & 0 & 0 \\ 0 & 0 & \frac{1}{J_y} & 0 \\ 0 & 0 & 0 & \frac{1}{J_z} \\ \end{array}\right] \left[\begin{array}{cccc} k_1 & k_1 & k_1 & k_1 \\ 0 & -\ell k_1 & 0 & \ell k_1 \\ \ell k_1 & 0 & -\ell k_1 & 0 \\ -k_2 & k_2 & -k_2 & k_2 \end{array}\right]^{-1} \left[\begin{array}{c} \delta_f\\ \delta_r\\ \delta_b\\ \delta_\ell \end{array}\right] + \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ \hline 0 \\ 0 \\ 0 \\ \hline -gS_\theta \\ gS_\phi C_\theta \\ gC_\phi C_\theta \\ \hline 0 \\ 0 \\ 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dfbd76199ec24769a2fab7d91200e5dc_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{p}\\ \dot{q}\\ \dot{r} \end{array}\right] =- \left[\begin{array}{c} \frac{J_z-J_y}{J_x}qr \\ \frac{J_x-J_z}{J_y}pr \\ \frac{J_y-J_x}{J_z}pq \end{array}\right] + \left[\begin{array}{c} \frac{1}{J_x}\tau_\phi\\ \frac{1}{J_y}\tau_\theta\\ \frac{1}{J_z}\tau_\psi \end{array}\right] \simeq \left[\begin{array}{c} \frac{1}{J_x}\tau_\phi\\ \frac{1}{J_y}\tau_\theta\\ \frac{1}{J_z}\tau_\psi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f6a1e8b9f0e32ed0de052e40acd5d9e8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{array}\right] = \left[\begin{array}{ccc} 1 & S_\phi T_\theta & C_\phi T_\theta \\ 0 & C_\phi & -S_\phi \\ 0 & \frac{S_\phi}{C_\theta} & \frac{C_\phi}{C_\theta} \end{array}\right] \left[\begin{array}{c} p \\ q \\ r \end{array}\right] \simeq \left[\begin{array}{c} p \\ q \\ r \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7588cb998bf45f4453bd790068da25cd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \ddot{\phi} \\ \ddot{\theta} \\ \ddot{\psi} \end{array}\right] \simeq \left[\begin{array}{c} \dot{p}\\ \dot{q}\\ \dot{r} \end{array}\right] \simeq \left[\begin{array}{c} \frac{1}{J_x}\tau_\phi\\ \frac{1}{J_y}\tau_\theta\\ \frac{1}{J_z}\tau_\psi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c00140559d247b19ba35379d4f2fc7d2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{p}_x \\ \dot{p}_y \\ \dot{p}_z \end{array}\right] = {R}_{v1}^b \left[\begin{array}{c} u \\ v \\ w \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-07b55ee0eb520a01571a66c82273a1b1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \ddot{p}_x \\ \ddot{p}_y \\ \ddot{p}_z \end{array}\right] = \underbrace{\dot{R}_{v1}^b}_{\simeq0} \left[\begin{array}{c} {u}\\ {v}\\ {w} \end{array}\right] + {R}_{v1}^b \left[\begin{array}{c} \dot{u}\\ \dot{v}\\ \dot{w} \end{array}\right] \simeq {R}_{v1}^b \left[\begin{array}{c} \dot{u}\\ \dot{v}\\ \dot{w} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b6a4f91764dbe1ccc821cb66b6c128a3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \ddot{p}_x \\ \ddot{p}_y \\ \ddot{p}_z \end{array}\right] \simeq \left[\begin{array}{ccc} C_\theta & S_\phi S_\theta & C_\phi S_\theta \\ 0 & C_\phi & -S_\phi \\ -S_\theta &S_\phi C_\theta &C_\phi C_\theta \end{array}\right] (g \left[\begin{array}{c} -S_\theta \\ S_\phi C_\theta \\ C_\phi C_\theta \end{array}\right] +\frac{1}{m} \left[\begin{array}{c} 0\\ 0\\ -F \end{array}\right]) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-806c2333ecc5b9e2f2176af3d06ac631_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \left[\begin{array}{c} 0 \\ 0 \\ g \end{array}\right] -\frac{1}{m}F \left[\begin{array}{ccc} C_\phi S_\theta \\ -S_\phi \\ C_\phi C_\theta \end{array}\right] \simeq \left[\begin{array}{c} 0 \\ 0 \\ g-\frac{1}{m}F \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a012c160125fa47849e9b54d7a6be80e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} \dot{p}_z \\ \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \\\hline \ddot{z} \\ \ddot{\phi} \\ \ddot{\theta} \\ \ddot{\psi} \\ \end{array}\right] }_{\dot{x}} = \underbrace{ \left[\begin{array}{cccc|cccc} 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\\hline 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array}\right] }_{A} % \left[\begin{array}{c|c} % 0_{4\times4} & I_4 \\\hline % 0_{4\times4} & 0_{4\times4} % \end{array}\right] \underbrace{ \left[\begin{array}{c} {p_z} \\ {\phi} \\ {\theta} \\ {\psi} \\\hline \dot{z} \\ \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \\ \end{array}\right] }_{x} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c2d526861def4102dd037941437ebbd2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{+ \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\\hline -\frac{k_f}{m} & -\frac{k_f}{m} & -\frac{k_f}{m} & -\frac{k_f}{m} \\ 0 & -\frac{\ell k_f}{J_x} & 0 & \frac{\ell k_f}{J_x} \\ \frac{\ell k_f}{J_y} & 0 & -\frac{\ell k_f}{J_y} & 0 \\ -\frac{k_\tau}{J_z} & \frac{k_\tau}{J_z} & -\frac{k_\tau}{J_z} & \frac{k_\tau}{J_z} \\ \end{array}\right] }_{B} % \left[\begin{array}{c} % 0_{4\times4} \\ % B_2 \\ % \end{array}\right] \underbrace{ \left[\begin{array}{c} \delta_f-\delta^* \\ \delta_r-\delta^* \\ \delta_b-\delta^* \\ \delta_\ell-\delta^* \\ \end{array}\right] }_{u} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b01d89585d73ec5fff8e27c5c03036e2_l3.png)
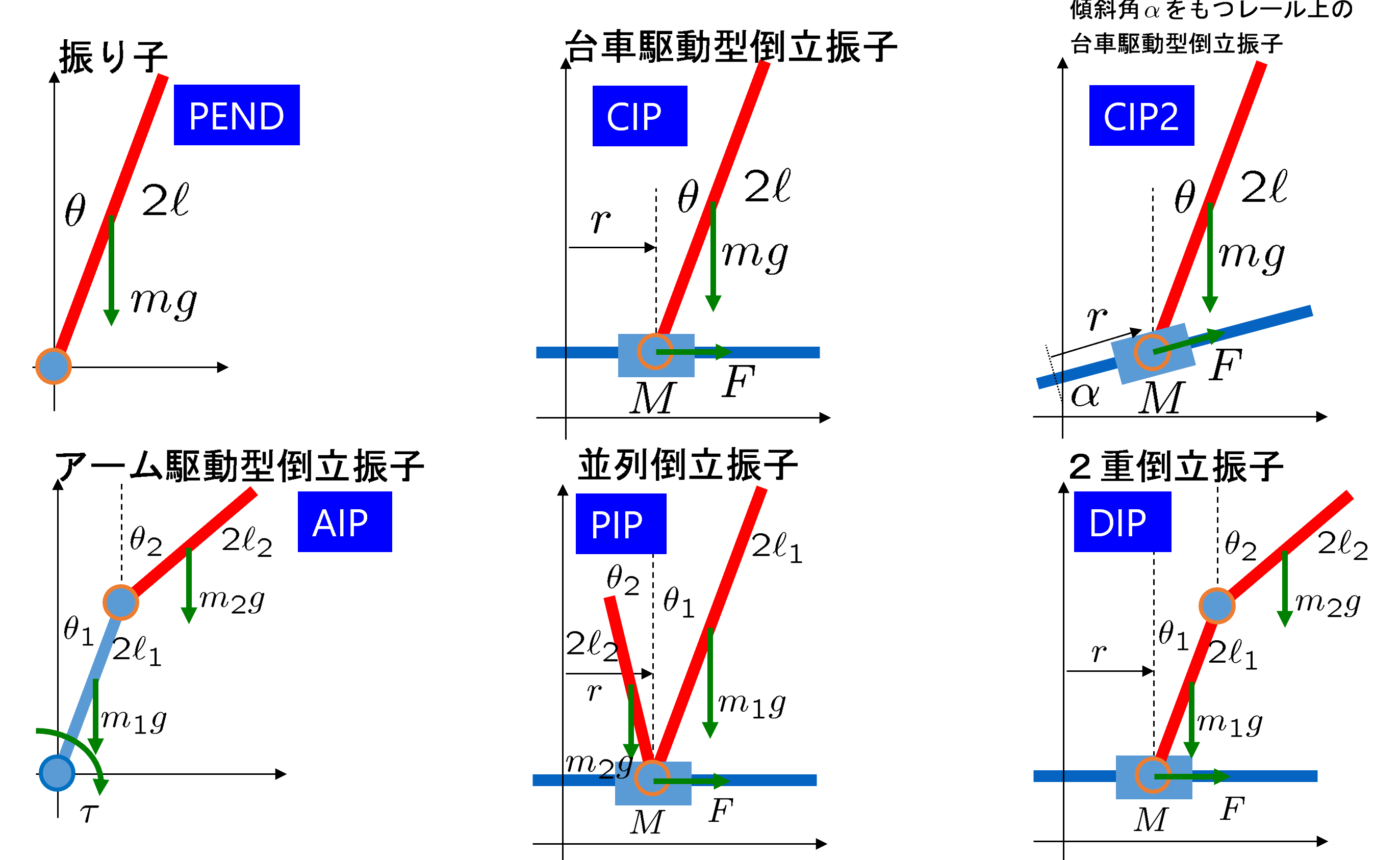 図1 様々な倒立振子
図1 様々な倒立振子![Rendered by QuickLaTeX.com (2.1)\quad \begin{array}{l} \displaystyle{\underbrace{ \left[\begin{array}{ccc} M+m & m\ell\cos\theta \\ m\ell\cos\theta & \frac{4}{3}m\ell^2 \end{array}\right] }_{M(\xi_1)} \underbrace{ \left[\begin{array}{c} \ddot{r} \\ \ddot{\theta} \end{array}\right] }_{\dot{\xi}_2}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 & -m\ell\sin\theta\dot{\theta} \\ 0 & 0 \end{array}\right] }_{C(\xi_1,\xi_2)} \underbrace{ \left[\begin{array}{c} \dot{r} \\ \dot{\theta} \end{array}\right] }_{\dot{\xi}_1}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0\\ -m\ell g\sin\theta \end{array}\right] }_{G(\xi_1)} = \underbrace{ \left[\begin{array}{c} 1 \\ 0 \end{array}\right] F}_{\tilde{F}}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b6b8157fad48af615f079cdbabc05028_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2.5)\quad \frac{d}{dt}\left[\begin{array}{c} r\\ \theta-\theta^*\\ \dot{r}\\ \dot{\theta} \end{array}\right] = \left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & -\frac{3gm}{4M+m} & 0 & 0\\ 0 & \frac{3(M+m)g}{(4M+m)\ell} & 0 & 0\\ \end{array}\right] \left[\begin{array}{c} r\\ \theta-\theta^*\\ \dot{r}\\ \dot{\theta} \end{array}\right] + \left[\begin{array}{c} 0\\ 0\\ \frac{4}{4M+m}\\ \frac{3}{(4M+m)\ell} \end{array}\right] F }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fae8887f4f90143f54cd71d63289bc0f_l3.png)
![Rendered by QuickLaTeX.com (3.1)\quad \begin{array}{l} \displaystyle{\underbrace{ \left[\begin{array}{ccc} M+m & m\ell\cos(\theta+\alpha) \\ m\ell\cos(\theta+\alpha) & \frac{4}{3}m\ell^2 \end{array}\right] }_{M(\xi_1)} \underbrace{ \left[\begin{array}{c} \ddot{r} \\ \ddot{\theta} \end{array}\right] }_{\dot{\xi}_2}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 & -m\ell\sin(\theta+\alpha)\dot{\theta} \\ 0 & 0 \end{array}\right] }_{C(\xi_1,\xi_2)} \underbrace{ \left[\begin{array}{c} \dot{r} \\ \dot{\theta} \end{array}\right] }_{\dot{\xi}_1}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} (M+m)g\sin\alpha\\ -m\ell g\sin\theta \end{array}\right] }_{G(\xi_1)} = \left[\begin{array}{c} 1 \\ 0 \end{array}\right] F} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9e90c77e32ef0131c7f6472d28283498_l3.png)
![Rendered by QuickLaTeX.com (3.5)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} r\\ \theta-\theta^*\\ \dot{r}\\ \dot{\theta} \end{array}\right] = \left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & -\frac{6\cos\alpha mg}{8M+(5-3\cos2\alpha)m} & 0 & 0\\ 0 & \frac{6(M+m)g}{(8M+(5-3\cos2\alpha)m)\ell} & 0 & 0\\ \end{array}\right] \left[\begin{array}{c} r\\ \theta-\theta^*\\ \dot{r}\\ \dot{\theta} \end{array}\right]}\\ \displaystyle{+ \left[\begin{array}{c} 0\\ 0\\ \frac{8}{8M+(5-3\cos2\alpha)m}\\ \frac{6\cos\alpha}{(8M+(5-3\cos2\alpha)m)\ell} \end{array}\right] (F-F^*)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-93deb9744dd26e8ee2880e1528f961ab_l3.png)
![Rendered by QuickLaTeX.com (4.1)\quad \begin{array}{l} \displaystyle{\underbrace{ \left[\begin{array}{ccc} (\frac{4}{3}m_1+4m_2)\ell_1^2 & 2m_2\ell_1\ell_2\cos(\theta_2-\theta_1)\\ 2m_2\ell_1\ell_2\cos(\theta_2-\theta_1) & \frac{4}{3}m_2\ell_2^2 \end{array}\right] }_{M(\xi_1)} \underbrace{ \left[\begin{array}{c} \ddot{\theta}_1 \\ \ddot{\theta}_2 \end{array}\right] }_{\dot{\xi}_2}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 & -2m_2\ell_1\ell_2\sin(\theta_2-\theta_1) \dot{\theta}_2\\ 2m_2\ell_1\ell_2\sin(\theta_2-\theta_1) \dot{\theta}_1 & 0\\ \end{array}\right] }_{C(\xi_1,\xi_2)} \underbrace{ \left[\begin{array}{c} \dot{\theta}_1 \\ \dot{\theta}_2 \end{array}\right] }_{\dot{\xi}_1}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} -(m_1+2m_2)\ell_1g\sin\theta_1\\ -m_2\ell_2g\sin\theta_2 \end{array}\right] }_{G(\xi_1)} = \underbrace{ \left[\begin{array}{c} 1 \\ 0 \end{array}\right] \tau}_{\tilde{\tau}}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-76a26f1d085c39daa570b8cee71ac8eb_l3.png)
![Rendered by QuickLaTeX.com (4.5a)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right] =}\\ \displaystyle{\left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \frac{3(m_1+2m_2)g}{(4m_1+3m_2)\ell_1} & -\frac{9m_2g}{2(4m_1+3m_2)\ell_1} & 0 & 0\\ -\frac{9(m_1+2m_2)g}{2(4m_1+3m_2)\ell_1} & \frac{9m_2g}{(4m_1+3m_2)\ell_2} & 0 & 0\\ \end{array}\right] \left[\begin{array}{c} \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right]}\\ \displaystyle{+ \left[\begin{array}{c} 0\\ 0\\ \frac{6}{2(4m_1+3m_2)\ell_1^2}\\ -\frac{9}{2(4m_1+3m_2)\ell_1\ell_2} \end{array}\right] (\tau-\tau^*)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a11a4d24890d0850335707e48115c732_l3.png)
![Rendered by QuickLaTeX.com (4.5b)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right] =}\\ \displaystyle{\left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ a_{31}(\alpha) & a_{32}(\alpha) & 0 & 0\\ a_{41}(\alpha) & a_{42}(\alpha) & 0 & 0 \end{array}\right] \left[\begin{array}{c} \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right]}\\ \displaystyle{+ \left[\begin{array}{c} 0\\ 0\\ \frac{6}{2(4m_1+3(4-3\cos^2\alpha)m_2)\ell_1^2}\\ -\frac{6}{2(4m_1+3(4-3\cos^2\alpha)m_2)\ell_1\ell_2} \end{array}\right] (\tau-\tau^*)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bbff369ea90195fe12e62e338448cbcd_l3.png)

![Rendered by QuickLaTeX.com (5.1)\quad \begin{array}{l} \displaystyle{\underbrace{ \left[\begin{array}{ccc} M+m_1+m_2 & (m_1+2m_2)\ell_1\cos\theta_1 & m_2\ell_2\cos\theta_2\\ (m_1+2m_2)\ell_1\cos\theta_1 & (\frac{4}{3}m_1+4m_2)\ell_1^2 & 2m_2\ell_1\ell_2\cos(\theta_2-\theta_1)\\ m_2\ell_2\cos\theta_2 & 2m_2\ell_1\ell_2\cos(\theta_2-\theta_1) & \frac{4}{3}m_2\ell_2^2 \end{array}\right] }_{M(\xi_1)} \underbrace{ \left[\begin{array}{c} \ddot{r} \\ \ddot{\theta}_1 \\ \ddot{\theta}_2 \end{array}\right] }_{\dot{\xi}_2}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 & -(m_1+2m_2)\ell_2\sin\theta_2 \dot{\theta}_1 & -m_2\ell_2\sin\theta_2 \dot{\theta}_2\\ 0 & 0 & 2m_2\ell_1\ell_2\sin(\theta_2-\theta_1) \dot{\theta}_2\\ 0 & 2m_2\ell_1\ell_2\sin(\theta_2-\theta_1) \dot{\theta}_1 & 0\\ \end{array}\right] }_{C(\xi_1,\xi_2)} \underbrace{ \left[\begin{array}{c} \dot{r} \\ \dot{\theta}_1 \\ \dot{\theta}_2 \end{array}\right] }_{\dot{\xi}_1}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 \\ (m_1+3m_2)\ell_1g\sin\theta_1\\ -m_2\ell_2g\sin\theta_2 \end{array}\right] }_{G(\xi_1)} = \underbrace{ \left[\begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right] F}_{\tilde{F}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-31c39d9c40fa5f71f3c50512937de667_l3.png)
![Rendered by QuickLaTeX.com (5.5)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} r\\ \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{r}\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right] =}\\ \displaystyle{\left[\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ 0 & -\frac{3m_1g}{4M+m_1+m_2} & -\frac{3m_2g}{4M+m_1+m_2} & 0 & 0 & 0\\ 0 & \frac{3(4m+4m_1+m_2)g}{4(4M+m_1+m_2)\ell_1} & \frac{9m_2g}{4(4M+m_1+m_2)\ell_1} & 0 & 0& 0\\ 0 & \frac{9gm_1}{4(4M+m_1+m_2)\ell_2} & \frac{3(4m+m_1+4m_2)g}{4(4M+m_1+m_2)\ell_2} & 0 & 0& 0\\ \end{array}\right] \left[\begin{array}{c} r\\ \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{r}\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right]}\\ \displaystyle{+ \left[\begin{array}{c} 0\\ 0\\ 0\\ \frac{4}{4M+m_1+m_2}\\ -\frac{3}{(4M+m_1+m_2)\ell_1}\\ -\frac{3}{(4M+m_1+m_2)\ell_2} \end{array}\right] F \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8554645545e9bed2d603331493dd90b7_l3.png)
![Rendered by QuickLaTeX.com (6.1)\quad \begin{array}{l} \displaystyle{\underbrace{ \left[\begin{array}{ccc} M+m_1+m_2 & m_1\ell_1\cos\theta_1 & -m_2\ell_2\cos\theta_2\\ m_1\ell_1\cos\theta_1 & \frac{4}{3}m_1\ell_1^2 & 0\\ -m_2\ell_2\cos\theta_2 & 0 & \frac{4}{3}m_2\ell_2^2 \end{array}\right] }_{M(\xi_1)} \underbrace{ \left[\begin{array}{c} \ddot{r} \\ \ddot{\theta}_1 \\ \ddot{\theta}_2 \end{array}\right] }_{\dot{\xi}_2}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 & -m_1\ell_2\sin\theta_2 \dot{\theta}_1 & -m_2\ell_2\sin\theta_2 \dot{\theta}_2\\ 0 & 0 & 0\\ 0 & 0 & 0\\ \end{array}\right] }_{C(\xi_1,\xi_2)} \underbrace{ \left[\begin{array}{c} \dot{r} \\ \dot{\theta}_1 \\ \dot{\theta}_2 \end{array}\right] }_{\dot{\xi}_1}}\\ \displaystyle{ +\underbrace{ \left[\begin{array}{ccc} 0 \\ -m_1\ell_1g\sin\theta_1\\ -m_2\ell_2g\sin\theta_2 \end{array}\right] }_{G(\xi_1)} = \underbrace{ \left[\begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right] F}_{\tilde{F}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-93481c5d4d113644bf7b152b46e9779f_l3.png)
![Rendered by QuickLaTeX.com (6.5)\quad \begin{array}{l} \displaystyle{ \frac{d}{dt}\left[\begin{array}{c} r\\ \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{r}\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right] =}\\ \displaystyle{ \left[\begin{array}{cccccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & -\frac{3m_1g}{Mm_1+m_1^2+(3M+m1)m_2} & -\frac{3m_2g}{Mm_1+m_1^2+(3M+m1)m_2} \\ 0 & \frac{3(4Mm_1+4m_1^2+3m_2^2+3(18M+13m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m1)m_2)\ell_1} & \frac{9(2M+m_1)m_2g}{(4Mm_1+m_1^2+(3M+m1)m_2)\ell_1} \\ 0 & \frac{9(2Mm_1+m_1^2+3(2M+m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} & \frac{3(4Mm_1+m_1^2+12(3M+m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} \\ \end{array}\right.}\\ \displaystyle{\left.\begin{array}{cccccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ \end{array}\right] \left[\begin{array}{c} r\\ \theta_1-\theta_1^*\\ \theta_2-\theta_2^*\\ \dot{r}\\ \dot{\theta}_1\\ \dot{\theta}_2 \end{array}\right]}\\ \displaystyle{+ \left[\begin{array}{c} 0\\ 0\\ 0\\ \frac{4m_1+3m_2}{4Mm_1+m_1^2+(3M+m1)m_2}\\ -\frac{3(2m_1+m2)}{2Mm_1+m_1^2+(3M+m1)m_2}\\ \frac{3m_1}{2(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} \end{array}\right] F} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0ded80f948ddab3f936f91c1c7ea13d2_l3.png)
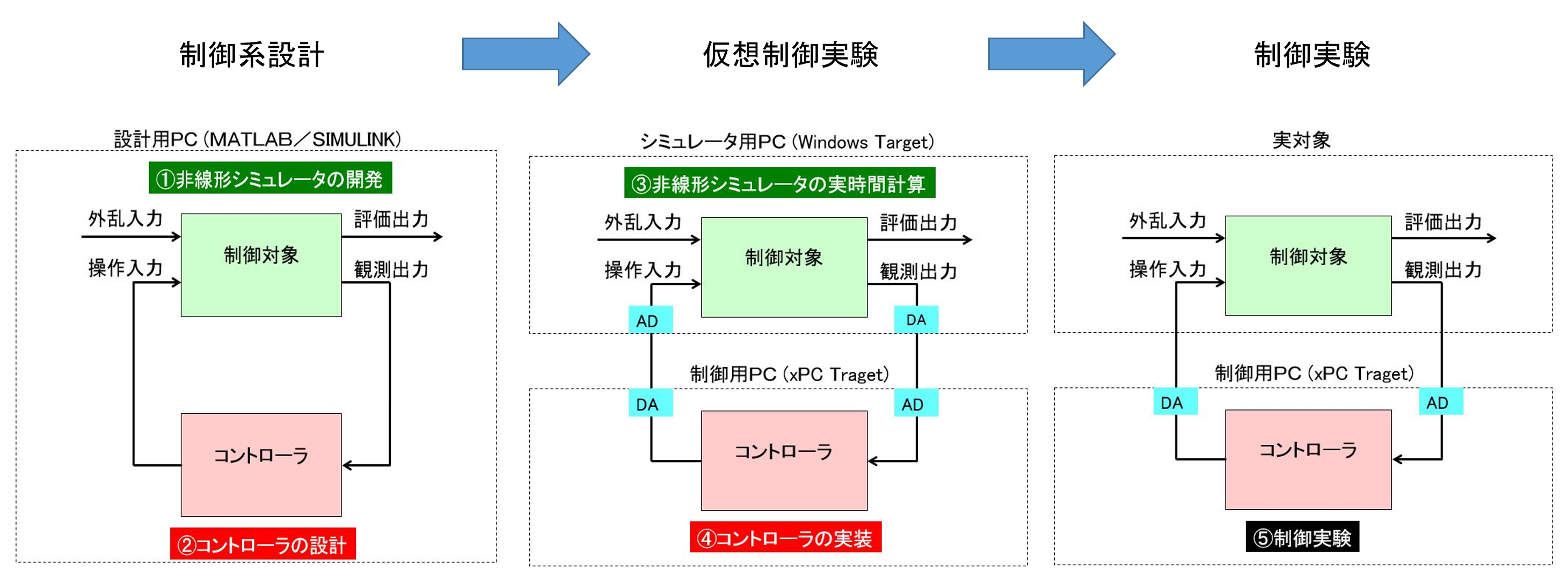 図1 HILS アプローチ
図1 HILS アプローチ 図2 単振り子
図2 単振り子 図3 単振り子の振動シミュレーション(モデルが線形か非線形か、初期状態を平衡状態周辺にとるかによる相違)
図3 単振り子の振動シミュレーション(モデルが線形か非線形か、初期状態を平衡状態周辺にとるかによる相違)![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \underbrace{ \left[\begin{array}{l} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{l} \omega(t) \\ -\frac{g}{L}\sin\theta(t) \end{array}\right] }_{f(x(t))} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ded67215525ba40fa5155a4367ed7405_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \underbrace{ \left[\begin{array}{l} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{g}{L}&0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{l} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ed5a0aa97035fe65dba8b64944a4a569_l3.png)
 図4 水タンクTANK
図4 水タンクTANK 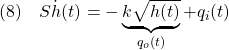
 図5 TANKの非線形シミュレータ
図5 TANKの非線形シミュレータ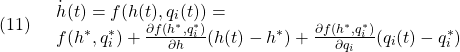
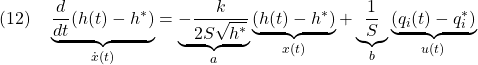
 図6 TANKの線形シミュレータ
図6 TANKの線形シミュレータ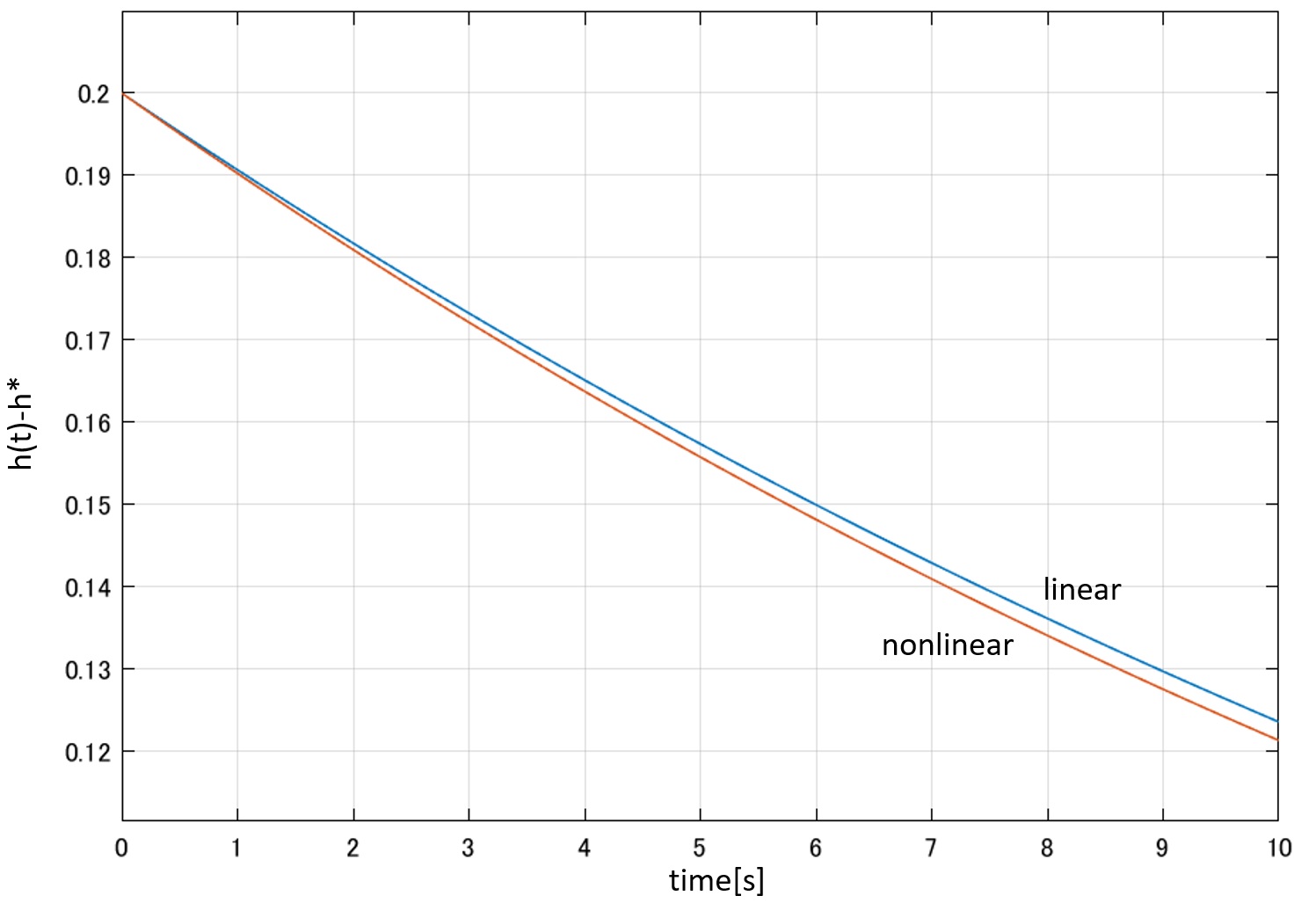 図7 TANKの非線形応答と線形応答の比較
図7 TANKの非線形応答と線形応答の比較 図8 TANKの非線形シミュレータと線形シミュレータ
図8 TANKの非線形シミュレータと線形シミュレータ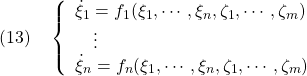
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \boxed{\dot{\xi}=f(\xi,\zeta)}\ \Leftrightarrow\ \underbrace{ \left[\begin{array}{l} \dot{\xi}_1 \\ \vdots \\ \dot{\xi}_n \end{array}\right] }_{\dot{\xi}} = \underbrace{ \left[\begin{array}{l} f_1(\xi,\zeta) \\ \quad\vdots \\ f_n(\xi,\zeta) \end{array}\right] }_{f(\xi,\zeta)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-92634287f13e8775d2c2a6ec25c7567c_l3.png)
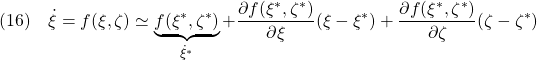
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad A=\frac{\partial\,f(\xi^*,\zeta^*)}{\partial\,\xi}= \left[\begin{array}{ccc} \frac{\partial f_1(\xi^*,\zeta^*)}{\partial \xi_1}&\cdots& \frac{\partial f_1(\xi^*,\zeta^*)}{\partial \xi_n}\\ \vdots&\ddots&\vdots\\ \frac{\partial f_n(\xi^*,\zeta^*)}{\partial \xi_1}&\cdots& \frac{\partial f_n(\xi^*,\zeta^*)}{\partial \xi_n} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9cbb1299b9fef4d94b388578973f2dd3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad B=\frac{\partial\,f(\xi^*,\zeta^*)}{\partial\,\zeta}= \left[\begin{array}{ccc} \frac{\partial f_1(\xi^*,\zeta^*)}{\partial \zeta_1}&\cdots& \frac{\partial f_1(\xi^*,\zeta^*)}{\partial \zeta_m}\\ \vdots&\ddots&\vdots\\ \frac{\partial f_n(\xi^*,\zeta^*)}{\partial \zeta_1}&\cdots& \frac{\partial f_n(\xi^*,\zeta^*)}{\partial \zeta_m} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-02d8fb9441471b4730389431ccc6f27c_l3.png)

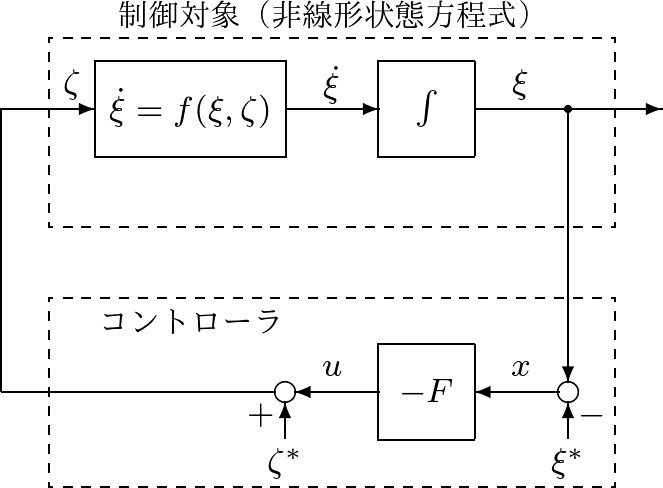
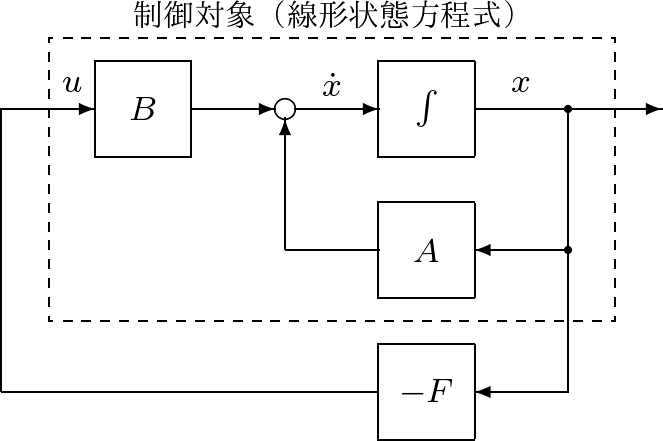
![Rendered by QuickLaTeX.com \displaystyle{(20)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{cc} \xi_1-\xi_1^* \\ \xi_2-\xi_2^* \end{array}\right] }_{\dot{x}=\dot{\xi}-\dot{\xi}^*}= \underbrace{ \left[\begin{array}{cc} \frac{\partial f_1(\xi^*,\tau^*)}{\partial \xi_1} & \frac{\partial f_1(\xi^*,\tau^*)}{\partial \xi_2} \\ \frac{\partial f_2(\xi^*,\tau^*)}{\partial \xi_1} & \frac{\partial f_2(\xi^*,\tau^*)}{\partial \xi_2} \end{array}\right] }_{A=\frac{\partial f(\xi^*,\tau^*)}{\partial \xi}} \underbrace{ \left[\begin{array}{l} \xi_1-\xi_1^* \\ \xi_2-\xi_2^* \end{array}\right] }_{x=\xi-\xi^*} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f2c5af558fdbb6c9d48962d44eed85a8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(22)\quad \underbrace{\frac{d}{dt} \left[\begin{array}{l} \xi_1 \\ \xi_2 \end{array}\right]}_{\dot{\xi}} =\underbrace{ \left[\begin{array}{l} \xi_2 \\ M^{-1}(\xi_1)(\zeta-C(\xi_1,\xi_2)\xi_2-G(\xi_1)) \end{array}\right]}_{f(\xi,\zeta)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5135df93ea761445ca840c16e381cc07_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(24)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{cc} \xi_1-\xi_1^* \\ \xi_2-\xi_2^* \end{array}\right] }_{\dot{x}}= \underbrace{ \left[\begin{array}{cc} 0 & I_n \\ A_{21} & A_{22} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{l} \xi_1-\xi_1^* \\ \xi_2-\xi_2^* \end{array}\right] }_{x}+ \underbrace{ \left[\begin{array}{cc} 0 \\ B_2 \end{array}\right] }_{B} \underbrace{ (\zeta-\zeta^*) }_{u} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-367b63505bbc335acbc7077f5650a169_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \underbrace{ \left[\begin{array}{l} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{3g}{4\ell}&0 \end{array}\right] }_{A_\alpha} \underbrace{ \left[\begin{array}{l} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aab7f16339e56d265534f36b3b8a9366_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{l} \theta(t)-\pi \\ \omega(t)-0 \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ \frac{3g}{4\ell}&0 \end{array}\right] }_{A_\beta} \underbrace{ \left[\begin{array}{l} \theta(t)-\pi \\ \omega(t)-0 \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-89b5ecb0d715edc56311f92b25c00853_l3.png)
 図2 剛体振り子と同じ周期をもつ単振り子の長さは?
図2 剛体振り子と同じ周期をもつ単振り子の長さは?
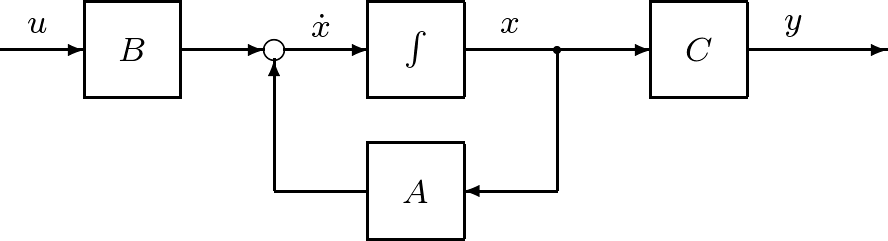 図1 状態空間表現(1)のブロック線図
図1 状態空間表現(1)のブロック線図 図2 マス・バネ・ダンパからなる機械系
図2 マス・バネ・ダンパからなる機械系![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \underbrace{ \left[\begin{array}{c} \dot{r}(t) \\ \dot{v}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{K}{M} & -\frac{D}{M} \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} r(t) \\ v(t) \end{array}\right] }_{x(t)}+ \underbrace{ \left[\begin{array}{c} 0 \\ \frac{1}{M} \end{array}\right] }_B u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0f9eee4a83cd00ce26d47f602e1c5d9a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \underbrace{r(t)}_{y(t)}= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} r(t) \\ v(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e6aa71a57291ccf1f09944a3b8846465_l3.png)
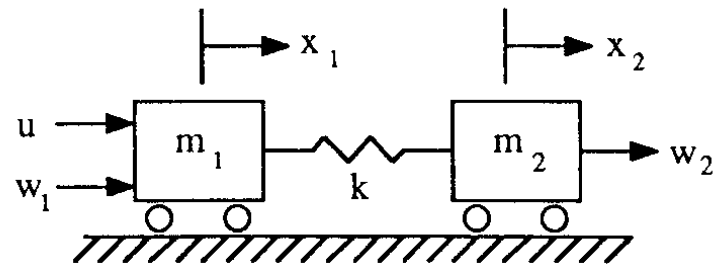
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \frac{d}{dt}\left[\begin{array}{c} x_1\\ x_2\\ \dot{x}_1\\ \dot{x}_2 \end{array}\right] = \left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{array}\right] \left[\begin{array}{c} x_1\\ x_2\\ \dot{x}_1\\ \dot{x}_2 \end{array}\right] + \left[\begin{array}{ccc} 0 & 0 & 0\\ 0 & 0 & 0\\ b_{31} & b_{32} & b_{33}\\ b_{41} & b_{42} & b_{43} \end{array}\right] \left[\begin{array}{c} u\\ w_1\\ w_2 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-797fe9e960cb81c588217b74e17d70fb_l3.png)
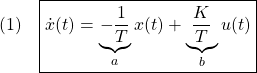
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \boxed{ \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] }_{\dot x} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{c} 0 \\ K\omega_n^2 \end{array}\right] }_{B} u(t) }}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-04009ed3d0edf5fa5a2060e9508b3422_l3.png)
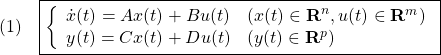
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \boxed{\left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right]= \left[\begin{array}{cc} A_1 & B_1C_2 \\ 0 & A_2 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] + \left[\begin{array}{cc} B_1D_2 \\ B_2 \end{array}\right] u_2(t) \\ y_1(t)= \left[\begin{array}{cc} C_1 & D_1C_2 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] +D_1D_2u_2(t) \end{array}\right.} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-36963521878ef7dd0808b96bae3bfff3_l3.png)
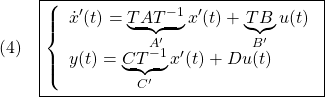
![Rendered by QuickLaTeX.com (4)\quad \begin{array}{l} \displaystyle{x(t)=e^{(a-bf)t}x(0)+\int_0^t e^{(a-bf)(t-\tau)}w\,d\tau}\\ \displaystyle{=e^{(a-bf)t}x(0)+\left[\frac{1}{-(a-bf)}e^{(a-bf)(t-\tau)}w\right]_0^t}\\ \displaystyle{=e^{(a-bf)t}x(0)+\frac{w}{-(a-bf)}(1-e^{(a-bf)t})}\\ \displaystyle{\rightarrow \frac{w}{-(a-bf)}\ne 0 \quad (t\rightarrow\infty)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-87ff2adf2a1f8bd25d390b2196807faa_l3.png)
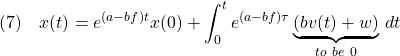
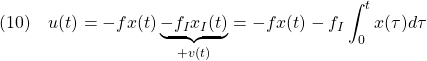
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad {\underbrace{ \left[\begin{array}{cc} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] }_{\dot{x}_E} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf_I \\ 1 & 0 \end{array}\right] }_{A_{EF}} \underbrace{ \left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] }_{x_E} + \underbrace{ \left[\begin{array}{cc} w \\ 0 \end{array}\right] }_{w_E}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-31b2a3c2e865a17fd4319135d80cb684_l3.png)
![Rendered by QuickLaTeX.com (14)\quad \begin{array}{l} \displaystyle{x_E(t)=\exp(A_{EF}t)x_E(0)+\int_0^t\exp(A_{EF}(t-\tau))w_E\,d\tau}\\ \displaystyle{=\exp(A_{EF}t)x_E(0)+\left[-\exp(A_{EF}(t-\tau))A_{EF}^{-1}w_E\right]_0^t}\\ \displaystyle{=\exp(A_{EF}t)x_E(0)-(I_2-\exp(A_{EF}t))A_{EF}^{-1}w_E}\\ \displaystyle{=\exp(A_{EF}t)(x_E(0)+A_{EF}^{-1}w_E)-A_{EF}^{-1}w_E}\\ \displaystyle{\rightarrow -A_{EF}^{-1}w_E \quad (t\rightarrow\infty)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3bca83642ec9ba9f633fe5e502d53148_l3.png)
![Rendered by QuickLaTeX.com (15)\quad \begin{array}{l} \displaystyle{\left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] \rightarrow - \left[\begin{array}{cc} a-bf & -bf_I \\ 1 & 0 \end{array}\right]^{-1} \left[\begin{array}{cc} w \\ 0 \end{array}\right]}\\ \displaystyle{ = -\frac{1}{bf_I} \left[\begin{array}{cc} 0 & bf_I \\ -1 & a-bf \end{array}\right] \left[\begin{array}{cc} w \\ 0 \end{array}\right] = \left[\begin{array}{cc} 0 \\ \frac{1}{bf_I}w \end{array}\right]} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b2e96500c3db9199db1fbc40cbaa0029_l3.png)
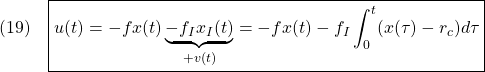
![Rendered by QuickLaTeX.com \displaystyle{(20)\quad \boxed{\underbrace{ \left[\begin{array}{cc} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] }_{\dot{x}_E} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf_I \\ 1 & 0 \end{array}\right] }_{A_{EF}} \underbrace{ \left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] }_{x_E} + \underbrace{ \left[\begin{array}{cc} w \\ -r_c \end{array}\right] }_{w_E}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ddef16b35db1273870bc586e72b3bb5a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(21)\quad \begin{array}{l} \displaystyle{\left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] \rightarrow - \left[\begin{array}{cc} a-bf & -bf_I \\ 1 & 0 \end{array}\right]^{-1} \left[\begin{array}{cc} w \\ -r_c \end{array}\right]}\\ \displaystyle{= -\frac{1}{bf_I} \left[\begin{array}{cc} 0 & bf_I \\ -1 & a-bf \end{array}\right] \left[\begin{array}{cc} w \\ -r_c \end{array}\right] = \left[\begin{array}{cc} r_c \\ \frac{1}{bf_I}w+\frac{a-bf}{bf_I}r_c \end{array}\right]} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f812ff0b7b34a62587cc56d0da3ad5fd_l3.png)
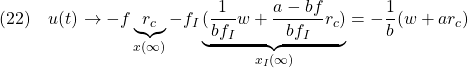
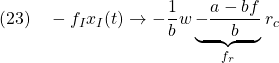
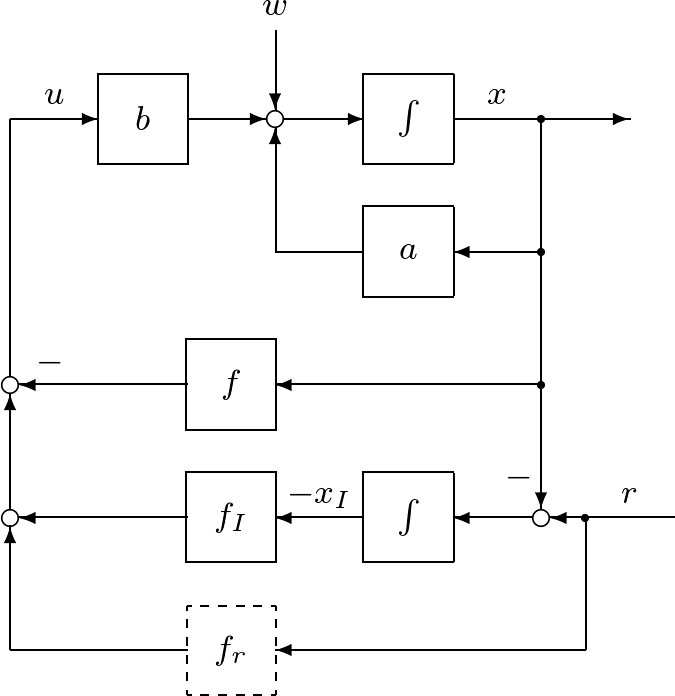
 図2 図1のシミュレーション例
図2 図1のシミュレーション例![Rendered by QuickLaTeX.com \displaystyle{(31)\quad \boxed{ \begin{array}{l} \left[\begin{array}{c} \dot{\hat{x}}(t) \\ \dot{x}_I(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} a-hc-bf & -bf_I \\ 0 & 0 \end{array}\right] }_{A_K} \left[\begin{array}{c} \hat{x}(t) \\ x_I(t) \end{array}\right] + \underbrace{ \left[\begin{array}{cc} h & 0\\ 1 & -1 \end{array}\right] }_{B_K} \left[\begin{array}{c} y(t) \\ r_c \end{array}\right]\\ u(t)= \underbrace{- \left[\begin{array}{cc} f & f_I \end{array}\right] }_{C_K} \left[\begin{array}{c} \hat{x}(t) \\ x_I(t) \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c9a64fdc6b3c7ee88c4b4ccbe8c58b7b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(33)\quad \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \\ \dot{\hat{x}}(t) \end{array}\right] = \left[\begin{array}{ccc} a & -bf_I & -bf \\ c & 0 & 0 \\ hc & -bf_I & a-hc-bf \end{array}\right] \left[\begin{array}{c} x(t) \\ x_I(t) \\ \hat{x}(t) \end{array}\right] + \left[\begin{array}{c} w \\ -r_c \\ 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ec175798327a5fc11b68b91a22172f0d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(34)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \\ e(t) \end{array}\right] = \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ -1 & 0 & 1 \end{array}\right] \left[\begin{array}{c} x(t) \\ x_I(t) \\ \hat{x}(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7ca97b463935b7f71dea225ffcb573f2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(35)\quad \boxed{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \\\hline \dot{e}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc|c} a-bf & -bf_I & -bf \\ c & 0 & 0 \\\hline 0 & 0 & a-hc \end{array}\right] }_{ A_{EF}'= \left[\begin{array}{c|c} A_{EF} & - \left[\begin{array}{cc} bf \\ 0 \end{array}\right] \\[5mm] \hline 0 & \widehat{a} \end{array}\right] } \left[\begin{array}{c} x(t) \\ x_I(t) \\\hline e(t) \end{array}\right] + \left[\begin{array}{c} w \\ -r_c \\\hline -w \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3a0c12a07d48d608c414bfef747b7ae3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(36)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \\\hline e(t) \end{array}\right] \ \rightarrow\ \underbrace{ \left[\begin{array}{c|c} A_{EF}^{-1} & -A_{EF}^{-1} \left[\begin{array}{cc} bf \\ 0 \end{array}\right] \widehat{a}^{-1} \\[5mm]\hline 0 & \widehat{a}^{-1} \end{array}\right] }_{A_{EF}'\,^{-1}} \left[\begin{array}{c} -w \\ r_c \\\hline w \end{array}\right] \quad (t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c8709893951656a10a2cf0aec18bef8b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(37)\quad \begin{array}{l} \displaystyle{\left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] \rightarrow \left[\begin{array}{cc} a-bf & -bf_I \\ c & 0 \end{array}\right]^{-1} \left[\begin{array}{cc} -w-bf\widehat{a}^{-1}w\\ r_c \end{array}\right]}\\ \displaystyle{= \frac{1}{cbf_I} \left[\begin{array}{cc} 0 & bf_I \\ -c & a-bf \end{array}\right] \left[\begin{array}{cc} -w-bf\widehat{a}^{-1}w\\ r_c \end{array}\right]}\\ \displaystyle{= \left[\begin{array}{cc} \frac{1}{c}r_c \\ \frac{1}{bf_I}w+\frac{1}{f_I}f\widehat{a}^{-1}w+\frac{a-bf}{cbf_I}r_c \end{array}\right]} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a0408f31040df6a4e4b055bc9c88bc05_l3.png)
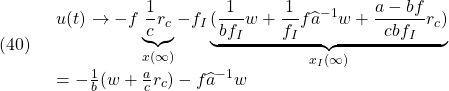
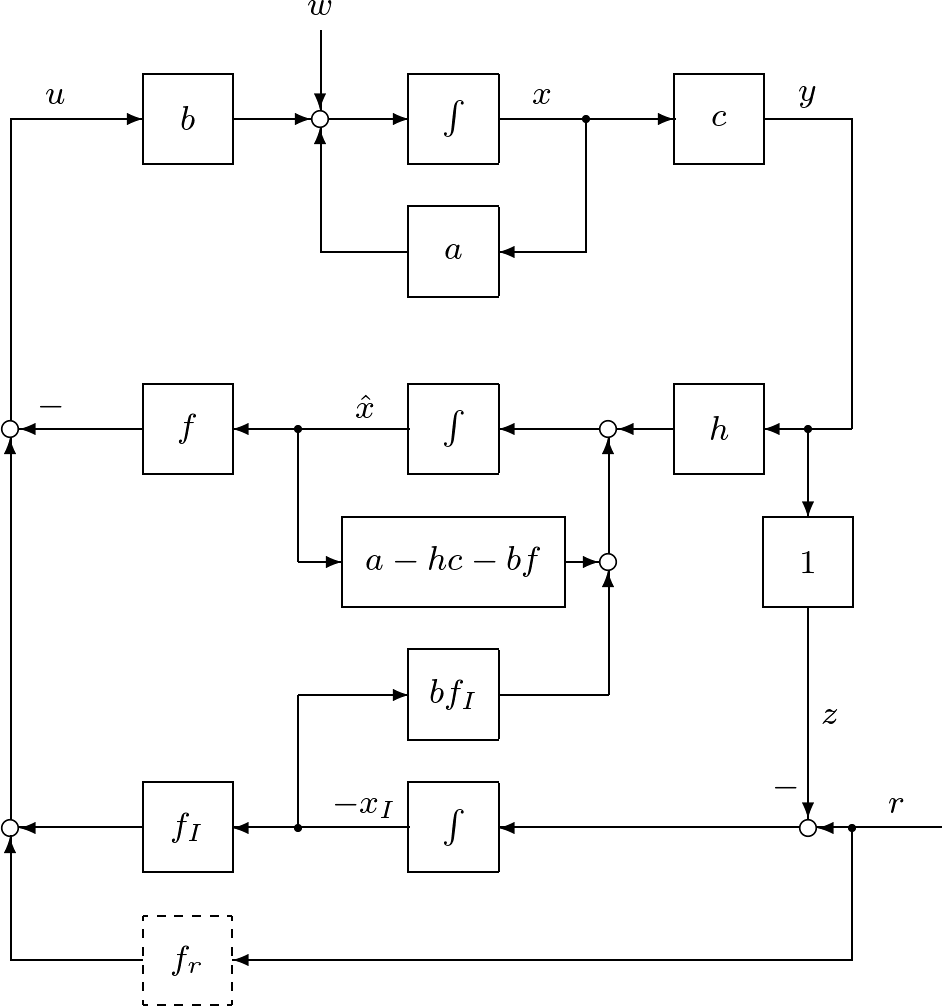 図3 積分動作を加えたオブザーバベースコントローラによる閉ループ系
図3 積分動作を加えたオブザーバベースコントローラによる閉ループ系![Rendered by QuickLaTeX.com \displaystyle{(41)\quad \underbrace{ \left[\begin{array}{cc} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] }_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf_I \\ c & 0 \end{array}\right] }_{A_{EF}} \underbrace{ \left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] }_{x_E(t)} + \underbrace{ \left[\begin{array}{cc} w \\ -r_c \end{array}\right] }_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f729fc6c953923d57572c53768579876_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(43)\quad \underbrace{ \left[\begin{array}{cc} qx(t)\\ ru(t) \end{array}\right] }_{y_{E}(t)} = \underbrace{ \left[\begin{array}{cc} q & 0 \\ -rf & -rf_I \end{array}\right] }_{C_{E}} \underbrace{ \left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] }_{x_{E}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0d18a388e7b6c8f9fa04453e84d71145_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(47)\quad \underbrace{\frac{d}{dt} \left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] }_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} a & 0 \\ c & 0 \end{array}\right] }_{A_E} \underbrace{ \left[\begin{array}{cc} x(t) \\ x_I(t) \end{array}\right] }_{x_E(t)} + \underbrace{ \left[\begin{array}{cc} b \\ 0 \end{array}\right] }_{B_E} u(t) + \underbrace{ \left[\begin{array}{cc} w \\ -r_c \end{array}\right] }_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4e152ba9118c145fdc3aa9097ad1291f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(48)\quad \underbrace{\frac{d}{dt} \left[\begin{array}{cc} x_\infty \\ x_{I\infty} \end{array}\right] }_{\dot{x}_{E\infty}=0} = \underbrace{ \left[\begin{array}{cc} a & 0 \\ c & 0 \end{array}\right] }_{A_E} \underbrace{ \left[\begin{array}{cc} x_\infty \\ x_{I\infty} \end{array}\right] }_{x_{E\infty}} + \underbrace{ \left[\begin{array}{cc} b \\ 0 \end{array}\right] }_{B_E} u_\infty + \underbrace{ \left[\begin{array}{cc} w \\ -r_c \end{array}\right] }_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-388e3b63a548f6ae3de1bca82350d6b8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(49)\quad \boxed{ \underbrace{\frac{d}{dt} \left[\begin{array}{cc} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{\dot{x}_{E1}(t)} = \underbrace{ \left[\begin{array}{cc} a & 0 \\ c & 0 \end{array}\right] }_{A_{E1}} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{x_{E1}(t)} + \underbrace{ \left[\begin{array}{cc} b \\ 0 \end{array}\right] }_{B_{E1}} \underbrace{(u(t)-u_\infty)}_{u_{E1}(t)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ef61060eeffd371eb2eb609612504541_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(50)\quad \underbrace{u(t)-u_\infty}_{u_{E1}(t)} =- \underbrace{ \left[\begin{array}{cc} f & f_I \end{array}\right] }_{F_E} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{x_{E1}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2de715ba671f8a4ff5fe87b581f7486f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(51)\quad \underbrace{\frac{d}{dt} \left[\begin{array}{cc} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{\dot{x}_{E1}(t)} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf_I \\ c & 0 \end{array}\right] }_{A_{EF}} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{x_{E1}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0ac4b58fae5895656374987e2e2dfb53_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(52)\quad \underbrace{ \left[\begin{array}{cc} q(x(t)-x_\infty) \\ r(u(t)-u_\infty) \end{array}\right] }_{y_{E1}(t)} = \underbrace{ \left[\begin{array}{cc} q & 0 \\ -rf & -rf_I \end{array}\right] }_{C_{E1}} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{x_{E1}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f6ff94e985ffd90ab5da603d6e28d94f_l3.png)
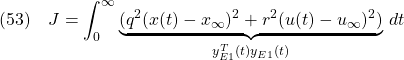
![Rendered by QuickLaTeX.com \displaystyle{(54)\quad \boxed{ \underbrace{\frac{d}{dt} \left[\begin{array}{cc} \dot{x}(t) \\ x(t)-r_c \end{array}\right] }_{\dot{x}_{E2}(t)} = \underbrace{ \left[\begin{array}{cc} a & 0 \\ c & 0 \end{array}\right] }_{A_{E2}} \underbrace{ \left[\begin{array}{cc} \dot{x}(t) \\ x(t)-r_c \end{array}\right] }_{x_{E2}(t)} + \underbrace{ \left[\begin{array}{cc} b \\ 0 \end{array}\right] }_{B_{E2}} \underbrace{\dot{u}(t)}_{u_{E2}(t)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d55bc528b4211e44104d9a016f1efe77_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(55)\quad \left[\begin{array}{cc} \dot{x}(t) \\ x(t)-r_c \end{array}\right] = \underbrace{ \left[\begin{array}{cc} a & b \\ c & 0 \end{array}\right] }_{S} \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b36ebc36ec3a8aa2b181e54a374490a4_l3.png)
![Rendered by QuickLaTeX.com (56)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} a & b \\ c & 0 \end{array}\right] }_{S} \frac{d}{dt} \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right]=\\ \underbrace{ \left[\begin{array}{cc} a & 0 \\ 1 & 0 \end{array}\right] }_{A_{E2}} \underbrace{ \left[\begin{array}{cc} a & b \\ c & 0 \end{array}\right] }_{S} \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] + \underbrace{ \left[\begin{array}{cc} b \\ 0 \end{array}\right] }_{B_{E2}} \underbrace{\dot{u}(t)}_{u_{E2}(t)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3fe9bb9955ebd8e2c8e93bbd706c8fe9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(57)\quad \boxed{\underbrace{ \frac{d}{dt} \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{\dot{x}_{E3}} = \underbrace{ \left[\begin{array}{cc} a & b \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}} + \underbrace{ \left[\begin{array}{cc} 0 \\ 1 \end{array}\right] }_{B_{E3}} \underbrace{\dot{u}(t)}_{u_{E3}(t)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c85ae085cc84c481ab12fad21f3f8ae0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(58)\quad \underbrace{\dot{u}(t)}_{u_{E3}(t)} =- \underbrace{ \left[\begin{array}{cc} k & k_I \end{array}\right] }_{K_E} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b8ffb28df7a25dd49c60692720881d34_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(59)\quad \underbrace{\frac{d}{dt} \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} a & b \\ -k & -k_I \end{array}\right] }_{A_{EK}} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-150f484db41dfcfd7bc2713f40cf1398_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(60)\quad \underbrace{ \left[\begin{array}{cc} q(x(t)-x_\infty) \\ r\dot{u}(t) \end{array}\right] }_{y_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} q & 0 \\ 0 & r\frac{d}{dt} \end{array}\right] }_{C_{E3}} \underbrace{ \left[\begin{array}{cc} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-36376901e37df555679c68adbb340194_l3.png)
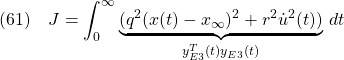
![Rendered by QuickLaTeX.com \displaystyle{(62)\quad \dot{u}(t) =- \underbrace{ \left[\begin{array}{cc} k & k_I \end{array}\right] }_{K_E} \underbrace{ \left[\begin{array}{cc} a & b \\ 1 & 0 \end{array}\right]^{-1} }_{S^{-1}} \left[\begin{array}{cc} \dot{x}(t) \\ x(t)-r_c \end{array}\right] =- \underbrace{ \left[\begin{array}{cc} f & f_I \end{array}\right] }_{F_E=K_ES^{-1}} \left[\begin{array}{cc} \dot{x}(t) \\ x(t)-r_c \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-84e71c3cc59f8a7feeedd162fdda01c6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(64)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} a & b \\ 0 & 0 \end{array}\right] }_{A_{E}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_{E}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0c41509ad03419a701e8ac16d5e5fdd9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(70)\quad \begin{array}{l} \dot{x}_K(t)=A_Kx_K(t)+B_K \left[\begin{array}{c} y(t) \\ r_c \end{array}\right]\\ u(t)=C_Kx_K(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a49a6c693b0b6603def7809f250eda5e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(71)\quad \begin{array}{l} A_K= \left[\begin{array}{cc} a-hc-bf & -bf_I \\ 0 & 0 \end{array}\right]\\ B_K= \left[\begin{array}{cc} h & 0\\ 1 & -1 \end{array}\right]\\ C_K=- \left[\begin{array}{cc} f & f_I \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-78a0c63e2aa625650bb1f5593550221b_l3.png)