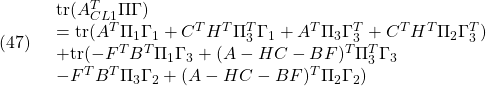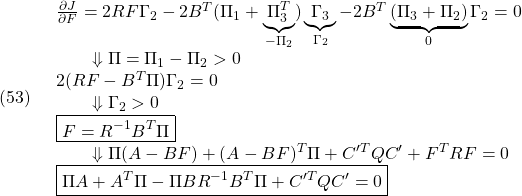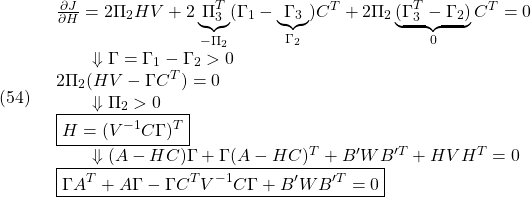特異値分解(Singular-Value Decomposition)
●![]() をサイズ
をサイズ![]() の行列(
の行列(![]() )とします。このとき、サイズ
)とします。このとき、サイズ![]() の直交行列
の直交行列![]() とサイズ
とサイズ![]() の直交行列
の直交行列![]() が存在して
が存在して
![]()
が成り立ちます。ここで、サイズ![]() の行列
の行列![]() は次を満たします。
は次を満たします。
![]()
![]()
●![]() だから、仮定
だから、仮定![]() より、
より、![]() は
は![]() 個の正固有値と
個の正固有値と![]() 個の零固有値をもち、互いに直交する固有ベクトルをもちます。そこで、
個の零固有値をもち、互いに直交する固有ベクトルをもちます。そこで、![]() の固有値の正の平方根を、大きい順に、
の固有値の正の平方根を、大きい順に、![]() のように表し、対応する固有ベクトル
のように表し、対応する固有ベクトル![]() を
を![]() を満足するようにとることができます。いま、
を満足するようにとることができます。いま、![]() を上のように、また
を上のように、また
![]()
とおくと、![]() は直交行列となり、つぎが成り立ちます。
は直交行列となり、つぎが成り立ちます。
![]()
第2式の左から、![]() をかけて
をかけて
![]()
また、![]() とおくと、第1式から
とおくと、第1式から![]() を得ます。そこで、
を得ます。そこで、![]() を
を![]() が直交行列となるように選ぶと
が直交行列となるように選ぶと
![]()
が成り立ちます。
●行列![]() の特異値分解は
の特異値分解は
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad A= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{U} \underbrace{ \left[\begin{array}{ccc} \sqrt{2} & 0 & 0 \\ 0 & 1 & 0 \end{array}\right] }_{\Sigma} \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ \frac{1}{\sqrt{2}} & 0 & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{array}\right]^T }_{V^T} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2af72a50a4707c3528e66ecddb5d79d3_l3.png)
のように与えられることを確かめます。
●![]() のサイズは
のサイズは![]() ですが、
ですが、![]() のサイズは
のサイズは![]() であるので、
であるので、![]() を計算すると
を計算すると![]() となります(サイズ
となります(サイズ![]() の行列
の行列![]() の特異値を手計算で求めるには、
の特異値を手計算で求めるには、![]() と
と![]() のが同じ非零固有値をもつことから、サイズの小さいほうの固有値計算を行えばよい)。これから、
のが同じ非零固有値をもつことから、サイズの小さいほうの固有値計算を行えばよい)。これから、![]() の固有値は
の固有値は![]() で、その正の平方根
で、その正の平方根![]() が特異値で、上の
が特異値で、上の![]() の対角成分の特異値は大きい順に並べる約束ですから
の対角成分の特異値は大きい順に並べる約束ですから
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ 0 & 2 \end{array}\right] }_{AA^T} \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{U} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{U} \underbrace{ \left[\begin{array}{cc} 2 & 0 \\ 0 & 1 \end{array}\right] }_{\Sigma_1^2} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6f51f7ede73c92e99db76c7c0af734a4_l3.png)
のように、![]() と
と![]() が決まります。つぎに、
が決まります。つぎに、![]() については、視察によって
については、視察によって
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 1 & 1 \end{array}\right] }_{A^TA} \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ x & 0 & -y \\ y & 0 & x \end{array}\right] }_{V} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ x & 0 & -y \\ y & 0 & x \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{ccc} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array}\right] }_{{\rm diag}\{\Sigma_1^2,0\}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-80803b0ba51318c2e2c0a244cacf7e45_l3.png)
とします。ここで、![]() と
と![]() が直交しており、
が直交しており、![]() の制約があります。上式から
の制約があります。上式から![]() が出て、
が出て、![]() と定まります。
と定まります。
行列のノルム
● ![]() から
から![]() への写像
への写像![]() の「伝達特性」をどう測るかを考えます。これはスカラの場合は正比例の関係
の「伝達特性」をどう測るかを考えます。これはスカラの場合は正比例の関係![]() ですから、比例定数
ですから、比例定数![]() に相当する量を求める話になります。
に相当する量を求める話になります。
サイズ![]() の行列
の行列![]() の次の特異値分解を考えます。
の次の特異値分解を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} A= \underbrace{ \left[\begin{array}{cc} U_1 & U_2 \end{array}\right] }_{U(m\times m)} \underbrace{ \left[\begin{array}{cc} {\rm diag}\{\sigma_1,\cdots,\sigma_k\} & 0_{k\times (n-k)} \\ 0_{(m-k)\times k} & 0_{(m-k)\times (n-k)} \end{array}\right] }_{\Sigma= \left[\begin{array}{cc} \Sigma_1 & 0 \\ 0 & 0 \end{array}\right] \quad(\sigma_1\ge\cdots\ge\sigma_k) } \underbrace{ \left[\begin{array}{cc} V_1^T \\ V_2^T \end{array}\right] }_{V(n\times n)^T}\\ =U_1(m\times k)\Sigma_1(k\times k)V_1(n\times k)^T \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dc89eab35a6815c659415bf9a11570b9_l3.png)
ここで、![]() で、
で、![]() と
と![]() は直交行列です。
は直交行列です。
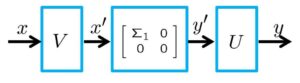
![]()
したがって、次のような3つの線形写像に分解されます。
●![]() 次元ベクトル
次元ベクトル![]() のノルムとして、次の3通りが知られています。
のノルムとして、次の3通りが知られています。
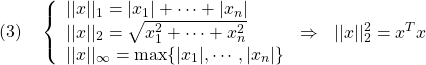
以下では、ベクトルのノルムとして、2番目の2ノルムを考えます。
このとき、次が成り立ちます。
![]()
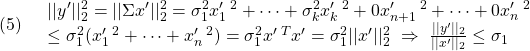
![]()
すなわち
![]()
したがって、線形写像![]() の伝達特性は、行列
の伝達特性は、行列![]() の2ノルム
の2ノルム
![]()
すなわち行列![]() の最大特異値
の最大特異値![]() (行列
(行列![]() または
または![]() の最大固有値の正の平方根)によって表されます。
の最大固有値の正の平方根)によって表されます。
●行列のノルムについて次式が成り立ちます。
![]()
(8)より
![]()
に注意して
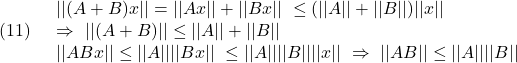
●一方、ベクトルの2ノルムについて次式が成り立ちます。
![]()
これらは(9)の特別な場合と考えられますが、ここでは直接導出してみます。
いま、![]() に関する2次方程式
に関する2次方程式
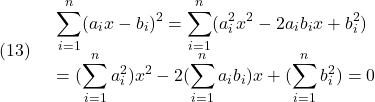
を考えると、この実数解は1個または0個となることから、この判別式は零または負でなければならないので

より
![]()
すなわち(12)の第2式が得られます。また、第1式は、次式から得られます。
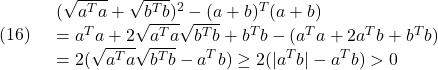
●ちなみに、行列のフロベニウスノルムは

で定義されます。これは
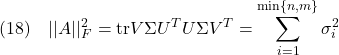
と表せるので、次式が成り立ちます。
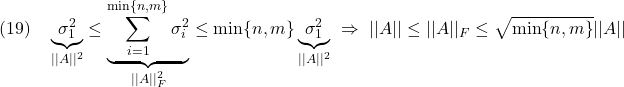
行列積のフロベニウスノルムについても

が成り立ちます。
連立1次方程式
次の線形方程式(連立1次方程式)を考えます。
![]()
ここで、![]() はフルランク(
はフルランク(![]() )とします。
)とします。
![]()
![]() の場合(未知数の数が方程式の数より大きい場合)、(1)はunder-determined(劣決定)と呼ばれ、
の場合(未知数の数が方程式の数より大きい場合)、(1)はunder-determined(劣決定)と呼ばれ、![]() の特異値分解を代入して次のように書けます。
の特異値分解を代入して次のように書けます。
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \begin{array}{l} \underbrace{U\left[\begin{array}{cc} \Sigma_1 & 0_{n\times m-n} \end{array}\right] \left[\begin{array}{c} V_1^H\\ V_2^H \end{array}\right]}_{A}x =U\Sigma_1V_1^Hx=b\\ \Sigma_1={\rm diag}\{\sigma_1,\cdots,\sigma_n\} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2633ba4a0b1a6e8db6ae07669f36a2f2_l3.png)
(2)の解候補として
![]()
を考えます。![]() より第1項と第2項は直交することから
より第1項と第2項は直交することから
![]()
(3)において![]() として得られる
として得られる![]() は、
は、![]() を最小化する最小ノルム解と呼ばれます。
を最小化する最小ノルム解と呼ばれます。
![]()
![]() の場合(未知数の数が方程式の数より小さい場合)、(1)はover-determined(過決定)と呼ばれ、
の場合(未知数の数が方程式の数より小さい場合)、(1)はover-determined(過決定)と呼ばれ、![]() の特異値分解を代入して次のように書けます。
の特異値分解を代入して次のように書けます。
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} U_1 & U_2 \end{array}\right] \left[\begin{array}{cc} \Sigma_1 \\ 0_{n-m\times m} \end{array}\right]V^H}_{A}x =U_1\Sigma_1V^Hx=b\\ \Sigma_1={\rm diag}\{\sigma_1,\cdots,\sigma_m\} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-89dad140495fae168ea6b37fa797cbe0_l3.png)
(5)の解候補として
![]()
を考えます。![]() において、
において、
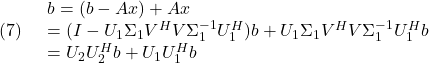
ここで、![]() より第1項と第2項は直交することから
より第1項と第2項は直交することから
![]()
(6)は![]() を最小化する最小2乗解と呼ばれます。
を最小化する最小2乗解と呼ばれます。
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array}\right]= \underbrace{\lambda_RI_2}_{X}+ \underbrace{\lambda_I \left[\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array}\right]}_{Y} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-90093f23486e9ebe543a4f748c41bfee_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{cc} \lambda & 1 \\ 0 & \lambda \end{array}\right]= \underbrace{\lambda I_2}_{X}+ \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right]}_{Y} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b6261249b8a119844a069dd65ff1df8e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{1^{\circ}\ \lambda(A)=\{\lambda_1,\lambda_2,\lambda_3\} \ \Rightarrow\ \Lambda_1=\left[\begin{array}{ccc} \lambda_1 & 0 & 0\\ 0 & \lambda_2 & 0\\ 0 & 0 & \lambda_3 \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3bd2b1a89b6bfe05ac946135ab4a5d46_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{2^{\circ}\ \lambda(A)=\{\lambda_R\pm j\lambda_I,\lambda\} \ \Rightarrow\ \Lambda_2=\left[\begin{array}{ccc} \lambda_R & \lambda_I & 0 \\ -\lambda_I & \lambda_R & 0 \\ 0 & 0 & \lambda \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8d85c1f19ccd0787c5b71e7d54877f24_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{3^{\circ}\ \lambda(A)=\{\lambda,\lambda,\lambda\} \ \Rightarrow\ \Lambda_3=\left[\begin{array}{ccc} \lambda & 1 & 0\\ 0 & \lambda & 1\\ 0 & 0 & \lambda \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a9eba9ac8ad743586bd7194d7fa3fa9d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{4^{\circ}\ \lambda(A)=\{\lambda,\lambda,\lambda'\} \ \Rightarrow\ \Lambda_4=\left[\begin{array}{ccc} \lambda & 1 & 0\\ 0 & \lambda & 0\\ 0 & 0 & \lambda' \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a07d669a93607f058df5310169859209_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{1^{\circ}\quad \exp(\Lambda_1 t)= \left[\begin{array}{ccc} e^{\lambda_1t} & 0 & 0\\ 0 & e^{\lambda_2 t} & 0\\ 0 & 0 & e^{\lambda_3 t} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a63717de8968d9c6311bc7099c27239e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{2^{\circ}\quad \exp(\Lambda_2 t)= \left[\begin{array}{ccc} e^{\lambda_R t}\cos(\lambda_It) & e^{\lambda_R t}\sin(\lambda_It) & 0\\ -e^{\lambda_R t}\sin(\lambda_It) & e^{\lambda_R t}\cos(\lambda_It) & 0\\ 0 & 0 & e^{\lambda t} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-13e0a88c983f834e8e6fbecebc725300_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{3^{\circ}\quad \exp(\Lambda_3 t)=e^{\lambda t} \left[\begin{array}{ccc} 1 & t & \frac{t^2}{2} \\ 0 & 1 & t \\ 0 & 0 & 1 \\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-017f57a48ebbb02c3f52a23e04f45293_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{4^{\circ}\quad \exp(\Lambda_4 t)= \left[\begin{array}{ccc} e^{\lambda t} & te^{\lambda t} & 0\\ 0 & e^{\lambda t} & 0\\ 0 & 0 & e^{\lambda t} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-657e4756bd61e0d0a2b833dfd26b89b3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{1^{\circ}\quad J(\lambda,m)= \left[\begin{array}{cccc} \lambda & 1 & & \\ & \lambda & \ddots & \\ & & \ddots & 1 \\ & & & \lambda \end{array}\right]\in{\bf R}^{m\times m} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-04756fbeb2c116fc5699aa675a993865_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{2^{\circ}\quad K(\lambda_{R},\lambda_{I},\ell)= \left[\begin{array}{c|c|cc|c} \begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array} & \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} & & \\ \hline & \begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array} & \ddots & & \\ \hline & & & & \\ \hline & & & \ddots & \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \\ \hline & & & & \begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array} \end{array}\right]\in{\bf R}^{2\ell\times 2\ell} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c2457aec06eab348db71633eafce1fb6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{1^{\circ}\quad \exp(J(\lambda,m)t)=e^{\lambda t} \left[\begin{array}{ccccc} 1 & t & \frac{t^2}{2} & \cdots & \frac{t^{m-1}}{(m-1)!} \\ & 1 & t & \ddots & \vdots \\ & & 1 & \ddots & \frac{t^2}{2} \\ & & & \ddots & t \\ & & & & 1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-214e860d644b198e7698b96f6af38b67_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ J(\lambda,m)= \underbrace{\lambda I_m}_{X}+ \underbrace{ \left[\begin{array}{cccc} 0 & 1 & & \\ & 0 & \ddots & \\ & & \ddots & 1 \\ & & & 0 \end{array}\right]}_{Y} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9840463b7dde1311b1a95f279ea67627_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ K(\lambda_{R},\lambda_{I},\ell)= \underbrace{\left[\begin{array}{cccc} \lambda_R & 1 & & \\ & \lambda_R & \ddots & \\ & & \ddots & 1 \\ & & & \lambda_R \end{array}\right] \otimes I_2 }_{X}+ \underbrace{I_\ell\otimes \lambda_I \left[\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array}\right] }_{Y} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c2321bffd746beb1183eafb2647ad175_l3.png)

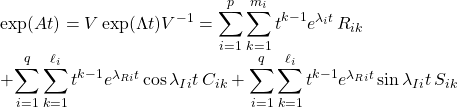
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{cc} v_{i1} \\ v_{i2} \end{array}\right] }_{v_i} = \lambda_i \underbrace{ \left[\begin{array}{cc} v_{i1} \\ v_{i2} \end{array}\right] }_{v_i}\quad(i=1,2)](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0831f4b46506687c014d958aea592423_l3.png)
![Rendered by QuickLaTeX.com \left\{\begin{array}{cc} Av_1=\lambda_1v_1\\ Av_2=\lambda_2v_2 \end{array}\right. \Leftrightarrow A \underbrace{ \left[\begin{array}{cc} v_1 & v_2 \end{array}\right] }_{V} = \underbrace{ \left[\begin{array}{cc} v_1 & v_2 \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda_1 & 0\\ 0 & \lambda_2 \end{array}\right] }_{\Lambda}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6d70b3d97f81ed2c410f999d9f9b0f72_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ J(\lambda,m)= \left[\begin{array}{cccc} \lambda & 1 & & \\ & \lambda & \ddots & \\ & & \ddots & 1 \\ & & & \lambda \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-10b37546f982ad32792ade27dcbb5bc5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ K(\lambda_{R},\lambda_{I},\ell)= \left[\begin{array}{c|c|cc|c} \begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array} & \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} & & \\ \hline & \begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array} & \ddots & & \\ \hline & & & & \\ \hline & & & \ddots & \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \\ \hline & & & & \begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6405a058d51a3c2f5859cfcee7d7fdcd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{1^{\circ}\ \lambda(A)=\{\lambda_1,\lambda_2,\lambda_3\} \ \Rightarrow\ \Lambda=\left[\begin{array}{ccc} \lambda_1 & 0 & 0\\ 0 & \lambda_2 & 0\\ 0 & 0 & \lambda_3 \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-84b04905b6ac45ff1964c63813a82081_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{2^{\circ}\ \lambda(A)=\{\lambda_R\pm j\lambda_I,\lambda\} \ \Rightarrow\ \Lambda=\left[\begin{array}{ccc} \lambda_R & \lambda_I & 0 \\ -\lambda_I & \lambda_R & 0 \\ 0 & 0 & \lambda \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a8c54381683d100c98707a0956c94b04_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{3^{\circ}\ \lambda(A)=\{\lambda,\lambda,\lambda\} \ \Rightarrow\ \Lambda=\left[\begin{array}{ccc} \lambda & 1 & 0\\ 0 & \lambda & 1\\ 0 & 0 & \lambda \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-76e61732a9aaced850d3e6e0c9170aec_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{4^{\circ}\ \lambda(A)=\{\lambda,\lambda,\lambda'\} \ \Rightarrow\ \Lambda=\left[\begin{array}{ccc} \lambda & 1 & 0\\ 0 & \lambda & 0\\ 0 & 0 & \lambda' \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2a9b6d31f9cc1646e9fdd22b4ac56857_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{cc} x_1\\ x_2 \end{array}\right] }_{x} \in{\rm\bf R}^2](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0fa82c1b4a8af7e3e26bf1f403b9c7db_l3.png)
](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-97304e22caaf0ac973a4c28144ad12f3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{{\rm rank}\left[\begin{array}{ccc} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{array}\right] ={\rm rank}\left[\begin{array}{ccc} \left[\begin{array}{ccc} a_{11} \\ a_{21} \\ a_{31} \end{array}\right] \left[\begin{array}{ccc} a_{12} \\ a_{22} \\ a_{32} \end{array}\right] \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0c416f3c23e28236351848860ebc9c23_l3.png)
![Rendered by QuickLaTeX.com \Leftrightarrow \underbrace{ \left[\begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{cc} x_1 \\ x_2 \end{array}\right] }_{x} = \underbrace{ \left[\begin{array}{cc} b_1 \\ b_2 \end{array}\right] }_{b}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1e69aad8154a0c48cc53582eb79dd64e_l3.png)
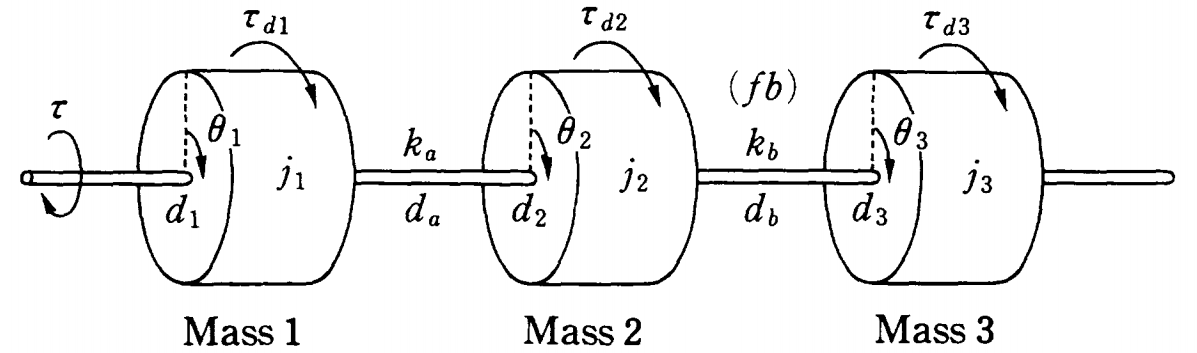
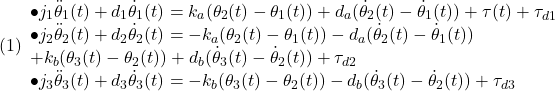
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{ccc} j_1 & 0 & 0\\ 0 & j_2 & 0\\ 0 & 0 & j_3 \end{array}\right] }_{J} \underbrace{ \left[\begin{array}{ccc} \ddot{\theta}_1(t)\\ \ddot{\theta}_2(t)\\ \ddot{\theta}_3(t) \end{array}\right] }_{\ddot{\xi}(t)} +\underbrace{ \left[\begin{array}{ccc} d_1+d_a & -d_a & 0\\ -d_a & d_2+d_a+d_b & -d_b\\ 0 & -d_b & d_3+d_b \end{array}\right] }_{D} \underbrace{ \left[\begin{array}{ccc} \dot{\theta}_1(t)\\ \dot{\theta}_2(t)\\ \dot{\theta}_3(t) \end{array}\right] }_{\dot{\xi}(t)}\\ +\underbrace{ \left[\begin{array}{ccc} k_a & -k_a & 0\\ -k_a & k_a+k_b & -k_b\\ 0 & -k_b & k_b \end{array}\right] }_{K} \underbrace{ \left[\begin{array}{ccc} {\theta}_1(t)\\ {\theta}_2(t)\\ {\theta}_3(t) \end{array}\right] }_{{\xi}(t)} = \underbrace{ \left[\begin{array}{ccc} 1\\ 0\\ 0 \end{array}\right] }_{E_{3\times1}}\tau(t) +\underbrace{ \left[\begin{array}{ccc} \tau_{d1}\\ \tau_{d2}\\ \tau_{d3} \end{array}\right] }_{\tau_{d}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f503c942853f86278fa2c1b5860489f2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \left[\begin{array}{c} \dot{\xi}(t)\\ \ddot{\xi}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} 0_{3\times3} & I_3\\ -J^{-1}K & -J^{-1}D \end{array}\right] }_{A(d_3/j_3,k_b/j_3)} \left[\begin{array}{c} {\xi}(t)\\ \dot{\xi}(t) \end{array}\right] + \left[\begin{array}{c} 0\\ J^{-1}E_{3\times1} \end{array}\right]\tau(t) + \left[\begin{array}{c} 0\\ J^{-1} \end{array}\right]\tau_d \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b27ed5b2207cc572494ae4bfcb986605_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \begin{array}{l} J^{-1}D={ \left[\begin{array}{ccc} d_1/j_1+d_a/j_1 & -d_a/j_1 & 0\\ -d_a/j_2 & d_2/j_2+d_a/j_2+d_b/j_2 & -d_b/j_2\\ 0 & -d_b/j_3 & d_3/j_3+d_b/j_3 \end{array}\right]\\ =(d_1/j_1)D_1+(d_2/j_2)D_2+(d_3/j_3)D_3\\ +(d_a/j_1)D_4+(d_a/j_2)D_5+(d_b/j_2)D_6+(d_b/j_3)D_7\\ J^{-1}K= \left[\begin{array}{ccc} k_a/j_1 & -k_a/j_1 & 0\\ -k_a/j_2 & k_a/j_2+k_b/j_2 & -k_b/j_2\\ 0 & -k_b/j_3 & k_b/j_3 \end{array}\right]\\ =(k_a/j_1)K_1+(k_a/j_2)K_2+(k_b/j_2)K_3+(k_b/j_3)K_4\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e79c3e7ebe83b4bd6c5f805aa18b7707_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \left[\begin{array}{c} \alpha\\ \beta \end{array}\right]= \underbrace{\frac{\alpha_2-\alpha}{\alpha_2-\alpha_1}\frac{\beta_2-\beta}{\beta_2-\beta_1}}_{p_{11}(\alpha,\beta)}\left[\begin{array}{c} \alpha_1\\ \beta_1 \end{array}\right]+ \underbrace{\frac{\alpha_2-\alpha}{\alpha_2-\alpha_1}\frac{\beta-\beta_1}{\beta_2-\beta_1}}_{p_{12}(\alpha,\beta)}\left[\begin{array}{c} \alpha_1\\ \beta_2 \end{array}\right]\\+ \underbrace{\frac{\alpha-\alpha_1}{\alpha_2-\alpha_1}\frac{\beta_2-\beta}{\beta_2-\beta_1}}_{p_{21}(\alpha,\beta)}\left[\begin{array}{c} \alpha_2\\ \beta_1 \end{array}\right]+ \underbrace{\frac{\alpha-\alpha_1}{\alpha_2-\alpha_1}\frac{\beta-\beta_1}{\beta_2-\beta_1}}_{p_{22}(\alpha,\beta)}\left[\begin{array}{c} \alpha_2\\ \beta_2 \end{array}\right] \\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-484fd6de8261d6cb87bf54fb54115386_l3.png)
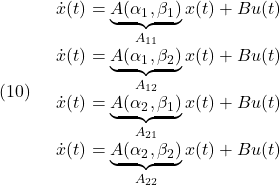
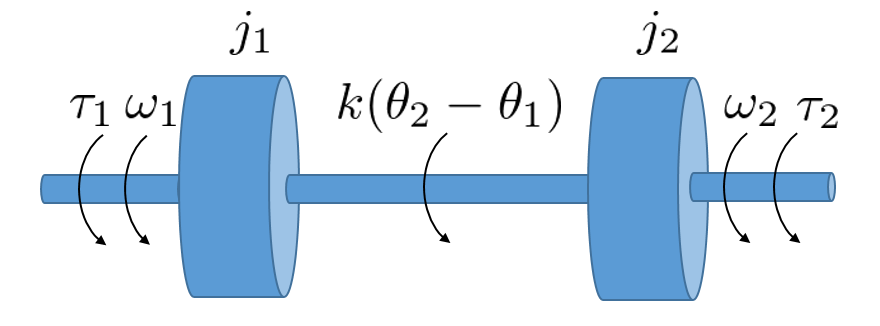
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \boxed{ \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\tau}_s(t)\\ \dot{\omega}_1(t)\\ \dot{\omega}_2(t) \end{array}\right] }_{\dot{\xi}(t)} = \underbrace{ \left[\begin{array}{cccc} 0 & k & -k\\ -1/j_1 & 0 & 0\\ 1/j_2 & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \tau_s(t)\\ \omega_1(t)\\ \omega_2(t) \end{array}\right] }_{\xi(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ 1/j_1 \\ 0 \end{array}\right] }_{B} \tau_1(t) + \underbrace{ \left[\begin{array}{c} 0\\ 0\\ 1/j_2 \end{array}\right] }_{w} \\ \omega_1(t)= \underbrace{ \left[\begin{array}{cccc} 0 & 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \tau_s(t)\\ \omega_1(t)\\ \omega_2(t) \end{array}\right] }_{\xi(t)}\\ \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c25f6b237c7c2e6cd097ce7e72e81495_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \left[\begin{array}{c} 0\\ 0\\ -1/j_2\\ \omega^* \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} 0 & k & -k & 0\\ -1/j_1 & 0 & 0 & 1/j_1\\ 1/j_2 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 \end{array}\right] }_{S= \left[\begin{array}{cc} A & B\\ C & 0 \end{array}\right] } \left[\begin{array}{c} \tau_s(\infty)\\ \omega_1(\infty)\\ \omega_2(\infty)\\ \tau_1(\infty) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-200a8504b885306bfa297096ead9dcfa_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \underbrace{ \left[\begin{array}{c} \tau_s(\infty)\\ \omega_1(\infty)\\ \omega_2(\infty)\\ \tau_1(\infty) \end{array}\right] }_{\left[\begin{array}{c} \xi_\infty \\ \tau_{1,\infty} \end{array}\right]} = \underbrace{ \left[\begin{array}{cccc} 0 & 0 & j_2 & 0\\ 0 & 0 & 0 & 1\\ -1/k & 0 & 0 & 1\\ 0 & j_1 & j_2 &0\end{array}\right] }_{S^{-1}} \left[\begin{array}{c} 0\\ 0\\ -1/j_2\\ \omega^* \end{array}\right] = \left[\begin{array}{c} -1\\ \omega^*\\ \omega^*\\ -1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f0d4e810a55a6a882407932aaab00e86_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \left[\begin{array}{c} \dot{\xi}(t) \\ \omega_1(t)-\omega^* \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_{1,\infty} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-47d30f4e17805a9a2ebaefe39021995e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \frac{d}{dt} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_{1,\infty} \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_{1,\infty} \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_{E3}} \dot{\tau}_1(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a0ff98500da4e2f52af6872960bbcfc1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \dot{\tau}_1(t) = K_{E3} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_{1,\infty} \end{array}\right] = \underbrace{ K_{E3}S^{-1} }_{ \left[\begin{array}{cccc} F_1 & F_2 & F_3 & F_4 \end{array}\right]} \left[\begin{array}{c} \dot{\xi}(t) \\ \omega_1(t)-\omega^* \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-20938eef1ea9c03b40aa65e259fc059d_l3.png)
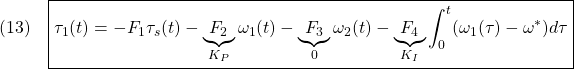
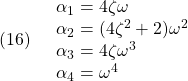
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \begin{array}{l} K_{E3}= \left[\begin{array}{cccc} 0 & 0 & 0 & 1 \end{array}\right]\\ \times \left[\begin{array}{cccc} B_{E3} & A_{E3}B_{E3} & A_{E3}^2B_{E3} & A_{E3}^3B_{E3} \end{array}\right]^{-1}\\ \times (A_{E3}^4+\alpha_1 A_{E3}^3+\alpha_2 A_{E3}^2+\alpha_3 A_{E3}+\alpha_4 I_4) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-753bbdf4eade430b3af666ccdd104bc1_l3.png)
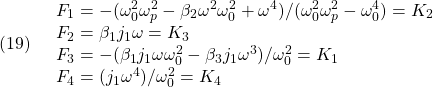
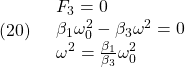
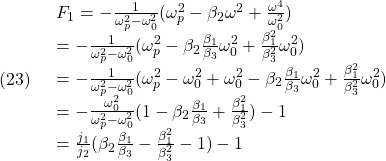
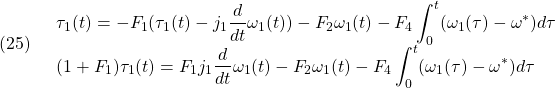
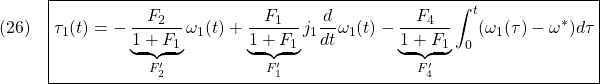
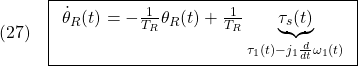
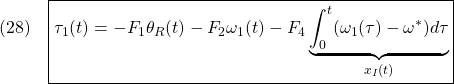
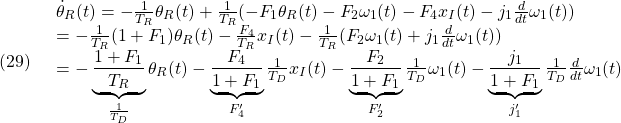
![Rendered by QuickLaTeX.com \displaystyle{(30)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_I(t)\\ \dot{\theta}_R(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} 0 & 0\\ -\frac{F'_4}{T_D} & -\frac{1}{T_D} \end{array}\right] }_{A_F} \left[\begin{array}{c} x_I(t)\\ \theta_R(t) \end{array}\right] + \underbrace{ \left[\begin{array}{cc} 1\\ -\frac{1}{T_D}(F'_2+j'_1\frac{d}{dt}) \end{array}\right] }_{B_F}\omega_1(t)\\ \tau_1(t)= \underbrace{ \left[\begin{array}{cccc} -F_4 & -F_1 \end{array}\right] }_{C_F} \left[\begin{array}{c} x_I(t)\\ \theta_R(t) \end{array}\right] +\underbrace{(-F_2)}_{D_F}\omega_1(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7e6311a39c4f39d2f6000e395385fed2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad \begin{array}{l} K(s)=\underbrace{ \left[\begin{array}{cccc} -F_4 & -F_1 \end{array}\right] }_{C_F} \underbrace{ \left[\begin{array}{cccc} s & 0\\ \frac{F'_4}{T_D} & s+\frac{1}{T_D} \end{array}\right]^{-1} }_{(sI-A_F)^{-1}} \underbrace{ \left[\begin{array}{cc} 1\\ -\frac{1}{T_D}(F'_2+j'_1s) \end{array}\right] }_{B_F} + \underbrace{(-F_2)}_{D_F}\\ = \left[\begin{array}{cccc} -F_4 & -F_1 \end{array}\right] \underbrace{ \left[\begin{array}{cccc} s & 0\\ \frac{F'_4}{T_D} & s+\frac{1}{T_D} \end{array}\right]^{-1} }_{ \frac{1}{s(s+\frac{1}{T_D})} \left[\begin{array}{cccc} s+\frac{1}{T_D} & 0\\ -\frac{F'_4}{T_D} & s \end{array}\right] } \left[\begin{array}{cc} 1\\ -\frac{1}{T_D}(F'_2+j'_1s) \end{array}\right] -F_2\\ =-F_4\frac{1}{s}+F_1 \frac{F'_4}{T_D}\frac{1}{s(s+\frac{1}{T_D})} +F_1 \frac{1}{s+\frac{1}{T_D}}\frac{1}{T_D}(F'_2+j'_1s)-F_2\\ =-(1+F_1 )(F'_2+F'_4\frac{1}{s})+F_1 \frac{1}{T_Ds+1}(F'_4\frac{1}{s}+F'_2+j'_1s)\\ =(-1-F_1 +F_1 \frac{1}{T_Ds+1}})(F'_2+F'_4\frac{1}{s})+F_1'\frac{j_1s}{T_Ds+1}}\\ =(-1-F_1 \frac{T_Ds}{T_Ds+1}})(F'_2+F'_4\frac{1}{s})+F_1'\frac{j_1s}{T_Ds+1}}\\ =(-1-F'_1\frac{T_Rs}{T_Ds+1}})(F'_2+F'_4\frac{1}{s})+F_1'\frac{j_1s}{T_Ds+1}}\\ =-F'_2-F'_4\frac{1}{s}-\frac{T_Rs}{T_Ds+1}}F'_1F'_2-\frac{T_Ds+1-T_Ds}{T_Ds+1}}T_RF'_1F'_4+F_1'\frac{j_1s}{T_Ds+1}}\\ =-F'_2-T_RF'_1F'_2-F'_4\frac{1}{s}-\frac{T_Rs}{T_Ds+1}}F'_1F'_2+\frac{T_Ds}{T_Ds+1}}T_RF'_1F'_4+F_1'\frac{j_1s}{T_Ds+1}}\\ =-\underbrace{(F'_2+T_RF'_1F'_2)}_{K_P}-\underbrace{F'_4}_{K_I}\frac{1}{s}-\frac{s}{T_Ds+1}}\underbrace{(T_RF'_1F'_2-T_DT_RF'_1F'_4-F_1'j_1)}}_{K_D}\\ %=F_P+F_I\frac{1}{s}+\frac{F_Ds}{Ts+1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4e1fa43bfe67aa01b18fdbf7cf206bd5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(33)\quad \boxed{ \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\tau}_s(t)\\ \dot{\omega}_1(t)\\ \dot{\omega}_2(t)\\ \dot{\tau}_1(t) \end{array}\right] }_{\dot{\xi}(t)} = \underbrace{ \left[\begin{array}{cccc} 0 & k & -k & 0\\ -1/j_1 & 0 & 0& 1/j_1\\ 1/j_2 & 0 & 0& 0\\ 0 & 0 & 0 & -1/T \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \tau_s(t)\\ \omega_1(t)\\ \omega_2(t)\\ \tau_1(t) \end{array}\right] }_{\xi(t)}\\ + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ 1/T \end{array}\right] }_{B} u(t) + \underbrace{ \left[\begin{array}{c} 0\\ 0\\ 1/j_2\\ 0 \end{array}\right] }_{w}\\ \dot{\theta}_1(t)= \underbrace{ \left[\begin{array}{cccc} 0 & 1 & 0& 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \tau_s(t)\\ \omega_1(t)\\ \omega_2(t)\\ \tau_1(t) \end{array}\right] }_{\xi(t)}\\ \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0face941bc9b742fd8c1a39a6ab8905e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(34)\quad \left[\begin{array}{c} 0\\ 0\\ -1/j_2\\ 0\\ \omega^* \end{array}\right] = \underbrace{ \left[\begin{array}{ccccc} 0 & k & -k & 0& 0\\ -1/j_1 & 0 & 0 & 1/j_1& 0\\ 1/j_2 & 0 & 0 & 0& 0\\ 0 & 0 & 0 & -1/T& 1/T\\ 0 & 1 & 0 & 0& 0 \end{array}\right] }_{S} \left[\begin{array}{c} \tau_s(\infty)\\ \omega_1(\infty)\\ \omega_2(\infty)\\ \tau_1(\infty)\\ u(\infty) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3bb52aeb5920c21402cde26565f91792_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(35)\quad \underbrace{ \left[\begin{array}{c} \tau_s(\infty)\\ \omega_1(\infty)\\ \omega_2(\infty)\\ \tau_1(\infty)\\ u(\infty) \end{array}\right] }_{\left[\begin{array}{c} \xi_\infty \\ u_\infty \end{array}\right]} = \underbrace{ \left[\begin{array}{ccccc} 0 & 0 & j_2 & 0& 0\\ 0 & 0 & 0 & 0& 1\\ -1 & 0 & 0 & 0& 1\\ 0 & j_1 & j_2 &0& 0\\ 0 & j_1 & j_2 &T& 0 \end{array}\right] }_{S^{-1}} \left[\begin{array}{c} 0\\ 0\\ -1/j_2\\ 0\\ \omega^* \end{array}\right] = \left[\begin{array}{c} -1\\ \omega^*\\ \omega^*\\ -1\\ -1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-384becd060fafe8dca8773e3c0ab725e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(36)\quad \left[\begin{array}{c} \dot{\xi}(t) \\ \omega_1(t)-\omega^* \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ u(t)-u_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-428e35cc70942d6dbf93edd87c4e25db_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(37)\quad \frac{d}{dt} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ u(t)-u_\infty \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ u(t)-u_\infty \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_{E3}} \dot{u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-06337a8f4ce7e3b2bf148980a4060511_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(38)\quad \dot{u}(t) = K_{E3} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ u(t)-u_\infty \end{array}\right] =\underbrace{ K_{E3}S^{-1} }_{ \left[\begin{array}{ccccc} K_2 & K_3 & K_1 & K_0& K_4 \end{array}\right]} \left[\begin{array}{c} \dot{\xi}(t) \\ \omega_1(t)-\omega^* \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c3735afe885bab43cef461836c34db22_l3.png)
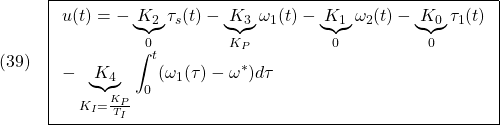
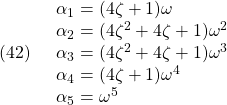
![Rendered by QuickLaTeX.com \displaystyle{(43)\quad \begin{array}{l} K_{E3}= \left[\begin{array}{ccccc} 0 & 0 & 0 & 0 &1 \end{array}\right]\\ \times \left[\begin{array}{ccccc} B_{E3} & A_{E3}B_{E3} & A_{E3}^2B_{E3} & A_{E3}^3B_{E3}& A_{E3}^4B_{E3} \end{array}\right]^{-1}\\ \times (A_{E3}^5+\alpha_1A_{E3}^4+\alpha_2A_{E3}^3+\alpha_3A_{E3}^2+\alpha_4A_{E3}+\alpha_5I_n) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c88f5d511bc275540dd02784c3de1ec1_l3.png)
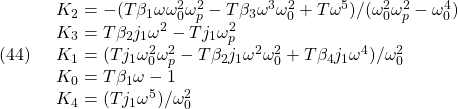
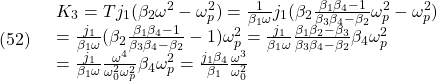
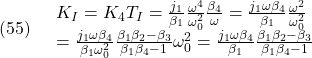
![Rendered by QuickLaTeX.com \displaystyle{(57)\quad \boxed{ \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\tau}_s(t)\\ \dot{\omega}_1(t)\\ \dot{\omega}_2(t)\\ \dot{x}_{D}(t)\\ \end{array}\right] }_{\dot{\xi}(t)} = \underbrace{ \left[\begin{array}{cccc} 0 & k & -k & 0\\ -1/j_1 & 0 & 0& 0\\ 1/j_2 & 0 & 0& 0\\ 0 & 1/T_D & 0 & -1/T_D \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \tau_s(t)\\ \omega_1(t)\\ \omega_2(t)\\ x_{D}(t)\\ \end{array}\right] }_{\xi(t)}\\ + \underbrace{ \left[\begin{array}{c} 0 \\ 1/j_1 \\ 0 \\ 0 \end{array}\right] }_{B} \tau_1(t) + \underbrace{ \left[\begin{array}{c} 0\\ 0\\ 1/j_2\\ 0 \end{array}\right] }_{w}\\ \omega_1(t)= \underbrace{ \left[\begin{array}{cccc} 0 & 1 & 0& 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \tau_s(t)\\ \omega_1(t)\\ \omega_2(t)\\ x_{D}(t)\\ \end{array}\right] }_{\xi(t)}\\ \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-43c48213c969f1206fa859c02ec68ff6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(58)\quad \left[\begin{array}{c} 0\\ 0\\ -1/j_2\\ 0\\ \omega^* \end{array}\right] = \underbrace{ \left[\begin{array}{ccccc} 0 & k & -k & 0& 0\\ -1/j_1 & 0 & 0& 0& 1/j_1 \\ 1/j_2 & 0 & 0& 0& 0\\ 0 & 1/T_D & 0 & -1/T_D& 0\\ 0 & 1 & 0 & 0& 0 \end{array}\right] }_{S} \left[\begin{array}{c} \tau_s(\infty)\\ \omega_1(\infty)\\ \omega_2(\infty)\\ x_{D}(\infty)\\ \tau_1(\infty) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-32cb895bdb660d3f9a735af3dc6e1f03_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(59)\quad \underbrace{ \left[\begin{array}{c} \tau_s(\infty)\\ \omega_1(\infty)\\ \omega_2(\infty)\\ x_{D}(\infty)\\ \tau_1(\infty) \end{array}\right] }_{\left[\begin{array}{c} \xi_\infty \\ \tau_\infty \end{array}\right]} = \underbrace{ \left[\begin{array}{ccccc} 0 & 0 & j_2 & 0& 0\\ 0 & 0 & 0 & 0& 1\\ -1/k & 0 & 0 & 0& 1\\ 0 & 0 & 0 &-1/T_D& 0\\ 0 & j_1 & j_2 &0& 0 \end{array}\right] }_{S^{-1}} \left[\begin{array}{c} 0\\ 0\\ -1/j_2\\ 0\\ \omega^* \end{array}\right] = \left[\begin{array}{c} -1\\ \omega^*\\ \omega^*\\ \omega^*\\ -1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-42e9671105c1457bff74113d4e882b97_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(60)\quad \left[\begin{array}{c} \dot{\xi}(t) \\ \omega_1(t)-\omega^* \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-451065a42216db1d57dd41f1a3b608e4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(61)\quad \frac{d}{dt} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_\infty \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_\infty \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_{E3}} \dot{u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f08c8362eba9a30ffbce176f269d3428_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(62)\quad \begin{array}{l} \dot{\tau}_1(t)(t) = K_{E3} \left[\begin{array}{c} \xi(t)-\xi_\infty \\ \tau_1(t)-\tau_\infty \end{array}\right]\\ =\underbrace{ K_{E3}S^{-1} }_{ \left[\begin{array}{ccccc} F_1(K_2) & F_2(K_3) & F_3(K_1) & F_4(K_0)& F_5(K_4) \end{array}\right]} \left[\begin{array}{c} \dot{\xi}(t) \\ \omega_1(t)-\omega^* \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-12a082ac3aaa6fa25b693f8371e7cdad_l3.png)
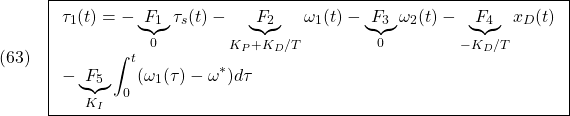
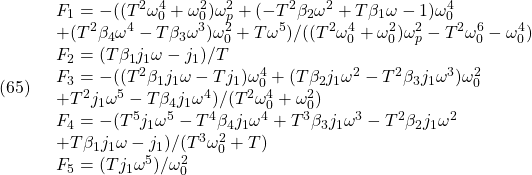
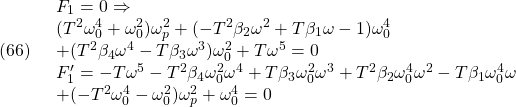
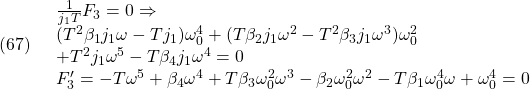
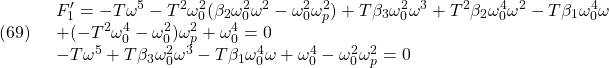
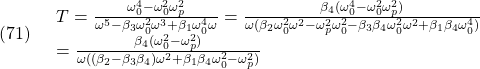
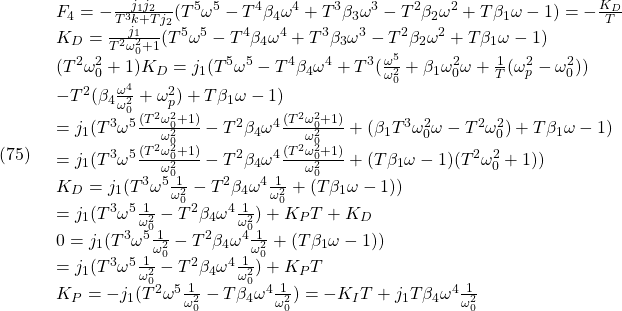
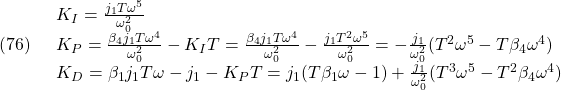
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad {\rm rank}\, \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S}=n+m }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2069deace994eb41f10ff0a9f788d3e6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \boxed{\begin{array}{rl} \left[\begin{array}{c} \dot{\hat{x}}(t) \\ \dot{x}_I(t) \end{array}\right] =& \underbrace{ \left[\begin{array}{cc} A-HC_M-BF & -BF_I \\ 0 & 0 \end{array}\right] }_{A_K} \left[\begin{array}{c} \hat{x}(t) \\ x_I(t) \end{array}\right]\\[10mm] &+ \underbrace{ \left[\begin{array}{cc} H & 0\\ C_S & -I_m \end{array}\right] }_{B_K} \left[\begin{array}{c} y(t) \\ r \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-977bf81afcea851483203c10814c5622_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \boxed{u(t)= \underbrace{- \left[\begin{array}{cc} F & F_I \end{array}\right] }_{C_K} \left[\begin{array}{c} \hat{x}(t) \\ x_I(t) \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d9ac340745aed0b88493ebd6fef302af_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \boxed{\left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \\ \dot{\hat{x}}(t) \end{array}\right] = \left[\begin{array}{ccc} A & -BF_I & -BF \\ C & 0 & 0 \\ HC_M & -BF_I & A-HC_M-BF \end{array}\right] \left[\begin{array}{c} x(t) \\ x_I(t) \\ \hat{x}(t) \end{array}\right] + \left[\begin{array}{c} w \\ -r \\ 0 \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-80e9ab84b8746522c22673f66ba84dda_l3.png)
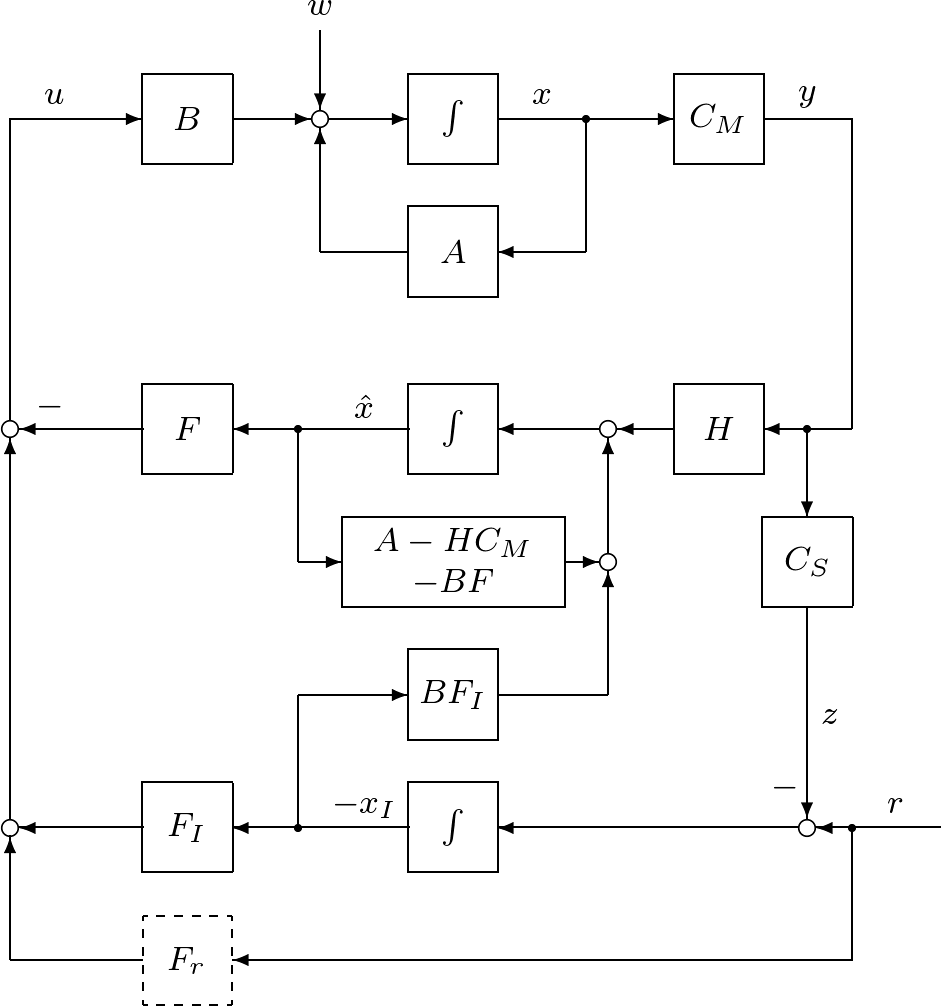 図1 積分動作を加えたオブザーバベースコントローラによる閉ループ系
図1 積分動作を加えたオブザーバベースコントローラによる閉ループ系![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \\ e(t) \end{array}\right] = \left[\begin{array}{ccc} I_n & 0 & 0 \\ 0 & I_m & 0 \\ -I_n & 0 & I_n \end{array}\right] \left[\begin{array}{c} x(t) \\ x_I(t) \\ \hat{x}(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b5d9f1751dc5c2977110972aa9b6df51_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \boxed{\left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \\\hline \dot{e}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc|c} A-BF & -BF_I & -BF \\ C & 0 & 0 \\\hline 0 & 0 & A-HC_M \end{array}\right] }_{ A_{EF}'= \left[\begin{array}{c|c} A_{EF} & - \left[\begin{array}{cc} B \\ 0 \end{array}\right] F \\[5mm] \hline 0 & \widehat{A} \end{array}\right] } \left[\begin{array}{c} x(t) \\ x_I(t) \\\hline e(t) \end{array}\right] + \left[\begin{array}{c} w \\ -r \\\hline -w \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e7fd58fcda89d55aeef7eae502bf33d5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \\\hline e(t) \end{array}\right] \ \rightarrow\ \underbrace{ \left[\begin{array}{c|c} A_{EF}^{-1} & -A_{EF}^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] F\widehat{A}^{-1} \\[5mm]\hline 0 & \widehat{A}^{-1} \end{array}\right] }_{A_{EF}'\,^{-1}} \left[\begin{array}{c} -w \\ r \\\hline w \end{array}\right] \quad (t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7dbdd90fdb25b174ea756263881e7ad1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(24)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0d41396e25f50798302fa74e0fcc7e0c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(26)\quad \int_0^\infty \left( \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right]^T Q_E \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] +{\dot u}^T(t)R_E{\dot u}(t)\right)\,dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e8a6e5b1e487b8f7d4c66618190de067_l3.png)
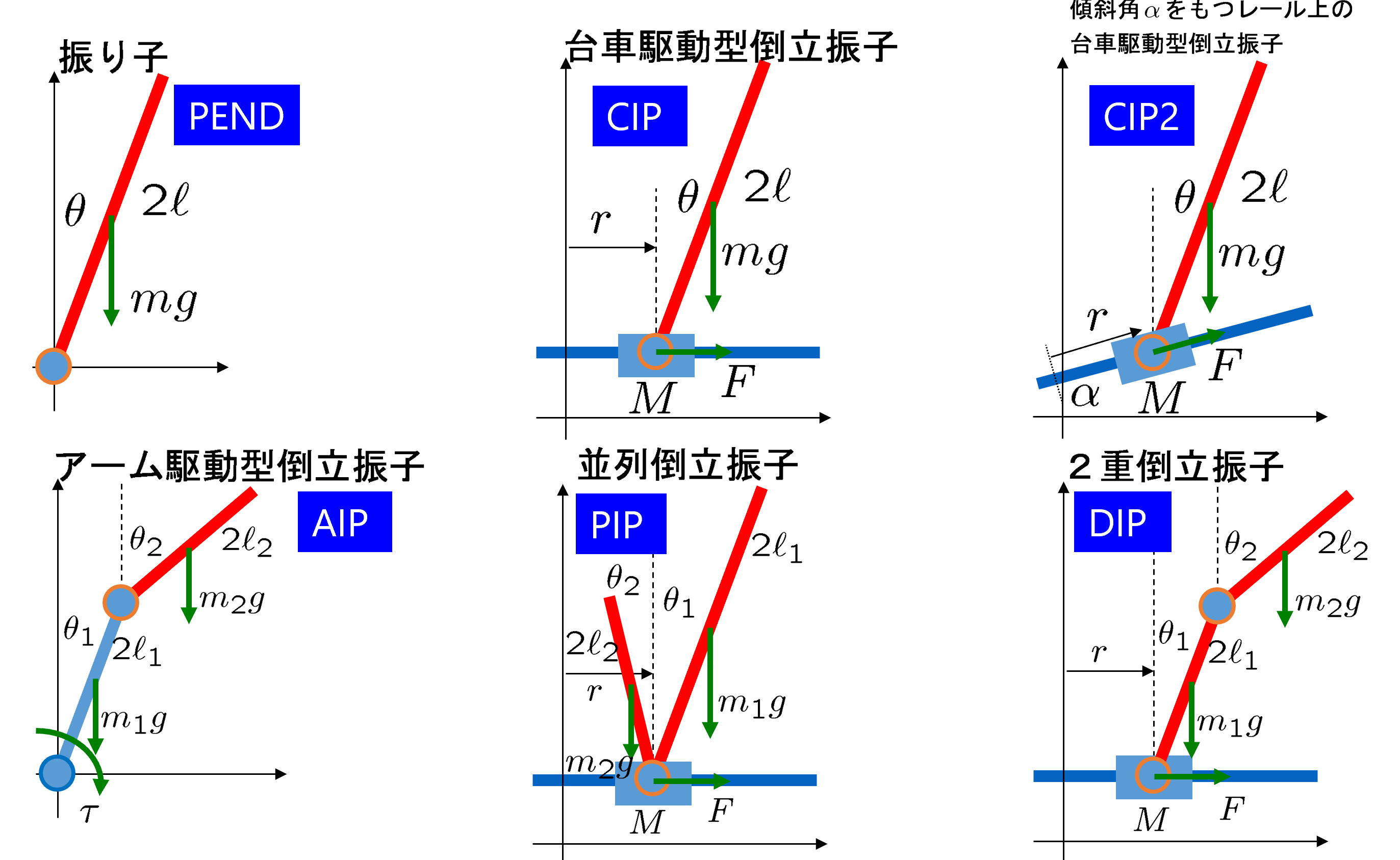 図1 様々な倒立振子
図1 様々な倒立振子![Rendered by QuickLaTeX.com \displaystyle{(2.1)\quad \frac{d}{dt}\left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & -\frac{3gm}{4M+m} & 0 & 0\\ 0 & \frac{3(M+m)g}{(4M+m)\ell} & 0 & 0\\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ 0\\ \frac{4}{4M+m}\\ \frac{3}{(4M+m)\ell} \end{array}\right] }_{B} \underbrace{F(t)}_{u(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-84a6ca484c9323a3fd95f4660cfea7d9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccc} f_1 & f_2 & f_3 & f_4 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (r(t)-r_c)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c730ca98f152a46bbeb44247cb831a1a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2.3)\quad \underbrace{r(t)}_{z(t)}= \underbrace{ \left[\begin{array}{cccc} 1 & 0 & 0 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b3d58870882b86ba47d53ab648e41923_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2.4)\quad \underbrace{\left[\begin{array}{c} 0\\ 0\\ 0\\ 0\\\hline r_c \end{array}\right] }_{\left[\begin{array}{c} -w \\ r_c \end{array}\right]} = \underbrace{\left[\begin{array}{cccc|c} 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & -\frac{3gm}{4M+m} & 0 & 0 & \frac{4}{4M+m}\\ 0 & \frac{3(M+m)g}{(4M+m)\ell} & 0 & 0 & \frac{3}{(4M+m)\ell}\\\hline 1 & 0 & 0 & 0 & 0 \end{array}\right] }_{S=\left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]} \underbrace{\left[\begin{array}{c} r_c\\ 0\\ 0\\ 0\\\hline 0 \end{array}\right] }_{\left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6e862f5ab4dc45e7e238f3e42b3b277a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2.5)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_{E}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c7d0b3f0821d3f8401967d391989d5f3_l3.png)
![Rendered by QuickLaTeX.com (3.1)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] = \underbrace{\left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ 0 & -\frac{6\cos\alpha mg}{8M+(5-3\cos2\alpha)m} & 0 & 0\\ 0 & \frac{6(M+m)g}{(8M+(5-3\cos2\alpha)m)\ell} & 0 & 0\\ \end{array}\right] }_{A(\alpha)} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)}}\\ \displaystyle{+ \underbrace{\left[\begin{array}{c} 0\\ 0\\ \frac{8}{8M+(5-3\cos2\alpha)m}\\ \frac{6\cos\alpha}{(8M+(5-3\cos2\alpha)m)\ell} \end{array}\right] }_{B(\alpha)} \underbrace{(F(t)-F^*)}_{u(t)}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e1dd7f9098a60203914c3ec06dcf5e98_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccc} f_1 & f_2 & f_3 & f_4 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta(t)\\ \dot{r}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (r(t)-r_c)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3a4cfa12b94bd29a0a664260285d99b8_l3.png)
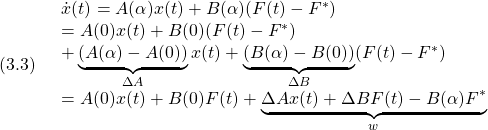
![Rendered by QuickLaTeX.com (4.1)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} \theta_1(t)\\ \theta_2(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] =}\\ \displaystyle{\underbrace{(\left[\begin{array}{cccc} 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1\\ \frac{3(m_1+2m_2)g}{(4m_1+3m_2)\ell_1} & -\frac{9m_2g}{2(4m_1+3m_2)\ell_1} & 0 & 0\\ -\frac{9(m_1+2m_2)g}{2(4m_1+3m_2)\ell_1} & \frac{9m_2g}{(4m_1+3m_2)\ell_2} & 0 & 0\\ \end{array}\right]+\Delta A) }_{A(\alpha)=A+\Delta A} \underbrace{\left[\begin{array}{c} \theta_1(t)\\ \theta_2(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] }_{x(t)}\\ \displaystyle{+ \underbrace{(\left[\begin{array}{c} 0\\ 0\\ \frac{6}{2(4m_1+3m_2)\ell_1^2}\\ -\frac{9}{2(4m_1+3m_2)\ell_1\ell_2} \end{array}\right]+\Delta B) }_{B(\alpha)=B+\Delta B} \underbrace{(\tau(t)-\tau^*)}_{u(t)}}\\ =Ax(t)+B\tau(t)+\underbrace{\Delta Ax(t)+\Delta B\tau(t)-B(\alpha)\tau^*}_{w} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6e5d5f40649f7ccecd6e3e7aea53bb6f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4.2)\quad \tau(t)= \underbrace{- \left[\begin{array}{cccc} f_1 & f_2 & f_3 & f_4 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} \theta_1(t)\\ \theta_2(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (\theta_1(t)-\alpha)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5a9d737b654d24c373c67149fdb430f1_l3.png)
![Rendered by QuickLaTeX.com (5.1)\quad \begin{array}{l} \displaystyle{\frac{d}{dt}\left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] =}\\ \displaystyle{\underbrace{\left[\begin{array}{cccccc} 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\ 0 & -\frac{3m_1g}{4M+m_1+m_2} & -\frac{3m_2g}{4M+m_1+m_2} & 0 & 0 & 0\\ 0 & \frac{3(4m+4m_1+m_2)g}{4(4M+m_1+m_2)\ell_1} & \frac{9m_2g}{4(4M+m_1+m_2)\ell_1} & 0 & 0& 0\\ 0 & \frac{9gm_1}{4(4M+m_1+m_2)\ell_2} & \frac{3(4m+m_1+4m_2)g}{4(4M+m_1+m_2)\ell_2} & 0 & 0& 0\\ \end{array}\right]}_{A} \left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right]}\\ \displaystyle{+ \underbrace{ \left[\begin{array}{c} 0\\ 0\\ 0\\ \frac{4}{4M+m_1+m_2}\\ -\frac{3}{(4M+m_1+m_2)\ell_1}\\ -\frac{3}{(4M+m_1+m_2)\ell_2} \end{array}\right] }_{B} \underbrace{F(t)}_{u(t)} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b146d12ebbd934f835113e9f5a66a050_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccccc} f_1 & f_2 & f_3 & f_4 & f_5 & f_6 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (r(t)-r_c)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a754530a145458dc98285892cb123a80_l3.png)
![Rendered by QuickLaTeX.com (6.1)\quad \begin{array}{l} \displaystyle{ \frac{d}{dt}\left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] =}\\ \displaystyle{ \left[\begin{array}{cccccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & -\frac{3m_1g}{Mm_1+m_1^2+(3M+m1)m_2} & -\frac{3m_2g}{Mm_1+m_1^2+(3M+m1)m_2} \\ 0 & \frac{3(4Mm_1+4m_1^2+3m_2^2+3(18M+13m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m1)m_2)\ell_1} & \frac{9(2M+m_1)m_2g}{(4Mm_1+m_1^2+(3M+m1)m_2)\ell_1} \\ 0 & \frac{9(2Mm_1+m_1^2+3(2M+m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} & \frac{3(4Mm_1+m_1^2+12(3M+m_1)m_2)g}{(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} \\ \end{array}\right.}\\ \displaystyle{\left.\begin{array}{cccccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1\\ 0 & 0 & 0\\ 0 & 0 & 0\\ 0 & 0 & 0\\ \end{array}\right] \left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right]}\\ \displaystyle{+ \underbrace{\left[\begin{array}{c} 0\\ 0\\ 0\\ \frac{4m_1+3m_2}{4Mm_1+m_1^2+(3M+m1)m_2}\\ -\frac{3(2m_1+m2)}{2Mm_1+m_1^2+(3M+m1)m_2}\\ \frac{3m_1}{2(4Mm_1+m_1^2+(3M+m_1)m_2)\ell_2} \end{array}\right] }_{B} \underbrace{F(t)}_{u(t)}} \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c0d8773e32ffbef0fd7275146dab4774_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6.2)\quad u(t)= \underbrace{- \left[\begin{array}{cccccc} f_1 & f_2 & f_3 & f_4 & f_5 & f_6 \end{array}\right] }_{-F} \underbrace{ \left[\begin{array}{c} r(t)\\ \theta_1(t)\\ \theta_2(t)\\ \dot{r}(t)\\ \dot{\theta}_1(t)\\ \dot{\theta}_2(t) \end{array}\right] }_{x(t)} +F_I\int_0^t (r(t)-r_c)dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-39932c622bf561d62c488e285deca01f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \boxed{\left[\begin{array}{c} -w \\ r \end{array}\right] = \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] \left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5a63c22e2c20de8035fdefcbe9d60119_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \boxed{{\rm rank}\, \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S}=n+m} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b2fcb8d3d07f55b008eda2e6a5836e50_l3.png)
 図1 積分動作を加えた状態フィードバックによる閉ループ系
図1 積分動作を加えた状態フィードバックによる閉ループ系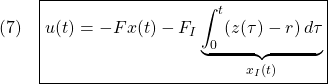
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \boxed{ %\underbrace{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] %}_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} A-BF & -BF_I \\ C & 0 \end{array}\right] }_{A_{EF}} %\underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] %}_{x_E(t)} + %\underbrace{ \left[\begin{array}{c} w \\ -r \end{array}\right] %}_{w_E} }}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a13e4e217df7e1cd4a8873612c945fbd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad A_{EF} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} - \left[\begin{array}{cc} B \\ 0 \end{array}\right] \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ae3e582f261444dac1f56aa447ce0eaa_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \begin{array}{ll} A_{EF}^{-1} =& S^{-1}+ S^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] \left(I_m- \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] S^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] \right)^{-1} \\[5mm] &\times \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] S^{-1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e0f009cac08e772a5836cd7f89991b53_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \boxed{A_{EF}^{-1} = \left[\begin{array}{cc} I_n & 0 \\ -F_I^{-1}F & -F_I^{-1} \end{array}\right] S^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0b2df9b56c6c85b1e3bfe245468fe652_l3.png)
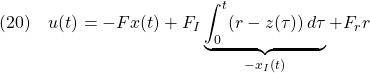
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \boxed{\frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] %}_{x_E(t)-x_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E1}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] %}_{x_E(t)-x_{E\infty}} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E1}} (u(t)-u_\infty)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2bcd3f36f880707fe8bc60b89fa6dbb6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(24)\quad \boxed{\frac{d}{dt} %\underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] %}_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} %\underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] %}_{\dot{x}_E(t)} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} {\dot u}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-acdd13f2ef2c1d92a0004a5f47cda17a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(25)\quad \left[\begin{array}{c} {\dot x}(t)-w \\ z(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-73ee9071a72e5208f32daf364e891bb9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(26)\quad \boxed{\left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-429e0ebfec7903d5dc5ce87f5046bed1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(27)\quad \boxed{\frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-69dd980e629d5d4d9cf34dc90dbc246d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(28)\quad \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cc8034db5edc1a000b2f2add912d9e66_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(29)\quad \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e7784673b16ee3dc6fc71b2e2e461a8c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(30)\quad u(t)-u_\infty=- \underbrace{\left[\begin{array}{cc} F & F_I \end{array}\right] }_{F_{E1}} \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-49e57cd33d9728f3bb2e32ce3cc5341c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad {\dot u}(t)=- \underbrace{\left[\begin{array}{cc} F & F_I \end{array}\right] }_{F_{E2}} \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-38d968135e7c7820854f8a99e80ed705_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(32)\quad {\dot u}(t)=- \underbrace{\left[\begin{array}{cc} K & K_I \end{array}\right] }_{K_{E3}} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a0dd224c0271441aad07fc15b5834f36_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(33)\quad {\dot u}(t)=- \underbrace{\left[\begin{array}{cc} K & K_I \end{array}\right] \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]^{-1} }_{K_{E3}S^{-1}} \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9efa6f3fc30539bde922fde97f38394c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(35)\quad \boxed{\left[\begin{array}{cc} F & F_I \end{array}\right] = \left[\begin{array}{cc} K & K_I \end{array}\right] \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-effa6673748e4582607e705f8cec8e0b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(36)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-09c7b450fba91ff4da2925235911deb2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(38)\quad \int_0^\infty \left( \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right]^T Q_E \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] +{\dot u}^T(t)R_E{\dot u}(t)\right)\,dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c670e9177dbb8cc950866876198e2e52_l3.png)
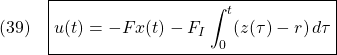
![Rendered by QuickLaTeX.com \displaystyle{(40)\quad \boxed{\left[\begin{array}{cc} F & F_I \end{array}\right] = \left[\begin{array}{cc} K & K_I \end{array}\right] \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right]^{-1}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bbcfc692f32dddd6063c223f23f96d7e_l3.png)
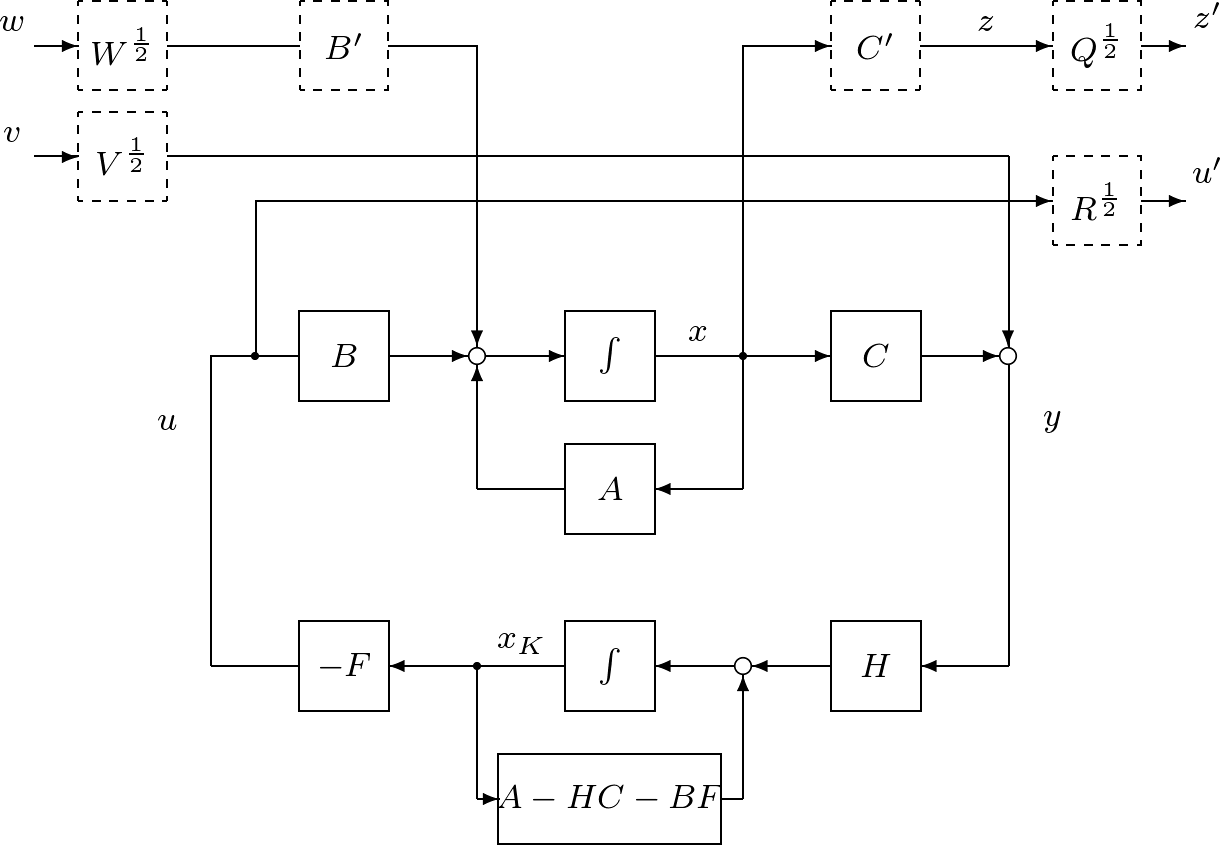 図1 LQG制御系設計の枠組み
図1 LQG制御系設計の枠組み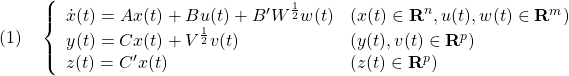
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \boxed{\begin{array}{l} \left[\begin{array}{cc} \dot{x}(t) \\ \dot{\hat{x}}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A & -BF \\ HC&A-HC-BF \end{array}\right] }_{A_{CL1}} \left[\begin{array}{cc} {x}(t) \\ \hat{x}(t) \end{array}\right] + \underbrace{ \left[\begin{array}{cc} B'W^{\frac{1}{2}} & 0 \\ 0 & HV^{\frac{1}{2}} \end{array}\right] }_{B_{CL1}} \left[\begin{array}{cc} {w}(t) \\ {v}(t) \end{array}\right]\\ \left[\begin{array}{cc} {y'}(t) \\ {u'}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} Q^{\frac{1}{2}}C' & 0 \\ 0 & -R^{\frac{1}{2}}F \end{array}\right] }_{C_{CL1}} \left[\begin{array}{cc} {x}(t) \\ \hat{x}(t) \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6e6de0ac1c24534b05d96168f970e1fc_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \boxed{\begin{array}{l} \left[\begin{array}{cc} \dot{x}(t) \\ \dot{e}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A-BF & -BF \\ 0 & A-HC \end{array}\right] }_{A_{CL2}} \left[\begin{array}{cc} {x}(t) \\ {e}(t) \end{array}\right] +\underbrace{ \left[\begin{array}{cc} B'W^{\frac{1}{2}} & 0 \\ -B'W^{\frac{1}{2}} & HV^{\frac{1}{2}} \end{array}\right] }_{B_{CL2}} \left[\begin{array}{cc} {w}(t) \\ {v}(t) \end{array}\right]\\ \left[\begin{array}{cc} {y'}(t) \\ {u'}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} Q^{\frac{1}{2}}C' & 0 \\ -R^{\frac{1}{2}}F & -R^{\frac{1}{2}}F \end{array}\right] }_{C_{CL2}} \left[\begin{array}{cc} {x}(t) \\ {e}(t) \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-81a989326d7d4a34c5752f6aecf84dec_l3.png)
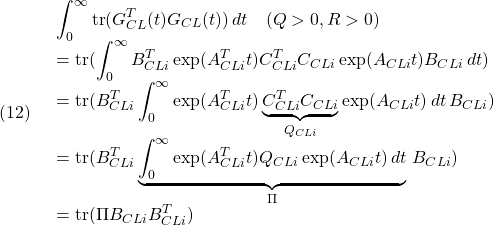
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \begin{array}{l} \Pi A_{CL1}= \left[\begin{array}{cc} \Pi_{1}&\Pi_{3} \\ \Pi_{3}^T&\Pi_{2} \end{array}\right] \left[\begin{array}{cc} A & -BF \\ HC&A-HC-BF \end{array}\right]\\ = \left[\begin{array}{cc} \Pi_{1}A+\Pi_{3}HC & -\Pi_{1}BF+\Pi_{3}(A-HC-BF)\\ \Pi_{3}^TA+\Pi_{2}HC & -\Pi_{3}^TBF+\Pi_{2}(A-HC-BF) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c429aa33a0e5684bc85b0263996ad5ef_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(19)\quad \begin{array}{l} A_{CL1}^T\Pi =(\Pi A_{CL1})^T\\ =\left[\begin{array}{cc} A^T\Pi_{1}+C^TH^T\Pi_{3}^T&\\ -F^TB^T\Pi_{1}+(A-HC-BF)^T\Pi_{3}^T & \end{array}\right.\\ \left.\begin{array}{cc} A^T\Pi_{3}+C^TH^T\Pi_{2}\\ -F^TB^T\Pi_{3}+(A-HC-BF)^T\Pi_{2} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c914ac5d6ae500873c120fe9e3c82eef_l3.png)
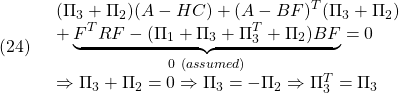
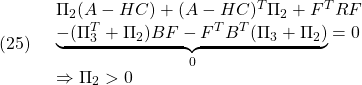
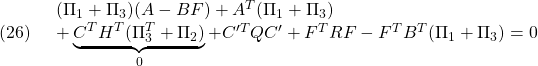
![Rendered by QuickLaTeX.com \displaystyle{(29)\quad \begin{array}{l} A_{CL1}\Gamma= \left[\begin{array}{cc} A & -BF \\ HC&A-HC-BF \end{array}\right] \left[\begin{array}{cc} \Gamma_{1}&\Gamma_{3} \\ \Gamma_{3}^T&\Gamma_{2} \end{array}\right]\\ =\left[\begin{array}{cc} A\Gamma_{1} -BF\Gamma_{3}^T &A\Gamma_{3} -BF\Gamma_{2}\\ HC\Gamma_{1}+(A-HC-BF)\Gamma_{3}^T &HC\Gamma_{3}+(A-HC-BF)\Gamma_{2} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b5efbe327872da02c0cdae613082e8a5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(30)\quad \begin{array}{l} \Gamma A_{CL1}^T =(A_{CL1}\Gamma)^T\\ =\left[\begin{array}{cc} \Gamma_{1}A^T -\Gamma_{3}F^TB^T & \Gamma_{1}C^TH^T+\Gamma_{3}(A-HC-BF)^T\\ \Gamma_{3}^TA^T -\Gamma_{2}F^TB^T & \Gamma_{3}^TC^TH^T+\Gamma_{2}(A-HC-BF)^T \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-166202eb44f8bebfc11fcdbb0cf09ab8_l3.png)
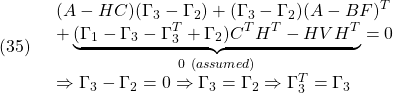
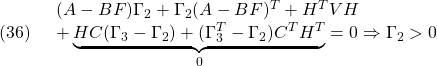
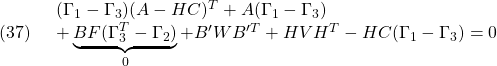
![Rendered by QuickLaTeX.com \displaystyle{(42)\quad \begin{array}{l} \Pi A_{CL1}\Gamma= \left[\begin{array}{cc} \Pi_{1}&\Pi_{3} \\ \Pi_{3}^T&\Pi_{2} \end{array}\right] \left[\begin{array}{cc} A & -BF \\ HC&A-HC-BF \end{array}\right] \Gamma\\ =\left[\begin{array}{cc} \Pi_{1}A+\Pi_{3}HC & -\Pi_{1}BF+\Pi_{3}(A-HC-BF)\\ \Pi_{3}^TA+\Pi_{2}HC & -\Pi_{3}^TBF+\Pi_{2}(A-HC-BF) \end{array}\right] \left[\begin{array}{cc} \Gamma_{1}&\Gamma_{3} \\ \Gamma_{3}^T&\Gamma_{2} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5cf2147ab153e0a23d8488f0452990da_l3.png)
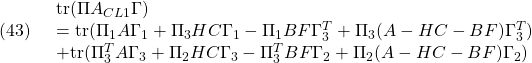
![Rendered by QuickLaTeX.com \displaystyle{(46)\quad \begin{array}{l} A_{CL1}^T\Pi\Gamma=(\Pi A_{CL1})^T\Gamma=\\ \left[\begin{array}{cc} A^T\Pi_{1}+C^TH^T\Pi_{3}^T&\\ -F^TB^T\Pi_{1}+(A-HC-BF)^T\Pi_{3}^T & \end{array}\right.\\ \left.\begin{array}{cc} A^T\Pi_{3}+C^TH^T\Pi_{2}\\ -F^TB^T\Pi_{3}+(A-HC-BF)^T\Pi_{2} \end{array}\right] \left[\begin{array}{cc} \Gamma_{1}&\Gamma_{3} \\ \Gamma_{3}^T&\Gamma_{2} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-98094a2e6a48cf9f59754bbc5f21fdef_l3.png)