| MATLAB |
%cSPIN_sf_gs.m
%-----
clear all close all
J1=1; J2=1; J3=0.5;
OMnom=2*pi; OMmin=0*OMnom; OMmax=2*OMnom;
A1=[0 (J2-J3)/J1;(J3-J1)/J2 0];
B=diag([1/J1 1/J2]); C=eye(2); D=zeros(2,2);
S0=[zeros(2,2) B;C D];
S1=zeros(4,4); S1(1:2,1:2)=A1;
%-----
J1=1; J2=1; J3=0.5;
OMnom=2*pi; OMmin=0*OMnom; OMmax=2*OMnom;
A1= OMmin*[0 (J2-J3)/J1;(J3-J1)/J2 0];
A2= OMmax*[0 (J2-J3)/J1;(J3-J1)/J2 0];
B=diag([1/J1 1/J2]);
B1=B; B2=B;
C1=[eye(2,2);zeros(2,2)];
D11=zeros(4,2);
D12=[zeros(2,2);eye(2,2)];
alpha=1; r=3; th=pi/4;
LMIs=sf_synlmi7(A1,A2,B1,B2,C1,D11,D12,alpha,r,th);
cobj=zeros(1,decnbr(LMIs));
cobj(1)=1;
[cost,xopt]=mincx(LMIs,cobj);
Y=dec2mat(LMIs,xopt,2);
Z1=dec2mat(LMIs,xopt,3);
Z2=dec2mat(LMIs,xopt,4);
F1=Z1/Y,pl1=eig(A1-B2*F1)
F2=Z2/Y,pl2=eig(A2-B2*F2)
%------
figure(1)
subplot(121),dregion(alpha,0,r,th,7*[-1,1,-1,1])
plot(real(pl1),imag(pl1),'*')
subplot(122), dregion(alpha,0,r,th,7*[-1,1,-1,1])
plot(real(pl2),imag(pl2),'*')
%------
prange=OMmax-OMmin; pmax=OMmax; pmin=OMmin;
sim("SPIN_sf_gs")
%-----
function LMIs=sf_synlmi7(A1,A2,B1,B2,C1,D11,D12,alpha,r,th)
[n,m]=size(B2);
sth=sin(th); cth=cos(th);
setlmis([]);
gam=lmivar(1,[1 0]);
Y=lmivar(1,[n 1]);
Z1=lmivar(2,[m n]);
Z2=lmivar(2,[m n]);
%
lmi11=newlmi;
lmiterm([lmi11,1,1,Y],A1,1,'s'); %#1:A*Y+Y*A'
lmiterm([lmi11,1,1,Z1],-B2,1,'s'); %#1:-(B2*Z+Z*B2')
lmiterm([lmi11,1,2,0],B1); %#1:B1
lmiterm([lmi11,2,2,gam],-1,1); %#1:-gam
lmiterm([lmi11,3,1,Y],C1,1); %#1:C1*Y
lmiterm([lmi11,3,1,Z1],-D12,1); %#1:D12*Z
lmiterm([lmi11,3,2,0],D11); %#1:D11
lmiterm([lmi11,3,3,gam],-1,1); %#1:-gam
lmi21=newlmi;
lmiterm([lmi21,1,1,Y],A1,1,'s'); %#2:A*Y+Y*A'
lmiterm([lmi21,1,1,Z1],-B2,1,'s'); %#2:-(B2*Z+Z'*B2')
lmiterm([lmi21,1,1,Y],2*alpha,1); %#2:2*alpha*Y
lmi31=newlmi;
lmiterm([lmi31,1,1,Y],-r,1); %#3:-r*Y
lmiterm([lmi31,1,2,Y],A1,1); %#3:A*Y
lmiterm([lmi31,1,2,Z1],-B2,1); %#3:-B2*Z
lmiterm([lmi31,2,2,Y],-r,1); %#3:-r*Y
lmi41=newlmi;
lmiterm([lmi41,1,1,Y],sth*A1,1,'s'); %#4:sth*(A*Y+Y*A')
lmiterm([lmi41,1,1,Z1],-sth*B2,1,'s');%#4:-sth*(B2*Z+Z'*B2')
lmiterm([lmi41,1,2,Y],cth*A1,1); %#4:cth*A*Y
lmiterm([lmi41,1,2,Y],1,-cth*A1'); %#4:-cth*Y*A'
lmiterm([lmi41,1,2,Z1],-cth*B2,1); %#4:-cth*B2*Z
lmiterm([lmi41,1,2,-Z1],1,cth*B2'); %#4:cth*Z'*B2'
lmiterm([lmi41,2,2,Y],sth*A1,1,'s'); %#4:sth*(A*Y+Y*A')
lmiterm([lmi41,2,2,Z1],-sth*B2,1,'s');%#4:-sth*(B2*Z+Z'*B2')
%
lmi12=newlmi;
lmiterm([lmi12,1,1,Y],A2,1,'s'); %#1:A*Y+Y*A'
lmiterm([lmi12,1,1,Z2],-B2,1,'s'); %#1:-(B2*Z+Z*B2')
lmiterm([lmi12,1,2,0],B1); %#1:B1
lmiterm([lmi12,2,2,gam],-1,1); %#1:-gam
lmiterm([lmi12,3,1,Y],C1,1); %#1:C1*Y
lmiterm([lmi12,3,1,Z2],-D12,1); %#1:D12*Z
lmiterm([lmi12,3,2,0],D11); %#1:D11
lmiterm([lmi12,3,3,gam],-1,1); %#1:-gam
lmi22=newlmi;
lmiterm([lmi22,1,1,Y],A2,1,'s'); %#2:A*Y+Y*A'
lmiterm([lmi22,1,1,Z2],-B2,1,'s'); %#2:-(B2*Z+Z'*B2')
lmiterm([lmi22,1,1,Y],2*alpha,1); %#2:2*alpha*Y
lmi32=newlmi;
lmiterm([lmi32,1,1,Y],-r,1); %#3:-r*Y
lmiterm([lmi32,1,2,Y],A2,1); %#3:A*Y
lmiterm([lmi32,1,2,Z2],-B2,1); %#3:-B2*Z
lmiterm([lmi32,2,2,Y],-r,1); %#3:-r*Y
lmi42=newlmi;
lmiterm([lmi42,1,1,Y],sth*A2,1,'s'); %#4:sth*(A*Y+Y*A')
lmiterm([lmi42,1,1,Z2],-sth*B2,1,'s');%#4:-sth*(B2*Z+Z'*B2')
lmiterm([lmi42,1,2,Y],cth*A2,1); %#4:cth*A*Y
lmiterm([lmi42,1,2,Y],1,-cth*A2'); %#4:-cth*Y*A'
lmiterm([lmi42,1,2,Z2],-cth*B2,1); %#4:-cth*B2*Z
lmiterm([lmi42,1,2,-Z2],1,cth*B2'); %#4:cth*Z'*B2'
lmiterm([lmi42,2,2,Y],sth*A2,1,'s'); %#4:sth*(A*Y+Y*A')
lmiterm([lmi42,2,2,Z2],-sth*B2,1,'s');%#4:-sth*(B2*Z+Z'*B2')
%
lmi5=newlmi;
lmiterm([-lmi5,1,1,Y],1,1); %#5:Y
lmi6=newlmi;
lmiterm([lmi6,1,1,gam],1,1); %#6:gam
lmiterm([-lmi6,1,1,0],1e3); %#6:1000
LMIs=getlmis;
end
%-----
%eof
|
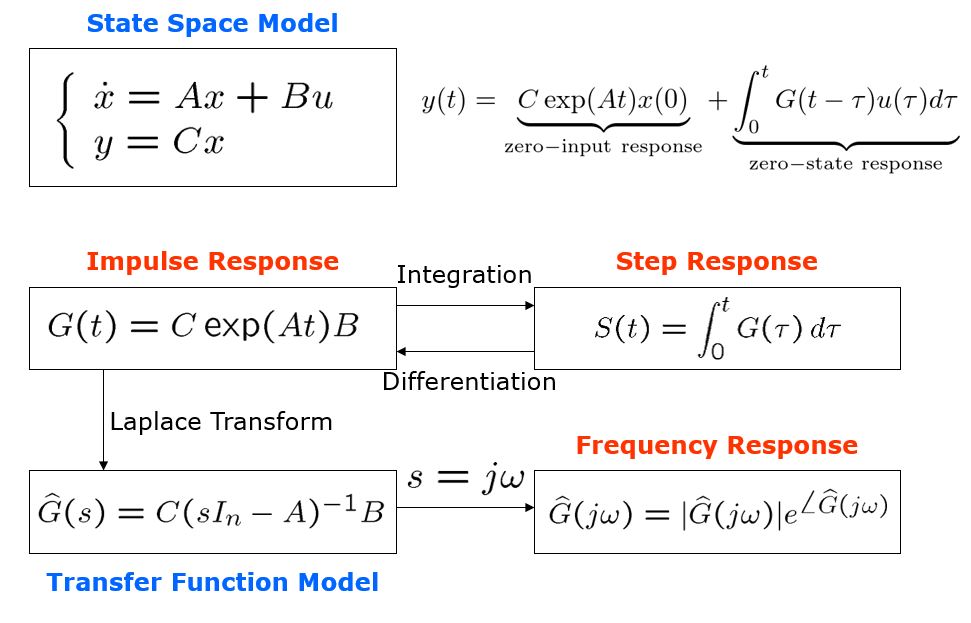
![]() 次系の
次系の![]() ノルムが
ノルムが![]() より小である条件は
より小である条件は![]() を用いて、次のように表されます。
を用いて、次のように表されます。
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \displaystyle{\sup_{u\in{\cal L}_2}\frac{||y(t)||_2}{||u(t)||_2} =\sup_{\omega\in{\rm\bf R}}||\hat{G}(j\omega)||_2<\gamma} \\ \displaystyle{\Leftrightarrow \exists X>0:\ \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D & -I \end{array}\right]<0} \\ \displaystyle{\Leftrightarrow \exists Y>0:\ \left[\begin{array}{ccc} YA^T+AY & B & YC^T \\ B^T & -\gamma^2 I & D^T \\ CY & D & -I \end{array}\right]<0} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cb76514d96e7c4115d9ea88e02ad0651_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \begin{array}{l} \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D &-I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{cc} A^TX+XA & XB \\ B^TX & -\gamma^2 I \end{array}\right] - \left[\begin{array}{cc} C^T\\ D^T \end{array}\right] (-I) %(-\gamma^{-1} I) \left[\begin{array}{cc} C & D \end{array}\right] <0 \\ \Leftrightarrow \left[\begin{array}{cc} A^TX+XA & XB \\ B^TX & 0 \end{array}\right] < \left[\begin{array}{cc} C^T & 0 \\ D^T & I \end{array}\right] \left[\begin{array}{cc} -I & 0 \\ 0 & \gamma^2 I \end{array}\right] \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5c2560cc668d6d0690878b8eedd8885c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \begin{array}{l} \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D & - I \end{array}\right]<0 \\ &\Leftrightarrow \forall \left[\begin{array}{c} x \\ u \end{array}\right]\ne0: \underbrace{ \left[\begin{array}{c} x \\ u \end{array}\right]^T \left[\begin{array}{cc} A^TX+XA & XB \\ B^TX & 0 \end{array}\right] \left[\begin{array}{c} x \\ u \end{array}\right] }_{\dot{V}(x)=\frac{d}{dt}(x^TXx)} \\ < \underbrace{ \left[\begin{array}{c} x \\ u \end{array}\right]^T \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right]^T \left[\begin{array}{cc} - I & 0 \\ 0 & \gamma^2 I \end{array}\right] \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right] \left[\begin{array}{c} x \\ u \end{array}\right] }_{s(u,y)=\gamma^2 u^Tu-y^Ty} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-474ab9036f2ca5939a3c709f1500ddf6_l3.png)
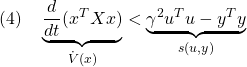
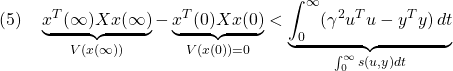
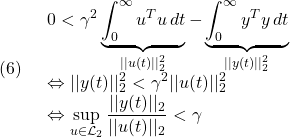
![]() から出力
から出力![]() への入出力特性は不変であることから
への入出力特性は不変であることから![Rendered by QuickLaTeX.com \displaystyle{(7) \begin{array}{l} \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D & -I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{ccc} A^TX+XA & X(B\sqrt{\gamma}) & (\frac{1}{\sqrt{\gamma}}C)^T \\ (B\sqrt{\gamma})^TX & - \gamma^2 I & D^T \\ (\frac{1}{\sqrt{\gamma}}C) & D & -I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{ccc} I & 0 & 0 \\ 0 & \sqrt{\gamma} I & 0 \\ 0 & 0 & \frac{1}{\sqrt{\gamma}} I \end{array}\right] \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma I & D^T \\ C & D &-\gamma I \end{array}\right] \left[\begin{array}{ccc} I & 0 & 0 \\ 0 & \sqrt{\gamma} I & 0 \\ 0 & 0 & \frac{1}{\sqrt{\gamma}} I \end{array}\right]<0 \\ \Leftrightarrow \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma I & D^T \\ C & D &-\gamma I \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9f78ef9deeaf1d5eba2e99bef8581c5e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \displaystyle{\sup_{u\in{\cal L}_2}\frac{||y(t)||_2}{||u(t)||_2} =\sup_{\omega\in{\rm\bf R}}||\hat{G}(j\omega)||_2<\gamma} \\ \displaystyle{\Leftrightarrow \exists X>0:\ \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma I & D^T \\ C & D & -\gamma I \end{array}\right]<0} \\ \displaystyle{\Leftrightarrow \exists Y>0:\ \left[\begin{array}{ccc} YA^T+AY & B & YC^T \\ B^T & -\gamma I & D^T \\ CY & D & -\gamma I \end{array}\right]<0} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0e630e89fa5b93c2df2468b74a26d002_l3.png)
![]() 2次振動系に対して、適当な
2次振動系に対して、適当な![]() を設定し、
を設定し、![]() ノルムと$の大小関係をチェックするプログラムを作成せよ。
ノルムと$の大小関係をチェックするプログラムを作成せよ。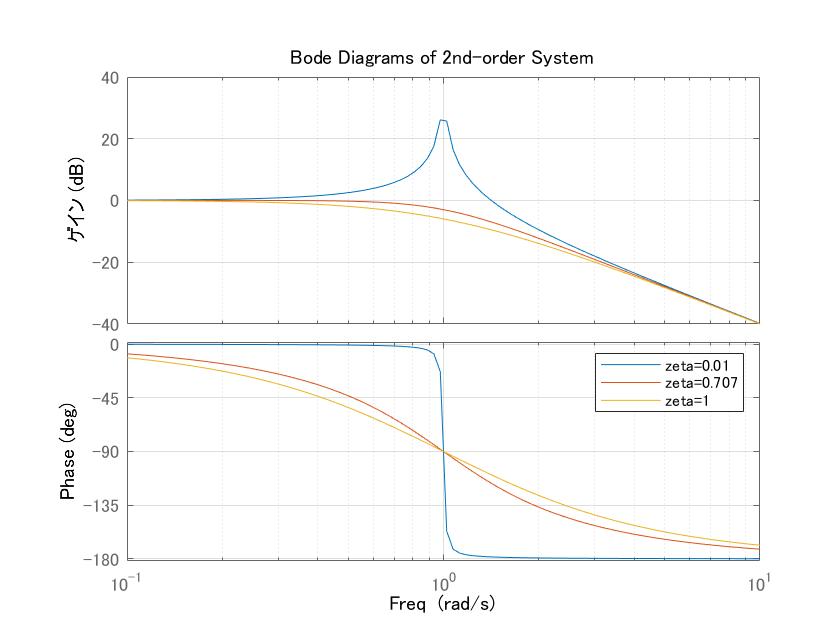
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \boxed{\begin{array}{l} A= \underbrace{ \left[\begin{array}{cc} U_1 & U_2 \end{array}\right] }_{U(m\times m)} \underbrace{ \left[\begin{array}{cc} {\rm diag}\{\sigma_1,\cdots,\sigma_k\} & 0_{k\times (n-k)} \\ 0_{(m-k)\times k} & 0_{(m-k)\times (n-k)} \end{array}\right] }_{\Sigma= \left[\begin{array}{cc} \Sigma_1 & 0 \\ 0 & 0 \end{array}\right] \quad(\sigma_1\ge\cdots\ge\sigma_k) } \underbrace{ \left[\begin{array}{cc} V_1^T \\ V_2^T \end{array}\right] }_{V(n\times n)^T}\\ =U_1(m\times k)\Sigma_1(k\times k)V_1(n\times k)^T \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1a8bdd72019cbda663e2a40b3a70d3b6_l3.png)
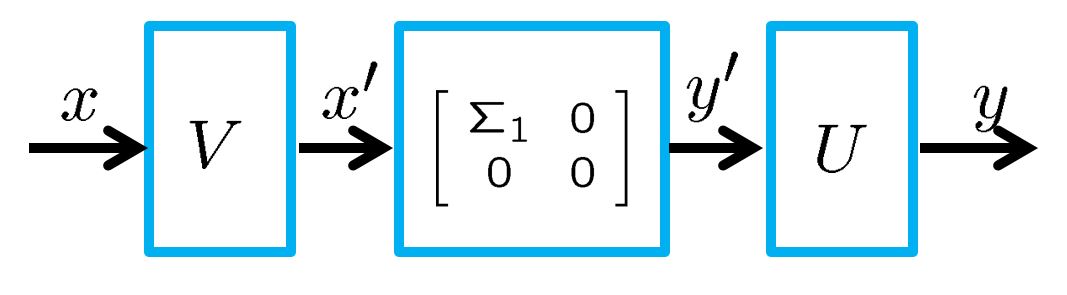 図3 特異値分解
図3 特異値分解
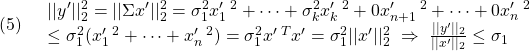
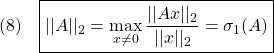
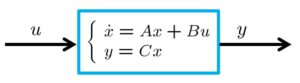
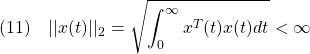
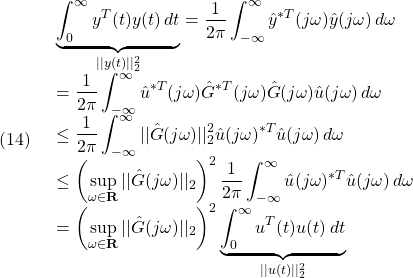
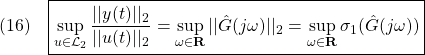

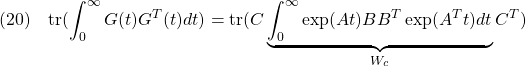
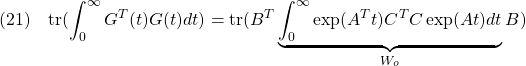
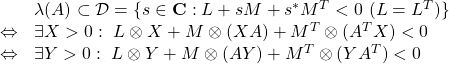
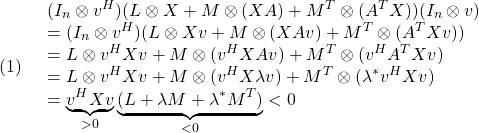
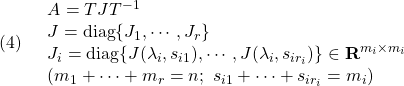
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad J(\lambda,k)=\left[\begin{array}{cccc} \lambda & 1 & & 0\\ 0 & \lambda & \ddots & \\ \vdots & \ddots & \ddots & 1 \\ 0 & \cdots & 0 & \lambda \end{array}\right]\in{\rm\bf R}^{k\times k} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ab96841e90e0d9dd55c8e1fbe6d37b58_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad T_\epsilon=\left[\begin{array}{cccc} 1 & 0 & \cdots & 0\\ 0 & \frac{1}{\epsilon} & \ddots & \vdots\\ \vdots & \ddots & \ddots & 0\\ 0 & \cdots & 0 & \frac{1}{\epsilon^{k-1}} \end{array}\right],\ T_\epsilon^{-1}=\left[\begin{array}{cccc} 1 & 0 & \cdots & 0\\ 0 & {\epsilon} & \ddots & \vdots\\ \vdots & \ddots & \ddots & 0\\ 0 & \cdots & 0 & {\epsilon^{k-1}} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-105301a3a42f7ab0eb9750acac26e2ce_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} T_\epsilon J(\lambda,k)T_\epsilon^{-1}\\ =T_\epsilon \left[\begin{array}{cccc} \lambda & 1 & & 0\\ 0 & \lambda & \ddots & \\ \vdots & \ddots & \ddots & 1 \\ 0 & \cdots & 0 & \lambda \end{array}\right] \left[\begin{array}{cccc} 1 & 0 & \cdots & 0\\ 0 & {\epsilon} & \ddots & \vdots\\ \vdots & \ddots & \ddots & 0\\ 0 & \cdots & 0 & {\epsilon^{k-1}} \end{array}\right]\\ =\left[\begin{array}{cccc} 1 & 0 & \cdots & 0\\ 0 & \frac{1}{\epsilon} & \ddots & \vdots\\ \vdots & \ddots & \ddots & 0\\ 0 & \cdots & 0 & \frac{1}{\epsilon^{k-1}} \end{array}\right] \left[\begin{array}{cccc} \lambda & \epsilon & & 0\\ 0 & \lambda\epsilon & \ddots & \\ \vdots & \ddots & \ddots & \epsilon^{k-1} \\ 0 & \cdots & 0 & \lambda\epsilon^{k-1} \end{array}\right]\\ =\left[\begin{array}{cccc} \lambda & \epsilon & & 0\\ 0 & \lambda & \ddots & \\ \vdots & \ddots & \ddots & \epsilon \\ 0 & \cdots & 0 & \lambda \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-517f70ee4d5a06e559e5f4be6fd4bd76_l3.png)
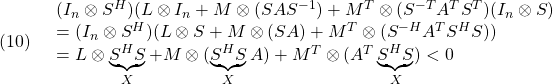

![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{lll} &&\lambda(A)\subset {\cal D}_3=\{s=x+jy\in{\rm\bf C}:\\ && \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]s + \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]^Ts^* <0 \}\nonumber\\ &&\Leftrightarrow \exists X>0:\ \left[\begin{array}{cc} \sin\theta(XA+A^TX) & \cos\theta(XA-A^TX) \\ -\cos\theta(XA-A^TX) & \sin\theta(XA+A^TX) \end{array}\right] <0 \nonumber\\ &&\Leftrightarrow \exists Y>0:\ \left[\begin{array}{cc} \sin\theta(AY+YA^T) & \cos\theta(AY-YA^T) \\ -\cos\theta(AY-YA^T) & \sin\theta(AY+YA^T) \end{array}\right] <0\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3b534e97017d8856b3ce56b56e0c3ab5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \begin{array}{lll} && \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]s + \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]^Ts^* <0 \nonumber\\ &\Leftrightarrow& \left[\begin{array}{cc} (s+s^*)\sin\theta & (s-s^*)\cos\theta \\ -(s-s^*)\cos\theta & (s+s^*)\sin\theta \end{array}\right] <0 \nonumber\\ &\Leftrightarrow& \left[\begin{array}{cc} 2x\sin\theta & 2jy\cos\theta \\ -2jy\cos\theta & 2x\sin\theta \end{array}\right] <0 \nonumber\\ &\Leftrightarrow& x\sin\theta-jy\cos\theta\frac{1}{x\sin\theta}(-j)y\cos\theta<0,\ x\sin\theta<0 \nonumber\\ &\Leftrightarrow& x^2\sin^2\theta-y^2\cos^2\theta>0,\ x<0 \nonumber\\ &\Leftrightarrow& \tan\theta>\frac{|y|}{-x},\ x<0 \nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0e18cdb9a2d398da5bbf4a4c180b6b22_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14) \begin{array}{lll} &&\left[\begin{array}{cc} v^{*T} & 0^{T}\\ 0^{T} & v^{*T} \end{array}\right] \left[\begin{array}{cc} \sin\theta(XA+A^TX) & \cos\theta(XA-A^TX) \\ -\cos\theta(XA-A^TX) & \sin\theta(XA+A^TX) \end{array}\right] \left[\begin{array}{cc} v & 0\\ 0 & v \end{array}\right] \nonumber\\ &=& \left[\begin{array}{cc} \sin\theta(v^{*T}X(\lambda v)+(\lambda^*v^{*T})Xv) & \cos\theta(v^{*T}X(\lambda v)-(\lambda^*v^{*T})Xv) \\ -\cos\theta(v^{*T}X(\lambda v)-(\lambda^*v^{*T})Xv) & \sin\theta(v^{*T}X(\lambda v)+(\lambda^*v^{*T})Xv) \end{array}\right] \nonumber\\ &=& \underbrace{ \left[\begin{array}{cc} (\lambda+\lambda^*)\sin\theta & (\lambda-\lambda^*)\cos\theta \\ -(\lambda-\lambda^*)\cos\theta & (\lambda+\lambda^*)\sin\theta \end{array}\right] }_{<0} \underbrace{v^{*T}Xv}_{>0}<0 \nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-285477ad44caf135647233332c329df5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(15) \begin{array}{lll} && \left[\begin{array}{cc} x_1^T & x_2^T \end{array}\right] \left[\begin{array}{cc} \sin\theta(XA+A^TX) & \cos\theta(XA-A^TX) \\ -\cos\theta(XA-A^TX) & \sin\theta(XA+A^TX) \end{array}\right] \left[\begin{array}{c} x_1\\ x_2 \end{array}\right] <0 \nonumber\\ &&\quad (\forall x_1,x_2\ne0)\nonumber\\ &\Leftrightarrow& \left[\begin{array}{cc} x_1^TX & x_2^TX \end{array}\right]\\ && \left[\begin{array}{cc} \sin\theta(AX^{-1}+X^{-1}A^T) & \cos\theta(AX^{-1}-X^{-1}A^T) \\ -\cos\theta(AX^{-1}-X^{-1}A^T) & \sin\theta(AX^{-1}+X^{-1}A^T) \end{array}\right] \left[\begin{array}{c} Xx_1\\ Xx_2 \end{array}\right] <0 \nonumber\\ &\Leftrightarrow& \left[\begin{array}{cc} y_1^T & y_2^T \end{array}\right] \left[\begin{array}{cc} \sin\theta(AY+YA^T) & \cos\theta(AY-YA^T) \\ -\cos\theta(AY-YA^T) & \sin\theta(AY+YA^T) \end{array}\right] \left[\begin{array}{c} y_1\\ y_2 \end{array}\right] <0 \nonumber\\ &&\quad (\forall y_1,y_2\ne0)\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-316c19f9344b2195c495883a36293683_l3.png)
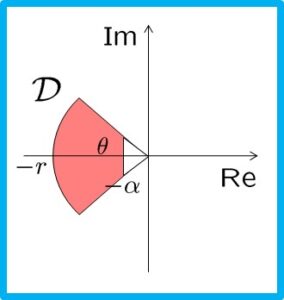
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \begin{array}{lll} && \lambda(A)\subset {\cal D}={\cal D}_1\cap{\cal D}_2\cap{\cal D}_3\nonumber\\ &&\Leftrightarrow \exists X>0:\nonumber\\ & & \left\{\begin{array}{l} 2\alpha X+XA+A^TX<0 \\ \left[\begin{array}{cc} -rX & XA \\ A^TX & -rX \end{array}\right]<0 \\ \left[\begin{array}{cc} \sin\theta(XA+A^TX) & \cos\theta(XA-A^TX) \\ -\cos\theta(XA-A^TX) & \sin\theta(XA+A^TX) \end{array}\right] <0 \end{array}\right.\nonumber\\ &&\Leftrightarrow \exists Y>0:\nonumber\\ & & \left\{\begin{array}{l} 2\alpha Y+AY+YA^T<0 \\ \left[\begin{array}{cc} -rY & AY \\ YA^T & -rY \end{array}\right]<0 \\ \left[\begin{array}{cc} \sin\theta(AY+YA^T) & \cos\theta(AY-YA^T) \\ -\cos\theta(AY-YA^T) & \sin\theta(AY+YA^T) \end{array}\right] <0 \end{array}\right.\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a5629f5f3a111b24527162f90eb8cad4_l3.png)
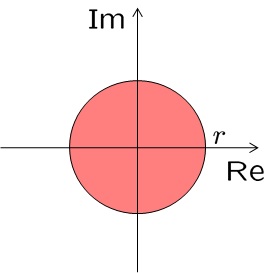
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{lll} &&\lambda(A)\subset {\cal D}_2=\{s=x+jy\in{\rm\bf C}: \left[\begin{array}{cc} -r & s \\ s^* & -r \end{array}\right] <0 \}\nonumber\\ &\Leftrightarrow& \exists X>0:\ \left[\begin{array}{cc} -rX & XA \\ A^TX & -rX \end{array}\right]<0 \nonumber\\ &\Leftrightarrow& \exists Y>0:\ \left[\begin{array}{cc} -rY & AY \\ YA^T & -rY \end{array}\right]<0\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5662d8b7c69301806b9c41c9e567c679_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \begin{array}{lll} && \left[\begin{array}{cc} -r & s \\ s^* & -r \end{array}\right]<0\\ &\Leftrightarrow& (-r)-s\frac{1}{(-r)}s^*<0,\ -r<0 \nonumber\\ &\Leftrightarrow& r^2-(x+jy)(x-jy)>0 \nonumber\\ &\Leftrightarrow& x^2+y^2<r^2 \nonumber\end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2a615e481d49cd65c7af58606dce9ebb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{lll} &&\left[\begin{array}{cc}v^{*T}&0^{T}\\0^{T}&v^{*T}\end{array}\right] \left[\begin{array}{cc}-rX&XA\\A^TX&-rX\end{array}\right] \left[\begin{array}{cc}v&0\\0&v\end{array}\right]\nonumber\\ &=& \left[\begin{array}{cc} -rv^{*T}Xv&v^{*T}X(\lambda v)\\ (\lambda^*v^{*T})Xv&-rv^{*T}Xv& \end{array}\right]\nonumber\\ &=& \underbrace{ \left[\begin{array}{cc} -r&\lambda\\\lambda^*&-r \end{array}\right] }_{<0} \underbrace{v^{*T}xv}_{>0}<0 \nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ee725f421be58c27c34f90905b890229_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{lll} && \left[\begin{array}{cc} x_1^T & x_2^T \end{array}\right] \left[\begin{array}{cc} -rX & XA \\ A^TX & -rX \end{array}\right] \left[\begin{array}{c} x_1\\ x_2 \end{array}\right] <0 \quad (\forall x_1,x_2\ne0)\nonumber\\ &\Leftrightarrow& \left[\begin{array}{cc} x_1^TX & x_2^TX \end{array}\right] \left[\begin{array}{cc} -rX^{-1} & AX^{-1} \\ X^{-1}A^T & -rX^{-1} \end{array}\right] \left[\begin{array}{c} Xx_1\\ Xx_2 \end{array}\right] <0 \nonumber\\ &\Leftrightarrow& \left[\begin{array}{cc} y_1^T & y_2^T \end{array}\right] \left[\begin{array}{cc} -rY & AY \\ YA^T & -rY \end{array}\right] \left[\begin{array}{c} y_1\\ y_2 \end{array}\right] <0 \quad (\forall y_1,y_2\ne0)\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c0fd523c8514218c28986c8a38f4dec1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \begin{array}{lll} &&\frac{x^2}{a^2}+\frac{y^2}{b^2}<1\Leftrightarrow\frac{(\frac{s+s^*}{2})^2}{a^2}+\frac{(\frac{s-s^*}{2j})^2}{b^2}<1 \\ &&\Leftrightarrow\ b^2(s+s^*)^2-a^2(s-s^*)^2<4a^2b^2\\ &&\Leftrightarrow\ (b(s+s^*)+a(s-s^*))(b(s+s^*)-a(s-s^*))<4a^2b^2 \\ &&\Leftrightarrow\ -4a^2b^2+((b+a)s+(b-a)s^*))((b-a)s+(b+a)s^*))<0 \\ &&\Leftrightarrow\ \left[\begin{array}{cc} -4a^2b^2 & (b+a)s+(b-a)s^* \\ (b-a)s+(b+a)s^* & -1 \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b25e3009225c1f9a4590486d7ac6c43d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(20)\quad \begin{array}{lll} &&\frac{x^2}{a^2}-\frac{y^2}{b^2}>1,\ x<-a\ \Leftrightarrow\ \frac{(\frac{s+s^*}{2})^2}{a^2}-\frac{(\frac{s-s^*}{2j})^2}{b^2}>1,\ \frac{s+s^*}{2}<-a}\\ &&\Leftrightarrow\ b^2(s+s^*)^2+a^2(s-s^*)^2>4a^2b^2,\ s+s^*+2a<0\\ &&\Leftrightarrow\ b^2(s+s^*+2a)(s+s^*-2a)+a^2(s-s^*)^2>0,\ s+s^*+2a<0\\ &&\Leftrightarrow\ b(s+s^*-2a)-\frac{-a^2(s-s^*)^2}{b(s+s^*+2a)}<0,b(s+s^*+2a)<0\\ &&\Leftrightarrow\ \left[\begin{array}{cc} b(s+s^*+2a) & a(s-s^*) \\ -a(s-s^*) & b(s+s^*-2a) \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-00ed2494a2b6bd5158edea1ece4fc648_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{lll} && \left[\begin{array}{cc} P & M \\ M^T & Q \end{array}\right]<0\\ &\Leftrightarrow& P-MQ^{-1}M^T<0,\ Q<0\\ &\Leftrightarrow& P<0,\ Q-M^TP^{-1}M<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1032be1b5ca3689d43f86d220f3f031c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \begin{array}{lll} & & \underbrace{ \left[\begin{array}{cc} P & M \\ M^T & Q \end{array}\right] }_{R} \\ &=& \left[\begin{array}{cc} I & MQ^{-1} \\ 0 & I \end{array}\right] \left[\begin{array}{cc} P-MQ^{-1}M^T & 0 \\ 0 & Q \end{array}\right] \left[\begin{array}{cc} I & 0 \\ Q^{-1}M^T & I \end{array}\right] \\ &=& \underbrace{ \left[\begin{array}{cc} I & 0 \\ M^TP^{-1} & I \end{array}\right] }_{T^T} \underbrace{ \left[\begin{array}{cc} P & 0 \\ 0 & Q-M^TP^{-1}M \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{cc} I & P^{-1}M \\ 0 & I \end{array}\right] }_{T} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c71f6a58283e2c1b2186c86022be5b68_l3.png)
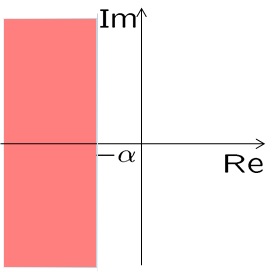
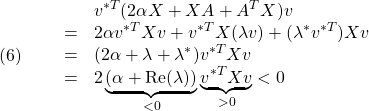
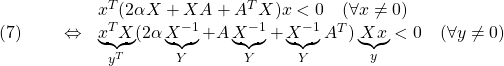
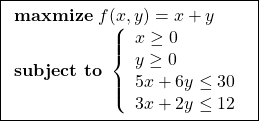
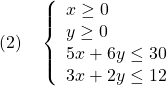
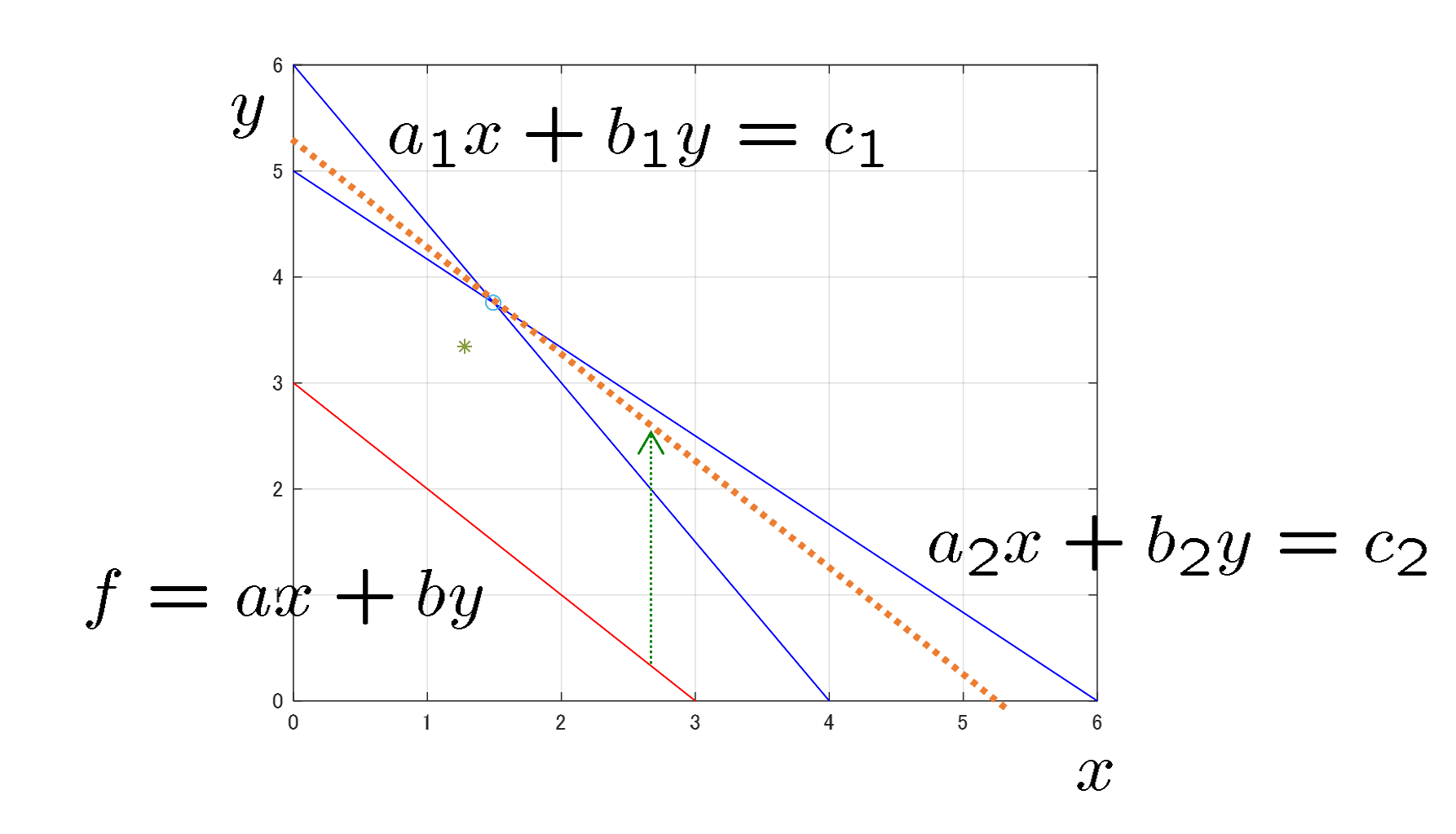 図1 線形計画問題の例
図1 線形計画問題の例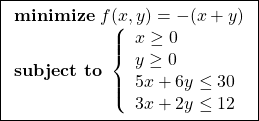
![Rendered by QuickLaTeX.com \displaystyle{(3) \underbrace{ \left[\begin{array}{c} \dot{\omega}_1(t) \\ \dot{\omega}_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & \Omega(t)\frac{J_2-J_3}{J_1} \\ \Omega(t)\frac{J_3-J_1}{J_2} & 0 \end{array}\right] }_{A(\Omega(t))} \underbrace{ \left[\begin{array}{c} \omega_1(t) \\ \omega_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} \frac{1}{J_1} & 0 \\ 0 & \frac{1}{J_2} \end{array}\right] }_{B} \underbrace{ \left[\begin{array}{c} \tau_1(t) \\ \tau_2(t) \end{array}\right] }_{u(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-06d0d0706f122470d4466143aac157d2_l3.png)
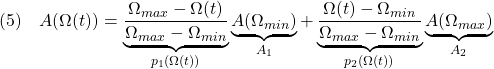
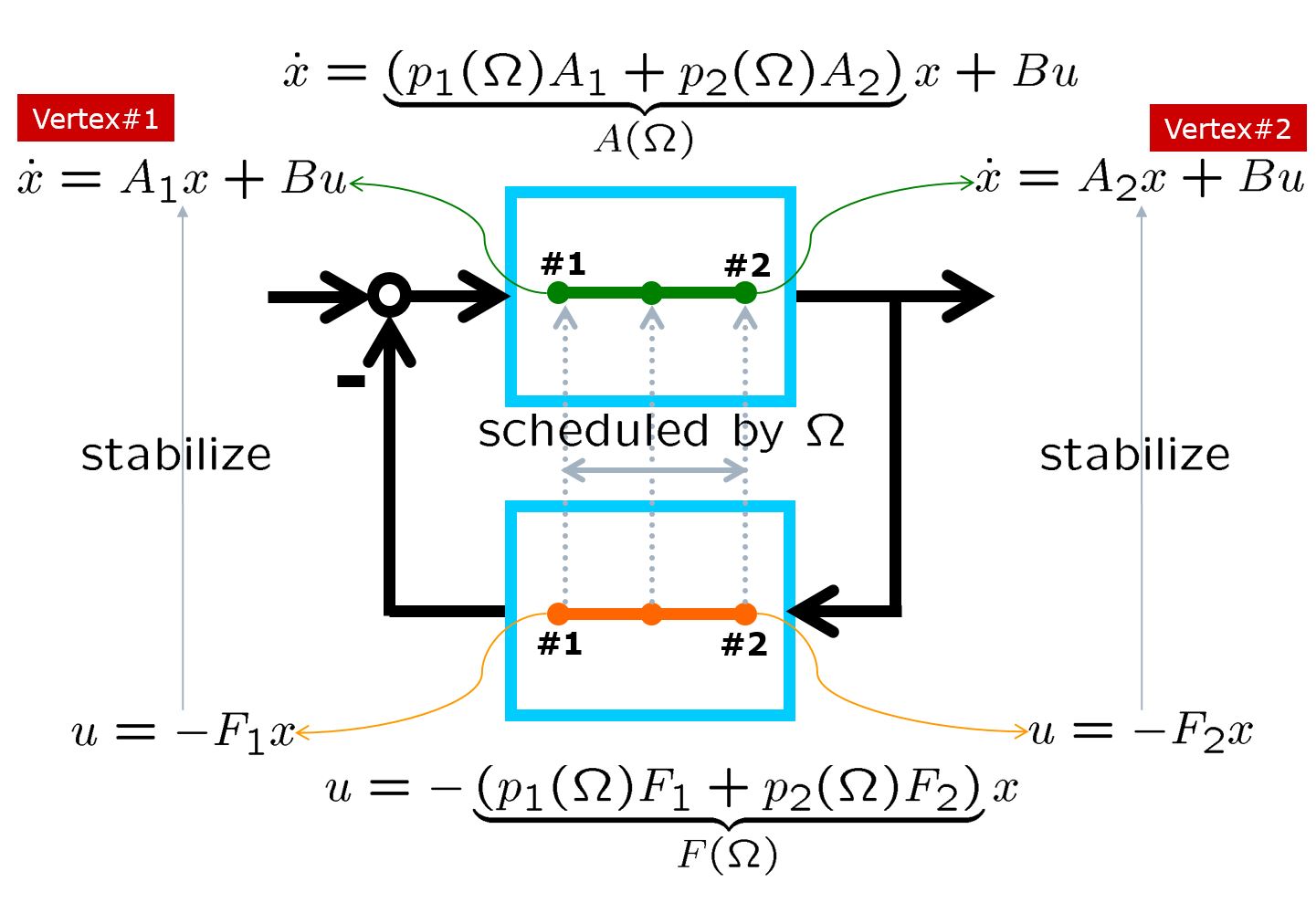 図3 LPV制御の枠組み
図3 LPV制御の枠組み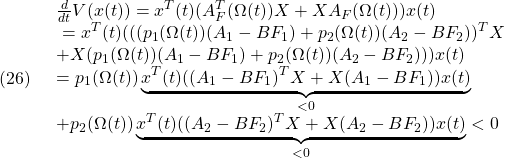
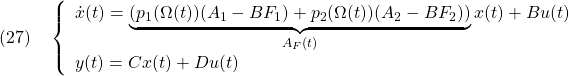
![Rendered by QuickLaTeX.com \displaystyle{(28)\quad \exists X_1>0:\ \left[\begin{array}{ccc} (A_1-BF_1)^TX_1+X_1(A_1-BF_1) & X_1B & C^T \\ B^TX_1 & -\gamma I & D^T \\ C & D & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4e0b94de7fd261c64c1ad459ff663479_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(29)\quad \exists X_2>0:\ \left[\begin{array}{ccc} (A_2-BF_2)^TX_2+X_2(A_2-BF_2) & X_2B & C^T \\ B^TX_2 & -\gamma I & D^T \\ C & D & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e6b89cd6a762615e4cf1bf7d4196430f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(30)\quad \left[\begin{array}{ccc} (A_1-BF_1)^TX+X(A_1-BF_1) & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D &-I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-54dee83aaf14f44301eff55fc1606abe_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad \left[\begin{array}{ccc} (A_1-BF_1)^TX+X(A_1-BF_1) & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D &-I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-740c33f1cb04f1a96dba09b1d8f767da_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right]^T \left[\begin{array}{cc} \begin{array}{c} ( p_1(\Omega(t))(A_1-BF_1)+p_2(\Omega(t))(A_2-BF_2) )^TX\\ +X( p_1(\Omega(t))(A_1-BF_1)+p_2(\Omega(t))(A_2-BF_2) ) \end{array} & XB \\ B^TX & 0 \end{array}\right] \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1fc23d0a361803d365380b86a013ae6e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ < \underbrace{(p_1(\Omega(t))+p_2(\Omega(t)))}_1 \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right]^T \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right]^T \left[\begin{array}{cc} - I & 0 \\ 0 & \gamma^2 I \end{array}\right] \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right] \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2d9183af6071904863cbae048501209a_l3.png)
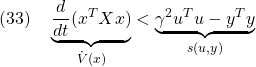
![Rendered by QuickLaTeX.com \displaystyle{(35)\quad P: \left\{\begin{array}{l} \dot{x}(t)=\underbrace{(p_1(\Omega(t))A_1+p_2(\Omega(t))A_2)}_{A(\Omega(t))}x(t)+B_1u_1(t)+B_2u_2(t) \\ \underbrace{ \left[\begin{array}{c} y(t)\\ u(t) \end{array}\right] }_{y_1(t)} = \underbrace{ \left[\begin{array}{c} C\\ 0 \end{array}\right] }_{C_1} x(t)+ \underbrace{ \left[\begin{array}{c} 0\\ 0 \end{array}\right] }_{D_{11}}u_1(t)+ \underbrace{ \left[\begin{array}{c} 0\\ I \end{array}\right] }_{D_{12}} u_2(t) \\ y_2(t)=x(t) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-427d73db7b01554c5df63c0e87878e0a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(37)\quad P_{CL}: \left\{\begin{array}{l} \dot{x}(t)=(A(\Omega(t))-B_2F(\Omega(t)))x(t)+B_1u_1(t) \\ y_1(t)= \underbrace{ \left[\begin{array}{c} C\\ -F \end{array}\right] }_{C_1-D_{12}F} x(t) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d78f3f099b3133c3acad786e1bf139f9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(40)\quad \left[\begin{array}{ccc} (A_1Y-B_2Z_1)^T+A_1Y-B_2Z_1 & B_1 & (C_1Y-D_{12}Z_1)^T \\ B_1^T & -\gamma I & D_{11}^T \\ C_1Y-D_{12}Z_1 & D_{11} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c7466d89622c237467830e9e7a4dde4f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(41)\quad \begin{array}{l} 2\alpha Y+A_1Y-B_2Z_1+(A_1Y-B_2Z_1)^T<0 \\ \left[\begin{array}{cc} -rY & A_1Y-B_2Z_1 \\ (A_1Y-B_2Z_1)^T & -rY \end{array}\right]<0 \\ \left[\begin{array}{cc} \sin\theta(A_1Y-B_2Z_1+(A_1Y-B_2Z_1)^T) & \\ -\cos\theta(A_1Y-B_2Z_1-(A_1Y-B_2Z_1)^T) & \end{array}\right. \\ \left.\begin{array}{cc} & \cos\theta(A_1Y-B_2Z_1-(A_1Y-B_2Z_1)^T) \\ & \sin\theta(A_1Y-B_2Z_1+(A_1Y-B_2Z_1)^T) \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e8f398812655a3aa43af25d448acd033_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(42)\quad \left[\begin{array}{ccc} (A_2Y-B_2Z_2)^T+A_2Y-B_2Z_2 & B_1 & (C_1Y-D_{12}Z_2)^T \\ B_1^T & -\gamma I & D_{11}^T \\ C_1Y-D_{12}Z_2 & D_{11} & -\gamma I \end{array}\right]<0 \\ }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4cce98efcffcefcc62a9d413a65d4bc4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(43)\quad \begin{array}{l} 2\alpha Y+A_1Y-B_2Z_2+(A_1Y-B_2Z_2)^T<0 \\ \left[\begin{array}{cc} -rY & A_1Y-B_2Z_2 \\ (A_1Y-B_2Z_2)^T & -rY \end{array}\right]<0 \\ \left[\begin{array}{cc} \sin\theta(A_2Y-B_2Z_2+(A_2Y-B_2Z_2)^T) & \\ -\cos\theta(A_2Y-B_2Z_2-(A_2Y-B_2Z_2)^T) & \end{array}\right. \\ \left.\begin{array}{cc} & \cos\theta(A_2Y-B_2Z_2-(A_2Y-B_2Z_2)^T) \\ & \sin\theta(A_2Y-B_2Z_2+(A_2Y-B_2Z_2)^T) \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-748f7d965c9e2ec369f760ff7e4cfe8d_l3.png)
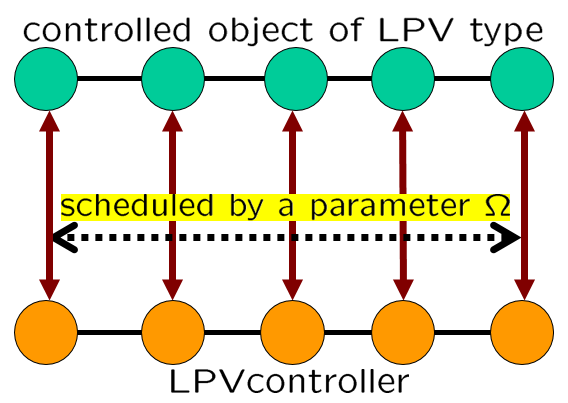 図4 LPV制御のイメージ
図4 LPV制御のイメージ 図5 LTI制御のイメージ
図5 LTI制御のイメージ 図6 LPV制御においてスケジューリングを止めた場合
図6 LPV制御においてスケジューリングを止めた場合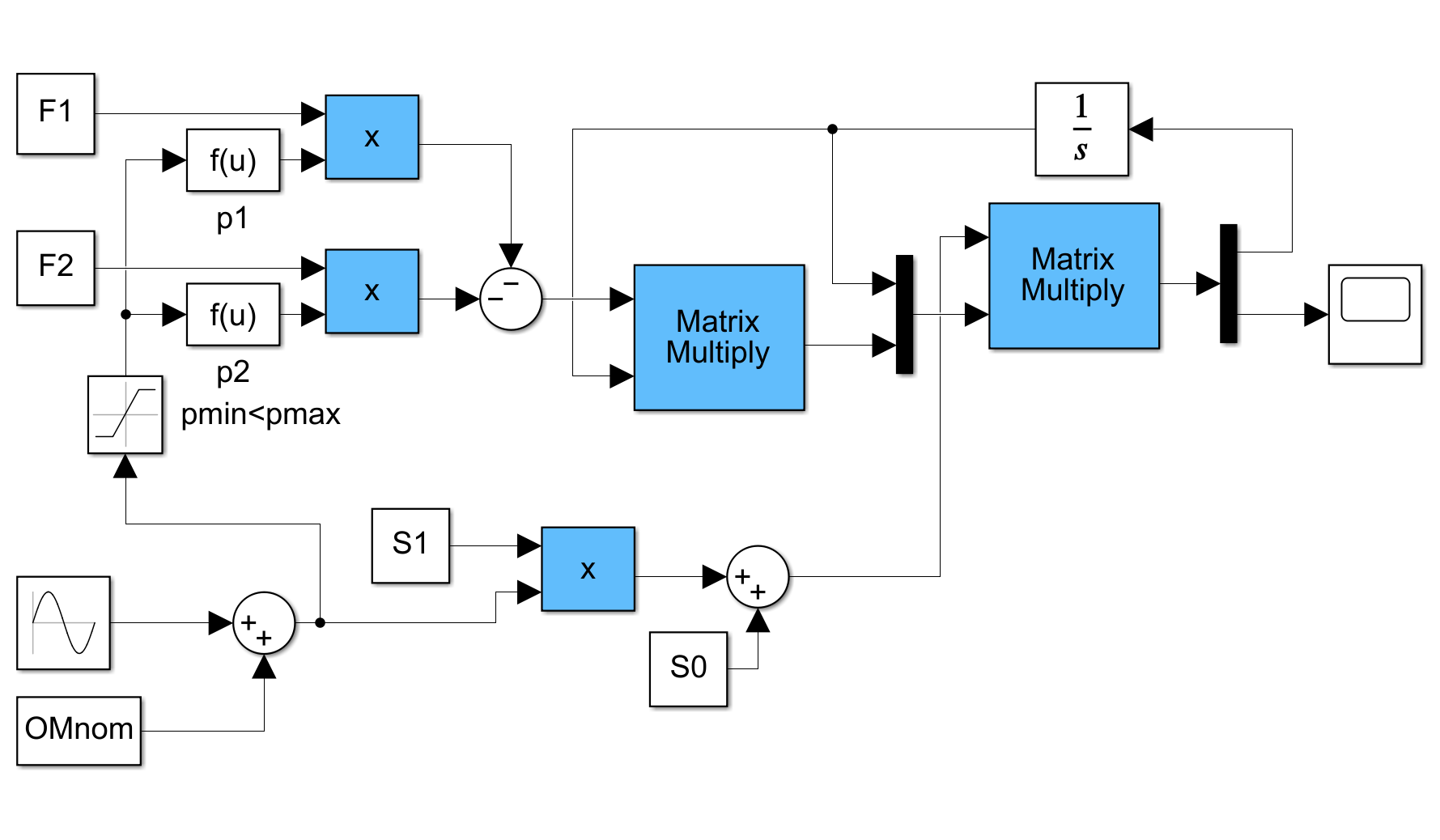
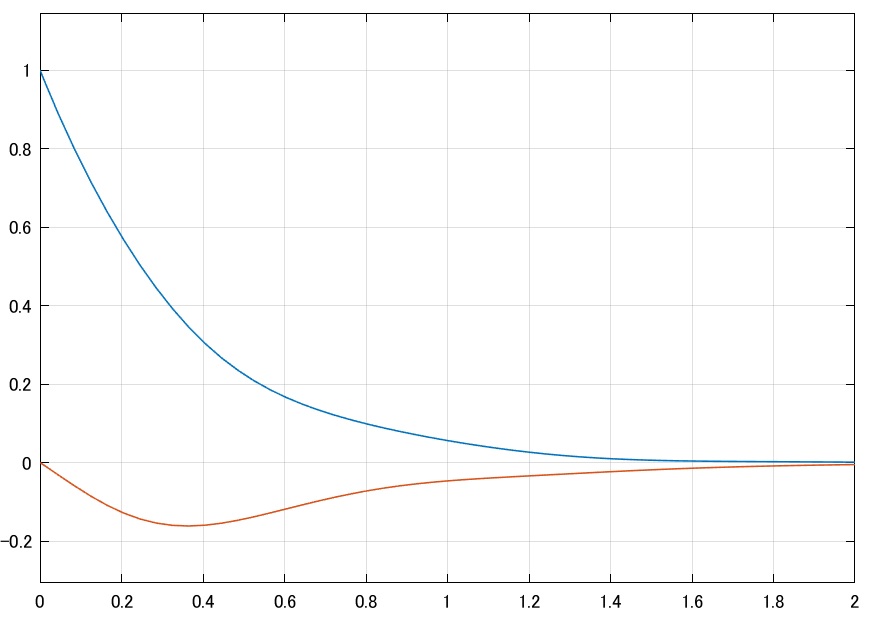 図7 回転体のLPV制御
図7 回転体のLPV制御
 図8 回転体の
図8 回転体の
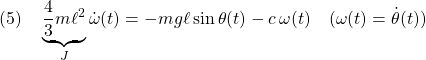
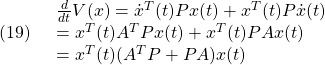
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \begin{array}{l} \displaystyle{A^T\int_0^\infty \exp(A^Tt)Q\exp(At)dt+\int_0^\infty \exp(A^Tt)Q\exp(At)dt\,A}\\ \displaystyle{=\int_0^\infty \frac{d}{dt}(\exp(A^Tt)Q\exp(At))\,dt}\\ \displaystyle{=\left[\exp(A^Tt)Q\exp(At)\right]_0^\infty=-Q<0} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8818d2570a2394fee7a40d1e57a29ee2_l3.png)
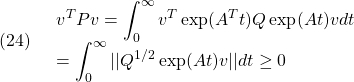
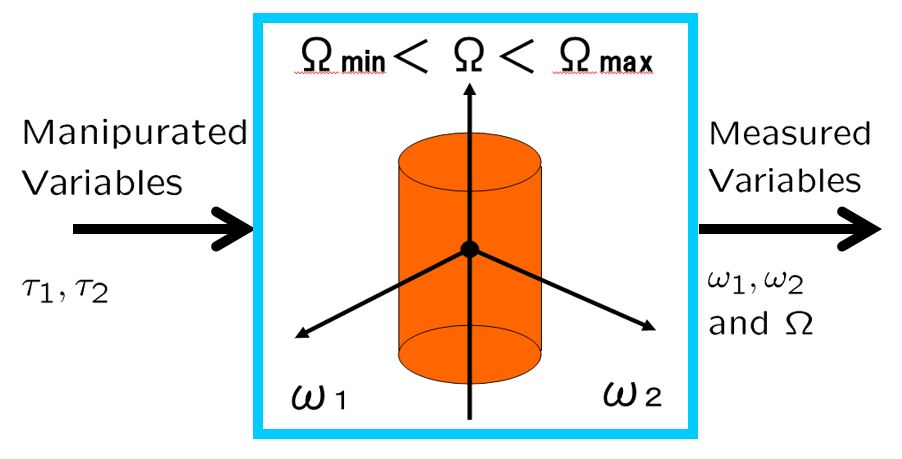 図1 パラメータ変動システムの例
図1 パラメータ変動システムの例 図2 パラメータ変動システムの応答シミュレーション例
図2 パラメータ変動システムの応答シミュレーション例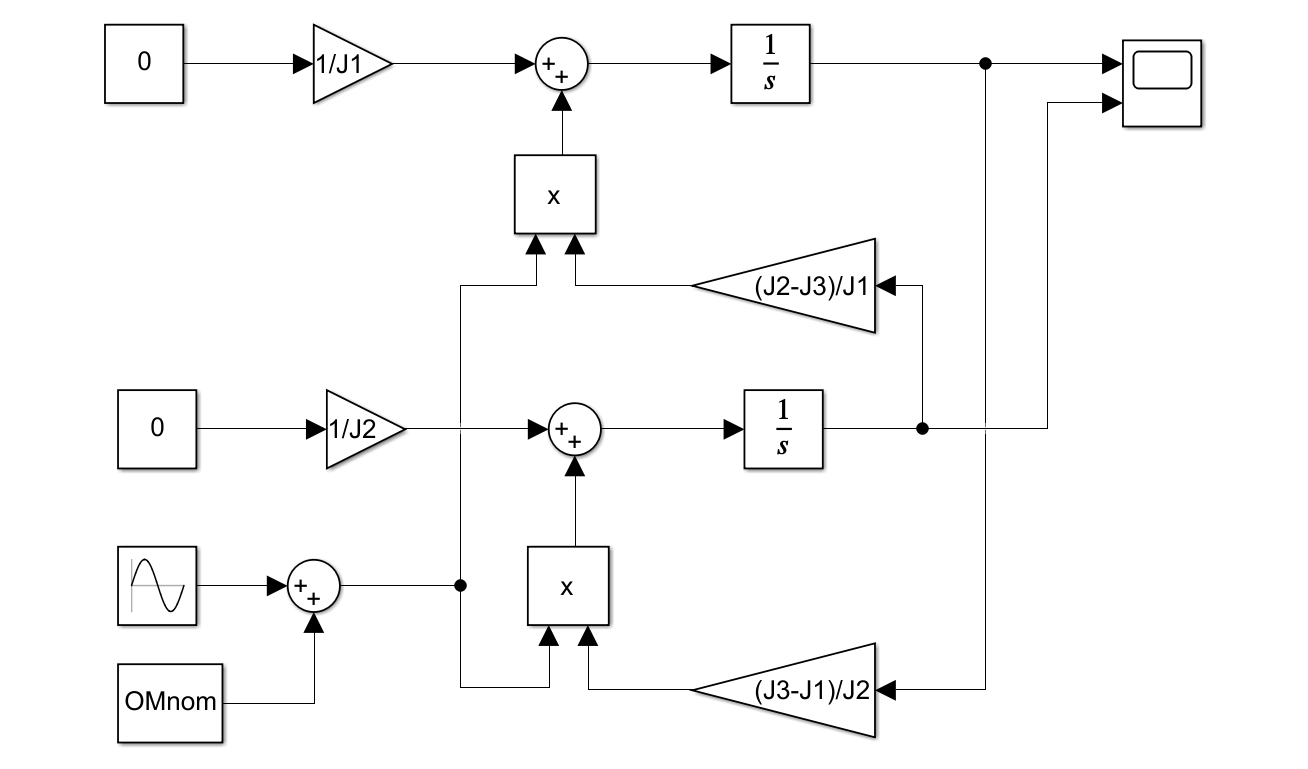 図3 SPIN0.slx
図3 SPIN0.slx