| MATLAB |
%cADIP_of_gs.m
%-----
clear all, close all
global ell1 ell2 th10 th20
ell1=0.13; ell2=0.15; m1=0.05; m2=0.03; g=9.8;
Ta=0.1; Ka=1;
th10=0; th20=0;
th1=0; th2=70/180*pi;
rymax=2*ell1*cos(th1); rymin=2*ell1*cos(th2); rynom=rymax;
rxmin=2*ell1*sin(th1); rxmax=2*ell1*sin(th2); rxnom=rxmax;
A0=[0 1 0 0;
3*g/(4*ell2) 0 -3*g/(4*ell2) 0;
0 0 0 0;
0 0 0 -1/Ta];
A1=[0 0 0 0;
0 0 0 0;
0 0 0 1;
0 0 0 0];
Amax=A0+rymax*A1;
Amin=A0+rymin*A1;
Anom=A0+rynom*A1;
B=[0;0;0;Ka/Ta];
CM=[1 0 0 0;
0 0 1 0];
DM=[0;0];
S0=[A0 B;CM DM];
S1=[A1 zeros(4,1);zeros(2,5)];
%-----
wD=0.02; wI=0.5; C0=CM(2,:);
AA1=[Amin zeros(4,1);-C0 0];
AA2=[Amax zeros(4,1);-C0 0];
B1=[zeros(4,1);1]; B2=[B;0];
C1=[zeros(1,4) wI;wD*C0*Anom 0]; D11=zeros(2,1); D12=[0;wD*C0*B];
C2=[CM zeros(2,1);zeros(1,4) 1]; D21=[0;0;0]; D22=[0;0;0];
%=====
alpha=0.1; r=50; th=90/180*pi;
LMIs=of_synlmi7(AA1,AA2,B1,B2,C1,C2,D11,D12,D21,D22,alpha,r,th);
cobj=zeros(1,decnbr(LMIs));
cobj(1)=1;
[cost,xopt]=mincx(LMIs,cobj);
gopt=dec2mat(LMIs,xopt,1)
R=dec2mat(LMIs,xopt,2);
S=dec2mat(LMIs,xopt,3);
%=====
ak1=dec2mat(LMIs,xopt,4);
bk1=dec2mat(LMIs,xopt,5);
ck1=dec2mat(LMIs,xopt,6);
dk1=dec2mat(LMIs,xopt,7);
[u,sd,v]=svd(eye(size(AA1,1))-R*S);
sd=diag(sqrt(1./diag(sd)));
Ni=sd*v'; Mti=u*sd;
AK1=Ni*(ak1-S*(AA1-B2*dk1*C2)*R-bk1*C2*R-S*B2*ck1)*Mti;
BK1=Ni*(bk1-S*B2*dk1);
CK1=(ck1-dk1*C2*R)*Mti;
DK1=dk1;
K1=[AK1 BK1;CK1 DK1];
%-----
pl1=eig(AA1)
ACL1=[AA1+B2*DK1*C2 B2*CK1;
BK1*C2 AK1];
plCL1=eig(ACL1)
figure(1)
dregion(-alpha,0,r,th,r*[-1,1,-1,1])
plot(real(pl1),imag(pl1),'x',real(plCL1),imag(plCL1),'*')
%-----
ACL1=[AA1+B2*DK1*C2 B2*CK1;BK1*C2 AK1];
BCL1=[B1+B2*DK1*D21;BK1*D21];
CCL1=[C2(1,:) zeros(1,5)];
AK1=[AK1 BK1(:,3);zeros(1,6)];
BK1=[BK1(:,1:2) zeros(5,1); -1 0 1];
CK1=[CK1 DK1(:,3)];
DK1=[DK1(:,1:2) 0];
SK1=[AK1 BK1;CK1 DK1];
%-----
w=logspace(-2,2,100);
ga_WS=20*log10(abs(wI./(i*w)));
ga_WT=20*log10(abs(wD*(i*w)));
G(:,:)=freqresp(ss(Amax,B,C0,[]),w); G=G.'; ga_G=20*log10(abs(G));
K(:,:)=freqresp(ss(AK1,BK1(:,1),CK1,DK1(:,1)),w); K=K.'; ga_K=20*log10(abs(K));
T(:,:)=freqresp(ss(ACL1,BCL1(:,1),CCL1(1,:),[]),w); T=T.'; ga_T=20*log10(abs(T));
ga_S=20*log10(abs(1-T));
figure(2)
subplot(121),semilogx(w,ga_G+ga_K,w,ga_WS,'b',w,-ga_WT,'r'),grid,legend('L','WS','1/WT')
subplot(122),semilogx(w,ga_T,'r',w,-ga_WT,'r',w,ga_S,'b',w,-ga_WS,'b'),grid,legend('T','1/WT','S','1/WS')
%=====
ak2=dec2mat(LMIs,xopt,8);
bk2=dec2mat(LMIs,xopt,9);
ck2=dec2mat(LMIs,xopt,10);
dk2=dec2mat(LMIs,xopt,11);
[u,sd,v]=svd(eye(size(AA2,1))-R*S);
sd=diag(sqrt(1./diag(sd)));
Ni=sd*v'; Mti=u*sd;
AK2=Ni*(ak2-S*(AA2-B2*dk2*C2)*R-bk2*C2*R-S*B2*ck2)*Mti;
BK2=Ni*(bk2-S*B2*dk2);
CK2=(ck2-dk2*C2*R)*Mti;
DK2=dk2;
K2=[AK2 BK2;CK2 DK2];
%-----
pl2=eig(AA2)
ACL2=[AA2+B2*DK2*C2 B2*CK2;
BK2*C2 AK2];
plCL2=eig(ACL2)
figure(3)
dregion(-alpha,0,r,th,r*[-1,1,-1,1])
plot(real(pl2),imag(pl2),'x',real(plCL2),imag(plCL2),'*')
%-----
ACL2=[AA2+B2*DK2*C2 B2*CK2;BK2*C2 AK2];
BCL2=[B1+B2*DK2*D21;BK2*D21];
CCL2=[C2(1,:) zeros(1,5)];
AK2=[AK2 BK2(:,3);zeros(1,6)];
BK2=[BK2(:,1:2) zeros(5,1); -1 0 1];
CK2=[CK2 DK2(:,3)];
DK2=[DK2(:,1:2) 0];
SK2=[AK2 BK2;CK2 DK2];
%-----
w=logspace(-2,2,100);
ga_WS=20*log10(abs(wI./(i*w)));
ga_WT=20*log10(abs(wD*(i*w)));
G(:,:)=freqresp(ss(Amin,B,C0,[]),w); G=G.'; ga_G=20*log10(abs(G));
K(:,:)=freqresp(ss(AK2,BK2(:,1),CK2,DK2(:,1)),w); K=K.'; ga_K=20*log10(abs(K));
T(:,:)=freqresp(ss(ACL2,BCL2(:,1),CCL2(1,:),[]),w); T=T.'; ga_T=20*log10(abs(T));
ga_S=20*log10(abs(1-T));
figure(4)
subplot(121),semilogx(w,ga_G+ga_K,w,ga_WS,'b',w,-ga_WT,'r'),grid,legend('L','WS','1/WT')
subplot(122),semilogx(w,ga_T,'r',w,-ga_WT,'r',w,ga_S,'b',w,-ga_WS,'b'),grid,legend('T','1/WT','S','1/WS')
%-----
prange=rymax-rymin; pmax=rymax; pmin=rymin;
%sim("ADIP_of_gs")
sim("ADIP_of_gs_2015a")
%-----
function LMIs=of_synlmi7(A1,A2,B1,B2,C1,C2,D11,D12,D21,D22,alpha,r,th)
[n,m]=size(B2); [p,n]=size(C2);
setlmis([]);
gam=lmivar(1,[1 0]);
[R,xxx,Rdec]=lmivar(1,[n 1]);
[S,xxx,Sdec]=lmivar(1,[n 1]);
Ak1=lmivar(2,[n n]);
Bk1=lmivar(2,[n p]);
Ck1=lmivar(2,[m n]);
Dk1=lmivar(2,[m p]);
Ak2=lmivar(2,[n n]);
Bk2=lmivar(2,[n p]);
Ck2=lmivar(2,[m n]);
Dk2=lmivar(2,[m p]);
%=====
lmiRS1=newlmi;
lmiterm([lmiRS1 1 1 R],A1,1,'s'); %#1:R*A'+AR
lmiterm([lmiRS1 1 1 Ck1],B2,1,'s'); %#1:Ck'*B2'+B2*Ck
lmiterm([lmiRS1 2 1 0],A1'); %#1:A'
lmiterm([lmiRS1 2 1 Ak1],1,1); %#1:Ak
lmiterm([lmiRS1 2 1 -Dk1],C2',B2'); %#1:C2'*Dk'*B2'
lmiterm([lmiRS1 2 2 S],1,A1,'s'); %#1:A'*S+S*A
lmiterm([lmiRS1 2 2 Bk1],1,C2,'s'); %#1:C2'*Bk'+Bk*C2
lmiterm([lmiRS1 1 3 0],B1); %#1:B1
lmiterm([lmiRS1 1 3 Dk1],B2,D21); %#1:B2*Dk*D21
lmiterm([lmiRS1 2 3 S],1,B1); %#1:S*B1
lmiterm([lmiRS1 2 3 Bk1],1,D21); %#1:Bk*D21
lmiterm([lmiRS1 3 3 gam],-1,1); %#1:-gam
lmiterm([lmiRS1 4 1 R],C1,1); %#1:C1*R
lmiterm([lmiRS1 4 1 Ck1],D12,1); %#1:D12*Ck
lmiterm([lmiRS1 4 2 0],C1); %#1:C1
lmiterm([lmiRS1 4 2 Dk1],D12,C2); %#1:D12*Dk*C2
lmiterm([lmiRS1 4 3 0],D11); %#1:D11
lmiterm([lmiRS1 4 3 Dk1],D12,D21); %#1:D12*Dk*D21
lmiterm([lmiRS1 4 4 gam],-1,1); %#1:-gam
%-----
lmiPL11=newlmi;
lmiterm([lmiPL11 1 1 R],A1,1,'s'); %#2:R*A'+A*R
lmiterm([lmiPL11 1 1 Ck1],B2,1,'s'); %#2:Ck'*B2'+B2*Ck
lmiterm([lmiPL11 2 1 Ak1],1,1); %#2:Ak
lmiterm([lmiPL11 1 2 0],A1); %#2:A
lmiterm([lmiPL11 1 2 Dk1],B2,C2); %#2:B2*Dk*C2
lmiterm([lmiPL11 2 2 S],1,A1,'s'); %#2:A'*S+S*A
lmiterm([lmiPL11 2 2 Bk1],1,C2,'s'); %#2:C2'*Bk'+Bk*C2
%
lmiterm([lmiPL11 1 1 R],2*alpha,1); %#2:2*alpha*R
lmiterm([lmiPL11 2 1 0],2*alpha); %#2:2*alpha*I
lmiterm([lmiPL11 2 2 S],2*alpha,1); %#2:2*alpha*S
%-----
lmiPL21=newlmi;
lmiterm([lmiPL21 1 1 R],-r,1); %#3:-r*R
lmiterm([lmiPL21 2 1 0],-r); %#3:-r*I
lmiterm([lmiPL21 2 2 S],-r,1); %#3:-r*S
%
lmiterm([lmiPL21 1 3 R],A1,1); %#3:A*R
lmiterm([lmiPL21 1 3 Ck1],B2,1); %#3:B2*Ck
lmiterm([lmiPL21 2 3 Ak1],1,1); %#3:Ak
lmiterm([lmiPL21 1 4 0],A1); %#3:A
lmiterm([lmiPL21 1 4 Dk1],B2,C2); %#3:B2*Dk*C2
lmiterm([lmiPL21 2 4 S],1,A1); %#3:S*A
lmiterm([lmiPL21 2 4 Bk1],1,C2); %#3:Bk*C2
%
lmiterm([lmiPL21 3 3 R],-r,1); %#3:-r*R
lmiterm([lmiPL21 4 3 0],-r); %#3:-r*I
lmiterm([lmiPL21 4 4 S],-r,1); %#3:-r*S
%-----
sth=sin(th); cth=cos(th);
lmiPL31=newlmi;
lmiterm([lmiPL31 1 1 R],sth*A1,1,'s'); %#4:sth*(R*A'+A*R)
lmiterm([lmiPL31 1 1 Ck1],sth*B2,1,'s');%#4:sth*(Ck'*B2'+B2*Ck)
lmiterm([lmiPL31 2 1 Ak1],sth,1); %#4:sth*(Ak)
lmiterm([lmiPL31 1 2 0],sth*A1); %#4:sth*(A)
lmiterm([lmiPL31 1 2 Dk1],sth*B2,C2); %#4:sth*(B2*Dk*C2)
lmiterm([lmiPL31 2 2 S],1,sth*A1,'s'); %#4:sth*(A'*S+S*A)
lmiterm([lmiPL31 2 2 Bk1],1,sth*C2,'s');%#4:sth*(C2'*Bk'+Bk*C2)
%
lmiterm([lmiPL31 1 3 R],cth*A1,1); %#1:cth*(A*R)
lmiterm([lmiPL31 1 3 R],1,-cth*A1'); %#1:cth*(-R*A')
lmiterm([lmiPL31 1 3 Ck1],cth*B2,1); %#1:cth*(B*Ck)
lmiterm([lmiPL31 1 3 -Ck1],-cth*B2',1); %#1:cth*(-Ck'*B')
lmiterm([lmiPL31 2 3 Ak1],cth,1); %#4:cth*(Ak)
lmiterm([lmiPL31 1 4 -Ak1],-cth,1); %#4:cth*(-Ak')
lmiterm([lmiPL31 1 4 0],A1); %#4:cth*(A)
lmiterm([lmiPL31 2 3 0],-A1'); %#4:cth*(-A')
lmiterm([lmiPL31 1 4 Dk1],cth*B2,C2); %#4:cth*(B2*Dk*C2)
lmiterm([lmiPL31 2 3 -Dk1],-cth*C2',B2');%#4:cth*(-C2'*Dk'*B2')
lmiterm([lmiPL31 2 4 S],1,cth*A1); %#4:cth*(S*A)
lmiterm([lmiPL31 2 4 S],-cth*A1',1); %#4:cth*(-A'*S)
lmiterm([lmiPL31 2 4 Bk1],1,cth*C2); %#4:cth*(Bk*C2)
lmiterm([lmiPL31 2 4 -Bk1],-cth*C2',1); %#4:cth*(-C2'*Bk')
%
lmiterm([lmiPL31 3 3 R],sth*A1,1,'s'); %#4:sth*(R*A'+A*R)
lmiterm([lmiPL31 3 3 Ck1],sth*B2,1,'s');%#4:sth*(Ck'*B2'+B2*Ck)
lmiterm([lmiPL31 4 3 Ak1],sth,1); %#4:sth*(Ak)
lmiterm([lmiPL31 3 4 0],sth*A1); %#4:sth*(A)
lmiterm([lmiPL31 3 4 Dk1],sth*B2,C2); %#4:sth*(B2*Dk*C2)
lmiterm([lmiPL31 4 4 S],1,sth*A1,'s'); %#4:sth*(A'*S+S*A)
lmiterm([lmiPL31 4 4 Bk1],1,sth*C2,'s');%#4:sth*(C2'*Bk'+Bk*C2)
%=====
lmiRS2=newlmi;
lmiterm([lmiRS2 1 1 R],A2,1,'s'); %#1:R*A'+AR
lmiterm([lmiRS2 1 1 Ck2],B2,1,'s'); %#1:Ck'*B2'+B2*Ck
lmiterm([lmiRS2 2 1 0],A2'); %#1:A'
lmiterm([lmiRS2 2 1 Ak2],1,1); %#1:Ak
lmiterm([lmiRS2 2 1 -Dk2],C2',B2'); %#1:C2'*Dk'*B2'
lmiterm([lmiRS2 2 2 S],1,A2,'s'); %#1:A'*S+S*A
lmiterm([lmiRS2 2 2 Bk2],1,C2,'s'); %#1:C2'*Bk'+Bk*C2
lmiterm([lmiRS2 1 3 0],B1); %#1:B1
lmiterm([lmiRS2 1 3 Dk2],B2,D21); %#1:B2*Dk*D21
lmiterm([lmiRS2 2 3 S],1,B1); %#1:S*B1
lmiterm([lmiRS2 2 3 Bk2],1,D21); %#1:Bk*D21
lmiterm([lmiRS2 3 3 gam],-1,1); %#1:-gam
lmiterm([lmiRS2 4 1 R],C1,1); %#1:C1*R
lmiterm([lmiRS2 4 1 Ck2],D12,1); %#1:D12*Ck
lmiterm([lmiRS2 4 2 0],C1); %#1:C1
lmiterm([lmiRS2 4 2 Dk2],D12,C2); %#1:D12*Dk*C2
lmiterm([lmiRS2 4 3 0],D11); %#1:D11
lmiterm([lmiRS2 4 3 Dk2],D12,D21); %#1:D12*Dk*D21
lmiterm([lmiRS2 4 4 gam],-1,1); %#1:-gam
%-----
lmiPL12=newlmi;
lmiterm([lmiPL12 1 1 R],A2,1,'s'); %#2:R*A'+A*R
lmiterm([lmiPL12 1 1 Ck2],B2,1,'s'); %#2:Ck'*B2'+B2*Ck
lmiterm([lmiPL12 2 1 Ak2],1,1); %#2:Ak
lmiterm([lmiPL12 1 2 0],A2); %#2:A
lmiterm([lmiPL12 1 2 Dk2],B2,C2); %#2:B2*Dk*C2
lmiterm([lmiPL12 2 2 S],1,A2,'s'); %#2:A'*S+S*A
lmiterm([lmiPL12 2 2 Bk2],1,C2,'s'); %#2:C2'*Bk'+Bk*C2
%
lmiterm([lmiPL12 1 1 R],2*alpha,1); %#2:2*alpha*R
lmiterm([lmiPL12 2 1 0],2*alpha); %#2:2*alpha*I
lmiterm([lmiPL12 2 2 S],2*alpha,1); %#2:2*alpha*S
%-----
lmiPL22=newlmi;
lmiterm([lmiPL22 1 1 R],-r,1); %#3:-r*R
lmiterm([lmiPL22 2 1 0],-r); %#3:-r*I
lmiterm([lmiPL22 2 2 S],-r,1); %#3:-r*S
%
lmiterm([lmiPL22 1 3 R],A2,1); %#3:A*R
lmiterm([lmiPL22 1 3 Ck2],B2,1); %#3:B2*Ck
lmiterm([lmiPL22 2 3 Ak2],1,1); %#3:Ak
lmiterm([lmiPL22 1 4 0],A2); %#3:A
lmiterm([lmiPL22 1 4 Dk2],B2,C2); %#3:B2*Dk*C2
lmiterm([lmiPL22 2 4 S],1,A2); %#3:S*A
lmiterm([lmiPL22 2 4 Bk2],1,C2); %#3:Bk*C2
%
lmiterm([lmiPL22 3 3 R],-r,1); %#3:-r*R
lmiterm([lmiPL22 4 3 0],-r); %#3:-r*I
lmiterm([lmiPL22 4 4 S],-r,1); %#3:-r*S
%-----
sth=sin(th); cth=cos(th);
lmiPL32=newlmi;
lmiterm([lmiPL32 1 1 R],sth*A2,1,'s'); %#4:sth*(R*A'+A*R)
lmiterm([lmiPL32 1 1 Ck2],sth*B2,1,'s');%#4:sth*(Ck'*B2'+B2*Ck)
lmiterm([lmiPL32 2 1 Ak2],sth,1); %#4:sth*(Ak)
lmiterm([lmiPL32 1 2 0],sth*A2); %#4:sth*(A)
lmiterm([lmiPL32 1 2 Dk2],sth*B2,C2); %#4:sth*(B2*Dk*C2)
lmiterm([lmiPL32 2 2 S],1,sth*A2,'s'); %#4:sth*(A'*S+S*A)
lmiterm([lmiPL32 2 2 Bk2],1,sth*C2,'s');%#4:sth*(C2'*Bk'+Bk*C2)
%
lmiterm([lmiPL32 1 3 R],cth*A2,1); %#1:cth*(A*R)
lmiterm([lmiPL32 1 3 R],1,-cth*A2'); %#1:cth*(-R*A')
lmiterm([lmiPL32 1 3 Ck2],cth*B2,1); %#1:cth*(B*Ck)
lmiterm([lmiPL32 1 3 -Ck2],-cth*B2',1); %#1:cth*(-Ck'*B')
lmiterm([lmiPL32 2 3 Ak2],cth,1); %#4:cth*(Ak)
lmiterm([lmiPL32 1 4 -Ak2],-cth,1); %#4:cth*(-Ak')
lmiterm([lmiPL32 1 4 0],A2); %#4:cth*(A)
lmiterm([lmiPL32 2 3 0],-A2'); %#4:cth*(-A')
lmiterm([lmiPL32 1 4 Dk2],cth*B2,C2); %#4:cth*(B2*Dk*C2)
lmiterm([lmiPL32 2 3 -Dk2],-cth*C2',B2');%#4:cth*(-C2'*Dk'*B2')
lmiterm([lmiPL32 2 4 S],1,cth*A2); %#4:cth*(S*A)
lmiterm([lmiPL32 2 4 S],-cth*A2',1); %#4:cth*(-A'*S)
lmiterm([lmiPL32 2 4 Bk2],1,cth*C2); %#4:cth*(Bk*C2)
lmiterm([lmiPL32 2 4 -Bk2],-cth*C2',1); %#4:cth*(-C2'*Bk')
%
lmiterm([lmiPL32 3 3 R],sth*A2,1,'s'); %#4:sth*(R*A'+A*R)
lmiterm([lmiPL32 3 3 Ck2],sth*B2,1,'s');%#4:sth*(Ck'*B2'+B2*Ck)
lmiterm([lmiPL32 4 3 Ak2],sth,1); %#4:sth*(Ak)
lmiterm([lmiPL32 3 4 0],sth*A2); %#4:sth*(A)
lmiterm([lmiPL32 3 4 Dk2],sth*B2,C2); %#4:sth*(B2*Dk*C2)
lmiterm([lmiPL32 4 4 S],1,sth*A2,'s'); %#4:sth*(A'*S+S*A)
lmiterm([lmiPL32 4 4 Bk2],1,sth*C2,'s');%#4:sth*(C2'*Bk'+Bk*C2)
%=====
posX=-newlmi;
lmiterm([posX 1 1 R],1,1); %#5:R
lmiterm([posX 2 1 0],1); %#5:I
lmiterm([posX 2 2 S],1,1); %#5:S
%-----
lmiDk1=-newlmi;
lmiterm([lmiDk1 1 1 0],1e2); %#6:1e2
lmiterm([lmiDk1 2 2 0],1e2); %#6:1e2
lmiterm([lmiDk1 2 1 Dk1],1,1); %#6:Dk
%-----
lmiDk2=-newlmi;
lmiterm([lmiDk2 1 1 0],1e2); %#6:1e2
lmiterm([lmiDk2 2 2 0],1e2); %#6:1e2
lmiterm([lmiDk2 2 1 Dk2],1,1); %#6:Dk
%-----
lmig=newlmi;
lmiterm([lmig,1,1,gam],1,1); %#7:gam
lmiterm([lmig,1,1,0],-1e3); %#7:1e3
LMIs=getlmis;
end
%-----
%eof
|
![]()
![]()
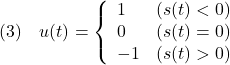
![]()
![]() の解は(
の解は(![]() に注意して)
に注意して)![]()
![]()
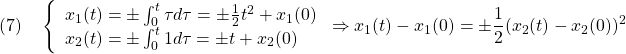
![]() 、
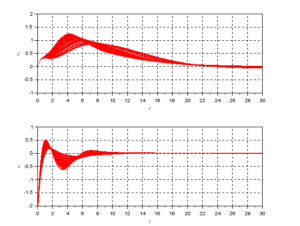
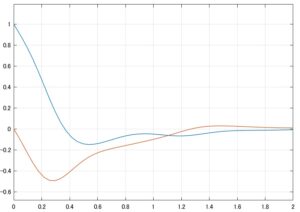
、![]() のときの状態軌道を図1に示します。
のときの状態軌道を図1に示します。
![]() のときの状態軌道
のときの状態軌道![]() の上側と下側にある(横に寝た)放物線を切り替えて状態軌道が構成されていることが分かります。ところが、原点に近くなると奇妙な現象が生じます。
の上側と下側にある(横に寝た)放物線を切り替えて状態軌道が構成されていることが分かります。ところが、原点に近くなると奇妙な現象が生じます。![]() 、
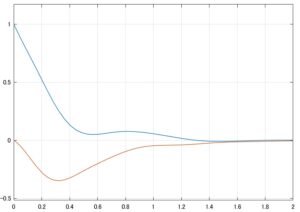
、![]() のときの状態軌道を図2に示します。
のときの状態軌道を図2に示します。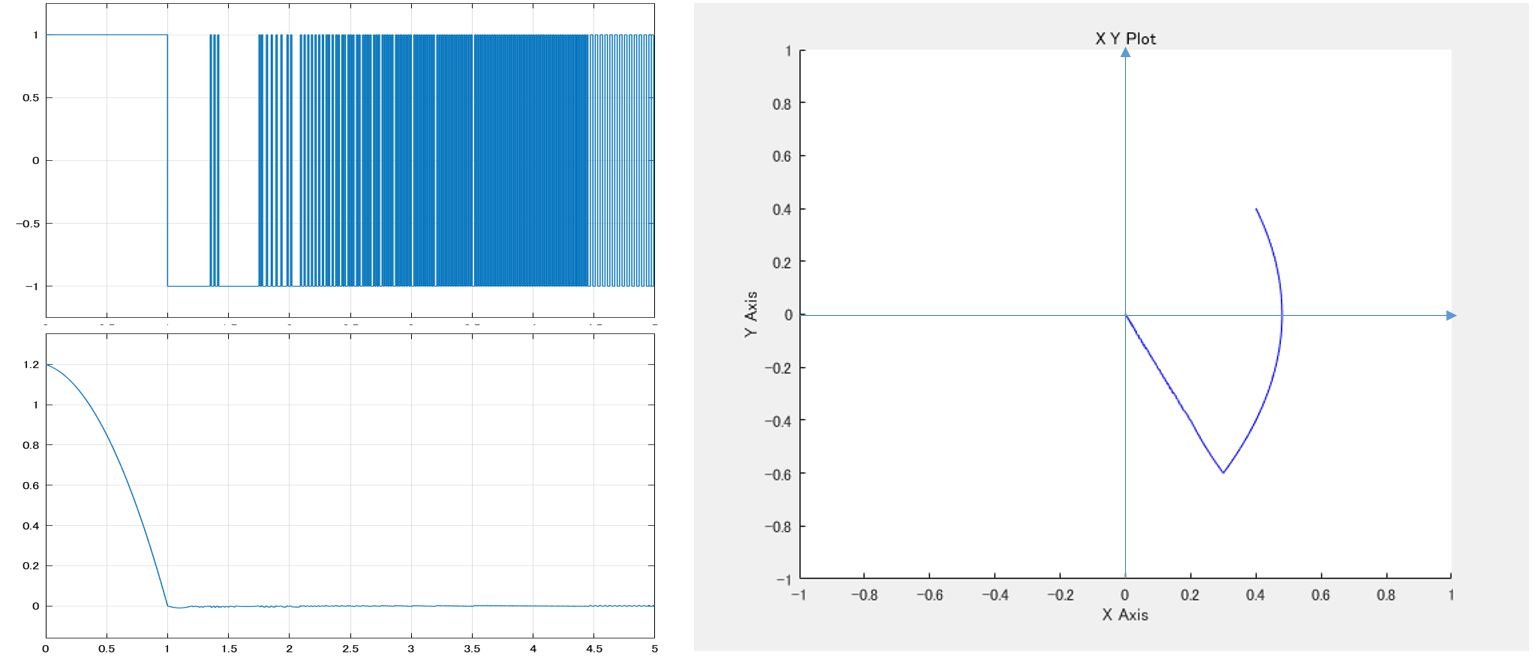
![]() のときの状態軌道
のときの状態軌道![]() に到達すると、この直線上に拘束されて原点まで滑っていることが分かります。一体、何が起こっているのでしょう?
に到達すると、この直線上に拘束されて原点まで滑っていることが分かります。一体、何が起こっているのでしょう?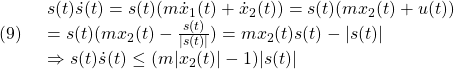
![]()
![]() は
は![]() 平面における
平面における![]() 軸の切片であることに注意します。(10)より、
軸の切片であることに注意します。(10)より、![]() のとき
のとき![]() なので切片
なので切片![]() は
は![]() 軸正の方から0に漸近します。一方、
軸正の方から0に漸近します。一方、![]() のとき
のとき![]() なので切片
なので切片![]() は
は![]() 軸負の方から0に漸近します。このことは状態は直線
軸負の方から0に漸近します。このことは状態は直線![]()
![]()
![]()
![]() に対して、可到達条件
に対して、可到達条件![]()
![]() とすると、次が成り立ちます。
とすると、次が成り立ちます。![]()
![]()
![]()
![]() を通したものが等価制御とよく合っていることがわかります。この1次システムはアクチュエータのダイナミックス(による帯域制限)を表しているとみなすことができます。
を通したものが等価制御とよく合っていることがわかります。この1次システムはアクチュエータのダイナミックス(による帯域制限)を表しているとみなすことができます。
![]() )
)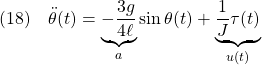
![]() ,
, ![]() とおいて、次の非線形状態方程式を得ます。
とおいて、次の非線形状態方程式を得ます。![]()
![]()
![]() とした場合のシミュレーション結果です。一見、図3と変わらないように見えます。
とした場合のシミュレーション結果です。一見、図3と変わらないように見えます。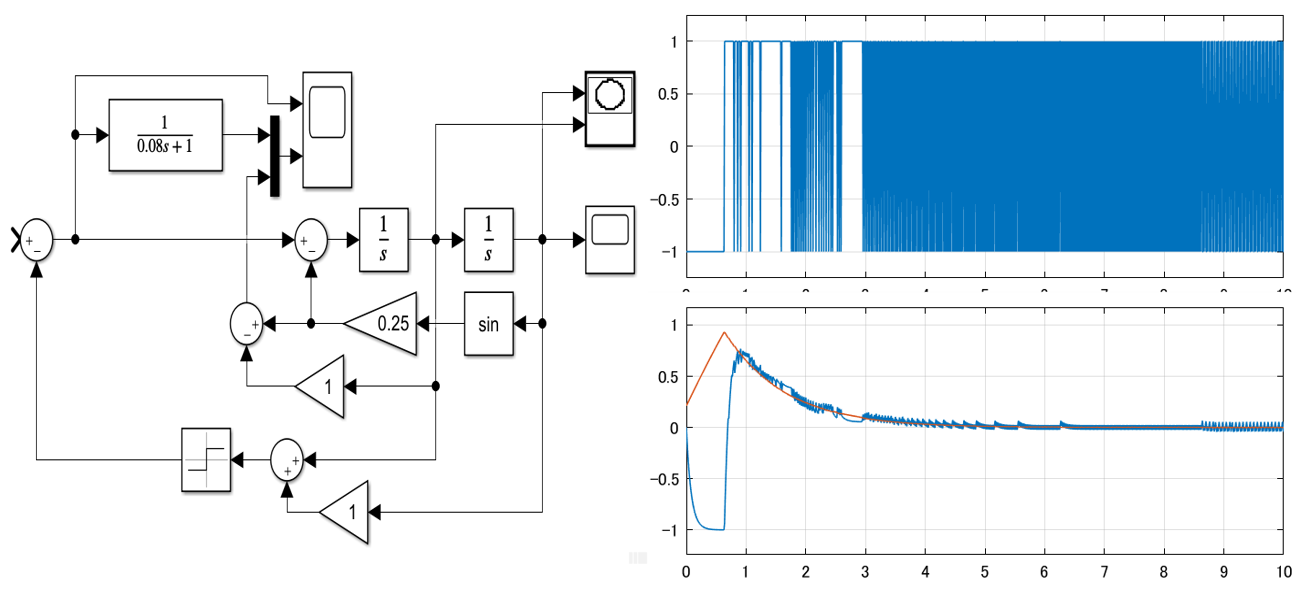
![]() )
)![]()
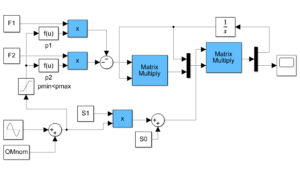
![]() smc11.slxとsmc12.slxを用いて、図1、図2のシミュレーションを行え。
smc11.slxとsmc12.slxを用いて、図1、図2のシミュレーションを行え。![]() smc13.slxとsmc14.slxを用いて、図3、図4のシミュレーションを行え。
smc13.slxとsmc14.slxを用いて、図3、図4のシミュレーションを行え。
![Rendered by QuickLaTeX.com \displaystyle{(1a)\quad \underbrace{ \left[\begin{array}{c|ccc} \alpha & m_1 & \dots &m_N \\ \hline m_1 & 1 & & 0 \\ \vdots & & \ddots & \\ m_N & 0 & & 1 \\ \end{array}\right] }_{M=\left[\begin{array}{cc} M_{11} & M_{12} \\ M_{21} & M_{22} \end{array}\right]} \underbrace{ \left[\begin{array}{c} \ddot{\theta} \\ \hline \ddot{r}_1 \\ \vdots \\ \ddot{r}_N \end{array}\right] }_{\ddot{\xi}} + \underbrace{ \left[\begin{array}{c|ccc} 0 & 0 & \dots &0 \\ \hline 0 & \Omega_1^2 & & 0 \\ \vdots & & \ddots & \\ 0 & 0 & & \Omega_N^2 \\ \end{array}\right] }_{K=\left[\begin{array}{cc} K_{11} & K_{12} \\ K_{21} & K_{22} \end{array}\right]} \underbrace{ \left[\begin{array}{c} \theta \\ \hline r_1 \\ \vdots \\ r_N \end{array}\right] }_{\xi} = \underbrace{ \left[\begin{array}{c} 1 \\ \hline 0 \\ \vdots \\ 0 \end{array}\right] }_{B_2} u' }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-346490e79fcc2267740093f5fde47d5f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1b)\quad \eta(\xi)= \underbrace{ \left[\begin{array}{c|ccc} 0 & \phi_1(\xi) & \dots &\phi_N(\xi) \end{array}\right] }_{C_1} \underbrace{ \left[\begin{array}{c} \theta \\ \hline r_1 \\ \vdots \\ r_N \end{array}\right] }_{\xi} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8a564535f5712a1756e4d97b569ada10_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2a)\quad \underbrace{ \left[\begin{array}{c} \dot{\xi} \\ \ddot{\xi} \end{array}\right] }_{\dot{x}} = \underbrace{ \left[\begin{array}{cc} 0_{N+1\times N+1} & I_{N+1} \\ M^{-1}K & 0_{N+1\times N+1} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \xi \\ \dot{\xi} \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{cc} 0_{N+1\times 1} \\ M^{-1}B_2 \end{array}\right] }_{B} u'}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-524df64b74898d10a9e6574263d3ca12_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2b)\quad \eta(\xi)= \underbrace{ \left[\begin{array}{cc} C_1 & 0_{1\times N} \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \xi \\ \dot{\xi} \end{array}\right] }_{x} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6e8294598be55b2b237fc74f95338ce8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{ \left[\begin{array}{c} m_1 \\ \vdots \\ m_N \\ \end{array}\right] }_{M_{21}} \ddot{\theta} + \underbrace{ \left[\begin{array}{c} \ddot{r}_1 \\ \vdots \\ \ddot{r}_N \end{array}\right] }_{\ddot{r}} + \underbrace{ \left[\begin{array}{ccc} \Omega_1^2 & & 0 \\ & \ddots & \\ 0 & & \Omega_N^2 \\ \end{array}\right] }_{K_{22}} \underbrace{ \left[\begin{array}{c} r_1 \\ \vdots \\ r_N \end{array}\right] }_{r} = \left[\begin{array}{c} 0 \\ \vdots \\ 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-83e03635bb43c77e2201d7335edf4248_l3.png)
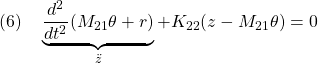
![Rendered by QuickLaTeX.com \displaystyle{(7a)\quad \underbrace{ \left[\begin{array}{c} \dot{z} \\ \dot{\theta} \\\hline \ddot{z} \\ \ddot{\theta} \end{array}\right] }_{\dot{x}} = \underbrace{ \left[\begin{array}{cc|cc} 0_{N\times N} & 0_{N\times 1} & I_N & 0_{N\times 1} \\ 0_{1\times N} & 0 & 0_{1\times N} & 1 \\\hline -K_{22} & K_{22}M_{21} & 0_{N\times N} & 0_{N\times 1} \\ 0_{1\times N} & 0 & 0_{1\times N} & -\frac{1}{T_a} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} {z} \\ {\theta} \\\hline \dot{z} \\ \dot{\theta} \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{cc} 0_{N\times 1} \\ 0 \\\hline 0_{N\times 1} \\ \frac{1}{T_a} \end{array}\right] }_{B} \dot{\theta}_c}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4e568bda7882b131b5b24ac100e86af6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7b)\quad \eta(\xi)= \underbrace{ \left[\begin{array}{ccc} \phi_1(\xi) & \cdots & \phi_N(\xi) \end{array}\right] \left[\begin{array}{cc|cc} I_N & -M_{21} & 0_{N\times N} & 0_{N\times 1} \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} {z} \\ {\theta} \\\hline \dot{z} \\ \dot{\theta} \end{array}\right] }_{x} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4598350d67871b8cea2146c9120e81d4_l3.png)

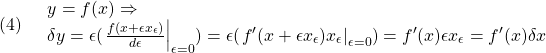
![Rendered by QuickLaTeX.com \displaystyle{ +\left[\rho A \int_0^{L} (x^2+{y}^2)\dot{\theta}+x\dot{y})\delta{\theta}dx\right]_{t_0}^{t_1}-\int_{t_0}^{t_1}\rho A \int_0^{L} \frac{d}{dt}((x^2+{y}^2)\dot{\theta}+x\dot{y})\delta{\theta}dxdt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f2118385d5eb945d389e6974e74e24cb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ +\left[\rho A \int_0^{L} (x\dot{\theta}+\dot{y}) \delta{y}dx\right]_{t_0}^{t_1}-\int_{t_0}^{t_1}\rho A \int_0^{L}\frac{d}{dt}(x\dot{\theta}+\dot{y})\delta{y}dxdt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cc6f74dcfcb568ed2b50d8e94189dc56_l3.png)
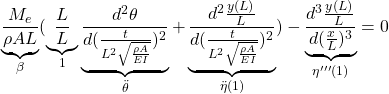
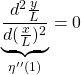
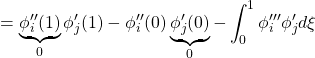
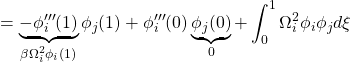
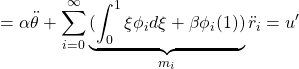
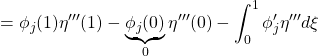
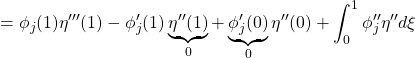
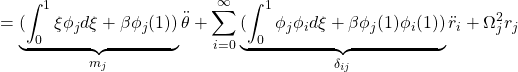
![Rendered by QuickLaTeX.com \displaystyle{(31a)\quad \underbrace{ \left[\begin{array}{c|ccc} \alpha & m_1 & \dots &m_N \\ \hline m_1 & 1 & & 0 \\ \vdots & & \ddots & \\ m_N & 0 & & 1 \\ \end{array}\right] }_{M=\left[\begin{array}{cc} M_{11} & M_{12} \\ M_{21} & M_{22} \end{array}\right]} \underbrace{ \left[\begin{array}{c} \ddot{\theta} \\ \hline \ddot{r}_1 \\ \vdots \\ \ddot{r}_N \end{array}\right] }_{\ddot{\xi}} + \underbrace{ \left[\begin{array}{c|ccc} 0 & 0 & \dots &0 \\ \hline 0 & \Omega_1^2 & & 0 \\ \vdots & & \ddots & \\ 0 & 0 & & \Omega_N^2 \\ \end{array}\right] }_{K=\left[\begin{array}{cc} K_{11} & K_{12} \\ K_{21} & M_{22} \end{array}\right]} \underbrace{ \left[\begin{array}{c} \theta \\ \hline r_1 \\ \vdots \\ r_N \end{array}\right] }_{\xi} = \underbrace{ \left[\begin{array}{c} 1 \\ \hline 0 \\ \vdots \\ 0 \end{array}\right] }_{B_2} u' }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-406d85fd430e037da5f5fde6fb0cad78_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(31b)\quad \eta(\xi)= \underbrace{ \left[\begin{array}{c|ccc} 0 & \phi_1(\xi) & \dots &\phi_N(\xi) \end{array}\right] }_{C_1} \underbrace{ \left[\begin{array}{c} \theta \\ \hline r_1 \\ \vdots \\ r_N \end{array}\right] }_{\xi} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ffc9ed02df3822a5d966a2c9ff2b13e0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(33a)\quad \underbrace{ \left[\begin{array}{c} \dot{\xi} \\ \ddot{\xi} \end{array}\right] }_{\dot{x}} = \underbrace{ \left[\begin{array}{cc} 0_{N+1\times N+1} & I_{N+1} \\ M^{-1}K & 0_{N+1\times N+1} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \xi \\ \dot{\xi} \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{cc} 0_{N+1\times 1} \\ M^{-1}B_2 \end{array}\right] }_{B} u'}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d04b4ccfb3bb84e6759113fd60916749_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(33b)\quad \eta(\xi)= \underbrace{ \left[\begin{array}{cc} C_1 & 0_{1\times N} \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \xi \\ \dot{\xi} \end{array}\right] }_{x} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3fe155c9c292f0b7a39bf25b09174740_l3.png)
 ,
, 
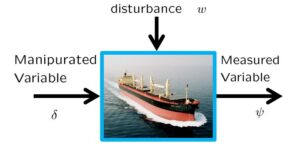
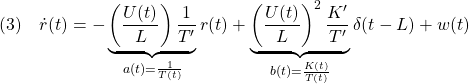
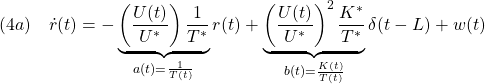
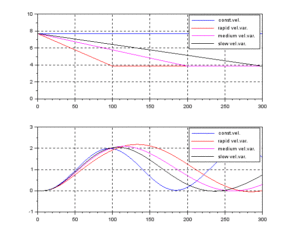
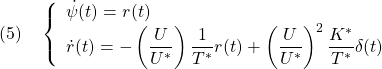
![Rendered by QuickLaTeX.com \displaystyle{(7a)\quad \underbrace{ \left[\begin{array}{c} \dot{\psi}(t) \\ \dot{r}(t) \\ \dot{\delta}(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0\\ 0 & -\left(\frac{U}{U^*}\right)\frac{1}{T^*} & \left(\frac{U}{U^*}\right)^2\frac{K^*}{T^*} \\ 0 & 0 & -\frac{1}{T_a} \end{array}\right] }_{A(U,U^2)} \underbrace{ \left[\begin{array}{c} \psi(t) \\ r(t) \\ \delta(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ \frac{K_a}{T_a} \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c40bbf2a01c1e41bb4cb2a38046541e9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7b)\quad \underbrace{ \psi(t) }_{y(t)} = \underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \psi(t) \\ r(t) \\ \delta(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-faf87c1ef2f82cfeaf915946a02f861a_l3.png)
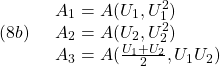
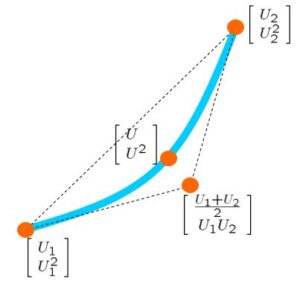
![Rendered by QuickLaTeX.com \displaystyle{(8c)\quad \begin{array}{l} p_1(U,U^2)=\frac{1}{p_0}\det \left[\begin{array}{cc} U-U_3 & U_2-U_3 \\ U^2-U_1U_2 & U_2^2-U_1U_2 \\ \end{array}\right]\\ p_2(U,U^2)=\frac{1}{p_0}\det \left[\begin{array}{cc} U_1-U_3 & U-U_3 \\ U_1^2-U_1U_2 & U^2-U_1U_2 \\ \end{array}\right]\\ p_3(U,U^2)=\frac{1}{p_0}\det \left[\begin{array}{cc} U_1-U_2 & U_2-U \\ U_1^2-U_2^2 & U_2^2-U^2 \\ \end{array}\right]\\ p_0=\det \left[\begin{array}{cc} U_1-U_2 & U_2-U_3 \\ U_1^2-U_2^2 & U_2^2-U_1U_2 \\ \end{array}\right]\\ p_1(U,U^2)+p_2(U,U^2)+p_3(U,U^2)=1 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7b82416721e9f2c01e1e17b0b24b075c_l3.png)
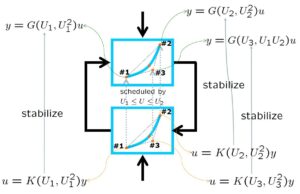
![Rendered by QuickLaTeX.com \displaystyle{(9a)\quad P: \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x} \\ \dot{x}_I \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A(U,U^2)& 0 \\ -C & 0 \end{array}\right] }_{A(U,U^2)} \left[\begin{array}{c} x \\ x_I \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_1} r + \underbrace{\left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_2} u\\ \underbrace{ \left[\begin{array}{c} y_{11} \\ y_{12} \end{array}\right] }_{y_1} = \underbrace{ \left[\begin{array}{cc} 0 &\omega_I\\ \omega_DCA(U,U^2) & 0 \end{array}\right] }_{C_1} \left[\begin{array}{c} x \\ x_I \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \end{array}\right] }_{D_{11}} r + \underbrace{ \left[\begin{array}{c} 0 \\ \omega_DCB \end{array}\right] }_{D_{12}} u\\ \underbrace{ \left[\begin{array}{c} y \\ x_I \end{array}\right] }_{y_2} = \underbrace{ \left[\begin{array}{cc} C & 0\\ 0 & 1 \end{array}\right] }_{C_2} \left[\begin{array}{c} x \\ x_I \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \end{array}\right] }_{D_{21}} r \end{array}\right.}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-34bf0da930252e74bd42cb1640969702_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10a)\quad K_0: \left\{\begin{array}{l} \dot{x}_K=A_K(U,U^2)x_K+ \underbrace{ \left[\begin{array}{cc} B_K^{(1)}(U,U^2) & B_K^{(2)}(U,U^2) \end{array}\right] }_{B_K(U,U^2)} \left[\begin{array}{c} y \\ x_I \end{array}\right] \\ u=C_K(U,U^2)x_K + \underbrace{ \left[\begin{array}{cc} D_K^{(1)}(U,U^2) & D_K^{(2)}(U,U^2) \end{array}\right] }_{D_K(U,U^2)} \left[\begin{array}{c} y \\ x_I \end{array}\right] \end{array}\right.}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a9bc3ecd695bd182e8c63d29351d1924_l3.png)
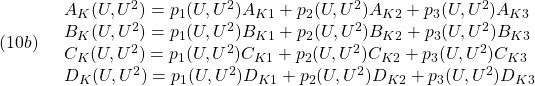
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad K: \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_K \\ \dot{x}_I \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A_K(U,U^2) & B_K^{(2)}(U,U^2) \\ 0 & 0 \end{array}\right] }_{A_K(U,U^2)} \left[\begin{array}{c} x_K \\ x_I \end{array}\right]\\ + \underbrace{ \left[\begin{array}{cc} B_K^{(1)}(U,U^2) & 0\\ -1& 1 \end{array}\right] }_{B_K(U,U^2)} \left[\begin{array}{c} y \\ r \end{array}\right] \\ u= \underbrace{ \left[\begin{array}{cc} C_K(U,U^2) & D_K^{(2)}(U,U^2) \end{array}\right] }_{C_K(U,U^2)} \left[\begin{array}{c} x_K \\ x_I \end{array}\right]\\ + \underbrace{ \left[\begin{array}{cc} D_K^{(1)}(U,U^2) & 0 \end{array}\right] }_{D_K(U,U^2)} \left[\begin{array}{c} y \\ r \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b11949446b4d75aac55c83f1105e175c_l3.png)






![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \boxed{P: \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x} \\ \dot{x}_I \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A& 0 \\ -C & 0 \end{array}\right] }_{A} \left[\begin{array}{c} x \\ x_I \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_1} r + \underbrace{\left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_2} u\\ \underbrace{ \left[\begin{array}{c} y_{11} \\ y_{12} \end{array}\right] }_{y_1} = \underbrace{ \left[\begin{array}{cc} 0 &\omega_I\\ \omega_DCA & 0 \end{array}\right] }_{C_1} \left[\begin{array}{c} x \\ x_I \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \end{array}\right] }_{D_{11}} r + \underbrace{ \left[\begin{array}{c} 0 \\ \omega_DCB \end{array}\right] }_{D_{12}} u\\ \underbrace{ \left[\begin{array}{c} y \\ x_I \end{array}\right] }_{y_2} = \underbrace{ \left[\begin{array}{cc} C & 0\\ 0 & 1 \end{array}\right] }_{C_2} \left[\begin{array}{c} x \\ x_I \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \end{array}\right] }_{D_{21}} r \end{array}\right.} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ff652eebac0dfbfce980306520dacf5b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad K_0: \left\{\begin{array}{l} \dot{x}_K=A_Kx_K+ \underbrace{ \left[\begin{array}{cc} B_{K1} & B_{K2} \end{array}\right] }_{B_K} \left[\begin{array}{c} y \\ x_I \end{array}\right] \\ u=C_Kx_K + \underbrace{ \left[\begin{array}{cc} D_{K1} & D_{K2} \end{array}\right] }_{D_K} \left[\begin{array}{c} y \\ x_I \end{array}\right] \end{array}\right.}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7dd72681c4a7787121d7e37cfd799a36_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad P_{CL}: \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x} \\ \dot{x}_K \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} A+B_2D_KC_2 & B_2C_K \\ B_KC_2 & A_K \end{array}\right] }_{A_{CL}} \left[\begin{array}{c} x \\ x_K \end{array}\right] + \underbrace{ \left[\begin{array}{ccc} B_1+B_2D_KD_{21} \\ B_KD_{21} \end{array}\right] }_{B_{CL}} r\\ \underbrace{ \left[\begin{array}{c} y_{11} \\ y_{12} \end{array}\right] }_{y_1} = \underbrace{ \left[\begin{array}{ccc} C_1+D_{12}D_KC_2 & D_{12}C_K \end{array}\right] }_{C_{CL}} \left[\begin{array}{c} x \\ x_K \end{array}\right] + \underbrace{ (D_{11}+D_{12}D_KD_{21}) }_{D_{CL}} r \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-741714e54da8d9e0f2096a7a04b58fe2_l3.png)
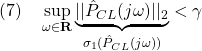
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \left[\begin{array}{ccc} \left[\begin{array}{cc} AR+B_2{\cal C}_K & A+B_2D_KC_2\\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right]+(*)^T & \left[\begin{array}{c} B_1+B_2D_KD_{21} \\ SB_1+{\cal B}_KD_{21} \end{array}\right] & (*)^T \\ (*)^T & -\gamma^2 I & (*)^T \\ \left[\begin{array}{cc} C_1R+D_{12}{\cal C}_K & C_1+D_{12}D_KC_2 \end{array}\right] & D_{11} & -I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-70227b027ea2dc86414260352f2ab59c_l3.png)
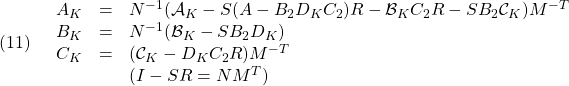
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \left[\begin{array}{cc} AR+B_2{\cal C}_K & A+B_2D_KC_2\\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right] +(*)^T %\nonumber\\&& +\alpha \left[\begin{array}{cc} R & I \\ I & S \end{array}\right]<0}\\ \left[\begin{array}{cc} -r \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] & \left[\begin{array}{cc} AR+B_2{\cal C}_K & A+B_2D_KC_2\\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right] \\ (*)^T & -r \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] \end{array}\right] <0\\ \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]\otimes \left[\begin{array}{cc} AR+B_2{\cal C}_K & A+B_2D_KC_2\\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right]+ (*)^T <0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4b17321a2dbe748dbe61f89fa2ec2fe7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \boxed{K: \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_K \\ \dot{x}_I \end{array}\right]= \left[\begin{array}{cc} A_K & B_{K2} \\ 0 & 0 \end{array}\right] \left[\begin{array}{c} x_K \\ x_I \end{array}\right] + \left[\begin{array}{cc} B_{K1} & 0\\ -1& 1 \end{array}\right] \left[\begin{array}{c} y \\ r \end{array}\right] \\ u= \left[\begin{array}{cc} C_K & D_{K2} \end{array}\right] \left[\begin{array}{c} x_K \\ x_I \end{array}\right] + \left[\begin{array}{cc} D_{K1} & 0 \end{array}\right] \left[\begin{array}{c} y \\ r \end{array}\right] \end{array}\right.} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5af64f9178784ac387be596d890834e7_l3.png)
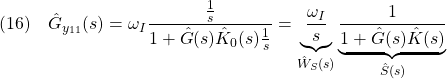
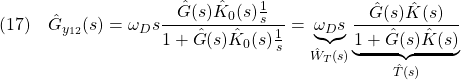
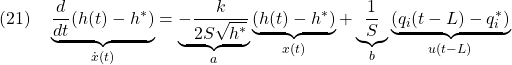
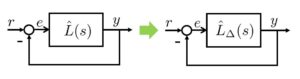
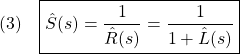
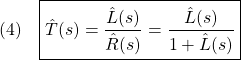
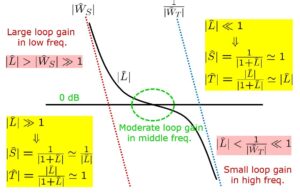
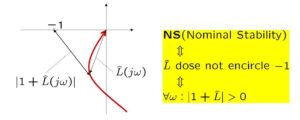




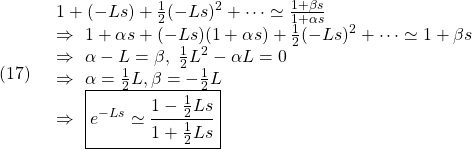
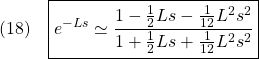
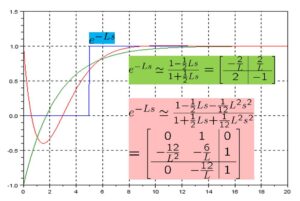
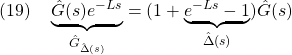
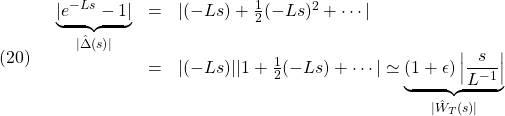

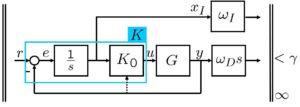
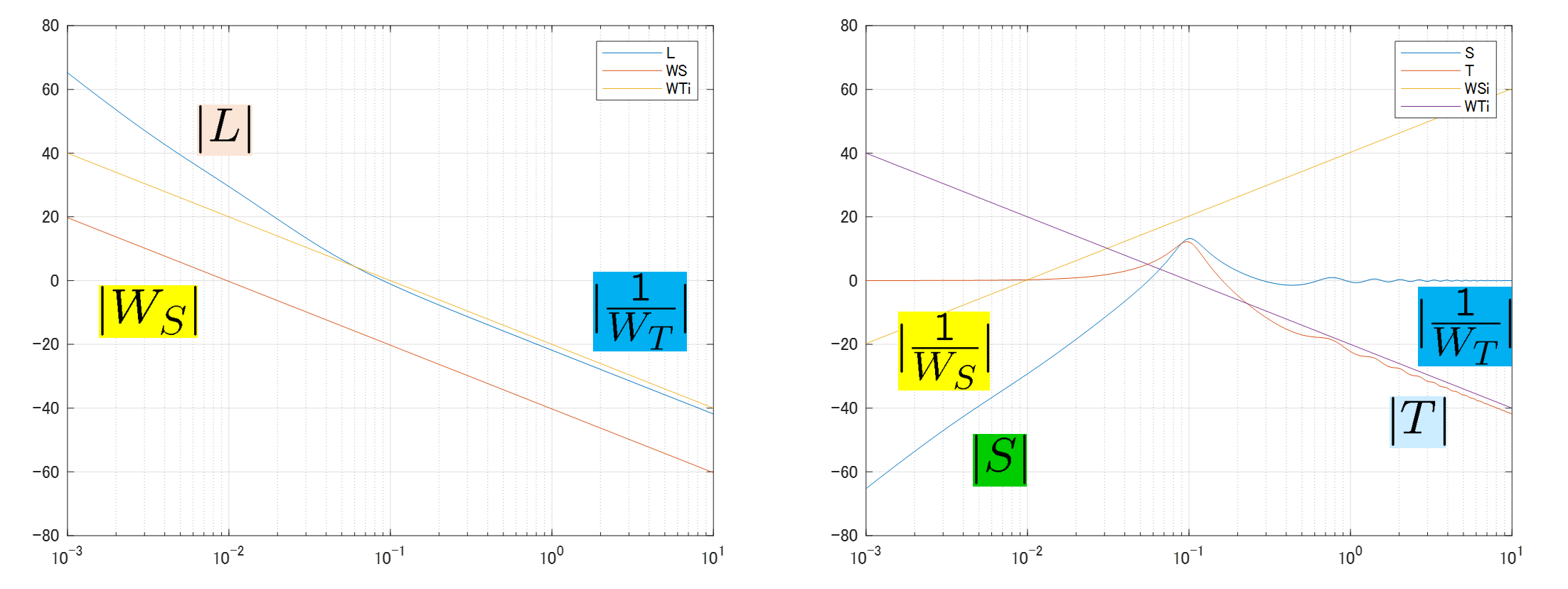 図10 開ループ整形と閉ループ整形
図10 開ループ整形と閉ループ整形
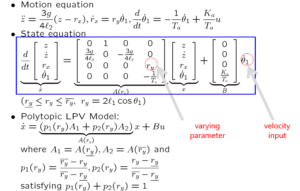
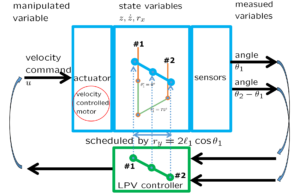

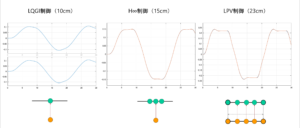
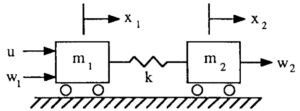

![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} m_1 & 0 \\ 0 & m_2 \end{array}\right] }_{M} \underbrace{ \left[\begin{array}{c} \ddot{x}_1(t)\\ \ddot{x}_2(t) \end{array}\right] }_{\ddot{x}(t)} +\underbrace{ \left[\begin{array}{cc} k & -k \\ -k & -k \end{array}\right] }_{K(k)} \underbrace{ \left[\begin{array}{ccc} {x}_1(t)\\ {x}_2(t) \end{array}\right] }_{{\xi}(t)} =\underbrace{ \left[\begin{array}{ccc} 1\\ 0 \end{array}\right] }_{E_{2\times1}}u(t) +\underbrace{ \left[\begin{array}{ccc} w_{1}\\ w_{2} \end{array}\right] }_{w_{d}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c378c02aa9343c10a7c74dacb7a82030_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \left[\begin{array}{c} \dot{\xi}(t)\\ \ddot{\xi}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} 0_{2\times2} & I_2\\ -M^{-1}K & -M^{-1}D \end{array}\right] }_{A(k)} \left[\begin{array}{c} {\xi}(t)\\ \dot{\xi}(t) \end{array}\right]\\ + \left[\begin{array}{c} 0_{2\times1}\\ M^{-1}E_{2\times1} \end{array}\right]u(t) + \left[\begin{array}{c} 0_{2\times2}\\ M^{-1} \end{array}\right]w_d \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b16d7bf6b82863e883f1235ec5f0459f_l3.png)
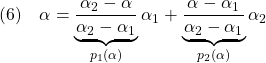
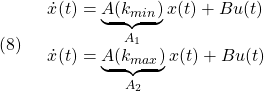
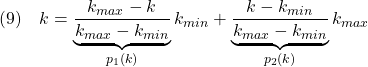

![Rendered by QuickLaTeX.com \displaystyle{(11) P: \left\{\begin{array}{l} \left[\begin{array}{c} \dot{\xi}\\ \ddot{\xi} \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} 0_{2\times2} & I_2\\ -M^{-1}K & -M^{-1}D \end{array}\right] }_{A(k)=p_1(k)A_1+p_2(k)A_2} \left[\begin{array}{c} {\xi}\\ \dot{\xi} \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0_{2\times2}\\ M^{-1} \end{array}\right] }_{B_1} w_d + \underbrace{ \left[\begin{array}{c} 0_{2\times1}\\ M^{-1}E_{2\times1} \end{array}\right] }_{B_2} u\\ \underbrace{ \left[\begin{array}{c} x_2-x_1 \\ x_1\\ 2u \end{array}\right] }_{y_1} = \underbrace{ \left[\begin{array}{cc|cc} -1 & 1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ \end{array}\right] }_{C_1} \left[\begin{array}{c} {\xi}\\ \dot{\xi} \end{array}\right] + \underbrace{ 0_{3\times2} }_{D_{11}} w_d + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 2 \end{array}\right] }_{D_{12}} u \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fd10d68cfea1b96cad0cc36a09499c1f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12) P: \left\{\begin{array}{l} \left[\begin{array}{c} \dot{\xi}\\ \ddot{\xi} \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} 0_{2\times2} & I_2\\ -M^{-1}K & -M^{-1}D \end{array}\right] }_{A(k)=p_1(k)A_1+p_2(k)A_2} \left[\begin{array}{c} {\xi}\\ \dot{\xi} \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0_{2\times2}\\ M^{-1} \end{array}\right] }_{B_1} w_d + \underbrace{ \left[\begin{array}{c} 0_{2\times1}\\ M^{-1}E_{2\times1} \end{array}\right] }_{B_2} u\\ \underbrace{ \left[\begin{array}{c} x_2-x_1 \\ x_1\\ 2u \end{array}\right] }_{y_1} = \underbrace{ \left[\begin{array}{cc|cc} -1 & 1 & 0 & 0\\ 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ \end{array}\right] }_{C_1} \left[\begin{array}{c} {\xi}\\ \dot{\xi} \end{array}\right] + \underbrace{ 0_{3\times2} }_{D_{11}} w_d + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 2 \end{array}\right] }_{D_{12}} u\\ \underbrace{ x_1 }_{y_2} = \underbrace{ \left[\begin{array}{cc|cc} 1 & 0 & 0 & 0 \end{array}\right] }_{C_2} \left[\begin{array}{c} {\xi}(t)\\ \dot{\xi}(t) \end{array}\right] + \underbrace{ 0_{1\times2} }_{D_{21}} w_d + \underbrace{ 0 }_{D_{22}} u \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b47f09bca2397aecd1d9f8e133a5ca01_l3.png)

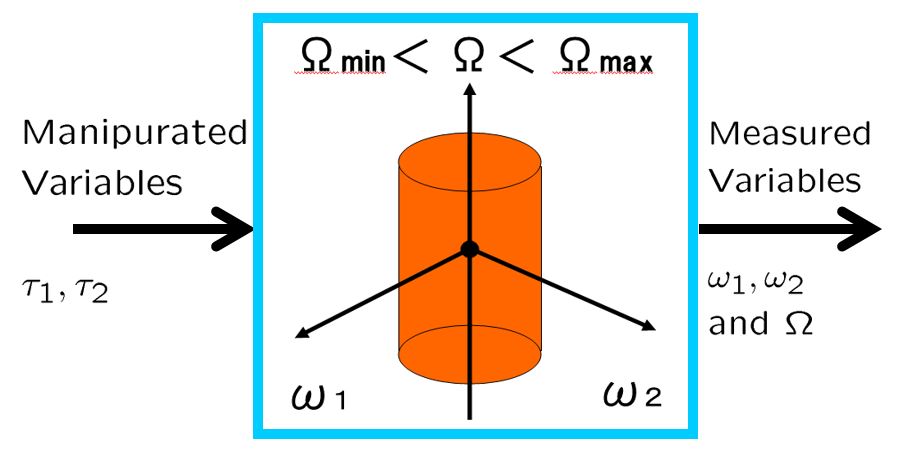
![Rendered by QuickLaTeX.com \displaystyle{(3) \underbrace{ \left[\begin{array}{c} \dot{\omega}_1(t) \\ \dot{\omega}_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & \Omega(t)\frac{J_2-J_3}{J_1} \\ -\Omega(t)\frac{J_3-J_1}{J_2} & 0 \end{array}\right] }_{A(\Omega(t))} \underbrace{ \left[\begin{array}{c} \omega_1(t) \\ \omega_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} \frac{1}{J_1} & 0 \\ 0 & \frac{1}{J_2} \end{array}\right] }_{B} \underbrace{ \left[\begin{array}{c} \tau_1(t) \\ \tau_2(t) \end{array}\right] }_{u(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-359a3b72faaf2d0a5cfc50d11ff3e826_l3.png)
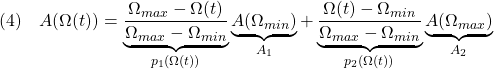
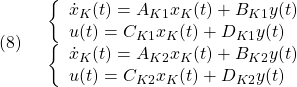
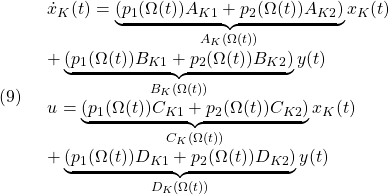
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_K(t) \end{array}\right] =(p_1(\Omega(t)) \underbrace{ \left[\begin{array}{ccc} A_1+BD_{K1}C & BC_{K1} \\ B_{K1}C & A_{K1} \end{array}\right] }_{A_{CL1}}\\ +p_2(\Omega(t)) \underbrace{ \left[\begin{array}{ccc} A_2+BD_{K2}C & BC_{K2} \\ B_{K2}C & A_{K2} \end{array}\right] }_{A_{CL2}} )\left[\begin{array}{c} x(t) \\ x_K(t) \end{array}\right]\\ =\underbrace{(p_1(\Omega(t))A_{CL1} +p_2(\Omega(t))A_{CL2} )}_{A_{CL}(\Omega(t))} \left[\begin{array}{c} x(t) \\ x_K(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8f0a038fe6a7bd2f5966695bcc3f718d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_K(t) \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} A_1+BD_{K1}C & BC_{K1} \\ B_{K1}C & A_{K1} \end{array}\right] }_{A_{CL1}} \left[\begin{array}{c} x(t) \\ x_K(t) \end{array}\right]\\ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_K(t) \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} A_2+BD_{K2}C & BC_{K2} \\ B_{K2}C & A_{K1} \end{array}\right] }_{A_{CL2}} \left[\begin{array}{c} x(t) \\ x_K(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e929ace4619cad2d177f258d9889a3c9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad P: \left\{\begin{array}{l} \dot{x}(t)=\underbrace{(p_1(\Omega(t))A^{(1)}+p_2(\Omega(t))A^{(2)})}_{A(\Omega(t))}x(t)+B_1u_1(t)+B_2u_2(t) \\ \underbrace{ \left[\begin{array}{c} y(t)\\ u(t) \end{array}\right] }_{y_1(t)} = \underbrace{ \left[\begin{array}{c} C\\ 0 \end{array}\right] }_{C_1} x(t)+ \underbrace{ \left[\begin{array}{c} 0\\ 0 \end{array}\right] }_{D_{11}}u_1(t)+ \underbrace{ \left[\begin{array}{c} 0\\ I \end{array}\right] }_{D_{12}} u_2(t) \\ y_2(t)=C_2x(t) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-faeda20d9d519080ed5b8cd13b046c7d_l3.png)
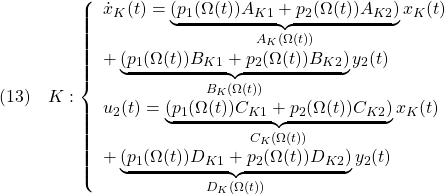
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad P_{CL}: \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_K(t) \end{array}\right] =\underbrace{(p_1(\Omega(t))A_{CL1} +p_2(\Omega(t))A_{CL2} )}_{A_{CL}(\Omega(t))} \left[\begin{array}{c} x(t) \\ x_K(t) \end{array}\right]\\ + \underbrace{ \left[\begin{array}{ccc} B_1 \\ 0 \end{array}\right] }_{B_{CL}} u_1(t)\\ y_1(t) = \underbrace{ \left[\begin{array}{ccc} C_1+D_{12}D_KC_2 & D_{12}C_K \end{array}\right] }_{C_{CL}} \left[\begin{array}{c} x(t) \\ x_K(t) \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-69093e258ea748ec8d4c740f25b24bcf_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17) \left[\begin{array}{ccc} \left[\begin{array}{cc} A^{(1)}R+B_2{\cal C}_K^{(1)} & A^{(1)}+B_2D_K^{(1)}C_2\\ {\cal A}_K^{(1)} & SA^{(1)}+{\cal B}_K^{(1)}C_2 \end{array}\right]+(*)^T & \left[\begin{array}{c} B_1+B_2D_K^{(1)}D_{21} \\ SB_1+{\cal B}_K^{(1)}D_{21} \end{array}\right] & (*)^T \\ (*)^T & -\gamma I & (*)^T \\ \left[\begin{array}{cc} C_1R+D_{12}{\cal C}_K^{(1)} & C_1+D_{12}D_K^{(1)}C_2 \end{array}\right] & D_{11} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0c84c35e2434d968a27708396729788c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18) \begin{array}{l} \left[\begin{array}{cc} A^{(1)}R+B_2{\cal C}_K^{(1)} & A^{(1)}+B_2D_K^{(1)}C_2\\ {\cal A}_K^{(1)} & SA^{(1)}+{\cal B}_K^{(1)}C_2 \end{array}\right] +(*)^T %\nonumber\\&& +\alpha \left[\begin{array}{cc} R & I \\ I & S \end{array}\right]<0} \\ \left[\begin{array}{cc} -r \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] & \left[\begin{array}{cc} A^{(1)}R+B_2{\cal C}_K^{(1)} & A^{(1)}+B_2D_K^{(1)}C_2\\ {\cal A}_K^{(1)} & SA^{(1)}+{\cal B}_K^{(1)}C_2 \end{array}\right] \\ (*)^T & -r \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] \end{array}\right] <0 \\ \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]\otimes \left[\begin{array}{cc} A^{(1)}R+B_2{\cal C}_K^{(1)} & A^{(1)}+B_2D_K^{(1)}C_2\\ {\cal A}_K^{(1)} & SA^{(1)}+{\cal B}_K^{(1)}C_2 \end{array}\right]+ (*)^T <0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-37825362e80092bdbffd30da63f679d5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(19) \left[\begin{array}{ccc} \left[\begin{array}{cc} A^{(2)}R+B_2{\cal C}_K^{(2)} & A^{(2)}+B_2D_K^{(2)}C_2\\ {\cal A}_K^{(2)} & SA^{(2)}+{\cal B}_K^{(2)}C_2 \end{array}\right]+(*)^T & \left[\begin{array}{c} B_1+B_2D_K^{(2)}D_{21} \\ SB_1+{\cal B}_K^{(2)}D_{21} \end{array}\right] & (*)^T \\ (*)^T & -\gamma I & (*)^T \\ \left[\begin{array}{cc} C_1R+D_{12}{\cal C}_K^{(2)} & C_1+D_{12}D_K^{(2)}C_2 \end{array}\right] & D_{11} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1f48b4c8d9a8b75d6d691d094c20694a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(20) \begin{array}{l} \left[\begin{array}{cc} A^{(2)}R+B_2{\cal C}_K^{(2)} & A^{(1)}+B_2D_K^{(2)}C_2\\ {\cal A}_K^{(2)} & SA^{(2)}+{\cal B}_K^{(2)}C_2 \end{array}\right] +(*)^T %\nonumber\\&& +\alpha \left[\begin{array}{cc} R & I \\ I & S \end{array}\right]<0} \\ \left[\begin{array}{cc} -r \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] & \left[\begin{array}{cc} A^{(2)}R+B_2{\cal C}_K^{(2)} & A^{(2)}+B_2D_K^{(2)}C_2\\ {\cal A}_K^{(2)} & SA^{(2)}+{\cal B}_K^{(2)}C_2 \end{array}\right] \\ (*)^T & -r \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] \end{array}\right] <0 \\ \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]\otimes \left[\begin{array}{cc} A^{(2)}R+B_2{\cal C}_K^{(2)} & A^{(2)}+B_2D_K^{(2)}C_2\\ {\cal A}_K^{(2)} & SA^{(2)}+{\cal B}_K^{(2)}C_2 \end{array}\right]+ (*)^T <0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e4f2f36e3876365a2a8058226ef8604d_l3.png)
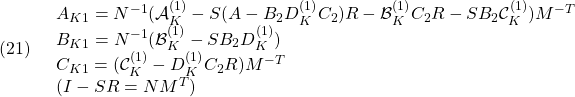
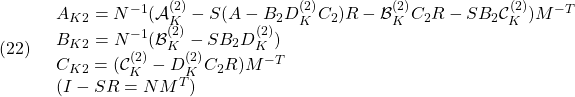
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \left[\begin{array}{ccc} Y_{CL}A_{CL1}^T+A_{CL1}Y_{CL} & B_{CL} & Y_{CL}C_{CL}^T \\ B_{CL}^T & -\gamma I & D_{CL}^T \\ C_{CL}Y_{CL} & D_{CL} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ae7b7271e03fda5eec4e707d46be1486_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(24)\quad \left[\begin{array}{ccc} Y_{CL}A_{CL2}^T+A_{CL2}Y_{CL} & B_{CL} & Y_{CL}C_{CL}^T \\ B_{CL}^T & -\gamma I & D_{CL}^T \\ C_{CL}Y_{CL} & D_{CL} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ebcd17b195f2caac772907fc0cd3745f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(26)\quad \left[\begin{array}{ccc} A_{CL1}^TX_{CL}+X_{CL}A_{CL1} & X_{CL}B_{CL} & C_{CL}^T \\ B_{CL}^TX_{CL} & -\gamma I & D_{CL}^T \\ C_{CL} & D_{CL} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-632d14c9b5efe00ba767e8f6195eb627_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(27)\quad \left[\begin{array}{ccc} A_{CL2}^TX_{CL}+X_{CL}A_{CL2} & X_{CL}B_{CL} & C_{CL}^T \\ B_{CL}^TX_{CL} & -\gamma I & D_{CL}^T \\ C_{CL} & D_{CL} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b21c8537a8ab0dfb4ea51a8573cb9bd9_l3.png)


![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{\left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_K(t) \end{array}\right]}_{\dot{\bar x}(t)} =\underbrace{(p_1(\Omega(t))A_{CL1} +p_2(\Omega(t))A_{CL2} )}_{A_{CL}(\Omega(t))} \underbrace{\left[\begin{array}{c} x(t) \\ x_K(t) \end{array}\right]}_{\bar{x}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-284947643aa6c7bcefd9ca89f26c3ed9_l3.png)
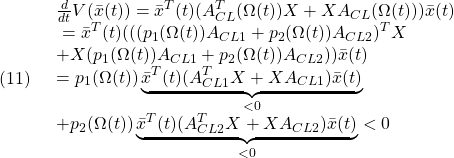
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad P_{CL}: \left\{\begin{array}{l} \underbrace{\left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_K(t) \end{array}\right]}_{\dot{\bar x}(t)} =\underbrace{(p_1(\Omega(t))A_{CL1} +p_2(\Omega(t))A_{CL2} )}_{A_{CL}(\Omega(t))} \underbrace{\left[\begin{array}{c} x(t) \\ x_K(t) \end{array}\right]}_{\bar{x}(t)}\\ + \underbrace{ \left[\begin{array}{ccc} B_1 \\ 0 \end{array}\right] }_{B_{CL}} u_1(t)\\ y_1(t) = \underbrace{ \left[\begin{array}{ccc} C_1+D_{12}D_KC_2 & D_{12}C_K \end{array}\right] }_{C_{CL}} \underbrace{\left[\begin{array}{c} x(t) \\ x_K(t) \end{array}\right]}_{\bar{x}(t)} \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7859b8904bfe69d3d2462b52727df585_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \exists X_1>0:\ \left[\begin{array}{ccc} A_{CL1}^TX_1+X_1A_{CL1} & X_1B_{CL} & C_{CL}^T \\ B_{CL}^TX_1 & -\gamma I & D_{CL}^T \\ C_{CL} & D_{CL} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-32121ac6448169e2c1b3ad70a6d1b8a1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \exists X_2>0:\ \left[\begin{array}{ccc} A_{CL2}^TX_2+X_2A_{CL2} & X_2B_{CL} & C_{CL}^T \\ B_{CL}^TX_2 & -\gamma I & D_{CL}^T \\ C_{CL} & D_{CL} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7dc86f448009472a06f5937161eabf0f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \left[\begin{array}{ccc} A_{CL1}^TX+XA_{CL1} & XB_{CL} & C_{CL}^T \\ B_{CL}^TX & -\gamma^2 I & D_{CL}^T \\ C_{CL} & D_{CL} &-I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0551f956ef678d8456cd257070a5515a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \left[\begin{array}{ccc} A_{CL1}^TX+XA_{CL1} & XB & C_{CL}^T \\ B_{CL}^TX & -\gamma^2 I & D_{CL}^T \\ C_{CL} & D_{CL} &-I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-182eed5588e5439f1a4fe8ccf23de8f8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \bar{x}(t) \\ u_1(t) \end{array}\right]^T \left[\begin{array}{cc} \begin{array}{c} ( p_1(\Omega(t))A_{CL1}+p_2(\Omega(t))A_{CL2} )^TX\\ +X( p_1(\Omega(t))A_{CL1}+p_2(\Omega(t))A_{CL2} ) \end{array} & XB_{CL} \\ B_{CL}^TX & 0 \end{array}\right] \left[\begin{array}{c} \bar{x}(t) \\ u_1(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-21fd65935890040936a03e1381b689d0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ < \underbrace{(p_1(\Omega(t))+p_2(\Omega(t)))}_1 \left[\begin{array}{c} \bar{x}(t) \\ u_1(t) \end{array}\right]^T \left[\begin{array}{cc} C_{CL} & D_{CL} \\ 0 & I \end{array}\right]^T \left[\begin{array}{cc} - I & 0 \\ 0 & \gamma^2 I \end{array}\right] \left[\begin{array}{cc} C_{CL} & D_{CL} \\ 0 & I \end{array}\right] \left[\begin{array}{c} \bar{x}(t) \\ u_1(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-efc3ed3c7e49e14825f76189803962fc_l3.png)
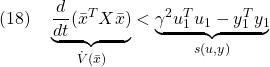
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad P: \left\{\begin{array}{l} \dot{x}(t)=\underbrace{(p_1(\Omega(t))A_1+p_2(\Omega(t))A_2)}_{A(\Omega(t))}x(t)+B_1u_1(t)+B_2u_2(t) \\ \underbrace{ \left[\begin{array}{c} y(t)\\ u(t) \end{array}\right] }_{y_1(t)} = \underbrace{ \left[\begin{array}{c} C\\ 0 \end{array}\right] }_{C_1} x(t)+ \underbrace{ \left[\begin{array}{c} 0\\ 0 \end{array}\right] }_{D_{11}}u_1(t)+ \underbrace{ \left[\begin{array}{c} 0\\ I \end{array}\right] }_{D_{12}} u_2(t) \\ y_2(t)=x(t) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5c52c28d5dc8099876feb3fc35d22c0a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad P_{CL}: \left\{\begin{array}{l} \dot{x}(t)=\underbrace{(p_1(\Omega(t))(A_1-B_2F_1)+p_2(\Omega(t))(A_2-B_2F_2))}_{A_F(\Omega(t))}x(t)+B_1u_1(t) \\ y_1(t)= \underbrace{ \left[\begin{array}{c} C\\ -F \end{array}\right] }_{C_1-D_{12}F} x(t) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-838ab14f36c266566a693aec4791304a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \left[\begin{array}{ccc} (A_1Y-B_2Z_1)^T+A_1Y-B_2Z_1 & B_1 & (C_1Y-D_{12}Z_1)^T \\ B_1^T & -\gamma I & D_{11}^T \\ C_1Y-D_{12}Z_1 & D_{11} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-50ae1d70b8404dd73e277a0933b482ce_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \begin{array}{l} 2\alpha Y+A_1Y-B_2Z_1+(A_1Y-B_2Z_1)^T<0 \\ \left[\begin{array}{cc} -rY & A_1Y-B_2Z_1 \\ (A_1Y-B_2Z_1)^T & -rY \end{array}\right]<0 \\ \left[\begin{array}{cc} \sin\theta(A_1Y-B_2Z_1+(A_1Y-B_2Z_1)^T) & \\ -\cos\theta(A_1Y-B_2Z_1-(A_1Y-B_2Z_1)^T) & \end{array}\right. \\ \left.\begin{array}{cc} & \cos\theta(A_1Y-B_2Z_1-(A_1Y-B_2Z_1)^T) \\ & \sin\theta(A_1Y-B_2Z_1+(A_1Y-B_2Z_1)^T) \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2e9b5aa7f67110719da98182197e19d2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(19)\quad \left[\begin{array}{ccc} (A_2Y-B_2Z_2)^T+A_2Y-B_2Z_2 & B_1 & (C_1Y-D_{12}Z_2)^T \\ B_1^T & -\gamma I & D_{11}^T \\ C_1Y-D_{12}Z_2 & D_{11} & -\gamma I \end{array}\right]<0 \\ }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-12d276ca145e5b9ab2496cceb04509bb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(20)\quad \begin{array}{l} 2\alpha Y+A_1Y-B_2Z_2+(A_1Y-B_2Z_2)^T<0 \\ \left[\begin{array}{cc} -rY & A_1Y-B_2Z_2 \\ (A_1Y-B_2Z_2)^T & -rY \end{array}\right]<0 \\ \left[\begin{array}{cc} \sin\theta(A_2Y-B_2Z_2+(A_2Y-B_2Z_2)^T) & \\ -\cos\theta(A_2Y-B_2Z_2-(A_2Y-B_2Z_2)^T) & \end{array}\right. \\ \left.\begin{array}{cc} & \cos\theta(A_2Y-B_2Z_2-(A_2Y-B_2Z_2)^T) \\ & \sin\theta(A_2Y-B_2Z_2+(A_2Y-B_2Z_2)^T) \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-078a99a65651029b51c2abe33836d299_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \left[\begin{array}{ccc} Y(A_1-B_2F)^T+(A_1-B_2F)Y & B_1 & Y(C_1-D_{12}F)^T \\ B_1^T & -\gamma I & D_{11}^T \\ (C_1-D_{12}F)Y & D_{11} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2495a37e41fa5d2eb8395dc1e0a92613_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(24)\quad \left[\begin{array}{ccc} Y(A_2-B_2F)^T+(A_2-B_2F)Y & B_1 & Y(C_1-D_{12}F)^T \\ B_1^T & -\gamma I & D_{11}^T \\ (C_1-D_{12}F)Y & D_{11} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-726386f3bcbb36ee571761f73067b759_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(25)\quad \left[\begin{array}{ccc} (A_1-BF_1)^TX+X(A_1-BF_1) & XB_1 & (C_1-D_{12}F)^T \\ B_1^TX_1 & -\gamma I & D_{11}^T \\ (C_1-D_{12}F) & D_{11} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bc5a1c5a1e9161235175c0b7f524f2ea_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(26)\quad \left[\begin{array}{ccc} (A_2-BF_2)^TX+X(A_2-BF_2) & XB_1 & (C_1-D_{12}F)^T \\ B_1^TX & -\gamma I & D_{11}^T \\ (C_1-D_{12}F) & D_{11} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fab9d12f17bd6d0fb7f7d46e76739e7c_l3.png)


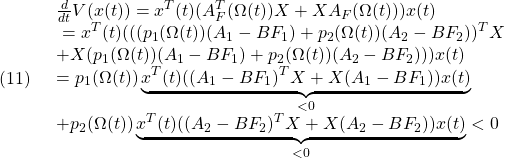
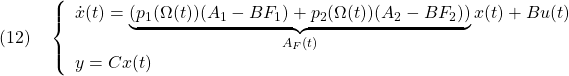
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \exists X_1>0:\ \left[\begin{array}{ccc} (A_1-BF_1)^TX_1+X_1(A_1-BF_1) & X_1B & C^T \\ B^TX_1 & -\gamma I & D^T \\ C & D & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-28301303802019e78fb62ed6637650b2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \exists X_2>0:\ \left[\begin{array}{ccc} (A_2-BF_2)^TX_2+X_2(A_2-BF_2) & X_2B & C^T \\ B^TX_2 & -\gamma I & D^T \\ C & D & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-677c72fc4448a2f17c5849d63dc4b8ad_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \left[\begin{array}{ccc} (A_1-BF_1)^TX+X(A_1-BF_1) & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D &-I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3e1b3029dd25fed1df0542788e32f52b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \left[\begin{array}{ccc} (A_1-BF_1)^TX+X(A_1-BF_1) & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D &-I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3a9dce011974e9852d76a5c15a462870_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right]^T \left[\begin{array}{cc} \begin{array}{c} ( p_1(\Omega(t))(A_1-BF_1)+p_2(\Omega(t))(A_2-BF_2) )^TX\\ +X( p_1(\Omega(t))(A_1-BF_1)+p_2(\Omega(t))(A_2-BF_2) ) \end{array} & XB \\ B^TX & 0 \end{array}\right] \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1fc23d0a361803d365380b86a013ae6e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ < \underbrace{(p_1(\Omega(t))+p_2(\Omega(t)))}_1 \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right]^T \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right]^T \left[\begin{array}{cc} - I & 0 \\ 0 & \gamma^2 I \end{array}\right] \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right] \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2d9183af6071904863cbae048501209a_l3.png)