一般には制御対象は非線形系ですが、ここでは重ね合わせの原理の成り立つ線形系(linear system)を考えます。また1入力1出力1次系(SISO 1st-order system)に限って、制御理論の概要を漸近安定性、時間応答、安定化制御、追値制御の4つに分けて述べます。
1次系の状態空間表現…Homework
[1] 制御対象が1入力1出力1次系の場合、そのモデルとして、次の状態空間表現が用いられます。
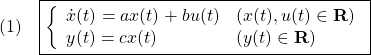
第1式は状態方程式とよばれ、![]() はそれぞれ時刻
はそれぞれ時刻![]() における状態変数、入力変数(アクチュエータを操作する)を表しています。また、第2式は出力方程式とよばれ、
における状態変数、入力変数(アクチュエータを操作する)を表しています。また、第2式は出力方程式とよばれ、![]() は時刻
は時刻![]() における出力変数(センサを用いて観測される)を表しています。
における出力変数(センサを用いて観測される)を表しています。![]() は実数の集合を表します。以下では状態空間表現(1)を簡単に1次系と参照します。
は実数の集合を表します。以下では状態空間表現(1)を簡単に1次系と参照します。
この状態空間表現は図3のようなブロック線図で表されます。
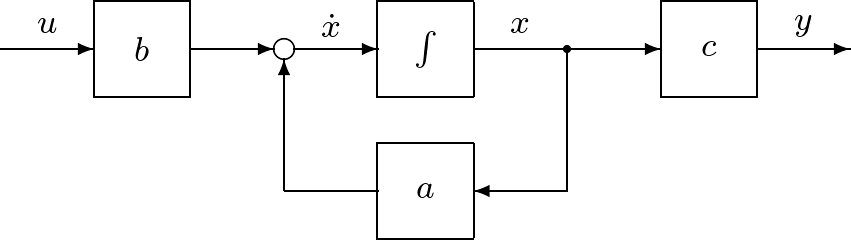
図1 1入力1出力1次系状態空間表現のブロック線図
●具体例を示すために、次図のような走行する車を考えます。

図2 走行する車
ニュートンの運動第2法則「質量×加速度=外力」を適用するため、車は質点とみなし、直線運動をしているとします。車の質量を![]() 、時刻
、時刻 ![]() における車の速度を
における車の速度を![]() 、車に働く外力(制動力)を
、車に働く外力(制動力)を ![]() とすると、車の運動方程式は次の微分方程式で与えられます。
とすると、車の運動方程式は次の微分方程式で与えられます。
![]()
ここで、![]() は車の加速度を表します。もし空気による抗力
は車の加速度を表します。もし空気による抗力![]() を考慮する場合は、車の運動方程式は次式となります。
を考慮する場合は、車の運動方程式は次式となります。
![]()
いま車は一定速度![]() で等速運動をしているとします。このとき加速度は零となるので
で等速運動をしているとします。このとき加速度は零となるので
![]()
を満たす一定の制動力![]() が定まります。実際には、この等速運動が何らかの原因により乱されたとき、これを速やかに元に戻すことが要求されます。そこで(3)から(4)を辺々引き算すると次式を得ます。
が定まります。実際には、この等速運動が何らかの原因により乱されたとき、これを速やかに元に戻すことが要求されます。そこで(3)から(4)を辺々引き算すると次式を得ます。
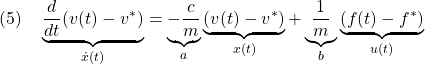
これが入力1出力1次系の状態方程式の一例です。ここで、![]() と
と![]() が、平衡状態
が、平衡状態![]() とこれを維持する平衡入力
とこれを維持する平衡入力![]() を表していることに留意します。
を表していることに留意します。
1次系の漸近安定性…Homework
[2] 1次系(1)で表される制御対象は平衡状態にあるとします(![]() )。いま平衡状態が乱され、時刻
)。いま平衡状態が乱され、時刻![]() において
において![]() となったとします。特に制動力を変えないとすると
となったとします。特に制動力を変えないとすると![]() です。このとき、元の平衡状態
です。このとき、元の平衡状態![]() に復帰できるならば、1次系(1)は漸近安定(asymptotically stable)であると言います。そこで
に復帰できるならば、1次系(1)は漸近安定(asymptotically stable)であると言います。そこで
![]()
の解
![]()
の振舞いを調べてみます。![]() のとき
のとき
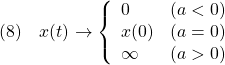
となるので、1次系(1)の漸近安定性の必要十分条件は
![]()
であることがわかります。
このように漸近安定性は、(1)において![]() とした自由系(unforced system)(6)に基づいて判定されることに留意してください。
とした自由系(unforced system)(6)に基づいて判定されることに留意してください。
●上の等速運動をしている車の例を考えます。いま突風による急激な速度変化のため![]() となり、特に制動力を変えないとすると
となり、特に制動力を変えないとすると![]() なので
なので
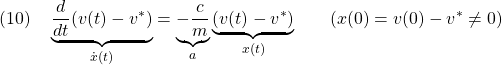
を解いて、元の速度![]() に復帰できるかを判断できます。ここで、
に復帰できるかを判断できます。ここで、![]() ですから、漸近安定であることが確かめられます。
ですから、漸近安定であることが確かめられます。
以上の議論は数学的には明らかですが、物理的にはどのような力が働いて平衡状態に戻るのでしょうか?それは空気抵抗![]() が速度の増減によって、逆方向に働くからといえます。速度に比例する抗力を減衰力、位置に比例する抗力を復元力といいます。モノつくりにおいて、これらを内在させることをパッシブ制御、コントローラ(補償器)を用いて補うことアクティブ制御といいます。
が速度の増減によって、逆方向に働くからといえます。速度に比例する抗力を減衰力、位置に比例する抗力を復元力といいます。モノつくりにおいて、これらを内在させることをパッシブ制御、コントローラ(補償器)を用いて補うことアクティブ制御といいます。
演習A01…Flipped Classroom
![]() 状態方程式
状態方程式![]() が与えられるときの漸近安定性の判定は、なぜ
が与えられるときの漸近安定性の判定は、なぜ![]() に基づいて行うのか説明せよ。
に基づいて行うのか説明せよ。
![]() MATLABまたはSCILABに次のコマンドを与えて、どのグラフが漸近安定であるか述べよ。
MATLABまたはSCILABに次のコマンドを与えて、どのグラフが漸近安定であるか述べよ。
| MATLAB |
|
| SCILAB |
|
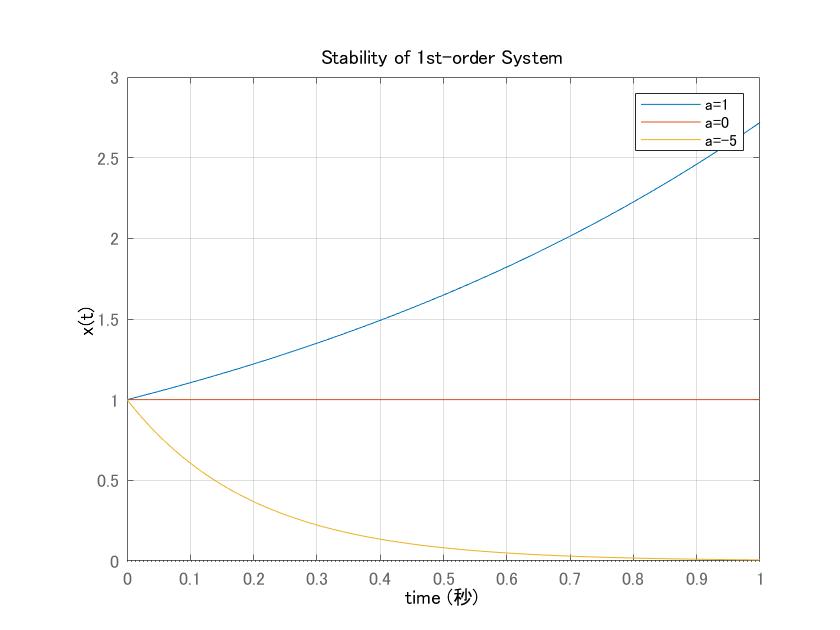 図3 どのグラフが漸近安定であるか?
図3 どのグラフが漸近安定であるか?