| MATLAB |
%beam1.m
%-----
clear all, close all
L=1; D=0.005; A=pi/4*D^2;
rho=7980; E=195000e6; I=pi/64*D^4;
J0=0.5*1*0.01; Me=0.1;
J=(J0+1/3*rho*A*L^3+Me*L^2)/(rho*A*L^3); beta=Me/(rho*A*L);
T=1/(L^2*sqrt(rho*A/(E*I)));
%-----
x=0:0.01:30;
y=err(x,beta);
figure(1)
plot(x,sign(y),[0 30],[0 0]); axis([0 30 -2 2]);
N=3;
% w=locate(N);
% om=[];
% for i=1:N
% x=fsolve(w(1,i),err); om=[om x];
% end
om=[1.3604444, 4.0789285, 7.1670195]
%-----
n_d=100; h=L/n_d; x=0:h:L; x=x';
y1=phi(1,x,om); y2=phi(2,x,om); y3=phi(3,x,om);
figure(2)
plot(x,y1,x,y2,x,y3)
%-----
y1=dphi(1,x,om); y2=dphi(2,x,om); y3=dphi(3,x,om);
figure(2)
plot(x,y1,x,y2,x,y3)
%-----
mode_fun=[];
for i=1:N, mode_fun =[mode_fun phi(i,x,om) ]; end
mode_dfun=[];
for i=1:N, mode_dfun=[mode_dfun dphi(i,x,om)]; end
%-----
t_simp=zeros(1, n_d+1);
t_simp(1,1)=1/3*h;
for i=1:(n_d+1)/2, t_simp(1,2*i)=2/3*h; t_simp(1,2*i+1)=4/3*h; end
t_simp(1,n_d+1)=1/3*h;
c_simp=t_simp(1,:);
%-----
for i=1:N
m(i) = c_simp*(x.*mode_fun(:,i))+beta*mode_fun(n_d+1,i);
OM2(i)=om(i)^4;
end
% M=[J m';m eye(N,N)];
% K=zeros(N+1,N+1); K(2:N+1,2:N+1)=diag(OM2);
% AA=[zeros(N+1,N+1) eye(N+1,N+1);
% -M\K zeros(N+1,N+1)];
% B =[zeros(N+1,1); M\eye(N+1,1)];
M21=m'; K22=diag(OM2);
AA=[zeros(N+1,N+1) eye(N+1,N+1);
[-K22 K22*m';zeros(1,N+1)] zeros(N+1,N+1)];
Ta=0.1;
AA(2*(N+1),2*(N+1))=-1/Ta;
B =[zeros(2*N+1,1); 1/Ta];
C=[eye(N,N) -M21 zeros(N,N+1)];
CC=[mode_fun*C;zeros(1,N),1,zeros(1,N+1)];
P=ss(AA,B,CC,[]);
G=tf(P);
w=logspace(-3,3,100);
figure(3)
for i=[1,21,41,61,81,101]
bode(G(i,1),w),hold on
end
%-----
sys=ss(AA,B,CC([1,21,41,61,81,101],:),[])
state0=(L/(E*I))*B;
%state0=zeros(8,1)
t0=0; t=0:T/1000:T;
figure(4)
initial(sys,state0,t)
%-----
[F,p]=opt(AA,B,eye(8,8),eye(8,8),1)
ACL=AA-B*F;
sysCL=ss(ACL,B,CC([1,21,41,61,81,101],:),[])
figure(5)
initial(sysCL,state0,t)
%====
function errval=err(x,beta)
errval=beta*x.*(cosh(x).*sin(x)-sinh(x).*cos(x))-(1+cosh(x).*cos(x));
end
%-----
function y=phi(i,x,om)
y=(sinh(om(i))+sin(om(i))).*(cosh(om(i)*x)-cos(om(i)*x))...
-(cosh(om(i))+cos(om(i))).*(sinh(om(i)*x)-sin(om(i)*x));
y=y/max(abs(y));
end
%-----
function y=dphi(i,x,om)
y=(sinh(om(i))+sin(om(i))).*(sinh(om(i)*x)+sin(om(i)*x))...
-(cosh(om(i))+cos(om(i))).*(cosh(om(i)*x)-cos(om(i)*x));
y=om(i)*y;
y=y/max(abs(y));
end
%-----
%eof
|

![Rendered by QuickLaTeX.com \displaystyle{(1a)\quad \underbrace{ \left[\begin{array}{c|ccc} \alpha & m_1 & \dots &m_N \\ \hline m_1 & 1 & & 0 \\ \vdots & & \ddots & \\ m_N & 0 & & 1 \\ \end{array}\right] }_{M=\left[\begin{array}{cc} M_{11} & M_{12} \\ M_{21} & M_{22} \end{array}\right]} \underbrace{ \left[\begin{array}{c} \ddot{\theta} \\ \hline \ddot{r}_1 \\ \vdots \\ \ddot{r}_N \end{array}\right] }_{\ddot{\xi}} + \underbrace{ \left[\begin{array}{c|ccc} 0 & 0 & \dots &0 \\ \hline 0 & \Omega_1^2 & & 0 \\ \vdots & & \ddots & \\ 0 & 0 & & \Omega_N^2 \\ \end{array}\right] }_{K=\left[\begin{array}{cc} K_{11} & K_{12} \\ K_{21} & K_{22} \end{array}\right]} \underbrace{ \left[\begin{array}{c} \theta \\ \hline r_1 \\ \vdots \\ r_N \end{array}\right] }_{\xi} = \underbrace{ \left[\begin{array}{c} 1 \\ \hline 0 \\ \vdots \\ 0 \end{array}\right] }_{B_2} u' }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-346490e79fcc2267740093f5fde47d5f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1b)\quad \eta(\xi)= \underbrace{ \left[\begin{array}{c|ccc} 0 & \phi_1(\xi) & \dots &\phi_N(\xi) \end{array}\right] }_{C_1} \underbrace{ \left[\begin{array}{c} \theta \\ \hline r_1 \\ \vdots \\ r_N \end{array}\right] }_{\xi} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8a564535f5712a1756e4d97b569ada10_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2a)\quad \underbrace{ \left[\begin{array}{c} \dot{\xi} \\ \ddot{\xi} \end{array}\right] }_{\dot{x}} = \underbrace{ \left[\begin{array}{cc} 0_{N+1\times N+1} & I_{N+1} \\ M^{-1}K & 0_{N+1\times N+1} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \xi \\ \dot{\xi} \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{cc} 0_{N+1\times 1} \\ M^{-1}B_2 \end{array}\right] }_{B} u'}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-524df64b74898d10a9e6574263d3ca12_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2b)\quad \eta(\xi)= \underbrace{ \left[\begin{array}{cc} C_1 & 0_{1\times N} \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \xi \\ \dot{\xi} \end{array}\right] }_{x} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6e8294598be55b2b237fc74f95338ce8_l3.png)
![]() を用いて
を用いて![]()
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{ \left[\begin{array}{c} m_1 \\ \vdots \\ m_N \\ \end{array}\right] }_{M_{21}} \ddot{\theta} + \underbrace{ \left[\begin{array}{c} \ddot{r}_1 \\ \vdots \\ \ddot{r}_N \end{array}\right] }_{\ddot{r}} + \underbrace{ \left[\begin{array}{ccc} \Omega_1^2 & & 0 \\ & \ddots & \\ 0 & & \Omega_N^2 \\ \end{array}\right] }_{K_{22}} \underbrace{ \left[\begin{array}{c} r_1 \\ \vdots \\ r_N \end{array}\right] }_{r} = \left[\begin{array}{c} 0 \\ \vdots \\ 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-83e03635bb43c77e2201d7335edf4248_l3.png)
![]()
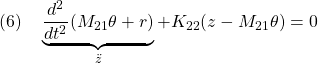
![Rendered by QuickLaTeX.com \displaystyle{(7a)\quad \underbrace{ \left[\begin{array}{c} \dot{z} \\ \dot{\theta} \\\hline \ddot{z} \\ \ddot{\theta} \end{array}\right] }_{\dot{x}} = \underbrace{ \left[\begin{array}{cc|cc} 0_{N\times N} & 0_{N\times 1} & I_N & 0_{N\times 1} \\ 0_{1\times N} & 0 & 0_{1\times N} & 1 \\\hline -K_{22} & K_{22}M_{21} & 0_{N\times N} & 0_{N\times 1} \\ 0_{1\times N} & 0 & 0_{1\times N} & -\frac{1}{T_a} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} {z} \\ {\theta} \\\hline \dot{z} \\ \dot{\theta} \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{cc} 0_{N\times 1} \\ 0 \\\hline 0_{N\times 1} \\ \frac{1}{T_a} \end{array}\right] }_{B} \dot{\theta}_c}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4e568bda7882b131b5b24ac100e86af6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7b)\quad \eta(\xi)= \underbrace{ \left[\begin{array}{ccc} \phi_1(\xi) & \cdots & \phi_N(\xi) \end{array}\right] \left[\begin{array}{cc|cc} I_N & -M_{21} & 0_{N\times N} & 0_{N\times 1} \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} {z} \\ {\theta} \\\hline \dot{z} \\ \dot{\theta} \end{array}\right] }_{x} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4598350d67871b8cea2146c9120e81d4_l3.png)
![]() m
m![]() m
m![]() kg/m
kg/m![]()
![]() N/mm
N/mm![]()
![]() m
m![]()
![]() m
m![]()
![]() kgm
kgm![]()
![]() kg
kg