|
私たちが制御したい対象が物である場合,その振る舞いは物理法則により記述される。一般に,動的な振る舞いを表す物理法則は微分方程式で表される。微分方程式というと尻込みする人もいるかもしれないが,最初は,ニュートンの運動第2法則 さて,制御を行うには対象の動的な振る舞い(状態変数の時間変化)を観測することが必要であり,そのためにセンサが用いられる。ここで,現実には,すべての状態変数にセンサを配置できるわけではなく,通常は状態変数の一部がセンサにより観測される。センサにより観測される変数と状態変数の間の関係式を,制御対象の「出力方程式」と呼ぶ。 本章では,動的な振る舞いが連立線形微分方程式で記述されるいくつかの制御対象に対して,状態方程式と出力方程式をペアにした「状態空間表現」を求める。これを図示した「ブロック線図」は,計算機シミュレーションを行う際にも有用である。 |
1.1 状態空間表現の導出例
1.1.1 ペースメーカ
|
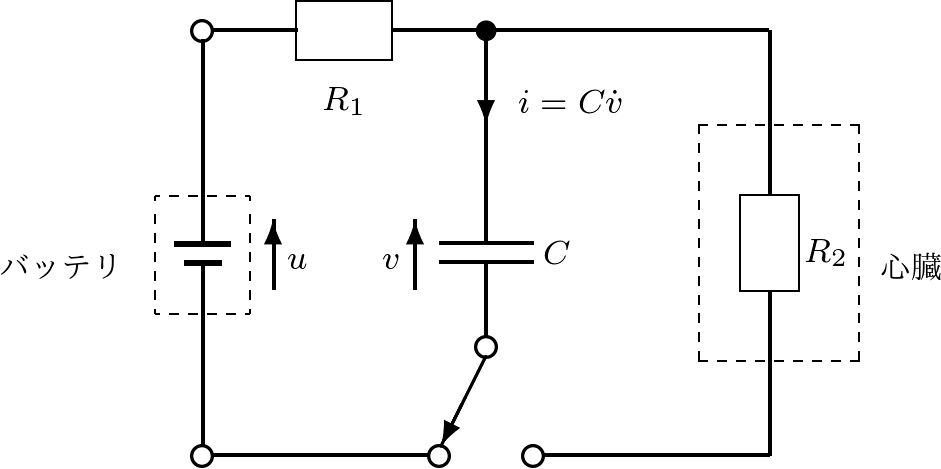
高齢化社会の到来に伴い,より優れた福祉・医療機器の開発が工学分野の大きなテーマの一つとなっている。図1.1に示すのは,心臓のペースメーカの簡単な原理図である。これは,まず左側の閉回路でコンデンサへの充電を行い,つぎにスイッチを切り替えてできる右側の閉回路で放電を行うという動作を周期的に繰り返すことにより,心臓のペースメーカの役割を果たそうとするものである。ここでは,状態方程式を導く最初の例として,このようなRC回路における充電と放電について考える。
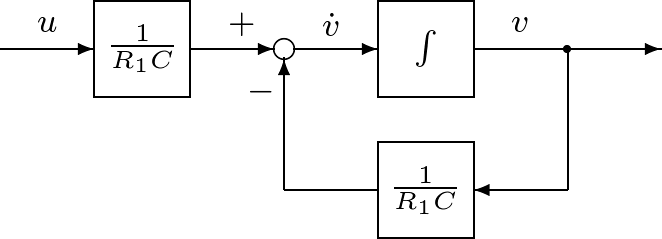
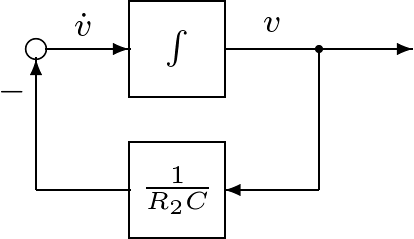
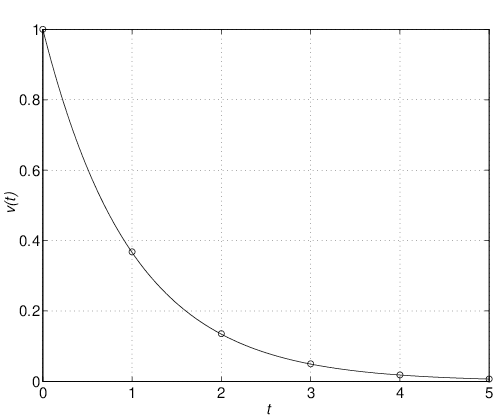
そのために,キルヒホッフの電圧則より,左側閉回路と右側閉回路の回路方程式を考えると,それぞれ (1) (2) となる。ここで, (3) 状態方程式(3)を図1.2のように図示し,これを状態方程式に基づくブロック線図と呼ぶ。この描き方のポイントは,式(3)の右辺を表すのに加え合わせ記号○を用いることと,また 同様に,式(2)から得られる状態方程式は (4) であり,これによるブロック線図は図1.3のように示される。 (5) と与えられることはよいであろう(式(4)に代入して確かめよ)。状態方程式(4)は入力変数をもたないが,状態変数の初期値によって,状態変数の時間的振る舞いが現れる。この意味で,1次系(4)は シミュレーション1.1 式(5)で表されるコンデンサ電圧 (6) によって近似計算しなさい。 |
*系はsystemの訳語。ここでは「××システム」を簡潔に「××系」と書く。
**本書では,時間応答のコンピュータによるシミュレーション(simulation)の欄を設けた。最終的には時間応答の数学的理解が大切であるが,まずは,なぜそのような時間的振る舞いが現れるのかを物理的イメージをもって考えながら,典型的な時間応答に親しみをもってほしい。なお,本書の数値計算については演習問題の【4】を参照のこと。
1.1.2 教室のドア
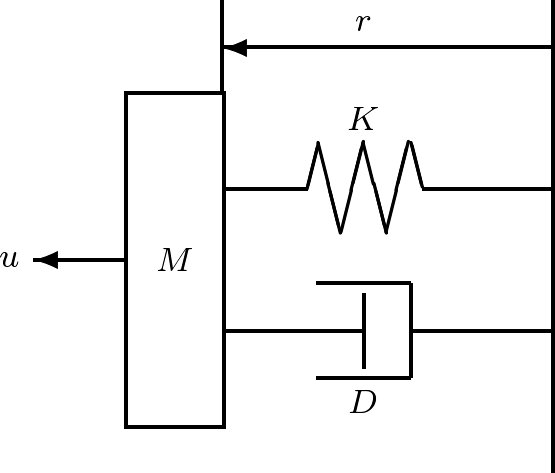
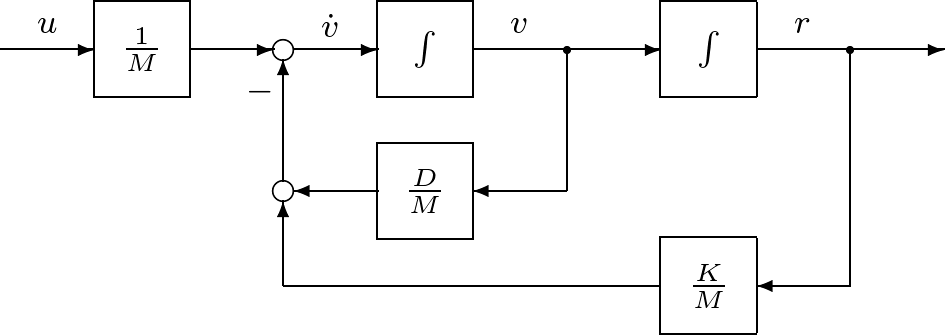
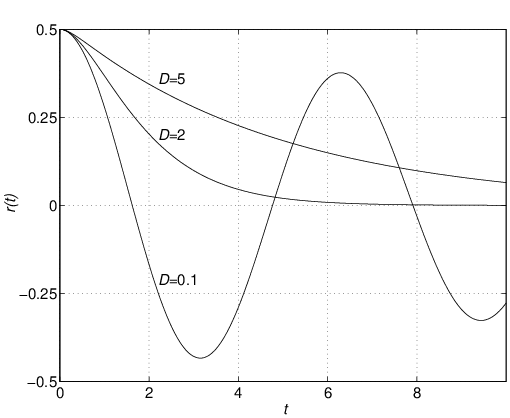
教室で物の動きを実感できるものに,図1.5に示すようなばねとダンパ 図1.5 緩衝装置をつけたドア このドアの運動は回転運動であるが,話しをわかりやすくするため,図1.6に示すような等価な直線運動として調べてみよう。その出発点は,ニュートンの運動第2法則 (7) である。ここで, (8) のように表すことができる。ここで,ダンパが第1項の力を,ばねが第2項の力を与える。 (9) を得る。 (10) (11) のような1階の連立線形微分方程式で表される。これらを行列表示すると (12) のような状態方程式を得る (13) を得るセンサはあるが,ドアの速度を計測するセンサはないものとする。このとき, (14) 以上から,ドアに対して,状態方程式(12)と出力方程式(14)からなる2次系(second-order system)としての状態空間表現を得た。 シミュレーション 式(12)において,
|
*ばねとダンパの特性値を調整するためのねじを回すことにより行われる。
**本書では,![]() のように書いて,△を○で定義・表記する(△は○に等しいとする)。
のように書いて,△を○で定義・表記する(△は○に等しいとする)。
1.1.3 直流モータ
|
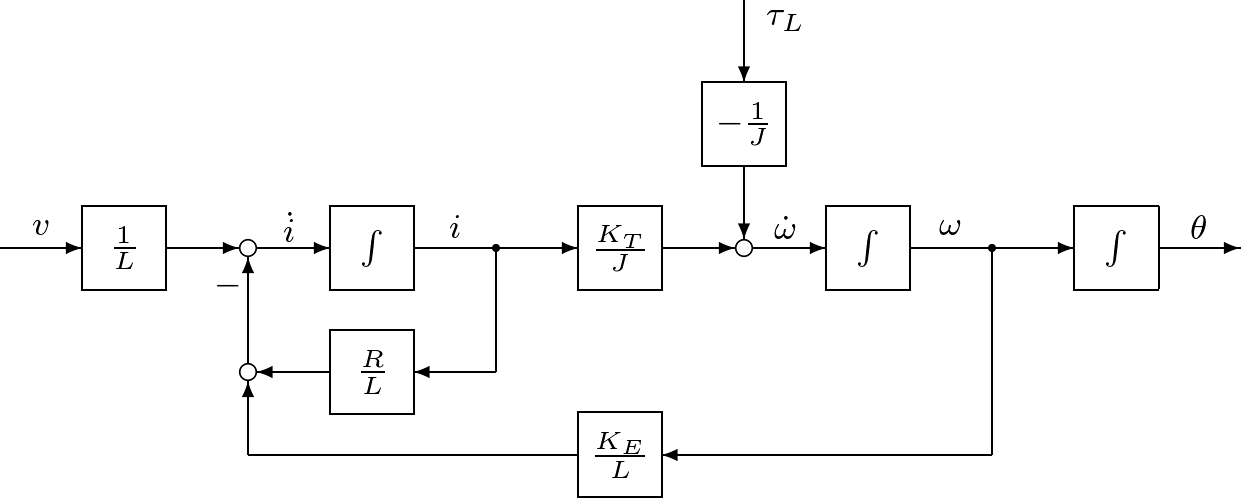
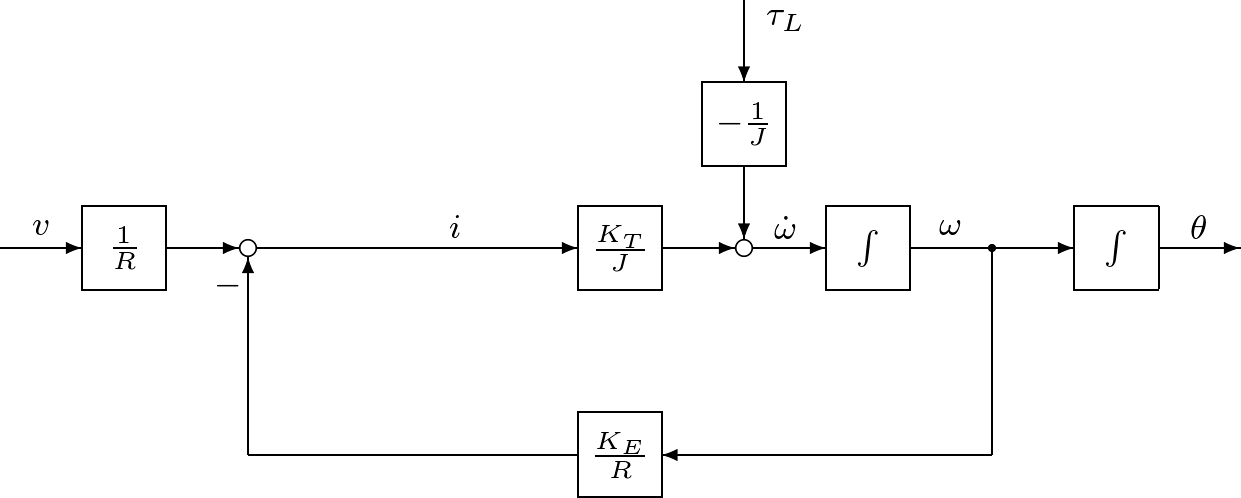
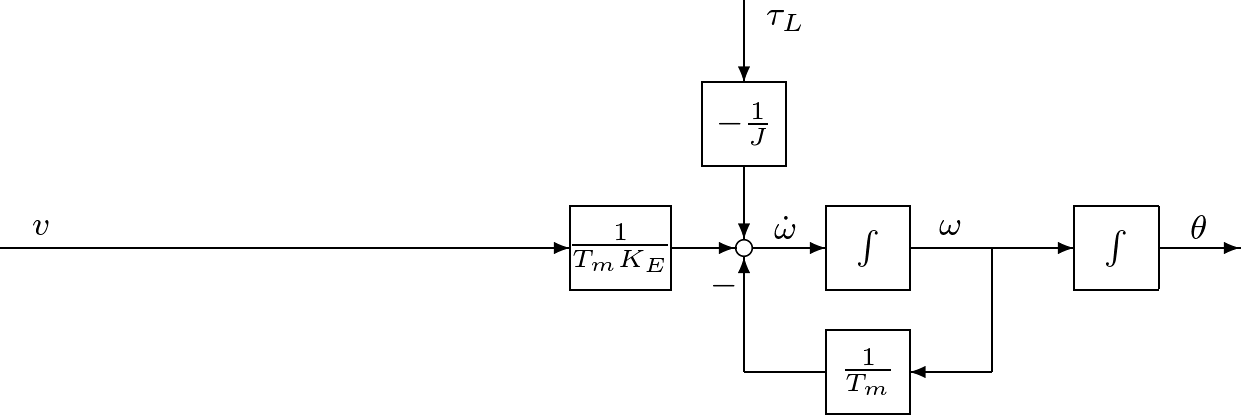
代表的なアクチュエータとしてモータがある。例えば図1.9に示すのは,ロボットアームを駆動する直流モータである。  図1.9 直流モータ このモデルは図1.10のように表される。 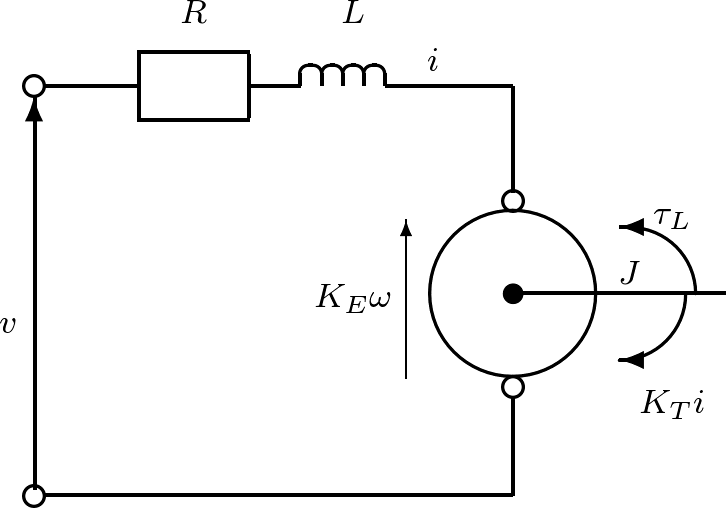 図1.10 直流モータのモデル このとき,つぎが成り立つ。 (15) (16) ここで,式(15)は機械系としての運動方程式であるが,電流による発生トルクの項 (17) (18) (19) のような状態方程式を得る。状態方程式(19)は二つの入力変数 (20) となる。このように,直流モータに対して,状態方程式(19)と出力方程式(20)からなる3次系(third-order system)としての状態空間表現を得た。つぎに一つのシミュレーション例を示す。 (21) で与えられ,上の例では (22) これから (23) (24) は直流モータの機械的時定数と呼ばれている。上の例で計算してみると (25) 式(19)と比較すると,状態空間表現の次数を1だけ減らしたことになる。 低次元化の過程を図1.12~図1.14に示しておく。 |
*式(18)は,式(19)のように物理パラメータどうしの演算を含まず,それらの変動の影響を考察するのに便利な形式であり,ディスクリプタ形式の状態方程式と呼ばれる。
**ここでは,2.1.3項で学ぶ時定数の知識を前提にしている。
1.2 状態空間表現へのモデリング
| 前節で述べた内容は,モデリング(modeling)という枠組でとらえられる。これは,何らかの対象に対して,目的に応じた科学的分析を通してそのモデルを得ようとするものである。私たちが扱う対象は,入力と出力をもつ動的システム 本書では,状態空間表現を次式のように書く。 (26) (27) ここで, |
*動的システムは,微分方程式・差分方程式のどちらで記述されるかによって連続時間系・離散時間系,重ね合わせの原理が成り立つか否かによって線形系・非線形系,常微分方程式か偏微分方程式かによって集中定数系・分布定数系,係数パラメータの時間依存性によって時変系・時不変系,入出力が確率過程であるか否かによって決定系・確率系などに分類される。
**非線形系の場合の取り扱いは7章で述べる。1~6章までは線形時不変系のみを扱う。
***他の数理モデルとして伝達関数表現がある。状態空間表現と伝達関数表現の間の相互関係については8章で述べる。
****他のアプローチとして,入力と出力の時系列データからモデリングを行うシステム同定がある。
1.3 状態空間表現の座標変換
| 状態空間表現を見やすくする一つの手段として,座標変換(coordinate transformation)があるので,これについて説明しよう。 いま, (28) (29) に対して,つぎの座標変換を行いたい。 (30) (31) に注意して (32) %すなわち (33) (34) となる。この結果を,参照しやすいようにつぎにまとめておく。 定理1.1 (35) (36) (37) 例題1.1 直流モータの状態方程式(25)において, (38) である。これに対して,座標変換 (39) を行うと,新しい状態方程式は (40) となることを示しなさい。 解答 座標変換後の (41) (42) のように得られる。 ここで,2次系の状態方程式が,二つの1次系の状態方程式 (43) に分離されており,入力から状態変数への影響の考察をしやすくなっていることに注意してほしい。 |
1.4 状態空間表現の直列結合
| 制御対象の状態空間表現を求める際に,図1.15に示すように,二つの部分システムの状態空間表現を求めておいて,これらを直列結合(serial connection)する場合がある。このときの結合システムの状態空間表現を求めることを考える。
まず,その結果を定理の形で示そう。 (44) (45) (46) (47) に対して, (48) (49) のように得られる。 証明 (50) (51) となる。第1式と (52) (53) に対して( (54) (55) を, 解答 定理1.2を用いて,直列結合の状態空間表現として (56) (57) が得られる 問1.4 例題1.2の直列結合の状態空間表現を,状態ベクトルが |
*ここで,![]() 行列の縦線と横線,
行列の縦線と横線,![]() 行列の横線は,状態ベクトルの要素
行列の横線は,状態ベクトルの要素![]() ,
,![]() のサイズに適合するように引かれている。
のサイズに適合するように引かれている。
演習問題
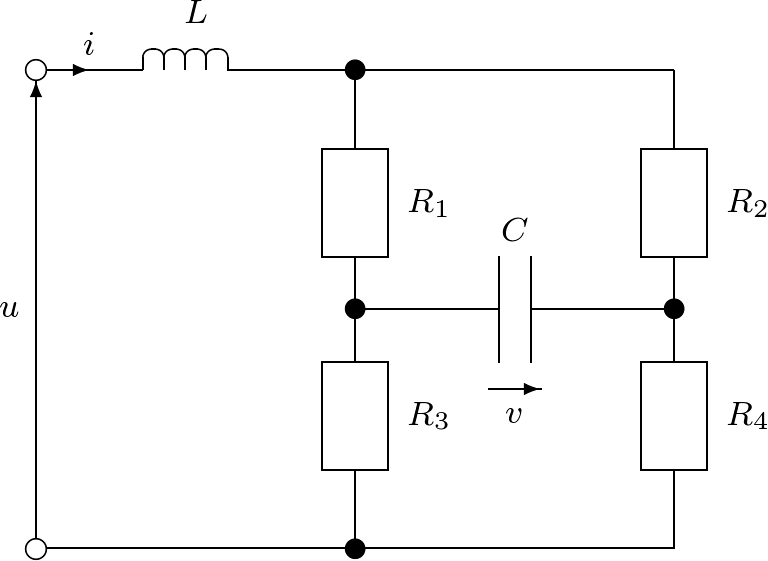
【1】 いろいろな計測装置の基礎となる電気回路の一つにブリッジ回路がある。 例えば,図1.16に示すブリッジ回路 (58) (59) で与えられる。いま,ブリッジ条件 (60) が成り立つとして,つぎの状態方程式を導出しなさい。 (61) この状態方程式に基づいて,平衡ブリッジ回路のブロック線図を描きなさい。
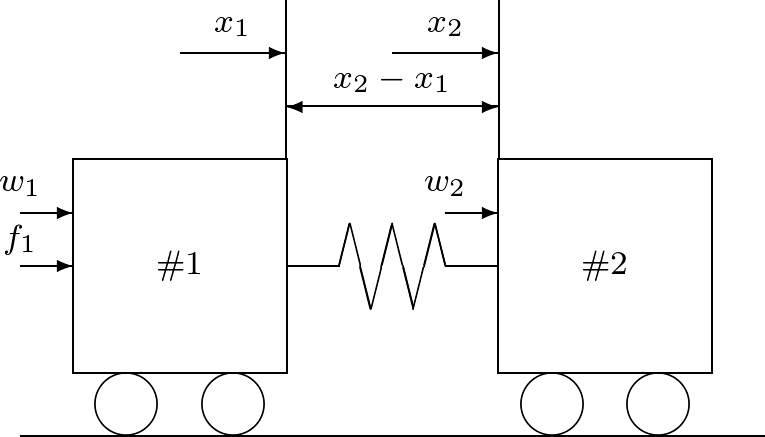
(62) (63) で与えられる。ここで, (64) この状態方程式に基づいて,連結台車のブロック線図を描きなさい。
MATLABとSIMULINKが手元にあれば,シミュレーション1.3と同一条件下で,直流モータの低次元化後の状態方程式25による角速度の応答を,低次元化前の状態方程式19によるものと比較しなさい。  図1.18 SIMULINKによる微分方程式のブロック表現 図1.18 SIMULINKによる微分方程式のブロック表現 |
*高橋・有本:回路網とシステム理論,コロナ社 (1974)のpp.65![]() 66から引用。
66から引用。
**B.Wie, D.2.Bernstein : Benchmark Problems for Robust Control Design, ACC Proc. pp.2047![]() 2048 (1992) から引用。
2048 (1992) から引用。
***The Student Edition of MATLAB-Version\,5 User’s Guide, Prentice Hall (1997)
****The Student Edition of SIMULINK-Version\,2 User’s Guide, Prentice Hall (1998)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} \dot{r}(t) \\ \dot{v}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{K}{M} & -\frac{D}{M} \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} r(t) \\ v(t) \end{array}\right] }_{x(t)}+ \underbrace{ \left[\begin{array}{c} 0 \\ \frac{1}{M} \end{array}\right] }_B u(t) \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1c7d500e812b8db8f7ef93fb748d863a_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{y_r(t)}_{y(t)}= \underbrace{ \left[\begin{array}{cc} c_r & 0 \end{array}\right] }_C \underbrace{ \left[\begin{array}{c} r(t) \\ v(t) \end{array}\right] }_{x(t)} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ba917ead63a659449c7ce89833f94df6_l3.png)
![Rendered by QuickLaTeX.com \begin{eqnarray*} %\begin{equation} %\renewcommand{\arraystretch}{1.3} %\begin{array}{rl} \underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & J & 0 \\ 0 & 0 & L \end{array}\right] }_{E} \left[\begin{array}{c} \dot{\theta}(t) \\ \dot{\omega}(t) \\ \dot{i}(t) \end{array}\right] & = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & K_T \\ 0 & -K_E & -R \end{array}\right] }_{A} \left[\begin{array}{c} \theta(t) \\ \omega(t) \\ i(t) \end{array}\right] \nonumber\\ & + \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ 0 & -1 \\ 1 & 0 \end{array}\right] }_{B} \left[\begin{array}{cc} v(t) \\ \tau_L(t) \end{array}\right] %\end{array} %\end{equation} \end{eqnarray*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8c9f17ab2cf165ed53693c17a0d06a1b_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} \dot{\theta}(t) \\ \dot{\omega}(t) \\ \dot{i}(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & \frac{K_T}{J} \\ 0 & -\frac{K_E}{L} & -\frac{R}{L} \end{array}\right] }_{E^{-1}A} \underbrace{ \left[\begin{array}{c} \theta(t) \\ \omega(t) \\ i(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ 0 & -\frac{1}{J} \\ \frac{1}{L} & 0 \end{array}\right] }_{E^{-1}B} \underbrace{ \left[\begin{array}{cc} v(t) \\ \tau_L(t) \end{array}\right] }_{u(t)} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-26653bd3a6e2a14d2a2dd8ae426bf5f9_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} y_\theta(t) \\ y_\omega(t) \end{array}\right] }_{y(t)}= \underbrace{ \left[\begin{array}{ccc} c_\theta & 0 & 0 \\ 0 & c_\omega & 0 \end{array}\right] }_C \underbrace{ \left[\begin{array}{c} \theta(t) \\ \omega(t) \\ i(t) \end{array}\right] }_{x(t)} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3d3a761f1082c0bb1c76cbac090b269d_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -\frac{1}{T_m} \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)}+ \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ \frac{1}{T_mK_E} & -\frac{1}{J} \end{array}\right] }_B \underbrace{ \left[\begin{array}{c} v(t)\\ \tau_L(t) \end{array}\right] }_{u(t)} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b6118b470740014f12ba99fab45c5044_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} \dot{\theta}(t)\\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -\frac{1}{T_m} \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} \theta(t)\\ \omega(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ \frac{1}{T_mK_E} \end{array}\right] }_B \underbrace{ v(t) }_{u(t)} % \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-06edd7a3c72279d04bbf853ea6c6bdd5_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} x'_1(t) \\ x'_2(t) \end{array}\right] }_{x'(t)} = \underbrace{ \left[\begin{array}{cc} 1 & T_m \\ 0 & -T_m \end{array}\right] }_T \underbrace{ \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)} % \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c6eae3ed06b9f97fd4eaffb60d82c161_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} \dot{x}'_1(t) \\ \dot{x}'_2(t) \end{array}\right] }_{\dot{x}'(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ 0 & -\frac{1}{T_m} \end{array}\right] }_{A'} \underbrace{ \left[\begin{array}{c} x'_1(t) \\ x'_2(t) \end{array}\right] }_{x'(t)} + \underbrace{ \left[\begin{array}{c} \frac{1}{K_E} \\ -\frac{1}{K_E} \end{array}\right] }_{B'} \underbrace{ v(t) }_{u(t)} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e26ebb2f15db7052666007c6f7713109_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{cc} 1 & T_m \\ 0 & -T_m \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ 0 & -\frac{1}{T_m} \end{array}\right] \left[\begin{array}{cc} 1 & 1 \\ 0 & -\frac{1}{T_m} \end{array}\right] }_{TAT^{-1}} = \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ 0 & -\frac{1}{T_m} \end{array}\right] }_{A'} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-063430e3eba82786ff27bab3362214fe_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{cc} 1 & T_m \\ 0 & -T_m \end{array}\right] \left[\begin{array}{cc} 0 \\ \frac{1}{T_mK_E} \end{array}\right] }_{TB} = \underbrace{ \left[\begin{array}{c} \frac{1}{K_E} \\ -\frac{1}{K_E} \end{array}\right] }_{B'} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-782f939b9de9db6e02c2932b3e39543c_l3.png)

![Rendered by QuickLaTeX.com \begin{equation*} \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_a(t) \end{array}\right]= \left[\begin{array}{cc|c} 0 & 1 & 0\\ -\omega_n^2 & -2\zeta\omega_n & K\omega_n^2 \\\hline 0 & 0 & -\frac{1}{T_a} \end{array}\right] \left[\begin{array}{c} x(t) \\ x_a(t) \end{array}\right]+ \left[\begin{array}{cc} 0 \\ 0 \\\hline \frac{K_a}{T_a} \end{array}\right] u_a(t) \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-375c43a38aaae14e657cf77df359e493_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \underbrace{ \left[\begin{array}{c} \dot{i}(t) \\ \dot{v}(t) \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} -\frac{1}{L}(\frac{R_1R_2}{R_1+R_2}+\frac{R_3R_4}{R_3+R_4})\ \ 0 \\ 0\ \ -\frac{1}{C}(\frac{1}{R_1+R_2}+\frac{1}{R_3+R_4}) \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} i(t) \\ v(t) \end{array}\right] }_{x(t)}+ \underbrace{ \left[\begin{array}{c} \frac{1}{L} \\ 0 \end{array}\right] }_B u(t) \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a8387d56c5b1e0a5d7e4371a7c5bf88f_l3.png)
![Rendered by QuickLaTeX.com \begin{equation*} \begin{array}{rcl} \underbrace{ \left[\begin{array}{c} \dot{x_1}(t) \\ \dot{x_2}(t) \\ \dot{v_1}(t) \\ \dot{v_2}(t) \end{array}\right] }_{\dot{x}(t)} &=& \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -\frac{k}{m_1} & \frac{k}{m_1} & 0 & 0 \\ \frac{k}{m_2} & -\frac{k}{m_2} & 0 & 0 \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \\ v_1(t) \\ v_2(t) \end{array}\right] }_{x(t)} \\ & & \hspace*{-1zw} + \underbrace{ \left[\begin{array}{ccc} 0 & 0 & 0 \\ 0 & 0 & 0 \\ \frac{1}{m_1} & 0 & \frac{1}{m_1} \\ 0 & \frac{1}{m_2} & 0 \end{array}\right] }_B \underbrace{ \left[\begin{array}{c} w_1(t)\\ w_2(t)\\ f_1(t) \end{array}\right] }_{u(t)} \end{array} \end{equation*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-726aaf73212dd3c34a1e3daca7912d95_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.8)\quad = \left[\begin{array}{cc|c} -a_1 & -a_2 & 1 \\ 1 & 0 & 0 \\\hline b_1 & b_2 & d \end{array}\right] = \left[\begin{array}{cc|c} 0 & 1 & 0 \\ -a_2 & -a_1 & 1 \\\hline b_2 & b_1 & d \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d7a3af5f4f8e549e8d5b0bc925920021_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.9)\quad = \left[\begin{array}{cc|c} -a_1 & 1 & b_1 \\ -a_2 & 0 & b_2 \\\hline 1 & 0 & d \end{array}\right] = \left[\begin{array}{cc|c} 0 & -a_2 & b_2 \\ 1 & -a_1 & b_1 \\\hline 0 & 1 & d \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-346bd4535c305aab672d107228824443_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \left[\begin{array}{cccc|c} -a_1 & \cdots & -a_{n-1} & -a_n & 1 \\ 1 & \cdots & 0 & 0 & 0 \\ \vdots & \ddots & \vdots & \vdots & 0 \\ 0 & \cdots & 1 & 0 & 0 \\ \hline b_1 & \cdots & b_{n-1} & b_n & d \\ \end{array}\right] = \left[\begin{array}{cccc|c} 0 & 1 & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & 0 \\ 0 & 0 & \cdots & 1 & 0 \\ -a_n & -a_{n-1} & \cdots & -a_1 & 1 \\ \hline b_n & b_{n-1} & \cdots & b_1 & d \\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1182e60b321b80d67da72737cf93a6aa_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \left[\begin{array}{cccc|c} -a_1 & 1 & \cdots & 0 & b_1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ -a_{n-1} & 0 & \cdots & 1 & b_{n-1} \\ -a_n & 0 & \cdots & 0 & b_n \\\hline 1 & 0 & \cdots & 0 & 0 \end{array}\right]\ = \left[\begin{array}{cccc|c} 0 & \cdots & 0 & -a_n & b_n \\ 1 & \cdots & 0 & -a_{n-1} & b_{n-1} \\ \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & \cdots & 1 & -a_1 & b_1 \\\hline 0 & \cdots & 0 & 1 & 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d5720a8829c9dfa241b03305b3b25411_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.11)\quad G(s)= \left[\begin{array}{cccc} G_{11}(s) & \cdots & G_{1m}(s) \\ \vdots & \ddots & \vdots \\ G_{p1}(s) & \cdots & G_{pm}(s) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7cb240795c5097204412352dfb980d8a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.13)\quad \left[\begin{array}{cccc} G_{11}(s) & \cdots & G_{1m}(s) \\ \vdots & \ddots & \vdots \\ G_{p1}(s) & \cdots & G_{pm}(s) \end{array}\right] = \left[\begin{array}{ccc|ccc} A_1 & \cdots & 0 & B_{1} \\ \vdots & \ddots & \vdots & \vdots \\ 0 & \cdots & A_p & B_{p} \\\hline C_{1} & \cdots & C_{p} & D \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d7220fda434ac07c20e2c4bea4de023f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.14)\quad A_i= \left[\begin{array}{ccc} A_{i1} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & A_{im} \end{array}\right] \ (i=1,\cdots,p) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-97d82178ac1ef7da5b4a4804aa5733aa_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.15)\quad B_i= \left[\begin{array}{ccc} B_{i1} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & B_{im} \end{array}\right] \ (i=1,\cdots,p) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-411bfaa56e8913f1d700b91bb4fb8318_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.16)\quad C_i= \left[\begin{array}{ccc} C_{i1} & \cdots & 0 \\ \vdots & \ddots & \vdots \\ 0 & \cdots & C_{im} \end{array}\right] \ (i=1,\cdots,p) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-229691483d6d651a5baff611990e829b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.17)\quad D= \left[\begin{array}{ccc} D_{11} & \cdots & D_{1m} \\ \vdots & \ddots & \vdots \\ D_{p1} & \cdots & D_{pm} \end{array}\right] \ (i=1,\cdots,p) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-26d78920b61bbc58ffebe39615ed38bd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.19)\quad G(s)&=& \left[\begin{array}{cccc|c} -a_1I_m & \cdots & -a_{n-1}I_m & -a_nI_m & I_m \\ I_m & \cdots & 0 & 0 & 0 \\ \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & \cdots & I_m & 0 & 0 \\\hline G_1 & \cdots & G_{n-1} & G_n & D \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2147338b5b2e2e48c7ca64d574ff9446_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.20)\quad &=& \left[\begin{array}{cccc|c} 0 & I_m & \cdots & 0 & 0 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ 0 & 0 & \cdots & I_m & 0 \\ -a_nI_m & -a_{n-1}I_m & \cdots & -a_1I_m & I_m \\\hline G_n & G_{n-1} & \cdots & G_1 & D \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f4b3e34a1cb231f0c99ea3fcdddb6b69_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.21)\quad G(s)&=& \left[\begin{array}{cccc|c} -a_1I_p & I_p & \cdots & 0 & G_1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ -a_{n-1}I_p & 0 & \cdots & I_p & G_{n-1} \\ -a_nI_p & 0 & \cdots & 0 & G_n \\\hline I_p & 0 & \cdots & 0 & D \end{array}\right]\ }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6978afaef8daedb2ce9dccb7a11256cd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.22)\quad &=& \left[\begin{array}{cccc|c} 0 & \cdots & 0 & -a_nI_p & G_n \\ I_p & \cdots & 0 & -a_{n-1}I_p & G_{n-1} \\ \vdots & \ddots & \vdots & \vdots & \vdots \\ 0 & \cdots & I_p & -a_1I_p & G_1 \\\hline 0 & \cdots & 0 & I_p & D \end{array}\right]\ }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-025c74ce69e17aa7f048aa587bdca393_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \frac{s+1}{s^2+3s+2} = \left[\begin{array}{cc|c} -3 & -2 & 1 \\ 1 & 0 & 0 \\\hline 1 & 1 & 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-820089b2535805b0088531f9b06f3193_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ G(s)= \left[\begin{array}{ccc|c} -1 & 0 & 0 & 1 \\ 0 & -3 & -2 & 1\\ 0 & 1 & 0 & 0 \\\hline 1 & 0 & 0 & 0 \\ 0 & 1 & 1 & 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-238da7f8aef65560e4a36b8bccfed84f_l3.png)
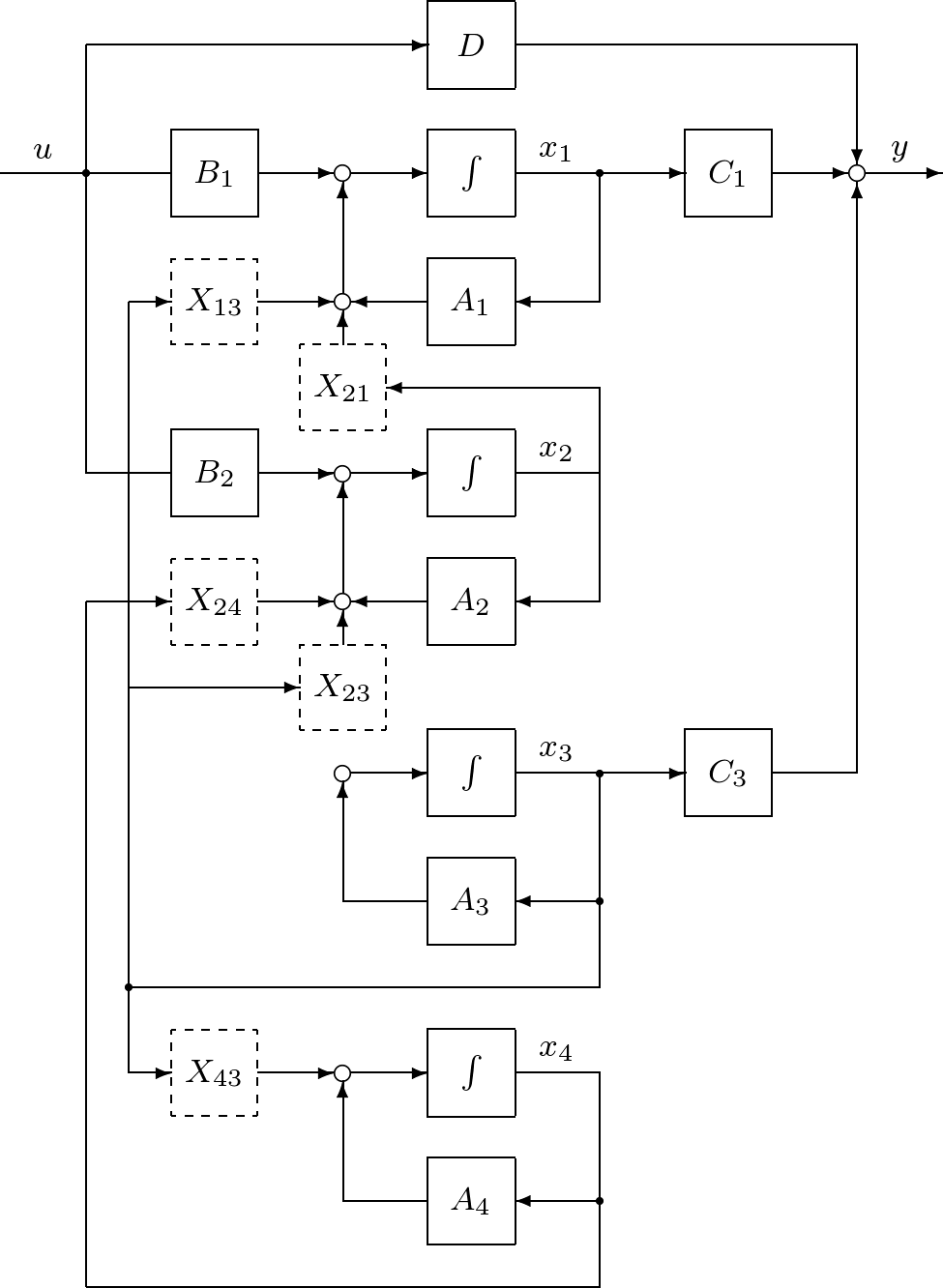
![Rendered by QuickLaTeX.com \displaystyle{(8.23)\quad \left[\begin{array}{c|c} TAT^{-1} & TB \\\hline CT^{-1} & D \end{array}\right] = \left[\begin{array}{cccc|c} A_1 & 0 & X_{13} & 0 & B_1 \\ X_{21} & A_2 & X_{23} & X_{24} & B_2 \\ 0 & 0 & A_3 & 0 & 0 \\ 0 & 0 & X_{43} & A_4 & 0 \\\hline C_1 & 0 & C_3 & 0 & 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aca4fee72af4083324246c35ea634544_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.25)\quad \left[\begin{array}{cc|c} A_1 & 0 & B_1 \\ X_{21} & A_2 & B_2 \\\hline C_1 & 0 & 0 \end{array}\right]=G(s) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fd69efff248bd3d7a38c87a6a5d2be09_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.26)\quad \left[\begin{array}{cc|c} A_1 & X_{13} & B_1 \\ 0 & A_3 & 0 \\\hline C_1 & C_3 & 0 \end{array}\right]=G(s) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1abfe9504b1b05046e408992203637e4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.27)\quad \left[\begin{array}{c|c} T^TAT & T^TB \\\hline CT & D \end{array}\right] = \left[\begin{array}{ccccc|c} A_1 & X & \cdots & X & X & B_1 \\ B_2 & A_2 & \cdots & X & X & 0 \\ 0 & \ddots & \ddots & \vdots & \vdots & \vdots \\ \vdots & \ddots & B_{k-1} & A_{k-1} & X & 0 \\ 0 & \cdots & 0 & B_k & A_k & 0 \\\hline X & X & \cdots & X & X & D \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bebfa6a7ec1e3d3439827215b71906b0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.28)\quad \left[\begin{array}{c|c} T^TAT & T^TB \\\hline CT & D \end{array}\right] = \left[\begin{array}{ccccc|c} A_1 & C_2 & \cdots & 0 & 0 & X \\ X & A_2 & \ddots & \vdots & \vdots & \vdots \\ \vdots & \vdots & \ddots & C_{k-1} & 0 & X \\ X & X & \cdots & A_{k-1} & C_k & X \\ X & X & \cdots & X & A_k & X \\\hline C_1 & 0 & \cdots & 0 & 0 & D \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6ceafd83a60c165e75fa6ea4fd8f23d0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ T= \left[\begin{array}{ccc} -0.7071 & 0.5774 & -0.4082 \\ -0.7071 & -0.5774 & 0.4082 \\ 0 & 0.5774 & 0.8165 \end{array}\right], \ m_1=1,\ m_2=1,\ m_3=0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-92e087299ea77ed3a043849cc9d65e7f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c|c} T^TAT & T^TB \\\hline CT & D \end{array}\right] = \left[\begin{array}{ccc|c} -2.0000 & -0.0000 & 1.7321 & -1.4142 \\ -1.2247 & -1.0000 & 2.1213 & 0 \\ 0 & 0 & -1.0000 & 0 \\\hline -0.7071 & 0.5774 & -0.4082 & 0 \\ -0.7071 & 0 & 1.2247 & 0 \\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d9e9c93cf1d7970d3a1ea2722b808e91_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ G(s)= \left[\begin{array}{cc|c} -2.0000 & -0.0000 & -1.4142\\ -1.2247 & -1.0000 & 0\\\hline -0.7071 & 0.5774 & 0\\ -0.7071 & 0 & 0\\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f66d12e6d25d761cc6ef7e5a4317680b_l3.png)
![Rendered by QuickLaTeX.com \left[\begin{array}{cc|c} 0 & 1 & 0 \\ -\frac{12}{L^2} & -\frac{6}{L} & 1 \\\hline 0 & -\frac{12}{L} & 1 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8791b10c9e8d24f0e89ba1c36b7e8e1d_l3.png)
![Rendered by QuickLaTeX.com \frac{s+2}{s^2+3s+2} = \left[\begin{array}{cc|c} -3 & -2 &1 \\ 1 & 0 & 0 \\\hline 1 & 2 & 0 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-02a700ac2acf1e2c1c049368c35a65e4_l3.png) ,
,![Rendered by QuickLaTeX.com G(s)= \left[\begin{array}{ccc|cc} -3 & -2 & 0 & 1 & 0 \\ 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & -2 & 0 & 1\\\hline 1 & 2 & 1& 0 & 0 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-53234bc4586d74cb92e6abe08b23456c_l3.png)
![Rendered by QuickLaTeX.com T= \left[\begin{array}{ccc} -0.4082 & -0.1826 & -0.8944 \\ -0.8165 & -0.3651 & 0.4472 \\ -0.4082 & 0.9129 & 0.0000 \\ \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-13752e35a12134b463334aaadd894e68_l3.png) ,
,![Rendered by QuickLaTeX.com \left[\begin{array}{c|c} T^TAT & T^TB \\\hline CT & D \end{array}\right] = \left[\begin{array}{ccc|cc} -1.1667 & 0.3727 & -0.0000 & -0.4082 & -0.4082 \\ 0.3727 & -1.8333 & -0.0000 & -0.1826 & 0.9129 \\ -2.7386 & -1.2247 & -2.0000 & -0.8944 & 0.0000 \\\hline -2.4495 & 0 & -0.0000 & 0 & 0 \\ \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aeba8d0214bb2b2cf70900ced32e9e6e_l3.png)
![Rendered by QuickLaTeX.com G(s)= \left[\begin{array}{cc|cc} -1.1667 & 0.3727 & -0.4082 & -0.4082 \\ 0.3727 & -1.8333 & -0.1826 & 0.9129 \\\hline -2.4495 & 0 & 0 & 0 \\ \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8aef9bf8d730cb671be66a87e3fdd8f7_l3.png)

![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{c} \dot{\theta}\\ \ddot{\theta} \end{array}\right] }_{\dot \xi} = \underbrace{ \left[\begin{array}{c} \dot{\theta}\\ \frac{3g}{4\ell}\sin\theta \end{array}\right] }_{f(\xi)}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2a78ef4b7d2b88e22f838f474b01b538_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{c} f_1(\xi)\\ f_2(\xi) \end{array}\right] }_{f(\xi)} \simeq \underbrace{\left. \left[\begin{array}{cc} 0 & 1 \\ \frac{\partial f_2}{\partial\theta} & \frac{\partial f_2}{\partial\dot{\theta}} \end{array}\right]\right|_{{\theta=\theta^*}\atop{\dot{\theta}=0\ }} }_{A} \underbrace{ \left[\begin{array}{c} \theta-\theta^*\\ \dot{\theta} \end{array}\right] }_{x=\xi-\xi^*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-40619fb8aefc66df2a9f1690d2b51bed_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ \frac{d}{dt} \left[\begin{array}{c} \theta-\theta^*\\ \dot{\theta} \end{array}\right] }_{\dot x} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ \frac{3g}{4\ell}\cos\theta^* & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \theta-\theta^*\\ \dot{\theta} \end{array}\right] }_{x}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e20bbd8807203333d0f192d00bf9a3ef_l3.png)
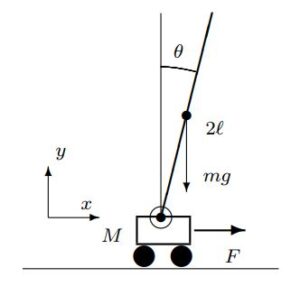
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{cc} M+m & m\ell\cos\theta \\ m\ell\cos\theta & \frac{4}{3}m\ell^2 \end{array}\right] }_{M(\theta)} \underbrace{ \left[\begin{array}{c} \ddot{r}\\ \ddot{\theta} \end{array}\right] }_{\ddot{\xi}_1} + \underbrace{ \left[\begin{array}{cc} 0 & -m\ell\dot{\theta}\sin\theta \\ 0 & 0 \end{array}\right] }_{C(\theta)} \underbrace{ \left[\begin{array}{c} \dot{r}\\ \dot{\theta} \end{array}\right] }_{\dot{\xi}_1}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c3ca9545327d374f12a7a3b48f8bd6d8_l3.png) \\
\\![Rendered by QuickLaTeX.com + \underbrace{ \left[\begin{array}{c} 0 \\ -m\ell g\sin\theta \end{array}\right] }_{G(\theta)} = \underbrace{ \left[\begin{array}{c} F\\ 0 \end{array}\right] }_{\zeta}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dff2f69ef0d1c2deefbae29b72fb58f3_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{c} \dot{\xi}_1\\ \ddot{\xi}_1 \end{array}\right] }_{\dot \xi} = \underbrace{ \left[\begin{array}{c} \dot{\xi}_1\\ -M(\theta)^{-1}(\zeta-C(\theta)\dot{\xi}_1-G(\theta)) \end{array}\right] }_{f(\xi,\zeta)}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f427ac559f4a9bf3589bed5bf3b87104_l3.png)
![Rendered by QuickLaTeX.com \xi^* =\left[\begin{array}{c} 0 \\ \theta^* \\ 0 \\ 0 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-494e62c3407794d38dafa6f7008aea42_l3.png) (
(![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{c} \dot{r}\\ \dot{\theta}\\ f_3(r,\theta,\dot{r},\dot{\theta})\\ f_4(r,\theta,\dot{r},\dot{\theta})\\ \end{array}\right] }_{f(\xi,\zeta)} \simeq \underbrace{\left. \left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ \frac{\partial f_3}{\partial r} & \frac{\partial f_3}{\partial\theta} & \frac{\partial f_3}{\partial\dot{r}} & \frac{\partial f_3}{\partial\dot{\theta}} \\ \frac{\partial f_4}{\partial r} & \frac{\partial f_4}{\partial\theta} & \frac{\partial f_4}{\partial\dot{r}} & \frac{\partial f_4}{\partial\dot{\theta}} \end{array}\right] \right|_{{{{{r=0}\atop{\theta=\theta^*}}\atop{\dot{r}=0}}\atop{\dot{\theta}=0}}\atop{F^*=0}} }_{A} \underbrace{ \left[\begin{array}{c} r \\ \theta-\theta^* \\ \dot{r} \\ \dot{\theta} \end{array}\right] }_{x=\xi-\xi^*}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-28af87870eb0ee575637ef26ea72751e_l3.png)
![Rendered by QuickLaTeX.com + \underbrace{\left. \left[\begin{array}{c} 0 \\ 0 \\ \frac{\partial f_3}{\partial F} \\ \frac{\partial f_4}{\partial F} \end{array}\right] \right|_{{{{{r=0}\atop{\theta=\theta^*}}\atop{\dot{r}=0}}\atop{\dot{\theta}=0}}\atop{F^*=0}} }_{B} \underbrace{ F }_{u}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c6c66c6fa11494395e52f2856f245118_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ \frac{d}{dt} \left[\begin{array}{c} r \\ \theta \\ \dot{r} \\ \dot{\theta} \end{array}\right] }_{\dot x} = \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & -\frac{3mg}{4M+m} & 0 & 0 \\ 0 & \frac{3(M+m)g}{(4M+m)\ell} & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} r \\ \theta \\ \dot{r} \\ \dot{\theta} \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{cccc} 0 \\ 0 \\ \frac{4}{4M+m} \\ -\frac{3}{(4M+m)\ell} \\ \end{array}\right] }_{B} \underbrace{ F }_{u}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ba8959ac6db881665315c9c4984ce39d_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ \frac{d}{dt} \left[\begin{array}{c} r \\ \theta-\pi \\ \dot{r} \\ \dot{\theta} \end{array}\right] }_{\dot x} = \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & -\frac{3mg}{4M+m} & 0 & 0 \\ 0 & -\frac{3(M+m)g}{(4M+m)\ell} & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} r \\ \theta-\pi \\ \dot{r} \\ \dot{\theta} \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{cccc} 0 \\ 0 \\ \frac{4}{4M+m} \\ \frac{3}{(4M+m)\ell} \\ \end{array}\right] }_{B} \underbrace{ F }_{u}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-55c9a98a3b25a90144337fc86d41c888_l3.png) \\
\\
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{c} r \\ \theta \end{array}\right] }_{y_M} = \underbrace{ \left[\begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{array}\right] }_{C_M} \underbrace{ \left[\begin{array}{c} r \\ \theta \\ \dot{r} \\ \dot{\theta} \end{array}\right] }_{x}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6baa8fc6b84d2586dd49b58ef433c5fe_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ r }_{z} = \underbrace{ \left[\begin{array}{cccc} 1 & 0 \end{array}\right] }_{C_S} \underbrace{ \left[\begin{array}{c} r \\ \theta \end{array}\right] }_{y_M} = \underbrace{ \left[\begin{array}{cccc} 1 & 0 & 0 & 0 \end{array}\right] }_{C=C_SC_M} \underbrace{ \left[\begin{array}{c} r \\ \theta \\ \dot{r} \\ \dot{\theta} \end{array}\right] }_{x}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-05c56d73b83531ae91ffbf08372ccd6a_l3.png)
![Rendered by QuickLaTeX.com S=\left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] = \left[\begin{array}{cccc:c} 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & -\frac{3mg}{4M+m} & 0 & 0 & \frac{3}{4M+m}\\ 0 & \frac{3(M+m)g}{(4M+m)\ell} & 0 & 0 & -\frac{3}{(4M+m)\ell} \\ \hdashline 1 & 0 & 0 & 0 & 0 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-23f8500a01f8e1021ee1d64e187eff87_l3.png)
![Rendered by QuickLaTeX.com \left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right] = \left[\begin{array}{c} r_\infty \\ \theta_\infty \\ \dot{r}_\infty \\ \dot{\theta}_\infty \\\hdashline u_\infty \end{array}\right] =S^{-1} \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \\\hdashline r^* \end{array}\right] = \left[\begin{array}{c} r^* \\ 0 \\ 0 \\ 0 \\\hdashline 0 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-964e005b0fd9999c976a917896e43759_l3.png)
![Rendered by QuickLaTeX.com \frac{d}{dt} \underbrace{ \left[\begin{array}{c} x-x_\infty \\ u-u_\infty \end{array}\right] }_{x_{E3}} = \underbrace{ \left[\begin{array}{cccc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x-x_\infty \\ u-u_\infty \end{array}\right] }_{x_{E3}} + \underbrace{ \left[\begin{array}{cccc} 0 \\ 1 \\ \end{array}\right] }_{B_{E3}} \dot{u}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f23734294bd218f2bca348f310c80f7b_l3.png)
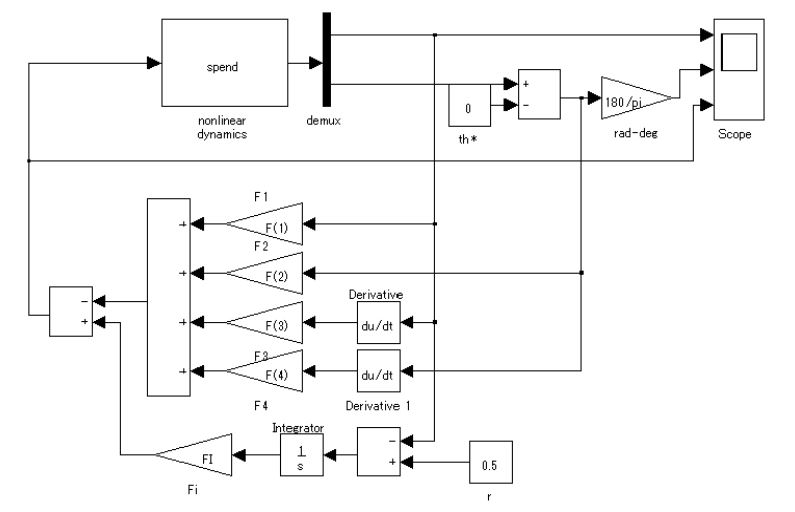

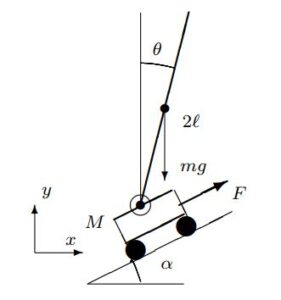
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{cc} M+m & m\ell\cos(\theta+\alpha) \\ m\ell\cos(\theta+\alpha) & \frac{4}{3}m\ell^2 \end{array}\right] }_{M(\theta)} \underbrace{ \left[\begin{array}{c} \ddot{r}\\ \ddot{\theta} \end{array}\right] }_{\ddot{\xi}_1} + \underbrace{ \left[\begin{array}{cc} 0 & -m\ell\dot{\theta}\sin(\theta+\alpha) \\ 0 & 0 \end{array}\right] }_{C(\theta)} \underbrace{ \left[\begin{array}{c} \dot{r}\\ \dot{\theta} \end{array}\right] }_{\dot{\xi}_1}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b6922d7711b2f0f96db4501e90739345_l3.png)
![Rendered by QuickLaTeX.com + \underbrace{ \left[\begin{array}{c} 0 \\ -m\ell g\sin\theta \end{array}\right] }_{G(\theta)} = \underbrace{ \left[\begin{array}{c} F-(M+m)g\sin\alpha\\ 0 \end{array}\right] }_{\zeta}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d1078acd06df1fb0cd7feb9d9fffcb18_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ \frac{d}{dt} \left[\begin{array}{c} r \\ \theta \\ \dot{r} \\ \dot{\theta} \end{array}\right] }_{\dot x} = \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & -\frac{6mg\cos\alpha}{8M+(5-3\cos2\alpha)m} & 0 & 0 \\ 0 & \frac{6(M+m)g}{(8M+(5-3\cos2\alpha)m)\ell} & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} r \\ \theta \\ \dot{r} \\ \dot{\theta} \end{array}\right] }_{x}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-92877f60035f32a0435dbc3738e4be0d_l3.png) \\
\\![Rendered by QuickLaTeX.com + \underbrace{ \left[\begin{array}{cccc} 0 \\ 0 \\ \frac{8}{8M+(5-3\cos2\alpha)m} \\ -\frac{6\cos\alpha}{(8M+(5-3\cos2\alpha)m)\ell} \\ \end{array}\right] }_{B} \underbrace{ (F-(M+m)g\sin\alpha) }_{u}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-62f774fb9a1f073d682e3fbb5ca13050_l3.png)
 図6.1 外乱入力をもつ1次系
図6.1 外乱入力をもつ1次系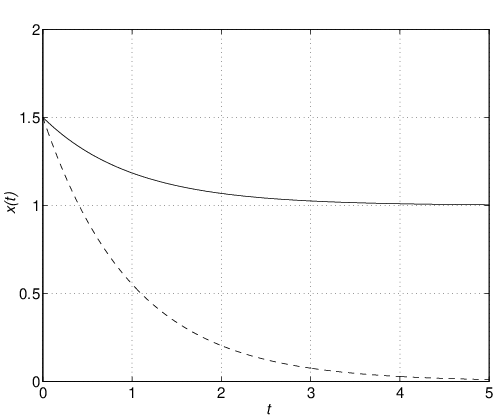
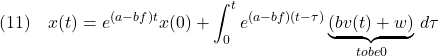
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \underbrace{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] }_{\dot{x}_E(t)} = %\underbrace{ \left[\begin{array}{cc} a & 0 \\ 1 & 0 \end{array}\right] %}_{A_E} \underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] }_{x_E(t)} + %\underbrace{ \left[\begin{array}{c} b \\ 0 \end{array}\right] %}_{B_E} u(t) + \underbrace{ \left[\begin{array}{c} w \\ 0 \end{array}\right] }_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ed7888e66cf423a299c78119493e2a8f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad u(t)=-fx(t) %\underbrace{ -f_Ix_I(t) %}_{+v(t)} =- \underbrace{ \left[\begin{array}{cc} f & f_I \end{array}\right] }_{F_E} \underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] }_{x_E(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5541d2dd02a7b6ebe166310f4c922b7f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \underbrace{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] }_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf_I \\ 1 & 0 \end{array}\right] }_{A_{EF}} \underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] }_{x_E(t)} + \underbrace{ \left[\begin{array}{c} w \\ 0 \end{array}\right] }_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9ce54a9bb373b31ef22c017c0033d328_l3.png)

![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] \ \rightarrow\ \left[\begin{array}{c} 0 \\ \displaystyle{\frac{w}{bf_I}} \end{array}\right] \quad (t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-730cb6e0547a706ae11a604fcf3f76b4_l3.png)
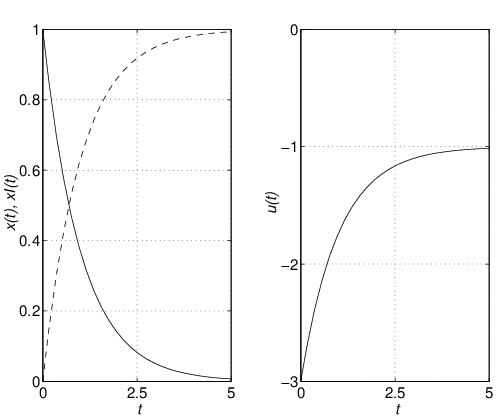

![Rendered by QuickLaTeX.com \displaystyle{(31)\quad %\underbrace{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] %}_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} a-bf & -bf_I \\ 1 & 0 \end{array}\right] }_{A_{EF}} %\underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] %}_{x_E(t)} + %\underbrace{ \left[\begin{array}{c} w \\ -r \end{array}\right] %}_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-107de515677af73c8cfa3d74309054d6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(32)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] \ \rightarrow\ \underbrace{ \displaystyle{\frac{1}{bf_I}} \left[\begin{array}{cc} 0 & bf_I \\ -1 & a-bf \end{array}\right] }_{A_{EF}^{-1}} \left[\begin{array}{c} -w \\ r \end{array}\right] \quad (t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d1efa2ea9c0128df30789fc39ea551f4_l3.png)
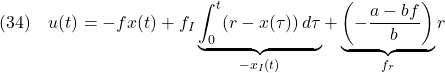
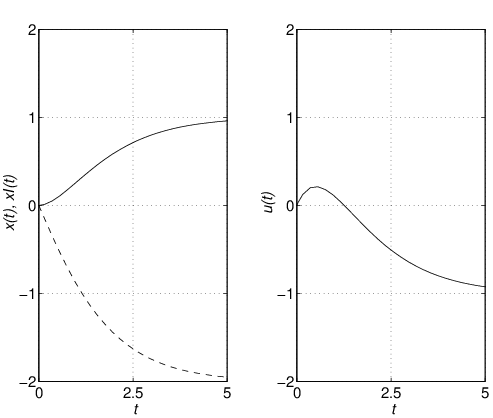
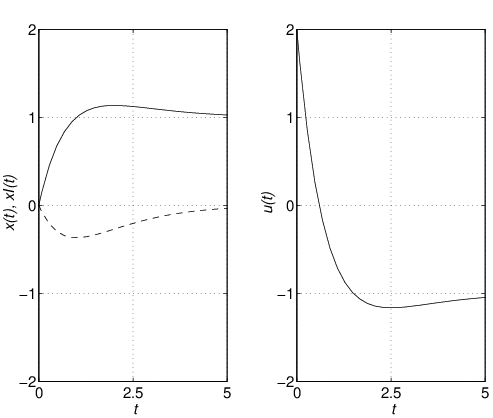
![Rendered by QuickLaTeX.com \displaystyle{(41)\quad {\rm rank}\, \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S}=n+m }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6d7d661fc9e59a3b704afda235a27be2_l3.png)
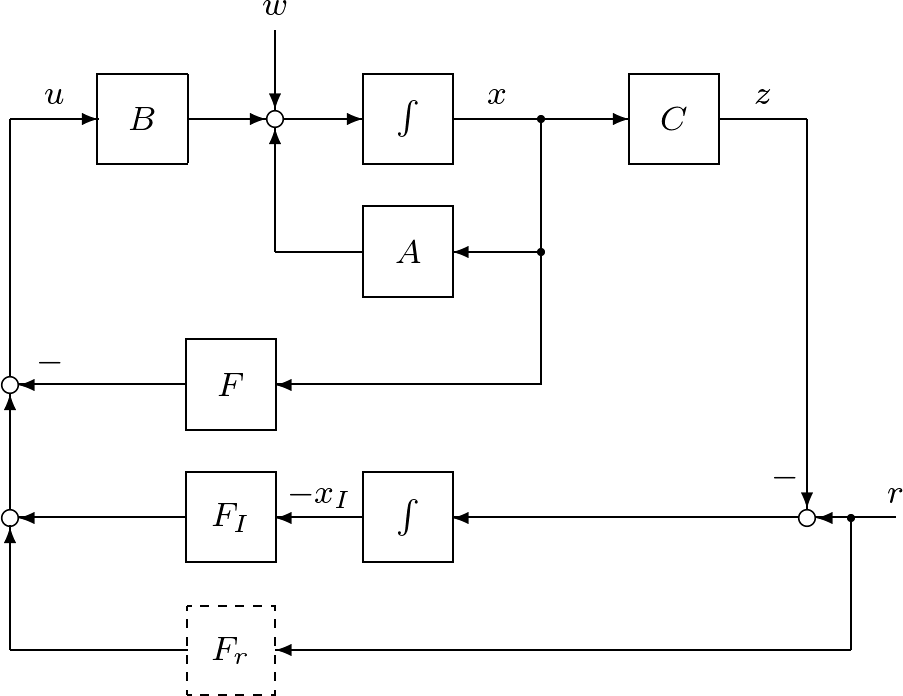
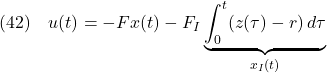
![Rendered by QuickLaTeX.com \displaystyle{(46)\quad %\underbrace{ \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \end{array}\right] %}_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} A-BF & -BF_I \\ C & 0 \end{array}\right] }_{A_{EF}} %\underbrace{ \left[\begin{array}{c} x(t) \\ x_I(t) \end{array}\right] %}_{x_E(t)} + %\underbrace{ \left[\begin{array}{c} w \\ -r \end{array}\right] %}_{w_E} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eae149cb8e48771ddf2829382730be8f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(47)\quad A_{EF} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} - \left[\begin{array}{cc} B \\ 0 \end{array}\right] \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bdd5074b66a5f1df70acdb96f25154a5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(48)\quad \begin{array}{ll} A_{EF}^{-1} =& S^{-1}+ S^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] \left(I_m- \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] S^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] \right)^{-1} \\[5mm] &\times \left[\begin{array}{cc} F & F_I+I_m \end{array}\right] S^{-1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9d2c5a73b40a6bad18b71d793037dc0d_l3.png)
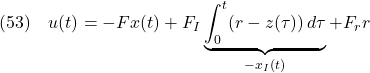
![Rendered by QuickLaTeX.com \displaystyle{(58)\quad \begin{array}{rl} \left[\begin{array}{c} \dot{\hat{x}}(t) \\ \dot{x}_I(t) \end{array}\right] =& \underbrace{ \left[\begin{array}{cc} A-HC_M-BF & -BF_I \\ 0(m\times n) & 0(m\times m) \end{array}\right] }_{A_K} \left[\begin{array}{c} \hat{x}(t) \\ x_I(t) \end{array}\right]\\[10mm] &+ \underbrace{ \left[\begin{array}{cc} H & 0(n\times m)\\ C_S & -I_m \end{array}\right] }_{B_K} \left[\begin{array}{c} y(t) \\ r \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0674921b2ea4d9a7a9554aeb4e94375f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(59)\quad u(t)= \underbrace{- \left[\begin{array}{cc} F & F_I \end{array}\right] }_{C_K} \left[\begin{array}{c} \hat{x}(t) \\ x_I(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1eaa990f79c14f18c22d28baecc3287b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(61)\quad \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \\ \dot{\hat{x}}(t) \end{array}\right] = \left[\begin{array}{ccc} A & -BF_I & -BF \\ C & 0 & 0 \\ HC_M & -BF_I & A-HC_M-BF \end{array}\right] \left[\begin{array}{c} x(t) \\ x_I(t) \\ \hat{x}(t) \end{array}\right] + \left[\begin{array}{c} w \\ -r \\ 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5628b37e548005d81b699f0317cfbcd2_l3.png)
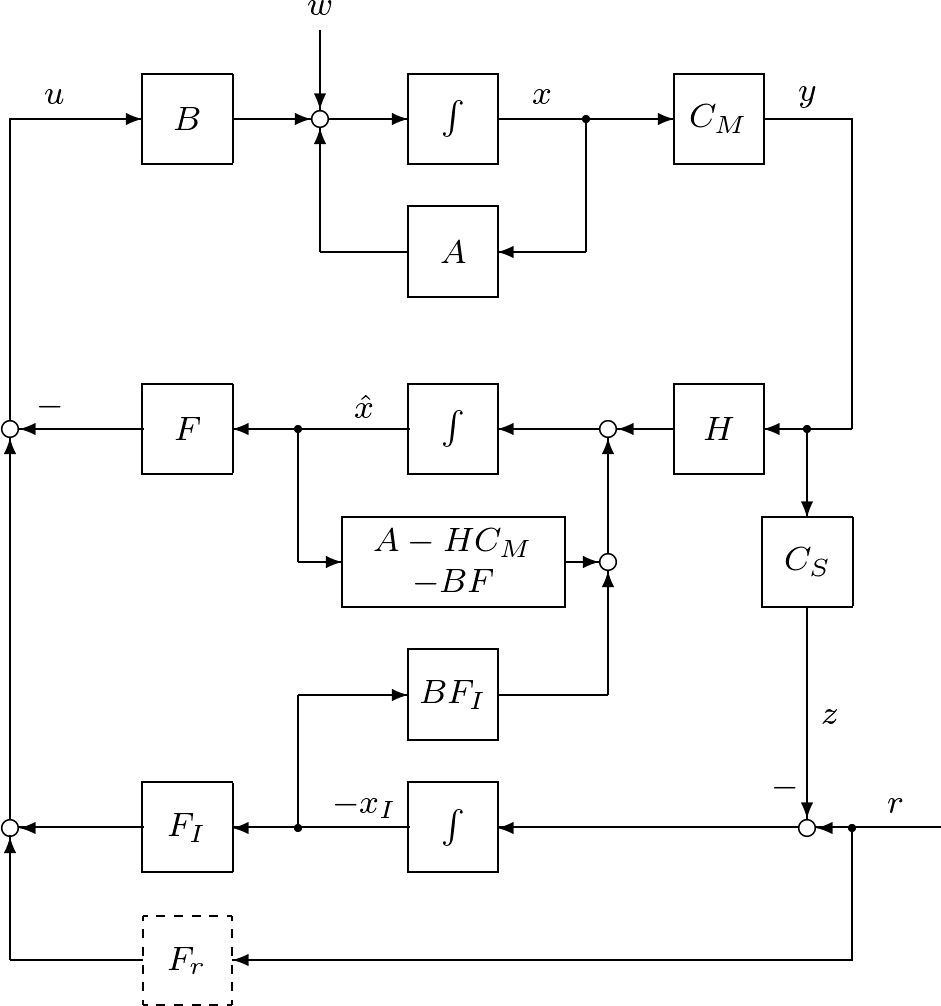
![Rendered by QuickLaTeX.com \displaystyle{(62)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \\ e(t) \end{array}\right] = \left[\begin{array}{ccc} I_n & 0 & 0 \\ 0 & I_m & 0 \\ -I_n & 0 & I_n \end{array}\right] \left[\begin{array}{c} x(t) \\ x_I(t) \\ \hat{x}(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-398042fbd4912104fef837986adc51a1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(63)\quad \left[\begin{array}{c} \dot{x}(t) \\ \dot{x}_I(t) \\\hline \dot{e}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc|c} A-BF & -BF_I & -BF \\ C & 0 & 0 \\\hline 0 & 0 & A-HC_M \end{array}\right] }_{ A_{EF}'= \left[\begin{array}{c|c} A_{EF} & - \left[\begin{array}{cc} B \\ 0 \end{array}\right] F \\[5mm] \hline 0 & \widehat{A} \end{array}\right] } \left[\begin{array}{c} x(t) \\ x_I(t) \\\hline e(t) \end{array}\right] + \left[\begin{array}{c} w \\ -r \\\hline -w \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b776ef380292f9c7b97e082e1356466d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(64)\quad \left[\begin{array}{c} x(t) \\ x_I(t) \\\hline e(t) \end{array}\right] \ \rightarrow\ \underbrace{ \left[\begin{array}{c|c} A_{EF}^{-1} & -A_{EF}^{-1} \left[\begin{array}{cc} B \\ 0 \end{array}\right] F\widehat{A}^{-1} \\[5mm]\hline 0 & \widehat{A}^{-1} \end{array}\right] }_{A_{EF}'\,^{-1}} \left[\begin{array}{c} -w \\ r \\\hline w \end{array}\right] \quad (t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3d3d576874ceeaf93880948df0adb803_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(69)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] %}_{x_E(t)-x_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E1}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] %}_{x_E(t)-x_{E\infty}} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E1}} (u(t)-u_\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f6e3bc338005f728c3c6b147eb039e9e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(70)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] %}_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} %\underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] %}_{\dot{x}_E(t)} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-966078beee574786867caed4fcd2d943_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(71)\quad \left[\begin{array}{c} {\dot x}(t)-w \\ z(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1426f7e0895fd79de17dc34732b3e43c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(72)\quad \left[\begin{array}{c} {\dot x}(t) \\ z(t)-r \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c1612c9c215faae7214a621c77652b77_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(73)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-61e355172bd112774aad674a10e1d6b1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(74)\quad \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-47811d4d699fd4de1d937f73c0245ddb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(75)\quad \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-46729c351e496ba40060fc93a706a112_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(76)\quad \underbrace{ \left[\begin{array}{cc} 0 & I_m \end{array}\right] }_{C_{E2}} \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S} = \underbrace{ \left[\begin{array}{cc} C & 0 \end{array}\right] }_{C_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4ea560477a3448b751379c9a95240132_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(78)\quad \frac{d}{dt} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E}} %\underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] %}_{{\tilde x}_E(t)-{\tilde x}_{E\infty}} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-40c26e612ca99e6fd4cd79c47fb7d193_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(80)\quad \int_0^\infty \left( \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right]^T Q_E \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] +{\dot u}^T(t)R_E{\dot u}(t)\right)\,dt }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-91e30617eef32873dec337f41b4b0942_l3.png)
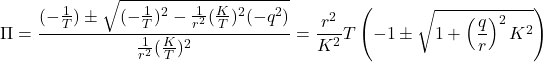
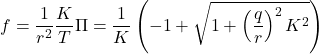
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{l} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right] + \left[\begin{array}{cc} 0 & 0 \\ 1 & 0 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ - \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{c} 0 \\ 1 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] + \left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right]\\ = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c0fe9f8513553f489bdfd16b398f4af9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] %}_{\dot{x}(t)} = %\underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -2\zeta\omega_n \end{array}\right] %}_{A} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] + %\underbrace{ \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] %}_{B} \\ y(t)= %\underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] %}_{C} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1fce5372a6e13e3b5578a08abeba594c_l3.png)
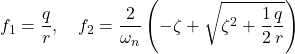
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{l} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ 0 & -2\zeta\omega_n \end{array}\right] + \left[\begin{array}{cc} 0 & 0 \\ 1 & -2\zeta\omega_n \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]\\ - \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] r^{-2} \left[\begin{array}{cc} 0 & \omega_n^2 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] + \left[\begin{array}{c} 1 \\ 0 \end{array}\right] q^{2} \left[\begin{array}{cc} 1 & 0 \end{array}\right]\\ % \left[\begin{array}{cc} % q_1^2 & 0 \\ % 0 & q_2^2 % \end{array}\right] = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-276692b36c29cb26f7eb5ce869645673_l3.png)
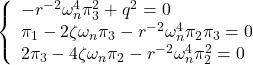
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{l} \left[\begin{array}{cc} f_1 & f_2 \end{array}\right]=r^{-2} \left[\begin{array}{cc} 0 & \omega_n^2 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]=r^{-2}\omega_n^2 \left[\begin{array}{cc} \pi_3 & \pi_2 \end{array}\right]\\ = \left[\begin{array}{cc} \frac{q}{r} & \frac{2}{\omega_n}\left(-\zeta+\sqrt{\zeta^2+\frac{1}{2}\frac{q}{r}}\right) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c3d6734e1d1303cee73bacf9ffc4267f_l3.png)
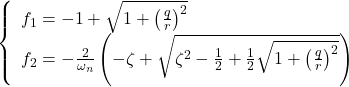
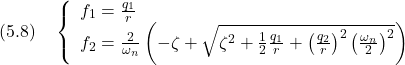
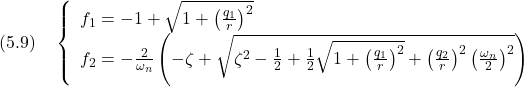
![Rendered by QuickLaTeX.com \displaystyle{(5.10)\quad \underbrace{ \left[\begin{array}{cc} A & -BR^{-1}B^T \\ -C^TQC & -A^T \end{array}\right]}_{M(2n\times 2n)} \underbrace{ \left[\begin{array}{c} V_1 \\ V_2 \end{array}\right]}_{V^-(2n\times n)} = \underbrace{ \left[\begin{array}{c} V_1 \\ V_2 \end{array}\right]}_{V^-(2n\times n)} \underbrace{ {\rm diag}\{\lambda_1,\cdots,\lambda_n\} }_{\Lambda^-(n\times n)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-835801247f79b1b7c7493fad4e900dbd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\ \dot{x}_3(t) \end{array}\right] %}_{\dot{x}(t)} = \left[\begin{array}{cccc} 0 & 1 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & -1 \end{array}\right] %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \\ x_3(t) \end{array}\right] %}_{x(t)} + \left[\begin{array}{cc} 0 & 0 \\ 1 & -1 \\ 0 & 1 \\ \end{array}\right] \left[\begin{array}{c} u_1(t) \\ u_2(t) \end{array}\right] \\ \left[\begin{array}{c} y_1(t) \\ y_2(t) \end{array}\right] = \left[\begin{array}{cccc} 1 & 0 & 0 \\ 0 & 0 & 1 \\ \end{array}\right] %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \\ x_3(t) \end{array}\right] %}_{x(t)} \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dae10affe1e50a41b97b2aaeb226a5bd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\ \dot{x}_3(t) \\ \dot{x}_4(t) \end{array}\right] %}_{\dot{x}(t)} = \left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -1 & 1 & 0 & 0 \\ 1 & -1 & 0 & 0 \end{array}\right] %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \\ x_3(t) \\ x_4(t) \end{array}\right] %}_{x(t)} + \left[\begin{array}{c} 0 \\ 0 \\ 1 \\ 0 \end{array}\right] u(t) \\ y(t) = \left[\begin{array}{cccc} 0 & 1 & 0 & 0 \end{array}\right] %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \\ x_3(t) \\ x_4(t) \end{array}\right] %}_{x(t)} \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4e0489ca273b85f434222050e1404718_l3.png)
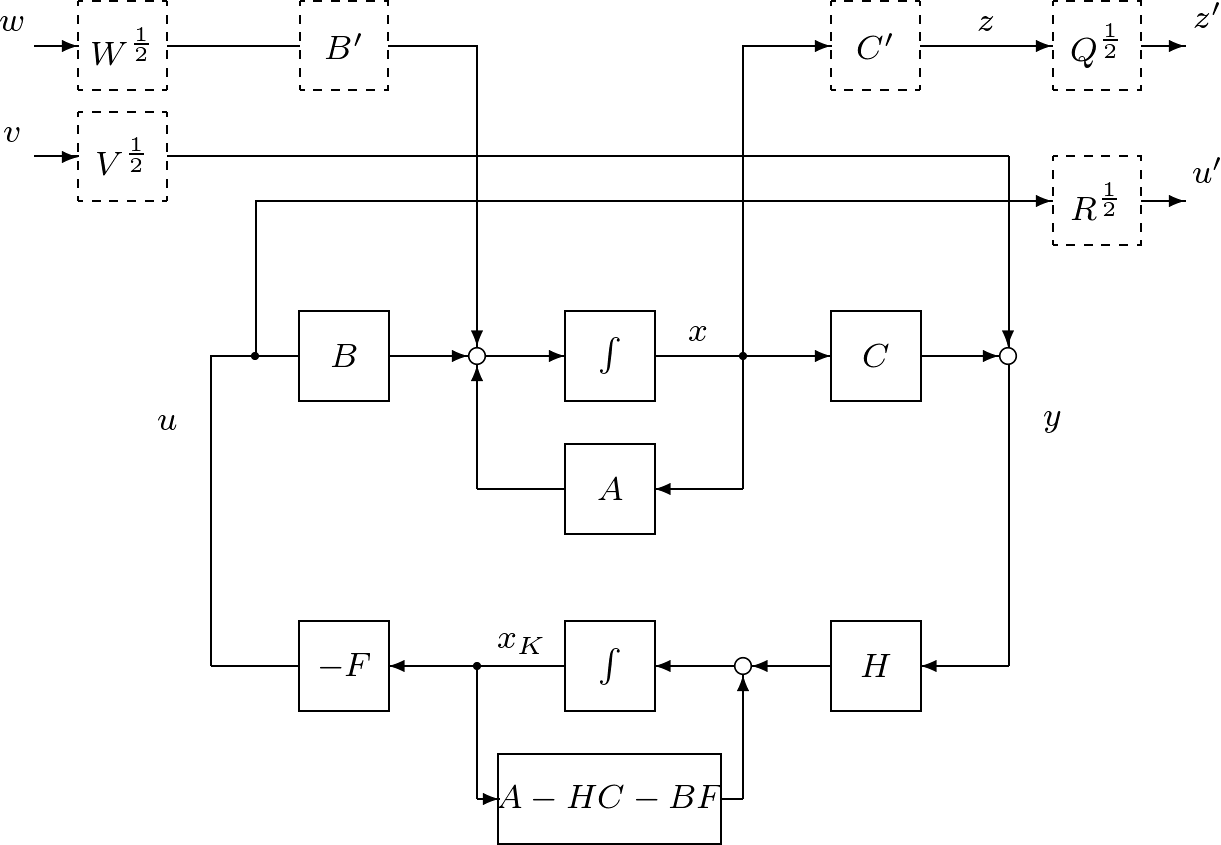
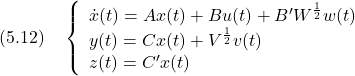
![Rendered by QuickLaTeX.com \displaystyle{(5.14)\quad \left\{\begin{array}{rcl} \left[\begin{array}{cc} \dot{x}(t) \\ \dot{\hat{x}}(t) \end{array}\right]&=& \underbrace{ \left[\begin{array}{cc} A & -BF \\ HC&A-HC-BF \end{array}\right] }_{A_{CL}} \left[\begin{array}{cc} {x}(t) \\ \hat{x}(t) \end{array}\right] \\ &&+ \underbrace{ \left[\begin{array}{cc} B'W^{\frac{1}{2}} & 0 \\ 0 & HV^{\frac{1}{2}} \end{array}\right] }_{B_{CL}} \left[\begin{array}{cc} {w}(t) \\ {v}(t) \end{array}\right] \\ \left[\begin{array}{cc} {z'}(t) \\ {u'}(t) \end{array}\right] &=& \underbrace{ \left[\begin{array}{cc} Q^{\frac{1}{2}}C' & 0 \\ 0 & -R^{\frac{1}{2}}F \end{array}\right] }_{C_{CL}} \left[\begin{array}{cc} {x}(t) \\ \hat{x}(t) \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1b91a2937df2ee79c45fd36c4cd78be7_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{ll} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ 0 & -1 \end{array}\right] + \left[\begin{array}{cc} 0 & 0 \\ 1 & -1 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]- \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \\ \times \left[\begin{array}{c} 0 \\ 1 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] + \left[\begin{array}{c} 1 \\ 0 \end{array}\right] \left[\begin{array}{cc} 1 & 0 \end{array}\right] = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-77abcc710f7d176292ed41df61fb44dd_l3.png)
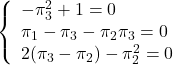
![Rendered by QuickLaTeX.com \begin{array}{ll} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array}\right] + \left[\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right]- \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \\ \times \left[\begin{array}{c} 0 \\ 1 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] + \left[\begin{array}{c} 1 \\ 0 \end{array}\right] \left[\begin{array}{cc} 1 & 0 \end{array}\right] = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c3be713e989b828432150c9bf7d0a7fe_l3.png)
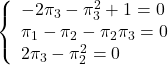
![Rendered by QuickLaTeX.com \begin{array}{ll} \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] + \left[\begin{array}{cc} 0 & -\omega_n^2 \\ 1 & -2\zeta\omega_n \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] - \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] \\ \times \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] r^{-2} \left[\begin{array}{cc} 0 & \omega_n^2 \end{array}\right] \left[\begin{array}{cc} \pi_1 & \pi_3 \\ \pi_3 & \pi_2 \end{array}\right] + \left[\begin{array}{c} 1 \\ 0 \end{array}\right] q^2 \left[\begin{array}{cc} 1 & 0 \end{array}\right] = \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \end{array}\right] \end{array}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e4281eae5d3310b57d2a3cdb66eb7865_l3.png)
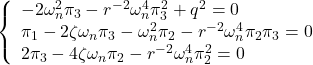
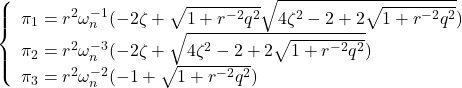
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\ \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{x(t)}+ \underbrace{ \left[\begin{array}{cc} 0 \\ 1 \end{array}\right] }_{B} u(t)\\ y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{x(t)} \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b4716f40d1006ce97470291edbcab935_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ {\rm det}(\lambda I_2-A)= {\rm det}\left[\begin{array}{cc} \lambda & -1 \\ 0 & \lambda \end{array}\right] =\lambda^2+\underbrace{0}_{a_1}\lambda+\underbrace{0}_{a_2} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4a8163de84bd0261dff1fa933592b34c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\ \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{x(t)}+ \underbrace{ \left[\begin{array}{cc} 0 \\ 1 \end{array}\right] }_{B} u(t)\\ y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 1 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{x(t)} \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cb616bd20ad3679652dda6f9def23eb8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{x}(t)\\ \dot{\hat{x}}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} a & -bf \\ hc & a-hc-bf \end{array}\right] }_{A_F} \left[\begin{array}{c} {x}(t)\\ {\hat{x}}(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7399b50c26a8ee8f72f43f1c373710a1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{lll} &&{\rm det}(\lambda I_2-A_F) ={\rm det} \left[\begin{array}{cc} \lambda-a & bf \\ -hc & \lambda-a+hc+bf \end{array}\right]\\ &&=(\lambda-a)(\lambda-a+hc+bf)+bfhc\\ &&=\lambda^2-(a-bf+a-hc)\lambda+(a-bf)(a-hc)\\ &&=(\lambda-(a-bf))(\lambda-(a-hc))=0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-773a683e5ed9d01a0b5fb9fed4d9fa15_l3.png)
![Rendered by QuickLaTeX.com {\rm rank}\, \underbrace{ \left[\begin{array}{c} C \\ CA \\ \vdots\\ CA^{n-1} \end{array}\right] }_{observability\ matrix} =n](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6253173de124e69f731cff9f00238073_l3.png)
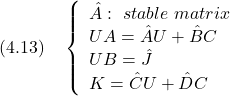
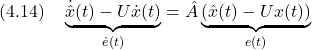
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{y}(t) \\ \ddot{y}(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & I_p \\ A_{21} & A_{22} \end{array}\right] }_A \underbrace{ \left[\begin{array}{c} y(t) \\ \dot{y}(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} 0 \\ B_2 \end{array}\right] }_B u(t) \\ y(t)= \underbrace{ \left[\begin{array}{cc} I_p & 0 \end{array}\right] }_C \underbrace{ \left[\begin{array}{c} y(t) \\ \dot{y}(t) \end{array}\right] }_{x(t)} \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dd502a7f8d2f5cdb3309be9babf3c735_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \dot{\hat{x}}(t)= \underbrace{(A_{22}-L)}_{\hat{A}}\hat{x}(t) +\underbrace{(A_{21}+(A_{22}-L)L)}_{\hat{B}}y(t) +\underbrace{B_{2}}_{\hat{J}}u(t)\\ z(t)= \underbrace{ \left[\begin{array}{c} 0 \\ I_p \end{array}\right] }_{\hat{C}} \hat{x}(t) + \underbrace{ \left[\begin{array}{c} I_p \\ L \end{array}\right] }_{\hat{D}} y(t) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d2e714a3407b24c35a02e8bde698f9a0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{cc} A_{21} & A_{22}-L \\ I_p & 0\\ 0 & I_p \end{array}\right] }_{ \left[\begin{array}{cc} UA \\ I_{2p} \end{array}\right]} = \underbrace{ \left[\begin{array}{cc} A_{22}-L & A_{21}+(A_{22}-L)L\\ 0 & I_p\\ I_p & L \end{array}\right] }_{ \left[\begin{array}{cc} \hat{A} & \hat{B} \\ \hat{C} & \hat{D} \end{array}\right]} \underbrace{ \left[\begin{array}{cc} -L & I_p \\ I_p & 0 \end{array}\right] }_{ \left[\begin{array}{cc} U \\ C \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4437dc03385f40f22d80730c9970d4e5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ u(t)= \underbrace{ \left[\begin{array}{cc} K_1 & K_2 \end{array}\right] }_K \underbrace{ \left[\begin{array}{c} y(t) \\ \dot{y}(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-38415ee373992f2396ca53180700b8cb_l3.png)
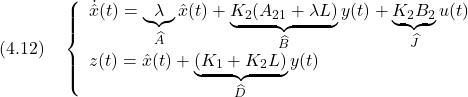
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{cc} K_2A_{21} & K_2(A_{22}-L) \\ K_1 & K_2 \end{array}\right] }_{ \left[\begin{array}{cc} UA \\ K \end{array}\right]} = \underbrace{ \left[\begin{array}{cc} \lambda & K_2(A_{21}+\lambda L) \\ 1 & K_1+K_2L \end{array}\right] }_{ \left[\begin{array}{cc} \hat{A} & \hat{B} \\ \hat{C} & \hat{D} \end{array}\right]} \underbrace{ \left[\begin{array}{cc} -K_2L & K_2 \\ I_p & 0 \end{array}\right] }_{ \left[\begin{array}{cc} U \\ C \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-af379103f3c6d8408714f762d43eaae9_l3.png)
![Rendered by QuickLaTeX.com {\rm det}(\lambda I_2-A)= {\rm det}\left[\begin{array}{cc} \lambda & -1 \\ 0 & \lambda \end{array}\right] =\lambda^2+\underbrace{0}_{a_1}\lambda+\underbrace{0}_{a_2}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-683fa53a06a69cdf8560c0f6dd23d977_l3.png)
![Rendered by QuickLaTeX.com {\rm rank}\, \left[\begin{array}{c} C \\ A-\lambda_i I_2 \end{array}\right]= {\rm rank} \left[\begin{array}{ccc} 1 & 0 \\ 0 & 1 \\ 0 & 0 \end{array}\right]= 2\ \ (i=1,2)](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-30cd66cd7df59213c8b0268c2be8051e_l3.png)
![Rendered by QuickLaTeX.com {\rm rank}\, \left[\begin{array}{c} C \\ A-\lambda_i I_2 \end{array}\right]= {\rm rank} \left[\begin{array}{ccc} 0 & 1 \\ 0 & 1 \\ 0 & 0 \end{array}\right]= 1\ \ (i=1,2)](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3ebec8ef15f1eec0c91cca84d38ca025_l3.png)
![Rendered by QuickLaTeX.com {\rm rank}\, \left[\begin{array}{c} C \\ A-\lambda_1 I_2 \end{array}\right]= {\rm rank} \left[\begin{array}{ccc} 1 & 1 \\ 0 & 1 \\ 0 & -1 \end{array}\right]= 2](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eeba5efd60e4377e2987397eae0f3d4a_l3.png)
![Rendered by QuickLaTeX.com {\rm rank}\, \left[\begin{array}{c} C \\ A-\lambda_2 I_2 \end{array}\right]= {\rm rank} \left[\begin{array}{ccc} 1 & 1 \\ -1 & 1 \\ 0 & 0 \end{array}\right]= 1](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-062a4b6b19aa5147e9e189c402950ecf_l3.png)
![Rendered by QuickLaTeX.com \left\{\begin{array}{l} \dot{\hat{x}}(t)= \underbrace{-L}_{A_{22}-L} \hat{x}(t) \underbrace{-L^2}_{A_{21}+(A_{22}-L)L} y(t)+ \underbrace{1}_{B_{2}} u(t)\\ z(t)= \left[\begin{array}{c} 0 \\ 1 \end{array}\right] \hat{x}(t) + \left[\begin{array}{c} 1 \\ L \end{array}\right] y(t) \end{array}\right.](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d477eebdabe870a1925aa162c9c0ac2f_l3.png)
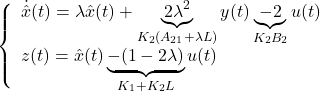
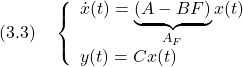
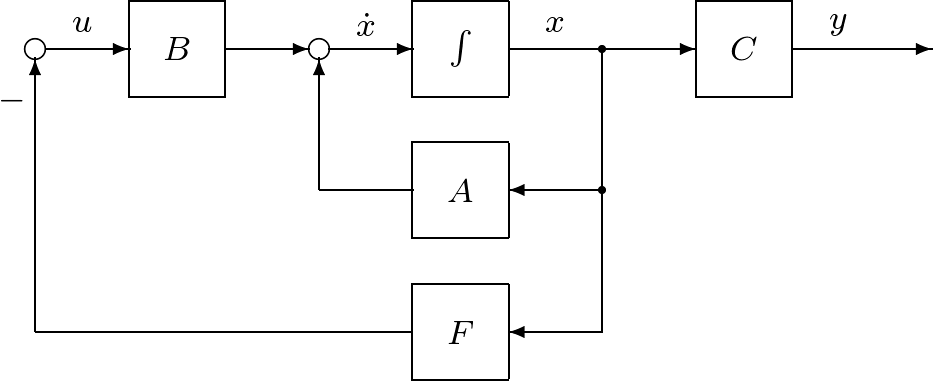
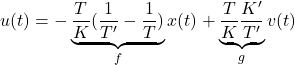
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] }_{\dot x} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5932569bcea6f83e90d462d598332ff4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ u(t)=- \underbrace{ \left[\begin{array}{cc} \frac{1}{\omega_n^2}(\omega_n'\,^2-\omega_n^2) & \frac{2}{\omega_n^2}(\zeta'\omega_n'-\zeta\omega_n) \end{array}\right] }_{F} \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] +\underbrace{\frac{\omega_n'\,^2}{\omega_n^2}}_Gv(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-265415e99e8b4aed32c5f7a8ce5fbc90_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{lll} &&A-BF= \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] - \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right]\\ && \times \left[\begin{array}{cc} \frac{1}{\omega_n^2}(\omega_n'\,^2-\omega_n^2) & \frac{2}{\omega_n^2}(\zeta'\omega_n'-\zeta\omega_n) \end{array}\right] =\left[\begin{array}{cc} 0 & 1 \\ -\omega_n'\,^2 & -2\zeta'\omega_n' \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f0d26f2790cc8788d788deb679fa2869_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3.8)\quad \begin{array}{lll} F&=&\left[\begin{array}{cccc} a_n'-a_n & \cdots & a_2'-a_2 & a_1'-a_1 \end{array}\right] \nonumber\\ &\times& \left[\begin{array}{ccccc} a_{n-1} & a_{n-2} & \cdots & a_1 & 1 \\ a_{n-2} & a_{n-3} & \cdots & 1 & 0 \\ \vdots & \vdots & \cdots & \vdots & \vdots \\ a_2 & a_1 & \cdots & 0 & 0 \\ a_1 & 1 & \cdots & 0 & 0 \\ 1 & 0 & \cdots & 0 & 0 \end{array}\right]^{-1} \nonumber\\ &\times& \left[\begin{array}{cccc} B & AB &\cdots & A^{n-1}B \end{array}\right]^{-1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-76067715bdbc7d9b8029b271b91a27de_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\ \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{{x}(t)}+ \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f8bc98dd7c81e82779b6017dbc6cb85e_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\ \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -1 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{{x}(t)}+ \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B} u(t)](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9040963fdd9acf7b39f1bf812fa99c88_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\ \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{{x}(t)}+ \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B} u(t)](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f5aff16fd9935d4b51dc9dea0f54e64b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\ \end{array}\right] }_{\dot{x}(t)}= \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ 0 & -1 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{{x}(t)}+ \underbrace{ \left[\begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array}\right] }_{B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5b7a0db163b44996055239c4cf8ec6aa_l3.png)
![Rendered by QuickLaTeX.com u(t)=- \underbrace{ \left[\begin{array}{cc} 1 & 1 \\ 1 & -1 \end{array}\right] }_{F} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{{x}(t)}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8a1880804ad575edaa4ce349005ec561_l3.png)
![Rendered by QuickLaTeX.com u(t)=- \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ 1 & -2 \end{array}\right] }_{F} \underbrace{ \left[\begin{array}{c} {x}_1(t) \\ {x}_2(t) \\ \end{array}\right] }_{{x}(t)}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d7681a2997f575f972ebd16c2a6cf272_l3.png)
![Rendered by QuickLaTeX.com A= \left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & -1 & 1 \\ 0 & 0 & -1 \end{array}\right] ,\ B= \left[\begin{array}{c} 0 \\ 1 \\ 0 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6cc304a4620ea5dad9c5361bc465956f_l3.png)
![Rendered by QuickLaTeX.com A= \left[\begin{array}{ccc} 0 & 1 & 0 \\ -1 & -1 & 0 \\ 0 & 0 & 2 \end{array}\right] ,\ B= \left[\begin{array}{cc} 0 & 0 \\ 1 & -1 \\ 0 & 1 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f6830e3d13f543452788ce6893c98e2d_l3.png)
![Rendered by QuickLaTeX.com {\rm det}(\lambda I_2-A)= {\rm det}\left[\begin{array}{cc} \lambda & -1 \\ 0 & \lambda+1 \end{array}\right] =\lambda(\lambda+1) =\lambda^2+\underbrace{1}_{a_1}\lambda+\underbrace{0}_{a_2}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-65acea39d75710f02f1e7c20e6043964_l3.png)
![Rendered by QuickLaTeX.com {\rm det}(\lambda I_2-A)= {\rm det}\left[\begin{array}{cc} \lambda & -1 \\ 1 & \lambda \end{array}\right] =\lambda^2+1 =\lambda^2+\underbrace{0}_{a_1}\lambda+\underbrace{1}_{a_2}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3d9ad5dbdcf90b601c9c329ce2b16c08_l3.png)
![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} B & AB & A^2B \end{array}\right]= \left[\begin{array}{ccc} 0 & 1 & -1 \\ 1 & -1 & 1 \\ 0 & 0 & 0 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-067a828760d4077d69d7af72f096c285_l3.png) 。この階数は2で,システムの次数3より小さい。したがって,この3次系は不可制御である。
。この階数は2で,システムの次数3より小さい。したがって,この3次系は不可制御である。![Rendered by QuickLaTeX.com \left[\begin{array}{ccc} B & AB & A^2B \end{array}\right]= \left[\begin{array}{cccccc} 0 & 0 & 1 &-1 &-1 & 1\\ 1 &-1 &-1 & 1 & 0 & 0\\ 0 & 1 & 0 & 2 & 0 & 4 \end{array}\right]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b6489685f970d758a91f786a979180de_l3.png) 。この階数は3で,システムの次数3と等しい。
。この階数は3で,システムの次数3と等しい。![Rendered by QuickLaTeX.com {\rm rank} \left[\begin{array}{cc} B & A-\lambda_1 I_3 \end{array}\right]= {\rm rank} \left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 1 & 0 & -1 & 1 \\ 0 & 0 & 0 & -1 \end{array}\right]= 3](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8ac387d8c9e926e0876ad2511344ba70_l3.png)
![Rendered by QuickLaTeX.com {\rm rank} \left[\begin{array}{cc} B & A-\lambda_3 I_3 \end{array}\right]= {\rm rank} \left[\begin{array}{ccccc} 0 & 0 & -2 & 1 & 0 \\ 1 & -1 & 0 & -2 & 1 \\ 0 & 1 & 0 & 0 & -2 \end{array}\right]= 3](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-24936c92a1e90e689dc378bb582c938c_l3.png)
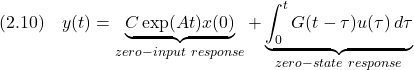
![Rendered by QuickLaTeX.com \displaystyle{(2.17)\quad \left\{\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] }_{\dot x} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] }_{B} u(t) \\ y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] }_{x} \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d6fa93bcbfb96d93d94f9d66f5d59230_l3.png)
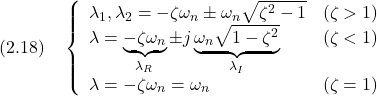
![Rendered by QuickLaTeX.com \displaystyle{(2.19)\quad A= \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda_1 & \lambda_2 \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda_1& 0\\ 0 & \lambda_2 \end{array}\right] }_{\Lambda} \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda_1 & \lambda_2 \end{array}\right]^{-1} }_{V^{-1}} \quad (\zeta>1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dc4be3c5282d75dff407233f401f3cae_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2.20)\quad A= \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ \lambda_R & \lambda_I \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array}\right] }_{\Lambda} \underbrace{ \frac{1}{\lambda_I} \left[\begin{array}{cc} \lambda_I & 0 \\ -\lambda_R & 1 \end{array}\right] }_{V^{-1}} \quad (\zeta<1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b54e86b94889450f0dc10eed7c12eb0a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2.21)\quad A= \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda & \lambda+1 \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda & 1\\ 0 & \lambda \end{array}\right] }_{\Lambda} \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda & \lambda+1 \end{array}\right]^{-1} }_{V^{-1}} \quad (\zeta<1)(\zeta=1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7de86a3d34cbcf41a4444cfcb326f29b_l3.png)
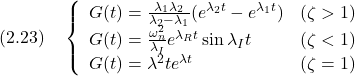
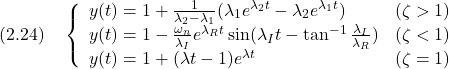
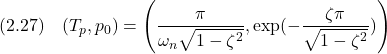
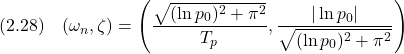
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right]= \left[\begin{array}{cc} 0 & 1 \\ -1 & -0.02 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] + \left[\begin{array}{c} 0 \\ 1 \end{array}\right]u(t)\\ y(t)= \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-05f0daf3113d159b35c6b96888f71b3a_l3.png)
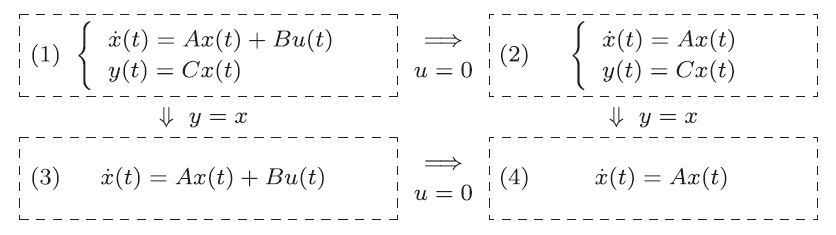
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} \dot{r}(t) \\ \dot{v}(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{K}{M} & -\frac{D}{M} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} r(t) \\ v(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ \frac{1}{M} \end{array}\right] }_{B} \underbrace{f(t)}_{u(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ef4faf86d94fdce557ed8f6c9622d05a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -\frac{D}{J} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ \frac{1}{J} \end{array}\right] }_{B} \underbrace{\tau(t)}_{u(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-484074821cf6000dcc2b08dea90f306d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{\theta(t)}_{y(t)}= \underbrace{\ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \underbrace{\ \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b42c6bcd1d0e4b9b623948c7f0f93a13_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{\omega(t)}_{y(t)}= \underbrace{\ \left[\begin{array}{cc} 0 & 1 \end{array}\right] }_{C} \underbrace{\ \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d37f011e7ffcd8701510840b8bd72ac5_l3.png)

![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] %}_{\dot x} = %\underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] %}_{A} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] %}_{x} + %\underbrace{ \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] %}_{B} u(t) \\ y(t) = %\underbrace{ \left[\begin{array}{cc} c_1 & 0 \end{array}\right] %}_{C} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] %}_{x} \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-587f36fed37f9953e05fef2eaa5ad043_l3.png)
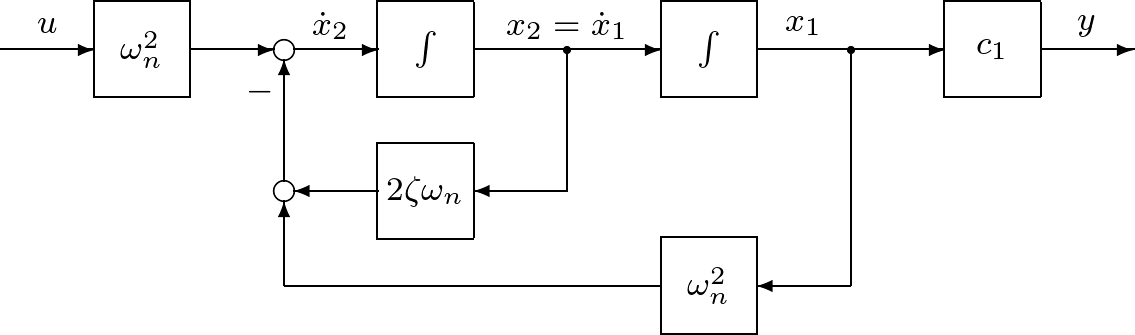
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] %}_{\dot x} = %\underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -2\zeta\omega_n \end{array}\right] %}_{A} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] %}_{x} + %\underbrace{ \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] %}_{B} u(t) \\ y(t) = %\underbrace{ \left[\begin{array}{cc} 0 & c_2 \end{array}\right] %}_{C} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] %}_{x} \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8a12ef04ab77525067dea6216a718e66_l3.png)
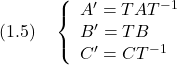
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] = \left[\begin{array}{cc} 0 & -a_2 \\ 1 & -a_1 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] + \left[\begin{array}{c} 1 \\ 0 \end{array}\right] u(t) \nonumber \\ y(t)= \left[\begin{array}{cc} 0 & 1 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5720ce663fe820bc4a73f858fe7621af_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{cc} a_1 & 1 \\ 1 & 0 \end{array}\right] \left[\begin{array}{c} \dot{x}_1'(t) \\ \dot{x}_2'(t) \end{array}\right] = \left[\begin{array}{cc} 0 & -a_2 \\ 1 & -a_1 \end{array}\right] \left[\begin{array}{cc} a_1 & 1 \\ 1 & 0 \end{array}\right] \left[\begin{array}{c} x_1'(t) \\ x_2'(t) \end{array}\right] + \left[\begin{array}{c} 1 \\ 0 \end{array}\right] u \nonumber \\ y(t)= \left[\begin{array}{cc} 0 & 1 \end{array}\right] \left[\begin{array}{cc} a_1 & 1 \\ 1 & 0 \end{array}\right] \left[\begin{array}{c} x_1'(t) \\ x_2'(t) \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9f217759c530ad775b8cdfc5b7b9a2ef_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1'(t) \\ \dot{x}_2'(t) \end{array}\right] = \left[\begin{array}{cc} 0 & 1 \\ -a_2 & -a_1 \end{array}\right] \left[\begin{array}{c} x_1'(t) \\ x_2'(t) \end{array}\right] + \left[\begin{array}{c} 0 \\ 1 \end{array}\right] u(t) \nonumber \\ y(t)= \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{c} x_1'(t) \\ x_2'(t) \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8d290b3e89fcdf34fb69dc7492113ca4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] %}_{\dot x} = %\underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] %}_{A} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] %}_{x} + %\underbrace{ \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] %}_{B} u(t) \\ y(t) = %\underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] %}_{C} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] %}_{x} \end{array}\right. \quad(\zeta<1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8d2c7b5e69c9ce679c9d94e4d7689851_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] = \left[\begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] + \left[\begin{array}{c} b_{1} \\ b_{2} \end{array}\right] u(t) \nonumber \\ y(t) = \underbrace{ \left[\begin{array}{cc} c_1 & c_2 \end{array}\right] }_C \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] \quad(c_1\ne0) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8c3073a3cfb73fa13da8cfc86d6d81b5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} x_1'(t) \\ x_2'(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} t_{11} & t_{12} \\ t_{21} & t_{22} \end{array}\right] }_T \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a9bd1162c0064ff2b9cb7912de1ef12a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ y(t) = \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C'} \left[\begin{array}{c} x'_1(t) \\ x'_2(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ba2c71909620ee072e89a08a075e05d3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1.8)\quad \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] = \left[\begin{array}{cc} A_1 & B_1C_2 \\ 0 & A_2 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] + \left[\begin{array}{c} B_1D_2 \\ B_2 \end{array}\right] u_2(t) \\ y_1(t)= \left[\begin{array}{cc} C_1 & D_1C_2 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] +D_1D_2u_2(t) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-45f3ee32db1b8df2414978f4caf6c253_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] = \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] + \left[\begin{array}{c} 0 \\ 1 \end{array}\right] u(t) \nonumber \\ y(t) = \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2b423f8999f810877f8f1248966b0da9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_{L1}(t) \\ \dot{x}_{L2}(t) \end{array}\right] = \left[\begin{array}{cc} 0 & 1 \\ -\frac{12}{L^2} & -\frac{6}{L} \end{array}\right] \left[\begin{array}{c} x_{L1}(t) \\ x_{L2}(t) \end{array}\right] + \left[\begin{array}{c} 0 \\ 1 \end{array}\right] u_L(t) \nonumber \\ y_L(t) = \left[\begin{array}{cc} 0 & -\frac{12}{L} \end{array}\right] \left[\begin{array}{c} x_{L1}(t) \\ x_{L2}(t) \end{array}\right] +u_L(t) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-376fc34690563a81806abd6dcfef597b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{x}_1 \\ \dot{v}_1 \\ \dot{x}_2 \\ \dot{v}_2 \end{array}\right] = \left[\begin{array}{cccc} 0 & 1 & 0 & 0 \\ -1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & -1 & 0 \\ \end{array}\right] \left[\begin{array}{c} x_1 \\ v_1 \\ x_2 \\ v_2 \end{array}\right] + \left[\begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \end{array}\right] u }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3e0fbd089d806f623d6ef6059995bbce_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{x}_1 \\ \dot{x}_2 \\ \dot{v}_1 \\ \dot{v}_2 \end{array}\right] = \left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -1 & 1 & 0 & 0 \\ 1 & -1 & 0 & 0 \\ \end{array}\right] \left[\begin{array}{c} x_1 \\ x_2 \\ v_1 \\ v_2 \end{array}\right] + \left[\begin{array}{c} 0 \\ 0 \\ 1 \\ 0 \end{array}\right] u }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-12f427b283fd383668530bb9278fee32_l3.png)
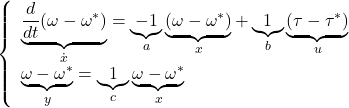
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1 \\ \dot{x}_2 \\ \end{array}\right] = \left[\begin{array}{cccc} 0 & 1 \\ -a_2 & -a_1 \\ \end{array}\right] \left[\begin{array}{c} x_1 \\ x_2 \\ \end{array}\right] + \left[\begin{array}{c} 0 \\ 1 \\ \end{array}\right] u \\ y = \left[\begin{array}{cccc} 1 & 0 \end{array}\right] \left[\begin{array}{c} x_1 \\ x_2 \\ \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cce49d29fd930bdb75330eaf2f6abd9b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_2 \\ \dot{x}_1 \\ \end{array}\right] = \left[\begin{array}{cccc} -a_1 & -a_2 \\ 1 & 0 \\ \end{array}\right] \left[\begin{array}{c} x_2 \\ x_1 \\ \end{array}\right] + \left[\begin{array}{c} 1 \\ 0 \\ \end{array}\right] u \\ y = \left[\begin{array}{cccc} 0 & 1 \end{array}\right] \left[\begin{array}{c} x_2 \\ x_1 \\ \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6201e8183d7a0bb863f9ffa2d66fdab9_l3.png)
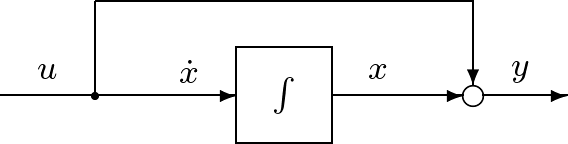
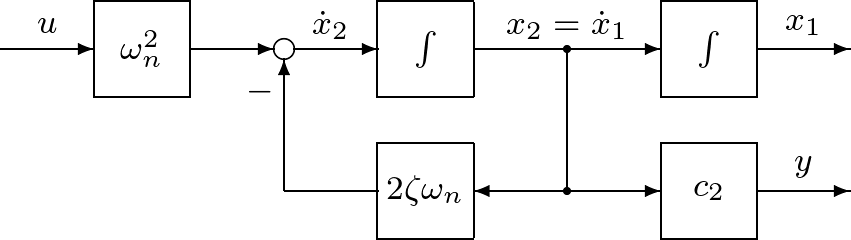
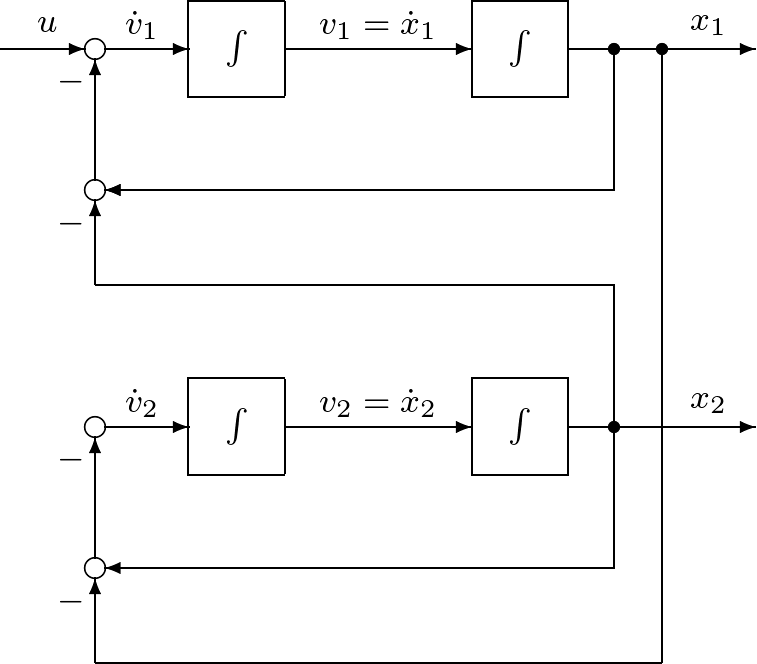
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{cc} 1 & 0 \\ -\zeta\omega_n & \omega_n\sqrt{1-\zeta^2} \end{array}\right] \left[\begin{array}{c} \dot{x}_1' \\ \dot{x}_2' \end{array}\right] \nonumber \\ = \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] \left[\begin{array}{cc} 1 & 0 \\ -\zeta\omega_n & \omega_n\sqrt{1-\zeta^2} \end{array}\right] \left[\begin{array}{c} x_1' \\ x_2' \end{array}\right] + \left[\begin{array}{c} 0 \\ 1 \end{array}\right] u \nonumber \\ y= \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{cc} 1 & 0 \\ -\zeta\omega_n & \omega_n\sqrt{1-\zeta^2} \end{array}\right] \left[\begin{array}{c} x_1' \\ x_2' \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-548a07a10980959e629ac59779c43482_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{cc} 1 & 0 \\ -\zeta\omega_n & \omega_n\sqrt{1-\zeta^2} \end{array}\right]^{-1} = \frac{1}{\omega_n\sqrt{1-\zeta^2}} \left[\begin{array}{cc} \omega_n\sqrt{1-\zeta^2} & 0 \\ \zeta\omega_n & 1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f28070aaad5ed40f0568a9a63d302400_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1' \\ \dot{x}_2' \end{array}\right] = \left[\begin{array}{cc} -\zeta\omega_n & \omega_n\sqrt{1-\zeta^2} \\ -\omega_n\sqrt{1-\zeta^2} & -\zeta\omega_n \end{array}\right] \left[\begin{array}{c} x_1' \\ x_2' \end{array}\right] + \left[\begin{array}{c} 0 \\ \frac{1}{\omega_n\sqrt{1-\zeta^2}} \end{array}\right] u \nonumber \\ y= \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{c} x_1' \\ x_2' \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bbcf1c94073c8ce9361d2eb6b4ab2f6e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C'} \underbrace{ \left[\begin{array}{cc} t_{11} & t_{12} \\ t_{21} & t_{22} \end{array}\right] }_T = \underbrace{ \left[\begin{array}{cc} c_1 & c_2 \end{array}\right] }_C \quad(Tは正則) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eb2b3f3ede67ce2ed7004c9f814b44c5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\\hdashline \dot{x}_{L1}(t) \\ \dot{x}_{L2}(t) \end{array}\right] = \left[\begin{array}{cc:cc} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & -\frac{12}{L} \\\hdashline 0 & 0 & 0 & 1 \\ 0 & 0 & -\frac{12}{L^2} & -\frac{6}{L} \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \\ \hdashline x_{L1}(t) \\ x_{L2}(t) \end{array}\right] + \left[\begin{array}{c} 0 \\ 1 \\ \hdashline 0 \\ 1 \end{array}\right] u_L(t) \\ y(t)= \left[\begin{array}{cc:cc} 1 & 0 & 0 & 0 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \\ \hdashline x_{L1}(t) \\ x_{L2}(t) \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-60c141da6506e0e4b9f90fda362de68e_l3.png)