|
【本章のねらい】 ・状態空間表現を導き,その構造をブロック線図で表す。 ・状態空間表現に対する操作として座標変換と直列結合を行う。 |
1.1 状態空間表現の導出とブロック線図
|
古典制御では,主に1入力1出力をもつ線形ダイナミカルシステム(線形系)の入出力特性に注目し,これを伝達関数で表した。一方,現代制御では,多入出力をもつ線形系において,「まず入力が状態に影響を及ぼし,つぎに状態の一部が出力として現れる」と考え,前者を状態方程式で,後者を出力方程式で表す。すなわち,状態方程式と出力方程式をペアにした状態空間表現
を求めることが出発点となる。ここで,実ベクトル 以下では,(1.1)式の状態空間表現で表される
ここで,(1)は直達項 ここでは,制御対象のダイナミクスは連立された線形常微分方程式で表されるとし,これから連立1階線形微分方程式の行列表現を導いて状態方程式を得る。 例題1.1 つぎの運動方程式を考える。
ここで,
これを行列表現して,
演習1.1 つぎの運動方程式から2次自由系の状態方程式を導出せよ。
演習1.2 つぎの連成した運動方程式から,
例題1.2 つぎの運動方程式を考える。
ここで,
これを行列表現すると,
(1)
(2)
演習1.3 例題1.2の(2)を考える。角速度を 演習1.4 つぎの2階線形常微分方程式から,
MATLABを用いて状態空間表現 sys を定義するには,たとえば例題1.2の(1)で, %state_space.m ここで, sys.a,sys.b,sys.c,sys.d を用いる。たとえば sys.a(2,2)=-0.1 また, %state_space_cont.m もし状態方程式だけを指定する場合は,C=[]; D=[]; または C=eye(size(A)); D=0; とする。 |
SCILABを用いて状態空間表現 sys を定義するには,たとえば例題1.2の(1)で,![]() の場合,つぎのコマンドを与えればよい。
の場合,つぎのコマンドを与えればよい。
//state_space.m
A=[0 1;0 -0.01]; B=[0;1]; C=[1 0]; D=0;
sys=syslin(A,B,C,D)
ここで,![]() 行列,
行列,![]() 行列,
行列,![]() 行列,
行列,![]() 行列を参照するには,それぞれ
行列を参照するには,それぞれ
sys.a,sys.b,sys.c,sys.d
を用いる。たとえば![]() 行列の
行列の![]() 要素を-0.1に変更するには,つぎのコマンドを与えればよい。
要素を-0.1に変更するには,つぎのコマンドを与えればよい。
A(2,2)=-0.1; sys.a=A
また,![]() 行列,
行列,![]() 行列が存在しない自由系 sys0 を定義するには,つぎのコマンドを与えればよい。
行列が存在しない自由系 sys0 を定義するには,つぎのコマンドを与えればよい。
//state_space_cont.m
A=[0 1;0 -0.01]; B=[]; C=[1 0]; D=[];
sys0=syslin(A,B,C,D)
もし状態方程式だけを指定する場合は,C=[]; D=[]; または C=eye(size(A)); D=zeros(size(A,1),size(B,2)); とする。
|
さて,状態空間表現のブロック線図を作成することにより,どのように入力変数から状態変数を経て出力変数につながるかを表すことができる。これは,Simulinkなどを用いた時間応答シミュレーションに役に立つ。
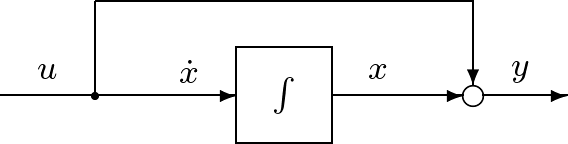
例題1.3 つぎの1次系の状態空間表現をブロック線図で表せ。
解答 積分器の出力を
演習1.5 つぎの1次系の状態空間表現をブロック線図で表せ。
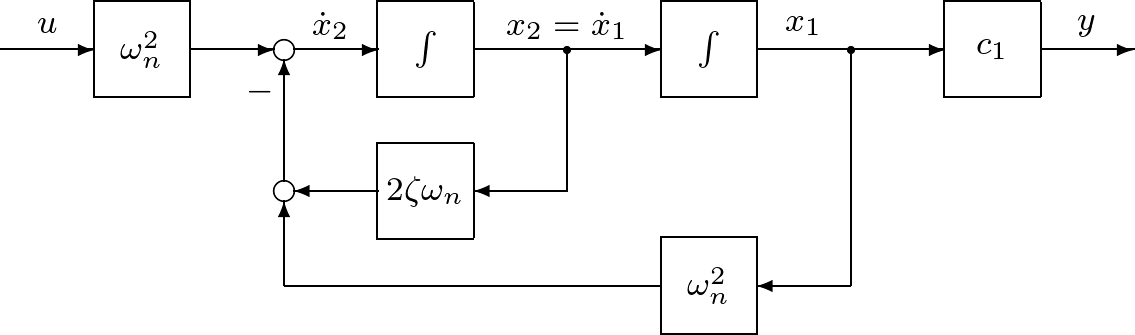
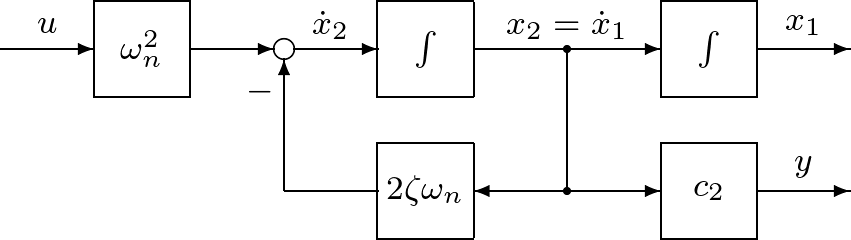
例題1.4 つぎの2次系の状態空間表現をブロック線図で表せ。
解答 演習1.6 つぎの2次系の状態空間表現をブロック線図で表せ。
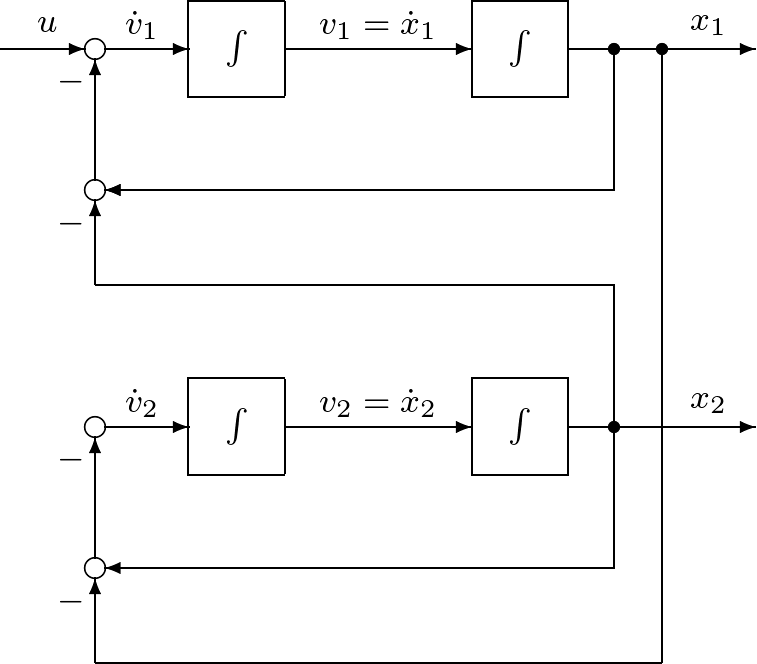
演習1.7 演習1.2 で得られた状態空間表現について,ブロック線図を描け。 |
1.2 状態空間表現の座標変換と直列結合
|
に対して,座標変換
を行うと,つぎの状態空間表現を得る。
ただし,変換後の係数行列は次式で与えられる。
例題1.5 2次系の状態空間表現
に対して,つぎの座標変換を行え。
解答 状態空間表現に
を代入して
この状態方程式の左から
をかけて,つぎの状態空間表現を得る。
演習1.8 2次系の状態空間表現
に対して,つぎの座標変換を行え。
演習1.9 2次系の状態空間表現
に対して,どのような座標変換
を行なえば,出力方程式をつぎの形にできるか。
さて,つぎの2つの状態空間表現を考える。
例題1.6 1次系の状態空間表現
の入力に,むだ時間を1次系として近似したときの状態空間表現
の出力を結合して得られるシステムの状態空間表現を求めよ。
に
と合わせて
のように得られる。また,出力方程式は
のように得られる。 演習1.10 2次系
の入力に,むだ時間を2次系として近似したときの状態空間表現
の出力を結合して得られるシステムの状態空間表現を求めよ。 MATLABを用いて座標変換を行うために,たとえば演習1.8で, %coordinate_transformation.m |
SCILABを用いて座標変換を行うために,たとえば演習1.8で,![]() の場合,つぎのコマンドを与えればよい。
の場合,つぎのコマンドを与えればよい。
//coordinate_transformation.m
om=1; zeta=0.01;
A=[0 1;-om^2 -2*zeta*om]; B=[0;om^2]; C=[1 0]; D=0;
sys1=syslin(‘c’,A,B,C,D);
T=[1 0;-zeta*om om*sqrt(1-zeta^2)];
sys2=ss2ss(sys1,T)
|
つぎに,MATLABを用いて直列結合を行うためには,たとえば演習1.10で %serial_connection.m ここで, sys1 と sys2 の順番に注意する。 最後に,状態空間表現から伝達関数行列表現(8章の(8.2)式を参照。)を求めるには,コマンド tf を用いる。たとえば,上のむだ時間を2次系として近似したときの状態空間表現 sys2 の伝達関数を求めるには,コマンド tf(sys2) を与えればよい。 |
つぎに,SCILABを用いて直列結合を行うためには,たとえば演習1.10で![]() の場合,つぎのコマンドを与えればよい。
の場合,つぎのコマンドを与えればよい。
//serial_connection.m
A1=[0 1;0 0]; B1=[0;1]; C1=[1 0]; D1=0;
sys1=syslin(‘c’,A1,B1,C1,D1);
L=1;
A2=[0 1;-12/L^2 -6/L]; B2=[0;1]; C2=[0 -12/L]; D2=1;
sys2=syslin(‘c’,A2,B2,C2,D2);
sys=sys1*sys2
ここで, sys1 と sys2 の順番に注意する。
最後に,状態空間表現から伝達関数行列表現(8章の(8.2)式を参照。)を求めるには,コマンド ss2tf を用いる。たとえば,上のむだ時間を2次系として近似したときの状態空間表現 sys2 の伝達関数を求めるには,コマンド ss2tf(sys2) を与えればよい。
演習問題の解答
|
演習1.1
演習1.2
または
演習1.3 一定のトルク
演習1.4
または
演習1.5
演習1.6
演習1.7
演習1.8 状態空間表現に
を代入して
この状態方程式の左から
をかけて,つぎの状態空間表現を得る。
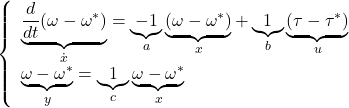
演習1.9
を満足させればよいので,たとえば 演習1.10
|
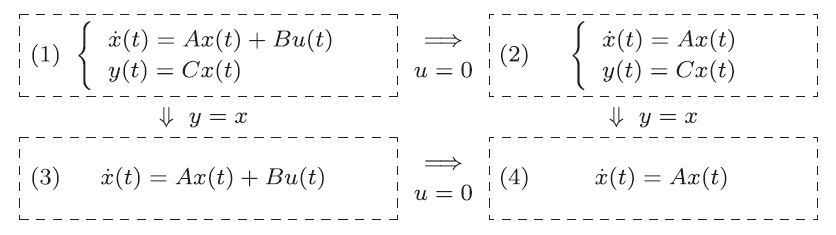
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} \dot{r}(t) \\ \dot{v}(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{K}{M} & -\frac{D}{M} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} r(t) \\ v(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ \frac{1}{M} \end{array}\right] }_{B} \underbrace{f(t)}_{u(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ef4faf86d94fdce557ed8f6c9622d05a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -\frac{D}{J} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ \frac{1}{J} \end{array}\right] }_{B} \underbrace{\tau(t)}_{u(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-484074821cf6000dcc2b08dea90f306d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{\theta(t)}_{y(t)}= \underbrace{\ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \underbrace{\ \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b42c6bcd1d0e4b9b623948c7f0f93a13_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{\omega(t)}_{y(t)}= \underbrace{\ \left[\begin{array}{cc} 0 & 1 \end{array}\right] }_{C} \underbrace{\ \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d37f011e7ffcd8701510840b8bd72ac5_l3.png)

![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] %}_{\dot x} = %\underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] %}_{A} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] %}_{x} + %\underbrace{ \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] %}_{B} u(t) \\ y(t) = %\underbrace{ \left[\begin{array}{cc} c_1 & 0 \end{array}\right] %}_{C} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] %}_{x} \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-587f36fed37f9953e05fef2eaa5ad043_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] %}_{\dot x} = %\underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & -2\zeta\omega_n \end{array}\right] %}_{A} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] %}_{x} + %\underbrace{ \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] %}_{B} u(t) \\ y(t) = %\underbrace{ \left[\begin{array}{cc} 0 & c_2 \end{array}\right] %}_{C} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] %}_{x} \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8a12ef04ab77525067dea6216a718e66_l3.png)
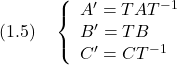
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] = \left[\begin{array}{cc} 0 & -a_2 \\ 1 & -a_1 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] + \left[\begin{array}{c} 1 \\ 0 \end{array}\right] u(t) \nonumber \\ y(t)= \left[\begin{array}{cc} 0 & 1 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5720ce663fe820bc4a73f858fe7621af_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{cc} a_1 & 1 \\ 1 & 0 \end{array}\right] \left[\begin{array}{c} \dot{x}_1'(t) \\ \dot{x}_2'(t) \end{array}\right] = \left[\begin{array}{cc} 0 & -a_2 \\ 1 & -a_1 \end{array}\right] \left[\begin{array}{cc} a_1 & 1 \\ 1 & 0 \end{array}\right] \left[\begin{array}{c} x_1'(t) \\ x_2'(t) \end{array}\right] + \left[\begin{array}{c} 1 \\ 0 \end{array}\right] u \nonumber \\ y(t)= \left[\begin{array}{cc} 0 & 1 \end{array}\right] \left[\begin{array}{cc} a_1 & 1 \\ 1 & 0 \end{array}\right] \left[\begin{array}{c} x_1'(t) \\ x_2'(t) \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9f217759c530ad775b8cdfc5b7b9a2ef_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1'(t) \\ \dot{x}_2'(t) \end{array}\right] = \left[\begin{array}{cc} 0 & 1 \\ -a_2 & -a_1 \end{array}\right] \left[\begin{array}{c} x_1'(t) \\ x_2'(t) \end{array}\right] + \left[\begin{array}{c} 0 \\ 1 \end{array}\right] u(t) \nonumber \\ y(t)= \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{c} x_1'(t) \\ x_2'(t) \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8d290b3e89fcdf34fb69dc7492113ca4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] %}_{\dot x} = %\underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] %}_{A} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] %}_{x} + %\underbrace{ \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] %}_{B} u(t) \\ y(t) = %\underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] %}_{C} %\underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] %}_{x} \end{array}\right. \quad(\zeta<1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8d2c7b5e69c9ce679c9d94e4d7689851_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] = \left[\begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] + \left[\begin{array}{c} b_{1} \\ b_{2} \end{array}\right] u(t) \nonumber \\ y(t) = \underbrace{ \left[\begin{array}{cc} c_1 & c_2 \end{array}\right] }_C \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] \quad(c_1\ne0) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8c3073a3cfb73fa13da8cfc86d6d81b5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} x_1'(t) \\ x_2'(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} t_{11} & t_{12} \\ t_{21} & t_{22} \end{array}\right] }_T \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a9bd1162c0064ff2b9cb7912de1ef12a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ y(t) = \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C'} \left[\begin{array}{c} x'_1(t) \\ x'_2(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ba2c71909620ee072e89a08a075e05d3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1.8)\quad \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] = \left[\begin{array}{cc} A_1 & B_1C_2 \\ 0 & A_2 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] + \left[\begin{array}{c} B_1D_2 \\ B_2 \end{array}\right] u_2(t) \\ y_1(t)= \left[\begin{array}{cc} C_1 & D_1C_2 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] +D_1D_2u_2(t) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-45f3ee32db1b8df2414978f4caf6c253_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] = \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] + \left[\begin{array}{c} 0 \\ 1 \end{array}\right] u(t) \nonumber \\ y(t) = \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2b423f8999f810877f8f1248966b0da9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_{L1}(t) \\ \dot{x}_{L2}(t) \end{array}\right] = \left[\begin{array}{cc} 0 & 1 \\ -\frac{12}{L^2} & -\frac{6}{L} \end{array}\right] \left[\begin{array}{c} x_{L1}(t) \\ x_{L2}(t) \end{array}\right] + \left[\begin{array}{c} 0 \\ 1 \end{array}\right] u_L(t) \nonumber \\ y_L(t) = \left[\begin{array}{cc} 0 & -\frac{12}{L} \end{array}\right] \left[\begin{array}{c} x_{L1}(t) \\ x_{L2}(t) \end{array}\right] +u_L(t) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-376fc34690563a81806abd6dcfef597b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{x}_1 \\ \dot{v}_1 \\ \dot{x}_2 \\ \dot{v}_2 \end{array}\right] = \left[\begin{array}{cccc} 0 & 1 & 0 & 0 \\ -1 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ 1 & 0 & -1 & 0 \\ \end{array}\right] \left[\begin{array}{c} x_1 \\ v_1 \\ x_2 \\ v_2 \end{array}\right] + \left[\begin{array}{c} 0 \\ 1 \\ 0 \\ 0 \end{array}\right] u }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3e0fbd089d806f623d6ef6059995bbce_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{x}_1 \\ \dot{x}_2 \\ \dot{v}_1 \\ \dot{v}_2 \end{array}\right] = \left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -1 & 1 & 0 & 0 \\ 1 & -1 & 0 & 0 \\ \end{array}\right] \left[\begin{array}{c} x_1 \\ x_2 \\ v_1 \\ v_2 \end{array}\right] + \left[\begin{array}{c} 0 \\ 0 \\ 1 \\ 0 \end{array}\right] u }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-12f427b283fd383668530bb9278fee32_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1 \\ \dot{x}_2 \\ \end{array}\right] = \left[\begin{array}{cccc} 0 & 1 \\ -a_2 & -a_1 \\ \end{array}\right] \left[\begin{array}{c} x_1 \\ x_2 \\ \end{array}\right] + \left[\begin{array}{c} 0 \\ 1 \\ \end{array}\right] u \\ y = \left[\begin{array}{cccc} 1 & 0 \end{array}\right] \left[\begin{array}{c} x_1 \\ x_2 \\ \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cce49d29fd930bdb75330eaf2f6abd9b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_2 \\ \dot{x}_1 \\ \end{array}\right] = \left[\begin{array}{cccc} -a_1 & -a_2 \\ 1 & 0 \\ \end{array}\right] \left[\begin{array}{c} x_2 \\ x_1 \\ \end{array}\right] + \left[\begin{array}{c} 1 \\ 0 \\ \end{array}\right] u \\ y = \left[\begin{array}{cccc} 0 & 1 \end{array}\right] \left[\begin{array}{c} x_2 \\ x_1 \\ \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6201e8183d7a0bb863f9ffa2d66fdab9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{cc} 1 & 0 \\ -\zeta\omega_n & \omega_n\sqrt{1-\zeta^2} \end{array}\right] \left[\begin{array}{c} \dot{x}_1' \\ \dot{x}_2' \end{array}\right] \nonumber \\ = \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] \left[\begin{array}{cc} 1 & 0 \\ -\zeta\omega_n & \omega_n\sqrt{1-\zeta^2} \end{array}\right] \left[\begin{array}{c} x_1' \\ x_2' \end{array}\right] + \left[\begin{array}{c} 0 \\ 1 \end{array}\right] u \nonumber \\ y= \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{cc} 1 & 0 \\ -\zeta\omega_n & \omega_n\sqrt{1-\zeta^2} \end{array}\right] \left[\begin{array}{c} x_1' \\ x_2' \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-548a07a10980959e629ac59779c43482_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{cc} 1 & 0 \\ -\zeta\omega_n & \omega_n\sqrt{1-\zeta^2} \end{array}\right]^{-1} = \frac{1}{\omega_n\sqrt{1-\zeta^2}} \left[\begin{array}{cc} \omega_n\sqrt{1-\zeta^2} & 0 \\ \zeta\omega_n & 1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f28070aaad5ed40f0568a9a63d302400_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1' \\ \dot{x}_2' \end{array}\right] = \left[\begin{array}{cc} -\zeta\omega_n & \omega_n\sqrt{1-\zeta^2} \\ -\omega_n\sqrt{1-\zeta^2} & -\zeta\omega_n \end{array}\right] \left[\begin{array}{c} x_1' \\ x_2' \end{array}\right] + \left[\begin{array}{c} 0 \\ \frac{1}{\omega_n\sqrt{1-\zeta^2}} \end{array}\right] u \nonumber \\ y= \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{c} x_1' \\ x_2' \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bbcf1c94073c8ce9361d2eb6b4ab2f6e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C'} \underbrace{ \left[\begin{array}{cc} t_{11} & t_{12} \\ t_{21} & t_{22} \end{array}\right] }_T = \underbrace{ \left[\begin{array}{cc} c_1 & c_2 \end{array}\right] }_C \quad(Tは正則) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eb2b3f3ede67ce2ed7004c9f814b44c5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \\\hdashline \dot{x}_{L1}(t) \\ \dot{x}_{L2}(t) \end{array}\right] = \left[\begin{array}{cc:cc} 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & -\frac{12}{L} \\\hdashline 0 & 0 & 0 & 1 \\ 0 & 0 & -\frac{12}{L^2} & -\frac{6}{L} \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \\ \hdashline x_{L1}(t) \\ x_{L2}(t) \end{array}\right] + \left[\begin{array}{c} 0 \\ 1 \\ \hdashline 0 \\ 1 \end{array}\right] u_L(t) \\ y(t)= \left[\begin{array}{cc:cc} 1 & 0 & 0 & 0 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \\ \hdashline x_{L1}(t) \\ x_{L2}(t) \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-60c141da6506e0e4b9f90fda362de68e_l3.png)