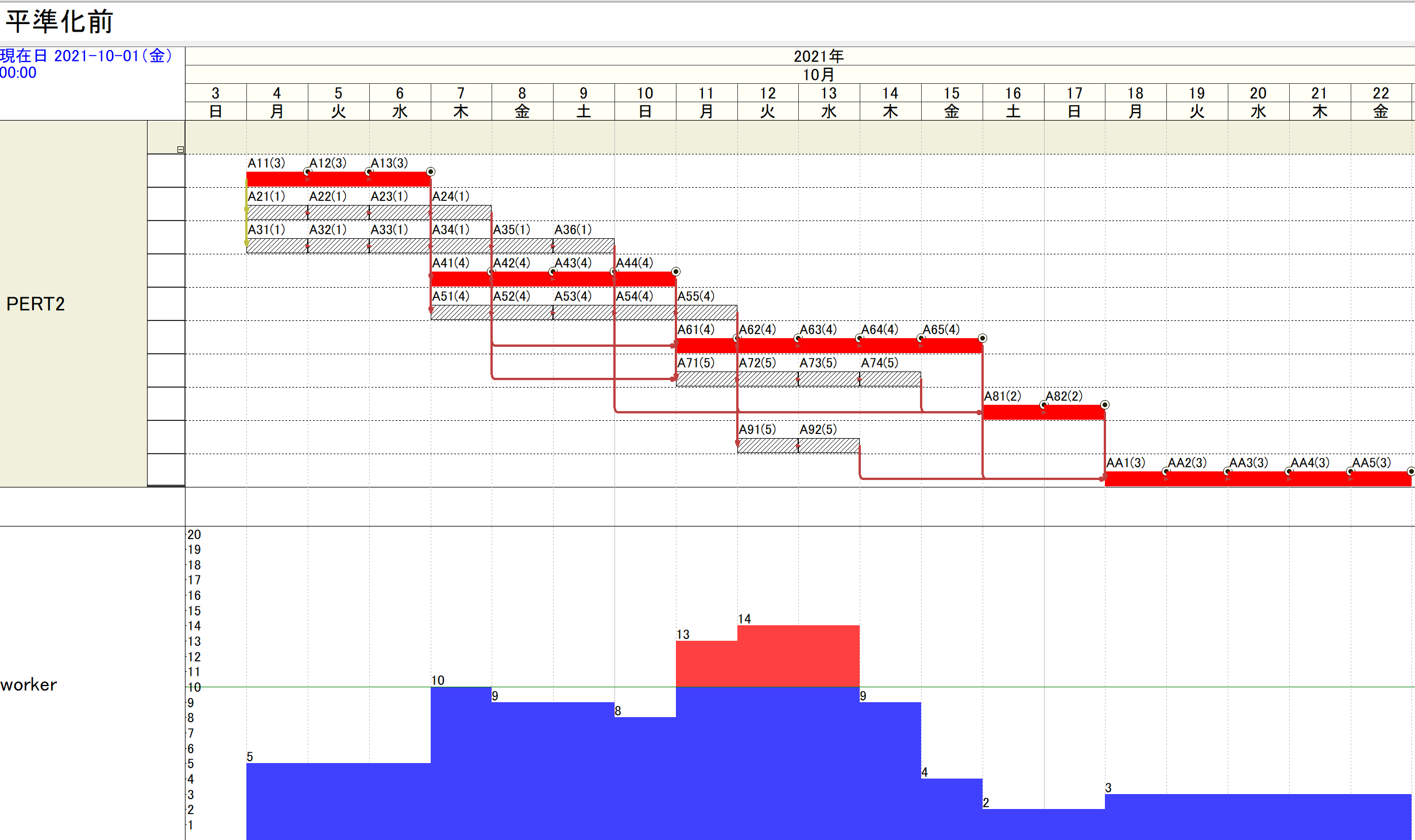
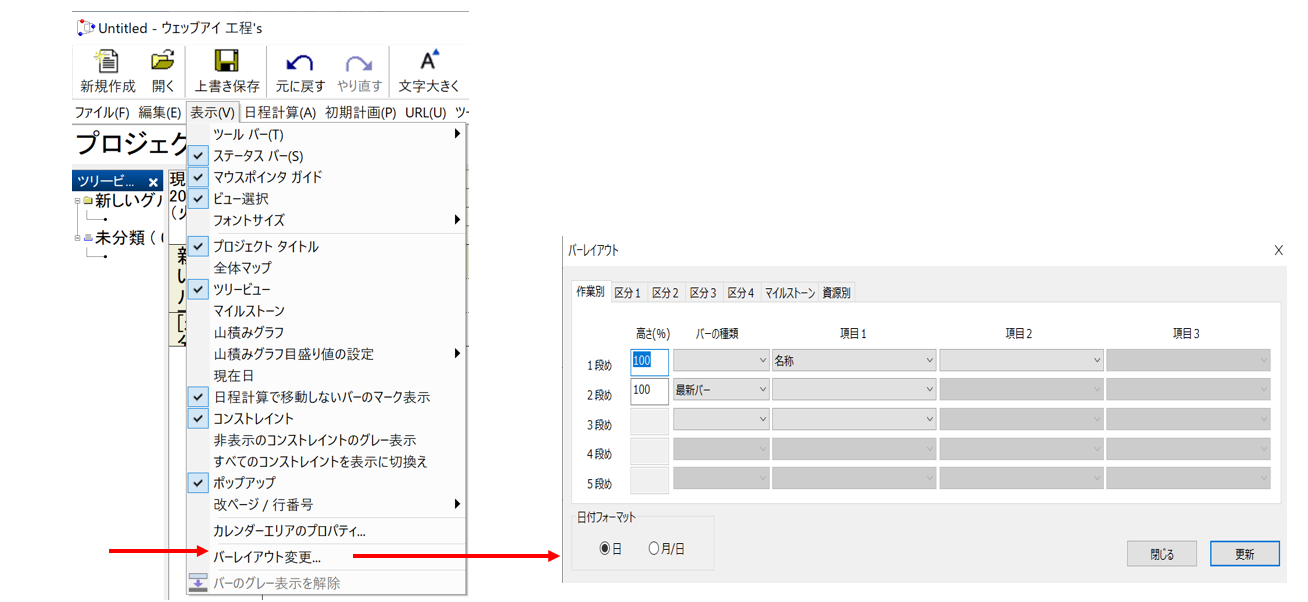
OptSeqによる平準化
以下では、「工程’s」による平準化で扱った同じ問題を考えます。
●まず山積みを行うプログラムは次のようになります。
#prob11.py
from optseq import *
#=====リソース
prob11=Model()
res1=ex.addResource("Resource",capacity={(0,"inf"):20}) #10
#-----データセット
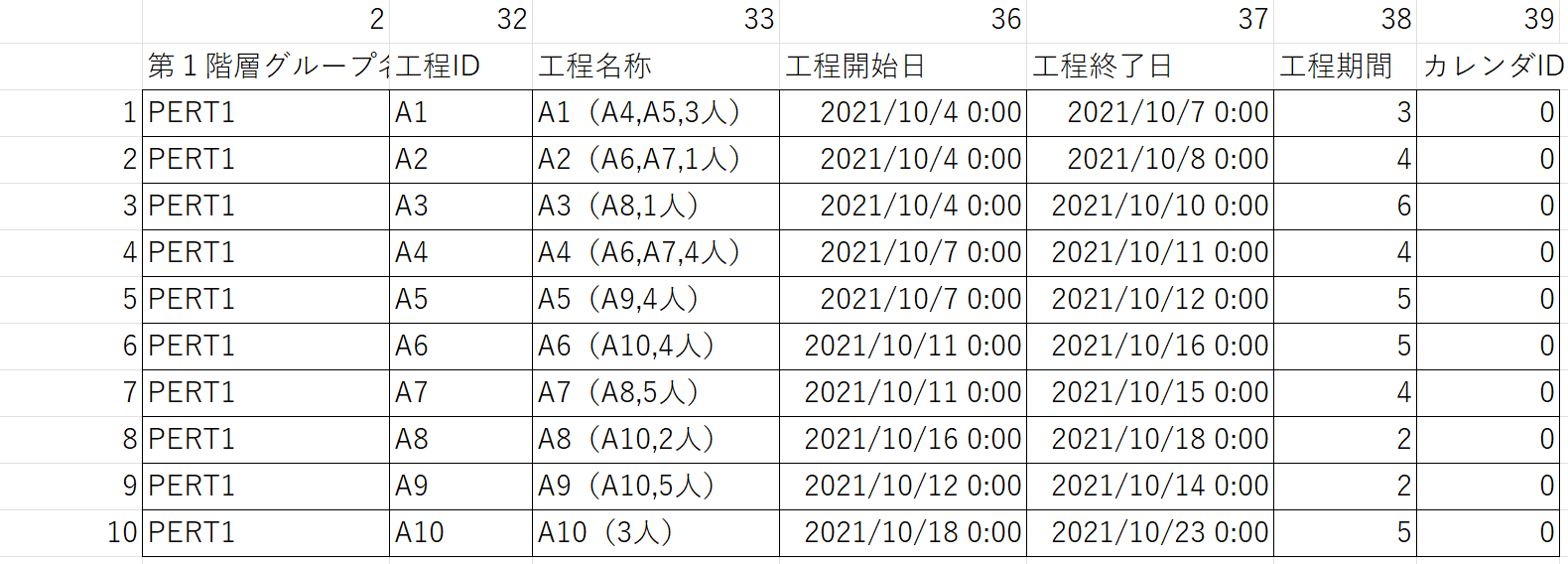
#i:[期間、後続、納期]
data={\
1:[3,[4,5],3],\
2:[4,[6,7],1],\
3:[6,[9] ,1],\
4:[4,[6,7],4],\
5:[5,[8] ,4],\
6:[4,[10] ,5],\
7:[5,[9], 4],\
8:[2,[10] ,5],\
9:[2,[10] ,2],\
10:[5,[0] ,3],\
}
#=====アクティビティ
act={}
for i in data:
act[i]=prob11.addActivity("Act[{0}]".format(i))
#=====先行制約
for i in data:
for j in data[i][1]:
if j>0: prob11.addTemporal(act[i],act[j])
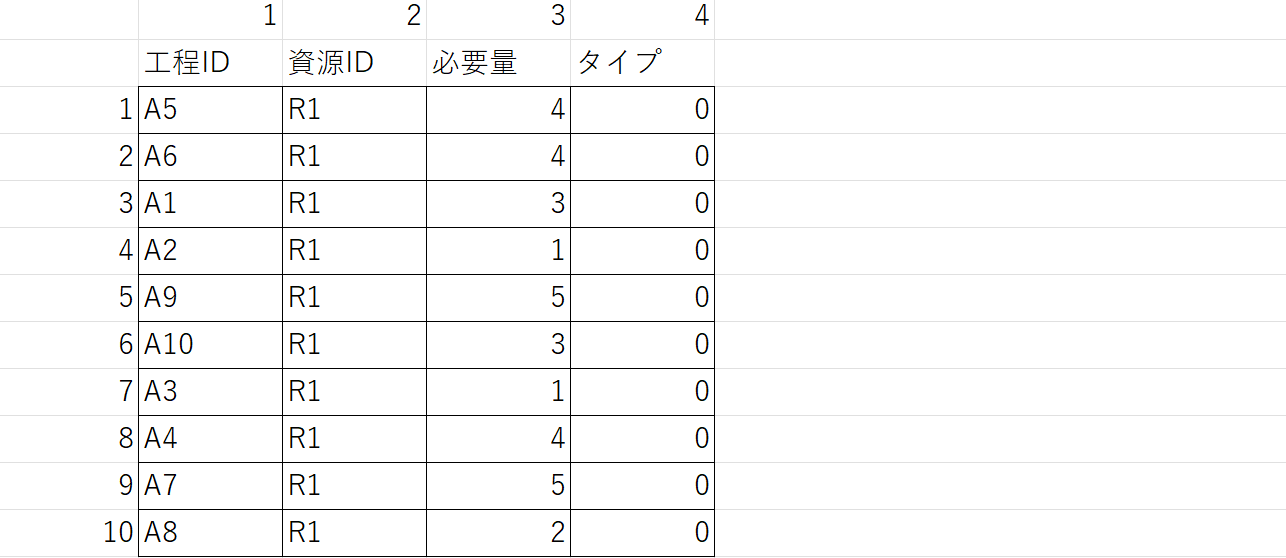
#====資源制約
mode={}
for i in data:
mode[i]=Mode("Mode[{0:02d}]".format(i),data[i][0])
mode[i].addResource(res1,requirement=data[i][2])
act[i].addModes(mode[i])
#=====最適化
prob11.Params.Makespan=True
prob11.Params.TimeLimit=1
#prob11.Params.OutputFlag=True
prob11.optimize()
prob11.write("prob11.txt")
prob11.writeExcel("prob11.csv")
#=====prob11.txt
# activity mode duration 1 2 3 4 5 6 7 8 910111213141516171819
#---------------------------------------------------------------------
# Act[1] Mode[01] 3 ======
# Act[2] Mode[02] 4 ========
# Act[3] Mode[03] 6 ============
# Act[4] Mode[04] 4 ========
# Act[5] Mode[05] 5 ==========
# Act[6] Mode[06] 4 ========
# Act[7] Mode[07] 5 ==========
# Act[8] Mode[08] 2 ====
# Act[9] Mode[09] 2 ====
# Act[10] Mode[10] 5 ==========
#---------------------------------------------------------------------
# resource usage/capacity
#---------------------------------------------------------------------
# Resource 5 5 510 9 9 8131414 9 4 2 2 3 3 3 3 3
# 20202020202020202020202020202020202020
#---------------------------------------------------------------------
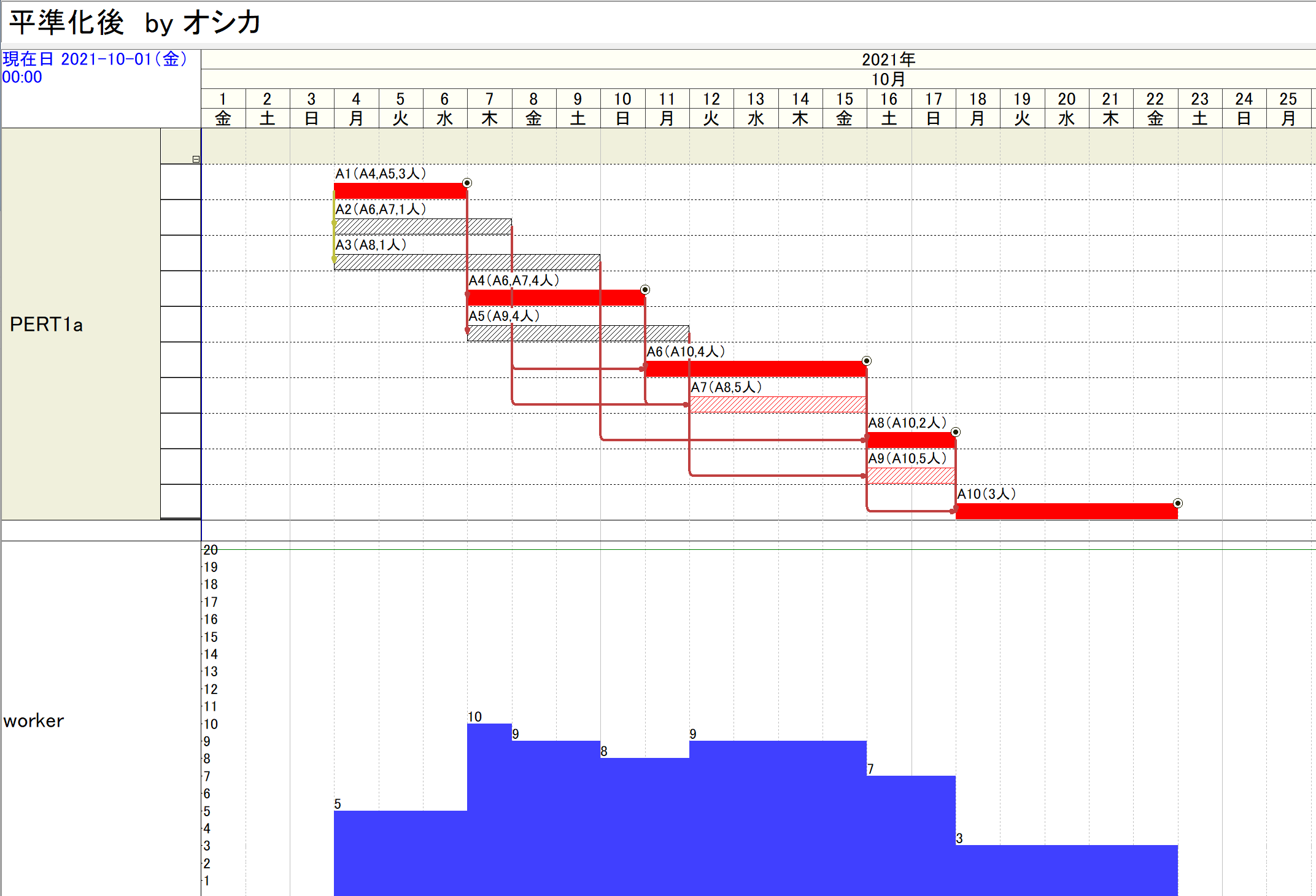
このプログラムを実行して、次の結果を得ます。
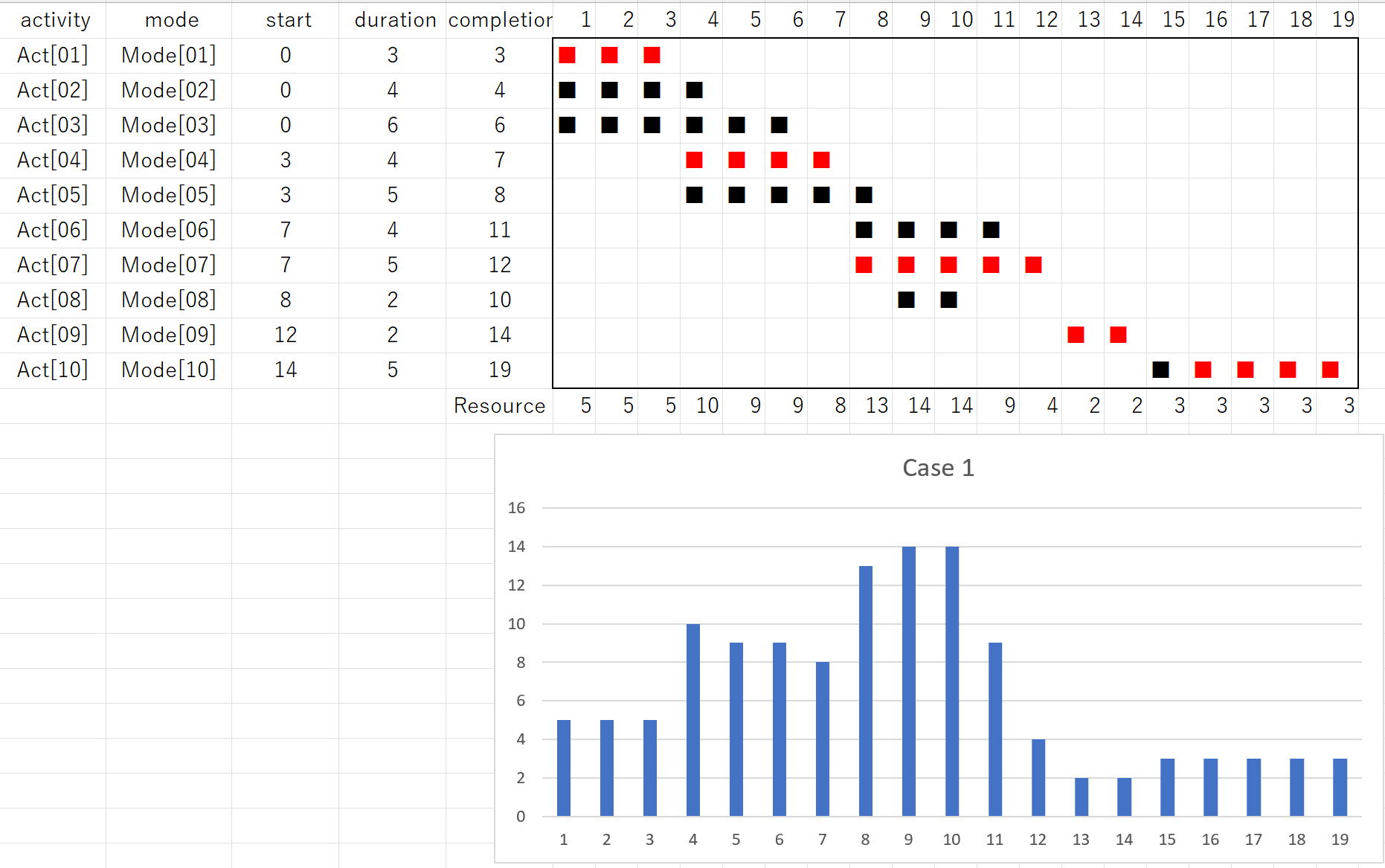
この結果は「工程’s」では次のように得られていました。
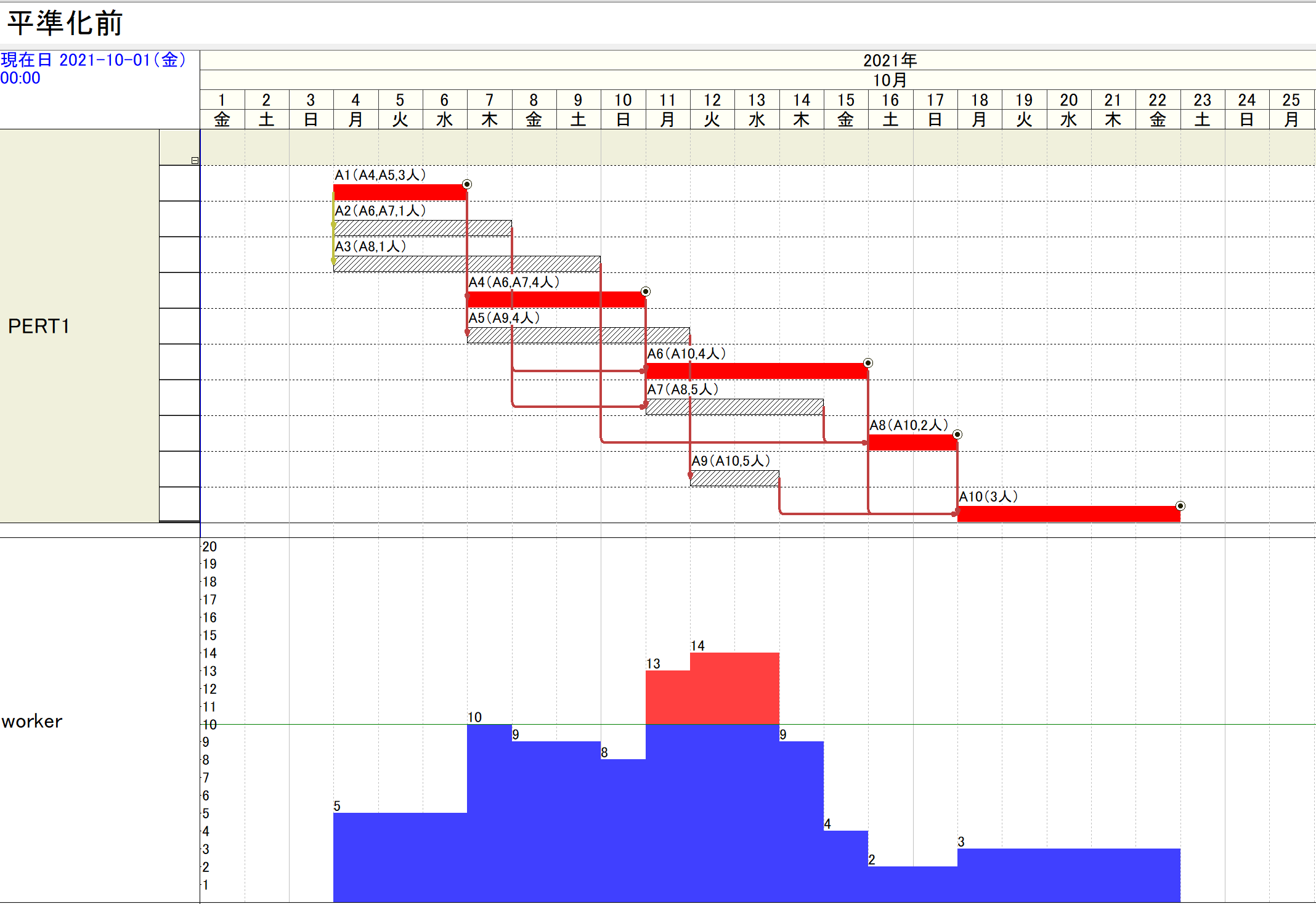
●これに対してOptSeqでは、次のような平準化が可能です。

これを行うプログラムを次に示します。データセットでは、各作業を1人で行う場合の作業期間が登録されています。これを小作業の並列化という手法を用いて平準化しています。
#prob12.py
from optseq import *
#=====リソース
prob12=Model()
res1=ex.addResource("Resource",capacity={(0,"inf"):10})
#-----データセット
#i:[期間、後続、納期]
data={\
1:[9,[4,5] ,1],\
2:[4,[6,7] ,1],\
3:[6,[9] ,1],\
4:[16,[6,7],1],\
5:[20,[8] ,1],\
6:[20,[10] ,1],\
7:[20,[9] ,1],\
8:[10,[10] ,1],\
9:[4,[10] ,1],\
10:[15,[0] ,1],\
}
#=====アクティビティ
act={}
for i in data:
act[i]=prob12.addActivity("Act[{0}]".format(i))
#=====先行制約
for i in data:
for j in data[i][1]:
if j>0: prob12.addTemporal(act[i],act[j])
#====資源制約
mode={}
for i in data:
mode[i]=Mode("Mode[{0:02d}]".format(i),data[i][0])
mode[i].addResource(res1,requirement=data[i][2])
mode[i].addParallel(1,data[i][0],10)
act[i].addModes(mode[i])
#=====最適化
prob12.Params.Makespan=True
prob12.Params.TimeLimit=1
#prob11.Params.OutputFlag=True
prob12.optimize()
prob12.write("prob12.txt")
prob12.writeExcel("prob12.csv")
#=====prob12.txt
# activity mode duration 1 2 3 4 5 6 7 8 910111213
#---------------------------------------------------------
# Act[1] Mode[01] 9 *6*3
# Act[2] Mode[02] 4 *4
# Act[3] Mode[03] 6 *6
# Act[4] Mode[04] 16 *10*6
# Act[5] Mode[05] 20 *4*10*6
# Act[6] Mode[06] 20 *4*10*6
# Act[7] Mode[07] 20 *4*10*6
# Act[8] Mode[08] 10 *4*6
# Act[9] Mode[09] 4 *4
# Act[10] Mode[10] 15 *10*5
#---------------------------------------------------------
# resource usage/capacity
#---------------------------------------------------------
# Resource 10 910101010101010101010 5
# 10101010101010101010101010
#---------------------------------------------------------
このプログラムを実行して、次の結果を得ます。
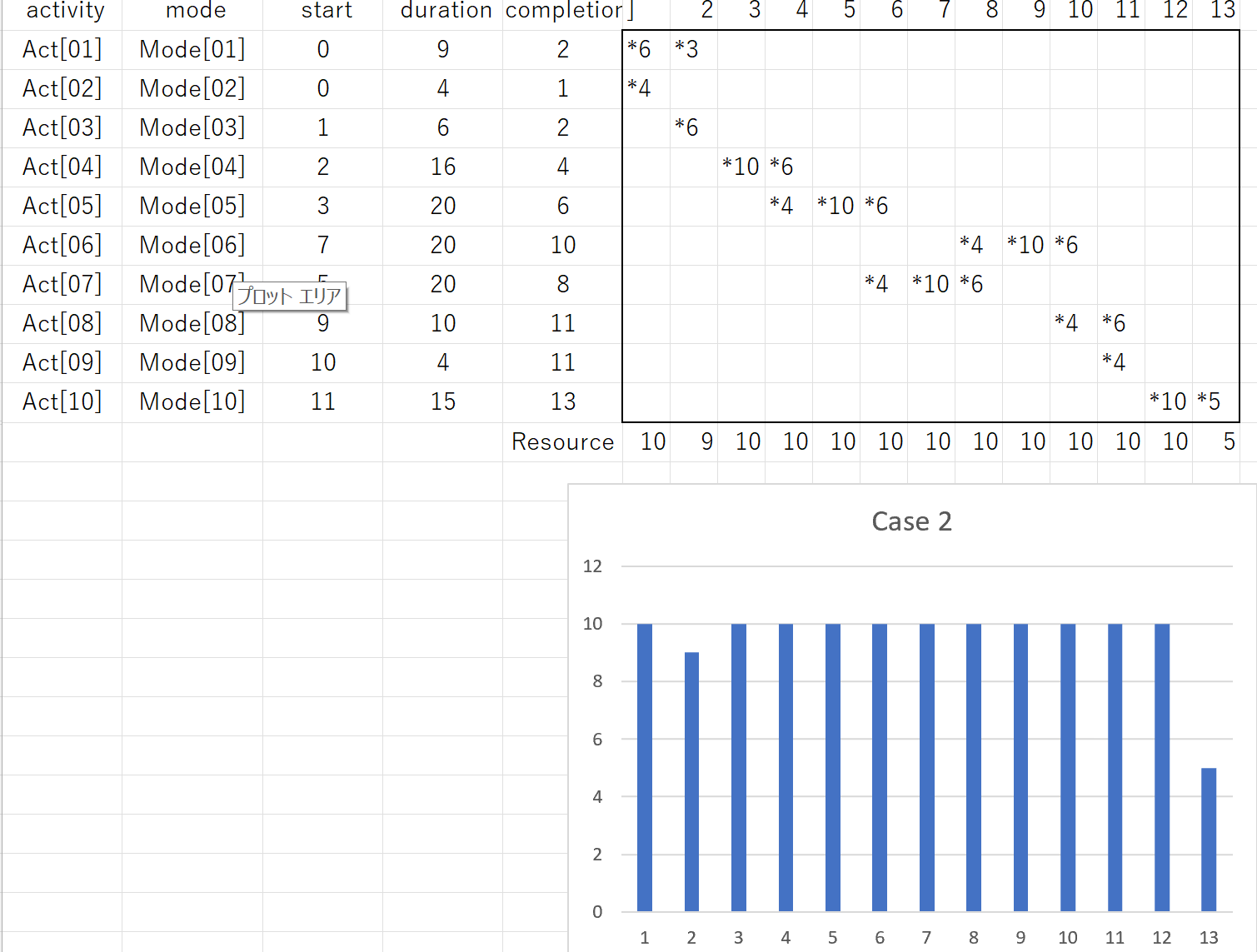
●上の例は配員計画を基に作業期間を定めており、日程計画と配員計画の同時計画を達成しています。次の例は、作業期間が未知の仮想作業を定義し、作業設備の確保も併せて達成しようとしています。
##prob13.py
from optseq import *
#=====リソース
prob13=Model()
res1=prob13.addResource("Resource1",capacity={(0,"inf"):10}) #10
res2=prob13.addResource("Resource2",capacity={(0,"inf"):10}) #10
#-----データセット
#i:[期間、後続、納期]
data={\
1:[9,[4,5] ,1],\
2:[4,[6,7] ,1],\
3:[6,[9] ,1],\
4:[16,[6,7],1],\
5:[20,[8] ,1],\
6:[20,[10] ,1],\
7:[20,[9] ,1],\
8:[10,[10] ,1],\
9:[4,[10] ,1],\
10:[15,[0] ,1],\
}
#=====アクティビティ
act={}
for i in data:
act[i]=prob13.addActivity("Act[{0}]".format(i))
#=====先行制約
for i in data:
for j in data[i][1]:
if j>0: prob13.addTemporal(act[i],act[j])
#====資源制約
mode={}
for i in data:
mode[i]=Mode("Mode[{0:02d}]".format(i),data[i][0])
mode[i].addResource(res1,requirement=data[i][2])
mode[i].addParallel(1,data[i][0],10)
act[i].addModes(mode[i])
#====仮想作業
dact={}
for i in data:
dact[i]=prob13.addActivity("DAct[{0:02d}]".format(i))
prob13.addTemporal(act[i],dact[i],tempType="SS")
prob13.addTemporal(act[i],dact[i],tempType="CC")
dmode={}
for i in data:
dmode[i]=Mode("DMode[{0:02d}]".format(i))
dmode[i].addBreak(0,0)
dmode[i].addResource(res2,{(0,"inf"):1},"break")
dact[i].addModes(dmode[i])
#=====最適化
prob13.Params.Makespan=True
prob13.Params.TimeLimit=1
#prob13.Params.OutputFlag=True
prob13.optimize()
prob13.write("prob13.txt")
prob13.writeExcel("prob13.csv")
#=====prob13.txt
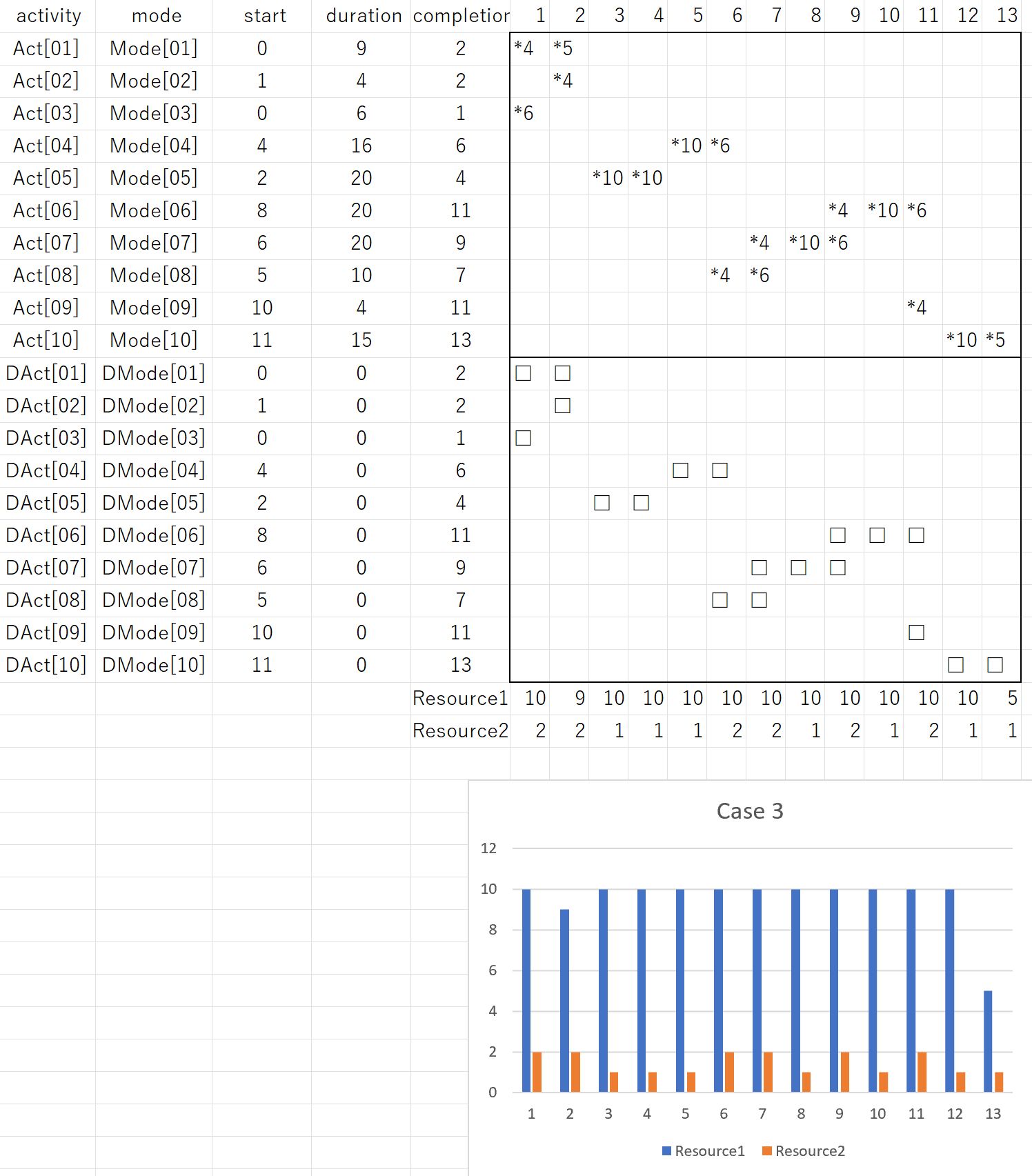
# activity mode duration 1 2 3 4 5 6 7 8 910111213
#---------------------------------------------------------
# Act[1] Mode[01] 9 *4*5
# Act[2] Mode[02] 4 *4
# Act[3] Mode[03] 6 *6
# Act[4] Mode[04] 16 *10*6
# Act[5] Mode[05] 20 *10*10
# Act[6] Mode[06] 20 *4*10*6
# Act[7] Mode[07] 20 *4*10*6
# Act[8] Mode[08] 10 *4*6
# Act[9] Mode[09] 4 *4
# Act[10] Mode[10] 15 *10*5
# DAct[01] DMode[01] 0 ....
# DAct[02] DMode[02] 0 ..
# DAct[03] DMode[03] 0 ..
# DAct[04] DMode[04] 0 ....
# DAct[05] DMode[05] 0 ....
# DAct[06] DMode[06] 0 ......
# DAct[07] DMode[07] 0 ......
# DAct[08] DMode[08] 0 ....
# DAct[09] DMode[09] 0 ..
# DAct[10] DMode[10] 0 ....
#---------------------------------------------------------
# resource usage/capacity
#---------------------------------------------------------
# Resource1 10 910101010101010101010 5
# 10101010101010101010101010
#---------------------------------------------------------
# Resource2 2 2 1 1 1 2 2 1 2 1 2 1 1
# 2 2 2 2 2 2 2 2 2 2 2 2 2
このプログラムを実行して、次の結果を得ます。
![Rendered by QuickLaTeX.com \[\displaystyle{\boxed{\begin{array}{cl} {\bf min}&\ Objective\ Function\\ {start\ times}&\\ {\bf subject\ to}&1^\circ\ Precedence\ Constraints\\ &2^\circ\ Resource\ Constraints \end{array}}}\]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e06beb8547aee1ddb83a85eeb795ffb6_l3.png)