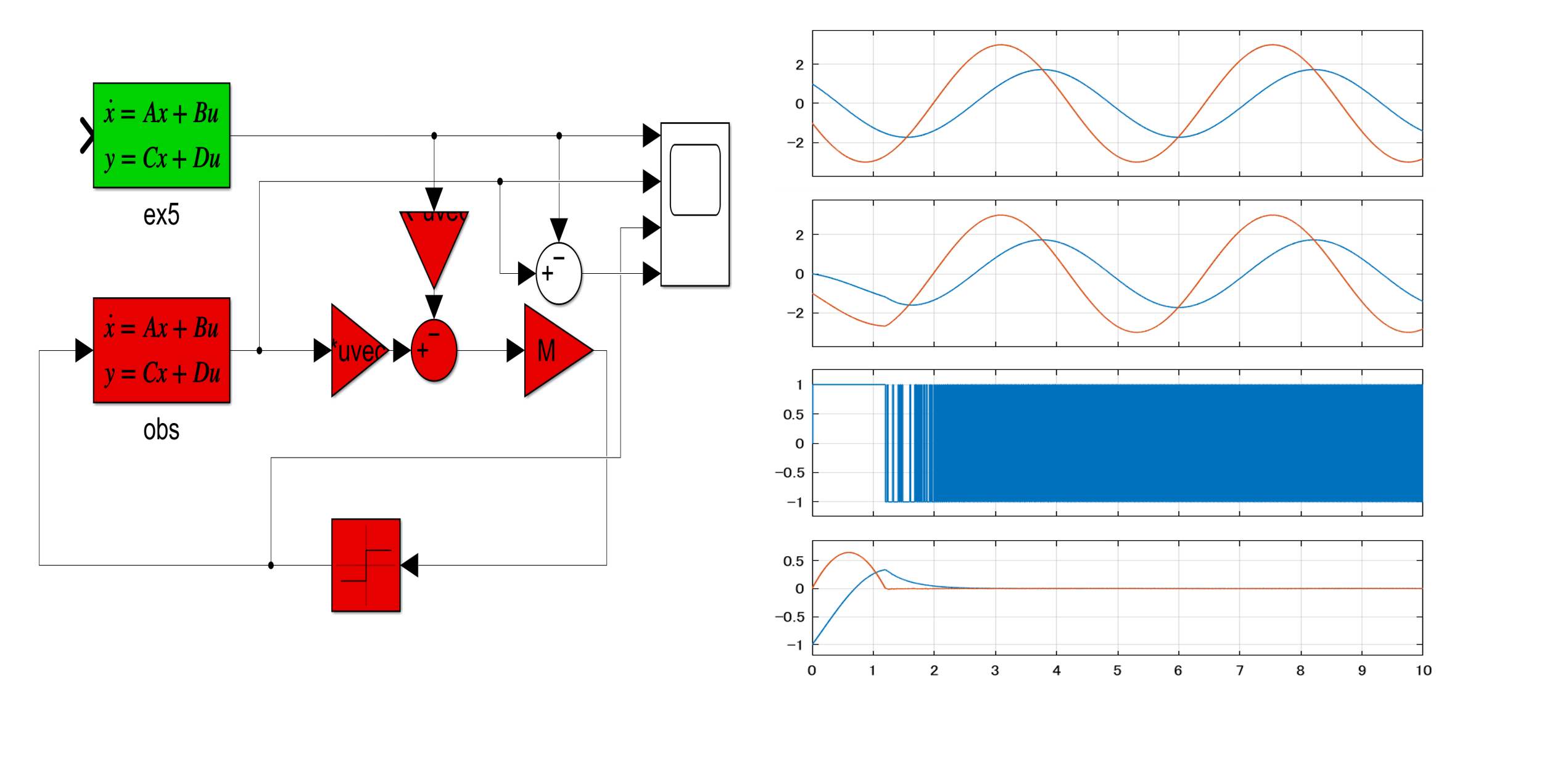
YMCPBの線形モデル
●制御対象YMCPBの運動方程式として次式を考えます。
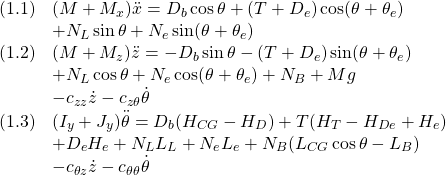
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(1')\quad \begin{array}{l} \left[\begin{array}{ccc} M+M_x & 0 & 0 \\ 0 & M+M_z & 0\\ 0 & 0 & I_y+J_y \end{array}\right] \left[\begin{array}{c} \ddot{x}\\ \ddot{z}\\ \ddot{\theta} \end{array}\right]= \left[\begin{array}{ccc} 0 & 0 & 0 \\ 0 & c_{zz} & c_{z\theta}\\ 0 & c_{\theta z} & c_{\theta\theta} \end{array}\right] \left[\begin{array}{c} \dot{x}\\ \dot{z}\\ \dot{\theta} \end{array}\right]\\ +\left[\begin{array}{c} D_b\cos\theta+(T+D_e)\cos(\theta+\theta_e)\\ -D_b\sin\theta-(T+D_e)\sin(\theta+\theta_e)\\ D_b(H_{CG}-H_D)+T(H_T-H_{De}+H_e)+D_eH_e \end{array}\right]\\ +\left[\begin{array}{c} N_L\sin\theta+N_e\sin(\theta+\theta_e)\\ N_L\cos\theta+N_e\cos(\theta+\theta_e)\\ N_LL_L+N_eL_e \end{array}\right] + \left[\begin{array}{c} 0 \\ N_B+Mg\\ N_B(L_{CG}\cos\theta-L_B) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5fcbf114446e6f6006a4add51667c0b6_l3.png)
ここで、![]() はそれぞれサージ、ヒーブ、ピッチを、
はそれぞれサージ、ヒーブ、ピッチを、![]() はそれぞれスラスト、船外機取付角を表しています。その他の物理パラメータの説明はここでは省略します。
はそれぞれスラスト、船外機取付角を表しています。その他の物理パラメータの説明はここでは省略します。
●いま状態変数ベクトルと操作変数ベクトルをそれぞれ
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \xi=\left[\begin{array}{c} x\\ z\\ \theta\\\hline \dot{x}\\ \dot{z}\\ \dot{\theta} \end{array}\right],\ \zeta=\left[\begin{array}{c} T\\ \theta_e \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-289b718cdf08a7268cfcc44b2dd308bb_l3.png)
ととると、次の非線形状態方程式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(3.1)\quad \underbrace{\frac{d}{dt}\left[\begin{array}{c} x\\ z\\ \theta\\\hline \dot{x}\\ \dot{z}\\ \dot{\theta} \end{array}\right]}_{\dot{\xi}}= \underbrace{ \left[\begin{array}{c} f_1(x,z,\theta,\dot{x},\dot{z},\dot{\theta},T,\theta_e)\\ f_2(x,z,\theta,\dot{x},\dot{z},\dot{\theta},T,\theta_e)\\ f_3(x,z,\theta,\dot{x},\dot{z},\dot{\theta},T,\theta_e)\\\hline f_4(x,z,\theta,\dot{x},\dot{z},\dot{\theta},T,\theta_e)\\ f_5(x,z,\theta,\dot{x},\dot{z},\dot{\theta},T,\theta_e)\\ f_6(x,z,\theta,\dot{x},\dot{z},\dot{\theta},T,\theta_e) \end{array}\right]}_{f(\xi,\zeta)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-986df1fe9bf874b3902a899fdb7379ed_l3.png)
ただし
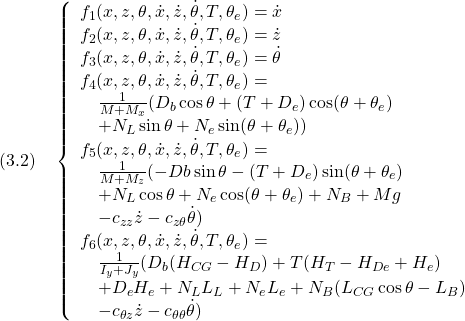
●制御対象YMCPBに対する制御目的は、あるスラスト![]() と取付角
と取付角![]() の下で、巡航速度
の下で、巡航速度![]() で走行するとき、一定の姿勢
で走行するとき、一定の姿勢![]() を保つこととします。これは、次の平衡状態
を保つこととします。これは、次の平衡状態![]() を、次の平衡入力
を、次の平衡入力![]() によって保持することとみなすことができます。
によって保持することとみなすことができます。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \xi^*=\left[\begin{array}{c} V^*t\\ z^*\\ \theta^*\\\hline V^*\\ 0\\ 0 \end{array}\right],\ \zeta^*=\left[\begin{array}{c} T^*\\ \theta_e^* \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5f6437de0791e355b2bdc371e694f78d_l3.png)
この平衡状態と平衡入力を定めるためには、![]() と
と![]() を所与として、残りの
を所与として、残りの![]() を次の非線形連立方程式を解いて求めます。
を次の非線形連立方程式を解いて求めます。
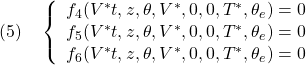
したがって、次式が成り立つことに注意します。
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad f(\xi^*,\zeta^*)= \left[\begin{array}{c} V^*\\ 0\\ 0\\\hline 0\\ 0\\ 0 \end{array}\right]=\frac{d}{dt}\xi^* }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7f31cdd4dd69a9639cb450150aaf8339_l3.png)
●この平衡状態![]() と平衡入力
と平衡入力![]() の回りで、非線形状態方程式
の回りで、非線形状態方程式![]() を線形近似します。
を線形近似します。
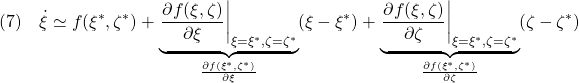
ここで(6)に注意して、線形状態方程式
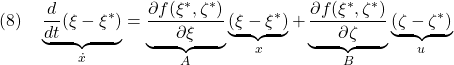
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \begin{array}{c} \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-V^*t\\ z(t)-z^*\\ \theta(t)-\theta^*\\\hline \dot{x}(t)-V^*\\ \dot{z}(t)\\ \dot{\theta}(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{ccc|ccc} 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\\hline 0 & a_{42} & a_{43} & a_{44} & a_{45} & a_{46} \\ 0 & a_{52} & a_{53} & a_{54} & a_{55} & a_{56} \\ 0 & a_{62} & a_{63} & a_{64} & a_{65} & a_{66} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x(t)-V^*t\\ z(t)-z^*\\ \theta(t)-\theta^*\\\hline \dot{x}(t)-V^*\\ \dot{z}(t)\\ \dot{\theta}(t) \end{array}\right] }_{x(t)}\\ + \underbrace{ \left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\\hline b_{41} & b_{42} \\ b_{51} & b_{52} \\ b_{61} & b_{62} \end{array}\right] }_{B} \underbrace{ \left[\begin{array}{c} T(t)-T^*\\ \theta_e(t)-\theta_e^*\\ \end{array}\right] }_{u(t)} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9015be8df754f0e7d33ca667c6ed948c_l3.png)
を得ます。
●次の5組のデータセットが与えられています。
| 艇 | 艇質量[kg] | 長手方向重心位置[m] | 備考 | |
| No1 | SPTM247 | 2709 | 1.9756 | INM抵抗試験レポートC2620-07CT18-RAP01による |
| No2 | SPTM247 | 2813 | 1.925 | 2021/8/2重量重心測定結果より |
| No3 | SPTM247 | 2845 | 1.937 | 2022/1/19重量重心測定結果より |
| No4 | SPTM247 | 2945 | 1.937 | No3重量に+100kg |
| No5 | SPTM247 | 2745 | 1.937 | No3重量に-100kg |
各データセットは、133個(![]() )の平衡状態と平衡入力と
)の平衡状態と平衡入力と![]() 行列を含みます(
行列を含みます(![]() 行列と
行列と![]() 行列は固定)。これらは、たとえば、データセットNo1に対しては図1のようにグラフ化されます。
行列は固定)。これらは、たとえば、データセットNo1に対しては図1のようにグラフ化されます。
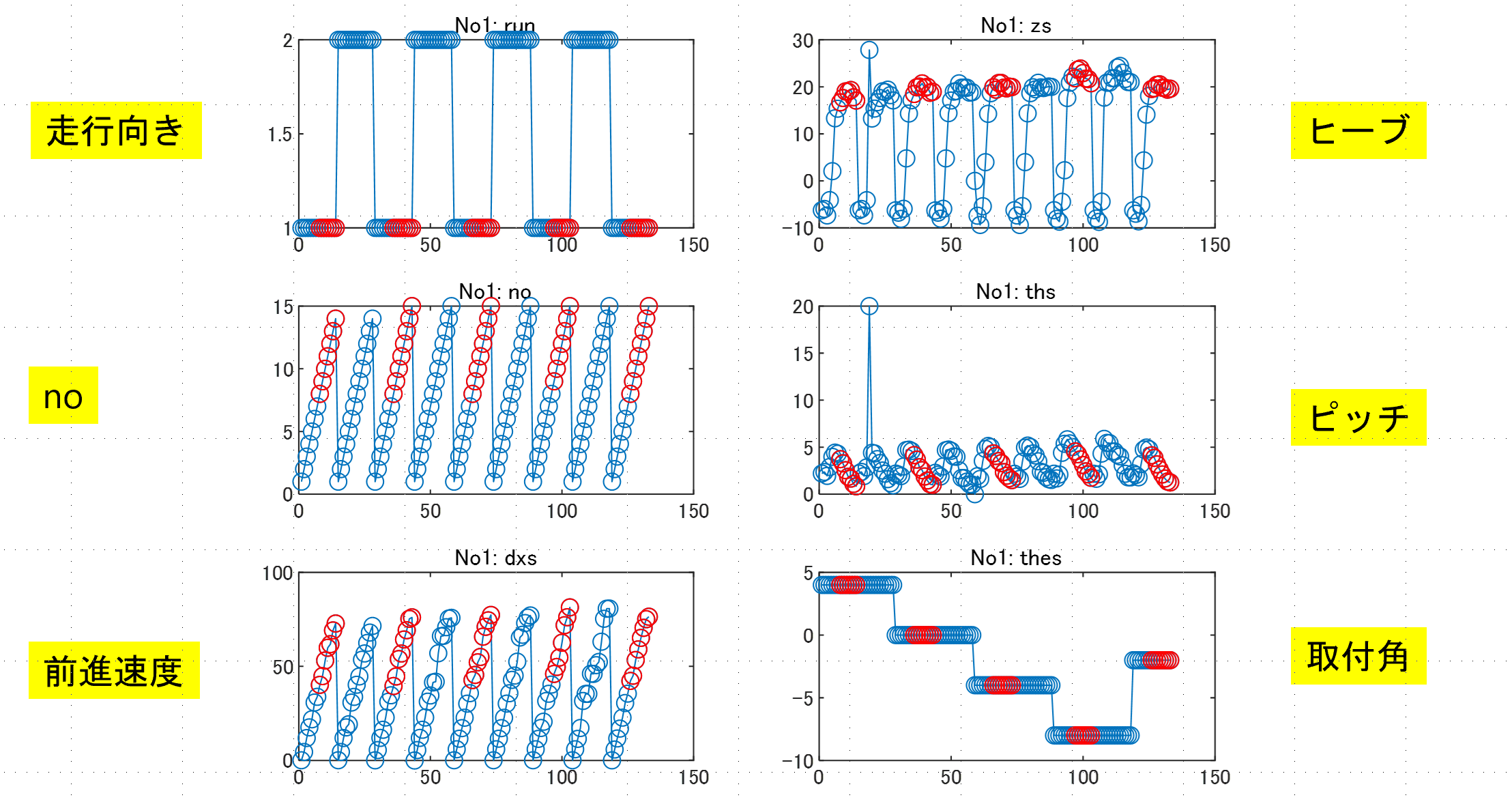
図1 データセットNo1における平衡状態
ここで、赤い〇の平衡状態は、制御系の設計および評価のために選ばれた、次表に示す39点です。![]() の場合の平衡状態回りの線形モデルについてコントローラを設計します。
の場合の平衡状態回りの線形モデルについてコントローラを設計します。
| run | k | ||
| -4 deg | run1 | 8,9,10,11,12,13,14 | |
| 0 deg | run1 | 36,37,38,39,40,41,42,43 | |
| 4 deg | run1 | 66,67,68,69,70,71,72,73 | |
| 8 deg | run1 | 96,97,98,99,100,101,102,103 | |
| 2 deg | run1 | 126,127,128,129,130,131,132,133 |
またデータセットNo1に対する行列![]() の固有値は図2のようにグラフ化されます。
の固有値は図2のようにグラフ化されます。
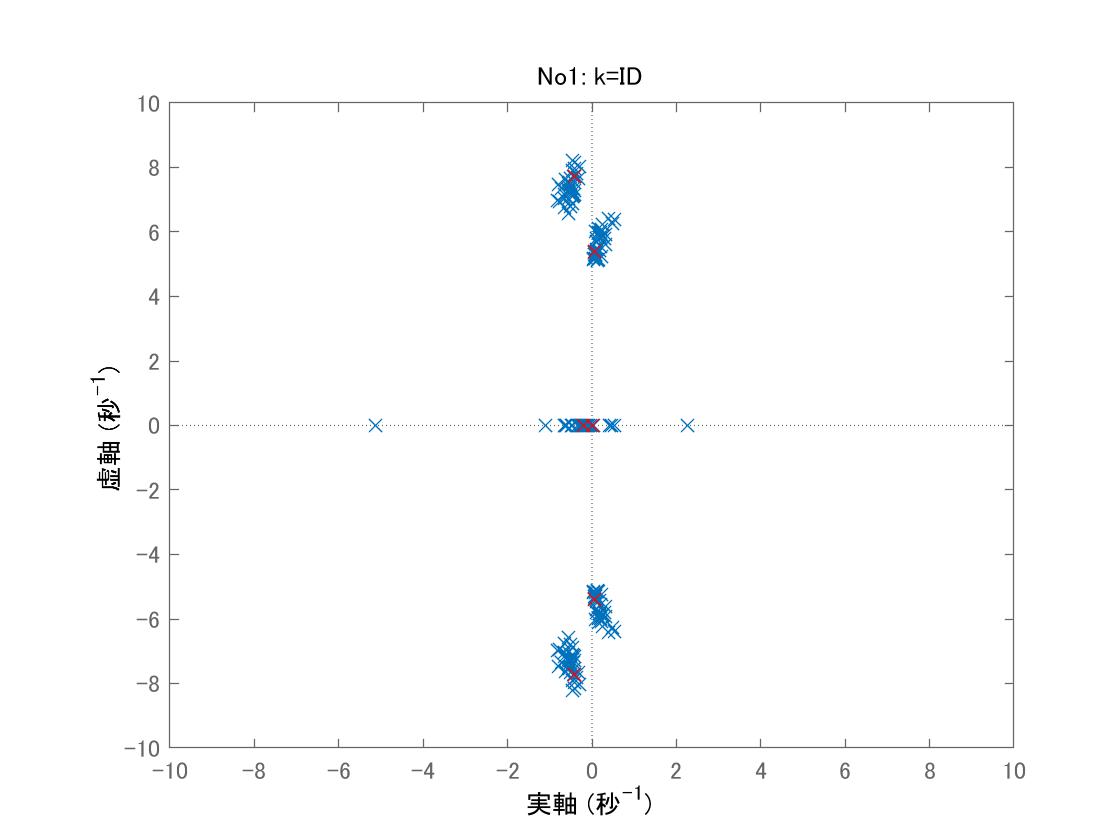
図2 データセットNo1における行列![]() の固有値
の固有値
各線形モデルに対して複素固有値が2対、実固有値が2個(うち1個は零)あることがわかります。不安定な複素固有値はピッチの振舞いに、安定な複素固有値はヒーブの振舞いに、非零実固有値は速度変動に関係しています。速度変動が発散する場合があることが気になるところです。
制御系設計用線形モデル
●制御系設計用線形モデルを得るために、まずアクチュエータについては、船外機の取付角を操作するためにレバーを引いた期間だけ一定の角速度![]() で回転するものとします。これを次式で表します。
で回転するものとします。これを次式で表します。
![]()
ここで、![]() は操作入力
は操作入力![]() が正のとき
が正のとき![]() 、負のとき
、負のとき![]() の値をとるものとします。すなわち
の値をとるものとします。すなわち
![]()
したがって、制御対象の状態方程式(9)とアクチュエータ(10)を合わせて、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{c} \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-V^*t\\ z(t)-z^*\\ \theta(t)-\theta^*\\\hline \dot{x}(t)-V^*\\ \dot{z}(t)\\ \dot{\theta}(t)\\\hline \theta_e(t)-\theta_e^* \end{array}\right] }_{\dot{x}_a(t)} = \underbrace{ \left[\begin{array}{ccc|ccc|c} 0 & 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0\\\hline 0 & a_{42} & a_{43} & a_{44} & a_{45} & a_{46} & b_{42}\\ 0 & a_{52} & a_{53} & a_{54} & a_{55} & a_{56} & b_{52}\\ 0 & a_{62} & a_{63} & a_{64} & a_{65} & a_{66} & b_{62}\\\hline 0 & 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right] }_{A_a} \underbrace{ \left[\begin{array}{c} x(t)-V^*t\\ z(t)-z^*\\ \theta(t)-\theta^*\\\hline \dot{x}(t)-V^*\\ \dot{z}(t)\\ \dot{\theta}(t)\\\hline \theta_e(t)-\theta_e^* \end{array}\right] }_{x_a(t)}\\ + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 0 \\\hline 0 \\ 0 \\ 0 \\\hline \omega_e \end{array}\right] }_{B_a}u_e(t) + \left[\begin{array}{c} 0 \\ 0 \\ 0 \\\hline b_{41} \\ b_{51} \\ b_{61} \\\hline 0 \end{array}\right]\underbrace{(T(t)-T^*)}_{0} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d60d11235671d929a5e705c533a692dc_l3.png)
また状態変数のうち、![]() 、
、![]() 、
、![]() が計測できるものとします。このとき、状態方程式(12)に対する観測方程式は次式で表されます。
が計測できるものとします。このとき、状態方程式(12)に対する観測方程式は次式で表されます。
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{y(t)} = \underbrace{ \left[\begin{array}{ccc|ccc|c} 0 & 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x(t)-V^*t\\ z(t)-z^*\\ \theta(t)-\theta^*\\\hline \dot{x}(t)-V^*\\ \dot{z}(t)\\ \dot{\theta}(t)\\\hline \theta_e(t)-\theta_e^* \end{array}\right] }_{x(t)} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-19a5fd67356f5063740009700e8d5cd0_l3.png)
●制御対象YMCPBに対する制御目的は、あるスラスト![]() と取付角
と取付角![]() の下で、巡航速度
の下で、巡航速度![]() で走行するとき、一定の姿勢
で走行するとき、一定の姿勢![]() を保つこととします。この制御目的に照らして、サージ方向の状態変数は省いてよく、また操作変数も船外機取付角に限定することができます。ヒーブ方向の状態変数を残すか省くかによって、次の2種類の線形モデルが考えられます。
を保つこととします。この制御目的に照らして、サージ方向の状態変数は省いてよく、また操作変数も船外機取付角に限定することができます。ヒーブ方向の状態変数を残すか省くかによって、次の2種類の線形モデルが考えられます。
5次元モデル
![Rendered by QuickLaTeX.com \displaystyle{(14.1)\quad \begin{array}{l} \underbrace{ \frac{d}{dt} \left[\begin{array}{c} z(t)-z^*\\ \theta(t)-\theta^*\\ \dot{z}(t)\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{ccccc} 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ a_{52} & a_{53} & a_{55} & a_{56} & b_{52}\\ a_{62} & a_{63} & a_{65} & a_{66} & b_{62}\\ 0 & 0 & 0 & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} z(t)-z^*\\ \theta(t)-\theta^*\\ \dot{z}(t)\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{x(t)}\\ + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \\ \omega_e \end{array}\right] }_{B} u_e(t) + \left[\begin{array}{c} 0 \\ 0 \\ a_{54} \\ a_{64} \\ 0 \end{array}\right] \underbrace{(\dot{x}(t)-V^*)}_{0} + \left[\begin{array}{c} 0 \\ 0 \\ b_{51} \\ b_{61} \\ 0 \end{array}\right]\underbrace{(T(t)-T^*)}_{0} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b66229e291e6a7c831c272149ccfd762_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14.2)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{y(t)} = \underbrace{ \left[\begin{array}{ccccc} 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 1 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} z(t)-z^*\\ \theta(t)-\theta^*\\ \dot{z}(t)\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{x(t)} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-64265721f5befad0ff0fa09174416663_l3.png)
データセットNo1に対する行列![]() の固有値は図3のようにグラフ化されます。ここで、安定な固有値はヒーブの振舞いに、不安定な固有値はピッチの振舞いに関係しています。
の固有値は図3のようにグラフ化されます。ここで、安定な固有値はヒーブの振舞いに、不安定な固有値はピッチの振舞いに関係しています。
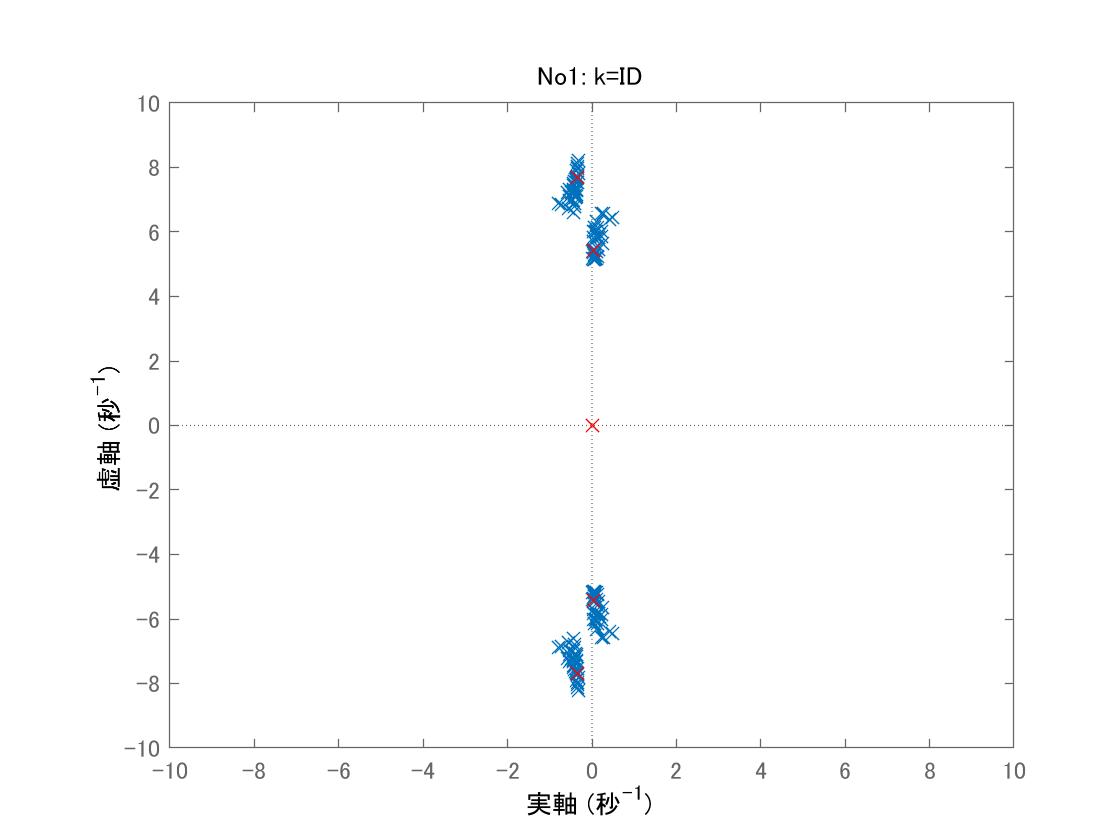
図3 データセットNo1を用いた5次元モデルの行列![]() の固有値
の固有値
3次元モデル
![Rendered by QuickLaTeX.com \displaystyle{(15.1)\quad \begin{array}{l} \underbrace{ \frac{d}{dt} \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0\\ a_{63} & a_{66} & b_{62}\\ 0 & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ \omega_e \end{array}\right] }_{B} u_e(t)\\ + \underbrace{\left[\begin{array}{cc} 0 & 0 \\ a_{62} & a_{65} \\ 0 & 0 \end{array}\right] \left[\begin{array}{c} z(t)-z^*\\ \dot{z}(t) \end{array}\right]}_{w(t)} + \left[\begin{array}{cc} 0 & 0 \\ a_{64} & b_{61} \\ 0 & 0 \end{array}\right] \underbrace{\left[\begin{array}{c} \dot{x}(t)-V^* \\ T(t)-T^* \end{array}\right]}_{0} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bf87259f32e1c8fdd86639d65f233881_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(15.2)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{y(t)} = \underbrace{ \left[\begin{array}{ccccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{x(t)} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2a21e890f7313ffc080ff529f06666fc_l3.png)
データセットNo1に対する行列![]() の固有値は図4のようにグラフ化されます。これからピッチに対応する固有値は不安定であることが分かります。
の固有値は図4のようにグラフ化されます。これからピッチに対応する固有値は不安定であることが分かります。
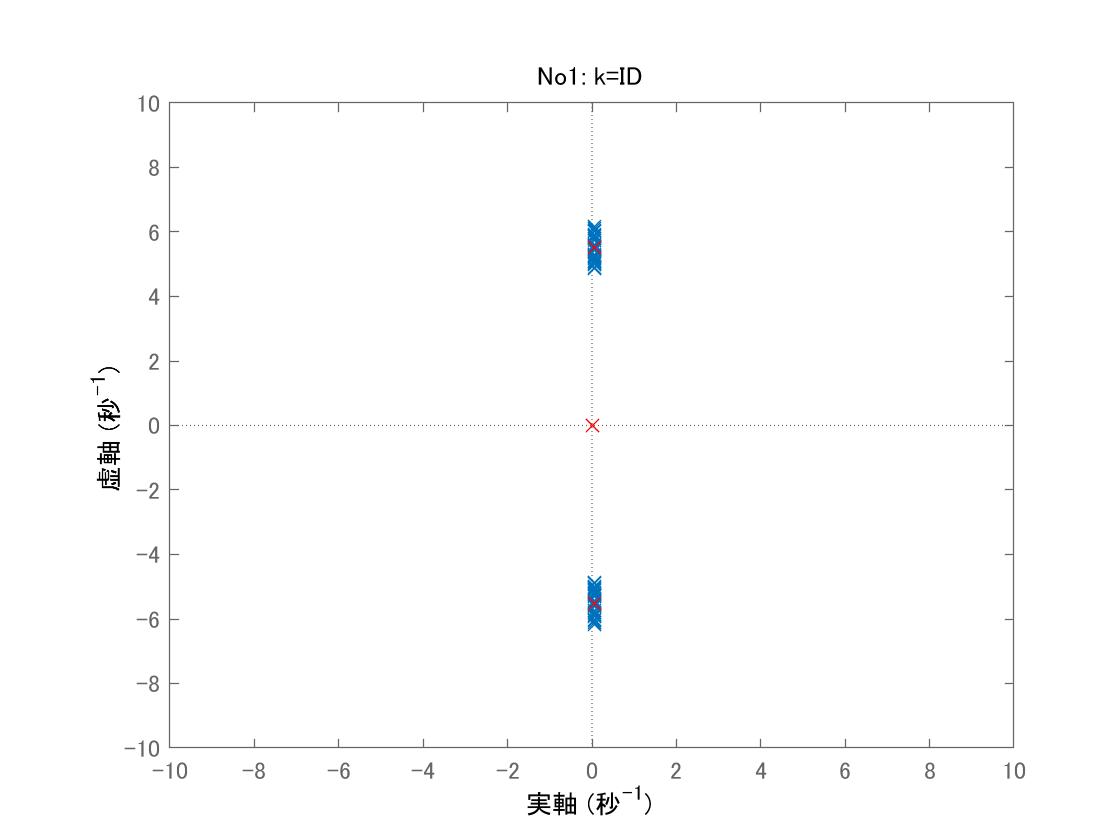
図4 データセットNo1を用いた3次元モデルの行列![]() の固有値
の固有値
●制御目的を達成する制御系を設計する立場から、2つのモデルを比較してみます。まず制御則として次式を考えます。
![]()
ここで、右辺第1項は状態フィードバック、第2項は船外機取付角をある収納状態![]() から所定の平衡入力値
から所定の平衡入力値![]() に設定するための積分動作です。
に設定するための積分動作です。
5次元モデル(14.1)の場合は、ヒーブに関する状態変数を計測できないので、状態オブザーバを用いてこれらを推定して、状態フィードバックを実施することになります。
一方3次元モデル(15.1)の場合は、状態フィードバックは実施できますが、ヒーブの振舞いの影響が外乱![]() として現れますので、これを抑制する必要があります。そのヒーブの振舞いは次式で表されます。
として現れますので、これを抑制する必要があります。そのヒーブの振舞いは次式で表されます。
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \begin{array}{l} \underbrace{ \frac{d}{dt} \left[\begin{array}{c} z(t)-z^*\\ \dot{z}(t) \end{array}\right] }_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{ccccc} 0 & 1 \\ a_{52} & a_{55} \end{array}\right] }_{A'} \underbrace{ \left[\begin{array}{c} z(t)-z^*\\ \dot{z}(t)\\ \end{array}\right] }_{x'(t)}\\ + \underbrace{ \left[\begin{array}{ccccc} 0 & 1 & 0\\ a_{53} & a_{56} & b_{52} \end{array}\right] }_{B'} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{y(t)}\\ + \left[\begin{array}{c} 0 \\ a_{54} \end{array}\right] \underbrace{(\dot{x}(t)-V^*)}_{0} + \left[\begin{array}{c} 0 \\ b_{51} \end{array}\right]\underbrace{(T(t)-T^*)}_{0} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d470e645c52cb94809030f2a1033637f_l3.png)
これからヒーブの振舞いには操作入力![]() は直接影響を及ぼさず、ピッチを通して間接的に影響すること分かります。ただ、これは漸近安定(
は直接影響を及ぼさず、ピッチを通して間接的に影響すること分かります。ただ、これは漸近安定(![]() は安定行列)なので、ピッチの安定化を速やかにできれば(
は安定行列)なので、ピッチの安定化を速やかにできれば(![]() が零に収束すれば)、(17)は考慮しなくともよいことになります。しかしながら、3次元モデルに対する状態フィードバックを5次元モデルに適用して、閉ループ系が漸近安定かどうかを調べておくことが考えられます。
が零に収束すれば)、(17)は考慮しなくともよいことになります。しかしながら、3次元モデルに対する状態フィードバックを5次元モデルに適用して、閉ループ系が漸近安定かどうかを調べておくことが考えられます。
制御系設計に3次元モデルを用いる場合は、状態オブザーバが不要となる利点がありますが、ヒーブの振舞いの影響が抑制されていることを確かめるために、5次元モデルに対する閉ループシミュレ-ションを行うことが重要になります。
●以上の結果を、![]() の場合の平衡状態回りの線形モデルについて数値で確認しておきます。
の場合の平衡状態回りの線形モデルについて数値で確認しておきます。
まず元の線形モデル(12)の行列![]() とその固有値は次のようになります。
とその固有値は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle{(18.1)\quad A= \left[\begin{array}{cccccc} 0 & 0 & 0 & 1.0000 & 0 & 0\\ 0 & 0 & 0 & 0 & 1.0000 & 0\\ 0 & 0 & 0 & 0 & 0 & 1.0000\\ 0 & 8.3458 & -6.9684 & -0.2549 & 0 & 0\\ 0 & -58.4515 & 67.9416 & 0.4686 & -0.7383 & -0.0369\\ 0 & 0.4559 & -30.3422 & -0.1922 & -0.0117 & 0.1175 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4b36eb6e0cb7156f03d9bf7681c55879_l3.png)
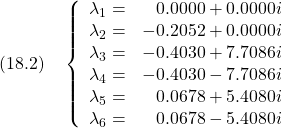
5次元モデル(14.1)における行列![]() とその固有値は次のようになります。
とその固有値は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle{(19.1)\quad A= \left[\begin{array}{ccccc} 0 & 0 & 1.0000 & 0 & 0\\ 0 & 0 & 0 & 1.0000 & 0\\ -58.4515 & 67.9416 & -0.7383 & -0.0369 & -0.0797\\ 0.4559 & -30.3422 & -0.0117 & 0.1175 & -2.7873\\ 0 & 0 & 0 & 0 & 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-385eb5461b75f3eab0188fc4a0c28dcf_l3.png)
これからサージに関わる状態変数を除いた場合、ヒーブとピッチに関わる固有値![]() がほぼ引き継がれることが分かります。
がほぼ引き継がれることが分かります。
一方3次元モデル(15.1)における行列![]() とその固有値は次のようになります。
とその固有値は次のようになります。
![Rendered by QuickLaTeX.com \displaystyle{(20.1)\quad A= \left[\begin{array}{ccc} 0 & 1.0000 & 0\\ -30.3422 & 0.1175 & -2.7873\\ 0 & 0 & 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-df1140cc4fabe39af15eb5dede652c01_l3.png)

これからさらにヒーブに関わる状態変数を除いた場合、ピッチに関わる固有値![]() がほぼ引き継がれることが分かります。
がほぼ引き継がれることが分かります。
●ヒーブとピッチに関わる固有値![]() の可制御性と可観測性を、5次元モデルを用いて調べてみます。
の可制御性と可観測性を、5次元モデルを用いて調べてみます。
![Rendered by QuickLaTeX.com \displaystyle{(21)\quad \left\{\begin{array}{l} \underline{\sigma}(\left[\begin{array}{cc} B & A-\lambda_1^{(5)} I_5 \end{array}\right])=0.0048^{*}\\ \underline{\sigma}(\left[\begin{array}{cc} B & A-\lambda_2^{(5)} I_5 \end{array}\right])=0.0048^{*}\\ \underline{\sigma}(\left[\begin{array}{cc} B & A-\lambda_3^{(5)} I_5 \end{array}\right])=0.0106\\ \underline{\sigma}(\left[\begin{array}{cc} B & A-\lambda_4^{(5)} I_5 \end{array}\right])=0.0106\\ \underline{\sigma}(\left[\begin{array}{cc} B & A-\lambda_5^{(5)} I_5 \end{array}\right])=0.1140\\ \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a7e4cf96c547aedfac2c36a38d07ed50_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(22)\quad \left\{\begin{array}{l} \underline{\sigma}(\left[\begin{array}{cc} C^T & A^T-\lambda_1^{(5)} I_5 \end{array}\right])=0.0146^{*}\\ \underline{\sigma}(\left[\begin{array}{cc} C^T & A^T-\lambda_2^{(5)} I_5 \end{array}\right])=0.0146^{*}\\ \underline{\sigma}(\left[\begin{array}{cc} C^T & A^T-\lambda_3^{(5)} I_5 \end{array}\right])=0.3129\\ \underline{\sigma}(\left[\begin{array}{cc} C^T & A^T-\lambda_4^{(5)} I_5 \end{array}\right])=0.3129\\ \underline{\sigma}(\left[\begin{array}{cc} C^T & A^T-\lambda_5^{(5)} I_5 \end{array}\right])=0.9940\\ \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9da4f1036a5ce1b33a3e76163bc55f97_l3.png)
(21)から、すべての固有値について行列![]() の最小特異値は正ですから、形式的には可制御性は成り立つと判定できます。ただ、*印の値が示すように、ヒーブはピッチに比べて相対的に可制御性の程度が弱く、状態フィードバックによる固有値の変更が難しいと言えます。したがって、制御対象は可制御でなく、むしろ可安定と判定することが考えられます。
の最小特異値は正ですから、形式的には可制御性は成り立つと判定できます。ただ、*印の値が示すように、ヒーブはピッチに比べて相対的に可制御性の程度が弱く、状態フィードバックによる固有値の変更が難しいと言えます。したがって、制御対象は可制御でなく、むしろ可安定と判定することが考えられます。
一方、(22)から、形式的には可観測性は成り立つと判定できます。ただ、*印の値が示すように、ヒーブはピッチに比べて相対的に可観測性の程度が弱く、状態オブザーバによる推定が難しいと言えます。
●操作入力(取付角)により、まずピッチが制御され、それがヒーブに影響を与えるという連成の仕組みを調べるために、(15.1)と(17)を数値で確かめてみます。
まず(15.1)は
![Rendered by QuickLaTeX.com \displaystyle{(15.1')\quad \begin{array}{l} \underbrace{ \frac{d}{dt} \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0\\ %a_{63} & a_{66} & b_{62}\\ -30.3422 & 0.1175 & -2.7873\\ 0 & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{x(t)}\\ + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ \omega_e \end{array}\right] }_{B} u_e(t) + \underbrace{\left[\begin{array}{cc} 0 & 0 \\ %a_{62} & a_{65} \\ 0.4559 & -0.0117 \\ 0 & 0 \end{array}\right] \left[\begin{array}{c} z(t)-z^*\\ \dot{z}(t) \end{array}\right]}_{w(t)} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6f7ec1b0d02eac3e57d854255ed386a7_l3.png)
となり、ヒーブのピッチへの影響を表す![]() に関わる係数
に関わる係数![]() の値がそれほど大きくなく、3次元モデルにおいても固有値が継承されることに注意します。
の値がそれほど大きくなく、3次元モデルにおいても固有値が継承されることに注意します。
一方(17)は
![Rendered by QuickLaTeX.com \displaystyle{(17')\quad \begin{array}{l} \underbrace{ \frac{d}{dt} \left[\begin{array}{c} z(t)-z^*\\ \dot{z}(t) \end{array}\right] }_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{ccccc} 0 & 1 \\ %a_{52} & a_{55} -58.4515 & -0.7383 \end{array}\right] }_{A'} \underbrace{ \left[\begin{array}{c} z(t)-z^*\\ \dot{z}(t)\\ \end{array}\right] }_{x'(t)}\\ + \underbrace{ \left[\begin{array}{ccccc} 0 & 1 & 0\\ %a_{53} & a_{56} & b_{52} 67.9416 & -0.0369 & -0.0797 \end{array}\right] }_{B'} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{y(t)} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dd41b1e619c39ebfa6602dc14ea3d00c_l3.png)
となります。これは漸近安定なので、ピッチの安定化が速やかに行えれば問題ないとと言えます。
●最後に、取付角からの伝達特性を調べておきます。
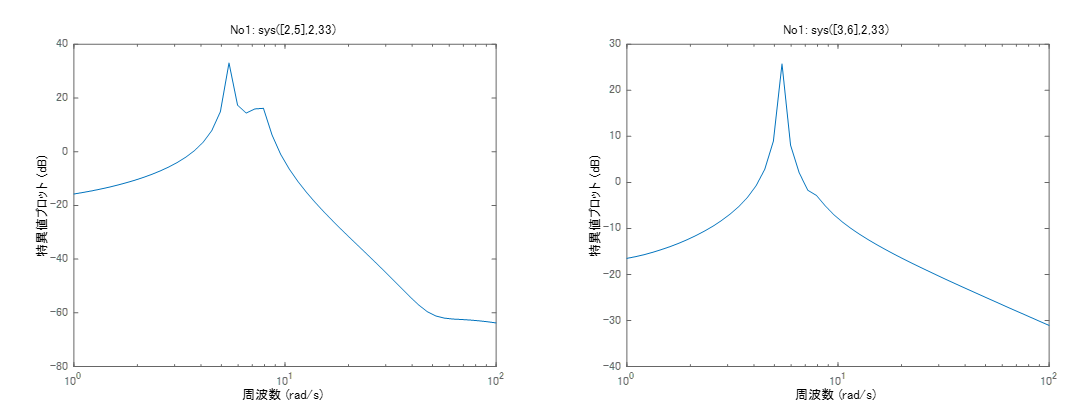
図5 取付角からヒーブまで(左図)とピッチまで(右図)の伝達特性
左図は2つの共振特性をもちますが、右図は(2つ目がほとんど消えていて)1つだけの共振特性をもちます。これから、ヒーブのピッチへの連成影響はほとんどないことがわかります。
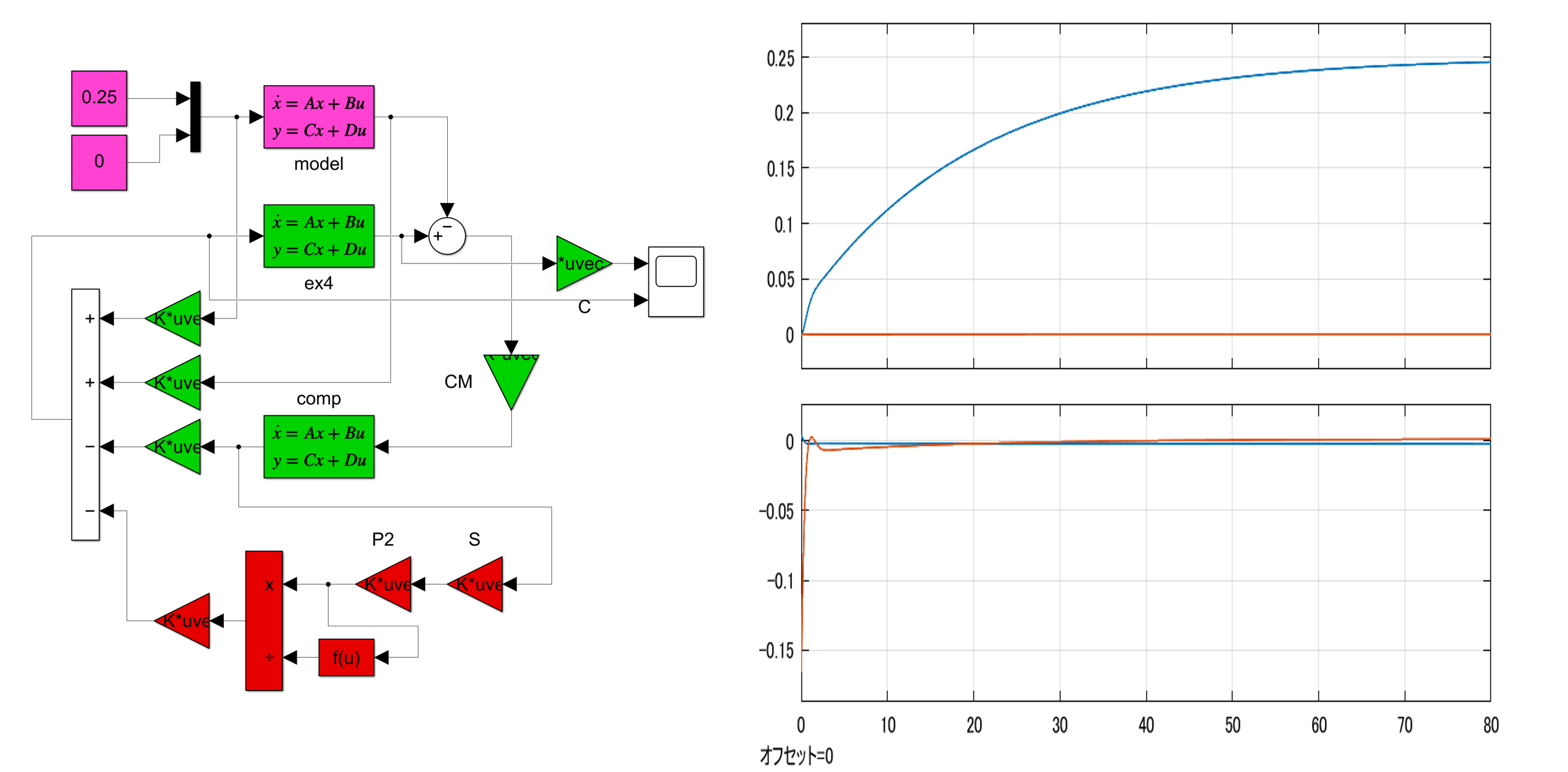
●以上の数値例の結果を得るためのプログラムを以下に示します。
| MATLAB |
|
参考:漸近安定性
|
【漸近安定性の定義とその等価な条件】 定義DA: 条件A1: |
漸近安定性とは、定義DAより、平衡状態が乱されたとき復帰できるかどうかにかかわる概念で、条件A1より、![]() 行列の固有値がすべて複素左半面にあることを調べて判定されます。
行列の固有値がすべて複素左半面にあることを調べて判定されます。
参考:可制御性・可安定性
|
【可安定性の定義とその等価な条件】 定義DS: 状態フィードバックにより安定化可能 条件S1: 【可制御性の定義とその等価な条件】 |
可安定性は、定義DSより、状態フィードバックにより安定化可能であることを意味し、条件S1が判定条件として知られています。一方、可制御性については、条件C4が判定条件として知られています。両者の相違は、すでに左半平面にある安定な固有値について関与(再配置)するかどうかにあります。可安定性の判定では不安定な固有値のみで条件S1を判定しますが、可制御性の判定ではすべて固有値について条件C4を判定します。
それでは、![]() に対して、条件S1と条件C4に出てくる行列
に対して、条件S1と条件C4に出てくる行列
![]()
の階数をどのようにして計算するかですが、これは![]() の非零特異値の数で決定します。したがって、条件S1と条件C4は、最小特異値が正かどうかで判定します。
の非零特異値の数で決定します。したがって、条件S1と条件C4は、最小特異値が正かどうかで判定します。
参考:可観測性・可検出性
|
【可検出性の定義とその等価な条件】 定義DD: 状態オブザーバを構成可能 条件D1: 【可観測性の定義とその等価な条件】 |
可検出性は、定義DDより、状態オブザーバを構成可能であることを意味し、条件D1が判定条件として知られています。状態オブザーバの![]() 行列は
行列は![]() と表され、オブザーバゲイン
と表され、オブザーバゲイン![]() は、仮想システム
は、仮想システム![]() に対する状態FB
に対する状態FB![]() による閉ループ系
による閉ループ系![]() を安定化して決定します。したがって、可検出性は
を安定化して決定します。したがって、可検出性は![]() の可安定性を意味します。一方、可観測性については、条件O4が判定条件として知られています。可検出性との相違は、すでに左半平面にある安定な
の可安定性を意味します。一方、可観測性については、条件O4が判定条件として知られています。可検出性との相違は、すでに左半平面にある安定な![]() の固有値について
の固有値について![]() で再配置するかどうかにあります。可検出性の判定では不安定な固有値のみで条件D1を判定しますが、可観測性の判定ではすべて固有値について条件O4を判定します。
で再配置するかどうかにあります。可検出性の判定では不安定な固有値のみで条件D1を判定しますが、可観測性の判定ではすべて固有値について条件O4を判定します。
それでは、![]() に対して、条件D1と条件O4に出てくる行列
に対して、条件D1と条件O4に出てくる行列
![]()
の階数をどのようにして計算するかですが、これは![]() の非零特異値の数で決定します。したがって、条件D1と条件O4は、最小特異値が正かどうかで判定します。
の非零特異値の数で決定します。したがって、条件D1と条件O4は、最小特異値が正かどうかで判定します。
参考:状態オブザーバ
●通常の状態オブザーバは
![]()
で表され
![]()
のように漸近的に元の状態を推定するものです。行列![]() はオブザーバゲインと呼ばれ、
はオブザーバゲインと呼ばれ、![]() は安定行列とするように選ばれます。
は安定行列とするように選ばれます。
によって表される漸近安定なシステムで、この出力が![]() に漸近するように構成するものです。そのためには、あるサイズ
に漸近するように構成するものです。そのためには、あるサイズ![]() の行列
の行列![]() に対して次式を満足させることが必要十分となります。
に対して次式を満足させることが必要十分となります。
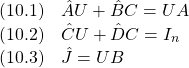
参考:最小実現
一般に,不可制御かつ不可観測な状態空間表現は適当な座標変換により,つぎの正準構造をもつように変換できることが知られています。
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \left[\begin{array}{c|c} TAT^{-1} & TB \\\hline CT^{-1} & D \end{array}\right] = \left[\begin{array}{cccc|c} A_1 & 0 & X_{13} & 0 & B_1 \\ X_{21} & A_2 & X_{23} & X_{24} & B_2 \\ 0 & 0 & A_3 & 0 & 0 \\ 0 & 0 & X_{43} & A_4 & 0 \\\hline C_1 & 0 & C_3 & 0 & 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4b2e92c732c0f76c1c7685becd70b05c_l3.png)
ここで,正方行列![]() ,
,![]() ,
,![]() ,
,![]() の次数は一意に定まり,
の次数は一意に定まり,![]() は可制御対,
は可制御対,![]() は可観測対です。この正準構造のブロック線図を図1に示します。
は可観測対です。この正準構造のブロック線図を図1に示します。

図1 正準構造のブロック線図
さて,つぎが成り立ちます。
![]()
すなわち,可制御かつ可観測な部分系が入力から出力までの伝達特性を表しています。
![Rendered by QuickLaTeX.com {\rm rank}\, \left[\begin{array}{c} C \\ CA \\ \vdots\\ CA^{n-1} \end{array}\right] =n](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c018f5737238e4ac298d377adf711de0_l3.png)
![Rendered by QuickLaTeX.com \boxed{{\rm rank} \left[\begin{array}{c} C \\ A-\lambda I_n \end{array}\right]=n}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-16e4ae46fa331c1889ac8dbffdb8b61a_l3.png) (
(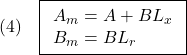
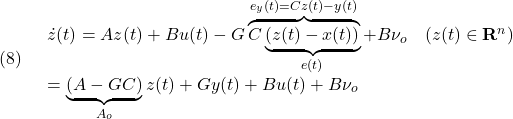
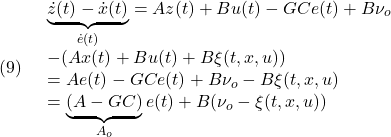
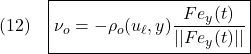
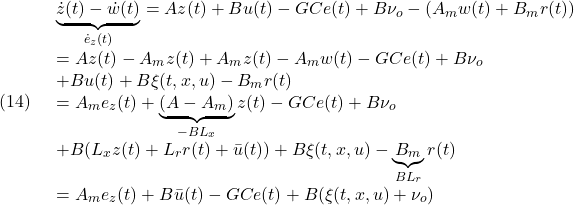
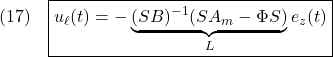
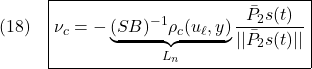
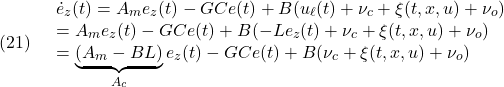
![Rendered by QuickLaTeX.com \displaystyle{(22)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} (u(t)+\xi(t,x,u)) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-afe711daafabb0f12e447bb07a3ace73_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} e_{z1}(t)\\ e_{z2}(t) \end{array}\right] }_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I_m \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} e_{z1}(t)\\ e_{z2}(t) \end{array}\right] }_{x(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d0776a59ef9ed32eda82a08310faf1f3_l3.png)
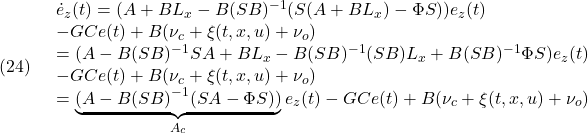
![Rendered by QuickLaTeX.com \displaystyle{(25)\quad \begin{array}{l} \underbrace{\left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right]}_{\bar{e}_z(t)}= \underbrace{\left[\begin{array}{cc} I_{n-m} & 0_{n\times m} \\ S_1 & S_2 \\ \end{array}\right]}_{\bar T} \underbrace{\left[\begin{array}{c} e_{z1}(t)\\ e_{z2}(t) \end{array}\right]}_{e_z(t)}\\ \Leftrightarrow \underbrace{\left[\begin{array}{c} e_{z1}(t)\\ e_{z2}(t) \end{array}\right]}_{e_z(t)}= \underbrace{\left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ -M & S_2^{-1} \\ \end{array}\right]}_{\bar{T}^{-1}} \underbrace{\left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right]}_{\bar{e}_z(t)}\quad(M=S_2^{-1}S_1) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-348e24095f272550ca7b0d85c1be93cf_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(26)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} I & 0 \\ -M & S_2^{-1} \\ \end{array}\right] }_{\bar{T}^{-1}} \underbrace{ \left[\begin{array}{c} \dot e_{z1}(t)\\ \dot s(t) \end{array}\right] }_{\dot{\bar{e}}_z(t)}\\ = (\left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] - \left[\begin{array}{c} 0\\ B_2 \end{array}\right] (\left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] \left[\begin{array}{c} 0\\ B_2 \end{array}\right])^{-1}\\ \times(\left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] -\Phi \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right]) ) \underbrace{ \left[\begin{array}{cc} I & 0 \\ -M & S_2^{-1} \\ \end{array}\right] }_{\bar{T}^{-1}} \underbrace{ \left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right] }_{\bar{e}_z(t)}\\ -G Ce(t)+\left[\begin{array}{c} 0\\ B_2 \end{array}\right](\nu_c+\xi(t,x,u)+\nu_o) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8b57169deafca1bae478ad161a8da6bc_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(27)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot e_{z1}(t)\\ \dot s(t) \end{array}\right] }_{\dot{\bar{e}}_z(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{\bar{T}} (\left[\begin{array}{cc} A_{11}-A_{12}M & A_{12}S_2^{-1} \\ A_{21}-A_{22}M & A_{22}S_2^{-1} \\ \end{array}\right] -\left[\begin{array}{c} 0\\ B_2 \end{array}\right](S_2B_2)^{-1}\\ \times(\left[\begin{array}{cc} S_1 & S_2 \end{array}\right] \left[\begin{array}{cc} A_{11}-A_{12}M & A_{12}S_2^{-1} \\ A_{21}-A_{22}M & A_{22}S_2^{-1} \\ \end{array}\right] -\Phi \left[\begin{array}{cc} 0 & I_m \\ \end{array}\right]) ) \underbrace{ \left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right] }_{\bar{e}_z(t)}\\ -\underbrace{\bar{T}G}_{\bar{G}} Ce(t) +\underbrace{\left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right]}_{\bar{T}} \left[\begin{array}{c} 0\\ B_2 \end{array}\right](\nu_c+\xi(t,x,u)+\nu_o)\\ = (\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22}\\ \end{array}\right] -\left[\begin{array}{c} 0\\ S_2B_2 \end{array}\right](S_2B_2)^{-1}\\ \times(\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22}\\ \end{array}\right] -\Phi \left[\begin{array}{cc} 0 & I_m \\ \end{array}\right]) ) \underbrace{ \left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right] }_{\bar{e}_z(t)}\\ -\bar{G} Ce(t)+\bar{B}(\nu_c+\xi(t,x,u)+\nu_o)\\ =\underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ 0 & \Phi\\ \end{array}\right]}_{A_c} \underbrace{ \left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right] }_{\bar{e}_z(t)} -\bar{G} Ce(t) +\underbrace{\left[\begin{array}{c} 0\\ S_2B_2 \end{array}\right]}_{\bar{B}}(\nu_c+\xi(t,x,u)+\nu_o) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2b1c5781518b0452b1e2a88534ac95c5_l3.png)
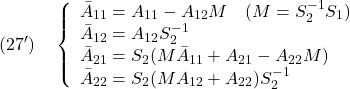
![Rendered by QuickLaTeX.com \displaystyle{(28)\quad \begin{array}{l} \left[\begin{array}{c} \dot{e}(t)\\ \dot{\bar{e}}_z(t) \end{array}\right]= \underbrace{\left[\begin{array}{cc} A_o & 0\\ -\bar{G}C & A_c \end{array}\right]}_{A_G} \left[\begin{array}{c} e(t)\\ \bar{e}_z(t) \end{array}\right]\\ + \left[\begin{array}{c} 0\\ \bar{B} \end{array}\right]{\nu}_c + \left[\begin{array}{c} B\\ \bar{B} \end{array}\right]\nu_o + \left[\begin{array}{c} -B\\ \bar{B} \end{array}\right]\xi(t,x,\hat{u}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4780b23f37e18adf37d5716a3c232cfb_l3.png)

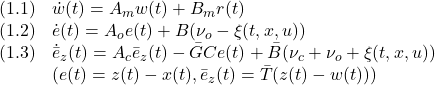
![Rendered by QuickLaTeX.com \displaystyle{(1.4)\quad \begin{array}{l} A_m=A+BL_x,\ B_m=BL_r\\ A_o=A-GC\\ A_c=\bar{T}(A_m-BL)\bar{T}^{-1}\\ L=(SB)^{-1}(SA_m-\Phi S)\\ \bar{B}=\left[\begin{array}{c} 0\\ S_2B_2 \end{array}\right],\ \bar{G}=\bar{T}G \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5af9937c0ebb7b0466617bc2ea71afbe_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{\left[\begin{array}{cc} \bar{P}_1 & 0\\ 0 & \bar{P}_2 \end{array}\right]}_{\bar P} \underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]}_{A_c} +\underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]^T}_{A_c^T} \underbrace{\left[\begin{array}{cc} \bar{P}_1 & 0\\ 0 & \bar{P}_2 \end{array}\right]}_{\bar P}<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9f1e612deced36f7c7db9b14fc59dc21_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \underbrace{\left[\begin{array}{cc} P & 0\\ 0 & \bar{P} \end{array}\right]}_{P_G} \underbrace{\left[\begin{array}{cc} A_o & 0\\ -\bar{G}C & A_c \end{array}\right]}_{A_G} +\underbrace{\left[\begin{array}{cc} A_o & 0\\ -\bar{G}C & A_c \end{array}\right]^T}_{A_G^T} \underbrace{\left[\begin{array}{cc} P & 0\\ 0 & \bar{P} \end{array}\right]}_{P_G}<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dceeb6208f924a3f6efeaa77bb099a32_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} PA_o & 0\\ -\bar{P}\bar{G}C & \bar{P}A_c \end{array}\right]}_{P_GA_G}+ \underbrace{\left[\begin{array}{cc} PA_o & 0\\ -\bar{P}\bar{G}C & \bar{P}A_c \end{array}\right]^T}_{(P_GA_G)^T} =\left[\begin{array}{cc} -Q & -C^T\bar{G}^T\bar{P}\\ -\bar{P}\bar{G}C & \bar{P}A_c+A_c^T\bar{P} \end{array}\right]<0\\ \Leftrightarrow \bar{P}A_c+A_c^T\bar{P}+\bar{P}\bar{G}CQ^{-1}C^T\bar{G}^T\bar{P}<0\\ \Leftrightarrow A_c\bar{P}^{-1}+\bar{P}^{-1}A_c^T+\bar{G}CQ^{-1}C^T\bar{G}^T<0\\ \Leftrightarrow A_c\bar{P}^{-1}+\bar{P}^{-1}A_c^T+\bar{G}CQ^{-1}C^T\bar{G}^T=-\bar{Q}\quad(\bar{Q}>0) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c62b77d490c2fb89c0065a176246cf86_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{lll} && \left[\begin{array}{cc} P & M \\ M^T & Q \end{array}\right]<0\\ &\Leftrightarrow& P-MQ^{-1}M^T<0,\ Q<0\\ &\Leftrightarrow& P<0,\ Q-M^TP^{-1}M<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eee622434bc9e2fc505eb899dbb107cb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]}_{A_c} \underbrace{\left[\begin{array}{cc} \bar{P}_1^{-1} & 0\\ 0 & \bar{P}_2^{-1} \end{array}\right]}_{\bar{P}^{-1}} + \underbrace{\left[\begin{array}{cc} \bar{P}_1^{-1} & 0\\ 0 & \bar{P}_2^{-1} \end{array}\right]}_{\bar{P}^{-1}} \underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]^T}_{A_c^T}\\ +\underbrace{\left[\begin{array}{c} \bar{G}_1\\ \bar{G}_2 \end{array}\right]}_{\bar{G}} \underbrace{CQ^{-1}C^T}_{Q_{22}} \underbrace{\left[\begin{array}{c} \bar{G}_1\\ \bar{G}_2 \end{array}\right]^T}_{\bar{G}^T}\\ = \underbrace{\left[\begin{array}{cc} \bar{A}_{11}\bar{P}_1^{-1} & \bar{A}_{12}\bar{P}_2^{-1}\\ 0 & \Phi \bar{P}_2^{-1} \end{array}\right]}_{A_c\bar{P}^{-1}} + \underbrace{\left[\begin{array}{cc} \bar{A}_{11}\bar{P}_1^{-1} & \bar{A}_{12}\bar{P}_2^{-1}\\ 0 & \Phi \bar{P}_2^{-1} \end{array}\right]^T}_{(A_c\bar{P}^{-1})^T}\\ +\underbrace{\left[\begin{array}{cc} \bar{G}_1Q_{22}\bar{G}_1^T &\bar{G}_1Q_{22}\bar{G}_2^T\\ \bar{G}_2Q_{22}\bar{G}_1^T &\bar{G}_2Q_{22}\bar{G}_2^T \end{array}\right]}_{\bar{G}CQ^{-1}C^T\bar{G}^T}\\ = \left[\begin{array}{cc} \bar{A}_{11}\bar{P}_1^{-1}+\bar{P}_1^{-1}\bar{A}_{11}^T+\bar{G}_1Q_{22}\bar{G}_1^T & \bar{A}_{12}\bar{P}_2^{-1}+\bar{G}_1Q_{22}\bar{G}_2^T\\ \bar{P}_2^{-1}\bar{A}_{12}^T+\bar{G}_2Q_{22}\bar{G}_1^T & \Phi\bar{P}_2^{-1}+\bar{P}_2^{-1}\Phi^T+\bar{G}_2Q_{22}\bar{G}_2^T \end{array}\right]\\ = \left[\begin{array}{cc} -\hat{Q}_1+\bar{G}_1Q_{22}\bar{G}_1^T & \bar{A}_{12}\bar{P}_2^{-1}+\bar{G}_1Q_{22}\bar{G}_2^T\\ \bar{P}_2^{-1}\bar{A}_{12}^T+\bar{G}_2Q_{22}\bar{G}_1^T & -\hat{Q}_2+\bar{G}_2Q_{22}\bar{G}_2^T \end{array}\right]<0\\ \Leftrightarrow \left\{\begin{array}{l} \bar{G}_1Q_{22}\bar{G}_1^T +(\bar{A}_{12}\bar{P}_2^{-1}+\bar{G}_1Q_{22}\bar{G}_2^T)\\ \times(\bar{G}_2Q_{22}\bar{G}_2^T -\hat{Q}_2)^{-1}(\bar{P}_2^{-1}\bar{A}_{12}^T+\bar{G}_2Q_{22}\bar{G}_1^T) <\hat{Q}_1\\ \bar{G}_2Q_{22}\bar{G}_2^T <\hat{Q}_2 \end{array}\right. \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d2a4be3ea4336e3bad8a74302a1a87d8_l3.png)

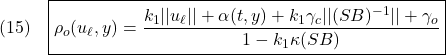
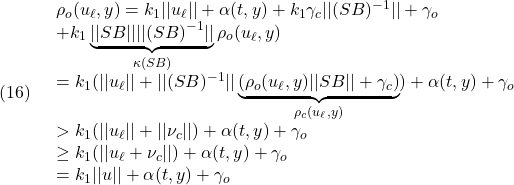
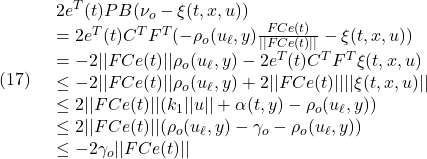
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \begin{array}{l} 2\bar{e}_z^T(t)\bar{P}\bar{B}(\nu_c+\nu_o+\xi(t,x,u))\\ =2\underbrace{\left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right]^T}_{\zeta^T(t)} \underbrace{\left[\begin{array}{cc} \bar{P}_1 & 0\\ 0 & \bar{P}_2 \end{array}\right]}_{\bar P} \underbrace{\left[\begin{array}{c} 0\\ S_2B_2 \end{array}\right]}_{\bar{B}}(\nu_c+\nu_o+\xi(t,x,u))\\ =-2s^T(t)\bar{P}_2(S_2B_2)\rho_o(u_\ell,y)\frac{FCe(t)}{||FCe(t)||}\\ -2s^T(t)\bar{P}_2(S_2B_2)(S_2B_2)^{-1}\rho_c(u_\ell,y) \frac{\bar{P}_2s(t)}{||\bar{P}_2s(t)||}+2s^T(t)\bar{P}_2(S_2B_2)\xi(t,x,u)\\ =-2s^T(t)\bar{P}_2(S_2B_2)\rho_o(u_\ell,y)\frac{B^TPe(t)}{||B^TPe(t)||}\\ -2s^T(t)\bar{P}_2\rho_c(u_\ell,y)\frac{\bar{P}_2s(t)}{||\bar{P}_2s(t)||}+2s^T(t)\bar{P}_2(S_2B_2)\xi(t,x,u)\\ \le 2||\bar{P}_2s(t)||||S_2B_2||\rho_o(u_\ell,y)-2\rho_c(u_\ell,y)||\bar{P}_2s(t)||\\ +2||\bar{P}_2s(t)||||S_2B_2||||\xi(t,x,u)||\\ \le 2||\bar{P}_2s(t)||(\rho_o(u_\ell,y)||S_2B_2||-\rho_c(u_\ell,y))\\ +2||\bar{P}_2s(t)||||S_2B_2||(k_1||u||+\alpha(t,y))\\ \le 2||\bar{P}_2s(t)||(\rho_c(u_\ell,y)-\gamma_c-\rho_c(u_\ell,y))\\ +2||\bar{P}_2s(t)||||S_2B_2||(\rho_o(u_\ell,y)-\gamma_o)\\ =-2\underbrace{(\gamma_c-||S_2B_2||(\rho_o(u_\ell,y)-\gamma_o))}_{\gamma_c'}||\bar{P}_2s(t)|| \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b653afff2b1cd408b6383ca8513746bc_l3.png)
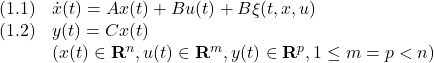
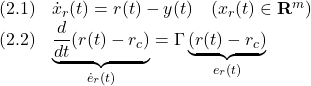
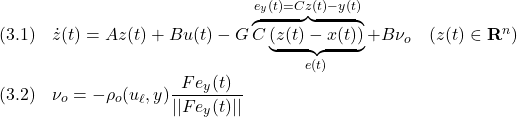
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \hat{u}(t)=\underbrace{-L\left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right]-L_rr(t)+L_{\dot r}\dot{r}(t)}_{\hat {u}_L}+\hat{\nu}_c\\ \displaystyle{\hat{\nu}_c=L_n\frac{P_2(S\left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right]-S_rr(t))}{||P_2(S\left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right]-S_rr(t))||}}\\ L=(S\tilde{B})^{-1}(S\tilde{A}-\Phi S)\\ L_r=(S\tilde{B})^{-1}(\Phi S_r+S_2MB_r)\\ L_{\dot r}=(S\tilde{B})^{-1}S_r\\ L_n=(S\tilde{B})^{-1}\rho_c(\hat{u}_L,y) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-024f6914b3128301f6c6ae196567ba16_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right] %}_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I_m \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right] %}_{x(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-027f6a001ff2fd6efdf5b3456395f8b3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \boxed{\begin{array}{l} \left[\begin{array}{c} \dot x_r(t)\\ \dot z(t) \end{array}\right] = \left[\begin{array}{cc} 0_{m\times m} & -C \\ 0_{n\times m} & A \\ \end{array}\right] \left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right] + \left[\begin{array}{c} I_p\\ -G \end{array}\right] e_y(t)\\ + \left[\begin{array}{c} r(t)\\ B(\hat{u}(t)+\nu_o) \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-65eb681dec39ab633fe7a5bbc2b85d2c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} \left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right]= \underbrace{\left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ S_1 & S_2 \\ \end{array}\right]}_{\bar T} \left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]\\ \Leftrightarrow \left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]= \underbrace{\left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ -M & S_2^{-1} \\ \end{array}\right]}_{\bar{T}^{-1}} \left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right]\quad(M=S_2^{-1}S_1) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4df32cc888cc01697c0d0a7a4a8de076_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \bar{T}^{-1} \left[\begin{array}{c} \dot{\tilde{z}}_1(t)\\ \dot{s}(t) \end{array}\right] = \underbrace{\left[\begin{array}{cc|c} 0_{m\times m} & -C_1 & -C_2 \\ 0_{n-m\times m} & A_{11} & A_{12} \\\hline 0_{m\times m} & A_{21} & A_{22} \end{array}\right]}_{\left[\begin{array}{cc} \tilde{A}_{11} & \tilde{A}_{12} \\ \tilde{A}_{21} & \tilde{A}_{22} \end{array}\right]} \left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ -M & S_2^{-1} \\ \end{array}\right] \left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right]\\ + \left[\begin{array}{c} I_p\\ -G_1\\\hline -G_2 \end{array}\right] e_y(t) + \left[\begin{array}{c} r(t)\\ 0\\\hline B_2(\hat{u}(t)+\nu_o) \end{array}\right]\\ = \underbrace{\left[\begin{array}{cc} \tilde{A}_{11}-\tilde{A}_{12}M & \tilde{A}_{12}S_2^{-1}\\ \tilde{A}_{21}-\tilde{A}_{22}M & \tilde{A}_{22}S_2^{-1} \end{array}\right]}_{\tilde{A}\bar{T}^{-1}} \left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right] - \left[\begin{array}{c} \bar{G}_1\\ G_2 \end{array}\right] e_y(t)\\ + \left[\begin{array}{c} B_rr(t)\\ B_2(\hat{u}(t)+\nu_o) \end{array}\right]\\ (\left[\begin{array}{c} G_1\\ G_2 \end{array}\right] =\left[\begin{array}{c} A_{12}C_2^{-1} \\ A_{22}C_2^{-1}-C_2^{-1}A_{22}^S \end{array}\right], \quad\bar{G}_1= \left[\begin{array}{c} -I_p\\ G_1 \end{array}\right]) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-da08553d36abc2e12fd0c39618cc6763_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \left[\begin{array}{c} \dot{\tilde{z}}_1(t)\\ \dot{s}(t) \end{array}\right] = \underbrace{\left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ S_1 & S_2 \\ \end{array}\right] \left[\begin{array}{cc} \tilde{A}_{11}-\tilde{A}_{12}M & \tilde{A}_{12}S_2^{-1}\\ \tilde{A}_{21}-\tilde{A}_{22}M & \tilde{A}_{22}S_2^{-1} \end{array}\right]}_{\bar{T}\tilde{A}\bar{T}^{-1}} \left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right]\\ - \left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ S_1 & S_2 \\ \end{array}\right] \left[\begin{array}{c} \bar{G}_1\\ G_2 \end{array}\right] e_y(t) + \left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ S_1 & S_2 \\ \end{array}\right] \left[\begin{array}{c} B_rr(t)\\ B_2(\hat{u}(t)+\nu_o) \end{array}\right]\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1da3c1791a8da84361163ffde267324f_l3.png)
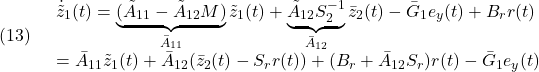
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \begin{array}{l} \dot{s}(t)= \underbrace{((S_1\bar{A}_{11}+S_2(\tilde{A}_{21}-\tilde{A}_{22}M))\tilde{z}_1(t)+(S_1\bar{A}_{12}+S_2\tilde{A}_{22}S_2^{-1})s(t)}_{S\tilde{A}\bar{T}^{-1}\left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right]=S\tilde{A}\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]}\\ -\underbrace{(S_1\bar{G}_1+S_2G_2)}_{\bar G_2}e_y(t)+S_1B_rr(t)\\ +\underbrace{S_2B_2}_{\Lambda}(L\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]+L_rr(t)+S_r\dot{r}(t)+\hat{\nu}_c+\nu_o)\\ =S\tilde{A}\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]-\bar{G}_2e_y(t)+S_1B_rr(t)\\ +\Lambda(-\Lambda^{-1}(S\tilde{A}-\Phi S)\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]-\Lambda^{-1}(\Phi S_r+S_2MB_r)r(t)+\Lambda^{-1}S_r\dot{r}(t))\\ +\Lambda(\hat{\nu}_c+\nu_o)\\ =S\tilde{A}\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]-\bar{G}_2e_y(t)+S_1B_rr(t)\\ -(S\tilde{A}-\Phi S)\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]-(\Phi S_r+S_2MB_r)r(t)+S_r\dot{r}(t)+\Lambda(\hat{\nu}_c+\nu_o)\\ =\Phi (\underbrace{S\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]}_{s(t)}-S_rr(t))+S_r\dot{r}(t)-\bar{G}_2e_y(t)+\Lambda(\hat{\nu}_c+\nu_o) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ebec66163067a3490f53ebceab553d5e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \begin{array}{l} \underbrace{\left[\begin{array}{c} \zeta_1(t)\\ \zeta_2(t) \end{array}\right]}_{\zeta(t)}= \left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right]+ \left[\begin{array}{c} \bar{A}_{11}^{-1}(\bar{A}_{12}S_r+B_r)r_c\\ -S_rr(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c676bab7a7f2b7c956feb633f175faa2_l3.png)
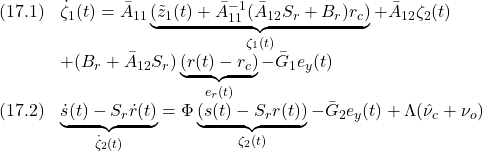
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \begin{array}{l} \underbrace{\left[\begin{array}{c} \dot \zeta_1(t)\\ \dot \zeta_2(t) \end{array}\right]}_{\dot{\zeta}(t)}= \underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]}_{A_c} \underbrace{\left[\begin{array}{c} \zeta_1(t)\\ \zeta_2(t) \end{array}\right]}_{\zeta(t)}\\ - \underbrace{\left[\begin{array}{c} \bar{G}_1\\ \bar{G}_2 \end{array}\right]}_{\bar{G}} \underbrace{e_y(t)}_{Ce(t)} + \underbrace{\left[\begin{array}{c} B_r+\bar{A}_{12}S_r\\ 0 \end{array}\right]}_{\bar{G}_r}e_r(t) + \underbrace{\left[\begin{array}{c} 0\\ \Lambda \end{array}\right]}_{\bar\Lambda}(\hat{\nu}_c+\nu_o) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e698246bb04c91be373318b20c960104_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(19)\quad \begin{array}{l} \left[\begin{array}{c} \dot{e}(t)\\ \dot \zeta(t) \end{array}\right]= \underbrace{\left[\begin{array}{cc} A_o & 0\\ -\bar{G}C & A_c \end{array}\right]}_{A_G} \left[\begin{array}{c} e(t)\\ \zeta(t) \end{array}\right]\\ + \left[\begin{array}{c} 0\\ \bar{G}_r \end{array}\right]e_r(t) + \left[\begin{array}{c} B\\ \bar\Lambda \end{array}\right]\nu_o + \left[\begin{array}{c} 0\\ \bar\Lambda \end{array}\right]\hat{\nu}_c - \left[\begin{array}{c} B\\ 0 \end{array}\right]\xi(t,x,\hat{u}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8e6c6626c17ebcf75a8e1b658d9e4738_l3.png)

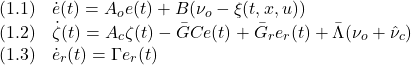
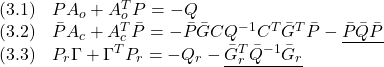

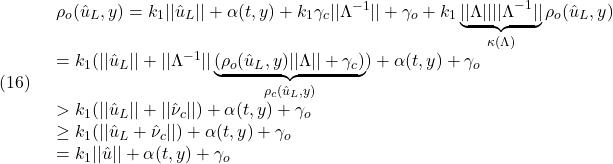
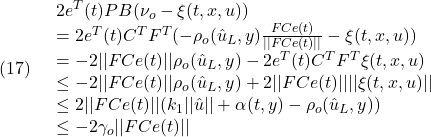
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \begin{array}{l} 2\zeta^T(t)\bar{P}\bar{\Lambda}(\nu_o+\hat{\nu}_c)\\ =2\underbrace{\left[\begin{array}{c} \zeta_1(t)\\ \zeta_2(t) \end{array}\right]^T}_{\zeta^T(t)} \underbrace{\left[\begin{array}{cc} \bar{P}_1 & 0\\ 0 & \bar{P}_2 \end{array}\right]}_{\bar P} \underbrace{\left[\begin{array}{c} 0\\ \Lambda \end{array}\right]}_{\bar\Lambda}(\nu_o+\hat{\nu}_c)\\ =-2\zeta_2^T(t)\bar{P}_2\Lambda\rho_o(\hat{u}_L,y)\frac{FCe(t)}{||FCe(t)||}-2\zeta_2^T(t)\bar{P}_2\Lambda\rho_c(\hat{u}_L,y)\Lambda^{-1} \frac{\bar{P}_2\zeta_2(t)}{||\bar{P}_2\zeta_2(t)||}\\ \le 2||\bar{P}_2\zeta_2(t)||||\Lambda||\rho_o(\hat{u}_L,y)-2\rho_c(\hat{u}_L,y)||\bar{P}_2\zeta_2(t)||\\ =2||\bar{P}_2\zeta_2(t)||(\rho_o(\hat{u}_L,y)||\Lambda||-\rho_c(\hat{u}_L,y))\\ =2||\bar{P}_2\zeta_2(t)||(\rho_c(\hat{u}_L,y)-\gamma_c-\rho_c(\hat{u}_L,y))\\ =-2\gamma_c||\bar{P}_2\zeta_2(t)|| \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-79955beab6ef0705346e5157fe6ced17_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad {\cal S}_c=\left\{\left[\begin{array}{c} e\\ \zeta_1\\ \zeta_2 \end{array}\right]\in{\bf R}^{2n+p}: \left\{\begin{array}{l} e_y(t)=Ce(t)=Cz(t)-y(t)=0\\ \zeta_2(t)=s(t)-S_rr(t)=0 \end{array}\right. \right\} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-198a3c5b246cf20144027bbb223bb2b6_l3.png)
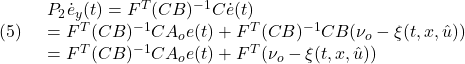
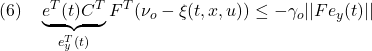
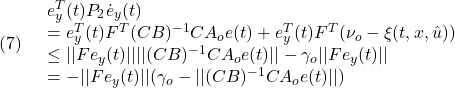
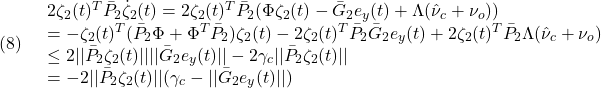
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \Omega_\eta=\left\{\left[\begin{array}{c} e\\ \zeta_1\\ \zeta_2 \end{array}\right]\in{\bf R}^{2n+p}: \left\{\begin{array}{l} ||(CB)^{-1}CA_oe(t)||<\gamma_o-\eta\\ ||\bar{G}_2e_y(t)||<\gamma_c-\eta \end{array}\right. \right\} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ba3afedc3c9f5d435d671a0460dfdda4_l3.png)
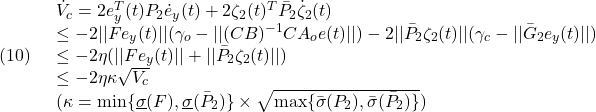
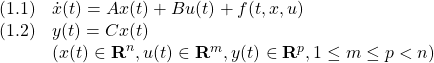
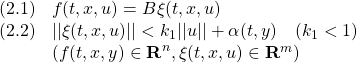
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{ll} (3.1) & \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t)\\ (3.2) & y(t) = \underbrace{ \left[\begin{array}{cc} C_1 & C_2 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6ec74dc0c4572a9c7fa91295a5ba283b_l3.png)
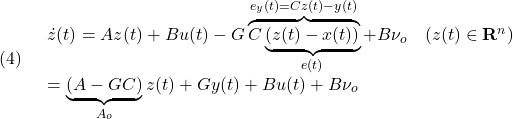
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} {\cal A}_{11} & {\cal A}_{12}\\ {\cal A}_{21} & {\cal A}_{22} \end{array}\right]}_{{\cal A}}\\ =\underbrace{\left[\begin{array}{cc} {A}_{11}-{A}_{12}C_2^{-1}C_1 & A_{12}C_2^{-1} \\ C_1{\cal A}_{11}+C_2A_{21}-C_2A_{22}C_2^{-1}C_1 & C_1A_{12}C_2^{-1}+C_2A_{22}C_2^{-1} \end{array}\right] }_{T_cAT_c^{-1}}\\ {\cal B}=\underbrace{\left[\begin{array}{c} 0 \\ C_2B_2 \end{array}\right] }_{T_cB}\\ {\cal C}=\underbrace{\left[\begin{array}{cc} 0 & I_p \end{array}\right] }_{CT_c^{-1}}\\ {\cal P}= \underbrace{\left[\begin{array}{cc} I_{n-p} & 0 \\ -C_2^{-1}C_1 & C_2^{-1} \end{array}\right]^T \left[\begin{array}{cc} P_1 & 0\\ 0 & P_2 \end{array}\right] \left[\begin{array}{cc} I_{n-p} & 0 \\ -C_2^{-1}C_1 & C_2^{-1} \end{array}\right] }_{T_c^TPT_c}\\ =\left[\begin{array}{cc} I_{n-p} & -C_1^TC_2^{-T} \\ 0 & C_2^{-T} \end{array}\right]^T \left[\begin{array}{cc} P_1 & 0 \\ -P_2C_2^{-1}C_1 & P_2C_2^{-1} \end{array}\right]\\ =\left[\begin{array}{cc} P_1+C_1^TC_2^{-T}P_2C_2^{-1}C_1 & -C_1^TC_2^{-T}P_2C_2^{-1}\\ -C_2^{-T}P_2C_2^{-1}C_1 & C_2^{-T}P_2C_2^{-1} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-23b25bc8ecbab40ee6e5976ebefccd82_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} G=\underbrace{\left[\begin{array}{cc} I_{n-p} & 0 \\ -C_2^{-1}C_1 & C_2^{-1} \end{array}\right] }_{T_c^{-1}} \underbrace{\left[\begin{array}{c} A_{12}C_2^{-1}\\ C_1A_{12}C_2^{-1}+C_2A_{22}C_2^{-1}-{\cal A}_{22}^s \end{array}\right] }_{\left[\begin{array}{c} {\cal A}_{12}\\ {\cal A}_{22}-{\cal A}_{22}^s \end{array}\right]}\\ =\left[\begin{array}{c} A_{12}C_2^{-1} \\ A_{22}C_2^{-1}-C_2^{-1}A_{22}^S \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6f55e042f0e71a68f90ee8ddf5588d0c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} P_1+C_1^TC_2^{-T}P_2C_2^{-1}C_1 & -C_1^TC_2^{-T}P_2C_2^{-1}\\ -C_2^{-T}P_2C_2^{-1}C_1 & C_2^{-T}P_2C_2^{-1} \end{array}\right] \left[\begin{array}{c} 0 \\ C_2B_2 \end{array}\right] }_{{\cal P}{\cal B}} = \underbrace{\left[\begin{array}{cc} 0 & I_p \end{array}\right]^T }_{{\cal C}^T} F^T\\ \Rightarrow F=(C_2^{-T}P_2C_2^{-1}C_2B_2)^T=B_2^TP_2C_2^{-1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d8371d4e684ace7595130cce38802819_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \boxed{\begin{array}{l} G= \left[\begin{array}{c} A_{12}C_2^{-1} \\ A_{22}C_2^{-1}-C_2^{-1}A_{22}^S \end{array}\right]\\ F=B_2^TP_2C_2^{-1} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-acc6f79294b0cb173b67e46276765b51_l3.png)
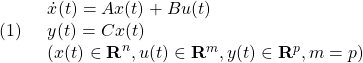
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \left[\begin{array}{c} \dot x_r(t)\\ \dot x(t) \end{array}\right] = \left[\begin{array}{c|cc} 0 & -C_1 & -C_2\\\hline 0 & A_{11} & A_{12} \\ 0 & A_{21} & A_{22} \end{array}\right] \left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right] + \left[\begin{array}{c} 0\\\hline 0\\ B_2 \end{array}\right] u(t) + \left[\begin{array}{c} I_m \\\hline 0 \\ 0 \end{array}\right] r(t)\\ (x_r(t)\in{\rm\bf R}^m, x(t)\in{\rm\bf R}^n) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1ab4b378422eddd1bff475a2408082e2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5a)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc|c} 0 & -C_1 & -C_2\\ 0 & A_{11} & A_{12} \\\hline 0 & A_{21} & A_{22} \end{array}\right] }_{\tilde{A}=\left[\begin{array}{cc} \tilde{A}_{11} & \tilde{A}_{12} \\ \tilde{A}_{21} & \tilde{A}_{22} \\ \end{array}\right]} \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0\\ 0\\\hline B_2 \end{array}\right] }_{\tilde{B}} u(t) + \left[\begin{array}{c} I_m \\ 0 \\\hline 0 \end{array}\right] r(t)\\ (x_1(t)\in{\rm\bf R}^n, x_2(t)\in{\rm\bf R}^m) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a01e5393ef83d3a307441de8778d577b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] %}_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I_m \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] %}_{x(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-01bb686061b94fbab2a0ff90e7d23f64_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} I_n & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right]\\ \Leftrightarrow \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} I_n & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-19e5643bcb296d8a517aba35bc4fe14e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8a)\quad \begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] %}_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right] }_{T_sA_ET_s^{-1}} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] %}_{x'(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ S_2B_2 \end{array}\right] }_{T_sB_E} u(t)\\ + \left[\begin{array}{cc} B_r \\ S_1B_r \end{array}\right] r(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a23595fe93cd3fb99284c6e90f61bcf1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8b)\quad \left\{\begin{array}{l} \bar{A}_{11}=\underbrace{ \left[\begin{array}{cc} 0 & -C_1 \\ 0 & A_{11} \end{array}\right]}_{\tilde{A}_{11}} -\underbrace{\left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right]}_{\tilde{A}_{12}}M\quad(M=S_2^{-1}S_1)\\ \bar{A}_{12}= \underbrace{\left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right]}_{\tilde{A}_{12}}S_2^{-1}\\ \bar{A}_{21}=S_2(M\bar{A}_{11} + \left[\begin{array}{cc} 0 & A_{21} \end{array}\right] -A_{22}M)\\ \bar{A}_{22}=S_2(M \left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right] +A_{22})S_2^{-1}\\ B_r=\left[\begin{array}{cc} I_m \\ 0 \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a8cb0e83576eef13d13b8f669a414ae8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} u(t)=u_L(t)+\nu_c\\ u_L(t)=-\underbrace{(S\tilde{B})^{-1}(S\tilde{A}-\Phi S)}_{L=L_{eq}+L_\Phi}\left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right]\\ -\underbrace{(S\tilde{B})^{-1}(\Phi S_r+S_1B_r)}_{L_r} r(t) +\underbrace{(S\tilde{B})^{-1}S_r}_{L_{\dot r}} \dot{r}(t)\\ \nu_c=-\underbrace{(S\tilde{B})^{-1}\rho_c(u_L,y)}_{L_n}\frac{P_2(s(t)-S_rr(t))}{||P_2(s(t)-S_rr(t))||} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4fa5c5c72c2ee8614e09bcaa4631f9d9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \hat{u}(t)=\underbrace{-L\left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right]-L_rr(t)+L_{\dot r}\dot{r}(t)}_{\hat{u}_L}+\hat{\nu}_c\\ \displaystyle{\hat{\nu}_c=-L_n\frac{P_2(S\left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right]-S_rr(t))}{||P_2(S\left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right]-S_rr(t))||}}\\ L=\Lambda^{-1}(S\tilde{A}-\Phi S)\\ L_r=\Lambda^{-1}(\Phi S_r+S_2MB_r)\\ L_{\dot r}=\Lambda^{-1}S_r\\ L_n=\Lambda^{-1}\rho_c(\hat{u}_L,y) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9b9975d5d229ccc8642e2fdd4c1c0561_l3.png)
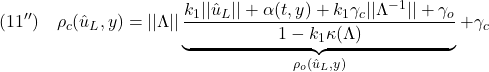
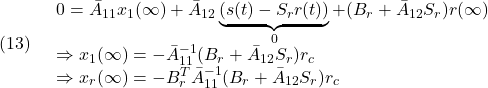
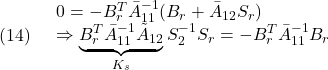
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \begin{array}{l} \left[\begin{array}{cc} I & 0\\ B_r^T\tilde{A}_{11}^{-1} & -K_s \end{array}\right]= \left[\begin{array}{cc} \tilde{A}_{11} & \tilde{A}_{12}\\ B_r^T & 0 \end{array}\right] \left[\begin{array}{cc} \bar{A}_{11}^{-1} & -\bar{A}_{11}^{-1}\tilde{A}_{12}\\ 0 & I \end{array}\right]\\ = \left[\begin{array}{cc} \tilde{A}_{11} & \tilde{A}_{12}\\ B_r^T & 0 \end{array}\right] \left[\begin{array}{cc} I & 0\\ -M & I \end{array}\right] \left[\begin{array}{cc} \bar{A}_{11}^{-1} & -\bar{A}_{11}^{-1}\tilde{A}_{12}\\ 0 & I \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-359f0d62c20de545dd87152fb1c6a94b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \begin{array}{l} {\rm det}\left[\begin{array}{cc} \tilde{A}_{11} & \tilde{A}_{12}\\ B_r^T & 0 \end{array}\right]\ne 0 \Leftrightarrow {\rm det}\left[\begin{array}{cc|c} 0 & -C_1 & -C_2\\ 0 & A_{11} & A_{12}\\\hline I & 0 & 0 \end{array}\right]\ne 0\\ \Leftrightarrow {\rm det}\left[\begin{array}{cc} -C_1 & -C_2\\ A_{11} & A_{12} \end{array}\right]\ne 0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8d7129e0a72d941b228a1e4ecda1d741_l3.png)
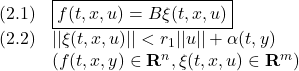
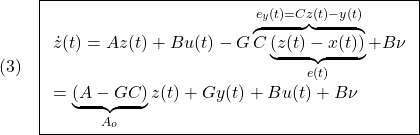
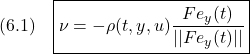
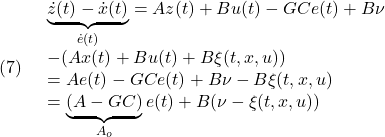
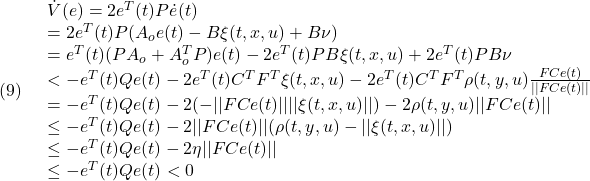
![Rendered by QuickLaTeX.com \displaystyle{(11.1)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{cc} {\bar A}_{11} & {\bar A}_{12} \\ {\bar A}_{21} & {\bar A}_{22} \\ \end{array}\right] }_{{\bar A}=TAT^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} + \boxed{\underbrace{ \left[\begin{array}{c} 0_{n-p\times p}\\ {\bar B}_{2} \end{array}\right] }_{{\bar B}=TB}} (u(t)+\xi(t))\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-df89f2c8c5027f65f3d1b001df56a333_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11.2)\quad y(t) = \boxed{\underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & I_p \\ \end{array}\right] }_{{\bar C}=CT^{-1}}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d15eb88c68556f6e054c3e64d14d9b4a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \dot{\hat x}(t)=A\hat{x}(t)+Bu(t)-G_\ell Ce(t)+G_n\nu\\ G_\ell=T_o^{-1}\left[\begin{array}{c} {\cal A}_{12}\\ {\cal A}_{22}-{\cal A}_{22}^{s} \end{array}\right]\\ G_n=||{\cal D}_{2}||T_o^{-1}\left[\begin{array}{c} 0_{n-p\times p}\\ I_p \end{array}\right]\\ \displaystyle{\nu=-\rho(t,y,u)\frac{P_2e_y(t)}{||P_2e_y(t)||} \quad(P_2{\cal A}_{22}^{s}+{\cal A}_{22}^{s}^TP_2<0)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4b315d5f9deb1d92118c05143cc36e33_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \boxed{G=(T_LT_bT_c)^{-1}\left[\begin{array}{c} {\cal A}_{12}\\ {\cal A}_{22}-{\cal A}_{22}^{s} \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-99565ec8e7483b355f59c24131882a38_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \bar{B}=TB= \left[\begin{array}{cc} I_{n-p} & {P}_{11}^{-1}{P}_{12} \\ 0 & I_p \end{array}\right] \left[\begin{array}{cc} {\tilde P}_{11} & {\tilde P}_{12} \\ {\tilde P}_{21} & {\tilde P}_{22} \end{array}\right] \left[\begin{array}{cc} 0 \\ I_p \end{array}\right] F^T\\ =\left[\begin{array}{cc} {\tilde P}_{12} + {P}_{11}^{-1}{P}_{12}{\tilde P}_{22} \\ {\tilde P}_{22} \end{array}\right] F^T= \underbrace{\left[\begin{array}{cc} 0 \\ {\tilde P}_{22}F^T \end{array}\right] }_{\left[\begin{array}{cc} 0 \\ {\bar B}_{2} \end{array}\right]} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ecf550e6e68e139dfd9b70a2c51821a0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \begin{array}{l} \bar{P}=T^{-T}PT^{-1}\\ = \left[\begin{array}{cc} I_{n-p} & 0 \\ -{P}_{12}^T{P}_{11}^{-1} & I_p \end{array}\right] \left[\begin{array}{cc} {P}_{11} & {P}_{12} \\ {P}_{21} & {P}_{22} \end{array}\right] \left[\begin{array}{cc} I_{n-p} & -{P}_{11}^{-1}{P}_{12} \\ 0 & I_p \end{array}\right]\\ = \left[\begin{array}{cc} {P}_{11} & {P}_{12} \\ 0 & {P}_{22}-{P}_{12}^T{P}_{11}^{-1}{P}_{12} \end{array}\right] \left[\begin{array}{cc} I_{n-p} & -{P}_{11}^{-1}{P}_{12} \\ 0 & I_p \end{array}\right]\\ =\underbrace{\left[\begin{array}{cc} {P}_{11} & 0 \\ 0 & {P}_{22}-{P}_{21}{P}_{11}^{-1}{P}_{12} \end{array}\right] }_{\left[\begin{array}{cc} {\bar P}_{1} & 0 \\ 0 & {\bar P}_{2} \end{array}\right]} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d939c6b48cf57392a69499adfa73c15a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \bar{A}=TAT^{-1}\\ = \left[\begin{array}{cc} I_{n-p} & {P}_{11}^{-1}{P}_{12} \\ 0 & I_p \end{array}\right] \left[\begin{array}{cc} {A}_{11} & {A}_{12} \\ {A}_{21} & {A}_{22} \end{array}\right] \left[\begin{array}{cc} I_{n-p} & -{P}_{11}^{-1}{P}_{12} \\ 0 & I_p \end{array}\right]\\ = \left[\begin{array}{cc} {A}_{11}+{P}_{11}^{-1}{P}_{12}{A}_{21} & {A}_{12}+ {P}_{11}^{-1}{P}_{12}{A}_{22}\\ {A}_{21} & {A}_{22} \end{array}\right] \left[\begin{array}{cc} I_{n-p} & -{P}_{11}^{-1}{P}_{12} \\ 0 & I_p \end{array}\right]\\ =\underbrace{\left[\begin{array}{cc} {A}_{11}+{P}_{11}^{-1}{P}_{12}{A}_{21} & * \\ {A}_{21} & {A}_{22}-{A}_{21}{P}_{11}^{-1}{P}_{12} \end{array}\right] }_{\left[\begin{array}{cc} {\bar A}_{11} & {\bar A}_{12} \\ {\bar A}_{21} & {\bar A}_{22} \end{array}\right]} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-818dd08ad7b025fcdf6ac9148b5e312b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \bar{A}_o=\underbrace{TA_oT^{-1} }_{\left[\begin{array}{cc} {\bar A}_{o11} & {\bar A}_{o12} \\ {\bar A}_{o21} & {\bar A}_{o22} \end{array}\right]} =T(A-GC)T^{-1}\\ =\underbrace{TAT^{-1}}_{ \left[\begin{array}{cc} {\bar A}_{11} & {\bar A}_{12} \\ {\bar A}_{21} & {\bar A}_{22} \end{array}\right]} -\underbrace{TGCT^{-1}} _{\left[\begin{array}{cc} 0 & TG \end{array}\right]} = \left[\begin{array}{cc} {\bar A}_{11} & * \\ {\bar A}_{21} & * \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ac09c08dae61878b5898912612961935_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \left[\begin{array}{cc} {\bar P}_{1} & 0 \\ 0 & {\bar P}_{2} \end{array}\right] \left[\begin{array}{cc} {\bar A}_{o11} & {\bar A}_{o12} \\ {\bar A}_{o21} & {\bar A}_{o22} \ \end{array}\right] +\left[\begin{array}{cc} {\bar A}_{o11} & {\bar A}_{o12} \\ {\bar A}_{o21} & {\bar A}_{o22} \ \end{array}\right]^T \left[\begin{array}{cc} {\bar P}_{1} & 0 \\ 0 & {\bar P}_{2} \end{array}\right]\\ =- \left[\begin{array}{cc} \bar{Q}_{11} & \bar{Q}_{12} \\ \bar{Q}_{12}^T & \bar{Q}_{22} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f9c197610a2dc08d37d7807a77250d9d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \underbrace{\left[\begin{array}{cc} 0 & I_p \end{array}\right]}_{\bar{C}^T}F^T=\underbrace{\left[\begin{array}{cc} {\bar P}_{1} & 0 \\ 0 & {\bar P}_{2} \end{array}\right]}_{\bar P}\underbrace{\left[\begin{array}{cc} 0 \\ {\bar B}_{2} \end{array}\right]}_{\bar B} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-25481cf05987d97cf1d660f8462287a3_l3.png)
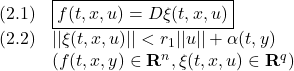
![Rendered by QuickLaTeX.com \displaystyle{(3.1)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{cc} {\cal A}_{11} & {\cal A}_{12} \\ {\cal A}_{21} & {\cal A}_{22} \\ \end{array}\right] }_{T_oAT_o^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} + \underbrace{ \left[\begin{array}{c} {\cal B}_{1}\\ {\cal B}_{2} \end{array}\right] }_{T_oB} u(t) +\boxed{ \underbrace{ \left[\begin{array}{c} 0_{n-p\times p}\\ {\cal D}_{2} \end{array}\right] }_{T_oD}} \xi(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c84baa48a735c227a2adb1d7a835b4a4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3.2)\quad y(t) = \boxed{\underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & I_p \\ \end{array}\right] }_{CT_o^{-1}}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-90635122c9b9569be2466b719f5f1954_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \boxed{\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\hat x}_1(t)\\ \dot{\hat y}(t) \end{array}\right] }_{\dot{\hat x}'(t)} = \underbrace{ \left[\begin{array}{cc} {\cal A}_{11} & {\cal A}_{12} \\ {\cal A}_{21} & {\cal A}_{22} \\ \end{array}\right] }_{T_oAT_o^{-1}} \underbrace{ \left[\begin{array}{c} \hat{x}_1(t)\\ \hat{y}(t) \end{array}\right] }_{\hat{x}'(t)} + \underbrace{ \left[\begin{array}{c} {\cal B}_{1}\\ {\cal B}_{2} \end{array}\right] }_{T_oB} u(t)\\ - \left[\begin{array}{c} {\cal A}_{12}\\ {\cal A}_{22}-{\cal A}_{22}^{s} \end{array}\right] \underbrace{(\hat{y}(t)-y(t))}_{e_y(t)} + \left[\begin{array}{c} 0_{n-p\times p}\\ I_p \end{array}\right] \nu \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-66e4a486014204d000a249eb1c1c592b_l3.png)
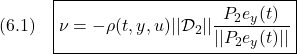
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \left[\begin{array}{c} \dot{\hat x}_1(t)-\dot{x}_1(t)\\ \dot{\hat y}(t)-\dot{y}(t) \end{array}\right] = \left[\begin{array}{cc} {\cal A}_{11} & {\cal A}_{12} \\ {\cal A}_{21} & {\cal A}_{22} \\ \end{array}\right] \left[\begin{array}{c} \hat{x}_1(t)-x_1(t)\\ \hat{y}(t)-y(t) \end{array}\right]\\ - \left[\begin{array}{cc} 0 & {\cal A}_{12}\\ 0 & {\cal A}_{22}-{\cal A}_{22}^{s} \end{array}\right] \left[\begin{array}{c} \hat{x}_1(t)-x_1(t)\\ \hat{y}(t)-y(t) \end{array}\right] + \left[\begin{array}{c} 0_{n-p}\\ \nu-{\cal D}_{2}\xi(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0c17498fb75a8ddddcfaced948ff16ca_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7')\quad \boxed{\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\hat x}_1(t)-\dot{x}_1(t)\\ \dot{\hat y}(t)-\dot{y}(t) \end{array}\right] }_{\left[\begin{array}{c} \dot{e}_1(t)\\ \dot{e}_y(t) \end{array}\right]} = \left[\begin{array}{cc} {\cal A}_{11} & 0_{n-p\times p} \\ {\cal A}_{21} & {\cal A}_{22}^{s} \\ \end{array}\right] \underbrace{ \left[\begin{array}{c} \hat{x}_1(t)-x_1(t)\\ \hat{y}(t)-y(t) \end{array}\right] }_{\left[\begin{array}{c} {e}_1(t)\\ {e}_y(t) \end{array}\right]}\\ + \left[\begin{array}{c} 0_{n-p}\\ \nu-{\cal D}_{2}\xi(t) \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eca857318ee4a936235a33d8531cf6bf_l3.png)
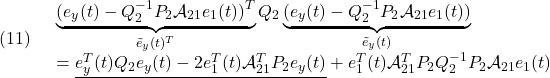
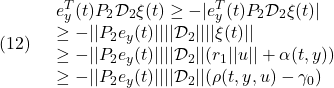
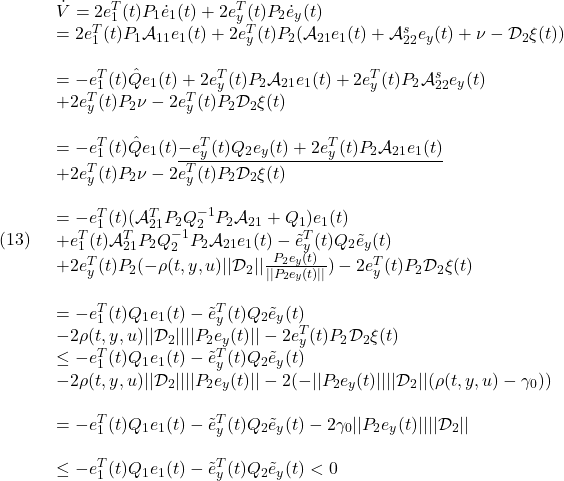
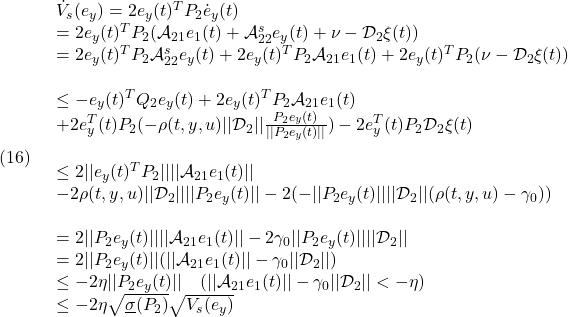
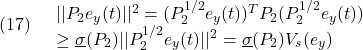
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\hat x}_1(t)\\ \dot{\hat y}(t) \end{array}\right] }_{\dot{\hat x}'(t)} = \underbrace{ \left[\begin{array}{cc} {\cal A}_{11} & {\cal A}_{12} \\ {\cal A}_{21} & {\cal A}_{22} \\ \end{array}\right] }_{T_oAT_o^{-1}} \underbrace{ \left[\begin{array}{c} \hat{x}_1(t)\\ \hat{y}(t) \end{array}\right] }_{\hat{x}'(t)} + \underbrace{ \left[\begin{array}{c} {\cal B}_{1}\\ {\cal B}_{2} \end{array}\right] }_{T_oB} u(t)\\ - \left[\begin{array}{c} {\cal A}_{12}\\ {\cal A}_{22}-{\cal A}_{22}^{s} \end{array}\right] \underbrace{(\hat{y}(t)-y(t))}_{e_y(t)} + \left[\begin{array}{c} 0_{n-p\times p}\\ I_p \end{array}\right] \nu \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-47ff921fcda56486a051274cf1f22315_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \boxed{\begin{array}{l} \dot{\hat x}(t)=A\hat{x}(t)+Bu(t)-G_\ell e_y(t)+G_n\nu\\ G_\ell=T_o^{-1}\left[\begin{array}{c} {\cal A}_{12}\\ {\cal A}_{22}-{\cal A}_{22}^{s} \end{array}\right]\\ G_n=||{\cal D}_{2}||T_o^{-1}\left[\begin{array}{c} 0_{n-p\times p}\\ I_p \end{array}\right]\\ \displaystyle{\nu=-\rho(t,y,u)\frac{P_2e_y(t)}{||P_2e_y(t)||} \quad(P_2{\cal A}_{22}^{s}+{\cal A}_{22}^{s}^TP_2<0)} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7107375b58980fcf0a852de479bd7ce3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{ll} (18.1*)&(T_aT_bT_c)A(T_aT_bT_c)^{-1}= \left[\begin{array}{cccc} A_{11}^o & A_{12}^o & A_{121}^m & A_{121}\\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m & A_{1221}\\ 0_{p-m\times r} & A_{21}^o & A_{22}^m & A_{1222}\\ A_{2120} & A_{2121} & A_{2122} & A_{22} \end{array}\right]\\ &(A_{11}^o\in{\rm\bf R}^{r\times r},A_{22}^o\in{\rm\bf R}^{n-p-r\times n-p-r},A_{22}^m\in{\rm\bf R}^{p-m\times p-m},A_{22}\in{\rm\bf R}^{m\times m})\\ (18.2*)&(T_aT_bT_c)B= \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\ B_2 \end{array}\right]\\ (18.3*)&C(T_aT_bT_c)^{-1}= \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-24aba4138d204a391e18f69edcd60c03_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{ll} (19.1)&(T_aT_bT_c)A(T_aT_bT_c)^{-1}= \underbrace{ \left[\begin{array}{cc|cc} A_{11}^o & A_{12}^o & A_{121}^m & A_{121}\\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m & A_{1221}\\\hline 0_{p-q\times r} & A_{21}^o & A_{22}^m & A_{1222}\\ A_{2120} & A_{2121} & A_{2122} & A_{22} \end{array}\right] }_{ \left[\begin{array}{c|c} A_{11} & *\\\hline A_{211} & *\\ * & * \end{array}\right] }\\ &(A_{11}\in{\rm\bf R}^{n-p\times n-p},A_{211}\in{\rm\bf R}^{p-q\times n-p})\\ (19.2)&(T_aT_bT_c)D= \left[\begin{array}{c} 0_{r\times q} \\ 0_{n-p-r\times q} \\ 0_{p-q\times q} \\ D_2 \end{array}\right]\\ (19.3)&C(T_aT_bT_c)^{-1}= \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0e35543abcf691542b05178054d4aac2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{ll} (21.1)&T_L(T_aT_bT_c)A(T_aT_bT_c)^{-1}= \underbrace{\left[\begin{array}{cc} I_{n-p} & \left[\begin{array}{cc} L & 0_{n-p\times q} \end{array}\right] \\ 0_{p\times n-p} & T \end{array}\right]}_{T_L} \left[\begin{array}{c|c} A_{11} & *\\\hline A_{211} & *\\ * & * \end{array}\right]T_L\\ &= \left[\begin{array}{c|c} A_{11}+LA_{211} & *\\\hline * & * \end{array}\right] \underbrace{\left[\begin{array}{cc} I_{n-p} & \left[\begin{array}{cc} L & 0_{n-p\times q} \end{array}\right] \\ 0_{p\times n-p} & T \end{array}\right]}_{T_L}\\ (21.2)&T_L(T_aT_bT_c)D= \underbrace{\left[\begin{array}{cc} I_{n-p} & \left[\begin{array}{cc} L & 0_{n-p\times q} \end{array}\right] \\ 0_{p\times n-p} & T \end{array}\right]}_{T_L} \left[\begin{array}{c} 0_{n-p\times q} \\ 0_{p-q\times q} \\ D_2 \end{array}\right]\\ (21.3)&C(T_aT_bT_c)^{-1}= \left[\begin{array}{cc} 0_{p\times n-p} & I_p \\ \end{array}\right] \underbrace{\left[\begin{array}{cc} I_{n-p} & \left[\begin{array}{cc} L & 0_{n-p\times q} \end{array}\right] \\ 0_{p\times n-p} & T \end{array}\right]}_{T_L} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-68fa24b51933a9c473610573a0e51069_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{ll} (22.1)&(T_LT_aT_bT_c)A(T_LT_aT_bT_c)^{-1}= \left[\begin{array}{c|c} A_{11}+LA_{211} & *\\\hline * & * \end{array}\right]\\ (22.2)&(T_LT_aT_bT_c)D= \left[\begin{array}{c} 0_{n-p\times q} \\ T\left[\begin{array}{c} 0_{p-q\times q} \\ D_2 \end{array}\right] \end{array}\right]\\ (22.3)&C(T_LT_aT_bT_c)^{-1}= \left[\begin{array}{cc} 0_{p\times n-p} & I_p \\ \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-92e44180ccc9fb5eea4f190d7391699c_l3.png)
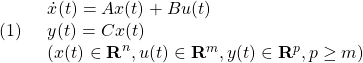
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} = \underbrace{ \left[\begin{array}{cc} N_c^T \\ C \\ \end{array}\right] }_{T_c} x(t) \Leftrightarrow x(t)= \underbrace{ \left[\begin{array}{cc} N_c^T \\ C \\ \end{array}\right]^{-1} }_{T_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4db3d40a6624450f2c64ca791f380fe1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3.1)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{cc} A_{c11} & A_{c12} \\ A_{c21} & A_{c22} \\ \end{array}\right] }_{T_cAT_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} + \underbrace{ \left[\begin{array}{c} B_{c1}\\ B_{c2} \end{array}\right] }_{T_cB} u(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-644186c09de8b1938a61eb3a18489a90_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3.2)\quad y(t) = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & I_p \\ \end{array}\right] }_{CT_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-58c311e6be5fde3b8343f975d58b0d2a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4.1)\quad \boxed{\begin{array}{l} \left[\begin{array}{c} \dot{\hat x}_1(t)\\ \dot{\hat y}(t) \end{array}\right] = \left[\begin{array}{cc} A_{c11} & A_{c12} \\ A_{c21} & A_{c22} \\ \end{array}\right] \left[\begin{array}{c} \hat{x}_1(t)\\ \hat{y}(t) \end{array}\right] + \left[\begin{array}{c} B_{c1}\\ B_{c2} \end{array}\right] u(t)\\ + \left[\begin{array}{c} L\\ -I_p \end{array}\right] \nu \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-be4b4ad4f240be627b5ee9bf2dfec609_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4.2)\quad \boxed{\nu=M \left[\begin{array}{c} {\rm sgn}(\hat{y}_1(t)-y_1(t))\\ \vdots\\ {\rm sgn}(\hat{y}_p(t)-y_p(t)) \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e7bc0ad75dd6f59af1617db5c3d71ce3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \underbrace{ \left[\begin{array}{c} \dot{\hat x}_1(t)-\dot{x}_1(t)\\ \dot{\hat y}(t)-\dot{y}(t) \end{array}\right] }_{\left[\begin{array}{c} \dot{e}_1(t)\\ \dot{e}_y(t) \end{array}\right]} = \left[\begin{array}{cc} A_{c11} & A_{c12} \\ A_{c21} & A_{c22} \\ \end{array}\right] \underbrace{ \left[\begin{array}{c} \hat{x}_1(t)-{x}_1(t)\\ \hat{y}(t)-{y}(t) \end{array}\right] }_{\left[\begin{array}{c} {e}_1(t)\\ {e}_y(t) \end{array}\right]} + \left[\begin{array}{c} 0\\ -\nu \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8c8ad91d08e2ba443b44f99ab4a83031_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7.1)\quad \boxed{\left[\begin{array}{c} \dot{\tilde e}_1(t)\\ \dot{e}_y(t) \end{array}\right] = \left[\begin{array}{cc} \tilde{A}_{c11} & \tilde{A}_{c12} \\ \tilde{A}_{c21} & \tilde{A}_{c22} \\ \end{array}\right] \left[\begin{array}{c} \tilde{e}_1(t)\\ {e}_y(t) \end{array}\right] + \left[\begin{array}{c} 0\\ -I_p \end{array}\right]\nu} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c3e4c6bfa8770bfcf9a5e2e1e89effae_l3.png)
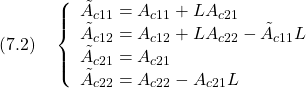
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \begin{array}{l} e^T_y(t)\dot{e}_y(t)=e^T_y(t)(\tilde{A}_{c21}\tilde{e}_1(t)+\tilde{A}_{c22}{e}_y(t)-\nu)\\\\ =e^T_y(t)\tilde{A}_{c21}\tilde{e}_1(t)+e^T_y(t)\tilde{A}_{c22}{e}_y(t)\\ -M \left[\begin{array}{c} \hat{y}_1(t)-y_1(t)\\ \vdots\\ \hat{y}_p(t)-y_p(t) \end{array}\right]^T \left[\begin{array}{c} {\rm sgn}(\hat{y}_1(t)-y_1(t))\\ \vdots\\ {\rm sgn}(\hat{y}_p(t)-y_p(t)) \end{array}\right]\\\\ =e^T_y(t)\tilde{A}_{c21}\tilde{e}_1(t)+e^T_y(t)\frac{1}{2}(\tilde{A}_{c22}+\tilde{A}^T_{c22}){e}_y(t)\\ -M(|\hat{y}_1(t)-y_1(t)|+\cdots+|\hat{y}_p(t)-y_p(t)|)\\\\ \le e^T_y(t)\tilde{A}_{c21}\tilde{e}_1(t)+\frac{1}{2}\bar\sigma(\tilde{A}_{c22}+\tilde{A}^T_{c22})e^T_y(t){e}_y(t)\\ -M(|\hat{y}_1(t)-y_1(t)|+\cdots+|\hat{y}_p(t)-y_p(t)|)\\\\ \le ||e_y(t)||(||\tilde{A}_{c21}\tilde{e}_1(t)||+\frac{1}{2}\bar\sigma(\tilde{A}_{c22}+\tilde{A}^T_{c22})||{e}_y(t)||)\\ -M(|\hat{y}_1(t)-y_1(t)|+\cdots+|\hat{y}_p(t)-y_p(t)|)\\\\ < ||e_y(t)||(M-\eta)-M(|\hat{y}_1(t)-y_1(t)|+\cdots+|\hat{y}_p(t)-y_p(t)|)\\ \le -\eta||e_y(t)||+M\underbrace{(||e_y(t)||-(|\hat{y}_1(t)-y_1(t)|+\cdots+|\hat{y}_p(t)-y_p(t)|))}_{\le0}\\ \le -\eta||e_y(t)||<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e20cc8c96c530a7504d6d40df37a524b_l3.png)
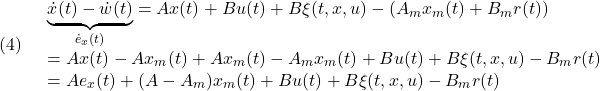
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \dot{x}(t)=Ax(t)+Bu(t)\\ x(t)= \left[\begin{array}{ll} \phi & bank\ angle\\ r & yaw\ rate\\ p & roll\ rate\\ \beta & sideslip\ angle\\ x_5 & washed-out\ filter\ state \end{array}\right],\quad u(t)= \left[\begin{array}{ll} \delta_r & rudder\ deflection\\ \delta_a & aileron\ deflection \end{array}\right]\\ A=\left[\begin{array}{rrrrr} 0 & 0 & 1.0000 & 0 & 0\\ 0 & -0.1540 & -0.0042 & 1.5400 & 0\\ 0 & 0.2490 & -1.0000 & -5.2000 & 0\\ 0.0386 & -0.9960 & -0.0003 & -0.1170 & 0\\ 0 & 0.5000 & 0 & 0 & -0.5000 \end{array}\right],\quad\\ B=\left[\begin{array}{rr} 0 & 0 \\ -0.7440 & -0.0320 \\ 0.3370 & -1.1200 \\ 0.0200 & 0\\ 0 & 20 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8622180be357918528164e3d543e7c84_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \begin{array}{l} y(t)=C_Mx(t),\ z(t)=Cx(t)\\ y(t)= \left[\begin{array}{ll} r_{wo} & washed-out\ yaw\ rate\\ p & roll\ rate\\ \beta & sideslip\ angle\\ \phi & bank\ angle \end{array}\right],\quad z(t)= \left[\begin{array}{ll} \phi & bank\ angle\\ \beta & sideslip\ angle \end{array}\right]\\ C_M=\left[\begin{array}{rrrrr} 0 & 1 & 0 & 0 & -1\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 1 & 0 & 0 & 0 & 0 \end{array}\right],\quad C=\left[\begin{array}{rrrrr} 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a47cabffa6576dc1b9f48be4914a76a7_l3.png)

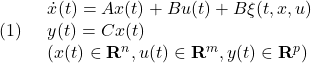
![Rendered by QuickLaTeX.com \displaystyle{(18.1^*)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x'''_1(t)\\ \dot x'''_2(t) \end{array}\right] }_{\dot{x}'''(t)} = \underbrace{ \left[\begin{array}{ccc|c} A_{11}^o & A_{12}^o & A_{121}^m & A_{121}\\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m & A_{1221}\\ 0_{p-m\times r} & A_{21}^o & A_{22}^m & A_{1222}\\\hline A_{2120} & A_{2121} & A_{2122} & A_{22} \end{array}\right] }_{(T_aT_bT_c)A(T_aT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)}\\ + \underbrace{ \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline B_2 \end{array}\right] }_ {(T_aT_bT_c)B} \underbrace{(u(t)+\xi(t,x,u))}_{u'(t)}\\ (A_{11}^o\in{\rm\bf R}^{r\times r},A_{22}^o\in{\rm\bf R}^{n-p-r\times n-p-r},A_{22}^m\in{\rm\bf R}^{p-m\times p-m},A_{22}\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-712c9ee206bbfdfc0320ee7fb2c01281_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18.2^*)\quad \begin{array}{l} y(t) = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] }_{C(T_aT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c2d502c3e8c7b30de092731cc5418e3d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2')\quad \begin{array}{l} \dot{x}_c(t)=Hx_c(t)+Dy(t)\\ =Hx_c(t)+ \left[\begin{array}{cc} 0_{p\times n-p} & DT \\ \end{array}\right] %\underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] %}_{x'''(t)} \\ =Hx_c(t)+ \left[\begin{array}{cc} D_1C_1 & D_2 \\ \end{array}\right] %\underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] %}_{x'''(t)} \\ =Hx_c(t)+D_1C_1x'''_1(t)+D_2x'''_2(t)\\ (DT=\left[\begin{array}{cc} D_1 & D_2 \end{array}\right], D_1\in{\rm\bf R}^{m\times p-m}, D_2\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9c519f23b2642a1398b44d297648888d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3')\quad \begin{array}{l} s(t)=F_cx_c(t)+Fy(t)\\ =Hx_c(t)+ \left[\begin{array}{cc} 0_{p\times n-p} & FT \\ \end{array}\right] %\underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] %}_{x'''(t)} \\ =Hx_c(t)+ \left[\begin{array}{cc} F_1C_1 & F_2 \\ \end{array}\right] %\underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] %}_{x'''(t)} \\ =Hx_c(t)+F_1C_1x'''_1(t)+F_2x'''_2(t)\\ (FT=\left[\begin{array}{cc} F_1 & F_2 \end{array}\right], F_1\in{\rm\bf R}^{m\times p-m}, F_2\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c3a63f48d662d8ce45ee20bfb786b893_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x'''_1(t)\\\hline \dot x'''_2(t)\\\hline\hline \dot x_c(t) \end{array}\right] }_{\dot{x}'''(t)} = \left[\begin{array}{c|c||c} \left.\begin{array}{ccc} A_{11}^o & A_{12}^o & A_{121}^m \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m \\ \end{array}\right.& \left.\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222} \end{array}\right.& \left.\begin{array}{cc} 0_{r\times q} \\ 0_{n-p-r\times q} \\ 0_{p-m\times q} \end{array}\right. \\\hline \left.\begin{array}{ccc} A_{211} & A_{2121} &A_{2122} \end{array}\right.& \left.\begin{array}{cc} A_{22} \end{array}\right.& 0_{m\times q} \\\hline\hline %D_1C_1 \left.\begin{array}{cc} 0_{q\times r} & D_1\tilde{C}_1 \end{array}\right. & D_2 & H \end{array}\right]\\ \times \underbrace{ \left[\begin{array}{c} x'''_1(t)\\\hline x'''_2(t)\\\hline\hline x_c(t) \end{array}\right] }_{x'''(t)} + \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline B_2\\\hline\hline 0_{q\times m} \end{array}\right] u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1968121e3a5d1a000f172ea9ce55a016_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x'''_1(t)\\\hline \dot x_c(t)\\\hline\hline \dot x'''_2(t) \end{array}\right] }_{\dot{x}'''(t)} = \left[\begin{array}{c|c||c} \left.\begin{array}{ccc} A_{11}^o & A_{12}^o & A_{121}^m \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m \\ \end{array}\right.& \left.\begin{array}{cc} 0_{r\times q} \\ 0_{n-p-r\times q} \\ 0_{p-m\times q} \end{array}\right. & \left.\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222} \end{array}\right. \\\hline %D_1C_1 \left.\begin{array}{ccc} 0_{q\times r} & D_1\tilde{C}_1 \end{array}\right. & \left.\begin{array}{cc} H \end{array}\right. & D_2 \\\hline\hline \left.\begin{array}{ccc} A_{211} & A_{2121} &A_{2122} \end{array}\right. & 0_{m\times q} & A_{22} \end{array}\right]\\ \times \underbrace{ \left[\begin{array}{c} x'''_1(t)\\\hline x_c(t)\\\hline\hline x'''_2(t) \end{array}\right] }_{x'''(t)} + \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline 0_{q\times m}\\\hline\hline B_2\\ \end{array}\right] u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-954b2e74e37e5828afcfbe39a920d5cb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\\hline x_c(t)\\\hline\hline x''''_2(t)\\ \end{array}\right] }_{x''''(t)} = \underbrace{ \left[\begin{array}{ccc|c||c} I_{r} & 0 & 0 & 0& 0 \\ 0 & I_{n-p-r} & 0 & 0& 0 \\ 0 & 0 & I_{p-m} & 0 & 0\\\hline 0 & 0 & 0 & I_q &0 \\\hline\hline 0 & 0 & K & K_c & I_m \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\\hline x_c(t)\\\hline\hline x'''_2(t)\\ \end{array}\right] }_{x'''(t)}\\ (K=F_2^{-1}F_1, K_c=F_2^{-1}F_c) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bb2718c0970f9bbdf8747a901f89c9ab_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x'''_r(t)\\ \dot x'''_{11}(t)\\ \dot x'''_{12}(t)\\\hline \dot x_c(t)\\\hline \dot x''''_2(t) \end{array}\right] }_{\dot{x}''''(t)} = \left[\begin{array}{c|c} \left[\begin{array}{c|c} \left.\begin{array}{ccc} A_{11}^o & A_{12}^o & A_{121}^m \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m \\ \end{array}\right. & \left.\begin{array}{cc} 0_{r\times q} \\ 0_{n-p-r\times q} \\ 0_{p-m\times q} \end{array}\right. \\\hline %D_1C_1 \left.\begin{array}{cc} 0_{q\times r} & D_1\tilde{C}_1 \end{array}\right. & H \end{array}\right]\\ - \left[\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222}\\\hline D_2 \end{array}\right] \left[\begin{array}{ccccc} 0_{m\times r} & K\tilde{C}_1 & K_c \end{array}\right] & \left.\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222}\\\hline D_2 \end{array}\right. \\\hline \left.\begin{array}{ccc|c} A_{211} & A_{2121} &A_{2122} & 0_{m\times q} \end{array}\right. & A_{22} \end{array}\right]\\ \times \underbrace{ \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\\hline x_c(t)\\\hline x''''_2(t)\\ \end{array}\right] }_{x''''(t)} + \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline 0_{q\times m}\\\hline B_2 \end{array}\right] u'(t)\\ = \underbrace{ \left[\begin{array}{c|c} \left.\begin{array}{c|c} \left.\begin{array}{ccc} A_{11}^o & A_{12}^o & A_{121}^m-A_{121}K \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m-A_{1221}K \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m-A_{1222}K \end{array}\right. & \left.\begin{array}{cc} -A_{121}K_c\\ -A_{1221}K_c\\ -A_{1222}K_c\\ \end{array}\right. \\\hline %(D_1-D_2K)C_1 \left.\begin{array}{cc} 0_{q\times r} & D(D_1-D_2K)\tilde{C}_1 \end{array}\right. & H-D_2K_c \end{array}\right. & \left.\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222}\\\hline D_2 \end{array}\right.\\\hline \left.\begin{array}{ccc|c} A_{211} & A_{2121} &A_{2122} & 0_{m\times q} \end{array}\right. & A_{22} \end{array}\right] }_{ \left[\begin{array}{cc} \tilde{\cal A}_{11} & \tilde{\cal A}_{12} \\ \tilde{\cal A}_{21} & \tilde{\cal A}_{22} \end{array}\right]} \\ \times \underbrace{ \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\\hline x_c(t)\\\hline x''''_2(t)\\ \end{array}\right] }_{x''''(t)} + \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline 0_{q\times m}\\\hline B_2 \end{array}\right] u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1a787fcbba242095e1c00febe98dcfe6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \left[\begin{array}{c} \dot x'''_{11}(t)\\ \dot x'''_{12}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A_{22}^o & A_{122}^m \\ A_{21}^o & A_{22}^m \\ \end{array}\right] }_{\tilde{A}_{11}} \left[\begin{array}{c} x'''_{11}(t)\\ x'''_{12}(t) \end{array}\right] + \underbrace{ \left[\begin{array}{cc} A_{1221} \\ A_{1222} \\ \end{array}\right] }_{A_{122}} \underbrace{x'''_{2}(t)}_{\tilde u(t)} \\ \underbrace{x'''_{12}(t)}_{\tilde y(t)} = \underbrace{ \left[\begin{array}{cc} 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right] }_{\tilde{C}_1}} \left[\begin{array}{c} x'''_{11}(t)\\ x'''_{12}(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0a20a7d2962db1ada4badc2bf0778a94_l3.png)
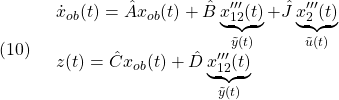
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad x_{ob}(t)\rightarrow \underbrace{ \left[\begin{array}{cc} I_{n-p-r} & -L^o \end{array}\right] }_{U} \left[\begin{array}{c} x'''_{11}(t)\\ x'''_{12}(t) \end{array}\right]= x'''_{11}(t)-L^ox'''_{12}(t) \quad(t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7c76952731eb4799d0b3b24379431e11_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \begin{array}{l} \left[\begin{array}{cc} \hat{A} & \hat{B}\\ \hat{C} & \hat{D} \end{array}\right] = \left[\begin{array}{c} U\tilde{A}_{11}\\ \left[\begin{array}{cc} {K}_1 & {K}_2 \end{array}\right] \end{array}\right] \left[\begin{array}{c} U\\ \tilde{C}_1 \end{array}\right]^{-1}\\ = \left[\begin{array}{c} \left[\begin{array}{cc} I_{n-p-r} & L^o \end{array}\right] \left[\begin{array}{cc} A_{22}^o & A_{122}^m \\ A_{21}^o & A_{22}^m \\ \end{array}\right]\\ \left[\begin{array}{cc} {K}_1 & {K}_2 \end{array}\right] \end{array}\right] \left[\begin{array}{cc} I_{n-p-r} & L^o\\ 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right]^{-1}\\ = \left[\begin{array}{cc} A_{22}^o+L^oA_{21}^o & A_{122}^m+L^oA_{22}^m \\ {K}_1 & {K}_2 \end{array}\right] \left[\begin{array}{cc} I_{n-p-r} & -L^o\\ 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right]\\ = \left[\begin{array}{cc} A_{22}^o+L^oA_{21}^o & A_{122}^m+L^oA_{22}^m-(A_{22}^o+L^oA_{21}^o)L^o \\ K_1 & K_2-K_1L^o \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0096b16ad8048d3787bdad7b1de35d39_l3.png)
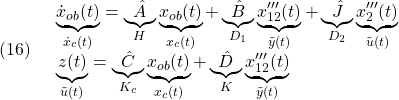
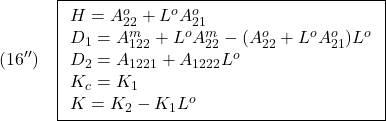
![Rendered by QuickLaTeX.com \displaystyle{(17.1)\quad \begin{array}{l} \left[\begin{array}{c} \dot x'''_r(t)\\ \dot x'''_{11}(t)\\ \dot x'''_{12}(t)\\ \dot x'''_2(t) \end{array}\right]= \left[\begin{array}{ccccc} A_{11}^o & A_{12}^o & A_{121}^m & A_{121} \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m & A_{1221} \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m & A_{1222} \\ A_{211} & A_{212} & A_{213} & A_{22} \end{array}\right] \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right]\\ + \left[\begin{array}{c} 0_{r\times m}\\ 0_{n-p-r\times m}\\ 0_{p-m\times m}\\ B_2\\ \end{array}\right] u(t)\\ (x'''_r(t)\in{\rm\bf R}^{r},x'''_{11}(t)\in{\rm\bf R}^{n-p-r},x'''_{12}(t)\in{\rm\bf R}^{p-m},x'''_{2}(t)\in{\rm\bf R}^{m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3e5a41c43ebb7a8d519dbce79ce8e0a3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17.2)\quad \begin{array}{l} y(t) = \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right]=T \left[\begin{array}{c} x'''_{12}(t)\\ x'''_2(t) \end{array}\right] \quad(T\in{\rm\bf R}^{p\times p}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-354531fad73a9f4ed2fb9035460b7345_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(19.1)\quad \underbrace{ \left[\begin{array}{c} \dot z_r(t)\\ \dot x_c(t)\\ \dot x'''_{12}(t)\\ \dot x'''_2(t) \end{array}\right] }_{\hat x(t)} = \underbrace{ \left[\begin{array}{ccccc} A_{11}^o & A_{12}^o & A_{121}^m-A_{12}^oL^o & A_{121} \\ 0_{q\times r} & H & D_1 & D_2 \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m-A_{21}^oL^o & A_{1222} \\ A_{211} & A_{212} & A_{213}-A_{212}L^o & A_{22} \end{array}\right] }_{\hat A} \underbrace{ \left[\begin{array}{c} z_r(t)\\ x_c(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right] }_{\hat x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-661ada8558710f28b5c81d3d52ca8358_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ + \underbrace{ \left[\begin{array}{ccccc} 0_{r\times r} & 0_{r\times m} \\ 0_{q\times r} & 0_{q\times m} \\ 0_{p-m\times r} & A_{21}^o \\ A_{211} & A_{212} \end{array}\right] }_{\hat A_e} \underbrace{ \left[\begin{array}{c} e_r(t)\\ e_c(t) \end{array}\right] }_{\hat{e}(t)} + \underbrace{ \left[\begin{array}{c} 0_{r\times m}\\ 0_{q\times m}\\ 0_{p-m\times m}\\ B_2\\ \end{array}\right] }_{\hat B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-35bbf3c7686c6043f5322df182777814_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(19.2)\quad \underbrace{ \left[\begin{array}{c} \dot e_r(t)\\ \dot e_c(t) \end{array}\right] }_{\dot{\hat{e}}(t)} = \underbrace{ \left[\begin{array}{cc} A_{11}^o & A_{12}^o \\ 0 & H \end{array}\right] }_{\hat{H}} \underbrace{ \left[\begin{array}{c} e_r(t)\\ e_c(t) \end{array}\right] }_{\hat{e}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eb43be95adf89038069e028493af823f_l3.png)
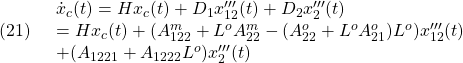
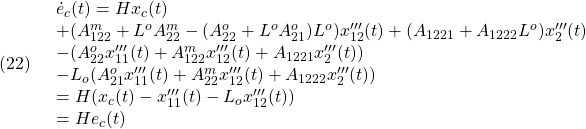
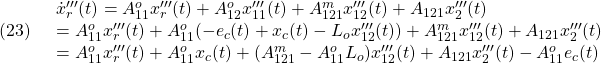
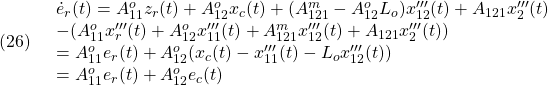
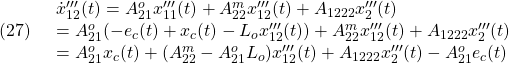
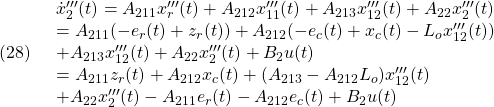
![Rendered by QuickLaTeX.com \displaystyle{(3'')\quad \begin{array}{l} s(t)=Hx_c(t)+F_1C_1x'''_1(t)+F_2x'''_2(t)\\ =\boxed{\underbrace{F_2\left[\begin{array}{cccc} 0_{m\times r} & K_c & K & I_m \end{array}\right]}_{S}} \underbrace{ \left[\begin{array}{c} z_r(t)\\ x_c(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right] }_{\hat x(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b40bb61a14d162099a8c5deefe1bb6ce_l3.png)
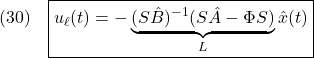
![Rendered by QuickLaTeX.com \displaystyle{(32)\quad \boxed{\begin{array}{l} \left[\begin{array}{c} \dot z_r(t)\\ \dot x_c(t) \end{array}\right] = \underbrace{ \left[\begin{array}{ccccc} A_{11}^o & A_{12}^o \\ 0_{q\times r} & H \end{array}\right] }_{\hat H} \left[\begin{array}{c} z_r(t)\\ x_c(t) \end{array}\right] + \underbrace{ \left[\begin{array}{ccccc} A_{121}^m-A_{12}^oL^o & A_{121} \\ D_1 & D_2 \end{array}\right]T' }_{\hat D} y(t)\\ \underbrace{ \left[\begin{array}{c} z_r(t)\\ x_c(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right] }_{\hat x(t)}= \underbrace{ \left[\begin{array}{ccccc} I_r & 0_{r\times q}\\ 0_{q\times r} & I_q\\ 0_{p-m\times r} & 0_{p-m\times q} \\ 0_{m\times r} & 0_{m\times q} \\ \end{array}\right]}_{\widehat{\cal C}} \left[\begin{array}{c} z_r(t)\\ x_c(t) \end{array}\right] + \underbrace{\left[\begin{array}{ccccc} 0_{r\times p-m} & 0_{r\times m} \\ 0_{q\times p-m} & 0_{q\times m} \\ I_{p-m} & 0_{p-m\times m}\\ 0_{m\times p-m} & I_m \end{array}\right]T' }_{\widehat{\cal D}} y(t) \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-87e3ff7ce930f9ed16d07870318d8f43_l3.png)
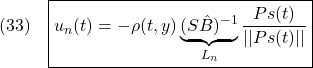

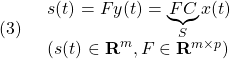
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} = \underbrace{ \left[\begin{array}{cc} N_c^T \\ C \\ \end{array}\right] }_{T_c} x(t) \Leftrightarrow x(t)= \underbrace{ \left[\begin{array}{cc} N_c^T \\ C \\ \end{array}\right]^{-1} }_{T_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ece730e4769618b1a1b4da039d7b9673_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5.1)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{cc} A_{c11} & A_{c12} \\ A_{c21} & A_{c22} \\ \end{array}\right] }_{T_cAT_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} + \underbrace{ \left[\begin{array}{c} B_{c1}\\ B_{c2} \end{array}\right] }_{T_cB} \underbrace{(u(t)+\xi(t,x,u))}_{u'(t)}\\ (B_{c2}\in{\rm\bf R}^{p\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-82e2bbb3826132d675e28645b6cdaee1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5.2)\quad y(t) = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & I_p \\ \end{array}\right] }_{CT_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a7a9e6b215ba844d91319c8cb51519fd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5.3)\quad s(t)= \underbrace{ \left[\begin{array}{cc} 0_{m\times n-p} & F \\ \end{array}\right] }_{FCT_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-81ca3ce18892566a004196f3e47aebc4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x''_1(t)\\ x''_2(t)\\ \end{array}\right] }_{x''(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-p} & -B_{c1}(B_{c2}^TB_{c2})^{-1}B_{c2}^T \\ 0_{p\times n-p} & T^T \end{array}\right] }_{T_b} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)}= \underbrace{ \left[\begin{array}{cc} I_{n-p} & B_{c1}(B_{c2}^TB_{c2})^{-1}B_{c2}^T \\ 0_{p\times n-p} & T \end{array}\right] }_{T_b^{-1}} \underbrace{ \left[\begin{array}{c} x''_1(t)\\ x''_2(t)\\ \end{array}\right] }_{x''(t)}\\ (x''_1(t)\in{\rm\bf R}^{n-p},x''_2(t)\in{\rm\bf R}^{p},T\in{\rm\bf R}^{p\times p}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f1c87f8de33e3f31e6f9bffbf4539320_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.1)\quad \underbrace{ \left[\begin{array}{c} \dot x''_1(t)\\ \dot x''_2(t) \end{array}\right] }_{\dot{x}''(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \end{array}\right] }_{(T_bT_c)A(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x''_1(t)\\ x''_2(t)\\ \end{array}\right] }_{x''(t)} + \underbrace{ \left[\begin{array}{c} 0_{n-p\times m}\\ B_2 \end{array}\right] }_ {(T_bT_c)B} u'(t)\\ }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fd900c29bf5651b6ba66e54daeac82a4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.2)\quad y(t) = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] }_{C(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x''_1(t)\\ x''_2(t)\\ \end{array}\right] }_{x''(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fb92fb33c1ef65dd6f2d56305d8605c5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.3)\quad \begin{array}{l} s(t)= \underbrace{ \left[\begin{array}{cc} 0_{m\times n-p} & FT \\ \end{array}\right] }_{FC(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x''_1(t)\\ x''_2(t)\\ \end{array}\right] }_{x''(t)} = \underbrace{ \left[\begin{array}{cc|c} 0_{m\times n-p} & F_1 & F_2 \\ \end{array}\right] }_{FC(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x''_1(t)\\ x''_2(t)\\ \end{array}\right] }_{x''(t)}\\ (FT=\left[\begin{array}{cc} F_1 & F_2 \end{array}\right], F_1\in{\rm\bf R}^{m\times p-m}, F_2\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-30c6c57fc79840cb7ba8a7963f16d627_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \tilde{x}''_1(t)\\ s(t) \end{array}\right] }_{\tilde{x}''(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ F_1C' & F_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} \tilde{x}''_1(t)\\ \tilde{x}''_2(t) \end{array}\right] }_{x''(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} \tilde{x}''_1(t)\\ \tilde{x}''_2(t) \end{array}\right] }_{x''(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -F_2^{-1}F_1C' & F_2^{-1} \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} \tilde{x}''_1(t)\\ s(t) \end{array}\right] }_{\tilde{x}''(t)}\\ (C'=\left[\begin{array}{cc} 0_{p-m\times n-p} & I_{p-m} \end{array}\right]) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-28d720f19c00491b7c997c513bad202b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \underbrace{ \left[\begin{array}{c} \dot{\tilde{x}}''_1(t)\\ \dot{s}(t) \end{array}\right] }_{\dot{\tilde{x}}''(t)} = \underbrace{ \left[\begin{array}{cc} \tilde{A}_{11} & \tilde{A}_{12} \\ \tilde{A}_{21} & \tilde{A}_{22} \end{array}\right] }_{\tilde{A}=(T_sT_bT_c)A(T_sT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} \tilde{x}''_1(t)\\ s(t) \end{array}\right] }_{\tilde{x}''(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \tilde{B}_2 \end{array}\right] }_{\tilde{B}=T_sT_bT_cB} u'(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-53712b6be774e1fea90c24f848d74bac_l3.png)
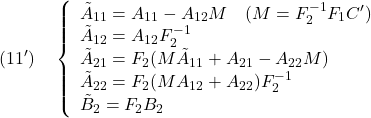
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \boxed{\tilde{A}_{11}=\underbrace{A_{11}}_{A'}-\underbrace{A_{12}}_{B'} \underbrace{F_2^{-1}F_1}_{K} \underbrace{\left[\begin{array}{cc} 0_{p-m\times n-p} & I_{p-m} \end{array}\right]}_{C'}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-507598a1b9847b9116034c01e1dba046_l3.png)
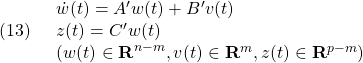
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \begin{array}{l} {\rm rank} \left[\begin{array}{cc} sI-A & B \end{array}\right]& ={\rm rank} \left[\begin{array}{cc} sI-(T_bT_c)A(T_bT_c)^{-1} & (T_bT_c)B \end{array}\right]\\ ={\rm rank} \left[\begin{array}{ccc} sI-A_{11} & -A_{12} & 0\\ -A_{21} & sI-A_{22} & B_2 \end{array}\right]\\ ={\rm rank} \left[\begin{array}{cc} sI-A_{11} & -A_{12} \end{array}\right]+m\\ ={\rm rank} \left[\begin{array}{cc} sI-A' & B' \end{array}\right]+m \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f0050e4228d42171173c44e1ab9f4b5b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \begin{array}{l} {\rm rank} \left[\begin{array}{c} sI-A' \\ C' \end{array}\right]\\ ={\rm rank} \left[\begin{array}{cc} sI-A_{1111} & -A_{1112} \\ -A_{1121} & sI-A_{1122} \\ 0 & I_{p-m} \end{array}\right]\ (A'=A_{11}= \left[\begin{array}{cc} A_{1111} & A_{1112} \\ A_{1121} & A_{1122} \end{array}\right])\\ ={\rm rank} \left[\begin{array}{c} sI-A_{1111} \\ A_{1121} \end{array}\right]+p-m\\ ={\rm rank} \left[\begin{array}{c} sI-T_{obs}A_{1111}T_{obs}^{-1} \\ A_{1121} T_{obs}^{-1} \end{array}\right]+p-m\\ (T_{obs}A_{1111}T_{obs}^{-1}= \left[\begin{array}{cc} A_{11}^o & A_{12}^o \\ 0_{n-p-r\times r} & A_{22}^o \end{array}\right], A_{1121} T_{obs}^{-1}= \left[\begin{array}{cc} 0_{p-m\times r} & A_{21}^o \end{array}\right] )\\ ={\rm rank} \left[\begin{array}{cc} sI-A_{11}^o & -A_{12}^o \\ 0_{n-p-r\times r} & sI-A_{22}^o\\ 0_{p-m\times r} & A_{21}^o \end{array}\right]+p-m\\ ={\rm rank}(sI-A_{11}^o)+ \underbrace{{\rm rank}\left[\begin{array}{cc} sI-A_{22}^o\\ A_{21}^o \end{array}\right]}_{n-p-r}+p-m \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-678a84f544a8ee5f97c48b3ee005d9e0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)} = \underbrace{ \left[\begin{array}{cc|c} T_{obs} & 0 & 0\\ 0 & I_{p-m} & 0 \\\hline 0 & 0 & I_m \end{array}\right] }_{T_a} \underbrace{ \left[\begin{array}{c} {x}''_1(t)\\ {x}''_2(t) \end{array}\right] }_{x''(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} {x}''_1(t)\\ {x}''_2(t) \end{array}\right] }_{x''(t)}= \underbrace{ \left[\begin{array}{cc|c} T_{obs}^{-1} & 0 & 0\\ 0 & I_{p-m} & 0 \\\hline 0 & 0 & I_m \end{array}\right] }_{T_a^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)}\\ (x'''_1(t)\in{\rm\bf R}^{n-m},x'''_2(t)\in{\rm\bf R}^{m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a761762bcf2a930d49f44e4cde5722c7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18.1)\quad \boxed{\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x'''_1(t)\\ \dot x'''_2(t) \end{array}\right] }_{\dot{x}'''(t)} = \underbrace{ \left[\begin{array}{ccc|c} A_{11}^o & A_{12}^o & A_{121}^m & A_{121}\\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m & A_{1221}\\ 0_{p-m\times r} & A_{21}^o & A_{22}^m & A_{1222}\\\hline A_{2120} & A_{2121} & A_{2122} & A_{22} \end{array}\right] }_{(T_aT_bT_c)A(T_aT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)}\\ + \underbrace{ \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline B_2 \end{array}\right] }_ {(T_aT_bT_c)B} u(t)\\ (A_{11}^o\in{\rm\bf R}^{r\times r},A_{22}^o\in{\rm\bf R}^{n-p-r\times n-p-r},A_{22}^m\in{\rm\bf R}^{p-m\times p-m}) \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2f4457165fe43f529be7658c079b9eff_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18.2)\quad \boxed{\begin{array}{l} y(t) = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] }_{C(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{cc|c} T_{obs}^{-1} & 0 & 0\\ 0 & I_{p-m} & 0 \\\hline 0 & 0 & I_m \end{array}\right] }_{T_a^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)}\\ = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] }_{C(T_aT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-05f9d91daa89c529f7c3464c13c2fd69_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12')\quad \begin{array}{l} T_{a'}\tilde{A}_{11}T_{a'}^{-1}=T_{a'}(A'-B'KC')T_{a'}^{-1} \quad (T_{a'}= \left[\begin{array}{cc} T_{obs} & 0 \\ 0 & I_{p-m} \end{array}\right])\\ =T_{a'}A_{11}T_{a'}^{-1}-T_{a'}A_{12} K \left[\begin{array}{ccc} 0_{p-m\times r} & 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right]T_{a'}^{-1}\\ = \underbrace{ \left[\begin{array}{c|cc} A_{11}^o & A_{12}^o & A_{121}^m \\\hline 0_{n-p-r\times r} & A_{22}^o & A_{122}^m \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m \end{array}\right]}_{T_{a'}A_{11}T_{a'}^{-1}} -\underbrace{\left[\begin{array}{ccc} A_{121}\\\hline A_{1221}\\ A_{1222} \end{array}\right]}_{T_{a'}A_{12}} \left[\begin{array}{ccc} 0_{p-m\times r} & 0_{p-m\times n-p-r} & K \end{array}\right]\\ = \left[\begin{array}{c|c} A_{11}^o & \left[\begin{array}{cc} A_{12}^o & A_{121}^m-A_{121}K \end{array}\right]\\\hline 0_{n-m-r\times r} & \left[\begin{array}{cc} A_{22}^o & A_{122}^m \\ A_{21}^o & A_{22}^m \end{array}\right] -\left[\begin{array}{c} A_{1221}\\ A_{1222} \end{array}\right] K\left[\begin{array}{cc} 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right] \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-63e4b25f1d738158680736e0e7e80f59_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(19)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} A_{22}^o & A_{122}^m \\ A_{21}^o & A_{22}^m \end{array}\right]}_{A''} - \underbrace{\left[\begin{array}{c} A_{1221}\\ A_{1222} \end{array}\right]}_{B''} K \underbrace{\left[\begin{array}{cc} 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right]}_{C''}\\ (A''\in{\rm\bf R}^{n-m-r\times n-m-r}, B''\in{\rm\bf R}^{n-m-r\times m}, C''\in{\rm\bf R}^{p-m\times n-m-r})\\ =\underbrace{\left[\begin{array}{cc} A_{22}^o & A_{122}^m \\ A_{21}^o & A_{22}^m \end{array}\right]}_{A''} - \underbrace{\left[\begin{array}{cc} B''_1 & 0_{n-m-r\times m-m'} \end{array}\right]}_{B''T_m} \underbrace{\left[\begin{array}{cc} K_1\\ K_2 \end{array}\right]}_{T_m^{-1}K} \underbrace{\left[\begin{array}{cc} 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right]}_{C''}\\ (T_m\in{\rm\bf R}^{m\times m}, B''_1\in{\rm\bf R}^{n-m-r\times m'}, K_1\in{\rm\bf R}^{m'\times p-m}, K_2\in{\rm\bf R}^{m-m'\times p-m})\\ =A''-B''_1K_1C'' \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f8caf2174f6b6ea2e5a122d260b19c35_l3.png)
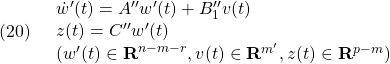
![Rendered by QuickLaTeX.com \displaystyle{(26)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ KC' & I_m \\ \end{array}\right] }_{\bar{T}_s} \underbrace{ \left[\begin{array}{c} {x}''_1(t)\\ {x}''_2(t) \end{array}\right] }_{x''(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} {x}''_1(t)\\ {x}''_2(t) \end{array}\right] }_{x''(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -KC' & I_m \end{array}\right] }_{\bar{T}_s^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)}\\ (C'=\left[\begin{array}{cc} 0_{p-m\times n-p} & I_{p-m} \end{array}\right]) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a09e0069834751decee9881760ac9db6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(27)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -KC' & I_m \end{array}\right] }_{\bar{T}_s^{-1}} \underbrace{ \left[\begin{array}{c} \dot{\bar{x}}''_1(t)\\ \dot{\bar{s}}(t) \end{array}\right] }_{\dot{\bar{x}}''(t)}\\ = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{(T_bT_c)A(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -KC' & I_m \end{array}\right] }_{\bar{T}_s^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{(T_bT_c)B} u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3b965cc92b91df561d39464b2a06eb0e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(28)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\bar{x}}''_1(t)\\ \dot{\bar{s}}(t) \end{array}\right] }_{\dot{\bar{x}}''(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ KC' & I_m \end{array}\right] }_{\bar{T}_s} \underbrace{ \left[\begin{array}{cc} A_{11}-A_{12}KC' & A_{12} \\ A_{21}-A_{22}KC' & A_{22} \end{array}\right] }_{(T_bT_c)A(\bar{T}_sT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)}\\ + \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ KC' & I_m \end{array}\right] }_{\bar{T}_s} \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3841b7fe89f905ef50150e9e6e841918_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(29.1)\quad \underbrace{ \left[\begin{array}{c} \dot{\bar{x}}''_1(t)\\ \dot{\bar{s}}(t) \end{array}\right] }_{\dot{\bar{x}}''(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22} \end{array}\right] }_{\bar{A}=(\bar{T}_sT_bT_c)A(\bar{T}_sT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \bar{B}_2 \end{array}\right] }_{\bar{B}=\bar{T}_sT_bT_cB} u'(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-22de0f3334d3536835a81c4149a15f5a_l3.png)
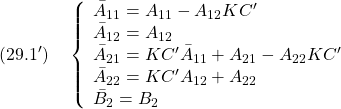
![Rendered by QuickLaTeX.com \displaystyle{(29.2)\quad \begin{array}{l} y(t) = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] }_{C(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -KC' & I_m \end{array}\right] }_{\bar{T}_s^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)}\\ = \underbrace{ \left[\begin{array}{cc} -TKC' & T \end{array}\right] }_{C(\bar{T}_sT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c45457f5b0c70ff7a60918110f867286_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(29.3)\quad \begin{array}{l} s(t)= \underbrace{ \left[\begin{array}{cc} 0_{m\times n-p} & FT \\ \end{array}\right] }_{FC(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -KC' & I_m \end{array}\right] }_{\bar{T}_s^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)}\\ = \underbrace{ \left[\begin{array}{cc|c} 0_{m\times n-p} & F_1 & F_2 \\ \end{array}\right] }_{FC(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{cc|c} I_{n-p}& 0 & 0\\ 0 & I_{p-m} & 0 \\\hline 0 & -K & I_m \end{array}\right] }_{\bar{T}_s^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)}\\ = \underbrace{ \left[\begin{array}{cc|c} 0_{m\times n-p} & 0_{m\times p-m} & F_2 \\ \end{array}\right] }_{FC(\bar{T}_sT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)}\\ (FT=\left[\begin{array}{cc} F_1 & F_2 \end{array}\right], F_1\in{\rm\bf R}^{m\times p-m}, F_2\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5ebe1bc0632a1704e6bdd06aca89f8c8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad \underbrace{ \left[\begin{array}{cc} 0 & \bar{B}_2^T \end{array}\right] }_{\bar{B}^T} \underbrace{ \left[\begin{array}{cc} P_1 & 0 \\ 0 & P_2 \end{array}\right] }_{P} =F \underbrace{ \left[\begin{array}{cc} -TKC' & T \end{array}\right] }_{\bar{C}}\\ \Rightarrow \bar{B}_2^TP_2=F_2 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-82f76df99883e6d0a1965e87719801b1_l3.png)
