| MATLAB |
%cSPIN_sf_gs.m
%-----
clear all close all
J1=1; J2=1; J3=0.5;
OMnom=2*pi; OMmin=0*OMnom; OMmax=2*OMnom;
A1=[0 (J2-J3)/J1;(J3-J1)/J2 0];
B=diag([1/J1 1/J2]); C=eye(2); D=zeros(2,2);
S0=[zeros(2,2) B;C D];
S1=zeros(4,4); S1(1:2,1:2)=A1;
%-----
J1=1; J2=1; J3=0.5;
OMnom=2*pi; OMmin=0*OMnom; OMmax=2*OMnom;
A1= OMmin*[0 (J2-J3)/J1;(J3-J1)/J2 0];
A2= OMmax*[0 (J2-J3)/J1;(J3-J1)/J2 0];
B=diag([1/J1 1/J2]);
B1=B; B2=B;
C1=[eye(2,2);zeros(2,2)];
D11=zeros(4,2);
D12=[zeros(2,2);eye(2,2)];
alpha=1; r=3; th=pi/4;
LMIs=sf_synlmi7(A1,A2,B1,B2,C1,D11,D12,alpha,r,th);
cobj=zeros(1,decnbr(LMIs));
cobj(1)=1;
[cost,xopt]=mincx(LMIs,cobj);
Y=dec2mat(LMIs,xopt,2);
Z1=dec2mat(LMIs,xopt,3);
Z2=dec2mat(LMIs,xopt,4);
F1=Z1/Y,pl1=eig(A1-B2*F1)
F2=Z2/Y,pl2=eig(A2-B2*F2)
%------
figure(1)
subplot(121),dregion(alpha,0,r,th,7*[-1,1,-1,1])
plot(real(pl1),imag(pl1),'*')
subplot(122), dregion(alpha,0,r,th,7*[-1,1,-1,1])
plot(real(pl2),imag(pl2),'*')
%------
prange=OMmax-OMmin; pmax=OMmax; pmin=OMmin;
sim("SPIN_sf_gs")
%-----
function LMIs=sf_synlmi7(A1,A2,B1,B2,C1,D11,D12,alpha,r,th)
[n,m]=size(B2);
sth=sin(th); cth=cos(th);
setlmis([]);
gam=lmivar(1,[1 0]);
Y=lmivar(1,[n 1]);
Z1=lmivar(2,[m n]);
Z2=lmivar(2,[m n]);
%
lmi11=newlmi;
lmiterm([lmi11,1,1,Y],A1,1,'s'); %#1:A*Y+Y*A'
lmiterm([lmi11,1,1,Z1],-B2,1,'s'); %#1:-(B2*Z+Z*B2')
lmiterm([lmi11,1,2,0],B1); %#1:B1
lmiterm([lmi11,2,2,gam],-1,1); %#1:-gam
lmiterm([lmi11,3,1,Y],C1,1); %#1:C1*Y
lmiterm([lmi11,3,1,Z1],-D12,1); %#1:D12*Z
lmiterm([lmi11,3,2,0],D11); %#1:D11
lmiterm([lmi11,3,3,gam],-1,1); %#1:-gam
lmi21=newlmi;
lmiterm([lmi21,1,1,Y],A1,1,'s'); %#2:A*Y+Y*A'
lmiterm([lmi21,1,1,Z1],-B2,1,'s'); %#2:-(B2*Z+Z'*B2')
lmiterm([lmi21,1,1,Y],2*alpha,1); %#2:2*alpha*Y
lmi31=newlmi;
lmiterm([lmi31,1,1,Y],-r,1); %#3:-r*Y
lmiterm([lmi31,1,2,Y],A1,1); %#3:A*Y
lmiterm([lmi31,1,2,Z1],-B2,1); %#3:-B2*Z
lmiterm([lmi31,2,2,Y],-r,1); %#3:-r*Y
lmi41=newlmi;
lmiterm([lmi41,1,1,Y],sth*A1,1,'s'); %#4:sth*(A*Y+Y*A')
lmiterm([lmi41,1,1,Z1],-sth*B2,1,'s');%#4:-sth*(B2*Z+Z'*B2')
lmiterm([lmi41,1,2,Y],cth*A1,1); %#4:cth*A*Y
lmiterm([lmi41,1,2,Y],1,-cth*A1'); %#4:-cth*Y*A'
lmiterm([lmi41,1,2,Z1],-cth*B2,1); %#4:-cth*B2*Z
lmiterm([lmi41,1,2,-Z1],1,cth*B2'); %#4:cth*Z'*B2'
lmiterm([lmi41,2,2,Y],sth*A1,1,'s'); %#4:sth*(A*Y+Y*A')
lmiterm([lmi41,2,2,Z1],-sth*B2,1,'s');%#4:-sth*(B2*Z+Z'*B2')
%
lmi12=newlmi;
lmiterm([lmi12,1,1,Y],A2,1,'s'); %#1:A*Y+Y*A'
lmiterm([lmi12,1,1,Z2],-B2,1,'s'); %#1:-(B2*Z+Z*B2')
lmiterm([lmi12,1,2,0],B1); %#1:B1
lmiterm([lmi12,2,2,gam],-1,1); %#1:-gam
lmiterm([lmi12,3,1,Y],C1,1); %#1:C1*Y
lmiterm([lmi12,3,1,Z2],-D12,1); %#1:D12*Z
lmiterm([lmi12,3,2,0],D11); %#1:D11
lmiterm([lmi12,3,3,gam],-1,1); %#1:-gam
lmi22=newlmi;
lmiterm([lmi22,1,1,Y],A2,1,'s'); %#2:A*Y+Y*A'
lmiterm([lmi22,1,1,Z2],-B2,1,'s'); %#2:-(B2*Z+Z'*B2')
lmiterm([lmi22,1,1,Y],2*alpha,1); %#2:2*alpha*Y
lmi32=newlmi;
lmiterm([lmi32,1,1,Y],-r,1); %#3:-r*Y
lmiterm([lmi32,1,2,Y],A2,1); %#3:A*Y
lmiterm([lmi32,1,2,Z2],-B2,1); %#3:-B2*Z
lmiterm([lmi32,2,2,Y],-r,1); %#3:-r*Y
lmi42=newlmi;
lmiterm([lmi42,1,1,Y],sth*A2,1,'s'); %#4:sth*(A*Y+Y*A')
lmiterm([lmi42,1,1,Z2],-sth*B2,1,'s');%#4:-sth*(B2*Z+Z'*B2')
lmiterm([lmi42,1,2,Y],cth*A2,1); %#4:cth*A*Y
lmiterm([lmi42,1,2,Y],1,-cth*A2'); %#4:-cth*Y*A'
lmiterm([lmi42,1,2,Z2],-cth*B2,1); %#4:-cth*B2*Z
lmiterm([lmi42,1,2,-Z2],1,cth*B2'); %#4:cth*Z'*B2'
lmiterm([lmi42,2,2,Y],sth*A2,1,'s'); %#4:sth*(A*Y+Y*A')
lmiterm([lmi42,2,2,Z2],-sth*B2,1,'s');%#4:-sth*(B2*Z+Z'*B2')
%
lmi5=newlmi;
lmiterm([-lmi5,1,1,Y],1,1); %#5:Y
lmi6=newlmi;
lmiterm([lmi6,1,1,gam],1,1); %#6:gam
lmiterm([-lmi6,1,1,0],1e3); %#6:1000
LMIs=getlmis;
end
%-----
%eof
|
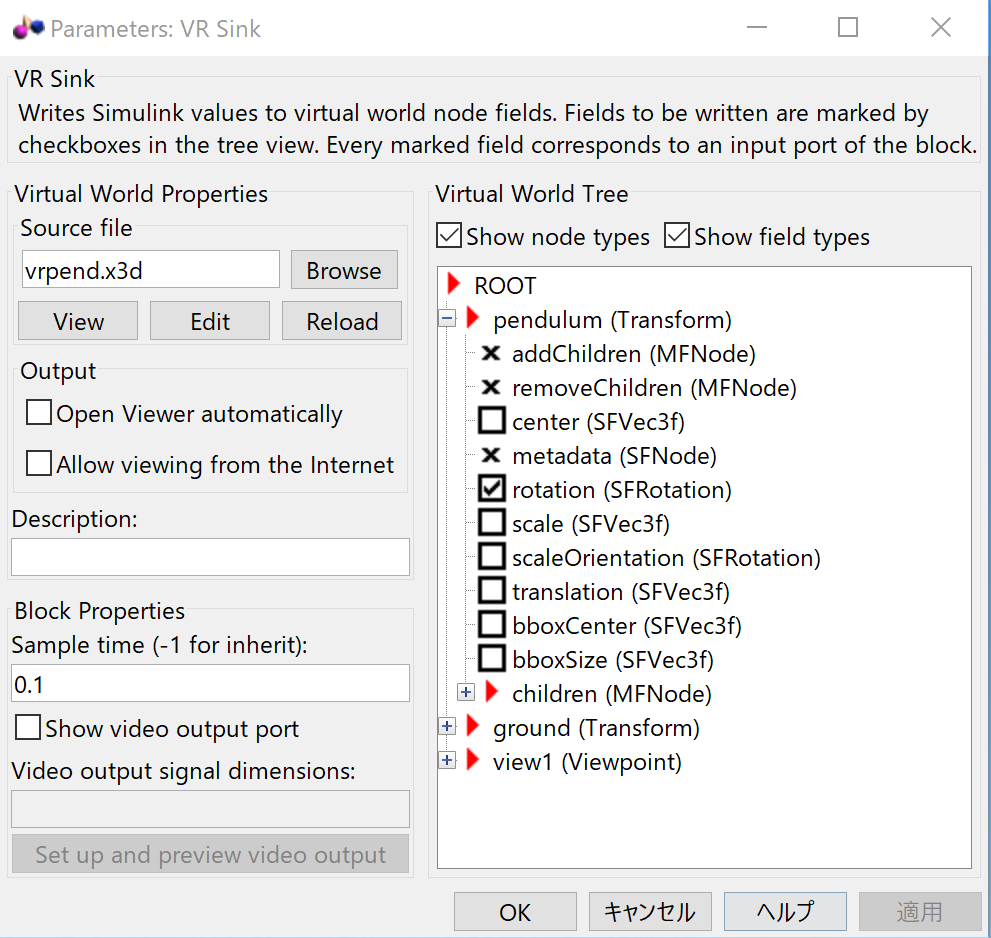
![]() が漸近安定であるための必要十分条件は、行列
が漸近安定であるための必要十分条件は、行列![]() の固有値がすべて複素左平面
の固有値がすべて複素左平面![]() に存在することでした。でも平衡状態
に存在することでした。でも平衡状態![]() に復帰するその過程はいつも好ましいとは言えません。たとえば、平衡状態
に復帰するその過程はいつも好ましいとは言えません。たとえば、平衡状態![]() に復帰する速さが適切であること、その過程が振動的でないこと、そして適切なサンプリング周期をもつ(絶対値が極端に大きな固有値をもたない)ことが必要です。そこで行列
に復帰する速さが適切であること、その過程が振動的でないこと、そして適切なサンプリング周期をもつ(絶対値が極端に大きな固有値をもたない)ことが必要です。そこで行列![]() の固有値が含まれる望ましい領域
の固有値が含まれる望ましい領域![]()
![]()
![]() (Linear Matrix Inequality)で表します。
(Linear Matrix Inequality)で表します。![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{lll} && \left[\begin{array}{cc} P & M \\ M^T & Q \end{array}\right]<0\\ &\Leftrightarrow& P-MQ^{-1}M^T<0,\ Q<0\\ &\Leftrightarrow& P<0,\ Q-M^TP^{-1}M<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1032be1b5ca3689d43f86d220f3f031c_l3.png)
![]() または
または![]() はシュール補元(Shure Complement)と呼ばれています。
はシュール補元(Shure Complement)と呼ばれています。![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \begin{array}{lll} & & \underbrace{ \left[\begin{array}{cc} P & M \\ M^T & Q \end{array}\right] }_{R} \\ &=& \left[\begin{array}{cc} I & MQ^{-1} \\ 0 & I \end{array}\right] \left[\begin{array}{cc} P-MQ^{-1}M^T & 0 \\ 0 & Q \end{array}\right] \left[\begin{array}{cc} I & 0 \\ Q^{-1}M^T & I \end{array}\right] \\ &=& \underbrace{ \left[\begin{array}{cc} I & 0 \\ M^TP^{-1} & I \end{array}\right] }_{T^T} \underbrace{ \left[\begin{array}{cc} P & 0 \\ 0 & Q-M^TP^{-1}M \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{cc} I & P^{-1}M \\ 0 & I \end{array}\right] }_{T} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c71f6a58283e2c1b2186c86022be5b68_l3.png)
![]()
![]()
![]() を考えます。
を考えます。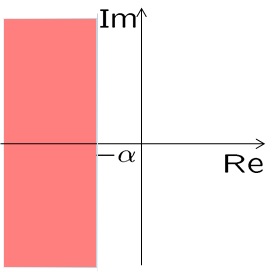
![]()
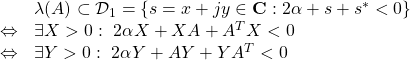
![]() が上図を表すことは、次のように確かめられます。
が上図を表すことは、次のように確かめられます。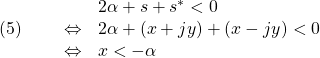
![]() とすると、次のように確かめられます(*は複素共役)。
とすると、次のように確かめられます(*は複素共役)。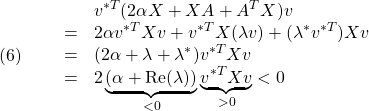
![]() とおくと、次が成り立ちます。
とおくと、次が成り立ちます。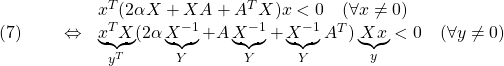
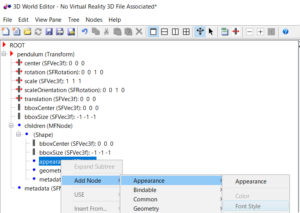
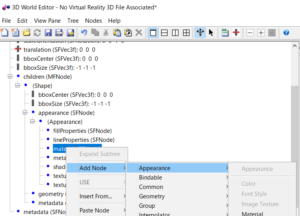
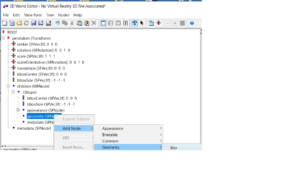
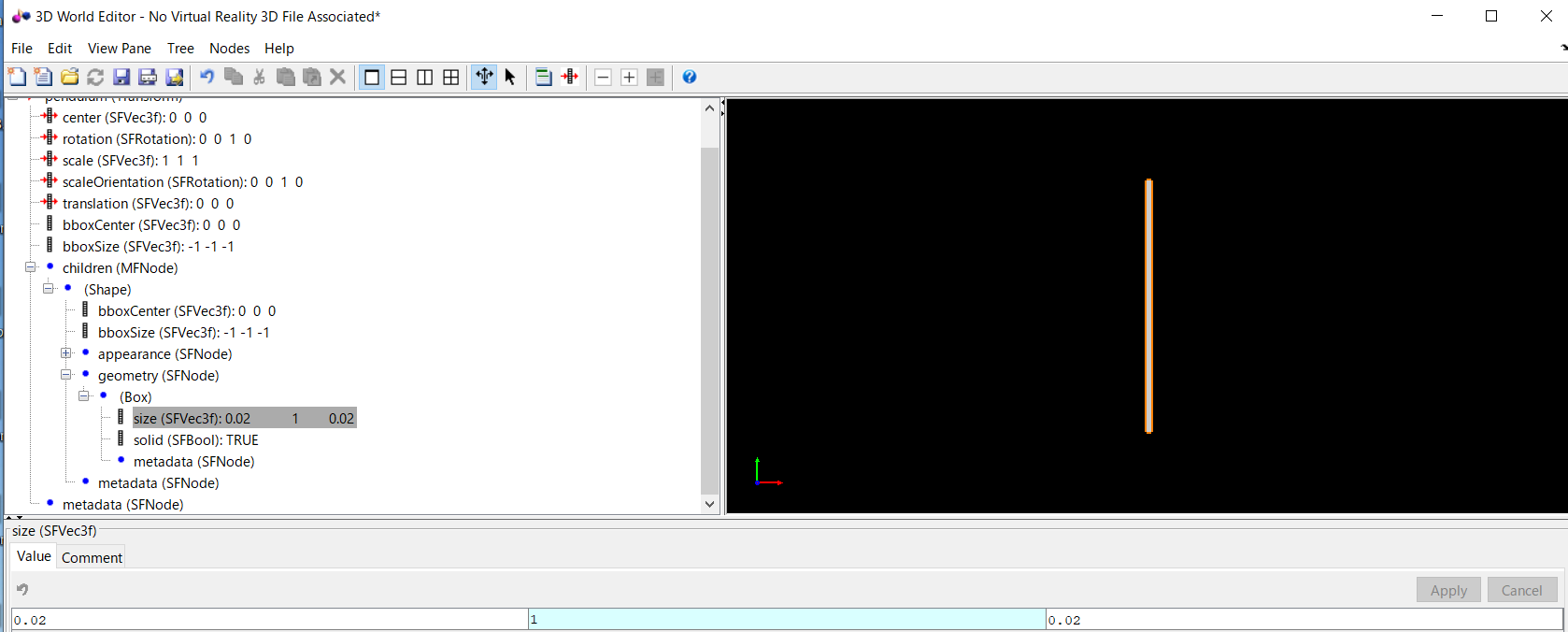
![]() α制約を調べる次のコードを説明せよ。
α制約を調べる次のコードを説明せよ。![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
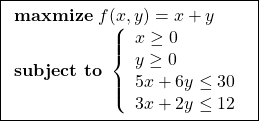
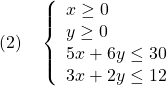
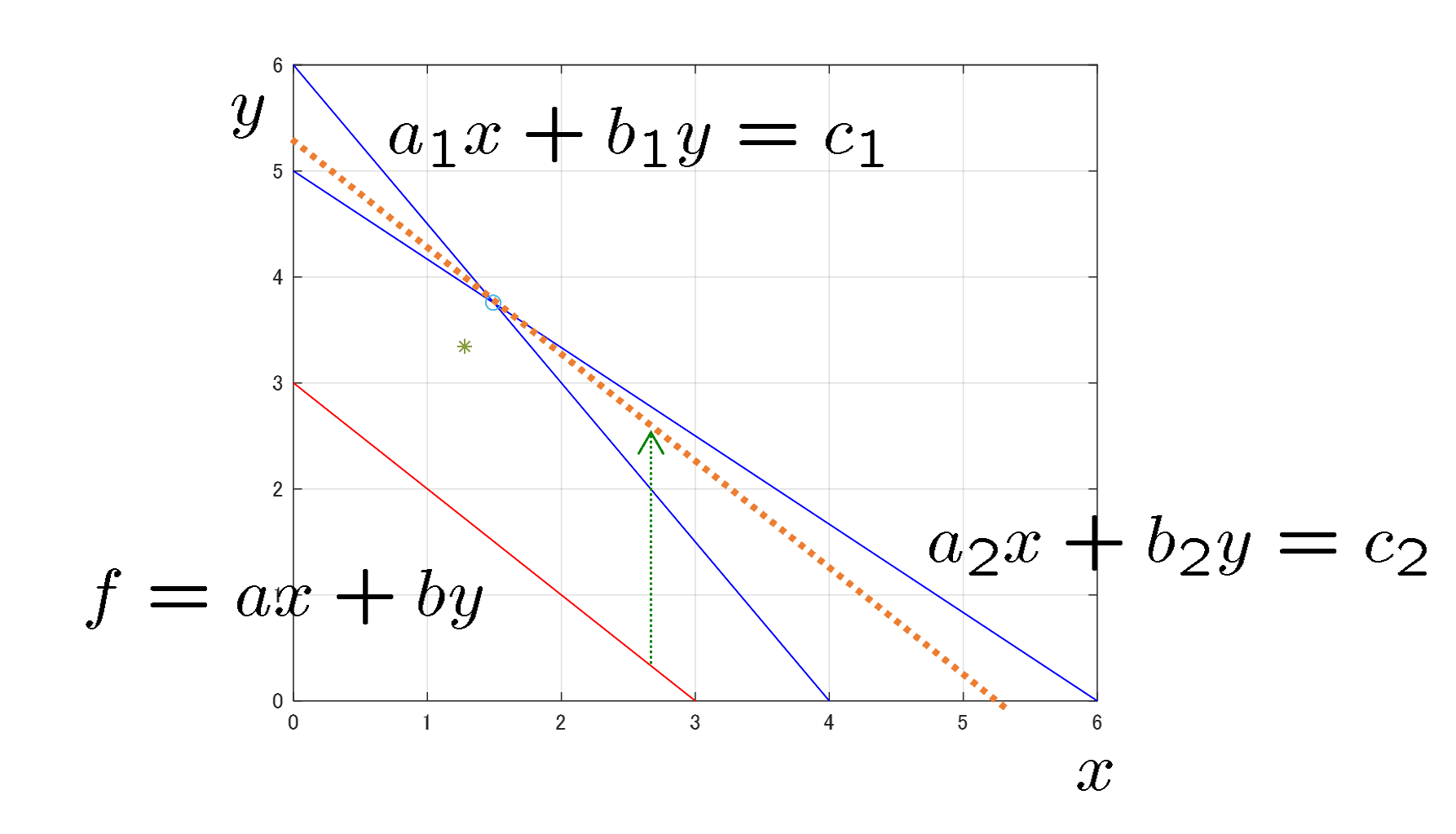 図1 線形計画問題の例
図1 線形計画問題の例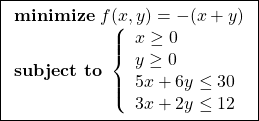
![Rendered by QuickLaTeX.com \displaystyle{(3) \underbrace{ \left[\begin{array}{c} \dot{\omega}_1(t) \\ \dot{\omega}_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & \Omega(t)\frac{J_2-J_3}{J_1} \\ \Omega(t)\frac{J_3-J_1}{J_2} & 0 \end{array}\right] }_{A(\Omega(t))} \underbrace{ \left[\begin{array}{c} \omega_1(t) \\ \omega_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} \frac{1}{J_1} & 0 \\ 0 & \frac{1}{J_2} \end{array}\right] }_{B} \underbrace{ \left[\begin{array}{c} \tau_1(t) \\ \tau_2(t) \end{array}\right] }_{u(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-06d0d0706f122470d4466143aac157d2_l3.png)
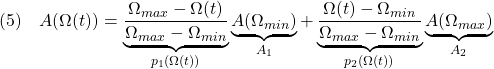
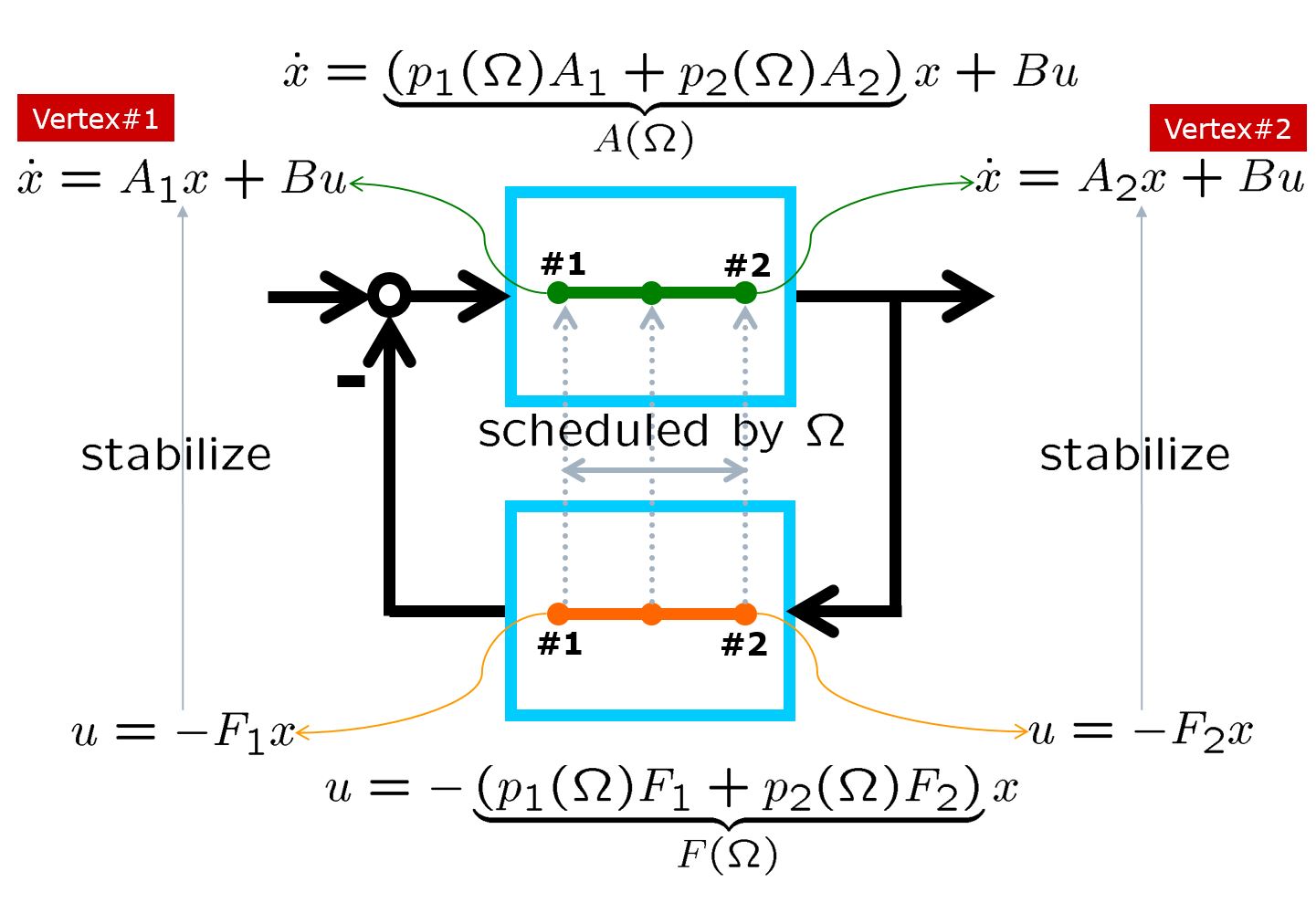 図3 LPV制御の枠組み
図3 LPV制御の枠組み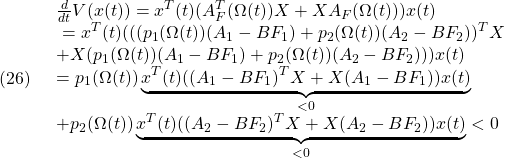
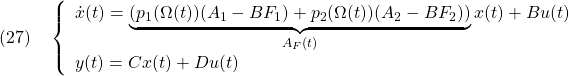
![Rendered by QuickLaTeX.com \displaystyle{(28)\quad \exists X_1>0:\ \left[\begin{array}{ccc} (A_1-BF_1)^TX_1+X_1(A_1-BF_1) & X_1B & C^T \\ B^TX_1 & -\gamma I & D^T \\ C & D & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4e0b94de7fd261c64c1ad459ff663479_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(29)\quad \exists X_2>0:\ \left[\begin{array}{ccc} (A_2-BF_2)^TX_2+X_2(A_2-BF_2) & X_2B & C^T \\ B^TX_2 & -\gamma I & D^T \\ C & D & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e6b89cd6a762615e4cf1bf7d4196430f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(30)\quad \left[\begin{array}{ccc} (A_1-BF_1)^TX+X(A_1-BF_1) & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D &-I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-54dee83aaf14f44301eff55fc1606abe_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad \left[\begin{array}{ccc} (A_1-BF_1)^TX+X(A_1-BF_1) & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D &-I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-740c33f1cb04f1a96dba09b1d8f767da_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right]^T \left[\begin{array}{cc} \begin{array}{c} ( p_1(\Omega(t))(A_1-BF_1)+p_2(\Omega(t))(A_2-BF_2) )^TX\\ +X( p_1(\Omega(t))(A_1-BF_1)+p_2(\Omega(t))(A_2-BF_2) ) \end{array} & XB \\ B^TX & 0 \end{array}\right] \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1fc23d0a361803d365380b86a013ae6e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ < \underbrace{(p_1(\Omega(t))+p_2(\Omega(t)))}_1 \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right]^T \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right]^T \left[\begin{array}{cc} - I & 0 \\ 0 & \gamma^2 I \end{array}\right] \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right] \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2d9183af6071904863cbae048501209a_l3.png)
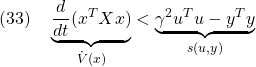
![Rendered by QuickLaTeX.com \displaystyle{(35)\quad P: \left\{\begin{array}{l} \dot{x}(t)=\underbrace{(p_1(\Omega(t))A_1+p_2(\Omega(t))A_2)}_{A(\Omega(t))}x(t)+B_1u_1(t)+B_2u_2(t) \\ \underbrace{ \left[\begin{array}{c} y(t)\\ u(t) \end{array}\right] }_{y_1(t)} = \underbrace{ \left[\begin{array}{c} C\\ 0 \end{array}\right] }_{C_1} x(t)+ \underbrace{ \left[\begin{array}{c} 0\\ 0 \end{array}\right] }_{D_{11}}u_1(t)+ \underbrace{ \left[\begin{array}{c} 0\\ I \end{array}\right] }_{D_{12}} u_2(t) \\ y_2(t)=x(t) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-427d73db7b01554c5df63c0e87878e0a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(37)\quad P_{CL}: \left\{\begin{array}{l} \dot{x}(t)=(A(\Omega(t))-B_2F(\Omega(t)))x(t)+B_1u_1(t) \\ y_1(t)= \underbrace{ \left[\begin{array}{c} C\\ -F \end{array}\right] }_{C_1-D_{12}F} x(t) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d78f3f099b3133c3acad786e1bf139f9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(40)\quad \left[\begin{array}{ccc} (A_1Y-B_2Z_1)^T+A_1Y-B_2Z_1 & B_1 & (C_1Y-D_{12}Z_1)^T \\ B_1^T & -\gamma I & D_{11}^T \\ C_1Y-D_{12}Z_1 & D_{11} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c7466d89622c237467830e9e7a4dde4f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(41)\quad \begin{array}{l} 2\alpha Y+A_1Y-B_2Z_1+(A_1Y-B_2Z_1)^T<0 \\ \left[\begin{array}{cc} -rY & A_1Y-B_2Z_1 \\ (A_1Y-B_2Z_1)^T & -rY \end{array}\right]<0 \\ \left[\begin{array}{cc} \sin\theta(A_1Y-B_2Z_1+(A_1Y-B_2Z_1)^T) & \\ -\cos\theta(A_1Y-B_2Z_1-(A_1Y-B_2Z_1)^T) & \end{array}\right. \\ \left.\begin{array}{cc} & \cos\theta(A_1Y-B_2Z_1-(A_1Y-B_2Z_1)^T) \\ & \sin\theta(A_1Y-B_2Z_1+(A_1Y-B_2Z_1)^T) \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e8f398812655a3aa43af25d448acd033_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(42)\quad \left[\begin{array}{ccc} (A_2Y-B_2Z_2)^T+A_2Y-B_2Z_2 & B_1 & (C_1Y-D_{12}Z_2)^T \\ B_1^T & -\gamma I & D_{11}^T \\ C_1Y-D_{12}Z_2 & D_{11} & -\gamma I \end{array}\right]<0 \\ }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4cce98efcffcefcc62a9d413a65d4bc4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(43)\quad \begin{array}{l} 2\alpha Y+A_1Y-B_2Z_2+(A_1Y-B_2Z_2)^T<0 \\ \left[\begin{array}{cc} -rY & A_1Y-B_2Z_2 \\ (A_1Y-B_2Z_2)^T & -rY \end{array}\right]<0 \\ \left[\begin{array}{cc} \sin\theta(A_2Y-B_2Z_2+(A_2Y-B_2Z_2)^T) & \\ -\cos\theta(A_2Y-B_2Z_2-(A_2Y-B_2Z_2)^T) & \end{array}\right. \\ \left.\begin{array}{cc} & \cos\theta(A_2Y-B_2Z_2-(A_2Y-B_2Z_2)^T) \\ & \sin\theta(A_2Y-B_2Z_2+(A_2Y-B_2Z_2)^T) \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-748f7d965c9e2ec369f760ff7e4cfe8d_l3.png)
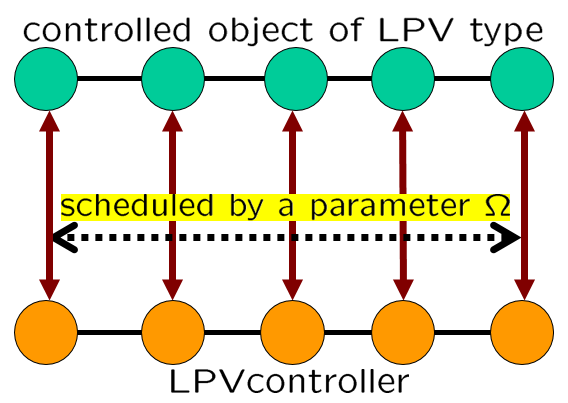 図4 LPV制御のイメージ
図4 LPV制御のイメージ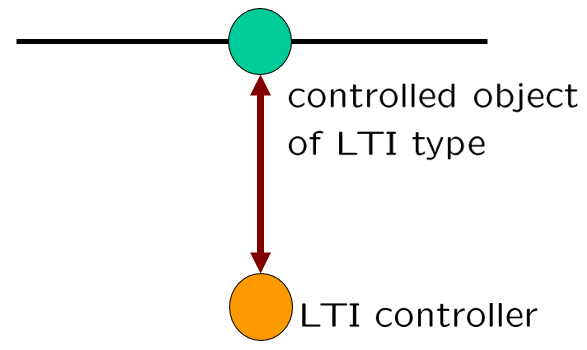 図5 LTI制御のイメージ
図5 LTI制御のイメージ 図6 LPV制御においてスケジューリングを止めた場合
図6 LPV制御においてスケジューリングを止めた場合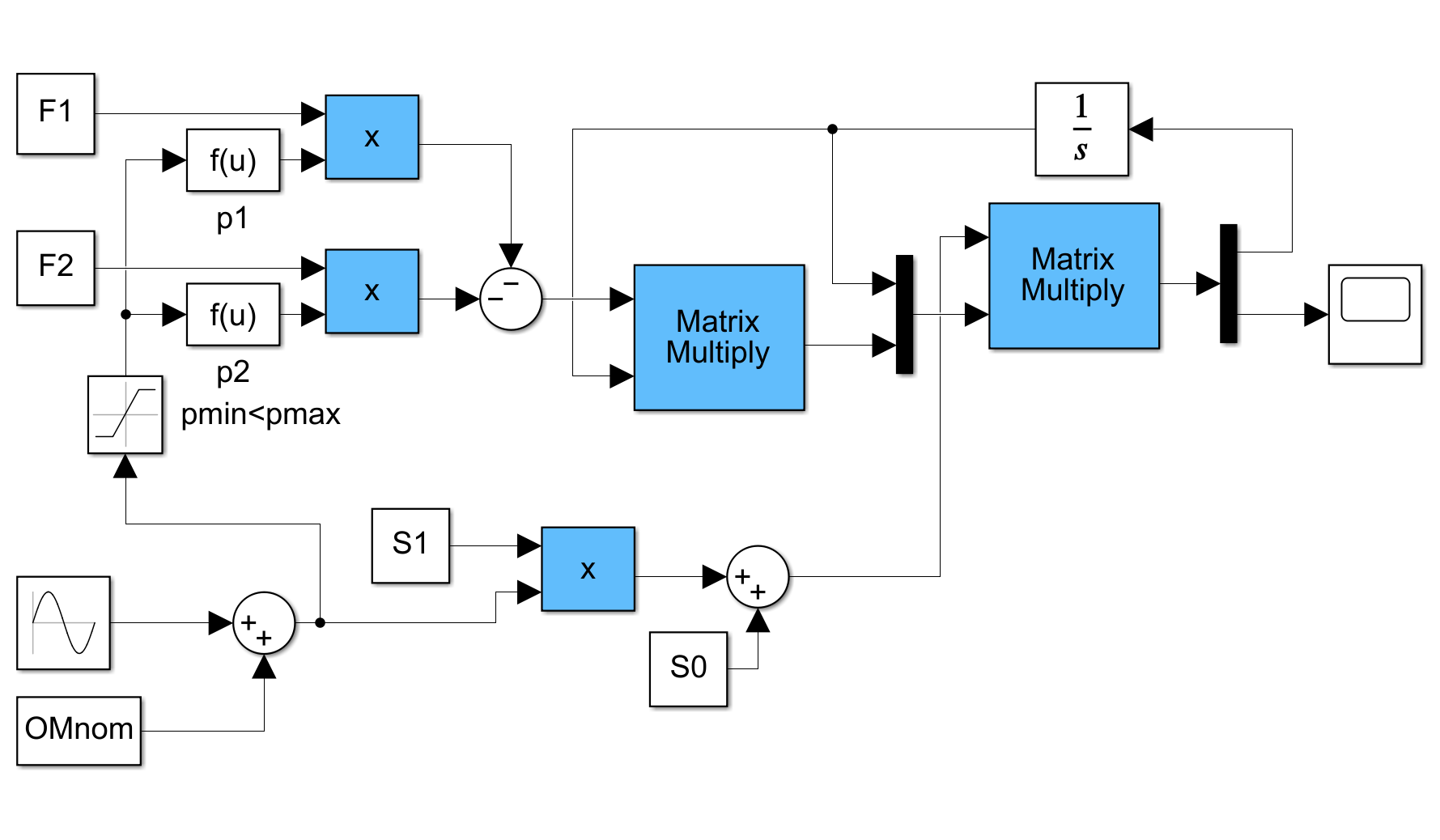
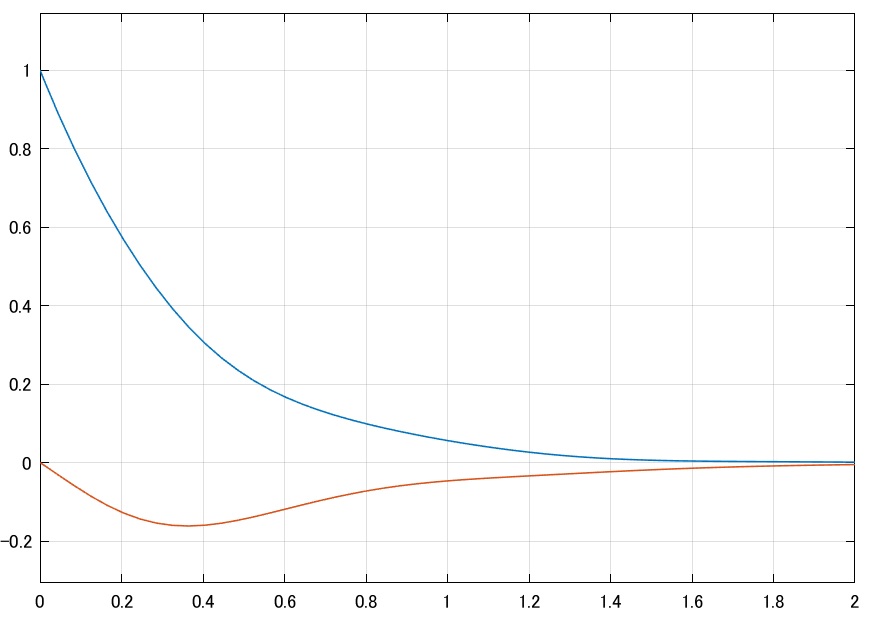 図7 回転体のLPV制御
図7 回転体のLPV制御
 図8 回転体の
図8 回転体の
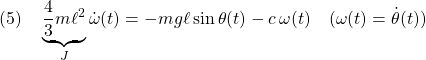
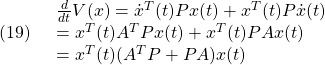
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \begin{array}{l} \displaystyle{A^T\int_0^\infty \exp(A^Tt)Q\exp(At)dt+\int_0^\infty \exp(A^Tt)Q\exp(At)dt\,A}\\ \displaystyle{=\int_0^\infty \frac{d}{dt}(\exp(A^Tt)Q\exp(At))\,dt}\\ \displaystyle{=\left[\exp(A^Tt)Q\exp(At)\right]_0^\infty=-Q<0} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8818d2570a2394fee7a40d1e57a29ee2_l3.png)
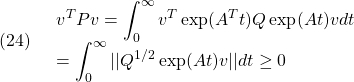
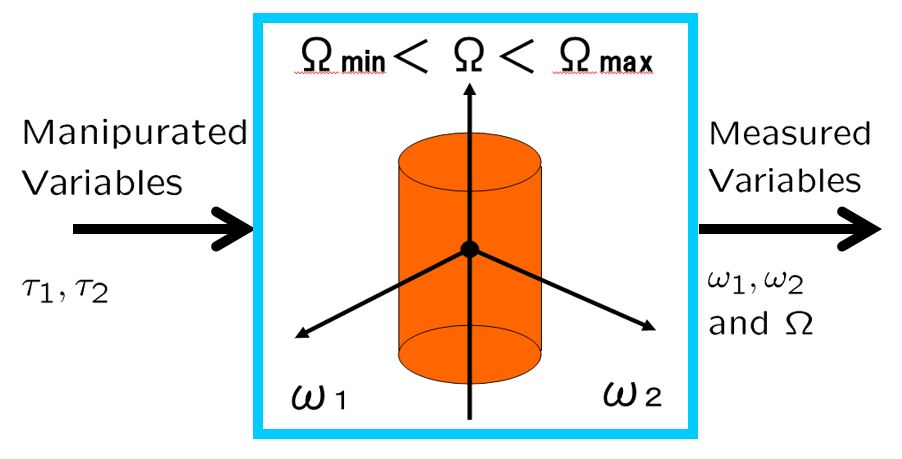 図1 パラメータ変動システムの例
図1 パラメータ変動システムの例 図2 パラメータ変動システムの応答シミュレーション例
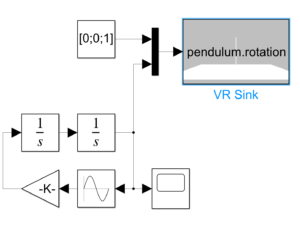
図2 パラメータ変動システムの応答シミュレーション例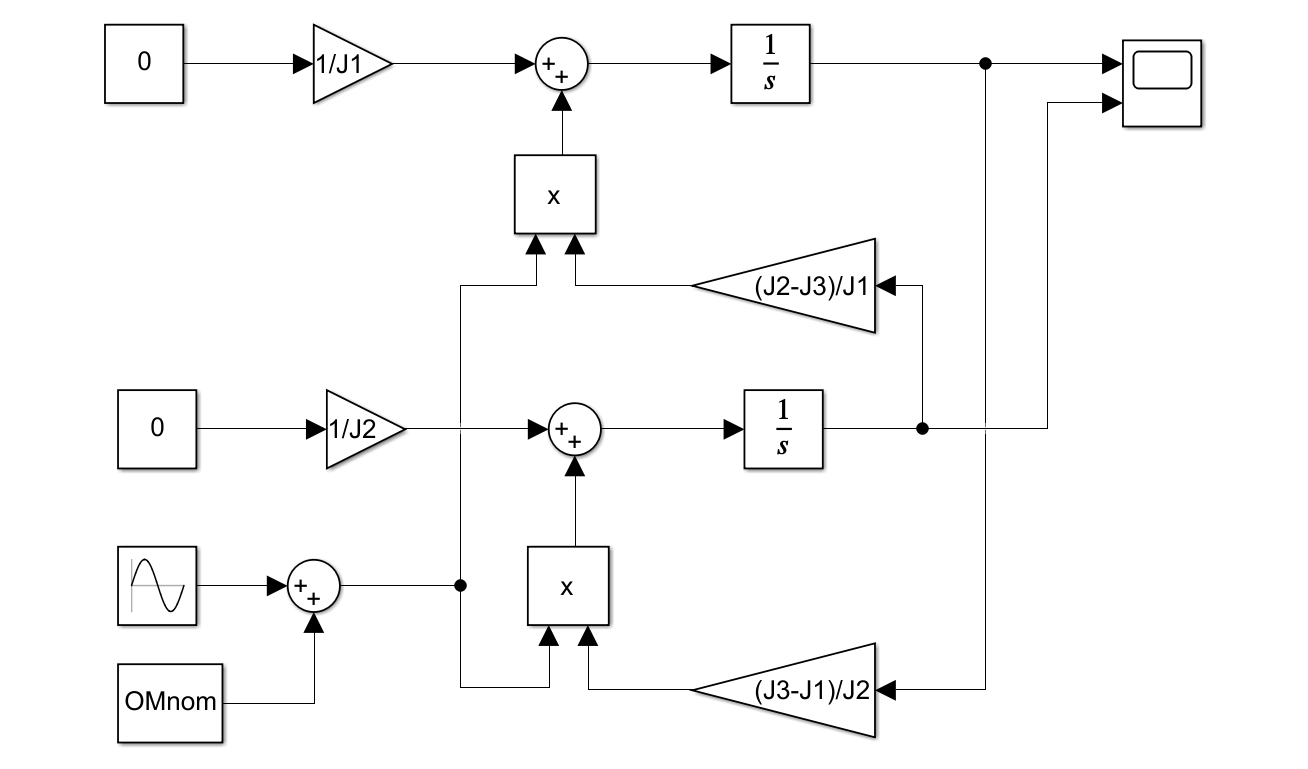 図3 SPIN0.slx
図3 SPIN0.slx
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad A= \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{U} \underbrace{ \left[\begin{array}{ccc} \sqrt{2} & 0 & 0 \\ 0 & 1 & 0 \end{array}\right] }_{\Sigma} \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ \frac{1}{\sqrt{2}} & 0 & -\frac{1}{\sqrt{2}} \\ \frac{1}{\sqrt{2}} & 0 & \frac{1}{\sqrt{2}} \end{array}\right]^T }_{V^T} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2af72a50a4707c3528e66ecddb5d79d3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ 0 & 2 \end{array}\right] }_{AA^T} \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{U} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{U} \underbrace{ \left[\begin{array}{cc} 2 & 0 \\ 0 & 1 \end{array}\right] }_{\Sigma_1^2} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6f51f7ede73c92e99db76c7c0af734a4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 1 \\ 0 & 1 & 1 \end{array}\right] }_{A^TA} \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ x & 0 & -y \\ y & 0 & x \end{array}\right] }_{V} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ x & 0 & -y \\ y & 0 & x \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{ccc} 2 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \end{array}\right] }_{{\rm diag}\{\Sigma_1^2,0\}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-80803b0ba51318c2e2c0a244cacf7e45_l3.png)
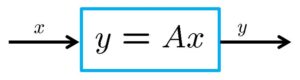
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} A= \underbrace{ \left[\begin{array}{cc} U_1 & U_2 \end{array}\right] }_{U(m\times m)} \underbrace{ \left[\begin{array}{cc} {\rm diag}\{\sigma_1,\cdots,\sigma_k\} & 0_{k\times (n-k)} \\ 0_{(m-k)\times k} & 0_{(m-k)\times (n-k)} \end{array}\right] }_{\Sigma= \left[\begin{array}{cc} \Sigma_1 & 0 \\ 0 & 0 \end{array}\right] \quad(\sigma_1\ge\cdots\ge\sigma_k) } \underbrace{ \left[\begin{array}{cc} V_1^T \\ V_2^T \end{array}\right] }_{V(n\times n)^T}\\ =U_1(m\times k)\Sigma_1(k\times k)V_1(n\times k)^T \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dc89eab35a6815c659415bf9a11570b9_l3.png)
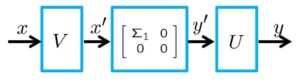
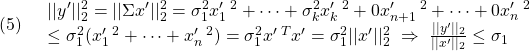
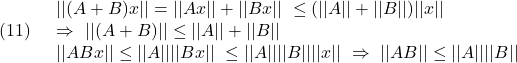
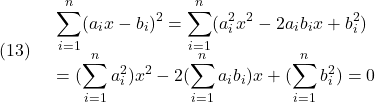
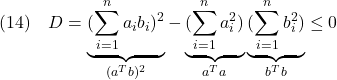
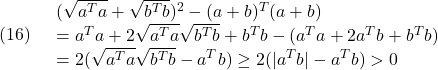
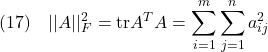
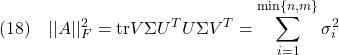
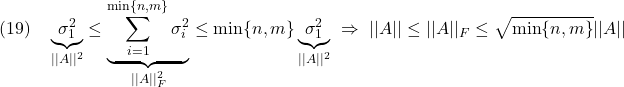
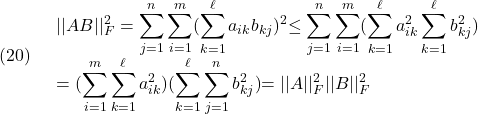
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \begin{array}{l} \underbrace{U\left[\begin{array}{cc} \Sigma_1 & 0_{n\times m-n} \end{array}\right] \left[\begin{array}{c} V_1^H\\ V_2^H \end{array}\right]}_{A}x =U\Sigma_1V_1^Hx=b\\ \Sigma_1={\rm diag}\{\sigma_1,\cdots,\sigma_n\} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2633ba4a0b1a6e8db6ae07669f36a2f2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} U_1 & U_2 \end{array}\right] \left[\begin{array}{cc} \Sigma_1 \\ 0_{n-m\times m} \end{array}\right]V^H}_{A}x =U_1\Sigma_1V^Hx=b\\ \Sigma_1={\rm diag}\{\sigma_1,\cdots,\sigma_m\} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-89dad140495fae168ea6b37fa797cbe0_l3.png)
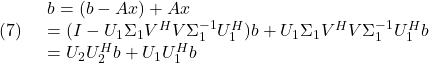
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array}\right]= \underbrace{\lambda_RI_2}_{X}+ \underbrace{\lambda_I \left[\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array}\right]}_{Y} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-90093f23486e9ebe543a4f748c41bfee_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{cc} \lambda & 1 \\ 0 & \lambda \end{array}\right]= \underbrace{\lambda I_2}_{X}+ \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right]}_{Y} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b6261249b8a119844a069dd65ff1df8e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{1^{\circ}\ \lambda(A)=\{\lambda_1,\lambda_2,\lambda_3\} \ \Rightarrow\ \Lambda_1=\left[\begin{array}{ccc} \lambda_1 & 0 & 0\\ 0 & \lambda_2 & 0\\ 0 & 0 & \lambda_3 \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3bd2b1a89b6bfe05ac946135ab4a5d46_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{2^{\circ}\ \lambda(A)=\{\lambda_R\pm j\lambda_I,\lambda\} \ \Rightarrow\ \Lambda_2=\left[\begin{array}{ccc} \lambda_R & \lambda_I & 0 \\ -\lambda_I & \lambda_R & 0 \\ 0 & 0 & \lambda \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8d85c1f19ccd0787c5b71e7d54877f24_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{3^{\circ}\ \lambda(A)=\{\lambda,\lambda,\lambda\} \ \Rightarrow\ \Lambda_3=\left[\begin{array}{ccc} \lambda & 1 & 0\\ 0 & \lambda & 1\\ 0 & 0 & \lambda \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a9eba9ac8ad743586bd7194d7fa3fa9d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{4^{\circ}\ \lambda(A)=\{\lambda,\lambda,\lambda'\} \ \Rightarrow\ \Lambda_4=\left[\begin{array}{ccc} \lambda & 1 & 0\\ 0 & \lambda & 0\\ 0 & 0 & \lambda' \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a07d669a93607f058df5310169859209_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{1^{\circ}\quad \exp(\Lambda_1 t)= \left[\begin{array}{ccc} e^{\lambda_1t} & 0 & 0\\ 0 & e^{\lambda_2 t} & 0\\ 0 & 0 & e^{\lambda_3 t} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a63717de8968d9c6311bc7099c27239e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{2^{\circ}\quad \exp(\Lambda_2 t)= \left[\begin{array}{ccc} e^{\lambda_R t}\cos(\lambda_It) & e^{\lambda_R t}\sin(\lambda_It) & 0\\ -e^{\lambda_R t}\sin(\lambda_It) & e^{\lambda_R t}\cos(\lambda_It) & 0\\ 0 & 0 & e^{\lambda t} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-13e0a88c983f834e8e6fbecebc725300_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{3^{\circ}\quad \exp(\Lambda_3 t)=e^{\lambda t} \left[\begin{array}{ccc} 1 & t & \frac{t^2}{2} \\ 0 & 1 & t \\ 0 & 0 & 1 \\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-017f57a48ebbb02c3f52a23e04f45293_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{4^{\circ}\quad \exp(\Lambda_4 t)= \left[\begin{array}{ccc} e^{\lambda t} & te^{\lambda t} & 0\\ 0 & e^{\lambda t} & 0\\ 0 & 0 & e^{\lambda t} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-657e4756bd61e0d0a2b833dfd26b89b3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{1^{\circ}\quad J(\lambda,m)= \left[\begin{array}{cccc} \lambda & 1 & & \\ & \lambda & \ddots & \\ & & \ddots & 1 \\ & & & \lambda \end{array}\right]\in{\bf R}^{m\times m} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-04756fbeb2c116fc5699aa675a993865_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{2^{\circ}\quad K(\lambda_{R},\lambda_{I},\ell)= \left[\begin{array}{c|c|cc|c} \begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array} & \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} & & \\ \hline & \begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array} & \ddots & & \\ \hline & & & & \\ \hline & & & \ddots & \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \\ \hline & & & & \begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array} \end{array}\right]\in{\bf R}^{2\ell\times 2\ell} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c2457aec06eab348db71633eafce1fb6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{1^{\circ}\quad \exp(J(\lambda,m)t)=e^{\lambda t} \left[\begin{array}{ccccc} 1 & t & \frac{t^2}{2} & \cdots & \frac{t^{m-1}}{(m-1)!} \\ & 1 & t & \ddots & \vdots \\ & & 1 & \ddots & \frac{t^2}{2} \\ & & & \ddots & t \\ & & & & 1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-214e860d644b198e7698b96f6af38b67_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ J(\lambda,m)= \underbrace{\lambda I_m}_{X}+ \underbrace{ \left[\begin{array}{cccc} 0 & 1 & & \\ & 0 & \ddots & \\ & & \ddots & 1 \\ & & & 0 \end{array}\right]}_{Y} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9840463b7dde1311b1a95f279ea67627_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ K(\lambda_{R},\lambda_{I},\ell)= \underbrace{\left[\begin{array}{cccc} \lambda_R & 1 & & \\ & \lambda_R & \ddots & \\ & & \ddots & 1 \\ & & & \lambda_R \end{array}\right] \otimes I_2 }_{X}+ \underbrace{I_\ell\otimes \lambda_I \left[\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array}\right] }_{Y} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c2321bffd746beb1183eafb2647ad175_l3.png)
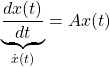
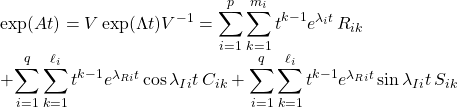
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{cc} v_{i1} \\ v_{i2} \end{array}\right] }_{v_i} = \lambda_i \underbrace{ \left[\begin{array}{cc} v_{i1} \\ v_{i2} \end{array}\right] }_{v_i}\quad(i=1,2)](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0831f4b46506687c014d958aea592423_l3.png)
![Rendered by QuickLaTeX.com \left\{\begin{array}{cc} Av_1=\lambda_1v_1\\ Av_2=\lambda_2v_2 \end{array}\right. \Leftrightarrow A \underbrace{ \left[\begin{array}{cc} v_1 & v_2 \end{array}\right] }_{V} = \underbrace{ \left[\begin{array}{cc} v_1 & v_2 \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda_1 & 0\\ 0 & \lambda_2 \end{array}\right] }_{\Lambda}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6d70b3d97f81ed2c410f999d9f9b0f72_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ J(\lambda,m)= \left[\begin{array}{cccc} \lambda & 1 & & \\ & \lambda & \ddots & \\ & & \ddots & 1 \\ & & & \lambda \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-10b37546f982ad32792ade27dcbb5bc5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ K(\lambda_{R},\lambda_{I},\ell)= \left[\begin{array}{c|c|cc|c} \begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array} & \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} & & \\ \hline & \begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array} & \ddots & & \\ \hline & & & & \\ \hline & & & \ddots & \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \\ \hline & & & & \begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6405a058d51a3c2f5859cfcee7d7fdcd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{1^{\circ}\ \lambda(A)=\{\lambda_1,\lambda_2,\lambda_3\} \ \Rightarrow\ \Lambda=\left[\begin{array}{ccc} \lambda_1 & 0 & 0\\ 0 & \lambda_2 & 0\\ 0 & 0 & \lambda_3 \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-84b04905b6ac45ff1964c63813a82081_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{2^{\circ}\ \lambda(A)=\{\lambda_R\pm j\lambda_I,\lambda\} \ \Rightarrow\ \Lambda=\left[\begin{array}{ccc} \lambda_R & \lambda_I & 0 \\ -\lambda_I & \lambda_R & 0 \\ 0 & 0 & \lambda \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a8c54381683d100c98707a0956c94b04_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{3^{\circ}\ \lambda(A)=\{\lambda,\lambda,\lambda\} \ \Rightarrow\ \Lambda=\left[\begin{array}{ccc} \lambda & 1 & 0\\ 0 & \lambda & 1\\ 0 & 0 & \lambda \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-76e61732a9aaced850d3e6e0c9170aec_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{4^{\circ}\ \lambda(A)=\{\lambda,\lambda,\lambda'\} \ \Rightarrow\ \Lambda=\left[\begin{array}{ccc} \lambda & 1 & 0\\ 0 & \lambda & 0\\ 0 & 0 & \lambda' \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2a9b6d31f9cc1646e9fdd22b4ac56857_l3.png)
![Rendered by QuickLaTeX.com \underbrace{ \left[\begin{array}{cc} x_1\\ x_2 \end{array}\right] }_{x} \in{\rm\bf R}^2](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0fa82c1b4a8af7e3e26bf1f403b9c7db_l3.png)
](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-97304e22caaf0ac973a4c28144ad12f3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{{\rm rank}\left[\begin{array}{ccc} a_{11} & a_{12} \\ a_{21} & a_{22} \\ a_{31} & a_{32} \end{array}\right] ={\rm rank}\left[\begin{array}{ccc} \left[\begin{array}{ccc} a_{11} \\ a_{21} \\ a_{31} \end{array}\right] \left[\begin{array}{ccc} a_{12} \\ a_{22} \\ a_{32} \end{array}\right] \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0c416f3c23e28236351848860ebc9c23_l3.png)
![Rendered by QuickLaTeX.com \Leftrightarrow \underbrace{ \left[\begin{array}{cc} a_{11} & a_{12} \\ a_{21} & a_{22} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{cc} x_1 \\ x_2 \end{array}\right] }_{x} = \underbrace{ \left[\begin{array}{cc} b_1 \\ b_2 \end{array}\right] }_{b}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1e69aad8154a0c48cc53582eb79dd64e_l3.png)