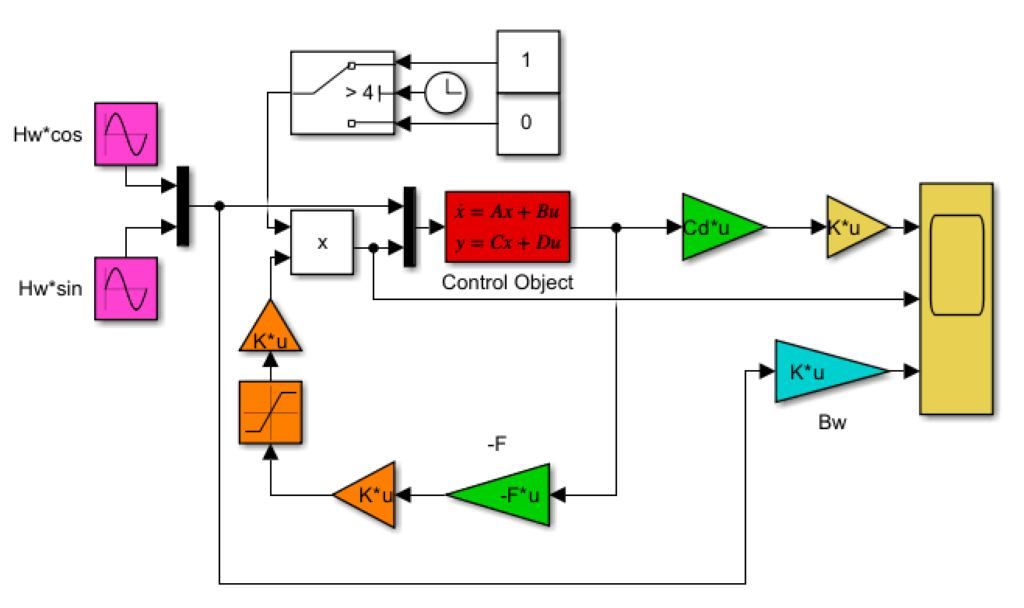
●制御対象(赤)
\left\{\begin{array}{l}
\dot{\vec x}=A(T_w){\vec x}+B(T_w)\vec{u}+B_w(T_w,\beta){\vec w},\ {\vec x}(0)={\vec x}_0\\
{\vec y}_M=C_M{\vec x}\\
y=\underbrace{C_SC_M}_{C}{\vec x}
\end{array}\right.
●外乱信号(赤紫)
{\vec w}=\left[\begin{array}{l}
H_w\sin\frac{2\pi}{T_w} t \\
H_w\cos\frac{2\pi}{T_w} t
\end{array}\right]
ここで、![]() とする。
とする。
●安定化制御則(緑)
\vec{u}=-F(T_w)\vec{x}
●推力配分(橙)
![]() は制御目的を達成するための望ましい
は制御目的を達成するための望ましい![]() であるが、これは4つのスラスタに次式で配分する。
であるが、これは4つのスラスタに次式で配分する。
\underbrace{\left[\begin{array}{c}F_1\\F_2\\F_3\\F_4\end{array}\right]}_{\vec F}=
\underbrace{\frac{1}{4}\left[\begin{array}{rrr} 1 & 1 & -1 \\ 1 & 1 & 1 \\ 1 & -1 & 1\\1 & -1 & -1 \end{array}\right]}_{G^\dag}
\underbrace{\left[\begin{array}{c}F_z\\F_\phi\\F_\theta\end{array}\right]}_{\vec\tau}
●推力制限(橙)
その際、次の制約が課される。
F_{min}\le F_k\le F_{max}\quad(k=1,2,3,4)
上のシミュレータは、この制約を考慮したものとなっている。
ここでは、F_{max}=2.5[kgf]、F_{min}=-2.5[kgf]を用いる(要チェック)。
●留意点
制約を受けた推力は次式で駆動力に変換されるが、推力制限がある場合は設計した駆動力が働かないので注意が必要である。
\underbrace{\left[\begin{array}{c}F_z\\F_\phi\\F_\theta\end{array}\right]}_{\vec\tau}=
\underbrace{\left[\begin{array}{rrrr} 1 & 1 & 1 & 1\\ 1 & 1 & -1 & -1\\ -1 & 1 & 1 & -1 \end{array}\right]}_{G}
\underbrace{\left[\begin{array}{c}F_1\\F_2\\F_3\\F_4\end{array}\right]}_{\vec F}
このとき、次の16ケースについて、上のシミュレータを用いてシミュレーションを行なう。ただし、短周期は![]() 、長周期は
、長周期は![]() とする。
とする。
| モデル/制御 | 横波短周期 | 横波長周期 | 斜波短周期 | 斜波長周期 |
|---|---|---|---|---|
| 2次系/LQ | Case 1.1 | Case 1.2 | Case 1.3 | Case 1.4 |
| 4次系/LQ | Case 1.5 | Case 1.6 | Case 1.7 | Case 1.8 |
| 6次系/LQ | Case 1.9 | Case 1.10 | Case 1.11 | Case 1.12 |
| 6次系/H∞ | Case 1.13 | Case 1.14 | Case 1.15 | Case 1.16 |
|
|
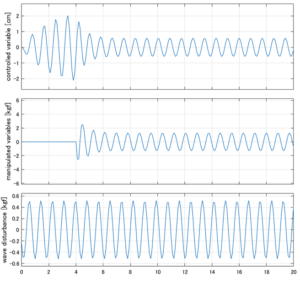
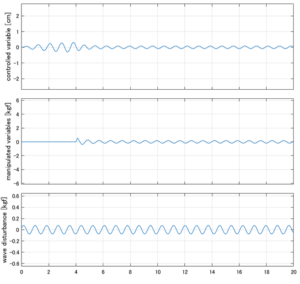
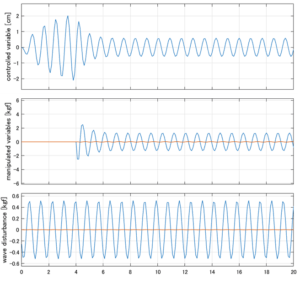
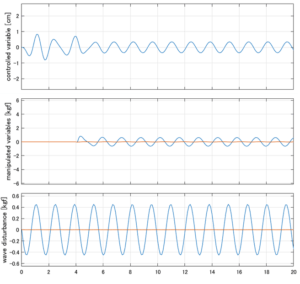
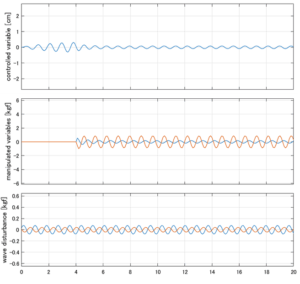
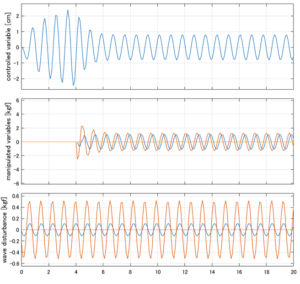
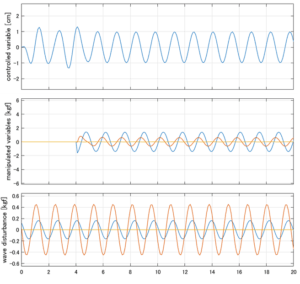
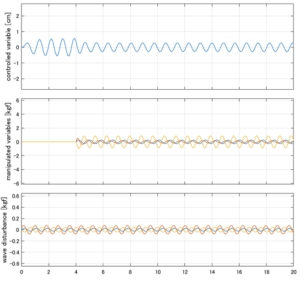
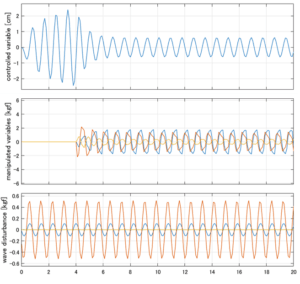
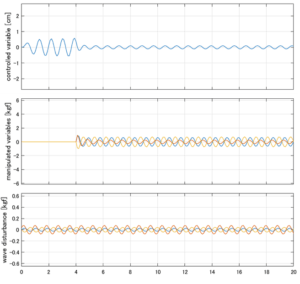
以下に、各ケースについてLQ制御系/H∞制御系の応答とゲイン線図を示す。前者の上段は制御点の応答[cm]、中段は操作入力[kgf]、下段は波浪外力[kgf]を示している。4秒までは制御なしで、4秒以降が制御ありの応答。制御点は横波・斜波とも右舷船首S1を取っている(横波の場合、右舷制御点の区別はない)。
2次モデルに対するLQ制御
2次モデルの状態変数はロールとその微分。ここではロールに浮体の半幅長さを掛けた制御点の縦変位の低減を図っている。
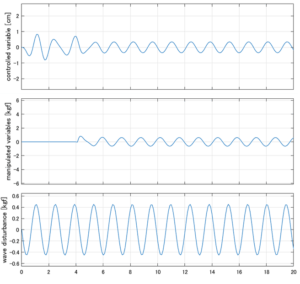
Case 1.1(横波、短周期規則波) Case 1.2(横波、長周期規則波)
Case 1.1コメント
●応答図上段:横波を受けて4秒までは制御点の縦変位は2cm程度まで大きく出る。4秒になると制御が始まり、1/10の0.2㎝程度まで低減される。
●応答図下段:浮体が受ける波浪外力を表している。計算式は
![]() を用いている。4秒までは5つの山がありますが、これを受けて制御点にも5つの山があることに注意。そして、4秒付近で、波浪外力は次の山に向かって負から正の方向に働いている。
を用いている。4秒までは5つの山がありますが、これを受けて制御点にも5つの山があることに注意。そして、4秒付近で、波浪外力は次の山に向かって負から正の方向に働いている。
●応答図中段:この外力を打ち消すように、4秒から制御動作が始まる。
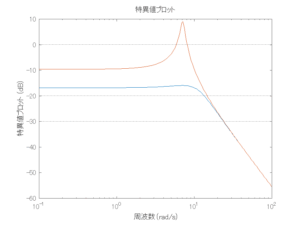
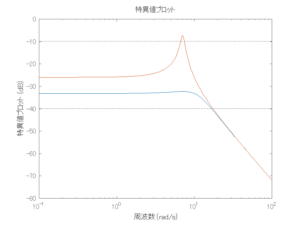
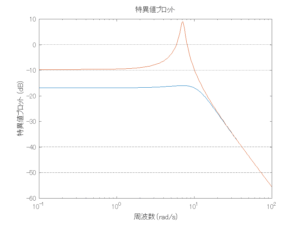
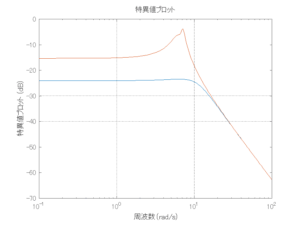
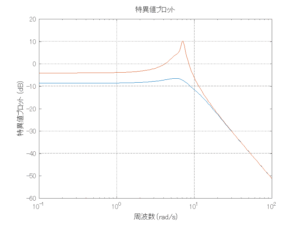
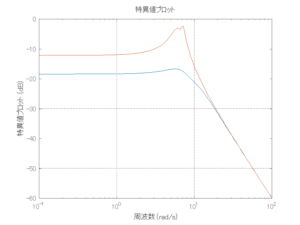
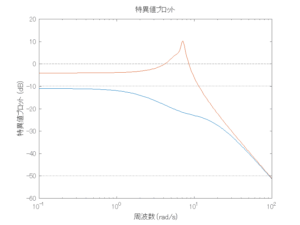
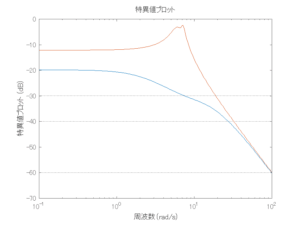
●波浪外力から制御点までのゲイン線図を、制御前の開ループ系(橙)と制御前の閉ループ系(青)について示している。波周期に対応する角周波数は![]() [rad/sec]です。閉ループ系のゲイン線図から、開ループ系のピークが抑制されていることが分かる。-20dBは1/10を意味する。
[rad/sec]です。閉ループ系のゲイン線図から、開ループ系のピークが抑制されていることが分かる。-20dBは1/10を意味する。
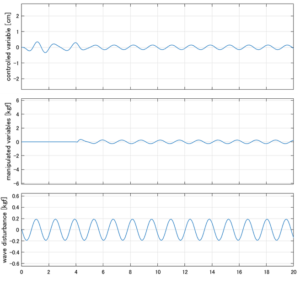
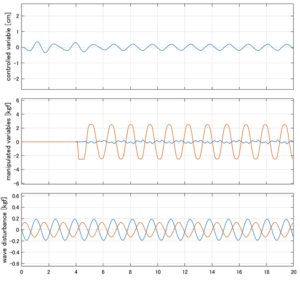
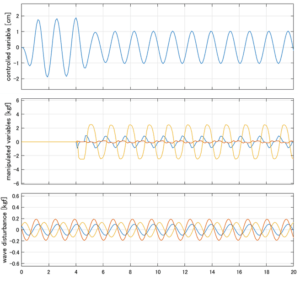
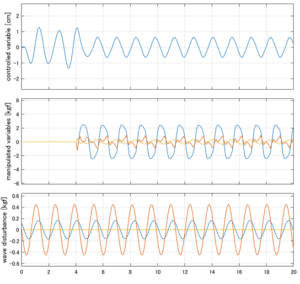
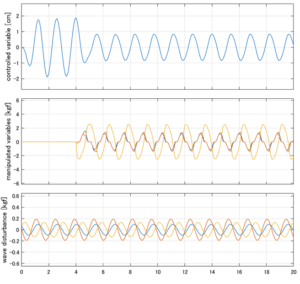
Case 1.2コメント
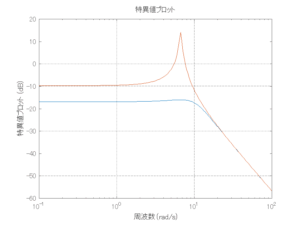
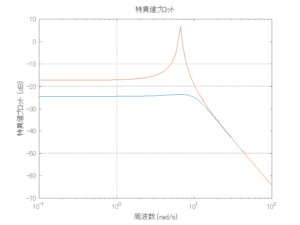
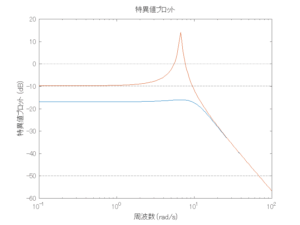
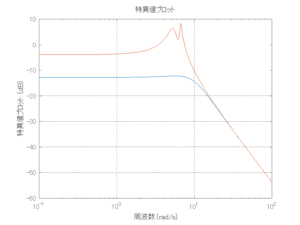
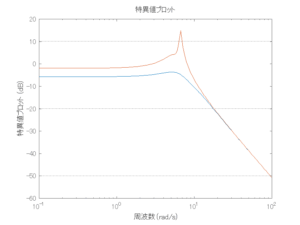
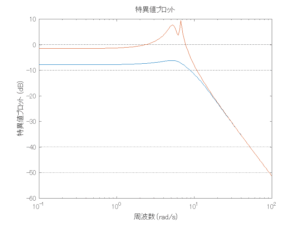
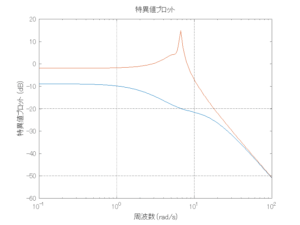
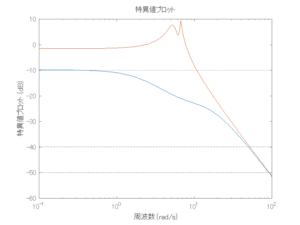
●波周期に対応する角周波数は![]() [rad/sec]。閉ループ系のゲイン線図から、開ループ系のピークが抑制されていることが分かる。
[rad/sec]。閉ループ系のゲイン線図から、開ループ系のピークが抑制されていることが分かる。
Case 1.3(斜波、短周期規則波) Case 1.4(斜波、長周期規則波)
Case 1.3コメント
●斜波のときは必ずピッチが生じるが、ここではロールだけに注目している。浮体が受ける波浪外力はCase1.1に比べて小さくなっている。
Case 1.4コメント
●斜波のときは必ずピッチが生じるが、ここではロールだけに注目している。浮体が受ける波浪外力はCase1.2に比べて小さくなっている。
4次モデルに対するLQ制御
4次モデルの状態変数はロールとピッチ、およびそれらの微分。ここではロールとピッチから計算される制御点の縦変位(ヒーブは入らないことに注意)の低減を図っている。
Case 1.5(横波、短周期規則波) Case 1.6(横波、長周期規則波)
Case 1.5コメント
●横波の場合はピッチは誘起されないので、Case1.1と同じになる。
●応答図中段:ピッチが誘起されないので、ピッチ駆動力(橙)は零。
Case 1.6コメント
●横波の場合はピッチは誘起されないので、Case1.2と同じになる。
●応答図中段:ピッチが誘起されないので、ピッチ駆動力(橙)は零。
Case 1.7(斜波、短周期規則波) Case 1.8(斜波、長周期規則波)
Case 1.7コメント
●応答図下段:ピッチ運動を誘起する波浪外力(橙)が生じている。計算式は ![]() を用いています。
を用いています。
●応答図中段:ピッチ運動を抑制するピッチ駆動力(橙)が生じている。
Case 1.8コメント
●長周期斜波の場合の波浪外力は、短周期の場合に比べて、大き目に出る模様。
6次モデルに対するLQ制御
6次モデルの状態変数はヒーブとロール、ピッチ、およびそれらの微分。ここではヒーブとロール、ピッチから計算される制御点の縦変位(ヒーブが加わことに注意)の低減を図っている。
Case 1.9(横波、短周期規則波) Case 1.10(横波、長周期規則波)
Case 1.9コメント
●横波の場合はピッチは誘起されないが、ヒーブが現れる。Case1.5との違いは、それに起因すると考えられる。
●応答図中段:青、赤、橙の順にヒーブ、ロール、ピッチに働く駆動力を表している。
●応答図下段:青、赤、橙の順にヒーブ、ロール、ピッチに働く波浪外力を表している。計算式は、それぞれ次を用いる。
![]()
![]()
![]()
Case 1.10コメント
●横波の場合はピッチは誘起されないが、ヒーブが現れます。Case1.6との違いは、それに起因すると考えられる。
Case 1.11(斜波、短周期規則波) Case 1.12(斜波、長周期規則波)
Case 1.11コメント
●斜波の場合はピッチが誘起され、ヒーブが現れる。Case1.7との違いは、それに起因すると考えらる。
Case 1.12コメント
●斜波の場合はピッチが誘起され、ヒーブが現れる。Case1.8との違いは、それに起因すると考えらる。
6次モデルに対するH∞制御
波浪外力から制御点までのゲイン線図は、LQ制御と比べて、波周期に対応する角周波数でより低減されていて、制御点縦変位の抑制も効いています。
Case 1.13(横波、短周期規則波) Case 1.14(横波、長周期規則波)
Case 1.13コメント
Case 1.14コメント
Case 1.15(斜波、短周期規則波) Case 1.16(斜波、長周期規則波)
Case 1.15コメント
Case 1.16コメント

![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \underbrace{ \left[\begin{array}{l} \dot{z}_1\\ \dot{z}_2 \end{array}\right]}_{\dot z}=- \underbrace{ \left[\begin{array}{cc} k_1 & 0\\ 0 & k_2 \end{array}\right]}_{K} \underbrace{ \left[\begin{array}{l} z_1\\ z_2 \end{array}\right]}_{z}+ \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -1 & 0 \end{array}\right]}_{S} \underbrace{ \left[\begin{array}{l} z_1\\ z_2 \end{array}\right]}_{z} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5ba0b9891c7ccb17dde0e6f7efa61211_l3.png)

![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} 1 & 0\\ 0 & m \end{array}\right]}_{M} \underbrace{ \left[\begin{array}{l} \dot{z}_1\\ \dot{z}_2 \end{array}\right]}_{\dot z}=- \underbrace{ \left[\begin{array}{cc} k_1+n_1(z_1) & 0\\ 0 & k_2+n_2(z_2) \end{array}\right]}_{K} \underbrace{ \left[\begin{array}{l} z_1\\ z_2 \end{array}\right]}_{z}\\ + \underbrace{ \left[\begin{array}{cc} 0 & 1\\ -1 & 0 \end{array}\right]}_{S} \underbrace{ \left[\begin{array}{l} z_1\\ z_2 \end{array}\right]}_{z} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7e30d4583990442c75248537bb56d2b1_l3.png)
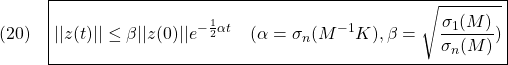

![Rendered by QuickLaTeX.com \displaystyle{(21)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & m \end{array}\right]}_{M} \underbrace{ \left[\begin{array}{l} \dot{z}_1\\ \dot{z}_2\\ \dot{z}_3 \end{array}\right]}_{\dot z}=- \underbrace{ \left[\begin{array}{ccc} k_1 & 0 & 0\\ 0 & k_2 & 0\\ 0 & 0 & d(v)+k_3 \end{array}\right]}_{K} \underbrace{ \left[\begin{array}{l} z_1\\ z_2\\ z_3 \end{array}\right]}_{z}\\+ \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0\\ -1 & 0 & 1\\ 0 & -1 & 0 \end{array}\right]}_{S} \underbrace{ \left[\begin{array}{l} z_1\\ z_2\\ z_3 \end{array}\right]}_{z} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e4c27a02e87a8a58ef7fe31f40061a45_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \underbrace{ \left[\begin{array}{cc} 1 & 0\\ 0 & m \end{array}\right]}_{M} \underbrace{ \left[\begin{array}{l} \dot{z}_1\\ \dot{z}_2 \end{array}\right]}_{\dot z}=- \underbrace{ \left[\begin{array}{cc} k_1 & 1\\ -1 & -k_2-d(v) \end{array}\right]}_{A} \underbrace{ \left[\begin{array}{l} z_1\\ z_2 \end{array}\right]}_{z}+ \underbrace{ \left[\begin{array}{c} 0 \\ -1 \end{array}\right]}_{b} (\hat{w}-w) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-da7a835f971ce5dac2d1a21c12164a35_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \dot{\hat{w}}=-p \underbrace{ \left[\begin{array}{cc} 0 & -1 \end{array}\right]}_{b^T} \underbrace{ \left[\begin{array}{l} z_1\\ z_2 \end{array}\right]}_{z} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c15da6d97348e4f96dbe7ef9aee6bada_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \frac{d}{dt} \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0\\ a_{63} & a_{66} & b_{62}\\ 0 & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} 0 \\ 0 \\ \Omega_e \end{array}\right] }_{B} u_e(t)\\ +\underbrace{ \left[\begin{array}{cccc} 0 & 0 & 0 & 0 \\ a_{62} & a_{64} & a_{65} & b_{61}\\ 0 & 0 & 0 & 0 \end{array}\right] \left[\begin{array}{c} z(t)-z^*\\ \dot{x}(t)-V^*\\ \dot{z}(t)\\ T(t)-T^* \end{array}\right] }_{w(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-44d46ce48189bf941958132e5f951657_l3.png)
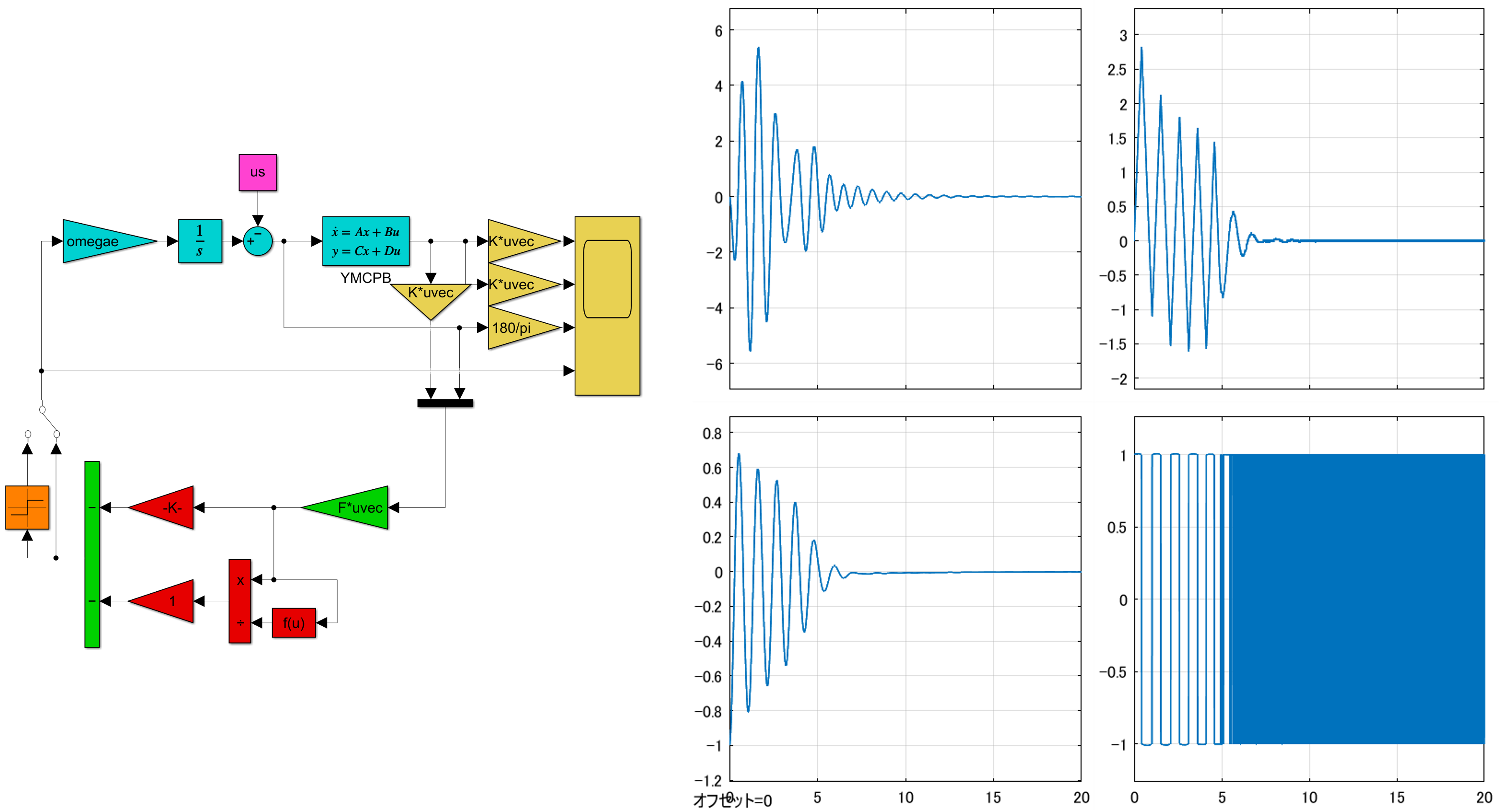
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t)\\ (x_1(t)=x(t)-x_\infty, x_2(t)=u(t)-u_\infty) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-287cdcd8e65d74ee36ec3b14429778da_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b29dc4a454912e8d6acde0686487f72b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1d43b39400a0f9614aa7f3662f3f8fc4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{x}'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right] }_{T_sA_{E3}T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ S_2 \end{array}\right] }_{T_sB_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ad4d0f30544fe9138bf4a06f0bbc0d3c_l3.png)
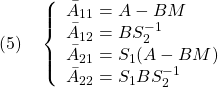
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad {\dot u}_\ell(t)=-\underbrace{(SB_{E3})^{-1}(SA_{E3}-\Phi S)}_{K_{E3}=\left[\begin{array}{cc} K_1 & K_2 \end{array}\right]}}x_{E3}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aa75a3fae556ffb1e063a6c3165e9f14_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad {\dot u}_\ell(t)=- \boxed{\underbrace{ (SB_{E3})^{-1}(SA_{E3}-\Phi S)S_E^{-1} }_{\left[\begin{array}{cc} F & F_I \end{array}\right]}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-17dcffd80184d45c409aa1d4e2fd454e_l3.png)
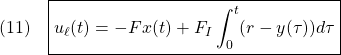
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad {\dot u}_n(t) =-(SB_{E3})^{-1}\rho\, {\rm sgn}( \boxed{\underbrace{ P_2SS_E^{-1} }_{\left[\begin{array}{cc} G & G_I \end{array}\right]}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)}) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-863369c4b058cffb357ac9501fed0507_l3.png)
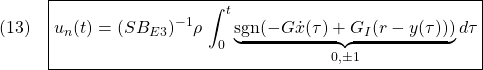
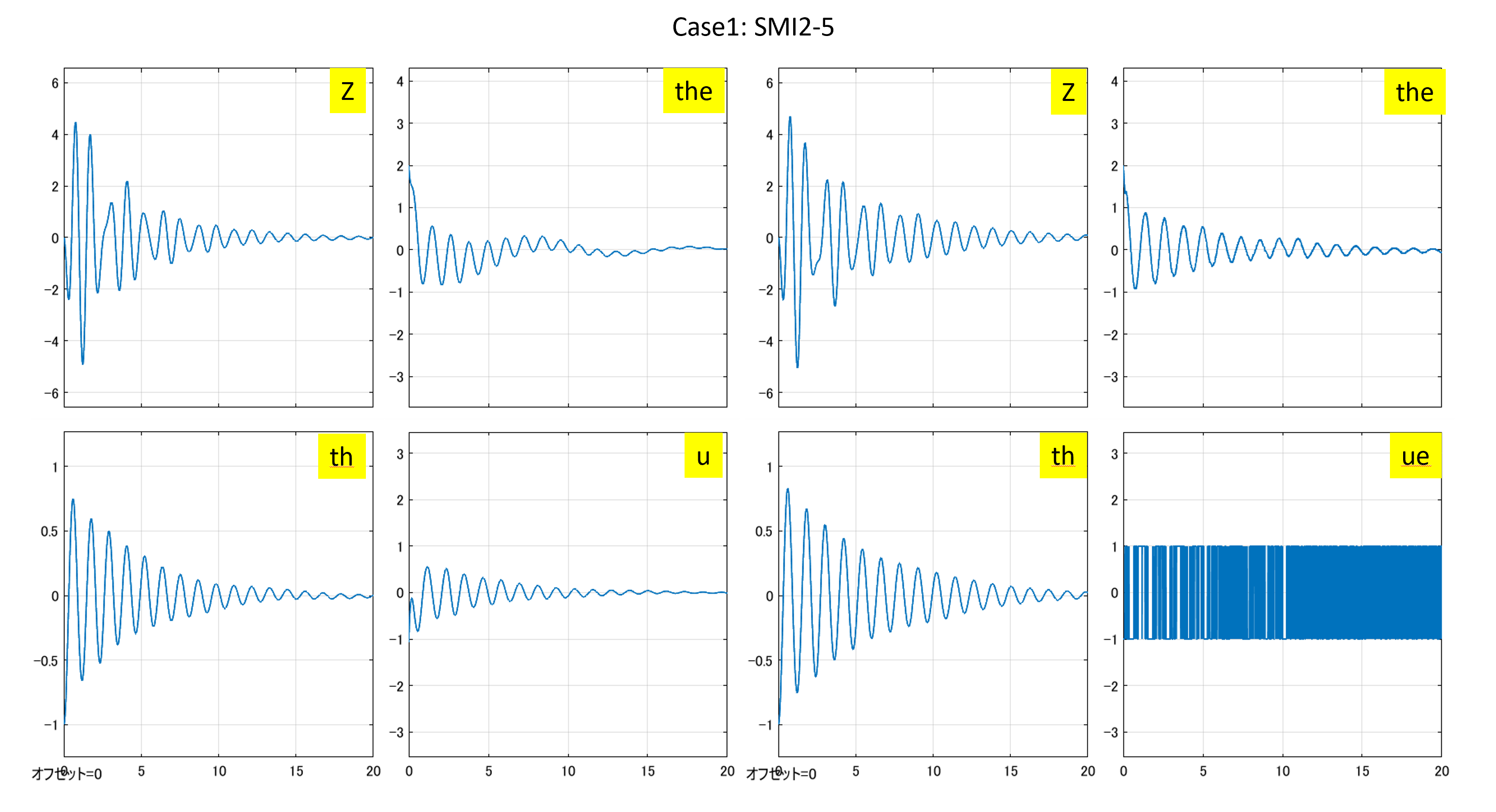
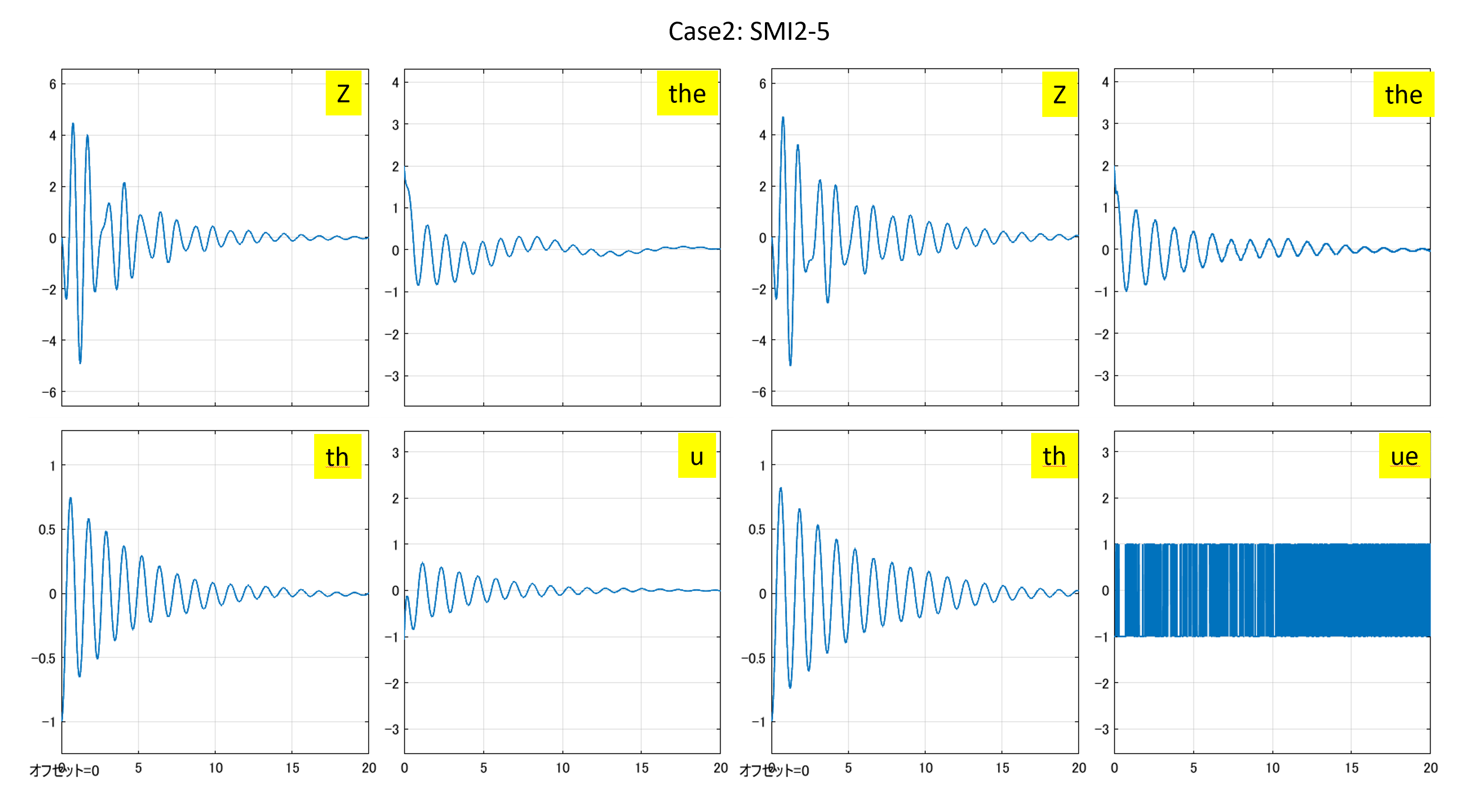
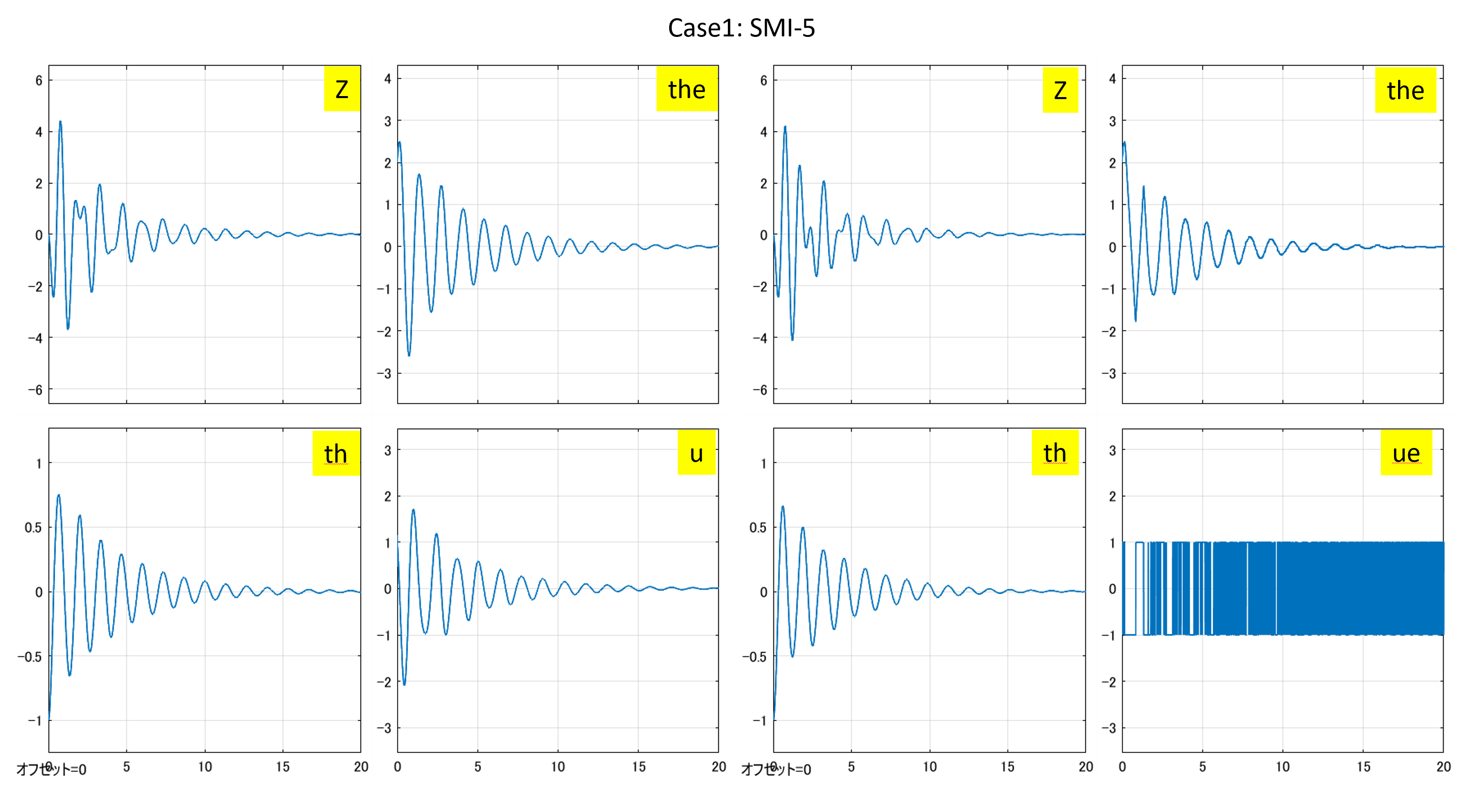
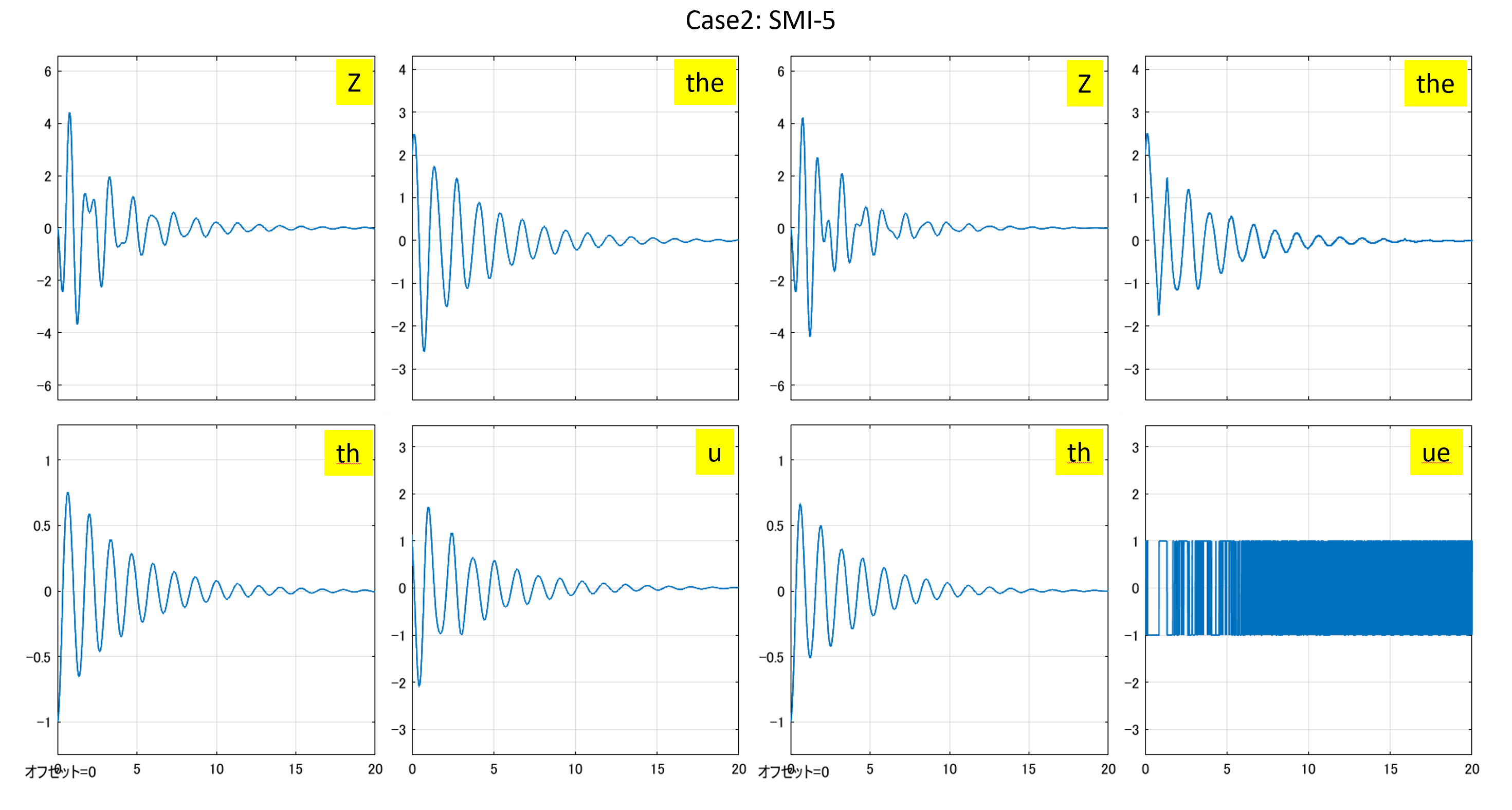
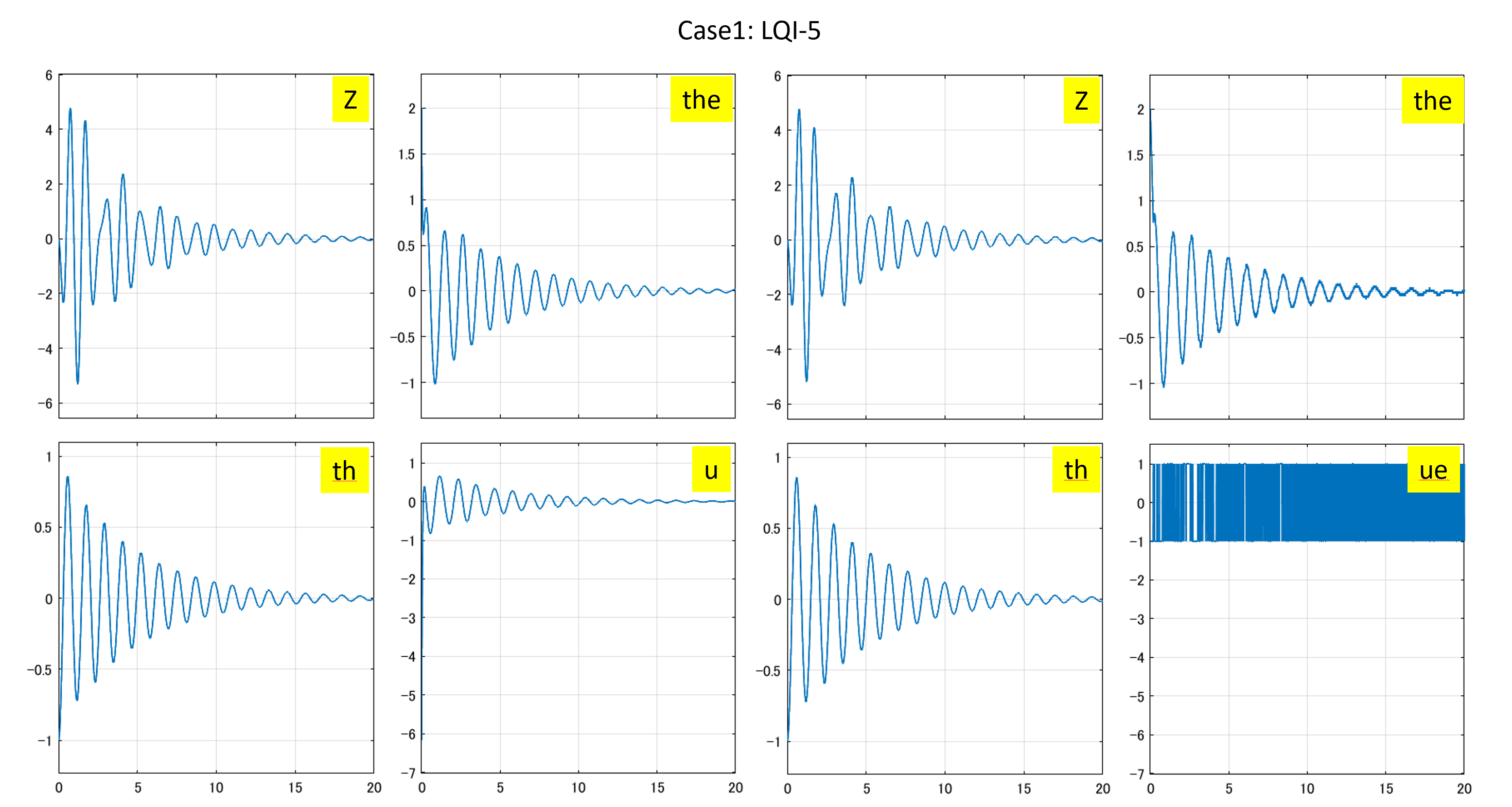
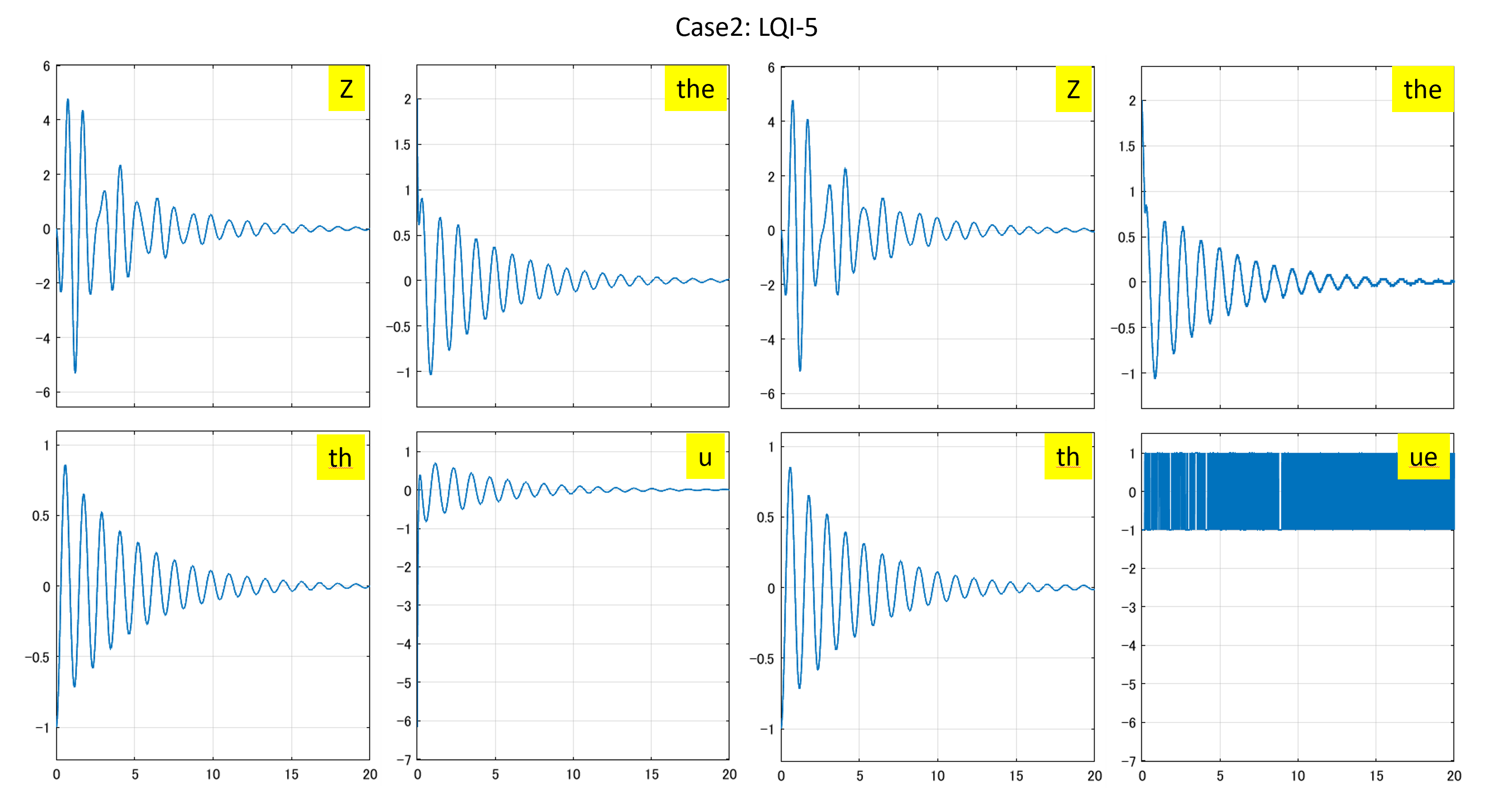
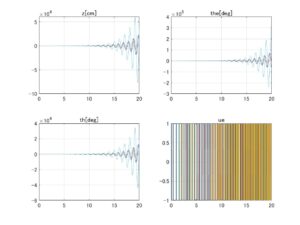 ⇒Case2:いくつかの動作点で不安定
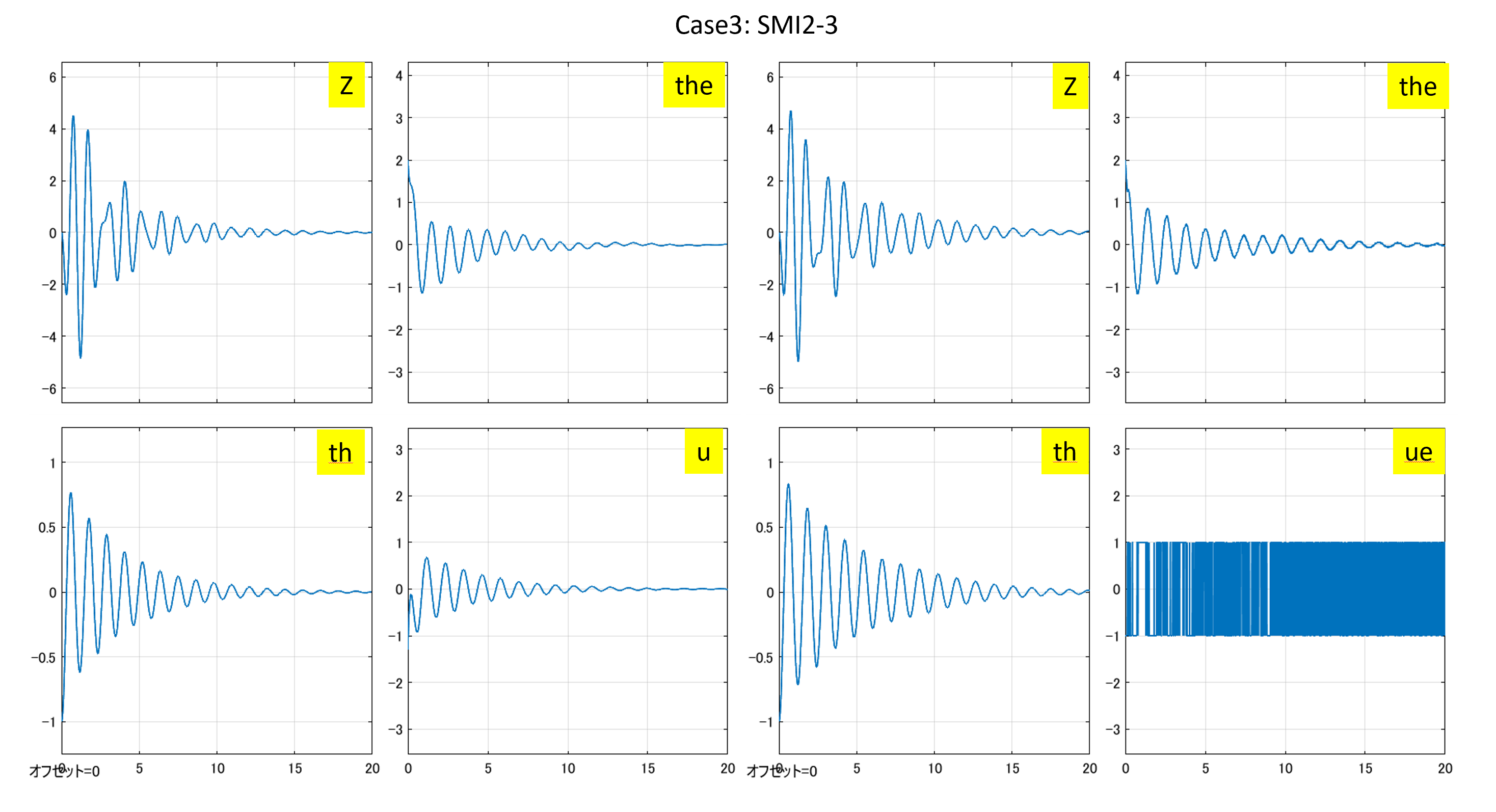
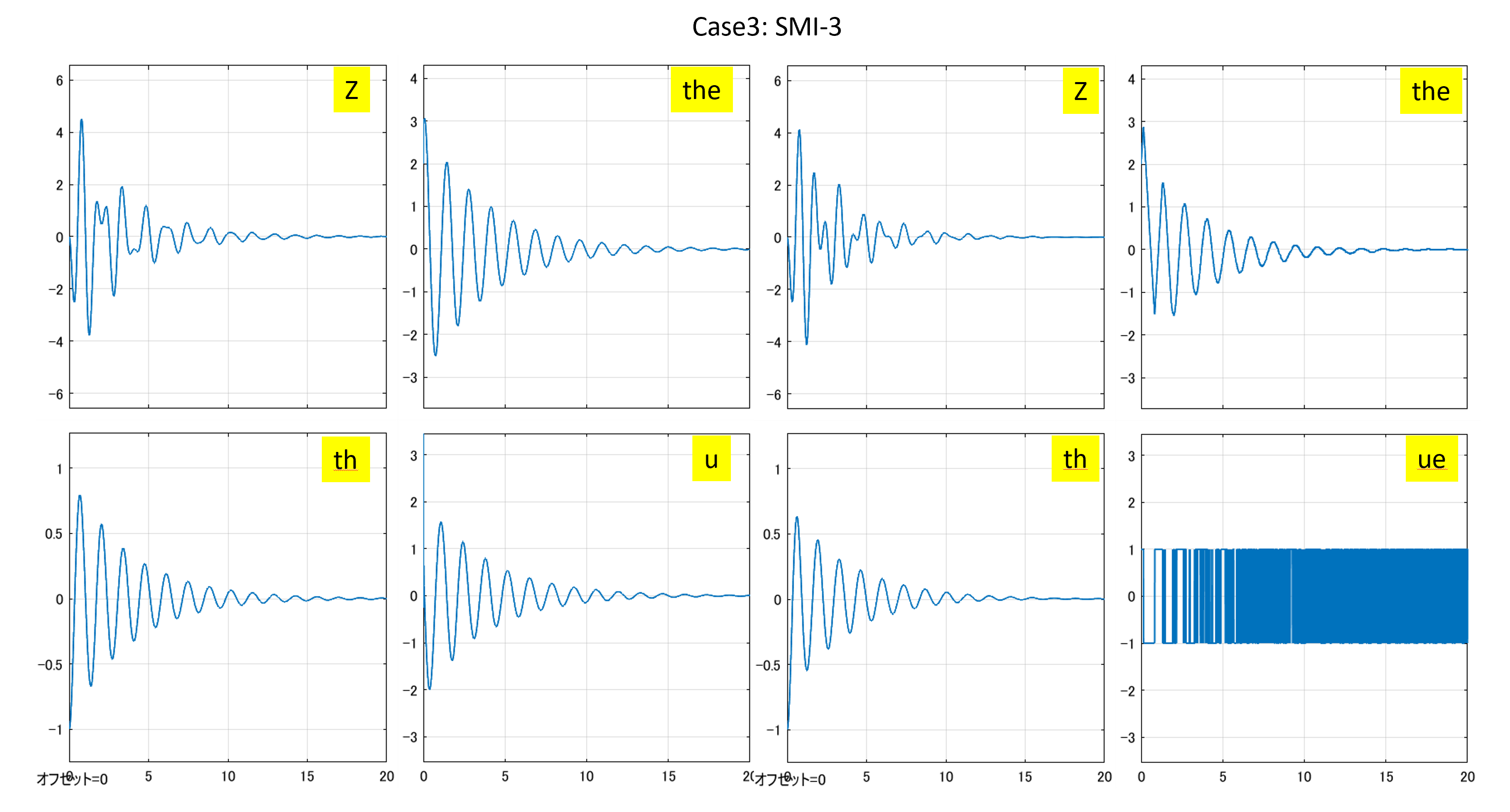
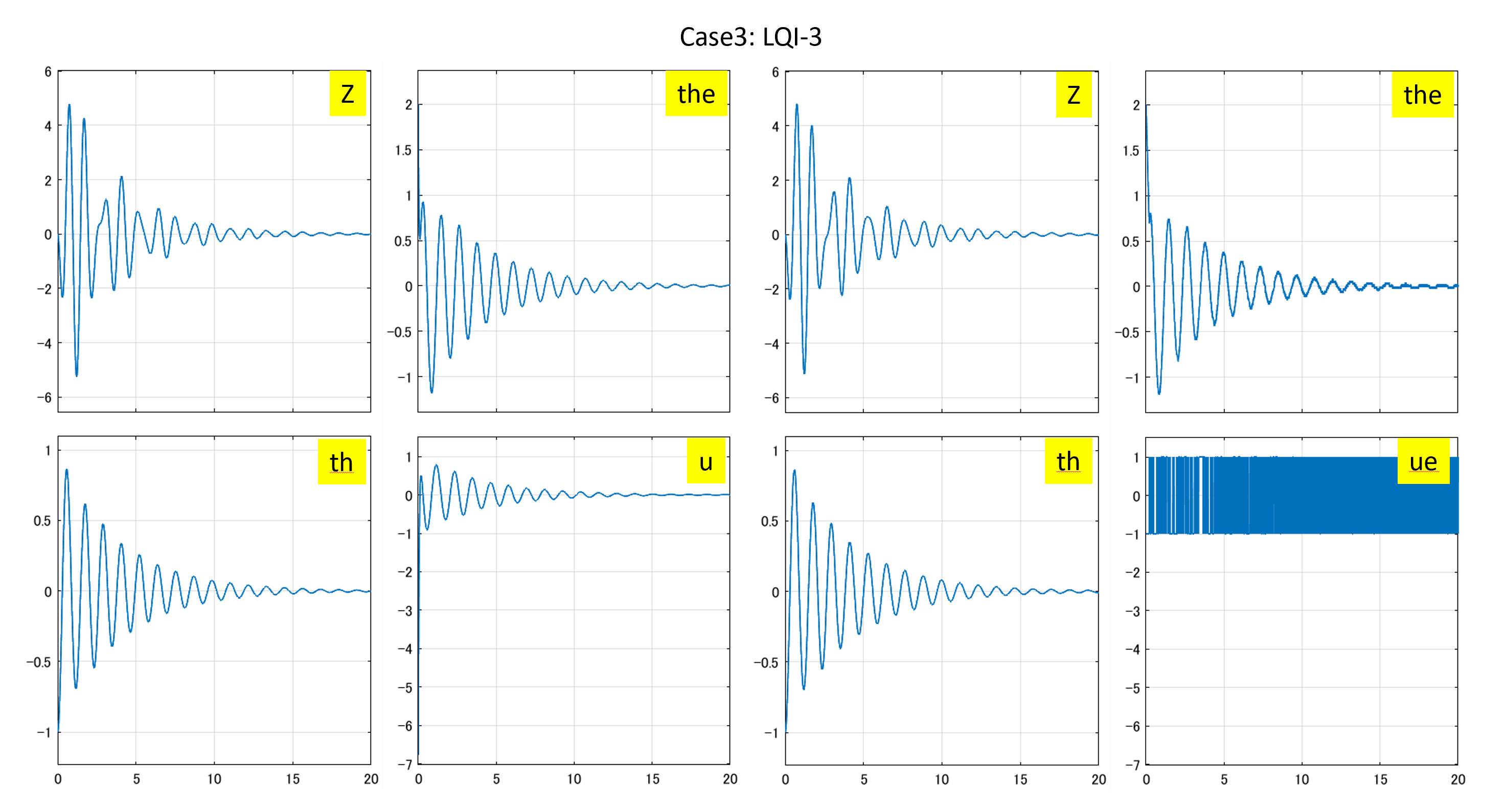
⇒Case2:いくつかの動作点で不安定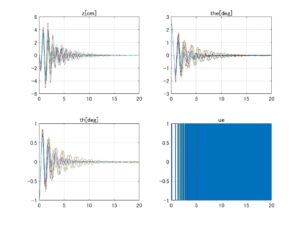 ⇒Case3:すべて安定
⇒Case3:すべて安定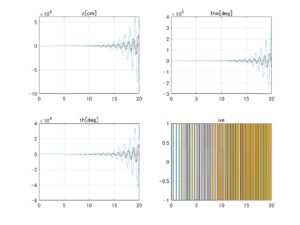 ⇒Case2:いくつかの動作点で不安定
⇒Case2:いくつかの動作点で不安定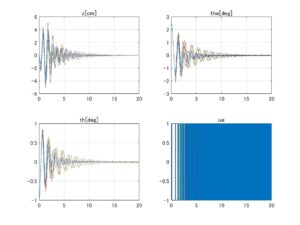 ⇒Case3:すべて安定
⇒Case3:すべて安定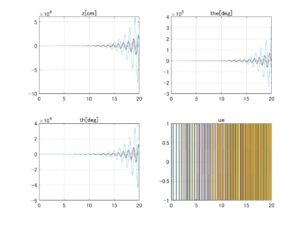 ⇒Case2:いくつかの動作点で不安定
⇒Case2:いくつかの動作点で不安定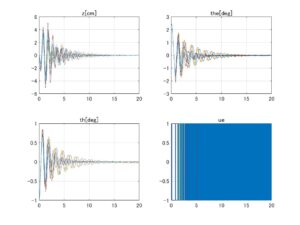 ⇒Case3:すべて安定
⇒Case3:すべて安定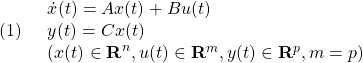
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \left[\begin{array}{c} \dot x_r(t)\\ \dot x(t) \end{array}\right] = \left[\begin{array}{c|cc} 0 & -C_1 & -C_2\\\hline 0 & A_{11} & A_{12} \\ 0 & A_{21} & A_{22} \end{array}\right] \left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right] + \left[\begin{array}{c} 0\\\hline 0\\ B_2 \end{array}\right] u(t) + \left[\begin{array}{c} I_m \\\hline 0 \\ 0 \end{array}\right] r(t)\\ (x_r(t)\in{\rm\bf R}^m, x(t)\in{\rm\bf R}^n) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1ab4b378422eddd1bff475a2408082e2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5a)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc|c} 0 & -C_1 & -C_2\\ 0 & A_{11} & A_{12} \\\hline 0 & A_{21} & A_{22} \end{array}\right] }_{A_E} \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0\\ 0\\\hline B_2 \end{array}\right] }_{B_E} u(t) + \left[\begin{array}{c} I_m \\ 0 \\\hline 0 \end{array}\right] r(t)\\ (x_1(t)\in{\rm\bf R}^n, x_2(t)\in{\rm\bf R}^m) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-374491b693fbc08a0a4648abd3e610d2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] %}_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I_m \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] %}_{x(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-01bb686061b94fbab2a0ff90e7d23f64_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} I_n & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right]\\ \Leftrightarrow \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} I_n & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-19e5643bcb296d8a517aba35bc4fe14e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8a)\quad \begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] %}_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right] }_{T_sA_ET_s^{-1}} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] %}_{x'(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ S_2B_2 \end{array}\right] }_{T_sB_E} u(t)\\ + \left[\begin{array}{cc} B_r \\ S_1B_r \end{array}\right] r(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a23595fe93cd3fb99284c6e90f61bcf1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8b)\quad \left\{\begin{array}{l} \bar{A}_{11}= \left[\begin{array}{cc} 0 & -C_1 \\ 0 & A_{11} \end{array}\right] -\left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right]M\\ \bar{A}_{12}= \left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right]S_2^{-1}\\ \bar{A}_{21}=S_2(M\bar{A}_{11} + \left[\begin{array}{cc} 0 & A_{21} \end{array}\right] -A_{22}M)\\ \bar{A}_{22}=S_2(M \left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right] +A_{22})S_2^{-1}\\ B_r=\left[\begin{array}{cc} I_m \\ 0 \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-24d62178408415d07b9cef2c8d0cfab3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad { \boxed{\begin{array}{l} u(t)=u_\ell(t)+u_n(t)\\ u_\ell(t)=-\underbrace{(SB_E)^{-1}(SA_E-\Phi S)}_{L=L_{eq}+L_\Phi}\left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right]\\ -\underbrace{(SB_E)^{-1}(\Phi S_r+S_1B_r)}_{L_r} r(t) +\underbrace{(SB_E)^{-1}S_r}_{L_{\dot r}} \dot{r}(t)\\ u_n(t)=-\underbrace{(SB_E)^{-1}\rho(t,x)}_{L_n}\frac{P_2(s(t)-S_rr(t))}{||P_2(s(t)-S_rr(t))||} \end{array}}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c4cbe9f1729638135b91b41ee797a570_l3.png)
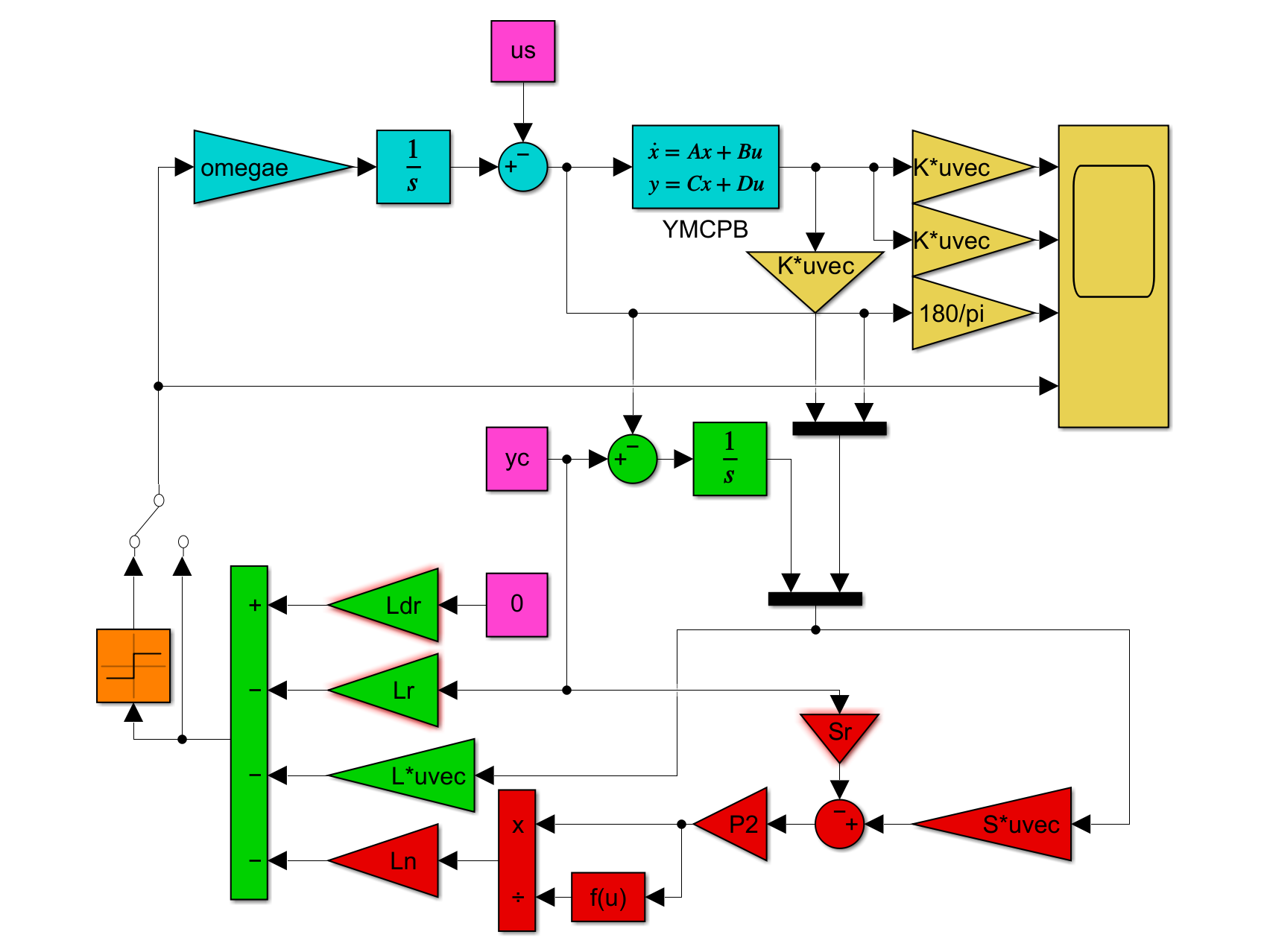
 ⇒Case2:いくつかの動作点で不安定
⇒Case2:いくつかの動作点で不安定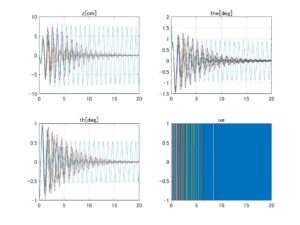 ⇒Case3:いくつかの動作点で不安定
⇒Case3:いくつかの動作点で不安定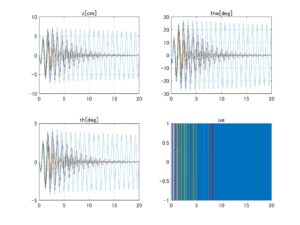 ⇒Case2:いくつかの動作点で不安定
⇒Case2:いくつかの動作点で不安定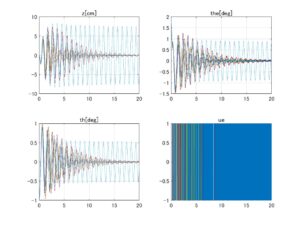 ⇒Case3:いくつかの動作点で不安定
⇒Case3:いくつかの動作点で不安定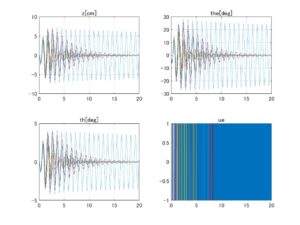 ⇒Case2:いくつかの動作点で不安定
⇒Case2:いくつかの動作点で不安定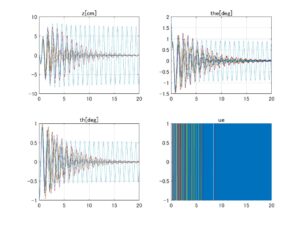 ⇒Case3:いくつかの動作点で不安定
⇒Case3:いくつかの動作点で不安定![Rendered by QuickLaTeX.com \displaystyle{(1.1)\quad \begin{array}{l} \underbrace{ \frac{d}{dt} \left[\begin{array}{c} z(t)-z^*\\ \theta(t)-\theta^*\\ \dot{z}(t)\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{ccccc} 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ a_{52} & a_{53} & a_{55} & a_{56} & b_{52}\\ a_{62} & a_{63} & a_{65} & a_{66} & b_{62}\\ 0 & 0 & 0 & 0 & 0 \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} z(t)-z^*\\ \theta(t)-\theta^*\\ \dot{z}(t)\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{x(t)}\\ + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \\ \omega_e \end{array}\right] }_{B} u(t) \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2ab91f82b36ff6c479a3662543135546_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(1.2)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{y(t)} = \underbrace{ \left[\begin{array}{ccccc} 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1 \end{array}\right] }_{C_M} \underbrace{ \left[\begin{array}{c} z(t)-z^*\\ \theta(t)-\theta^*\\ \dot{z}(t)\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{x(t)} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ab495fc33213399c94bb22d35ea16aa7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \theta_e(t)-\theta_e^* = \underbrace{ \left[\begin{array}{ccccc} 0 & 0 & 0 & 0 & 1 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} z(t)-z^*\\ \theta(t)-\theta^*\\ \dot{z}(t)\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{x(t)} \rightarrow \theta_e^c=0\quad(t\rightarrow\infty) \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b608779184f29f7dfe7199146bb182ff_l3.png)
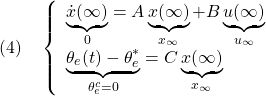
![Rendered by QuickLaTeX.com \displaystyle{(4')\quad \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\\hline \theta_e^c \\ \end{array}\right] = \underbrace{ \left[\begin{array}{ccccc|c} 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ a_{52} & a_{53} & a_{55} & a_{56} & b_{52}& 0\\ a_{62} & a_{63} & a_{65} & a_{66} & b_{62}& 0\\ 0 & 0 & 0 & 0 & 0 & \omega_e\\\hline 0 & 0 & 0 & 0 & 1 & 0 \end{array}\right] }_{S= \left[\begin{array}{cc} A & B\\ C & 0 \end{array}\right] } \left[\begin{array}{c} z_\infty\\ \theta_\infty\\ 0\\ 0\\ \theta_e^c \\\hline 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c97de0b2e36403d71388140469e2d777_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \underbrace{ \frac{d}{dt} \left[\begin{array}{c} (z(t)-z^*)-z_\infty\\ (\theta(t)-\theta^*)-\theta_\infty\\ \dot{z}(t)\\ \dot{\theta}(t)\\ (\theta_e(t)-\theta_e^*)-\theta_e^c \\\hline u(t) \end{array}\right] }_{\dot{x}_E(t)} = \underbrace{ \left[\begin{array}{ccccc|c} 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ a_{52} & a_{53} & a_{55} & a_{56} & b_{52}& 0\\ a_{62} & a_{63} & a_{65} & a_{66} & b_{62}& 0\\ 0 & 0 & 0 & 0 & 0 & \omega_e\\\hline 0 & 0 & 0 & 0 & 0 & 0 \end{array}\right] }_{A_E}\\ \times\underbrace{ \left[\begin{array}{c} (z(t)-z^*)-z_\infty\\ (\theta(t)-\theta^*)-\theta_\infty\\ \dot{z}(t)\\ \dot{\theta}(t)\\ (\theta_e(t)-\theta_e^*)-\theta_e^c \\\hline u(t) \end{array}\right] }_{x_E(t)} + \underbrace{ \left[\begin{array}{cccc} 0 \\ 0 \\ 0 \\ 0 \\ 0 \\\hline 1 \\ \end{array}\right] }_{B_E} \dot{u}(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-317e41c4ce1ea03263e1361d748dd7a7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \dot{u}(t)=- \underbrace{ \left[\begin{array}{ccccc|c} k_{1} & k_{2} & k_{3} & k_{4} & k_{5} & k_{6} \end{array}\right] }_{K_E} \underbrace{ \left[\begin{array}{c} (z(t)-z^*)-z_\infty\\ (\theta(t)-\theta^*)-\theta_\infty\\ \dot{z}(t)\\ \dot{\theta}(t)\\ (\theta_e(t)-\theta_e^*)-\theta_e^c \\\hline u(t) \end{array}\right] }_{x_E(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f5c8452e462ac8948c3cbf386db72361_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \left[\begin{array}{c} \frac{d}{dt} \left[\begin{array}{c} z(t)-z^*\\ \theta(t)-\theta^*\\ \dot{z}(t)\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \\\hline \end{array}\right]\\\hline (\theta_e(t)-\theta_e^*)-\theta_e^c \end{array}\right]=S \left[\begin{array}{c} (z(t)-z^*)-z_\infty\\ (\theta(t)-\theta^*)-\theta_\infty\\ \dot{z}(t)\\ \dot{\theta}(t)\\ (\theta_e(t)-\theta_e^*)-\theta_e^c \\\hline u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e858ba1cacf6b5a3e9c783dfa8edd49b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \dot{u}(t)=- \underbrace{ \left[\begin{array}{ccccc|c} k_{1} & k_{2} & k_{3} & k_{4} & k_{5} & k_{6} \end{array}\right]S^{-1} }_{F_E} \left[\begin{array}{c} \frac{d}{dt} \left[\begin{array}{c} z(t)-z^*\\ \theta(t)-\theta^*\\ \dot{z}(t)\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \\\hline \end{array}\right]\\\hline (\theta_e(t)-\theta_e^*)-\theta_e^c \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5274f5d7994ac45f370c81c83619df1b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad u(t) =- \underbrace{ \left[\begin{array}{ccccc} f_{1} & f_{2} & f_{3} & f_{4} & f_{5} \end{array}\right] }_{F} \underbrace{ \left[\begin{array}{c} z(t)-z^*\\ \theta(t)-\theta^*\\ \dot{z}(t)\\ \dot{\theta}(t)\\ \theta_e(t)-\theta_e^* \end{array}\right] }_{x(t)} +\underbrace{f_6}_{F_I}\int_0^t(\theta_e^c-(\theta_e(t)-\theta_e^*))dt} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-81adf7686a5ac0ccc4cd2c19c241dac1_l3.png)
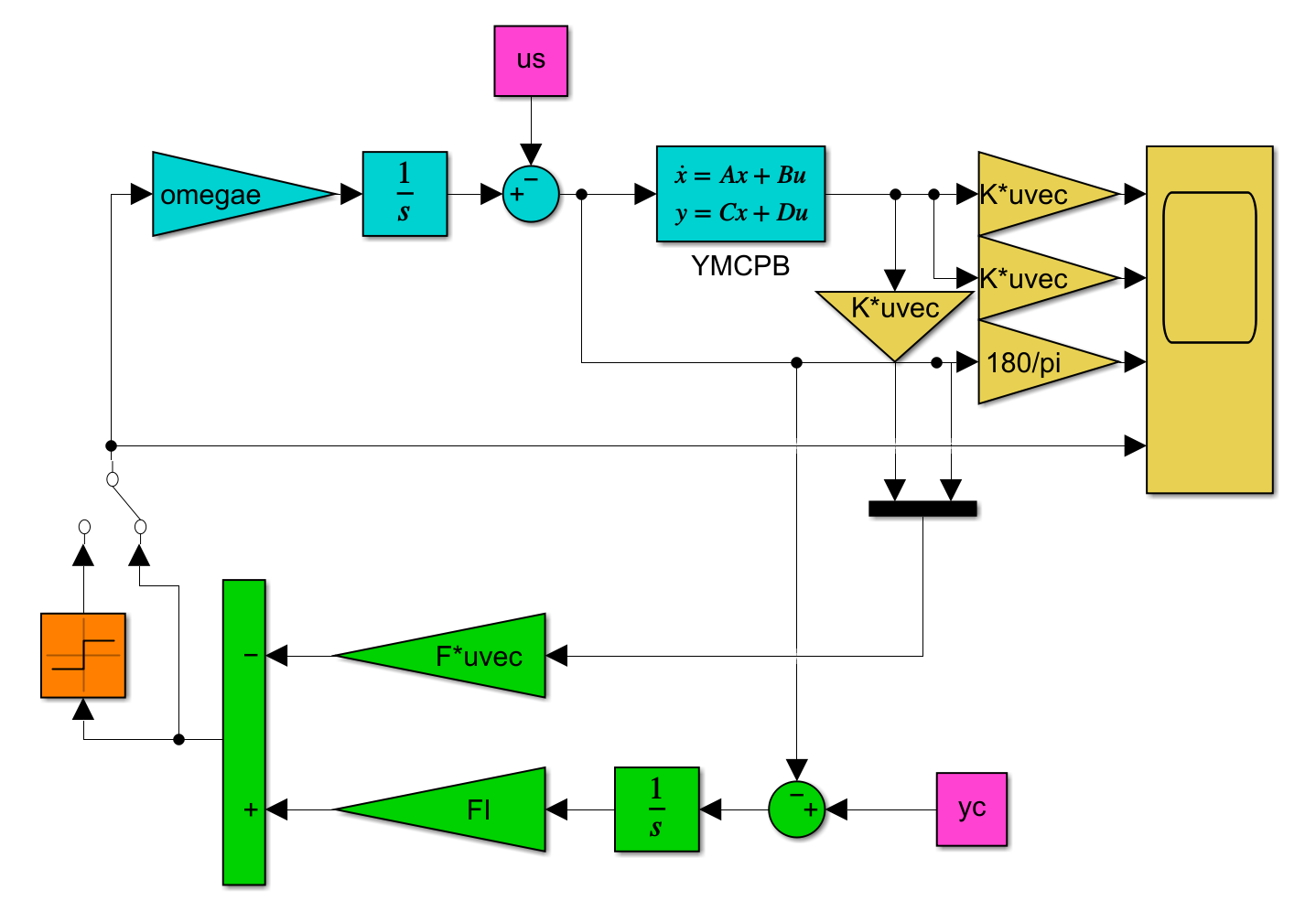
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \underbrace{ \frac{d}{dt} \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)\\\hline z(t)-z^*\\ \dot{z}(t) \end{array}\right] }_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{ccc|cc} 0 & 1 & 0 & 0 & 0 \\ a_{63} & 0 & b_{62} & a_{62} & 0 \\ 0 & 0 & 0 & 0 & 0 \\\hline 0 & 0 & 0 & 0 & 1 \\ a_{53} & 0 & b_{52} & a_{52} & 0 \end{array}\right] }_{A'=\left[\begin{array}{cc} A'_{11} & A'_{12}\\ A'_{21} & A'_{22} \end{array}\right] } \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)\\\hline z(t)-z^*\\ \dot{z}(t) \end{array}\right] }_{x'(t)}\\ + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ \omega_e\\\hline 0 \\ 0 \end{array}\right] }_{B'=\left[\begin{array}{cc} B'_1 \\ B'_2 \end{array}\right] } u(t) \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7fe85e46a1e1633fe91083e8fe93f2a6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t) \end{array}\right] }_{y(t)} = \underbrace{ \left[\begin{array}{ccc|cc} 1 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 \end{array}\right] }_{C'=[I_p\ 0]} \underbrace{ \left[\begin{array}{c} \theta(t)-\theta^*\\ \dot{\theta}(t)\\ \theta_e(t)\\\hline z(t)-z^*\\ \dot{z}(t) \end{array}\right] }_{x'(t)} \end{array}}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-26aac13c924dceec92a99cbc241a9571_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad U= \underbrace{\left[\begin{array}{ccc|cc} -\ell_{11} & -\ell_{12} & -\ell_{13} & 1 & 0 \\ -\ell_{21} & -\ell_{22} & -\ell_{23} & 0 & 1 \end{array}\right]}_{[-L\ I_{n-p}]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aa240c9d826b64c2ad7995e2b3c6a247_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \begin{array}{l} \left[\begin{array}{cc} \hat{A} & \hat{B} \end{array}\right]=UA' \left[\begin{array}{cc} U\\ C' \end{array}\right]^{-1}= \left[\begin{array}{cc} -L & I_{n-p} \end{array}\right] \left[\begin{array}{cc} A'_{11} & A'_{12}\\ A'_{21} & A'_{22} \end{array}\right] \left[\begin{array}{cc} 0 & I_p\\ I_{n-p}& L \end{array}\right]\\ =\left[\begin{array}{cc} A'_{22}-LA'_{12} & A'_{21}-LA'_{11}+\hat{A}L \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6668ff8720ac61955f63a1c860c85b76_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \hat{A} = \underbrace{\left[\begin{array}{ccc} 0 & 1 \\ a_{52} & 0 \end{array}\right]}_{A'_{22}}- \underbrace{\left[\begin{array}{ccc} \ell_{11} & \ell_{12} & \ell_{13} \\ \ell_{21} & \ell_{22} & \ell_{23} \end{array}\right]}_{L} \underbrace{\left[\begin{array}{ccc} 0 & 0 \\ a_{62} & 0 \\ 0 & 0 \end{array}\right]}_{A'_{12}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1f96c4d67fd044922c91fa9e1e1b2e71_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{cl} (18.1) &\left[\begin{array}{c} \dot{w}_1 \\ \dot{w}_2 \end{array}\right] = \underbrace{\left[\begin{array}{ccc} 0 & a_{52} \\ 1 & 0 \end{array}\right]}_{A'_{22}^T} \left[\begin{array}{c} w_1 \\ w_2 \end{array}\right]+ \underbrace{\left[\begin{array}{ccc} 0 & a_{62} & 0 \\ 0 & 0 & 0 \end{array}\right]}_{A'_{12}^T} \left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \end{array}\right]\\ (18.2) &\left[\begin{array}{c} v_1 \\ v_2 \\ v_3 \end{array}\right]=- \underbrace{\left[\begin{array}{ccc} \ell_{11} & \ell_{21} \\ \ell_{12} & \ell_{22} \\ \ell_{13} & \ell_{23} \end{array}\right]}_{L^T} \left[\begin{array}{c} w_1 \\ w_2 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0966560b08e71e8b9d05e93d3d1a2b46_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{cl} (19.1) &\left[\begin{array}{c} \dot{w}_1 \\ \dot{w}_2 \end{array}\right] = \left[\begin{array}{ccc} 0 & a_{52} \\ 1 & 0 \end{array}\right] \left[\begin{array}{c} w_1 \\ w_2 \end{array}\right]+ \left[\begin{array}{c} a_{62} \\ 0 \end{array}\right]v_2\\ (19.2) &v_2=- \left[\begin{array}{ccc} \ell_{12} & \ell_{22} \end{array}\right] \left[\begin{array}{c} w_1 \\ w_2 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2207f89283b711b6a3dac5da3343613c_l3.png)