2次安定性
[1] 非線形系
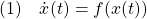
に対してリャプノフ関数
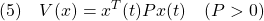
を考えます。これを微分して(1)を用いると((1)の解に沿って微分すると言います)
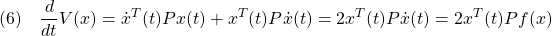
となります。このとき2次安定とは

が成り立つことを言います。これから次式を示すことができ、漸近安定性が成り立ちます。
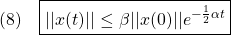
ただし
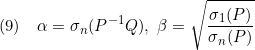
[2] 制御対象が平衡状態にあることは線形状態方程式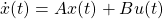 において、
において、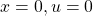 を意味します。そこで平衡状態が乱されて
を意味します。そこで平衡状態が乱されて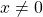 となる時刻を
となる時刻を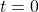 にとると、線形状態方程式は次式となります。
にとると、線形状態方程式は次式となります。
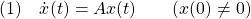
これに出力方程式
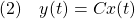
を考慮する場合も含めると、漸近安定性の判定法は次のようにまとめられます。
【漸近安定性の定義とその等価な条件】
定義DA: 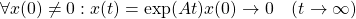
条件A0: 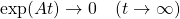
条件A1: 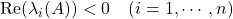
条件A2: 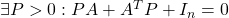
条件A3: 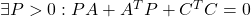 ただし、 ただし、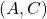 は可観測対 は可観測対
条件A4: 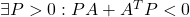
|
まず(1)が漸近安定とすると、条件A2のリャプノフ方程式から次式を得ます。
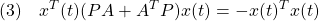
次に(1)に対してリャプノフ関数
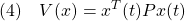
を考えるとき、(3)は2次安定性の条件
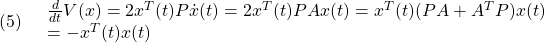
を意味します。これから漸近安定な線形系は2次安定であることが分かります。
●条件A2の両辺から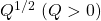 をかけて
をかけて
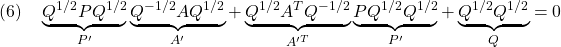
を得ます。 は可観測対なので条件A3を適用して(
は可観測対なので条件A3を適用して( をはずして)
をはずして)
条件A2′: 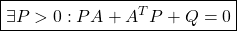 ただし、
ただし、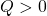
も漸近安定性の条件となることに注意します。
●たとえば、安定行列![Rendered by QuickLaTeX.com \displaystyle{ A= \left[\begin{array}{cc} 0 & 1 \\ -4 & -1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c6c1c66e1cf7b93bac3aad84f54e9744_l3.png)
が与えられるとき、リャプノフ方程式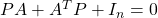 を満足する
を満足する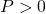 は
は
![Rendered by QuickLaTeX.com \displaystyle{ P=\left[\begin{array}{cc} 2.6250 & 0.1250\\ 0.1250 & 0.6250 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3885fe14c47a46dd2be67bc40c3c8e75_l3.png)
のように求まります。これはMATLABで次のコマンドを用いて計算できます。
ここで、P=lyap(A,Q) はリャプノフ方程式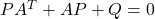 の解を求める関数であることに注意します。
の解を求める関数であることに注意します。
問題設定
[3] 制御対象の状態方程式として次式を考えます。
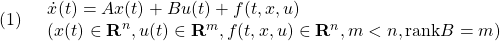
ここで、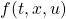 はモデル誤差、非線形要素、外乱などの影響を表し、有界かつ未知とします。これに対し、次のスイッチング関数を定義します。
はモデル誤差、非線形要素、外乱などの影響を表し、有界かつ未知とします。これに対し、次のスイッチング関数を定義します。
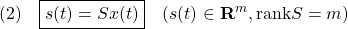
いま(1)の解が、ある時刻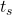 に対して
に対して
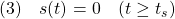
を満足するとき、スライディングモードが発生していると言います。
●以上の準備の下で、スライディングモード制御問題は次のように記述されます。
問題1: 動的システムの振る舞いが閉じ込められる超平面 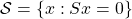 を定義するスイッチング関数を決定せよ。 を定義するスイッチング関数を決定せよ。
問題2: 有限時刻 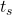 において状態を超平面内に拘束し、引き続き留まらせる( において状態を超平面内に拘束し、引き続き留まらせる(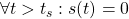 )ことのできるスライディングモード制御則(SM制御則)を設計せよ。 )ことのできるスライディングモード制御則(SM制御則)を設計せよ。 |
●いま、SM制御則を、2次安定性の条件
を、2次安定性
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad %\boxed{ \begin{array}{lll} V(\bar{x})= \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} P_1 & 0\\ 0 & P_2 \end{array}\right] }_{P} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}\\ \Rightarrow \dot{V}(\bar{x})\le - \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} Q_1 & 0\\ 0 & I \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} \end{array}}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a2747656c1f7d9559f971c1a26fd7023_l3.png)
すなわち
が成り立つように決定します( ,
,  ,
, 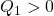 )。
)。
以下で示すように、このSM制御則は次式で表されます。

ここで、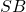 は正則行列であることを仮定しています。また設計パラメータは、スイッチング関数を決める行列
は正則行列であることを仮定しています。また設計パラメータは、スイッチング関数を決める行列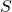 、安定行列
、安定行列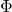 、スカラー
、スカラー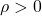 です。
です。
●2重積分器に対して、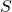 ,
,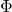 ,
,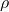 を適当に選んだときのSM制御則の計算は次のように行われます。
を適当に選んだときのSM制御則の計算は次のように行われます。
| MATLAB |
%cDINT_smc.m
%-----
clear all, close all
A=[0 1;
0 0];
B=[0;1];
C=eye(2);
D=zeros(2,1);
M=1;
S=[M 1];
Phi=-1;
P2=lyap(Phi,1);
P2S=P2*S;
Leq=inv(S*B)*S*A;
LPhi=-inv(S*B)*Phi*S;
L=Leq+LPhi;
rho=0.5;
Ln=inv(S*B)*rho;
x0=B;
sim('DINT_smc')
%-----
%eof
|
これを実行して、図1aのシミュレーション結果を得ます。

図1a 2重積分器のSM制御
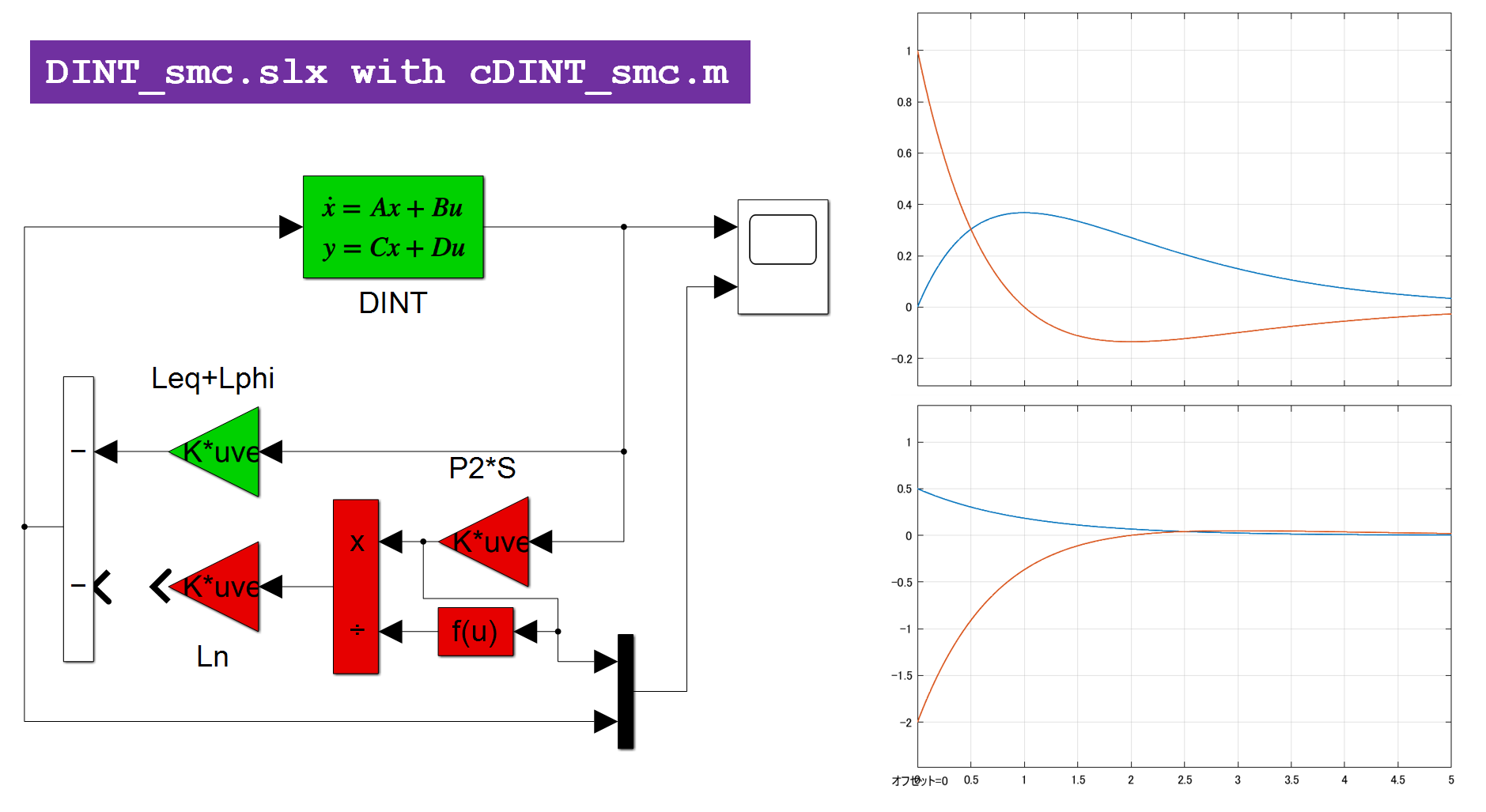
図1b 2重積分器の線形制御(SM制御のスイッチング項を外した場合)
図1bに、SM制御のスイッチング項を外した場合のシミュレーション結果を示します。これらからスイッチング項が速応性の改善に役立っていることが分かります。
●いま(1)において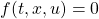 、すなわち
、すなわち
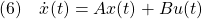
とし、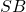 の正則性を仮定します。
の正則性を仮定します。 において、スライディングモード時の制御則は等価制御と呼ばれ、次式のように求められます。
において、スライディングモード時の制御則は等価制御と呼ばれ、次式のように求められます。
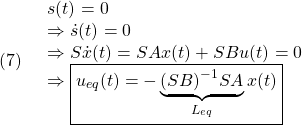
これによる閉ループ系は次式となります。
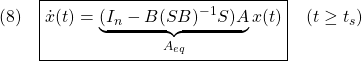
●いま(1)において の場合、適合サイズをもつ行列
の場合、適合サイズをもつ行列 を用いて
を用いて
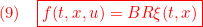
のように表されると仮定します。このとき、等価制御は
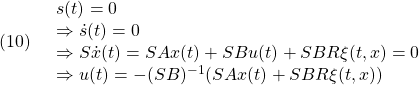
となります。これによる閉ループ系は次式となります。
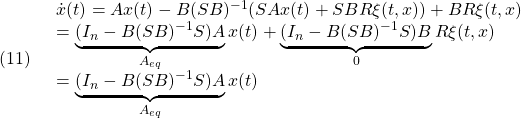
すなわちマッチング条件とよばれる(9)が成り立つとき、スライディングモード時は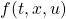 の影響を受けないことが分かります。
の影響を受けないことが分かります。
●剛体振子の運動方程式は次式で与えられました。
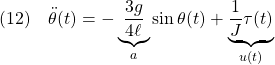
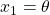 ,
, 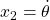 とおいて、次の非線形状態方程式を得ます。
とおいて、次の非線形状態方程式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right]= \left[\begin{array}{cc} x_2(t)\\ -a\sin x_1(t)+u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aa83e9dac52ad382b47bbc497cef2e6e_l3.png)
これは、次式のように、2重積分器に非線形項が加えられたものとみなすことができます。
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right]= \left[\begin{array}{cc} 0 & 1\\ 0 & 0 \end{array}\right] \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right]+ \left[\begin{array}{c} 0\\ 1 \end{array}\right] u(t)+ \left[\begin{array}{c} 0\\ -a\sin x_1(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fb895b4100fa03d5604bf0d34248d203_l3.png)
そこで、図1のSM制御則をそのまま用いたときの様子を調べてみます。図2は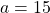 とした場合(
とした場合(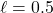 )のシミュレーション結果です。
)のシミュレーション結果です。
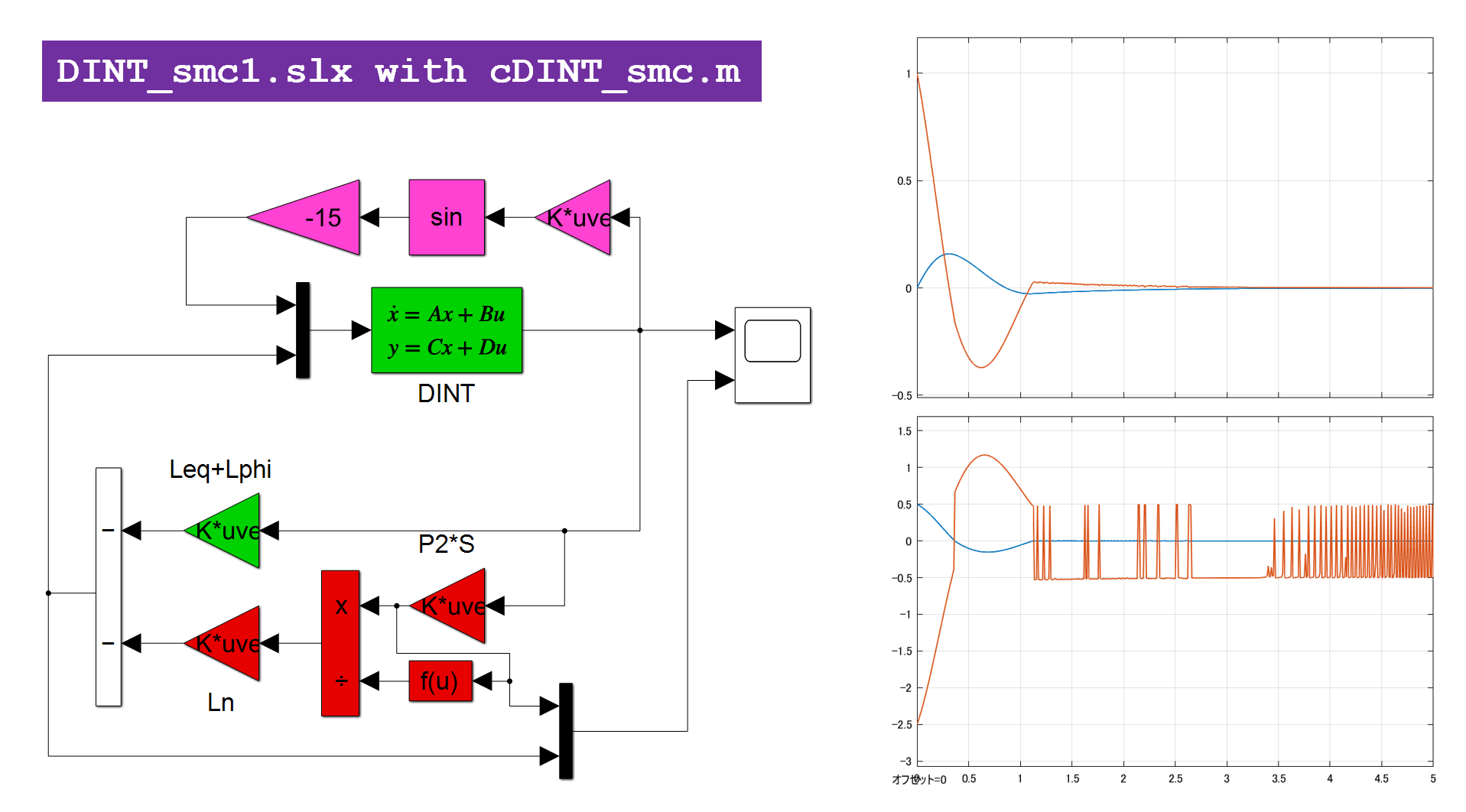
図2a 非線形項を考慮した場合のSM制御
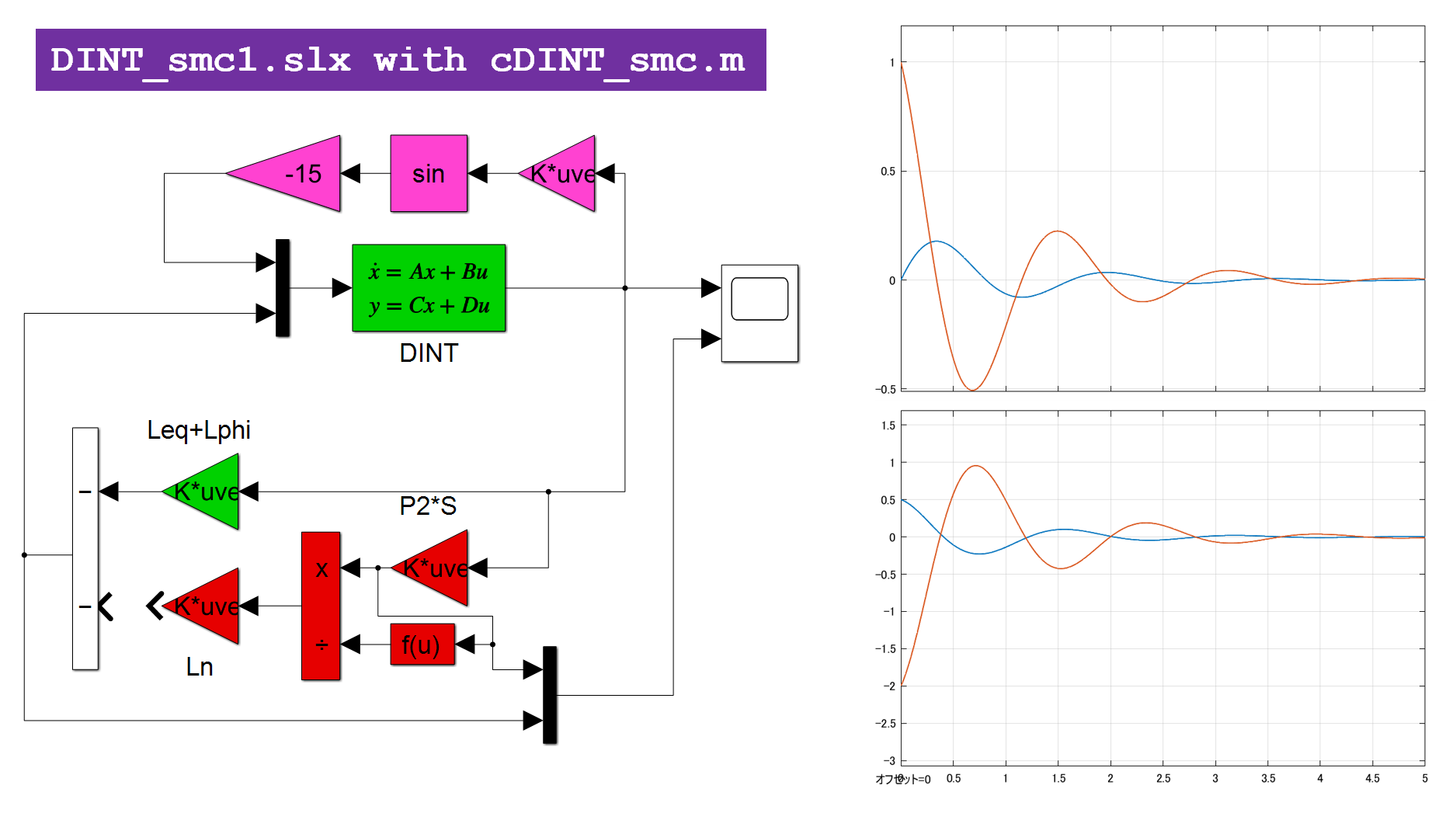
図2b 非線形項を考慮した場合の線形制御(SM制御のスイッチング項を外した場合)
図1のSM制御則は非線形項を考慮していないのですが、マッチング条件が満たされているので、非線形項の影響を抑制していることが分かります。これは図2bのスイッチング項がない場合と比べると明らかです。
SM制御則
[4] 制御対象の状態方程式として次式を考えます。
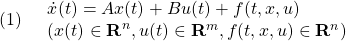
以下では、状態方程式とスイッチング関数は次のSMC標準形(regular form)をとるように座標変換されていると仮定します(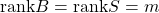 )。
)。
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \boxed{\underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t) + \underbrace{ \left[\begin{array}{l} f_u(t,x)\\ f_m(t,x,u) \end{array}\right] }_{f(t,x,u)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-492c810b2764797d15e8da449fa86719_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \boxed{s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} \ (M=S_2^{-1}S_1)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f362cf2f2a84558f6ce3b7cbfd623471_l3.png)
これに対して、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aa3c209c1893a28b597ab444a59fa480_l3.png)
を行って、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \boxed{ \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{\bar{x}}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22}\\ \end{array}\right] }_{\bar{A}=T_s A T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \bar{B}_2 \end{array}\right] }_{\bar{B}=T_sB} u(t)\\ + \underbrace{ \left[\begin{array}{c} f_u(t,x)\\ S_1f_u(t,x)+S_2f_m(t,x,u) \end{array}\right] }_{T_sf(t,x,u)} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8d94be87e2ee3e86130661d37570a682_l3.png)
ただし
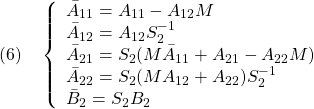
以下では、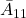 が安定行列となるようにスイッチング関数が選ばれていると仮定します。
が安定行列となるようにスイッチング関数が選ばれていると仮定します。
●SMC標準形に対する等価制御は、 として
として
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{cl} & s(t)=0\ \Rightarrow\ \dot{s}(t)=0\\ \Downarrow & by\ (5)\\ &\bar{A}_{21}x_1(t)+\bar{A}_{22}s(t)+\bar{B}_{2}u(t)=0\\ \Downarrow & \\ (7) & u_{eq}(t)=-\underbrace{\bar{B}_{2}^{-1}}_{([0\ I_m]T_sB)^{-1}} \underbrace{\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right]}_{[0\ I_m]T_sAT_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}\\ \Downarrow & by\ S=[0\ I_m]T_s, x=T_s^{-1}\bar{x}\\ (8) & \boxed{u_{eq}(t)=-\underbrace{(SB)^{-1}SA}_{L_\ell}x(t)}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2c000a36a1eddd1e979735e5c504c61b_l3.png)
のように得られます。線形制御則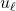 は、この等価制御をベースして
は、この等価制御をベースして
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{cl} (9) & u_{eq}(t)=-\underbrace{\bar{B}_{2}^{-1}}_{([0\ I_m]T_sB)^{-1}} (\underbrace{\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right]}_{[0\ I_m]T_sAT_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}-\Phi s(t))\\ \Downarrow & by\ S=[0\ I_m]T_s, x=T_s^{-1}\bar{x}\\ (10) & \boxed{u_\ell(t)=-\underbrace{(SB)^{-1}(SA-\Phi S)}_{L=L_{eq}+L_{phi}}x(t)}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f3c7ee69a5490d0416e346e8d6a29a04_l3.png)
のように構成します。ここで、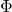 は適当に設定された安定行列です。
は適当に設定された安定行列です。
●このとき閉ループ系は次式で与えられます。
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{s}(t) \end{array}\right] = \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ 0 & \Phi \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ + \left[\begin{array}{c} f_u(t,x)\\ \bar{B}_{2}u_n(t)+S_2(Mf_u(t,x)+f_m(t,x,u)) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-08b0fd62ceefdfc7673e603a95165c27_l3.png)
これからスライディングモード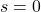 を達成するために
を達成するために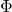 の影響を与えることが分かります。簡単な例で確かめると
の影響を与えることが分かります。簡単な例で確かめると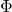 はダンピングを与え、速くスライディングモードを達成するためのパラメータであることが分かります。
はダンピングを与え、速くスライディングモードを達成するためのパラメータであることが分かります。
さて、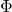 は安定行列なので
は安定行列なので
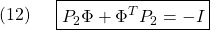
を満たす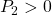 を選ぶことができます。これを用いて、スイッチング制御則
を選ぶことができます。これを用いて、スイッチング制御則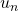 を
を
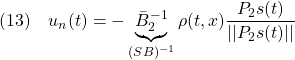
すなわち
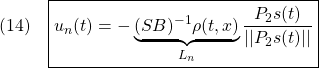
と定めます。線形制御則(10)とスイッチング制御則(14)を用いて、2次安定性を示すことができます。
スイッチング関数(1)
[5] スライディングモードの場合、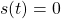 なので
なので
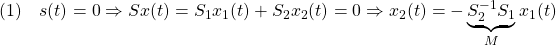
となって、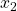 の振る舞いは
の振る舞いは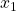 によって決まります。一方、
によって決まります。一方、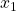 の振る舞いは
の振る舞いは
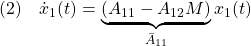
によって決まります。これは
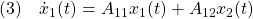
に対する安定化状態フィードバック
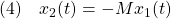
による閉ループ系とみなすことができます。
したがって、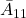 が安定行列となるようにスイッチング関数が選ぶためには、(3)に対する状態フィードバックによる安定化問題を解けばよいことが分かります。
が安定行列となるようにスイッチング関数が選ぶためには、(3)に対する状態フィードバックによる安定化問題を解けばよいことが分かります。
●そこで、次の2次形式評価関数を最小にするように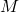 を決定する方法が提案されています。
を決定する方法が提案されています。
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \boxed{J=\int_0^\infty \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right]^T }_{x^T(t)} \underbrace{ \left[\begin{array}{cc} Q_{11} & Q_{12} \\ Q_{21} & Q_{22} \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} dt} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-13ff85a64857f296223fc5fc4db3a6fc_l3.png)
これは
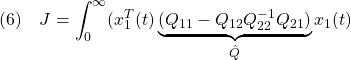
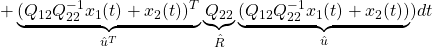
と書けます。ここで、(3)と(4)をそれぞれ
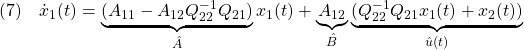
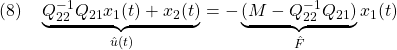
と書き直すと、次のような最適化制御問題の定式化ができていることがわかります。すなわち
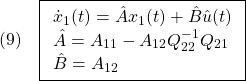
を2次系式評価関数
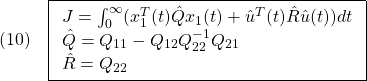
を最小にするように
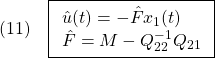
を求める問題です。この解は、リッカチ方程式
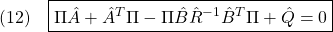
を解いて
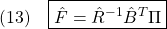
を求め、次式から を決めればよいことがわかります。
を決めればよいことがわかります。
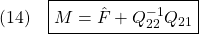
●2重積分器に対して、関数swflqrによるスイッチング関数Sの決定は次のように行われます。
| MATLAB |
%cDINT_smc1.m
%-----
clear all, close all
A=[0 1;
0 0];
B=[0;1];
C=eye(2);
D=zeros(2,1);
Mx=0.5; Tx=0.5;
Q=diag([1/Mx,Tx/Mx].^2);
S=swflqr(A,B,Q)
Phi=-1;
P2=lyap(Phi,1);
P2S=P2*S;
Leq=inv(S*B)*S*A;
LPhi=-inv(S*B)*Phi*S;
L=Leq+LPhi;
rho=0.5;
Ln=inv(S*B)*rho;
x0=B;
sim('DINT_smc')
%-----
%eof
|
これを実行して図3のシミュレーション結果を得ます。
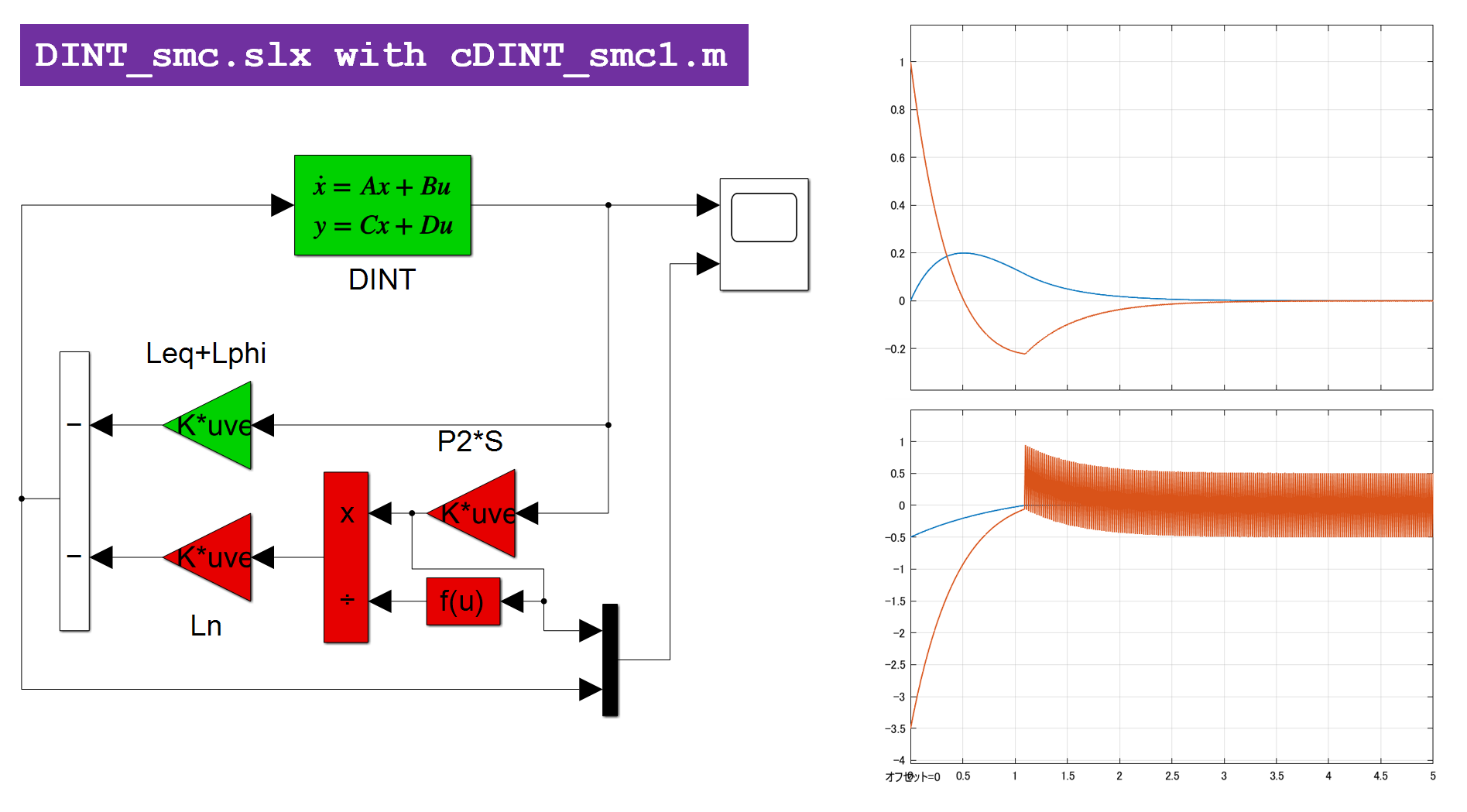
図3 関数swflqrによるスイッチング関数Sの決定
ここで、関数swflqrは、Edwards and Spurgeon によるものです。
スイッチング関数(2)
[6] 等価制御
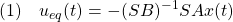
による閉ループ系は次式で表されました。
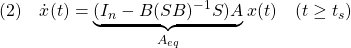
ここで
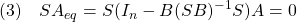
また、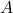 、
、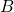 、
、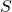 は、SMC標準形で与えられるとすると
は、SMC標準形で与えられるとすると
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} A_{eq}= \underbrace{ \left[\begin{array}{cc} I & 0 \\ -M & 0 \\ \end{array}\right] }_{I_n-B(SB)^{-1}S} \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right]= \left[\begin{array}{cc} A_{11} & A_{12} \\ -MA_{11} & -MA_{12} \\ \end{array}\right]\\ = \left[\begin{array}{cc} I & 0 \\ -M & I \\ \end{array}\right] \left[\begin{array}{cc} \bar{A}_{11} & A_{12} \\ 0 & 0 \\ \end{array}\right] \left[\begin{array}{cc} I & 0 \\ -M & I \\ \end{array}\right]^{-1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2474825aa676243c02182b9e5a87f0f1_l3.png)
となって、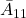 が安定行列なので、
が安定行列なので、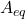 は
は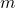 個の零固有値を持ちます。一方、
個の零固有値を持ちます。一方、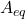 の非零固有値
の非零固有値 に対応する固有ベクトルを
に対応する固有ベクトルを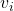 とすると、
とすると、
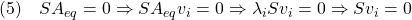
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad { \boxed{S[v_1\cdots v_{n-m}]=0 % \Rightarrow [v_1\cdots v_{n-m}]^TS^T=0}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-33964edd7a6349891872237b63b937ec_l3.png)
が成り立ちます。したがって、まず等価制御による閉ループ系の が望ましい固有値・固有ベクトルをもつように設計して、(5)から
が望ましい固有値・固有ベクトルをもつように設計して、(5)から を決定することが考えられます。
を決定することが考えられます。
●2重積分器に対して、関数swfvplによるスイッチング関数Sの決定は次のように行われます。
| MATLAB |
%cDINT_smc2.m
%-----
clear all, close all
A=[0 1;
0 0];
B=[0;1];
C=eye(2);
D=zeros(2,1);
lambda=-1;
nocomp=0;
specpos=rand(2,1)
specent=rand(2,1)
S=swfvpl(A,B,lambda,nocomp,specpos,specent)
Phi=-1;
P2=lyap(Phi,1);
P2S=P2*S;
Leq=inv(S*B)*S*A;
LPhi=-inv(S*B)*Phi*S;
L=Leq+LPhi;
rho=0.5;
Ln=inv(S*B)*rho;
x0=B;
sim('DINT_smc')
%-----
%eof
|
これを実行して図4のシミュレーション結果を得ます。
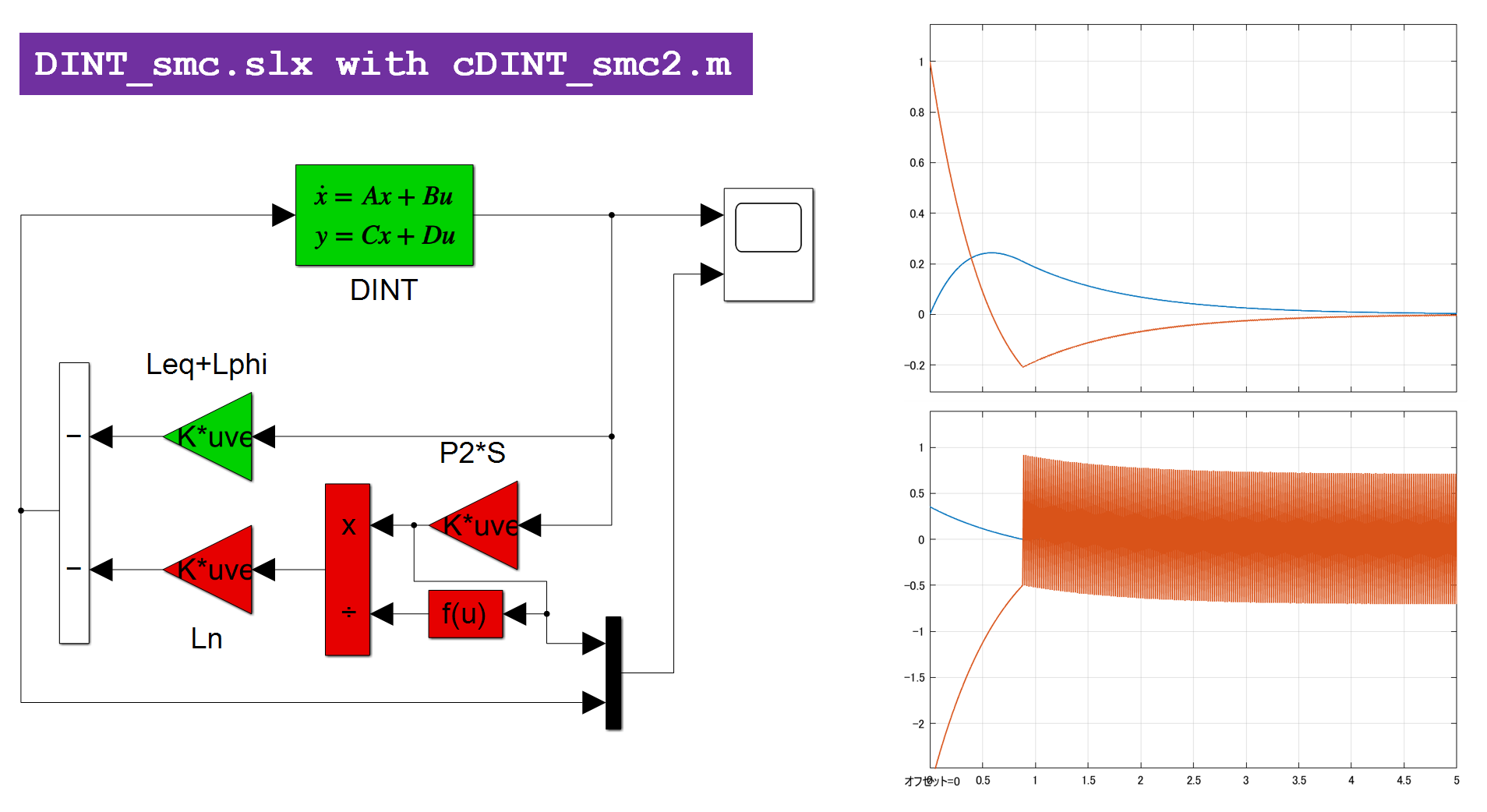
図4 関数swfvplによるスイッチング関数Sの決定
ここで、関数swfvplは、Edwards and Spurgeon によるものです。
積分動作の導入
[6] 定値外乱を受ける制御対象
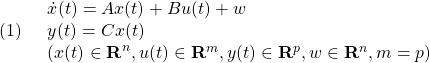
の出力を、次のコマンド(定値目標)
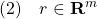
に追従させることを考えます。そのために、積分動作
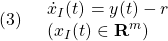
を考え、次の拡大系を構成します。
偏差系E3:
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3c19e131ef7f7e62fb75b0b722359667_l3.png)
を得ます。この偏差系E3が標準形となっていることに注意して、SMCを設計します。
(4)を、改めて次のように書きます。
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t)\\ (x_1(t)=x(t)-x_\infty, x_2(t)=u(t)-u_\infty) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3651de7cb254ab2cb45e5409ae9cd171_l3.png)
スイッチング関数として、次式を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-841f3fca38a28aec9d1c570b17f6f7ec_l3.png)
(15)に対して、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-94c9c19111e524fb6b7adf025beef334_l3.png)
を行って、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{x}'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right] }_{T_sA_{E3}T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ S_2 \end{array}\right] }_{T_sB_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-922fcb090845e1f769269f768e72eda3_l3.png)
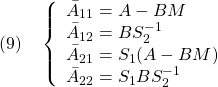
以下では、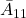 が安定行列となるようにスイッチング関数が選ばれていると仮定します。
が安定行列となるようにスイッチング関数が選ばれていると仮定します。
このとき、SM制御則を、2次安定性
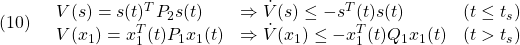
が成り立つように決定します(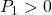 ,
, 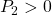 ,
, 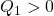 )。
)。
偏差系E3に対するSMCは次式で与えられます。
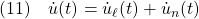
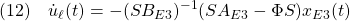
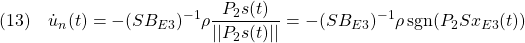
これらを積分して、制御対象(1)に対する積分動作をもつSMCを導出します。
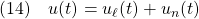
まず(12)は次式のように書けます。
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad {\dot u}_\ell(t)=- \boxed{\underbrace{ (SB_{E3})^{-1}(SA_{E3}-\Phi S)S_E^{-1} }_{\left[\begin{array}{cc} F & F_I \end{array}\right]}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-09bdbdbd69d8bc1d816020ba9b4ba6d8_l3.png)
これを積分して
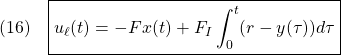
次に(13)は次式のように書けます。
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad {\dot u}_n(t) =-(SB_{E3})^{-1}\rho\, {\rm sgn}( \boxed{\underbrace{ P_2SS_E^{-1} }_{\left[\begin{array}{cc} G & G_I \end{array}\right]}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)}) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-88922723347229f2a9ac74335912e98d_l3.png)
これを積分すれば
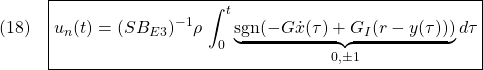
●2重積分器に対して、次のように行われます。
| MATLAB |
%cDINT_smci.m
%-----
clear all, close all
A=[0 1;
0 0];
B=[0;1];
C=[1 0];
D=0;
n=size(A,1); m=size(B,2); p=size(C,1);
AE=[A B;zeros(m,n+m)];
BE=[zeros(n,m);eye(m)];
SE=[A B;C D];
QE=eye(n+m);
S=-swflqr(AE,BE,QE)
Phi=-0.5;
Leq=inv(S*BE)*S*AE;
LPhi=-inv(S*BE)*Phi*S;
L=(Leq+LPhi)/SE;
F=L(1:2)
FI=L(3)
P2=lyap(Phi,1)
P2S=P2*S/SE;
G=P2S(1:2)
GI=P2S(3)
rho=1;
Ln=inv(S*BE)*rho
x0=zeros(2,1);
sim('DINT_smci')
%-----
%eof
|
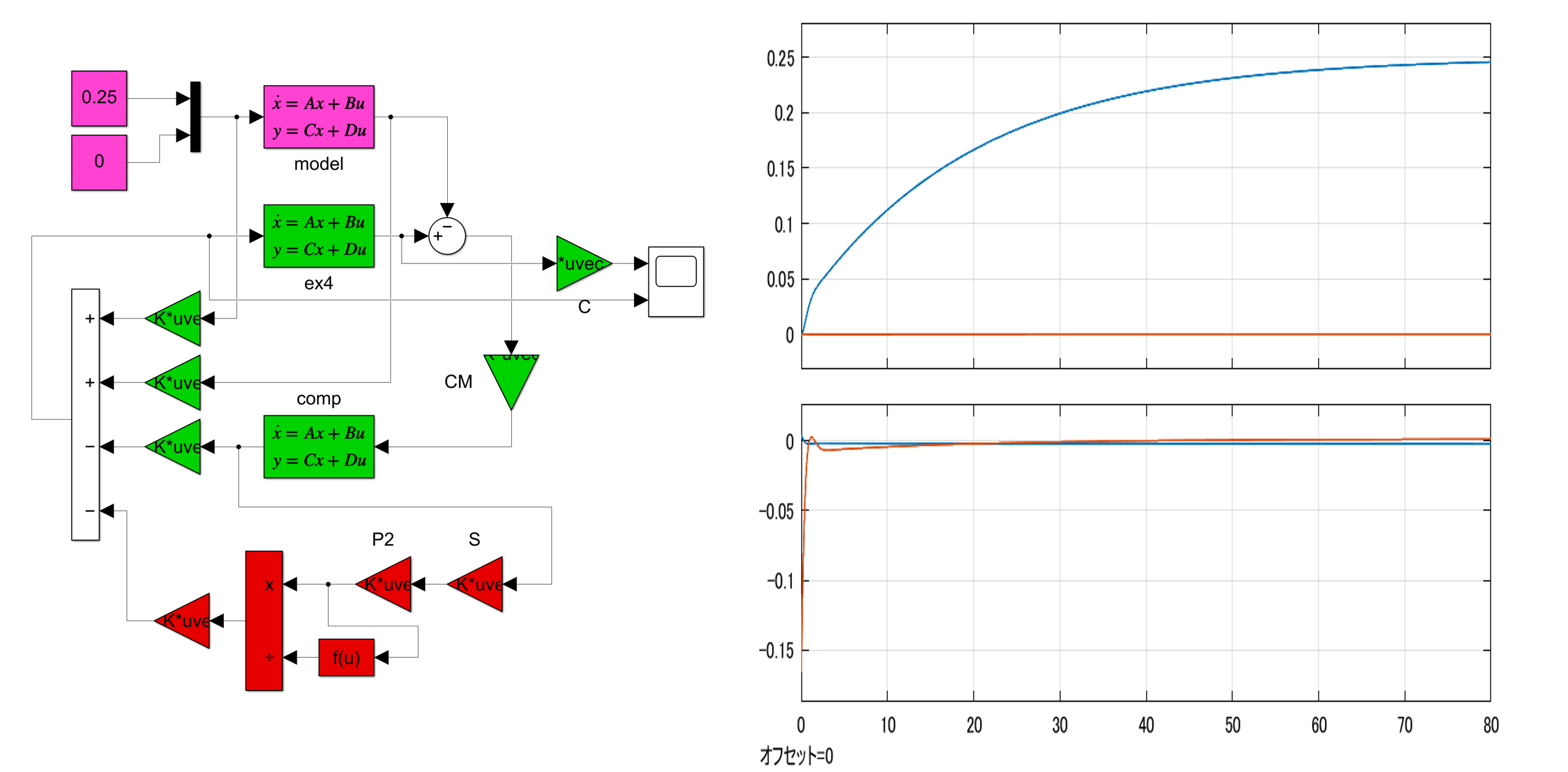
これを実行して図5のシミュレーション結果を得ます。
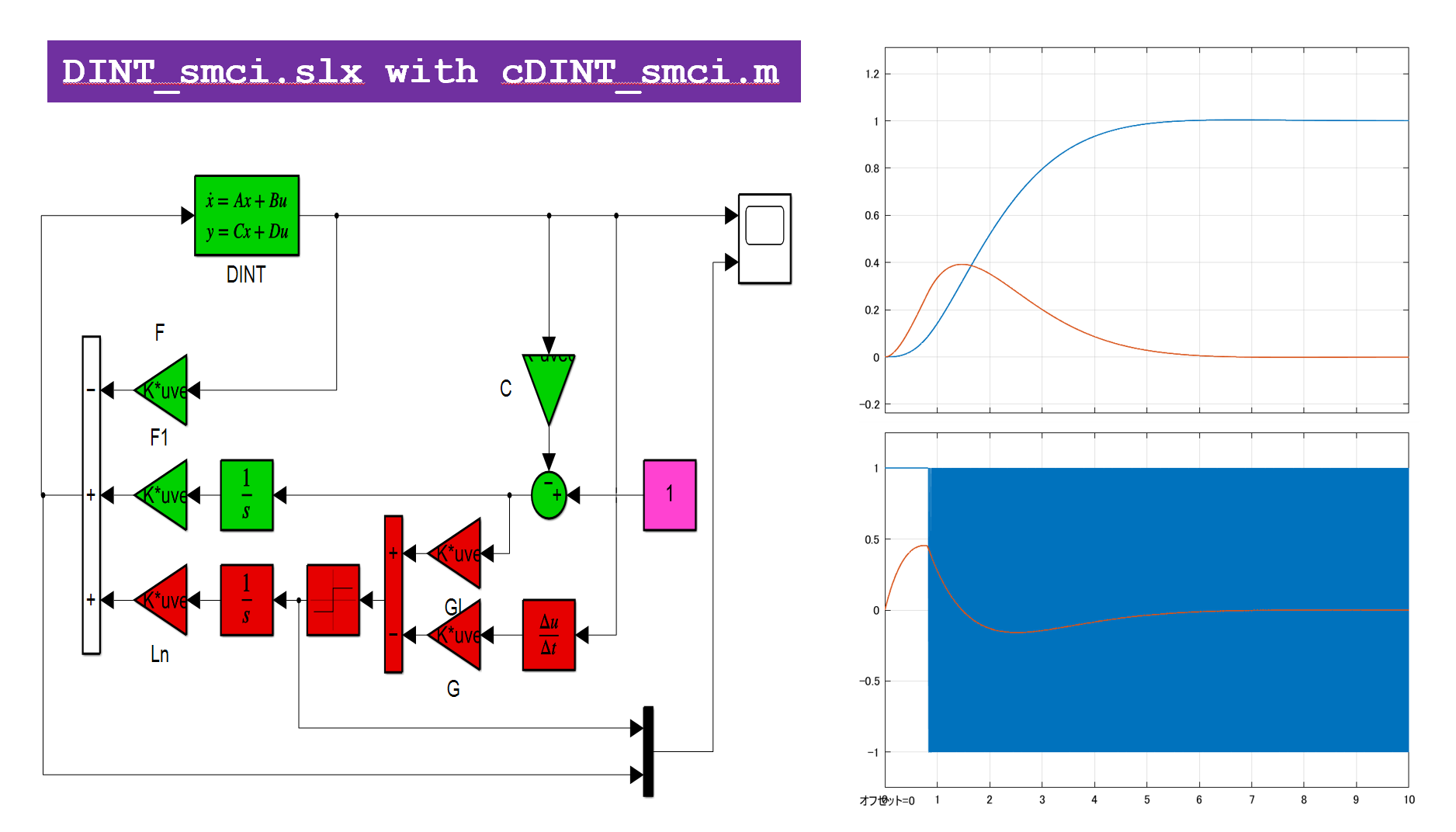
図5 積分動作を導入したSM制御
補遺:2次安定系のロバスト性…Homework
いま漸近安定な線形系
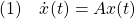
において次のようなモデルの不確かさがあるとします。
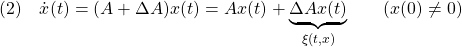
条件A2’より、適当な と
と に対して
に対して
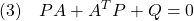
が成り立ちます。このとき
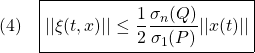
ならば、リャプノフ関数
に対して
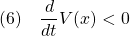
となって、リャプノフ安定となります。
●実際、
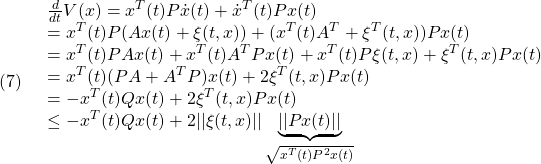
ここで、
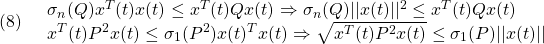
に注意して、(4)の下では
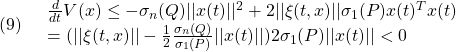
となります。
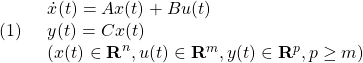
![]() は列フルランク、
は列フルランク、![]() は行フルランクをもち、
は行フルランクをもち、![]() は可観測対とします。
は可観測対とします。![]() を
を![]() の形にするために、座標変換
の形にするために、座標変換![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} = \underbrace{ \left[\begin{array}{cc} N_c^T \\ C \\ \end{array}\right] }_{T_c} x(t) \Leftrightarrow x(t)= \underbrace{ \left[\begin{array}{cc} N_c^T \\ C \\ \end{array}\right]^{-1} }_{T_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4db3d40a6624450f2c64ca791f380fe1_l3.png)
![]() は
は![]() を正則とする適当な行列)、次式を得ます。
を正則とする適当な行列)、次式を得ます。![Rendered by QuickLaTeX.com \displaystyle{(3.1)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{cc} A_{c11} & A_{c12} \\ A_{c21} & A_{c22} \\ \end{array}\right] }_{T_cAT_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} + \underbrace{ \left[\begin{array}{c} B_{c1}\\ B_{c2} \end{array}\right] }_{T_cB} u(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-644186c09de8b1938a61eb3a18489a90_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3.2)\quad y(t) = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & I_p \\ \end{array}\right] }_{CT_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-58c311e6be5fde3b8343f975d58b0d2a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4.1)\quad \boxed{\begin{array}{l} \left[\begin{array}{c} \dot{\hat x}_1(t)\\ \dot{\hat y}(t) \end{array}\right] = \left[\begin{array}{cc} A_{c11} & A_{c12} \\ A_{c21} & A_{c22} \\ \end{array}\right] \left[\begin{array}{c} \hat{x}_1(t)\\ \hat{y}(t) \end{array}\right] + \left[\begin{array}{c} B_{c1}\\ B_{c2} \end{array}\right] u(t)\\ + \left[\begin{array}{c} L\\ -I_p \end{array}\right] \nu \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-be4b4ad4f240be627b5ee9bf2dfec609_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4.2)\quad \boxed{\nu=M \left[\begin{array}{c} {\rm sgn}(\hat{y}_1(t)-y_1(t))\\ \vdots\\ {\rm sgn}(\hat{y}_p(t)-y_p(t)) \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e7bc0ad75dd6f59af1617db5c3d71ce3_l3.png)
![]() と
と![]() は設計パラメータです。
は設計パラメータです。![]() をフィードバックしますが、上のオブザーバは出力の推定誤差のスイッチング動作が加えられています。これにより、
をフィードバックしますが、上のオブザーバは出力の推定誤差のスイッチング動作が加えられています。これにより、![]() の超平面に載せることが考えられます。
の超平面に載せることが考えられます。![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \underbrace{ \left[\begin{array}{c} \dot{\hat x}_1(t)-\dot{x}_1(t)\\ \dot{\hat y}(t)-\dot{y}(t) \end{array}\right] }_{\left[\begin{array}{c} \dot{e}_1(t)\\ \dot{e}_y(t) \end{array}\right]} = \left[\begin{array}{cc} A_{c11} & A_{c12} \\ A_{c21} & A_{c22} \\ \end{array}\right] \underbrace{ \left[\begin{array}{c} \hat{x}_1(t)-{x}_1(t)\\ \hat{y}(t)-{y}(t) \end{array}\right] }_{\left[\begin{array}{c} {e}_1(t)\\ {e}_y(t) \end{array}\right]} + \left[\begin{array}{c} 0\\ -\nu \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8c8ad91d08e2ba443b44f99ab4a83031_l3.png)
![]()
![Rendered by QuickLaTeX.com \displaystyle{(7.1)\quad \boxed{\left[\begin{array}{c} \dot{\tilde e}_1(t)\\ \dot{e}_y(t) \end{array}\right] = \left[\begin{array}{cc} \tilde{A}_{c11} & \tilde{A}_{c12} \\ \tilde{A}_{c21} & \tilde{A}_{c22} \\ \end{array}\right] \left[\begin{array}{c} \tilde{e}_1(t)\\ {e}_y(t) \end{array}\right] + \left[\begin{array}{c} 0\\ -I_p \end{array}\right]\nu} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c3e4c6bfa8770bfcf9a5e2e1e89effae_l3.png)
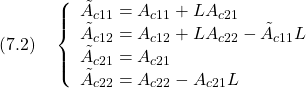
![]() が安定行列となるように
が安定行列となるように![]() が選ばれているとします。
が選ばれているとします。![]()
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \begin{array}{l} e^T_y(t)\dot{e}_y(t)=e^T_y(t)(\tilde{A}_{c21}\tilde{e}_1(t)+\tilde{A}_{c22}{e}_y(t)-\nu)\\\\ =e^T_y(t)\tilde{A}_{c21}\tilde{e}_1(t)+e^T_y(t)\tilde{A}_{c22}{e}_y(t)\\ -M \left[\begin{array}{c} \hat{y}_1(t)-y_1(t)\\ \vdots\\ \hat{y}_p(t)-y_p(t) \end{array}\right]^T \left[\begin{array}{c} {\rm sgn}(\hat{y}_1(t)-y_1(t))\\ \vdots\\ {\rm sgn}(\hat{y}_p(t)-y_p(t)) \end{array}\right]\\\\ =e^T_y(t)\tilde{A}_{c21}\tilde{e}_1(t)+e^T_y(t)\frac{1}{2}(\tilde{A}_{c22}+\tilde{A}^T_{c22}){e}_y(t)\\ -M(|\hat{y}_1(t)-y_1(t)|+\cdots+|\hat{y}_p(t)-y_p(t)|)\\\\ \le e^T_y(t)\tilde{A}_{c21}\tilde{e}_1(t)+\frac{1}{2}\bar\sigma(\tilde{A}_{c22}+\tilde{A}^T_{c22})e^T_y(t){e}_y(t)\\ -M(|\hat{y}_1(t)-y_1(t)|+\cdots+|\hat{y}_p(t)-y_p(t)|)\\\\ \le ||e_y(t)||(||\tilde{A}_{c21}\tilde{e}_1(t)||+\frac{1}{2}\bar\sigma(\tilde{A}_{c22}+\tilde{A}^T_{c22})||{e}_y(t)||)\\ -M(|\hat{y}_1(t)-y_1(t)|+\cdots+|\hat{y}_p(t)-y_p(t)|)\\\\ < ||e_y(t)||(M-\eta)-M(|\hat{y}_1(t)-y_1(t)|+\cdots+|\hat{y}_p(t)-y_p(t)|)\\ \le -\eta||e_y(t)||+M\underbrace{(||e_y(t)||-(|\hat{y}_1(t)-y_1(t)|+\cdots+|\hat{y}_p(t)-y_p(t)|))}_{\le0}\\ \le -\eta||e_y(t)||<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e20cc8c96c530a7504d6d40df37a524b_l3.png)
![]()
![]() となることを示しています。このとき(7.1)から
となることを示しています。このとき(7.1)から![]()
![]() も零の漸近するので、状態オブザーバ(4.1)が構成されていることが分かります。
も零の漸近するので、状態オブザーバ(4.1)が構成されていることが分かります。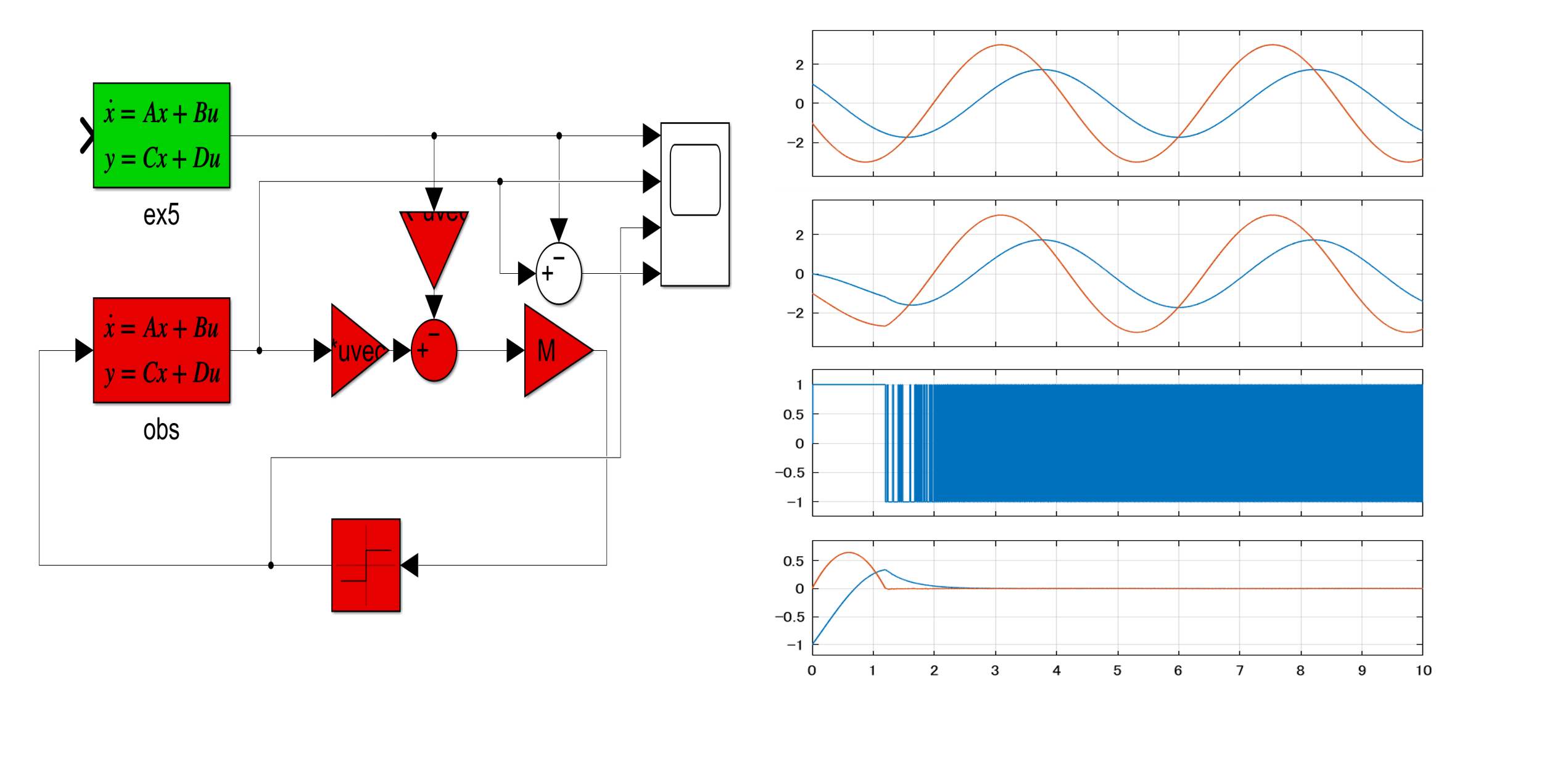
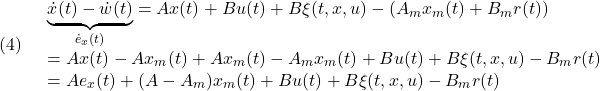
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \dot{x}(t)=Ax(t)+Bu(t)\\ x(t)= \left[\begin{array}{ll} \phi & bank\ angle\\ r & yaw\ rate\\ p & roll\ rate\\ \beta & sideslip\ angle\\ x_5 & washed-out\ filter\ state \end{array}\right],\quad u(t)= \left[\begin{array}{ll} \delta_r & rudder\ deflection\\ \delta_a & aileron\ deflection \end{array}\right]\\ A=\left[\begin{array}{rrrrr} 0 & 0 & 1.0000 & 0 & 0\\ 0 & -0.1540 & -0.0042 & 1.5400 & 0\\ 0 & 0.2490 & -1.0000 & -5.2000 & 0\\ 0.0386 & -0.9960 & -0.0003 & -0.1170 & 0\\ 0 & 0.5000 & 0 & 0 & -0.5000 \end{array}\right],\quad\\ B=\left[\begin{array}{rr} 0 & 0 \\ -0.7440 & -0.0320 \\ 0.3370 & -1.1200 \\ 0.0200 & 0\\ 0 & 20 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8622180be357918528164e3d543e7c84_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \begin{array}{l} y(t)=C_Mx(t),\ z(t)=Cx(t)\\ y(t)= \left[\begin{array}{ll} r_{wo} & washed-out\ yaw\ rate\\ p & roll\ rate\\ \beta & sideslip\ angle\\ \phi & bank\ angle \end{array}\right],\quad z(t)= \left[\begin{array}{ll} \phi & bank\ angle\\ \beta & sideslip\ angle \end{array}\right]\\ C_M=\left[\begin{array}{rrrrr} 0 & 1 & 0 & 0 & -1\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 1 & 0\\ 1 & 0 & 0 & 0 & 0 \end{array}\right],\quad C=\left[\begin{array}{rrrrr} 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a47cabffa6576dc1b9f48be4914a76a7_l3.png)

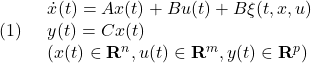
![Rendered by QuickLaTeX.com \displaystyle{(18.1^*)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x'''_1(t)\\ \dot x'''_2(t) \end{array}\right] }_{\dot{x}'''(t)} = \underbrace{ \left[\begin{array}{ccc|c} A_{11}^o & A_{12}^o & A_{121}^m & A_{121}\\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m & A_{1221}\\ 0_{p-m\times r} & A_{21}^o & A_{22}^m & A_{1222}\\\hline A_{2120} & A_{2121} & A_{2122} & A_{22} \end{array}\right] }_{(T_aT_bT_c)A(T_aT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)}\\ + \underbrace{ \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline B_2 \end{array}\right] }_ {(T_aT_bT_c)B} \underbrace{(u(t)+\xi(t,x,u))}_{u'(t)}\\ (A_{11}^o\in{\rm\bf R}^{r\times r},A_{22}^o\in{\rm\bf R}^{n-p-r\times n-p-r},A_{22}^m\in{\rm\bf R}^{p-m\times p-m},A_{22}\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-712c9ee206bbfdfc0320ee7fb2c01281_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18.2^*)\quad \begin{array}{l} y(t) = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] }_{C(T_aT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c2d502c3e8c7b30de092731cc5418e3d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2')\quad \begin{array}{l} \dot{x}_c(t)=Hx_c(t)+Dy(t)\\ =Hx_c(t)+ \left[\begin{array}{cc} 0_{p\times n-p} & DT \\ \end{array}\right] %\underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] %}_{x'''(t)} \\ =Hx_c(t)+ \left[\begin{array}{cc} D_1C_1 & D_2 \\ \end{array}\right] %\underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] %}_{x'''(t)} \\ =Hx_c(t)+D_1C_1x'''_1(t)+D_2x'''_2(t)\\ (DT=\left[\begin{array}{cc} D_1 & D_2 \end{array}\right], D_1\in{\rm\bf R}^{m\times p-m}, D_2\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9c519f23b2642a1398b44d297648888d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3')\quad \begin{array}{l} s(t)=F_cx_c(t)+Fy(t)\\ =Hx_c(t)+ \left[\begin{array}{cc} 0_{p\times n-p} & FT \\ \end{array}\right] %\underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] %}_{x'''(t)} \\ =Hx_c(t)+ \left[\begin{array}{cc} F_1C_1 & F_2 \\ \end{array}\right] %\underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] %}_{x'''(t)} \\ =Hx_c(t)+F_1C_1x'''_1(t)+F_2x'''_2(t)\\ (FT=\left[\begin{array}{cc} F_1 & F_2 \end{array}\right], F_1\in{\rm\bf R}^{m\times p-m}, F_2\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c3a63f48d662d8ce45ee20bfb786b893_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x'''_1(t)\\\hline \dot x'''_2(t)\\\hline\hline \dot x_c(t) \end{array}\right] }_{\dot{x}'''(t)} = \left[\begin{array}{c|c||c} \left.\begin{array}{ccc} A_{11}^o & A_{12}^o & A_{121}^m \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m \\ \end{array}\right.& \left.\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222} \end{array}\right.& \left.\begin{array}{cc} 0_{r\times q} \\ 0_{n-p-r\times q} \\ 0_{p-m\times q} \end{array}\right. \\\hline \left.\begin{array}{ccc} A_{211} & A_{2121} &A_{2122} \end{array}\right.& \left.\begin{array}{cc} A_{22} \end{array}\right.& 0_{m\times q} \\\hline\hline %D_1C_1 \left.\begin{array}{cc} 0_{q\times r} & D_1\tilde{C}_1 \end{array}\right. & D_2 & H \end{array}\right]\\ \times \underbrace{ \left[\begin{array}{c} x'''_1(t)\\\hline x'''_2(t)\\\hline\hline x_c(t) \end{array}\right] }_{x'''(t)} + \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline B_2\\\hline\hline 0_{q\times m} \end{array}\right] u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1968121e3a5d1a000f172ea9ce55a016_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x'''_1(t)\\\hline \dot x_c(t)\\\hline\hline \dot x'''_2(t) \end{array}\right] }_{\dot{x}'''(t)} = \left[\begin{array}{c|c||c} \left.\begin{array}{ccc} A_{11}^o & A_{12}^o & A_{121}^m \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m \\ \end{array}\right.& \left.\begin{array}{cc} 0_{r\times q} \\ 0_{n-p-r\times q} \\ 0_{p-m\times q} \end{array}\right. & \left.\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222} \end{array}\right. \\\hline %D_1C_1 \left.\begin{array}{ccc} 0_{q\times r} & D_1\tilde{C}_1 \end{array}\right. & \left.\begin{array}{cc} H \end{array}\right. & D_2 \\\hline\hline \left.\begin{array}{ccc} A_{211} & A_{2121} &A_{2122} \end{array}\right. & 0_{m\times q} & A_{22} \end{array}\right]\\ \times \underbrace{ \left[\begin{array}{c} x'''_1(t)\\\hline x_c(t)\\\hline\hline x'''_2(t) \end{array}\right] }_{x'''(t)} + \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline 0_{q\times m}\\\hline\hline B_2\\ \end{array}\right] u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-954b2e74e37e5828afcfbe39a920d5cb_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\\hline x_c(t)\\\hline\hline x''''_2(t)\\ \end{array}\right] }_{x''''(t)} = \underbrace{ \left[\begin{array}{ccc|c||c} I_{r} & 0 & 0 & 0& 0 \\ 0 & I_{n-p-r} & 0 & 0& 0 \\ 0 & 0 & I_{p-m} & 0 & 0\\\hline 0 & 0 & 0 & I_q &0 \\\hline\hline 0 & 0 & K & K_c & I_m \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\\hline x_c(t)\\\hline\hline x'''_2(t)\\ \end{array}\right] }_{x'''(t)}\\ (K=F_2^{-1}F_1, K_c=F_2^{-1}F_c) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bb2718c0970f9bbdf8747a901f89c9ab_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x'''_r(t)\\ \dot x'''_{11}(t)\\ \dot x'''_{12}(t)\\\hline \dot x_c(t)\\\hline \dot x''''_2(t) \end{array}\right] }_{\dot{x}''''(t)} = \left[\begin{array}{c|c} \left[\begin{array}{c|c} \left.\begin{array}{ccc} A_{11}^o & A_{12}^o & A_{121}^m \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m \\ \end{array}\right. & \left.\begin{array}{cc} 0_{r\times q} \\ 0_{n-p-r\times q} \\ 0_{p-m\times q} \end{array}\right. \\\hline %D_1C_1 \left.\begin{array}{cc} 0_{q\times r} & D_1\tilde{C}_1 \end{array}\right. & H \end{array}\right]\\ - \left[\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222}\\\hline D_2 \end{array}\right] \left[\begin{array}{ccccc} 0_{m\times r} & K\tilde{C}_1 & K_c \end{array}\right] & \left.\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222}\\\hline D_2 \end{array}\right. \\\hline \left.\begin{array}{ccc|c} A_{211} & A_{2121} &A_{2122} & 0_{m\times q} \end{array}\right. & A_{22} \end{array}\right]\\ \times \underbrace{ \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\\hline x_c(t)\\\hline x''''_2(t)\\ \end{array}\right] }_{x''''(t)} + \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline 0_{q\times m}\\\hline B_2 \end{array}\right] u'(t)\\ = \underbrace{ \left[\begin{array}{c|c} \left.\begin{array}{c|c} \left.\begin{array}{ccc} A_{11}^o & A_{12}^o & A_{121}^m-A_{121}K \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m-A_{1221}K \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m-A_{1222}K \end{array}\right. & \left.\begin{array}{cc} -A_{121}K_c\\ -A_{1221}K_c\\ -A_{1222}K_c\\ \end{array}\right. \\\hline %(D_1-D_2K)C_1 \left.\begin{array}{cc} 0_{q\times r} & D(D_1-D_2K)\tilde{C}_1 \end{array}\right. & H-D_2K_c \end{array}\right. & \left.\begin{array}{cc} A_{121}\\ A_{1221}\\ A_{1222}\\\hline D_2 \end{array}\right.\\\hline \left.\begin{array}{ccc|c} A_{211} & A_{2121} &A_{2122} & 0_{m\times q} \end{array}\right. & A_{22} \end{array}\right] }_{ \left[\begin{array}{cc} \tilde{\cal A}_{11} & \tilde{\cal A}_{12} \\ \tilde{\cal A}_{21} & \tilde{\cal A}_{22} \end{array}\right]} \\ \times \underbrace{ \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\\hline x_c(t)\\\hline x''''_2(t)\\ \end{array}\right] }_{x''''(t)} + \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline 0_{q\times m}\\\hline B_2 \end{array}\right] u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1a787fcbba242095e1c00febe98dcfe6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \left[\begin{array}{c} \dot x'''_{11}(t)\\ \dot x'''_{12}(t) \end{array}\right]= \underbrace{ \left[\begin{array}{cc} A_{22}^o & A_{122}^m \\ A_{21}^o & A_{22}^m \\ \end{array}\right] }_{\tilde{A}_{11}} \left[\begin{array}{c} x'''_{11}(t)\\ x'''_{12}(t) \end{array}\right] + \underbrace{ \left[\begin{array}{cc} A_{1221} \\ A_{1222} \\ \end{array}\right] }_{A_{122}} \underbrace{x'''_{2}(t)}_{\tilde u(t)} \\ \underbrace{x'''_{12}(t)}_{\tilde y(t)} = \underbrace{ \left[\begin{array}{cc} 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right] }_{\tilde{C}_1}} \left[\begin{array}{c} x'''_{11}(t)\\ x'''_{12}(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0a20a7d2962db1ada4badc2bf0778a94_l3.png)
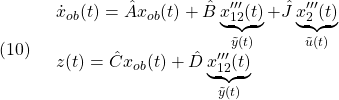
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad x_{ob}(t)\rightarrow \underbrace{ \left[\begin{array}{cc} I_{n-p-r} & -L^o \end{array}\right] }_{U} \left[\begin{array}{c} x'''_{11}(t)\\ x'''_{12}(t) \end{array}\right]= x'''_{11}(t)-L^ox'''_{12}(t) \quad(t\rightarrow\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7c76952731eb4799d0b3b24379431e11_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \begin{array}{l} \left[\begin{array}{cc} \hat{A} & \hat{B}\\ \hat{C} & \hat{D} \end{array}\right] = \left[\begin{array}{c} U\tilde{A}_{11}\\ \left[\begin{array}{cc} {K}_1 & {K}_2 \end{array}\right] \end{array}\right] \left[\begin{array}{c} U\\ \tilde{C}_1 \end{array}\right]^{-1}\\ = \left[\begin{array}{c} \left[\begin{array}{cc} I_{n-p-r} & L^o \end{array}\right] \left[\begin{array}{cc} A_{22}^o & A_{122}^m \\ A_{21}^o & A_{22}^m \\ \end{array}\right]\\ \left[\begin{array}{cc} {K}_1 & {K}_2 \end{array}\right] \end{array}\right] \left[\begin{array}{cc} I_{n-p-r} & L^o\\ 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right]^{-1}\\ = \left[\begin{array}{cc} A_{22}^o+L^oA_{21}^o & A_{122}^m+L^oA_{22}^m \\ {K}_1 & {K}_2 \end{array}\right] \left[\begin{array}{cc} I_{n-p-r} & -L^o\\ 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right]\\ = \left[\begin{array}{cc} A_{22}^o+L^oA_{21}^o & A_{122}^m+L^oA_{22}^m-(A_{22}^o+L^oA_{21}^o)L^o \\ K_1 & K_2-K_1L^o \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0096b16ad8048d3787bdad7b1de35d39_l3.png)
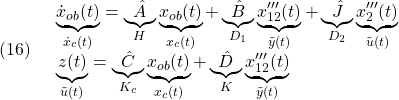
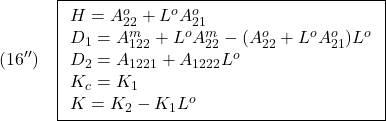
![Rendered by QuickLaTeX.com \displaystyle{(17.1)\quad \begin{array}{l} \left[\begin{array}{c} \dot x'''_r(t)\\ \dot x'''_{11}(t)\\ \dot x'''_{12}(t)\\ \dot x'''_2(t) \end{array}\right]= \left[\begin{array}{ccccc} A_{11}^o & A_{12}^o & A_{121}^m & A_{121} \\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m & A_{1221} \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m & A_{1222} \\ A_{211} & A_{212} & A_{213} & A_{22} \end{array}\right] \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right]\\ + \left[\begin{array}{c} 0_{r\times m}\\ 0_{n-p-r\times m}\\ 0_{p-m\times m}\\ B_2\\ \end{array}\right] u(t)\\ (x'''_r(t)\in{\rm\bf R}^{r},x'''_{11}(t)\in{\rm\bf R}^{n-p-r},x'''_{12}(t)\in{\rm\bf R}^{p-m},x'''_{2}(t)\in{\rm\bf R}^{m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3e5a41c43ebb7a8d519dbce79ce8e0a3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17.2)\quad \begin{array}{l} y(t) = \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] \left[\begin{array}{c} x'''_r(t)\\ x'''_{11}(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right]=T \left[\begin{array}{c} x'''_{12}(t)\\ x'''_2(t) \end{array}\right] \quad(T\in{\rm\bf R}^{p\times p}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-354531fad73a9f4ed2fb9035460b7345_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(19.1)\quad \underbrace{ \left[\begin{array}{c} \dot z_r(t)\\ \dot x_c(t)\\ \dot x'''_{12}(t)\\ \dot x'''_2(t) \end{array}\right] }_{\hat x(t)} = \underbrace{ \left[\begin{array}{ccccc} A_{11}^o & A_{12}^o & A_{121}^m-A_{12}^oL^o & A_{121} \\ 0_{q\times r} & H & D_1 & D_2 \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m-A_{21}^oL^o & A_{1222} \\ A_{211} & A_{212} & A_{213}-A_{212}L^o & A_{22} \end{array}\right] }_{\hat A} \underbrace{ \left[\begin{array}{c} z_r(t)\\ x_c(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right] }_{\hat x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-661ada8558710f28b5c81d3d52ca8358_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ + \underbrace{ \left[\begin{array}{ccccc} 0_{r\times r} & 0_{r\times m} \\ 0_{q\times r} & 0_{q\times m} \\ 0_{p-m\times r} & A_{21}^o \\ A_{211} & A_{212} \end{array}\right] }_{\hat A_e} \underbrace{ \left[\begin{array}{c} e_r(t)\\ e_c(t) \end{array}\right] }_{\hat{e}(t)} + \underbrace{ \left[\begin{array}{c} 0_{r\times m}\\ 0_{q\times m}\\ 0_{p-m\times m}\\ B_2\\ \end{array}\right] }_{\hat B} u(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-35bbf3c7686c6043f5322df182777814_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(19.2)\quad \underbrace{ \left[\begin{array}{c} \dot e_r(t)\\ \dot e_c(t) \end{array}\right] }_{\dot{\hat{e}}(t)} = \underbrace{ \left[\begin{array}{cc} A_{11}^o & A_{12}^o \\ 0 & H \end{array}\right] }_{\hat{H}} \underbrace{ \left[\begin{array}{c} e_r(t)\\ e_c(t) \end{array}\right] }_{\hat{e}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eb43be95adf89038069e028493af823f_l3.png)
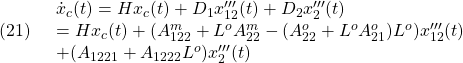
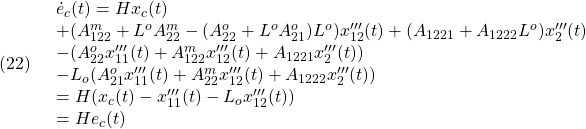
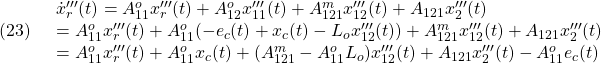
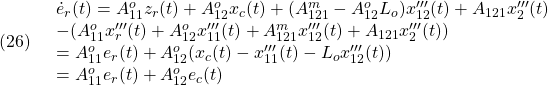
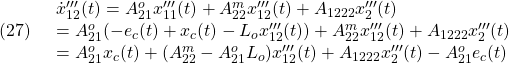
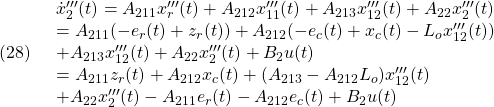
![Rendered by QuickLaTeX.com \displaystyle{(3'')\quad \begin{array}{l} s(t)=Hx_c(t)+F_1C_1x'''_1(t)+F_2x'''_2(t)\\ =\boxed{\underbrace{F_2\left[\begin{array}{cccc} 0_{m\times r} & K_c & K & I_m \end{array}\right]}_{S}} \underbrace{ \left[\begin{array}{c} z_r(t)\\ x_c(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right] }_{\hat x(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b40bb61a14d162099a8c5deefe1bb6ce_l3.png)
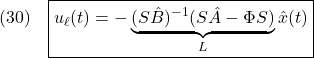
![Rendered by QuickLaTeX.com \displaystyle{(32)\quad \boxed{\begin{array}{l} \left[\begin{array}{c} \dot z_r(t)\\ \dot x_c(t) \end{array}\right] = \underbrace{ \left[\begin{array}{ccccc} A_{11}^o & A_{12}^o \\ 0_{q\times r} & H \end{array}\right] }_{\hat H} \left[\begin{array}{c} z_r(t)\\ x_c(t) \end{array}\right] + \underbrace{ \left[\begin{array}{ccccc} A_{121}^m-A_{12}^oL^o & A_{121} \\ D_1 & D_2 \end{array}\right]T' }_{\hat D} y(t)\\ \underbrace{ \left[\begin{array}{c} z_r(t)\\ x_c(t)\\ x'''_{12}(t)\\ x'''_2(t) \end{array}\right] }_{\hat x(t)}= \underbrace{ \left[\begin{array}{ccccc} I_r & 0_{r\times q}\\ 0_{q\times r} & I_q\\ 0_{p-m\times r} & 0_{p-m\times q} \\ 0_{m\times r} & 0_{m\times q} \\ \end{array}\right]}_{\widehat{\cal C}} \left[\begin{array}{c} z_r(t)\\ x_c(t) \end{array}\right] + \underbrace{\left[\begin{array}{ccccc} 0_{r\times p-m} & 0_{r\times m} \\ 0_{q\times p-m} & 0_{q\times m} \\ I_{p-m} & 0_{p-m\times m}\\ 0_{m\times p-m} & I_m \end{array}\right]T' }_{\widehat{\cal D}} y(t) \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-87e3ff7ce930f9ed16d07870318d8f43_l3.png)
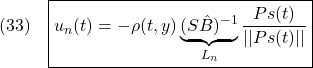

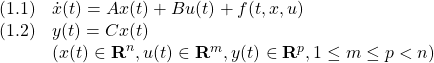
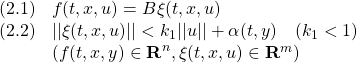
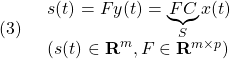
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} = \underbrace{ \left[\begin{array}{cc} N_c^T \\ C \\ \end{array}\right] }_{T_c} x(t) \Leftrightarrow x(t)= \underbrace{ \left[\begin{array}{cc} N_c^T \\ C \\ \end{array}\right]^{-1} }_{T_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ece730e4769618b1a1b4da039d7b9673_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5.1)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{cc} A_{c11} & A_{c12} \\ A_{c21} & A_{c22} \\ \end{array}\right] }_{T_cAT_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} + \underbrace{ \left[\begin{array}{c} B_{c1}\\ B_{c2} \end{array}\right] }_{T_cB} \underbrace{(u(t)+\xi(t,x,u))}_{u'(t)}\\ (B_{c2}\in{\rm\bf R}^{p\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-82e2bbb3826132d675e28645b6cdaee1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5.2)\quad y(t) = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & I_p \\ \end{array}\right] }_{CT_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a7a9e6b215ba844d91319c8cb51519fd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5.3)\quad s(t)= \underbrace{ \left[\begin{array}{cc} 0_{m\times n-p} & F \\ \end{array}\right] }_{FCT_c^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-81ca3ce18892566a004196f3e47aebc4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x''_1(t)\\ x''_2(t)\\ \end{array}\right] }_{x''(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-p} & -B_{c1}(B_{c2}^TB_{c2})^{-1}B_{c2}^T \\ 0_{p\times n-p} & T^T \end{array}\right] }_{T_b} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)}= \underbrace{ \left[\begin{array}{cc} I_{n-p} & B_{c1}(B_{c2}^TB_{c2})^{-1}B_{c2}^T \\ 0_{p\times n-p} & T \end{array}\right] }_{T_b^{-1}} \underbrace{ \left[\begin{array}{c} x''_1(t)\\ x''_2(t)\\ \end{array}\right] }_{x''(t)}\\ (x''_1(t)\in{\rm\bf R}^{n-p},x''_2(t)\in{\rm\bf R}^{p},T\in{\rm\bf R}^{p\times p}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f1c87f8de33e3f31e6f9bffbf4539320_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.1)\quad \underbrace{ \left[\begin{array}{c} \dot x''_1(t)\\ \dot x''_2(t) \end{array}\right] }_{\dot{x}''(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \end{array}\right] }_{(T_bT_c)A(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x''_1(t)\\ x''_2(t)\\ \end{array}\right] }_{x''(t)} + \underbrace{ \left[\begin{array}{c} 0_{n-p\times m}\\ B_2 \end{array}\right] }_ {(T_bT_c)B} u'(t)\\ }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fd900c29bf5651b6ba66e54daeac82a4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.2)\quad y(t) = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] }_{C(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x''_1(t)\\ x''_2(t)\\ \end{array}\right] }_{x''(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fb92fb33c1ef65dd6f2d56305d8605c5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8.3)\quad \begin{array}{l} s(t)= \underbrace{ \left[\begin{array}{cc} 0_{m\times n-p} & FT \\ \end{array}\right] }_{FC(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x''_1(t)\\ x''_2(t)\\ \end{array}\right] }_{x''(t)} = \underbrace{ \left[\begin{array}{cc|c} 0_{m\times n-p} & F_1 & F_2 \\ \end{array}\right] }_{FC(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x''_1(t)\\ x''_2(t)\\ \end{array}\right] }_{x''(t)}\\ (FT=\left[\begin{array}{cc} F_1 & F_2 \end{array}\right], F_1\in{\rm\bf R}^{m\times p-m}, F_2\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-30c6c57fc79840cb7ba8a7963f16d627_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \tilde{x}''_1(t)\\ s(t) \end{array}\right] }_{\tilde{x}''(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ F_1C' & F_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} \tilde{x}''_1(t)\\ \tilde{x}''_2(t) \end{array}\right] }_{x''(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} \tilde{x}''_1(t)\\ \tilde{x}''_2(t) \end{array}\right] }_{x''(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -F_2^{-1}F_1C' & F_2^{-1} \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} \tilde{x}''_1(t)\\ s(t) \end{array}\right] }_{\tilde{x}''(t)}\\ (C'=\left[\begin{array}{cc} 0_{p-m\times n-p} & I_{p-m} \end{array}\right]) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-28d720f19c00491b7c997c513bad202b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \underbrace{ \left[\begin{array}{c} \dot{\tilde{x}}''_1(t)\\ \dot{s}(t) \end{array}\right] }_{\dot{\tilde{x}}''(t)} = \underbrace{ \left[\begin{array}{cc} \tilde{A}_{11} & \tilde{A}_{12} \\ \tilde{A}_{21} & \tilde{A}_{22} \end{array}\right] }_{\tilde{A}=(T_sT_bT_c)A(T_sT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} \tilde{x}''_1(t)\\ s(t) \end{array}\right] }_{\tilde{x}''(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \tilde{B}_2 \end{array}\right] }_{\tilde{B}=T_sT_bT_cB} u'(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-53712b6be774e1fea90c24f848d74bac_l3.png)
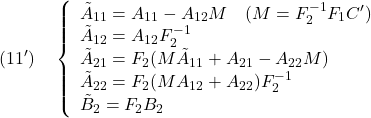
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \boxed{\tilde{A}_{11}=\underbrace{A_{11}}_{A'}-\underbrace{A_{12}}_{B'} \underbrace{F_2^{-1}F_1}_{K} \underbrace{\left[\begin{array}{cc} 0_{p-m\times n-p} & I_{p-m} \end{array}\right]}_{C'}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-507598a1b9847b9116034c01e1dba046_l3.png)
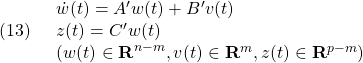
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \begin{array}{l} {\rm rank} \left[\begin{array}{cc} sI-A & B \end{array}\right]& ={\rm rank} \left[\begin{array}{cc} sI-(T_bT_c)A(T_bT_c)^{-1} & (T_bT_c)B \end{array}\right]\\ ={\rm rank} \left[\begin{array}{ccc} sI-A_{11} & -A_{12} & 0\\ -A_{21} & sI-A_{22} & B_2 \end{array}\right]\\ ={\rm rank} \left[\begin{array}{cc} sI-A_{11} & -A_{12} \end{array}\right]+m\\ ={\rm rank} \left[\begin{array}{cc} sI-A' & B' \end{array}\right]+m \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f0050e4228d42171173c44e1ab9f4b5b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \begin{array}{l} {\rm rank} \left[\begin{array}{c} sI-A' \\ C' \end{array}\right]\\ ={\rm rank} \left[\begin{array}{cc} sI-A_{1111} & -A_{1112} \\ -A_{1121} & sI-A_{1122} \\ 0 & I_{p-m} \end{array}\right]\ (A'=A_{11}= \left[\begin{array}{cc} A_{1111} & A_{1112} \\ A_{1121} & A_{1122} \end{array}\right])\\ ={\rm rank} \left[\begin{array}{c} sI-A_{1111} \\ A_{1121} \end{array}\right]+p-m\\ ={\rm rank} \left[\begin{array}{c} sI-T_{obs}A_{1111}T_{obs}^{-1} \\ A_{1121} T_{obs}^{-1} \end{array}\right]+p-m\\ (T_{obs}A_{1111}T_{obs}^{-1}= \left[\begin{array}{cc} A_{11}^o & A_{12}^o \\ 0_{n-p-r\times r} & A_{22}^o \end{array}\right], A_{1121} T_{obs}^{-1}= \left[\begin{array}{cc} 0_{p-m\times r} & A_{21}^o \end{array}\right] )\\ ={\rm rank} \left[\begin{array}{cc} sI-A_{11}^o & -A_{12}^o \\ 0_{n-p-r\times r} & sI-A_{22}^o\\ 0_{p-m\times r} & A_{21}^o \end{array}\right]+p-m\\ ={\rm rank}(sI-A_{11}^o)+ \underbrace{{\rm rank}\left[\begin{array}{cc} sI-A_{22}^o\\ A_{21}^o \end{array}\right]}_{n-p-r}+p-m \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-678a84f544a8ee5f97c48b3ee005d9e0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)} = \underbrace{ \left[\begin{array}{cc|c} T_{obs} & 0 & 0\\ 0 & I_{p-m} & 0 \\\hline 0 & 0 & I_m \end{array}\right] }_{T_a} \underbrace{ \left[\begin{array}{c} {x}''_1(t)\\ {x}''_2(t) \end{array}\right] }_{x''(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} {x}''_1(t)\\ {x}''_2(t) \end{array}\right] }_{x''(t)}= \underbrace{ \left[\begin{array}{cc|c} T_{obs}^{-1} & 0 & 0\\ 0 & I_{p-m} & 0 \\\hline 0 & 0 & I_m \end{array}\right] }_{T_a^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)}\\ (x'''_1(t)\in{\rm\bf R}^{n-m},x'''_2(t)\in{\rm\bf R}^{m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a761762bcf2a930d49f44e4cde5722c7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18.1)\quad \boxed{\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x'''_1(t)\\ \dot x'''_2(t) \end{array}\right] }_{\dot{x}'''(t)} = \underbrace{ \left[\begin{array}{ccc|c} A_{11}^o & A_{12}^o & A_{121}^m & A_{121}\\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m & A_{1221}\\ 0_{p-m\times r} & A_{21}^o & A_{22}^m & A_{1222}\\\hline A_{2120} & A_{2121} & A_{2122} & A_{22} \end{array}\right] }_{(T_aT_bT_c)A(T_aT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)}\\ + \underbrace{ \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\\hline B_2 \end{array}\right] }_ {(T_aT_bT_c)B} u(t)\\ (A_{11}^o\in{\rm\bf R}^{r\times r},A_{22}^o\in{\rm\bf R}^{n-p-r\times n-p-r},A_{22}^m\in{\rm\bf R}^{p-m\times p-m}) \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2f4457165fe43f529be7658c079b9eff_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18.2)\quad \boxed{\begin{array}{l} y(t) = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] }_{C(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{cc|c} T_{obs}^{-1} & 0 & 0\\ 0 & I_{p-m} & 0 \\\hline 0 & 0 & I_m \end{array}\right] }_{T_a^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)}\\ = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] }_{C(T_aT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} x'''_1(t)\\ x'''_2(t) \end{array}\right] }_{x'''(t)} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-05f9d91daa89c529f7c3464c13c2fd69_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12')\quad \begin{array}{l} T_{a'}\tilde{A}_{11}T_{a'}^{-1}=T_{a'}(A'-B'KC')T_{a'}^{-1} \quad (T_{a'}= \left[\begin{array}{cc} T_{obs} & 0 \\ 0 & I_{p-m} \end{array}\right])\\ =T_{a'}A_{11}T_{a'}^{-1}-T_{a'}A_{12} K \left[\begin{array}{ccc} 0_{p-m\times r} & 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right]T_{a'}^{-1}\\ = \underbrace{ \left[\begin{array}{c|cc} A_{11}^o & A_{12}^o & A_{121}^m \\\hline 0_{n-p-r\times r} & A_{22}^o & A_{122}^m \\ 0_{p-m\times r} & A_{21}^o & A_{22}^m \end{array}\right]}_{T_{a'}A_{11}T_{a'}^{-1}} -\underbrace{\left[\begin{array}{ccc} A_{121}\\\hline A_{1221}\\ A_{1222} \end{array}\right]}_{T_{a'}A_{12}} \left[\begin{array}{ccc} 0_{p-m\times r} & 0_{p-m\times n-p-r} & K \end{array}\right]\\ = \left[\begin{array}{c|c} A_{11}^o & \left[\begin{array}{cc} A_{12}^o & A_{121}^m-A_{121}K \end{array}\right]\\\hline 0_{n-m-r\times r} & \left[\begin{array}{cc} A_{22}^o & A_{122}^m \\ A_{21}^o & A_{22}^m \end{array}\right] -\left[\begin{array}{c} A_{1221}\\ A_{1222} \end{array}\right] K\left[\begin{array}{cc} 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right] \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-63e4b25f1d738158680736e0e7e80f59_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(19)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} A_{22}^o & A_{122}^m \\ A_{21}^o & A_{22}^m \end{array}\right]}_{A''} - \underbrace{\left[\begin{array}{c} A_{1221}\\ A_{1222} \end{array}\right]}_{B''} K \underbrace{\left[\begin{array}{cc} 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right]}_{C''}\\ (A''\in{\rm\bf R}^{n-m-r\times n-m-r}, B''\in{\rm\bf R}^{n-m-r\times m}, C''\in{\rm\bf R}^{p-m\times n-m-r})\\ =\underbrace{\left[\begin{array}{cc} A_{22}^o & A_{122}^m \\ A_{21}^o & A_{22}^m \end{array}\right]}_{A''} - \underbrace{\left[\begin{array}{cc} B''_1 & 0_{n-m-r\times m-m'} \end{array}\right]}_{B''T_m} \underbrace{\left[\begin{array}{cc} K_1\\ K_2 \end{array}\right]}_{T_m^{-1}K} \underbrace{\left[\begin{array}{cc} 0_{p-m\times n-p-r} & I_{p-m} \end{array}\right]}_{C''}\\ (T_m\in{\rm\bf R}^{m\times m}, B''_1\in{\rm\bf R}^{n-m-r\times m'}, K_1\in{\rm\bf R}^{m'\times p-m}, K_2\in{\rm\bf R}^{m-m'\times p-m})\\ =A''-B''_1K_1C'' \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f8caf2174f6b6ea2e5a122d260b19c35_l3.png)
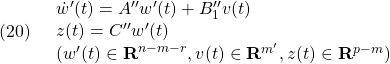
![Rendered by QuickLaTeX.com \displaystyle{(26)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ KC' & I_m \\ \end{array}\right] }_{\bar{T}_s} \underbrace{ \left[\begin{array}{c} {x}''_1(t)\\ {x}''_2(t) \end{array}\right] }_{x''(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} {x}''_1(t)\\ {x}''_2(t) \end{array}\right] }_{x''(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -KC' & I_m \end{array}\right] }_{\bar{T}_s^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)}\\ (C'=\left[\begin{array}{cc} 0_{p-m\times n-p} & I_{p-m} \end{array}\right]) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a09e0069834751decee9881760ac9db6_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(27)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -KC' & I_m \end{array}\right] }_{\bar{T}_s^{-1}} \underbrace{ \left[\begin{array}{c} \dot{\bar{x}}''_1(t)\\ \dot{\bar{s}}(t) \end{array}\right] }_{\dot{\bar{x}}''(t)}\\ = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{(T_bT_c)A(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -KC' & I_m \end{array}\right] }_{\bar{T}_s^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{(T_bT_c)B} u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3b965cc92b91df561d39464b2a06eb0e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(28)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\bar{x}}''_1(t)\\ \dot{\bar{s}}(t) \end{array}\right] }_{\dot{\bar{x}}''(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ KC' & I_m \end{array}\right] }_{\bar{T}_s} \underbrace{ \left[\begin{array}{cc} A_{11}-A_{12}KC' & A_{12} \\ A_{21}-A_{22}KC' & A_{22} \end{array}\right] }_{(T_bT_c)A(\bar{T}_sT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)}\\ + \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ KC' & I_m \end{array}\right] }_{\bar{T}_s} \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3841b7fe89f905ef50150e9e6e841918_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(29.1)\quad \underbrace{ \left[\begin{array}{c} \dot{\bar{x}}''_1(t)\\ \dot{\bar{s}}(t) \end{array}\right] }_{\dot{\bar{x}}''(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22} \end{array}\right] }_{\bar{A}=(\bar{T}_sT_bT_c)A(\bar{T}_sT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \bar{B}_2 \end{array}\right] }_{\bar{B}=\bar{T}_sT_bT_cB} u'(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-22de0f3334d3536835a81c4149a15f5a_l3.png)
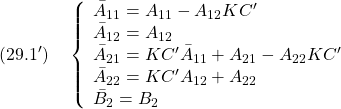
![Rendered by QuickLaTeX.com \displaystyle{(29.2)\quad \begin{array}{l} y(t) = \underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] }_{C(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -KC' & I_m \end{array}\right] }_{\bar{T}_s^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)}\\ = \underbrace{ \left[\begin{array}{cc} -TKC' & T \end{array}\right] }_{C(\bar{T}_sT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c45457f5b0c70ff7a60918110f867286_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(29.3)\quad \begin{array}{l} s(t)= \underbrace{ \left[\begin{array}{cc} 0_{m\times n-p} & FT \\ \end{array}\right] }_{FC(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -KC' & I_m \end{array}\right] }_{\bar{T}_s^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)}\\ = \underbrace{ \left[\begin{array}{cc|c} 0_{m\times n-p} & F_1 & F_2 \\ \end{array}\right] }_{FC(T_bT_c)^{-1}} \underbrace{ \left[\begin{array}{cc|c} I_{n-p}& 0 & 0\\ 0 & I_{p-m} & 0 \\\hline 0 & -K & I_m \end{array}\right] }_{\bar{T}_s^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)}\\ = \underbrace{ \left[\begin{array}{cc|c} 0_{m\times n-p} & 0_{m\times p-m} & F_2 \\ \end{array}\right] }_{FC(\bar{T}_sT_bT_c)^{-1}} \underbrace{ \left[\begin{array}{c} \bar{x}''_1(t)\\ \bar{s}(t) \end{array}\right] }_{\bar{x}''(t)}\\ (FT=\left[\begin{array}{cc} F_1 & F_2 \end{array}\right], F_1\in{\rm\bf R}^{m\times p-m}, F_2\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5ebe1bc0632a1704e6bdd06aca89f8c8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad \underbrace{ \left[\begin{array}{cc} 0 & \bar{B}_2^T \end{array}\right] }_{\bar{B}^T} \underbrace{ \left[\begin{array}{cc} P_1 & 0 \\ 0 & P_2 \end{array}\right] }_{P} =F \underbrace{ \left[\begin{array}{cc} -TKC' & T \end{array}\right] }_{\bar{C}}\\ \Rightarrow \bar{B}_2^TP_2=F_2 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-82f76df99883e6d0a1965e87719801b1_l3.png)

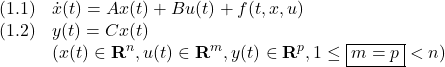
![Rendered by QuickLaTeX.com \displaystyle{(4.1)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} \underbrace{(u(t)+\xi(t,x,u))}_{u'(t)}\\ (x_1(t)\in{\rm\bf R}^{n-m}, x_2(t)\in{\rm\bf R}^m, B_2\in{\rm\bf R}^{m\times m}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9d9eabcd36c3ce62bf09a0d32ce9ea07_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4.2)\quad y(t)= \underbrace{ \left[\begin{array}{cc} C_{1} & C_{2} \\ \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)}\quad (y(t)\in{\rm\bf R}^m, C_2\in{\rm\bf R}^{m\times m}) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6b6bf798fce1fca1e7b12540a2a4e9a3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad s(t)=Fy(t)=F \underbrace{ \left[\begin{array}{cc} C_{1} & C_{2} \\ \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} =\underbrace{ \left[\begin{array}{cc} FC_{1} & FC_{2} \\ \end{array}\right] }_{S=FC} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a3e37089e535379edc227db046808e5a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ C_1 & C_2 \\ \end{array}\right] }_{T_y} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m}& 0 \\ -C_2^{-1}C_1 & C_2^{-1} \end{array}\right] }_{T_y^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-36294dfd18793309878ccd0d8385bbb5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ -M & C_2^{-1} \\ \end{array}\right] }_{T_y^{-1}} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{\bar{x}}(t)}\\ = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ -M & C_2^{-1} \\ \end{array}\right] }_{T_y^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-09b99785d09eb2ea3c9cda05273c87f9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{\bar{x}}(t)} = \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ C_1 & C_2 \\ \end{array}\right] }_{T_y} \underbrace{ \left[\begin{array}{cc} A_{11}-A_{12}M & A_{12}C_2^{-1} \\ A_{21}-A_{22}M & A_{22}C_2^{-1} \\ \end{array}\right] }_{AT_y^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)}\\ + \underbrace{ \left[\begin{array}{cc} I_{n-m} & 0 \\ C_1 & C_2 \\ \end{array}\right] }_{T_y} \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u'(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-576672e3c0ab015015806803be5be6e0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \boxed{ %\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{\bar{x}}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22}\\ \end{array}\right] }_{\bar{A}=T_y A T_y^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \bar{B}_2 \end{array}\right] }_{\bar{B}=T_yB} u'(t) %\end{array} }}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-551b974cb60f73d29035528b00414fb6_l3.png)
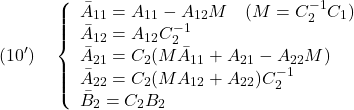
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \boxed{y(t)= \underbrace{ \left[\begin{array}{cc} 0 & I_{m} \\ \end{array}\right] }_{\bar{C}=CT_y^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6d572a784a0d5d01341f3c1a7bf72075_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \boxed{s(t)=Fy(t)= \underbrace{ \left[\begin{array}{cc} 0 & F \\ \end{array}\right] }_{F\bar{C}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{\bar{x}(t)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5b3fac9c95c90b06d76da8172b3c27ba_l3.png)
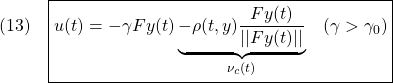
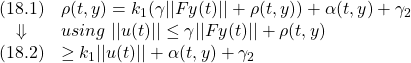
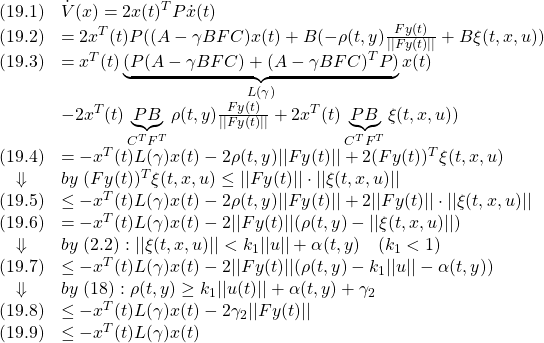
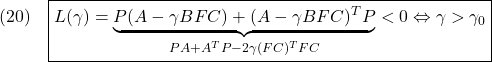
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{cl} (21.1) & L(\gamma)=PA+A^TP-2\gamma (FC)^TFC\\ (21.2) & =\underbrace{\left[ \begin{array}{cc} P_1 & 0 \\ 0 & P_2 \\ \end{array}\right]}_{P} \underbrace{\left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right]}_{A} + \underbrace{\left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right]^T}_{A^T} \underbrace{\left[\begin{array}{cc} P_1 & 0 \\ 0 & P_2 \\ \end{array}\right]}_{P}\\ &-2\gamma \underbrace{\left[\begin{array}{cc} 0 & F \\ \end{array}\right]^T}_{(FC)^T} \underbrace{\left[\begin{array}{cc} 0 & F \\ \end{array}\right]}_{FC}\\ (21.3) & =\left[ \begin{array}{cc} P_1A_{11}+A_{11}^TP_1 & P_1A_{12}+A_{21}^TP_2 \\ (P_1A_{12}+A_{21}^TP_2)^T & P_2A_{22}+A_{22}^TP_2 \\ \end{array}\right] -2\gamma \left[\begin{array}{cc} 0 & 0 \\ 0 & F^TF \\ \end{array}\right]\\ (21.4) & =\left[\begin{array}{cc} P_1A_{11}+A_{11}^TP_1 & P_1A_{12}+A_{21}^TP_2 \\ (P_1A_{12}+A_{21}^TP_2)^T & P_2A_{22}+A_{22}^TP_2-2\gamma F^TF \\ \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d90e2269d72fb880ea00c58c13b87908_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(22)\quad \begin{array}{l} \left[\begin{array}{cc} X & Z \\ Z^T & Y \end{array}\right]<0\\ \ \Leftrightarrow\ X-ZY^{-1}Z^T<0,\ Y<0 \\ \ \Leftrightarrow\ X<0,\ Y-Z^TX^{-1}Z<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5ad5723e74a49a0f86149626e8834da7_l3.png)
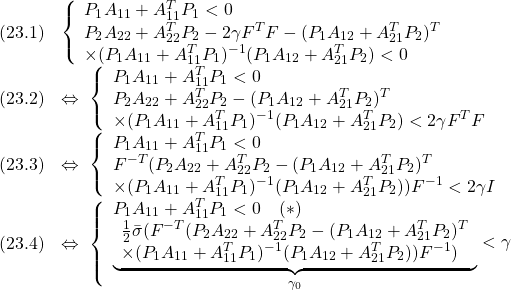
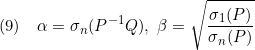
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad %\boxed{ \begin{array}{lll} V(\bar{x})= \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} P_1 & 0\\ 0 & P_2 \end{array}\right] }_{P} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}\\ \Rightarrow \dot{V}(\bar{x})\le - \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} Q_1 & 0\\ 0 & I \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} \end{array}}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a2747656c1f7d9559f971c1a26fd7023_l3.png)
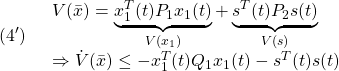



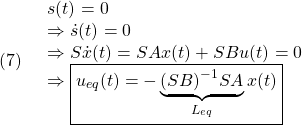
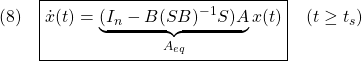
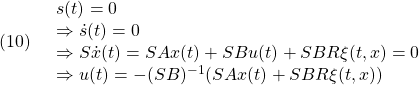
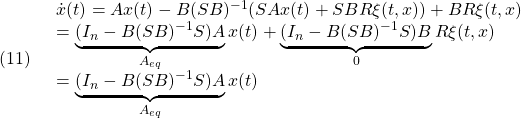
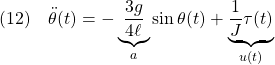


![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \boxed{\underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t) + \underbrace{ \left[\begin{array}{l} f_u(t,x)\\ f_m(t,x,u) \end{array}\right] }_{f(t,x,u)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-492c810b2764797d15e8da449fa86719_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \boxed{s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} \ (M=S_2^{-1}S_1)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f362cf2f2a84558f6ce3b7cbfd623471_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aa3c209c1893a28b597ab444a59fa480_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \boxed{ \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{\bar{x}}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22}\\ \end{array}\right] }_{\bar{A}=T_s A T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \bar{B}_2 \end{array}\right] }_{\bar{B}=T_sB} u(t)\\ + \underbrace{ \left[\begin{array}{c} f_u(t,x)\\ S_1f_u(t,x)+S_2f_m(t,x,u) \end{array}\right] }_{T_sf(t,x,u)} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8d94be87e2ee3e86130661d37570a682_l3.png)
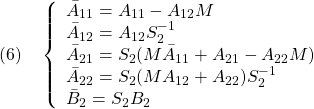
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{cl} & s(t)=0\ \Rightarrow\ \dot{s}(t)=0\\ \Downarrow & by\ (5)\\ &\bar{A}_{21}x_1(t)+\bar{A}_{22}s(t)+\bar{B}_{2}u(t)=0\\ \Downarrow & \\ (7) & u_{eq}(t)=-\underbrace{\bar{B}_{2}^{-1}}_{([0\ I_m]T_sB)^{-1}} \underbrace{\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right]}_{[0\ I_m]T_sAT_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}\\ \Downarrow & by\ S=[0\ I_m]T_s, x=T_s^{-1}\bar{x}\\ (8) & \boxed{u_{eq}(t)=-\underbrace{(SB)^{-1}SA}_{L_\ell}x(t)}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2c000a36a1eddd1e979735e5c504c61b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{cl} (9) & u_{eq}(t)=-\underbrace{\bar{B}_{2}^{-1}}_{([0\ I_m]T_sB)^{-1}} (\underbrace{\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right]}_{[0\ I_m]T_sAT_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}-\Phi s(t))\\ \Downarrow & by\ S=[0\ I_m]T_s, x=T_s^{-1}\bar{x}\\ (10) & \boxed{u_\ell(t)=-\underbrace{(SB)^{-1}(SA-\Phi S)}_{L=L_{eq}+L_{phi}}x(t)}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f3c7ee69a5490d0416e346e8d6a29a04_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{s}(t) \end{array}\right] = \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ 0 & \Phi \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ + \left[\begin{array}{c} f_u(t,x)\\ \bar{B}_{2}u_n(t)+S_2(Mf_u(t,x)+f_m(t,x,u)) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-08b0fd62ceefdfc7673e603a95165c27_l3.png)
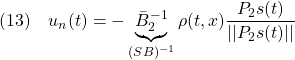
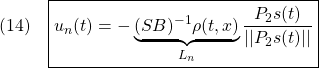
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \boxed{J=\int_0^\infty \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right]^T }_{x^T(t)} \underbrace{ \left[\begin{array}{cc} Q_{11} & Q_{12} \\ Q_{21} & Q_{22} \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} dt} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-13ff85a64857f296223fc5fc4db3a6fc_l3.png)
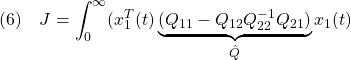
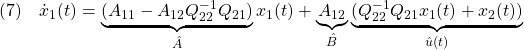
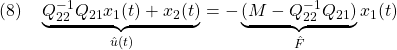
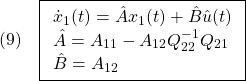
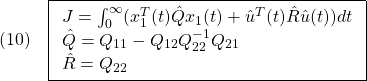
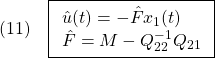

![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} A_{eq}= \underbrace{ \left[\begin{array}{cc} I & 0 \\ -M & 0 \\ \end{array}\right] }_{I_n-B(SB)^{-1}S} \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right]= \left[\begin{array}{cc} A_{11} & A_{12} \\ -MA_{11} & -MA_{12} \\ \end{array}\right]\\ = \left[\begin{array}{cc} I & 0 \\ -M & I \\ \end{array}\right] \left[\begin{array}{cc} \bar{A}_{11} & A_{12} \\ 0 & 0 \\ \end{array}\right] \left[\begin{array}{cc} I & 0 \\ -M & I \\ \end{array}\right]^{-1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2474825aa676243c02182b9e5a87f0f1_l3.png)

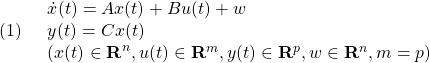
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3c19e131ef7f7e62fb75b0b722359667_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t)\\ (x_1(t)=x(t)-x_\infty, x_2(t)=u(t)-u_\infty) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3651de7cb254ab2cb45e5409ae9cd171_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-841f3fca38a28aec9d1c570b17f6f7ec_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-94c9c19111e524fb6b7adf025beef334_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{x}'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right] }_{T_sA_{E3}T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ S_2 \end{array}\right] }_{T_sB_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-922fcb090845e1f769269f768e72eda3_l3.png)
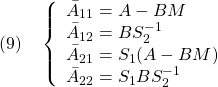
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad {\dot u}_\ell(t)=- \boxed{\underbrace{ (SB_{E3})^{-1}(SA_{E3}-\Phi S)S_E^{-1} }_{\left[\begin{array}{cc} F & F_I \end{array}\right]}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-09bdbdbd69d8bc1d816020ba9b4ba6d8_l3.png)
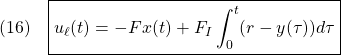
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad {\dot u}_n(t) =-(SB_{E3})^{-1}\rho\, {\rm sgn}( \boxed{\underbrace{ P_2SS_E^{-1} }_{\left[\begin{array}{cc} G & G_I \end{array}\right]}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)}) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-88922723347229f2a9ac74335912e98d_l3.png)
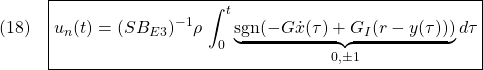

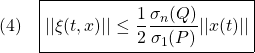
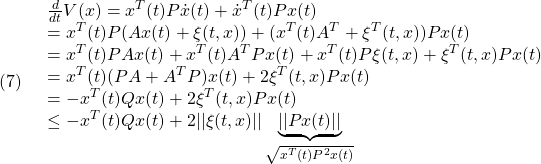
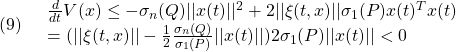
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{\dot{x}_{E1}(t)} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E1}} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ x_I(t)-x_{I\infty} \end{array}\right] }_{x_{E1}(t)} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E1}} (u(t)-u_\infty) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-31c37a9934e5cdea3c7a11d0c5575b8d_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{\dot{x}_{E2}(t)} = \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)} + \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3876d07fd5a0b32e63fa8f91e20b8ad7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \left[\begin{array}{c} {\dot x}(t)-w \\ y(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-28a64d5f6becf5dc458bf65746e1d706_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \left[\begin{array}{c} -w \\ r \end{array}\right] = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} \left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-70b5e47d55a371255ff67868bd470bbe_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d19845bc6a9ba5e6b6ffcc474aa170e5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e12324e6656148ca4b9a647055b6df5a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \underbrace{ \left[\begin{array}{cc} A & 0 \\ C & 0 \end{array}\right] }_{A_{E2}} \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-790b5d3825c0777b3d3285e5fd6b1394_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \underbrace{ \left[\begin{array}{c} B \\ 0 \end{array}\right] }_{B_{E2}} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} \underbrace{ \left[\begin{array}{c} 0 \\ I_m \end{array}\right] }_{B_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c15c3050bb3a9a40764927acc7268c81_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \underbrace{ \left[\begin{array}{cc} 0 & I_m \end{array}\right] }_{C_{E2}} \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} = \underbrace{ \left[\begin{array}{cc} C & 0 \end{array}\right] }_{C_{E3}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fa6e5db5cb4e863339f8797520d1a2b2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t)\\ (x_1(t)=x(t)-x_\infty, x_2(t)=u(t)-u_\infty) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-245a3ce1c7bbd57f344bac4b6ccdca9c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cdba45c2f46a4ded8109c4031c43eef8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-272d89e0452752b99489c956de386a73_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{x}'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right] }_{T_sA_{E3}T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ S_2 \end{array}\right] }_{T_sB_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5ab2f4f17de6fee9605aa2556d7f248c_l3.png)
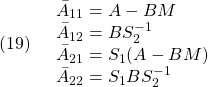
![Rendered by QuickLaTeX.com \displaystyle{(21)\quad \begin{array}{lll} V(\bar{x})= \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} P_1 & 0\\ 0 & P_2 \end{array}\right] }_{P} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}\\ \Rightarrow \dot{V}(\bar{x})\le - \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} Q_1 & 0\\ 0 & I \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7c77aa3ff56d9793c30ad999001a2185_l3.png)
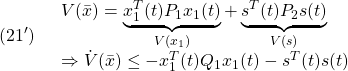
![Rendered by QuickLaTeX.com \displaystyle{(22)\quad \begin{array}{l} s(t)=0\Rightarrow\dot{s}(t)=0 \Rightarrow 0=\bar{A}_{21}x_1(t)+\bar{A}_{22}s(t)+S_2{\dot u}(t)\\ \Rightarrow {\dot u}_{eq}(t)=-\underbrace{S_2^{-1}}_{(SB_{E3})^{-1}} \underbrace{\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right]x'_{E3}(t)}_{SA_{E3}x_{E3}(t)}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3ad4a24162e39c9dd7341a0db806bc67_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \begin{array}{l} {\dot u}_\ell(t)=-\underbrace{S_2^{-1}}_{(SB_{E3})^{-1}} \underbrace{(\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right]x'_{E3}(t)-\Phi s(t))}_{(SA_{E3}-\Phi S)x_{E3}(t)}} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4da62d9774c6809e24338ce1ff05a030_l3.png)
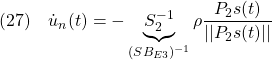
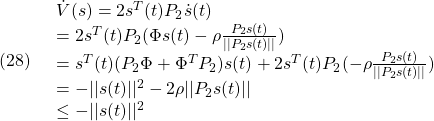
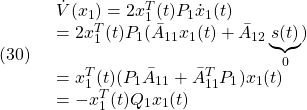
![Rendered by QuickLaTeX.com \displaystyle{(35)\quad {\dot u}_\ell(t)=- \underbrace{ (SB_{E3})^{-1}(SA_{E3}-\Phi S)S_E^{-1} }_{\left[\begin{array}{cc} F & F_I \end{array}\right]} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-edb851ab679593bf698b480644ba82ce_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(37)\quad {\dot u}_n(t) =-S_2^{-1}\rho\, {\rm sgn}( \underbrace{ P_2SS_E^{-1} }_{\left[\begin{array}{cc} G & G_I \end{array}\right]} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)}) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-913747aecf41d0c7b9c2a72e8ab5d520_l3.png)
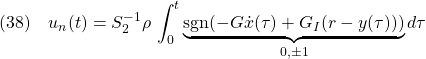
![Rendered by QuickLaTeX.com \displaystyle{(39)\quad \begin{array}{l} \underbrace{\dot{x}_1(t)}_{\dot{x}(t)}=\underbrace{(A-BM)}_{\bar{A}_{11}}x_1(t)+\underbrace{BS_2^{-1}}_{\bar{A}_{12}}\underbrace{(S_1x_1(t)+S_2x_2(t))}_{s(t)}\\ =(A-BM)x_1(t)+BS_2^{-1}S_2(Mx_1(t)+x_2(t))\\ =Ax_1(t)+Bx_2(t)\\ =Ax(t)+Bu(t)-\left[\begin{array}{cc} A & B \end{array}\right] \left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right]\\ =Ax(t)+Bu(t)-\left[\begin{array}{cc} A & B \end{array}\right]S_E^{-1} \left[\begin{array}{c} -w \\ r \end{array}\right]\\ =Ax(t)+Bu(t)-\left[\begin{array}{cc} I & 0 \end{array}\right] \left[\begin{array}{c} -w \\ r \end{array}\right]\\ =Ax(t)+Bu(t)+w \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2ba4e67edf54d3b4672c514eba81c975_l3.png)
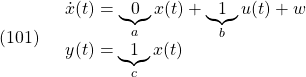
![Rendered by QuickLaTeX.com \displaystyle{(109)\quad \left[\begin{array}{c} -w \\ r \end{array}\right] = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{S_E} \left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right] \Rightarrow \left[\begin{array}{c} x_\infty \\ u_\infty \end{array}\right]= \left[\begin{array}{c} r \\ -w \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b6f19bc137b345cd02f056ded5359628_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(111)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ 1 \end{array}\right] }_{B_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-39ef4e33ccbbc6089ea56a80794721bd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(116)\quad s(t)= \underbrace{ \left[\begin{array}{cc} s_1 & s_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{s_2 \left[\begin{array}{cc} m & 1 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} \ (m=s_2^{-1}s_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0f6d44c1de2bf58be8fa0712e50791dd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(117)\quad \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ s_1 & s_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ -s_2^{-1}s_1 & s_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ae2c14797a0013427aaf5c62507328fe_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(118)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{x}'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} -m & s_2^{-1} \\ -s_1m & m \\ \end{array}\right] }_{T_sA_{E3}T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ s_2 \end{array}\right] }_{T_sB_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-09497ea1301736f936b51225906c697c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(123)\quad \begin{array}{l} {\dot u}_\ell(t)= -\underbrace{s_2^{-1}}_{(SB_{E3})^{-1}} \underbrace{(\left[\begin{array}{cc} -s_1m & m \\ \end{array}\right]x'_{E3}(t)-\Phi s(t))}_{(SA_{E3}-\Phi S)x_{E3}(t)}}\\ =-s_2^{-1}(\left[\begin{array}{cc} 0 & ms_2 \\ \end{array}\right]- \left[\begin{array}{cc} \Phi s_1 & \Phi s_2 \\ \end{array}\right])x_{E3}(t)\\ =-s_2^{-1}\left[\begin{array}{cc} -\Phi s_1 & ms_2-\Phi s_2 \\ \end{array}\right]x_{E3}(t)\\ =-\left[\begin{array}{cc} -\Phi m & m-\Phi \\ \end{array}\right] \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{S_E^{-1}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)}\\ =-\underbrace{(m-\Phi)}_{f}{\dot x}(t)+\underbrace{m(-\Phi)}_{f_I}(r-y(t))\\ \Rightarrow u_\ell(t)=-fx(t)+f_I\int_0^t (r-y(\tau))d\tau \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6aa7495d1adfe2e01b76d9d8229028e7_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(127)\quad \begin{array}{l} {\dot u}_n(t) =-s_2^{-1}\rho\, {\rm sgn}(\underbrace{-\frac{1}{2}\Phi^{-1}}_{p_2} \underbrace{ \left[\begin{array}{cc} s_1 & s_2 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}\right] }_{S_E^{-1}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)})\\ =\rho\, {\rm sgn}(\frac{1}{2}\Phi^{-1} \left[\begin{array}{cc} 1 & m \end{array}\right] \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right])\\ =\rho\, {\rm sgn}(-\underbrace{\frac{1}{2}(-\Phi^{-1})}_{g}{\dot x}(t)+\underbrace{\frac{1}{2}m(-\Phi^{-1})}_{g_I} (r-y(t)))\\ \Rightarrow u_n(t)=\rho\,\int_0^t\underbrace{{\rm sgn}(-g{\dot x}(\tau)+g_I(r-y(\tau)))}_{0,\pm 1}d\tau \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c70ad4d12c7dc10a4700d71c3c2e1719_l3.png)

![Rendered by QuickLaTeX.com \displaystyle{(201)\quad \begin{array}{l} \dot{x}(t)= \underbrace{\left[\begin{array}{cc} 0 & 1 \\ 0 & 0 \end{array}\right]}_{A}x(t) +\underbrace{\left[\begin{array}{cc} 0 \\ 1 \end{array}\right]}_{B}u(t)+ \left[\begin{array}{cc} 0 \\ w \end{array}\right]\\ y(t)=\underbrace{\left[\begin{array}{cc} 1 & 0 \end{array}\right]}_{C}x(t)\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ef113f64e22350dbc52f15182fe1a509_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(209)\quad \left[\begin{array}{c} 0 \\ -w \\ r \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \end{array}\right] }_{S_E} \left[\begin{array}{c} x_{1\infty} \\ x_{2\infty} \\ u_\infty \end{array}\right] \Rightarrow \left[\begin{array}{c} x_{1\infty} \\ x_{2\infty} \\ u_\infty \end{array}\right]= \left[\begin{array}{c} r \\ 0 \\ -w \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-69beeb3b2a284a9be405782120deebbd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(211)\quad \underbrace{ \frac{d}{dt} \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right] }_{B_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8e4db6573d9c0866d2409fc3290742b8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(216)\quad \begin{array}{l} s(t)= \underbrace{ \left[\begin{array}{ccc} s_{11} & s_{12} & s_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{s_2 \left[\begin{array}{ccc} m_1 & m_2 & 1 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)}\\ (m_1=s_2^{-1}s_{11},m_2=s_2^{-1}s_{12}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-400eb3876781e6270ec0fdecd65c935f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(217)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} = \underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ s_{11} & s_{12} & s_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)}\Leftrightarrow\\ \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ -s_2^{-1}s_{11} & -s_2^{-1}s_{12} & s_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-967eb06bf641a92d51f2f5dc0823ae03_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(218)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{x}'_{E3}(t)} = \underbrace{ \left[\begin{array}{ccc} 0 & 1 & 0\\ -m_1 & -m_2 & s_2^{-1} \\ -s_{12}m_1 & -s_{12}m_2 & m_2 \end{array}\right] }_{T_sA_{E3}T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ 0\\ s_2 \end{array}\right] }_{T_sB_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c09c2a528765c494ea49b0e4d526131e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(223)\quad \begin{array}{l} {\dot u}_\ell(t)= -\underbrace{s_2^{-1}}_{(SB_{E3})^{-1}} \underbrace{(\left[\begin{array}{ccc} -s_{12}m_1 & -s_{12}m_2 & m_2 \\ \end{array}\right]x'_{E3}(t)-\Phi s(t))}_{(SA_{E3}-\Phi S)x_{E3}(t)}}\\ =-s_2^{-1}(\left[\begin{array}{ccc} 0 & 0 & m_2s_2 \\ \end{array}\right]- \left[\begin{array}{ccc} \Phi s_{11} & \Phi s_{12} & \Phi s_2 \\ \end{array}\right])x_{E3}(t)\\ =-s_2^{-1}\left[\begin{array}{ccc} -\Phi s_{11} & -\Phi s_{12} & m_2s_2-\Phi s_2 \\ \end{array}\right]x_{E3}(t)\\ =-\left[\begin{array}{ccc} -\Phi m_1 & -\Phi m_2 & m_2-\Phi \\ \end{array}\right] \underbrace{ \left[\begin{array}{ccc} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right] }_{S_E^{-1}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)}\\ =-\underbrace{ \left[\begin{array}{cc} -\Phi m_2 & m_2-\Phi \\ \end{array}\right] }_{F}{\dot x}(t)+\underbrace{m_1(-\Phi)}_{F_I}(r-y(t))\\ \Rightarrow u_\ell(t)=-Fx(t)+F_I\int_0^t (r-y(\tau))d\tau \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a5fdce03c67f7578c2ac49db1237f4df_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(237)\quad \begin{array}{l} {\dot u}_n(t) =-s_2^{-1}\rho\, {\rm sgn}(\underbrace{-\frac{1}{2}\Phi^{-1}}_{p_2} \underbrace{ \left[\begin{array}{ccc} s_{11} & s_{12} & s_2 \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{ccc} 0 & 0 & 1 \\ 1 & 0 & 0 \\ 0 & 1 & 0 \end{array}\right] }_{S_E^{-1}} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)})\\ =s_2^{-1}\rho\, {\rm sgn}(\frac{1}{2}\Phi^{-1} \left[\begin{array}{ccc} s_{12} & s_2 & s_{11} \end{array}\right] \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right])\\ =\rho\, {\rm sgn}(\frac{1}{2}\Phi^{-1} \left[\begin{array}{ccc} m_2 & 1 & m_1 \end{array}\right] \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right])\\ =\rho\, {\rm sgn}(-\underbrace{\frac{1}{2}(-\Phi^{-1}) \left[\begin{array}{cc} m_2 & 1 \end{array}\right] }_{G}{\dot x}(t)+\underbrace{\frac{1}{2}m_1(-\Phi^{-1})}_{G_I} (r-y(t)))\\ \Rightarrow u_n(t)=\rho\,\int_0^t\underbrace{{\rm sgn}(-G{\dot x}(\tau)+G_I(r-y(\tau)))}_{0,\pm 1}d\tau \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fb6f2c2d66db55b55c3690dbc77615f3_l3.png)
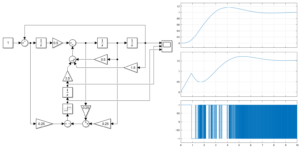
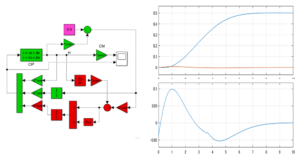
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} \dot{x}(t)=Ax(t)+Bu(t)\\ x(t)= \left[\begin{array}{ll} \theta & pitch\ angle\\ q & pitch\ rate\\ \alpha & angle\ of\ atack\\ \eta & elevator\ deflection\\ \delta & flap\ deflection \end{array}\right],\quad u(t)= \left[\begin{array}{ll} \eta_c & elevator\ command\\ \delta_c& flap\ comannd \end{array}\right]\\ A=\left[\begin{array}{rrrrr} 0 & 1 & 0 & 0 & 0\\ 0 &-1.99 & -13.41 & -18.95 & -3.60\\ 0 & 1 & -1.74 & -0.08 & -0.59\\ 0 & 0 & 0 & -20 & 0\\ 0 & 0 & 0 & 0 & -20 \end{array}\right],\quad B=\left[\begin{array}{rr} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 20 & 0\\ 0 & 20 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e8e30c3e5083c206da3951e3e40e9cfb_l3.png)

![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \begin{array}{l} \dot{x}(t)=Ax(t)+Bu(t)\\ x(t)= \left[\begin{array}{ll} \gamma=\theta-\alpha & fligt\ path\ angle\\ q & pitch\ rate\\ \alpha & angle\ of\ atack\\ \eta & elevator\ deflection\\ \delta & flap\ deflection \end{array}\right],\quad u(t)= \left[\begin{array}{ll} \eta_c & elevator\ command\\ \delta_c& flap\ comannd \end{array}\right]\\ A=\left[\begin{array}{rrrrr} 0 & 0 & 1.74 & 0.08 & 0.59\\ 0 &-1.99 & -13.41 & -18.95 & -3.60\\ 0 & 1 & -1.74 & -0.08 & -0.59\\ 0 & 0 & 0 & -20 & 0\\ 0 & 0 & 0 & 0 & -20 \end{array}\right],\quad B=\left[\begin{array}{rr} 0 & 0 \\ 0 & 0 \\ 0 & 0 \\ 20 & 0\\ 0 & 20 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b3ae110ebe0cc483c67a6db0b309e181_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} y(t)=Hx(t)\\ H= \left[\begin{array}{ccccc} 1 & 0 & 1 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c44cf07d269341a588b528f5aca4caf9_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(20)\quad { \boxed{\begin{array}{l} u(t)=u_\ell(t)+u_n(t)\\ u_\ell(t)=-\underbrace{(SB_E)^{-1}(SA_E-\Phi S)}_{L=L_{eq}+L_\Phi}\left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right]\\ -\underbrace{(SB_E)^{-1}(\Phi S_r+S_1B_r)}_{L_r} r(t) +\underbrace{(SB_E)^{-1}S_r}_{L_{\dot r}} \dot{r}(t)\\ u_n(t)=-\underbrace{(SB_E)^{-1}\rho(t,x)}_{L_n}\frac{P_2(s(t)-S_rr(t))}{||P_2(s(t)-S_rr(t))||} \end{array}}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-adc6bfdf1b50ea9ed3b1152bc4ee1729_l3.png)
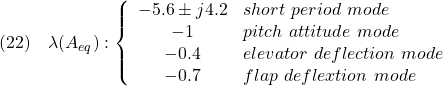
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad {\tt specpos}= \left[\begin{array}{ccccc} 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\\hline 1 & 1 & 1 & 1 & 1\\ 1 & 0 & 1 & 1 & 1\\ 0 & 1 & 1 & 0 & 1\\\hline 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0\\ \end{array}\right],\quad {\tt specent}= \left[\begin{array}{rrrrr} -1 & -1 & -1 & -1 & -1\\ -1 & -1 & -1 & -1 & -1\\\hline 0 & 0 & 1 & 0 & 1\\ 1 & -1 & 0 & 1 & 0\\ -1 & 1 & 0 & -1 & 0\\\hline -1 & -1 & -1 & -1 & -1\\ -1 & -1 & -1 & -1 & -1\\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0c718bed933ebbd16e58b62392705e36_l3.png)
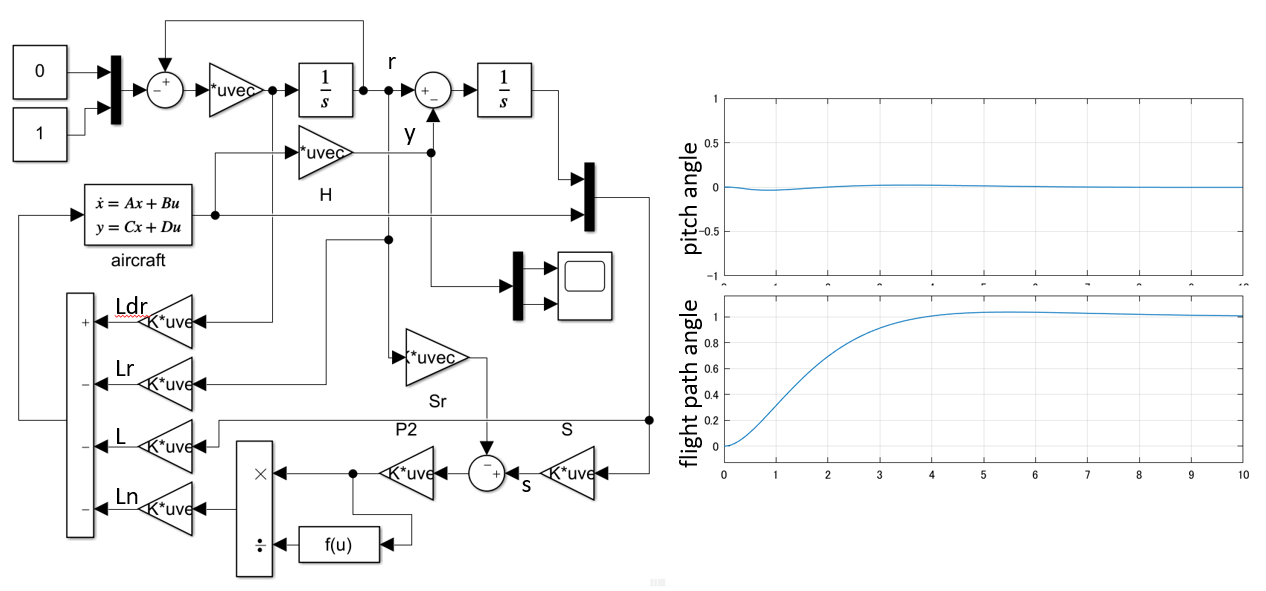
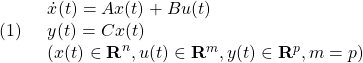
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \left[\begin{array}{c} \dot x_r(t)\\ \dot x(t) \end{array}\right] = \left[\begin{array}{c|cc} 0 & -C_1 & -C_2\\\hline 0 & A_{11} & A_{12} \\ 0 & A_{21} & A_{22} \end{array}\right] \left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right] + \left[\begin{array}{c} 0\\\hline 0\\ B_2 \end{array}\right] u(t) + \left[\begin{array}{c} I_m \\\hline 0 \\ 0 \end{array}\right] r(t)\\ (x_r(t)\in{\rm\bf R}^m, x(t)\in{\rm\bf R}^n) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1ab4b378422eddd1bff475a2408082e2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(5a)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc|c} 0 & -C_1 & -C_2\\ 0 & A_{11} & A_{12} \\\hline 0 & A_{21} & A_{22} \end{array}\right] }_{A_E} \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0\\ 0\\\hline B_2 \end{array}\right] }_{B_E} u(t) + \left[\begin{array}{c} I_m \\ 0 \\\hline 0 \end{array}\right] r(t)\\ (x_1(t)\in{\rm\bf R}^n, x_2(t)\in{\rm\bf R}^m) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-374491b693fbc08a0a4648abd3e610d2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] %}_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I_m \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] %}_{x(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-01bb686061b94fbab2a0ff90e7d23f64_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} I_n & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right]\\ \Leftrightarrow \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} I_n & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-19e5643bcb296d8a517aba35bc4fe14e_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8a)\quad \begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] %}_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right] }_{T_sA_ET_s^{-1}} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] %}_{x'(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ S_2B_2 \end{array}\right] }_{T_sB_E} u(t)\\ + \left[\begin{array}{cc} B_r \\ S_1B_r \end{array}\right] r(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a23595fe93cd3fb99284c6e90f61bcf1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(8b)\quad \left\{\begin{array}{l} \bar{A}_{11}= \left[\begin{array}{cc} 0 & -C_1 \\ 0 & A_{11} \end{array}\right] -\left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right]M\\ \bar{A}_{12}= \left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right]S_2^{-1}\\ \bar{A}_{21}=S_2(M\bar{A}_{11} + \left[\begin{array}{cc} 0 & A_{21} \end{array}\right] -A_{22}M)\\ \bar{A}_{22}=S_2(M \left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right] +A_{22})S_2^{-1}\\ B_r=\left[\begin{array}{cc} I_m \\ 0 \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-24d62178408415d07b9cef2c8d0cfab3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \boxed{ \begin{array}{lll} V(\bar{x})= \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t)-S_rr(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} P_1 & 0\\ 0 & P_2 \end{array}\right] }_{P} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t)-S_rr(t) \end{array}\right] }_{\bar{x}(t)}\\ \Rightarrow \dot{V}(\bar{x})\le - \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t)-S_rr(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} Q_1 & 0\\ 0 & I \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t)-S_rr(t) \end{array}\right] }_{\bar{x}(t)} \end{array}}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-174b6e0b351e183151b07a67d25fe6dc_l3.png)
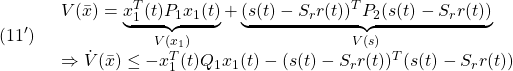
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{cl} (12.1) & s(t)=0\\ \Downarrow &\\ (12.2) & \dot{s}(t)=0\\ \Downarrow &\\ (12.3) & 0=S_2\bar{A}_{21}x_1(t)+S_2\bar{A}_{22}S_2^{-1}s(t)+S_2B_2u(t)\\ \Downarrow &\\ (12.4) & u_{eq}(t)=-\underbrace{(S_2B_2)^{-1}}_{([0\ I]T_sB_E)^{-1}} \underbrace{\left[\begin{array}{cc} S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right]}_{[0\ I]T_sA_ET_s^{-1}} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ \Downarrow & by\ S=[0\ I]T_s\\ (12.5) & u_{eq}(t)=-(SB_E)^{-1}SA_ET_s^{-1} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ \Downarrow & by\ (7),(8b)\\ (12.6) & u_{eq}(t)=-(SB_E)^{-1}SA_E \left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right]} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fc541c88c94f46e054237f8c4eb58974_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \begin{array}{l} u_\ell(t)=-(S_2B_2)^{-1} (\left[\begin{array}{cc} S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right]\left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]-\Phi s(t))\\ -(S_2B_2)^{-1}(\Phi S_r+S_1B_r)r(t)+(S_2B_2)^{-1}S_r\dot{r}(t)\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-523e59ff1e3266a531c8f91b270e4fc0_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13')\quad { \boxed{\begin{array}{l} u_\ell(t) =-\underbrace{(SB_E)^{-1}(SA_E-\Phi S)}_{L=L_{eq}+L_\Phi}\left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right]\\ -\underbrace{(SB_E)^{-1}(\Phi S_r+S_1B_r)}_{L_r} r(t) +\underbrace{(SB_E)^{-1}S_r}_{L_{\dot r}} \dot{r}(t)\\ \end{array}}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2d8158c14705344b0d2033bddb8e59ac_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \begin{array}{l} \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] = \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ + \left[\begin{array}{cc} 0\\ S_2B_2 \end{array}\right] (-(S_2B_2)^{-1} (\left[\begin{array}{cc} S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right]\left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]-\Phi s(t))\\ -(S_2B_2)^{-1}(\Phi S_r+S_1B_r)r(t)+(S_2B_2)^{-1}S_r\dot{r}(t)+u_n(t)) + \left[\begin{array}{cc} B_r \\ S_1B_r \end{array}\right] r(t)\\ = \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ + \left[\begin{array}{cc} 0\\ I_m \end{array}\right] \left[\begin{array}{cc} -S_2\bar{A}_{21} & -S_2\bar{A}_{22}S_2^{-1}+\Phi \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ + \left[\begin{array}{cc} 0\\ -(\Phi S_r+S_1B_r)r(t)+S_r\dot{r}(t)+S_2B_2u_n(t) \end{array}\right] + \left[\begin{array}{cc} B_r \\ S_1B_r \end{array}\right] r(t)\\ = \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ 0 & \Phi \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]+ \left[\begin{array}{cc} B_rr(t)\\ -\Phi S_rr(t)+S_r\dot{r}(t)+S_2B_2u_n(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7299445c3fbe65641193f7a4c068b664_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{s}(t)-S_r\dot{r}(t) \end{array}\right] = \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ 0 & \Phi \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t)-S_rr(t) \end{array}\right]\\ + \left[\begin{array}{cc} B_rr(t)\\ -\Phi S_rr(t)+S_r\dot{r}(t)+S_2B_2u_n(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2cbbaf4d3607cc033e3ec653af8d867e_l3.png)
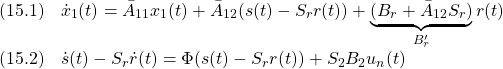
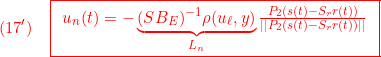
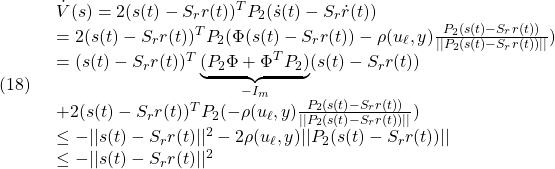
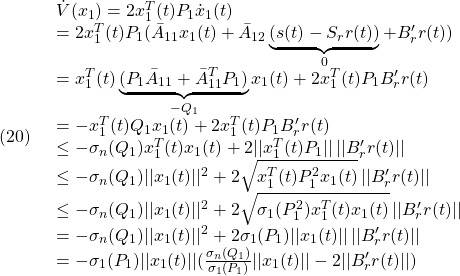


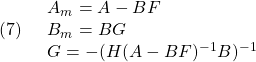
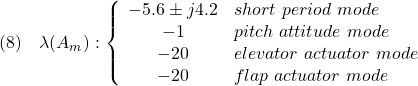
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad {\tt specpos}= \left[\begin{array}{ccc|cc} 1 & 1 & 1 & 0 & 0\\ 1 & 0 & 1 & 0 & 0\\ 0 & 1 & 1 & 0 & 0\\\hline 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 1\\ \end{array}\right],\quad {\tt specent}= \left[\begin{array}{rrr|rr} 0 & 0 & 1 & -1 & -1\\ 1 & -1 & 0 & -1 & -1\\ -1 & 1 & 0 & -1 & -1\\\hline -1 & -1 & -1 & 1 & -1\\ -1 & -1 & -1 & -1 & 1\\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9351aa1713d68cc420ab75e44c211a51_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} F=WV^{-1} =\left[\begin{array}{rrrrr} -1.9338 & -0.5744 & -2.1188 & 0.4750 & 0.1066\\ 1.9571 & 0.2253 & 3.1273 & -0.0694 & -0.0515 \end{array}\right]\\ W=\left[\begin{array}{rrrrr} 0.8445 & 1.9935 & -0.2742 & 0 & 0\\ -2.7055 & 1.2780 & 0.1767 & 0 & 0 \end{array}\right]\\ V=\left[\begin{array}{rrrrr} 0 & -0.0000 & 0.6667 & 0.0030 & -0.0313\\ 1.0000 & -9.5000 & -0.3333 & 0.9964 & 0.1493\\ -0.9286 & 1.0000 & -0.3333 & -0.0528 & 0.0238\\ -1.8252 & -2.2364 & 0.2886 & 1.0000 & -0.0649\\ 2.9860 & -2.6459 & -0.1860 & -0.0825 & 1.0000 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b86eb8a3dc0f557c2de880c6fc23d3ee_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \underbrace{ \left[\begin{array}{rr} 0.025 & 0\\ 0 & 0.025 \end{array}\right] }_{P_2} \underbrace{ \left[\begin{array}{rr} 20 & 0\\ 0 & 20 \end{array}\right] }_{\Phi} +(*)^T=-I }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dc78c4ca1633a74198c3d266be410408_l3.png)
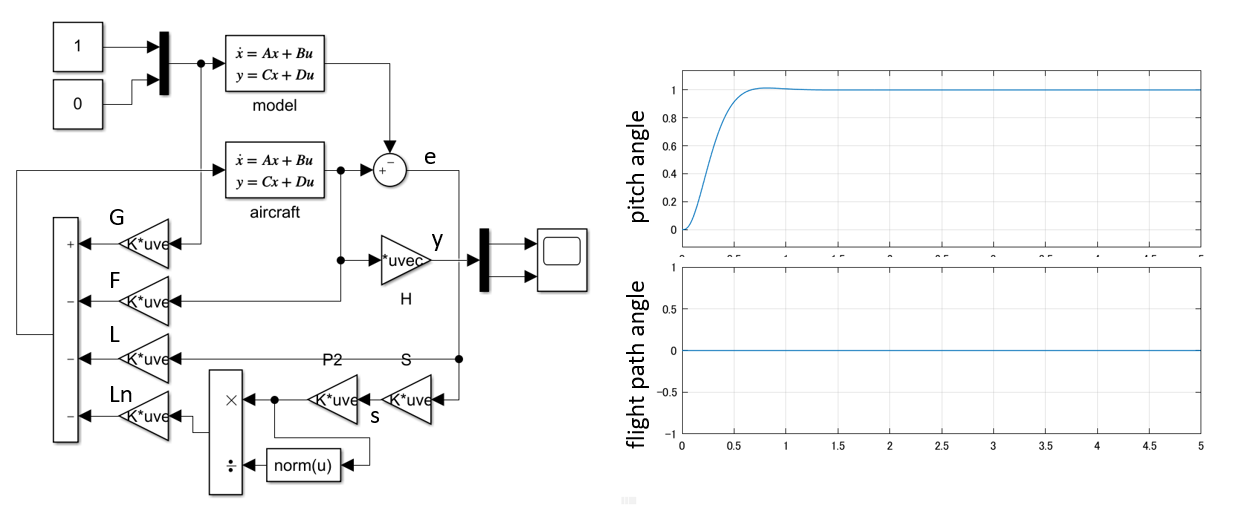 図2 モデル規範法によるSMC制御系応答
図2 モデル規範法によるSMC制御系応答