投稿者「cacsd」のアーカイブ
エクスポート
エクスポート
●「工程’s」のファイルにエクスポートを行うと、次のような13種類のTSVファイルが得られます。
ここで、次の3つのファイルに注目します。
・koutei.tsv ⇒作業の定義
・requirement.tsv ⇒要求リソース
・constraint.tsv ⇒先行制約
これらから、データセットを作成するのに必要な項目(以下の赤太字)を抽出します。
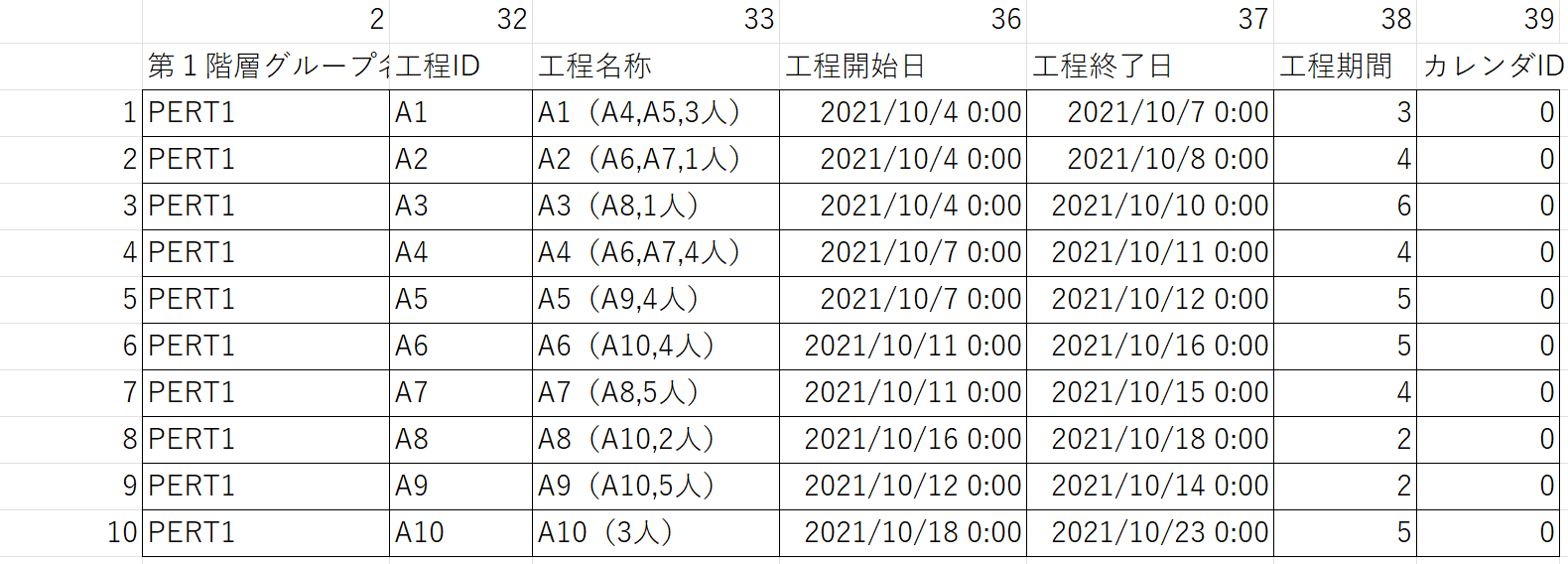
●koutei.tsvのレコードを構成するフィールド(129個)
| 第1階層グループID 第1階層グループ名称 第1階層グループ備考1 第1階層グループ備考2 第1階層グループ備考3 第1階層グループ備考4 第1階層グループ備考5 第1階層グループ備考6 第1階層グループ備考7 第1階層グループ備考8 第1階層グループ備考9 第1階層グループ備考10 第2階層グループID 第2階層グループ名称 第3階層グループID 第3階層グループ名称 第4階層グループID 第4階層グループ名称 第5階層グループID 第5階層グループ名称 第6階層グループID 第6階層グループ名称 第7階層グループID 第7階層グループ名称 第8階層グループID 第8階層グループ名称 第9階層グループID 第9階層グループ名称 第10階層グループID 第10階層グループ名称 行番号 工程ID 工程名称 初期工程開始日 初期工程終了日 工程開始日 工程終了日 工程期間 カレンダID 進捗度 数量 備考1 備考2 備考3 備考4 備考5 備考6 備考7 備考8 備考9 備考10 バーを移動しない 後続に影響しない範囲で遅く開始する 編集不可 左シンボル形状 中シンボル形状 右シンボル形状 左シンボル色 中シンボル色 右シンボル色 テキストの表示位置 URL表示名1 URL1 URL表示名2 URL2 URL表示名3 URL3 URL表示名4 URL4 URL表示名5 URL5 第1階層グループ非表示 第1階層グループバー非表示 第1階層グループ折りたたみ(バーチャート) 第1階層グループ折りたたみ(ツリービュー) 第1階層グループ名称の書き方 第2階層グループ非表示 第2階層グループバー非表示 第2階層グループ折りたたみ(バーチャート) 第2階層グループ折りたたみ(ツリービュー) 第2階層グループ名称の書き方 第3階層グループ非表示 第3階層グループバー非表示 第3階層グループ折りたたみ(バーチャート) 第3階層グループ折りたたみ(ツリービュー) 第3階層グループ名称の書き方 第4階層グループ非表示 第4階層グループバー非表示 第4階層グループ折りたたみ(バーチャート) 第4階層グループ折りたたみ(ツリービュー) 第4階層グループ名称の書き方 第5階層グループ非表示 第5階層グループバー非表示 第5階層グループ折りたたみ(バーチャート) 第5階層グループ折りたたみ(ツリービュー) 第5階層グループ名称の書き方 第6階層グループ非表示 第6階層グループバー非表示 第6階層グループ折りたたみ(バーチャート) 第6階層グループ折りたたみ(ツリービュー) 第6階層グループ名称の書き方 第7階層グループ非表示 第7階層グループバー非表示 第7階層グループ折りたたみ(バーチャート) 第7階層グループ折りたたみ(ツリービュー) 第7階層グループ名称の書き方 第8階層グループ非表示 第8階層グループバー非表示 第8階層グループ折りたたみ(バーチャート) 第8階層グループ折りたたみ(ツリービュー) 第8階層グループ名称の書き方 第9階層グループ非表示 第9階層グループバー非表示 第9階層グループ折りたたみ(バーチャート) 第9階層グループ折りたたみ(ツリービュー) 第9階層グループ名称の書き方 第10階層グループ非表示 第10階層グループバー非表示 第10階層グループ折りたたみ(バーチャート) 第10階層グループ折りたたみ(ツリービュー) 第10階層グループ名称の書き方 初期計画左シンボル形状 初期計画中シンボル形状 初期計画右シンボル形状 初期計画左シンボル色 初期計画中シンボル色 初期計画右シンボル色 拡張設定1 EOR |
PERTの例題について赤太字の項目を抜き出すと次のようになります。
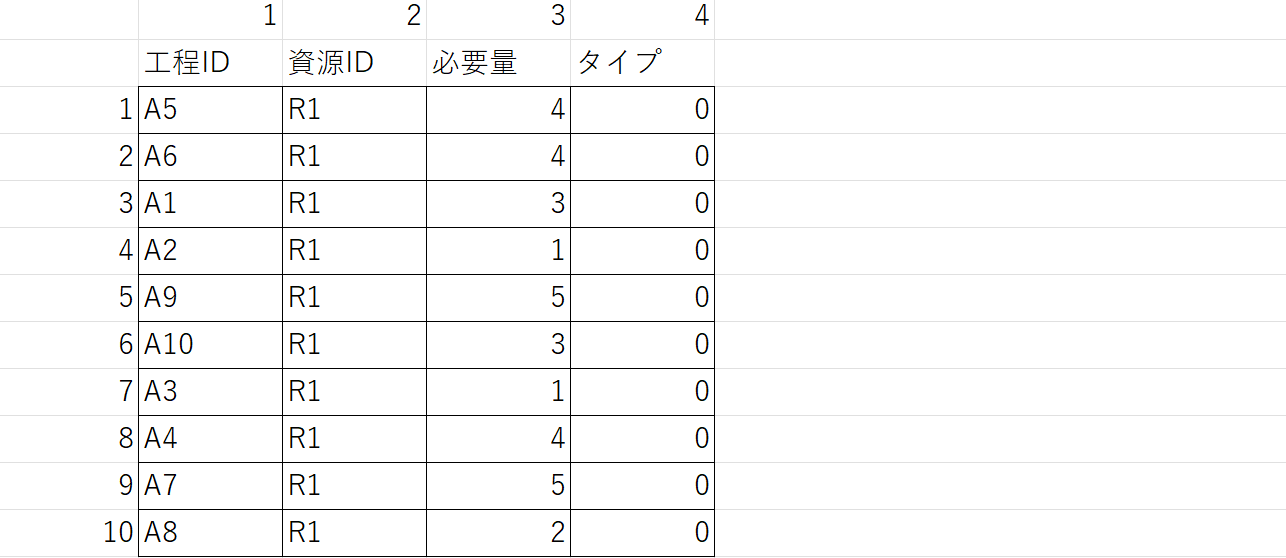
●requirement.tsvのレコードを構成するフィールド(5個)
| 工程ID 資源ID 必要量 タイプ EOR |
PERTの例題について赤太字の項目を抜き出すと次のようになります。
●constraint.tsvのレコードを構成するフィールド(26個)
| 先行工程ID 後続工程ID タイプ 作業間隔 カレンダID 備考 非表示 描画順序1 描画オフセット右1 描画オフセット下1 描画順序2 描画オフセット右2 描画オフセット下2 描画順序3 描画オフセット右3 描画オフセット下3 描画順序4 描画オフセット右4 描画オフセット下4 描画順序5 描画オフセット右5 描画オフセット下5 描画順序6 描画オフセット右6 描画オフセット下6 EOR |
PERTの例題について赤太字の項目を抜き出すと次のようになります。

データセットの作成
「工程’s」による平準化
「工程’s」による平準化…Homework
●作業情報が次表のように与えられる例を考えます。
| # | 作業名 | 作業時間 | 先行関係 | 作業員 | |
| 1 | A1 | 3 | 4 | 5 | 3 |
| 2 | A2 | 4 | 6 | 7 | 1 |
| 3 | A3 | 6 | 8 | 1 | |
| 4 | A4 | 4 | 6 | 7 | 4 |
| 5 | A5 | 5 | 9 | 4 | |
| 6 | A6 | 4 | 10 | 5 | |
| 7 | A7 | 5 | 8 | 4 | |
| 8 | A8 | 2 | 10 | 5 | |
| 9 | A9 | 2 | 10 | 2 | |
| 10 | A10 | 5 | 0 | 3 | |
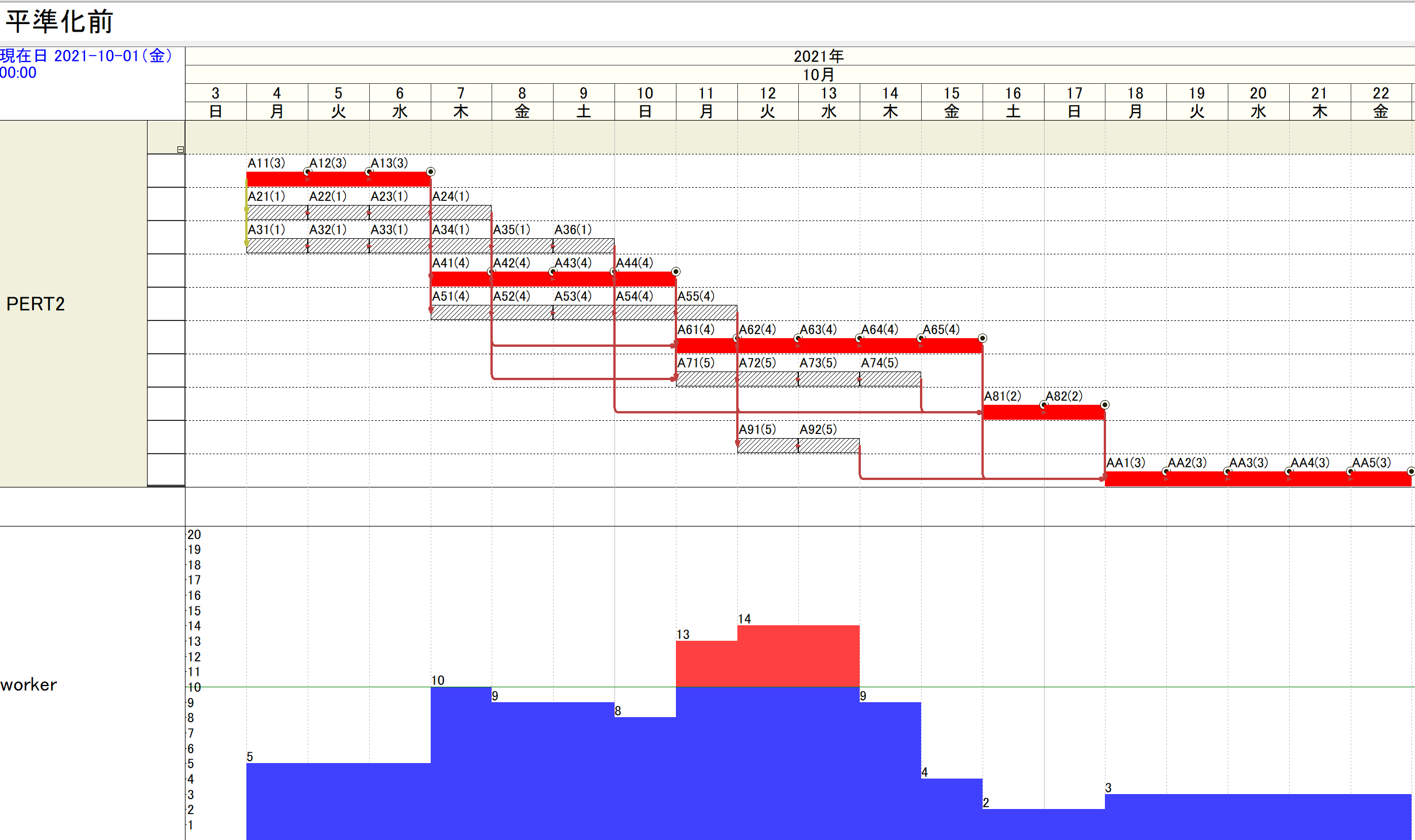
●山積みを行った結果を次に示します。毎日10名まで配員可能とすると、これをオーバーしていることが分かります。
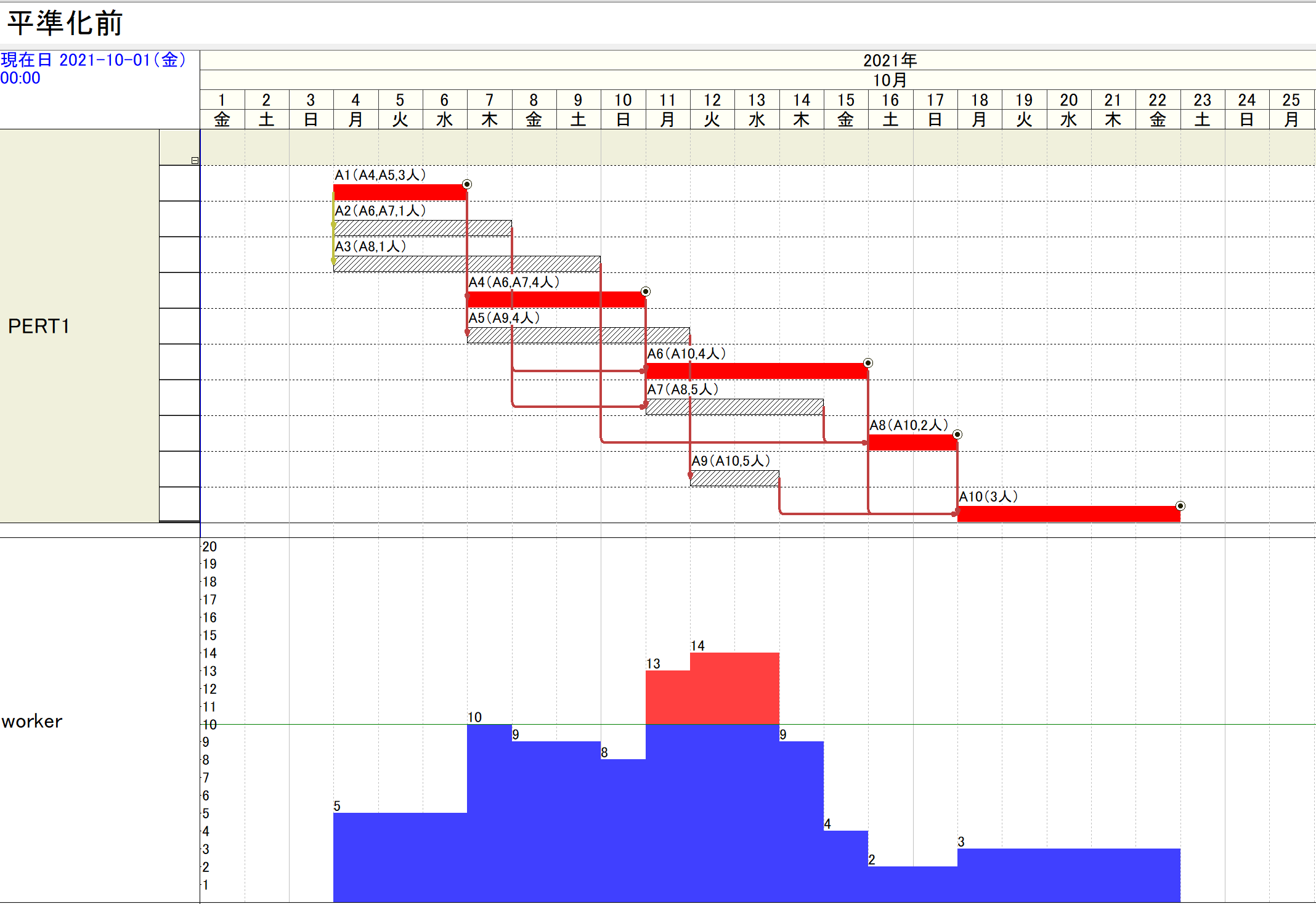
ここで、赤い作業の列がCPを表しています。通常は、CP以外の作業を前後させて平準化(山均し)を行います。
●「工程’s」の「オシカ」を用いて平準化を行った結果を次に示します。
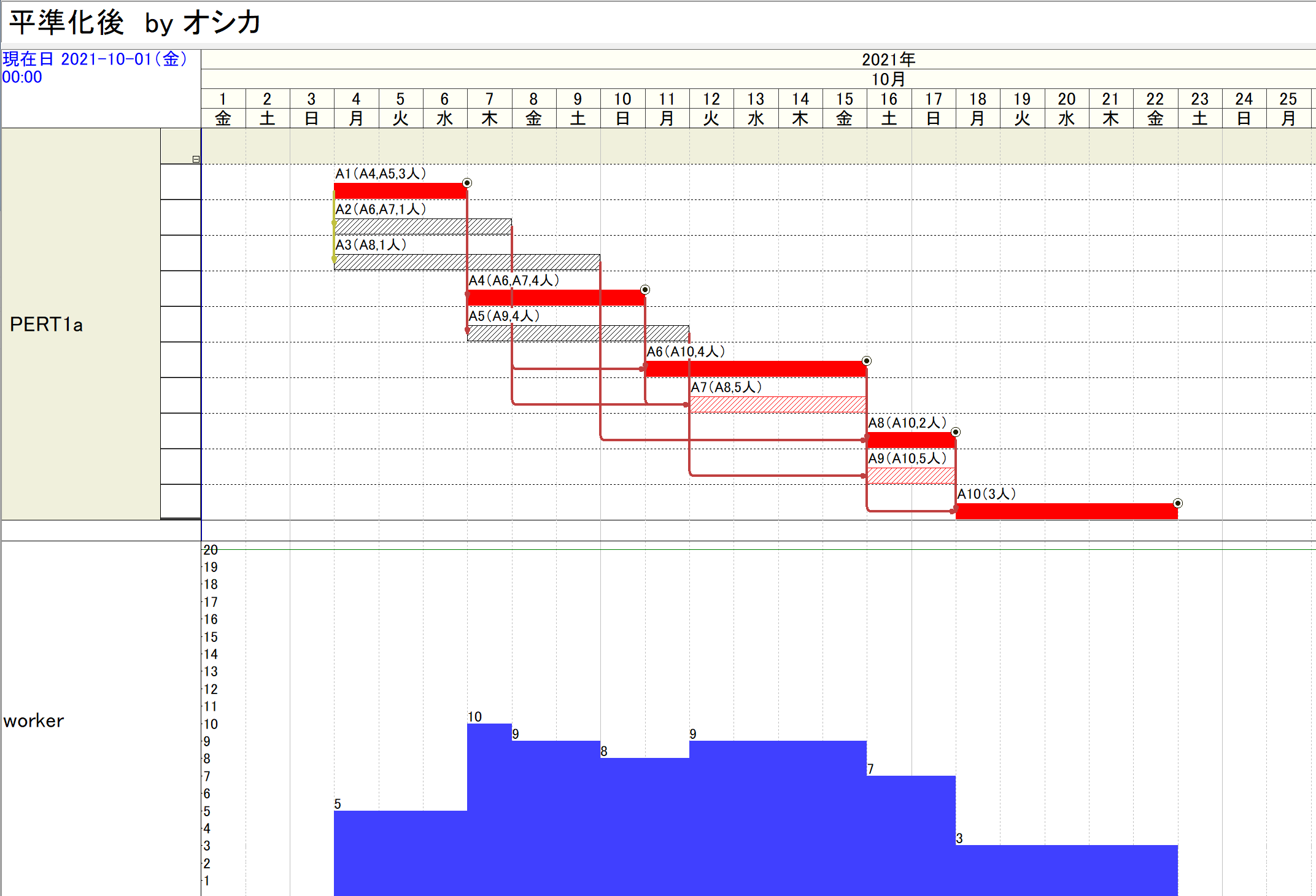
●以上は、各作業を作業期間中は毎日一定の配員で行う場合です。しかし日ごとに配員数を変えてよい場合を検討するために、次の山積みを行います。
●これを平準化して、次の結果を得ます。

本来は、作業81が始まるまでに作業A74を終わらせたいところですが、「工程’s」でそれが可能かどうかは現在検討中です。
●参考までに、別の方法で日ごとの配員数を変えながら(したがって作業期間を変えながら)、平準化を行った結果を次に示します。

ここで、10名の作業員はどの作業も担当できることを仮定しています。
基本操作
アクティティビティの定義と先行関係の付与…Homework
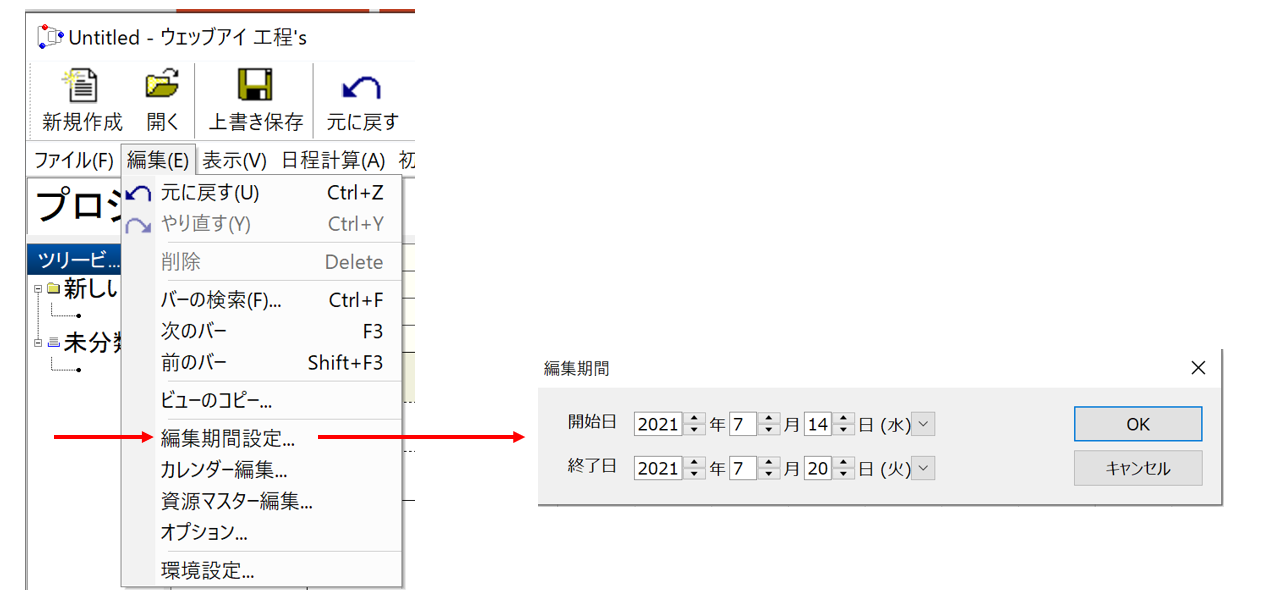
●操作1:編集期間の設定
●操作2:通し日の設定

●操作3:グループ名の定義(行の追加、行番号の定義)

●操作4:アクティビティの定義(名称の設定)

●操作5:シンボルの変更

●操作5:後続作業の定義、先行関係の付与
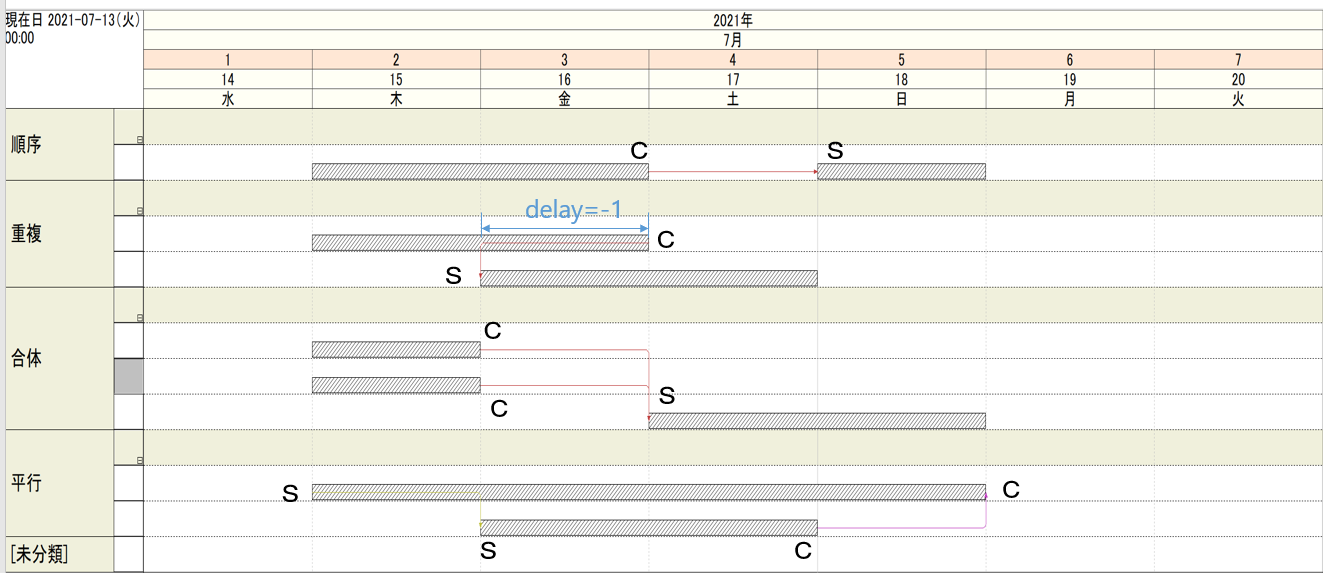
先行関係には、CS関係(完了⇒開始)、SC関係(開始⇒完了)、SS関係(開始⇒開始)、CC関係(完了⇒完了)の4種類がある。
●操作6:グループバーを非表示
●操作7:操作の取り消し
リソースの付与…Homework
●操作8:資源マスターの定義
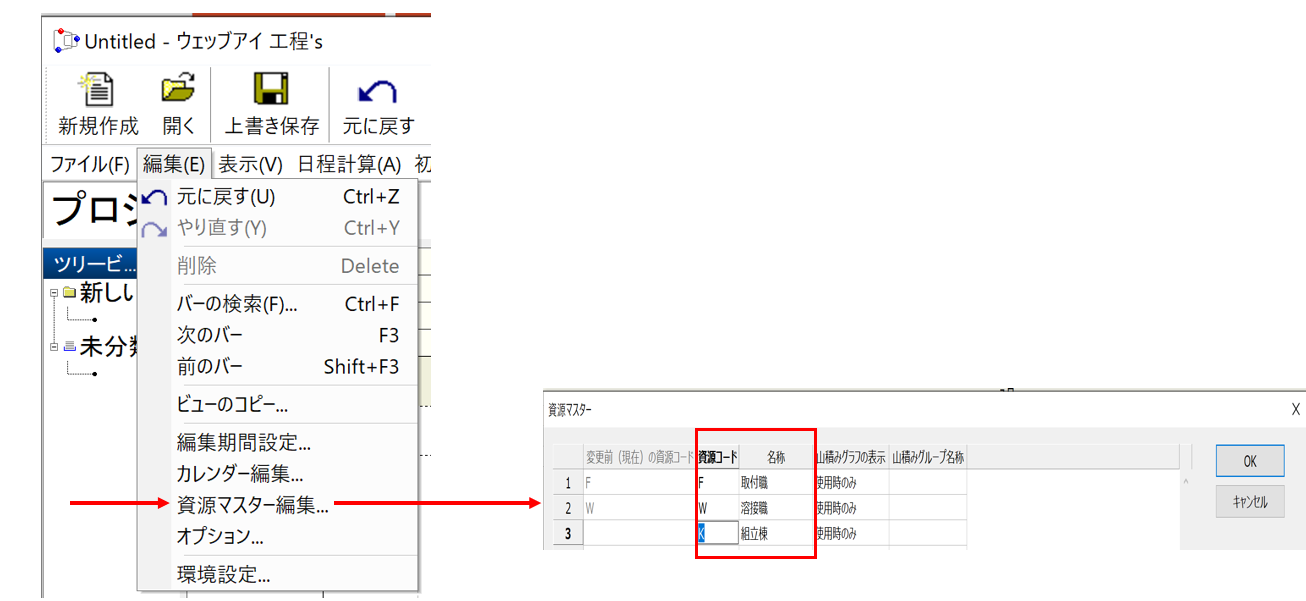
●操作9:必要資源の付与

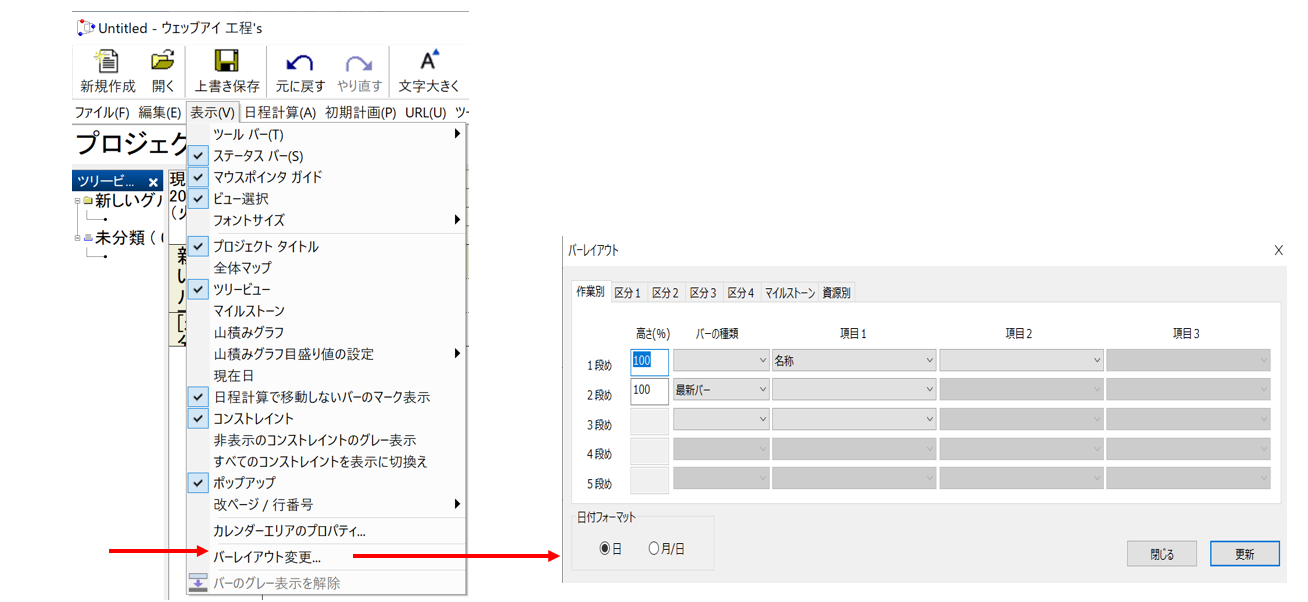
●操作10:バーレイアウトの変更
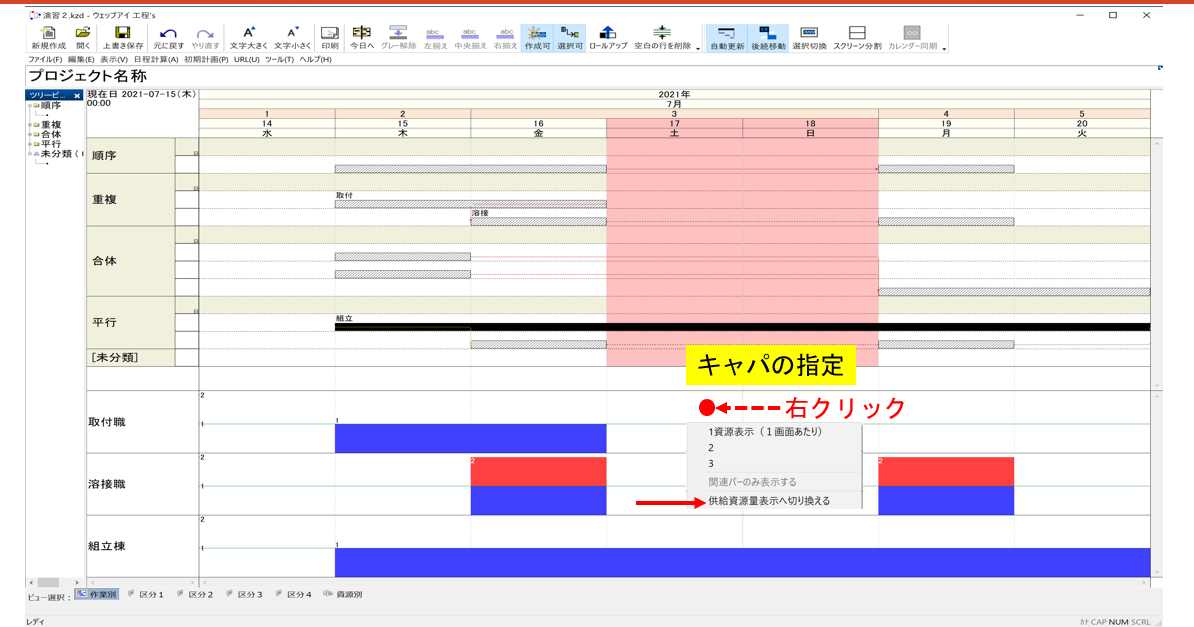
●操作11:キャパ(提供可能資源量)の付与
補遺:出力FB型追従SMI制御
補遺:出力FB型追従SMI制御…Homework
[1] 定値外乱を受ける制御対象
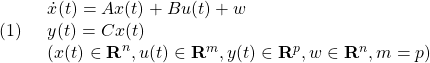
の出力を、次のコマンド(定値目標)
![]()
に追従させることを考えます。そのために、積分動作
![]()
を考え、次の拡大系を構成します。
![]()
定常状態では
![]()
を得ます(![]() ,
,![]() ,
,![]() は定数ベクトル)。
は定数ベクトル)。
●さて、関係式
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ C & 0 \end{array}\right] }_{S_E} \underbrace{ \left[\begin{array}{c} x(t)-x_\infty \\ u(t)-u_\infty \end{array}\right] }_{x_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d19845bc6a9ba5e6b6ffcc474aa170e5_l3.png)
を用いて、偏差系
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \begin{array}{l} \boxed{ \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} A & B \\ 0 & 0 \end{array}\right] }_{A_{E3}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ I_m \end{array}\right] }_{B_{E3}} {\dot u}(t)}\\ (x_1(t)=x(t)-x_\infty, x_2(t)=u(t)-u_\infty) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2d3658577af35dd369549e995357ea2d_l3.png)
を得ます。これはSM標準形となっていることに注意して、SM制御系を設計します。
●スイッチング関数として、次式を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1C & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} \ (M=S_2^{-1}S_1C) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-69cd20c627c9c293f7697843f1f90dc6_l3.png)
(15)に対して、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(17)\quad \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1C & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ -S_2^{-1}S_1C & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7e934ac1b10cbc9a5aedfe8a2c7344ed_l3.png)
を行って、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{x}'_{E3}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right] }_{T_sA_{E3}T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{x'_{E3}(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ S_2 \end{array}\right] }_{T_sB_{E3}} {\dot u}(t) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5ab2f4f17de6fee9605aa2556d7f248c_l3.png)
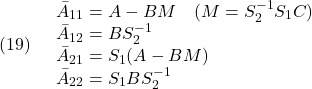
以下では、![]() が安定行列となるようにスイッチング関数が選ばれていると仮定します。
が安定行列となるようにスイッチング関数が選ばれていると仮定します。
●このとき、スライディングモード制御則(SM制御則、SMC則)
![]()
を、2次安定性
![Rendered by QuickLaTeX.com \displaystyle{(21)\quad \begin{array}{lll} V(\bar{x})= \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} P_1 & 0\\ 0 & P_2 \end{array}\right] }_{P} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}\\ \Rightarrow \dot{V}(\bar{x})\le - \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} Q_1 & 0\\ 0 & I \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7c77aa3ff56d9793c30ad999001a2185_l3.png)
すなわち
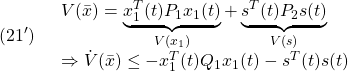
が成り立つように決定します(![]() ,
, ![]() ,
, ![]() )。
)。
可到達性の検討
等価制御は
![Rendered by QuickLaTeX.com \displaystyle{(22)\quad \begin{array}{l} s(t)=0\Rightarrow\dot{s}(t)=0 \Rightarrow 0=\bar{A}_{21}x_1(t)+\bar{A}_{22}s(t)+S_2{\dot u}(t)\\ \Rightarrow {\dot u}_{eq}(t)=-\underbrace{S_2^{-1}}_{(SB_{E3})^{-1}} \underbrace{\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right]x'_{E3}(t)}_{SA_{E3}x_{E3}(t)}} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3ad4a24162e39c9dd7341a0db806bc67_l3.png)
のように得られます。(20)の第1項![]() は、この等価制御をベースして
は、この等価制御をベースして
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad \begin{array}{l} {\dot u}_\ell(t)=-\underbrace{S_2^{-1}}_{(SB_{E3})^{-1}} \underbrace{(\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right]x'_{E3}(t)-\Phi s(t))}_{(SA_{E3}-\Phi S)x_{E3}(t)}} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4da62d9774c6809e24338ce1ff05a030_l3.png)
のように構成します(![]() は安定行列)。このとき閉ループ系は次式で与えられます。
は安定行列)。このとき閉ループ系は次式で与えられます。
![]()
すなわち
![]()
ここで、![]() は安定行列なので
は安定行列なので
![]()
を満たす![]() を選ぶことができます。これを用いて
を選ぶことができます。これを用いて
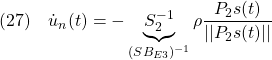
と選びます(![]() は定数)。このとき次式が成り立ちます。
は定数)。このとき次式が成り立ちます。
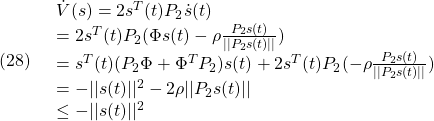
スライディングモードの検討
![]() は安定行列なので
は安定行列なので
![]()
を満たす![]() を選ぶことができます。
を選ぶことができます。
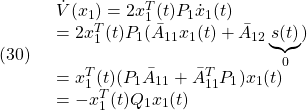
積分動作をもつSMC
上で求めた偏差系E3に対するSMCは次式で与えられました。
![]()
![]()
![]()
これらを積分して、制御対象(1)に対する積分動作をもつSMCを導出します。
![]()
まず(32)は(10)を用いて次式のように書けます。
![Rendered by QuickLaTeX.com \displaystyle{(35)\quad {\dot u}_\ell(t)=- \underbrace{ (SB_{E3})^{-1}(SA_{E3}-\Phi S)S_E^{-1} }_{\left[\begin{array}{cc} F & F_I \end{array}\right]} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-edb851ab679593bf698b480644ba82ce_l3.png)
これを積分して
![]()
次に(33)は(10)を用いて次式のように書けます。
![Rendered by QuickLaTeX.com \displaystyle{(37)\quad {\dot u}_n(t) =-S_2^{-1}\rho\, {\rm sgn}( \underbrace{ P_2SS_E^{-1} }_{\left[\begin{array}{cc} G & G_I \end{array}\right]} \underbrace{ \left[\begin{array}{c} {\dot x}(t) \\ y(t)-r \end{array}\right] }_{x_{E2}(t)}) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-913747aecf41d0c7b9c2a72e8ab5d520_l3.png)
これを積分すれば
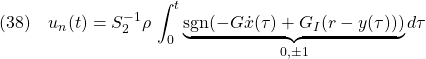
モデル規範・追従SM-OBS制御
モデル規範・SMオブザーバベース・追従SM制御…Homework
[1] 次の状態方程式で表される制御対象を考えます。
![]()
この状態が理想的なモデル
![]()
の状態を追従するように、すなわち
![]()
となるように制御則を決定したいとします。
以下では、(2)は適当な安定化状態フィードバックと入力変換を行って
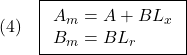
のように得られていると仮定します。
●モデル間の誤差は、(1)と(2)を辺々引き算して
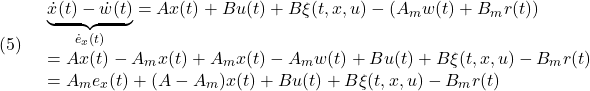
に従います。これは(4)を用いて次式となります。
![]()
●出力方程式は次式で与えられるとします。
![]()
状態フィードバックは使えないので、次のSMオブザーバを考えます。
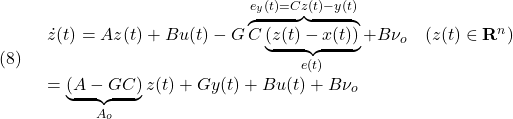
ここで、![]() は
は![]() が安定行列となるように選ばれているとします。
が安定行列となるように選ばれているとします。
SMオブザーバの誤差方程式は、(1)と(7)を辺々引き算して
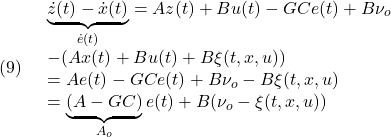
すなわち
![]()
となります。いま
![]()
を満足する![]() と、ある
と、ある![]() に対して
に対して
![]()
が満足されているものとします。このとき、![]() は次式で与えます。
は次式で与えます。
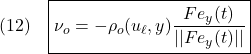
ただし
![]()
[2] SMオブザーバ(8)の状態((1)の状態の推定値)をモデル(2)の状態を追従させることを考えます。そのために次の制御則を考えます。
![]()
このとき、この場合のモデル間の誤差は、(8)と(2)を辺々引き算して
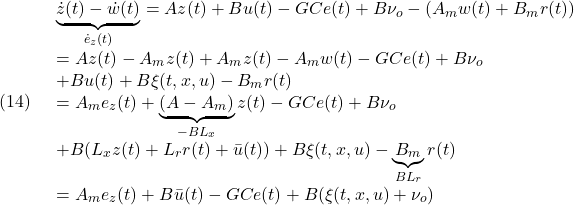
すなわち
![]()
に従います。これに対して、スライディングモード制御
![]()
を適用することを考えます。スイッチング関数は
![]()
とします。これはスイッチング関数(1)またはスイッチング関数(2)の方法で選定します。
●線形制御部を、次式のように決めます。
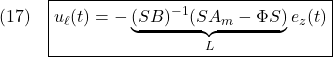
また、スイッチング部を、次式のように決めます。
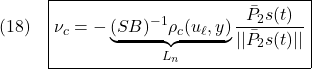
ここで、![]() は適当な安定行列
は適当な安定行列![]() を与えて
を与えて
![]()
の解として求め、また、次の関係を満たすものとします。
![]()
●(15),(18)を(14′)に代入して、モデル間の誤差は
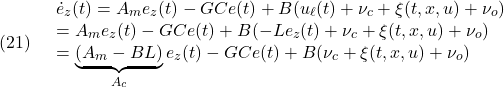
すなわち
![]()
に従います。
[3] 以下では、状態方程式は次のSM標準形をとるように座標変換されているとします。
![Rendered by QuickLaTeX.com \displaystyle{(22)\quad \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} (u(t)+\xi(t,x,u)) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-afe711daafabb0f12e447bb07a3ace73_l3.png)
これに応じて、スイッチング関数(16)を
![Rendered by QuickLaTeX.com \displaystyle{(23)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} e_{z1}(t)\\ e_{z2}(t) \end{array}\right] }_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I_m \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} e_{z1}(t)\\ e_{z2}(t) \end{array}\right] }_{x(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d0776a59ef9ed32eda82a08310faf1f3_l3.png)
と分割します。
(21)は、![]() と
と![]() に注意して
に注意して
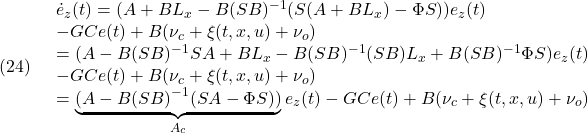
となります。これに対して座標変換
![Rendered by QuickLaTeX.com \displaystyle{(25)\quad \begin{array}{l} \underbrace{\left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right]}_{\bar{e}_z(t)}= \underbrace{\left[\begin{array}{cc} I_{n-m} & 0_{n\times m} \\ S_1 & S_2 \\ \end{array}\right]}_{\bar T} \underbrace{\left[\begin{array}{c} e_{z1}(t)\\ e_{z2}(t) \end{array}\right]}_{e_z(t)}\\ \Leftrightarrow \underbrace{\left[\begin{array}{c} e_{z1}(t)\\ e_{z2}(t) \end{array}\right]}_{e_z(t)}= \underbrace{\left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ -M & S_2^{-1} \\ \end{array}\right]}_{\bar{T}^{-1}} \underbrace{\left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right]}_{\bar{e}_z(t)}\quad(M=S_2^{-1}S_1) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-348e24095f272550ca7b0d85c1be93cf_l3.png)
を行うと、まず(25)を(24)に代入して
![Rendered by QuickLaTeX.com \displaystyle{(26)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} I & 0 \\ -M & S_2^{-1} \\ \end{array}\right] }_{\bar{T}^{-1}} \underbrace{ \left[\begin{array}{c} \dot e_{z1}(t)\\ \dot s(t) \end{array}\right] }_{\dot{\bar{e}}_z(t)}\\ = (\left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] - \left[\begin{array}{c} 0\\ B_2 \end{array}\right] (\left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] \left[\begin{array}{c} 0\\ B_2 \end{array}\right])^{-1}\\ \times(\left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] -\Phi \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right]) ) \underbrace{ \left[\begin{array}{cc} I & 0 \\ -M & S_2^{-1} \\ \end{array}\right] }_{\bar{T}^{-1}} \underbrace{ \left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right] }_{\bar{e}_z(t)}\\ -G Ce(t)+\left[\begin{array}{c} 0\\ B_2 \end{array}\right](\nu_c+\xi(t,x,u)+\nu_o) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8b57169deafca1bae478ad161a8da6bc_l3.png)
左から![]() をかけて
をかけて
![Rendered by QuickLaTeX.com \displaystyle{(27)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot e_{z1}(t)\\ \dot s(t) \end{array}\right] }_{\dot{\bar{e}}_z(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{\bar{T}} (\left[\begin{array}{cc} A_{11}-A_{12}M & A_{12}S_2^{-1} \\ A_{21}-A_{22}M & A_{22}S_2^{-1} \\ \end{array}\right] -\left[\begin{array}{c} 0\\ B_2 \end{array}\right](S_2B_2)^{-1}\\ \times(\left[\begin{array}{cc} S_1 & S_2 \end{array}\right] \left[\begin{array}{cc} A_{11}-A_{12}M & A_{12}S_2^{-1} \\ A_{21}-A_{22}M & A_{22}S_2^{-1} \\ \end{array}\right] -\Phi \left[\begin{array}{cc} 0 & I_m \\ \end{array}\right]) ) \underbrace{ \left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right] }_{\bar{e}_z(t)}\\ -\underbrace{\bar{T}G}_{\bar{G}} Ce(t) +\underbrace{\left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right]}_{\bar{T}} \left[\begin{array}{c} 0\\ B_2 \end{array}\right](\nu_c+\xi(t,x,u)+\nu_o)\\ = (\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22}\\ \end{array}\right] -\left[\begin{array}{c} 0\\ S_2B_2 \end{array}\right](S_2B_2)^{-1}\\ \times(\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22}\\ \end{array}\right] -\Phi \left[\begin{array}{cc} 0 & I_m \\ \end{array}\right]) ) \underbrace{ \left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right] }_{\bar{e}_z(t)}\\ -\bar{G} Ce(t)+\bar{B}(\nu_c+\xi(t,x,u)+\nu_o)\\ =\underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ 0 & \Phi\\ \end{array}\right]}_{A_c} \underbrace{ \left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right] }_{\bar{e}_z(t)} -\bar{G} Ce(t) +\underbrace{\left[\begin{array}{c} 0\\ S_2B_2 \end{array}\right]}_{\bar{B}}(\nu_c+\xi(t,x,u)+\nu_o) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2b1c5781518b0452b1e2a88534ac95c5_l3.png)
ただし
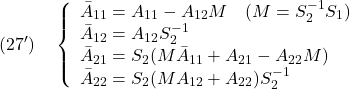
を得ます。ここで、![]() が安定行列となるように行列
が安定行列となるように行列![]() が選ばれているとします。
が選ばれているとします。
これを誤差方程式(9′)と合わせて、閉ループ系は次式で表されます。
![Rendered by QuickLaTeX.com \displaystyle{(28)\quad \begin{array}{l} \left[\begin{array}{c} \dot{e}(t)\\ \dot{\bar{e}}_z(t) \end{array}\right]= \underbrace{\left[\begin{array}{cc} A_o & 0\\ -\bar{G}C & A_c \end{array}\right]}_{A_G} \left[\begin{array}{c} e(t)\\ \bar{e}_z(t) \end{array}\right]\\ + \left[\begin{array}{c} 0\\ \bar{B} \end{array}\right]{\nu}_c + \left[\begin{array}{c} B\\ \bar{B} \end{array}\right]\nu_o + \left[\begin{array}{c} -B\\ \bar{B} \end{array}\right]\xi(t,x,\hat{u}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4780b23f37e18adf37d5716a3c232cfb_l3.png)
●以上に基づく設計手順を、数値例で示します。
| MATLAB |
|

図1 モデル規範・SMオブザーバベース・追従SM制御系のシミュレーション例
Note C93 閉ループ系の安定性
●閉ループ系のダイナミックスは次式で表されます。
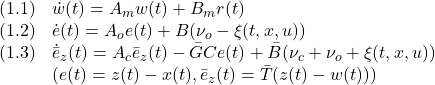
ただし
![Rendered by QuickLaTeX.com \displaystyle{(1.4)\quad \begin{array}{l} A_m=A+BL_x,\ B_m=BL_r\\ A_o=A-GC\\ A_c=\bar{T}(A_m-BL)\bar{T}^{-1}\\ L=(SB)^{-1}(SA_m-\Phi S)\\ \bar{B}=\left[\begin{array}{c} 0\\ S_2B_2 \end{array}\right],\ \bar{G}=\bar{T}G \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-5af9937c0ebb7b0466617bc2ea71afbe_l3.png)
これに対して次のリャプノフ関数を考えます。
![]()
ここで、正定行列![]() 、
、![]() は、それぞれ安定行列
は、それぞれ安定行列![]() 、
、![]() のリャプノフ行列とし、次のリャプノフ方程式の解とします。
のリャプノフ行列とし、次のリャプノフ方程式の解とします。
![]()
●![]() は、リャプノフ方程式
は、リャプノフ方程式
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{\left[\begin{array}{cc} \bar{P}_1 & 0\\ 0 & \bar{P}_2 \end{array}\right]}_{\bar P} \underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]}_{A_c} +\underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]^T}_{A_c^T} \underbrace{\left[\begin{array}{cc} \bar{P}_1 & 0\\ 0 & \bar{P}_2 \end{array}\right]}_{\bar P}<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9f1e612deced36f7c7db9b14fc59dc21_l3.png)
を満足するブロック対角行列とします。ここで、正定行列![]() 、
、![]() は、それぞれ安定行列
は、それぞれ安定行列![]() 、
、![]() に対する次のリャプノフ不等式の解です。
に対する次のリャプノフ不等式の解です。
![]()
![]()
このとき、![]() と
と![]() は、次のリャプノフ不等式の解を構成するとします。
は、次のリャプノフ不等式の解を構成するとします。
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \underbrace{\left[\begin{array}{cc} P & 0\\ 0 & \bar{P} \end{array}\right]}_{P_G} \underbrace{\left[\begin{array}{cc} A_o & 0\\ -\bar{G}C & A_c \end{array}\right]}_{A_G} +\underbrace{\left[\begin{array}{cc} A_o & 0\\ -\bar{G}C & A_c \end{array}\right]^T}_{A_G^T} \underbrace{\left[\begin{array}{cc} P & 0\\ 0 & \bar{P} \end{array}\right]}_{P_G}<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dceeb6208f924a3f6efeaa77bb099a32_l3.png)
これは次式と等価です。
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} PA_o & 0\\ -\bar{P}\bar{G}C & \bar{P}A_c \end{array}\right]}_{P_GA_G}+ \underbrace{\left[\begin{array}{cc} PA_o & 0\\ -\bar{P}\bar{G}C & \bar{P}A_c \end{array}\right]^T}_{(P_GA_G)^T} =\left[\begin{array}{cc} -Q & -C^T\bar{G}^T\bar{P}\\ -\bar{P}\bar{G}C & \bar{P}A_c+A_c^T\bar{P} \end{array}\right]<0\\ \Leftrightarrow \bar{P}A_c+A_c^T\bar{P}+\bar{P}\bar{G}CQ^{-1}C^T\bar{G}^T\bar{P}<0\\ \Leftrightarrow A_c\bar{P}^{-1}+\bar{P}^{-1}A_c^T+\bar{G}CQ^{-1}C^T\bar{G}^T<0\\ \Leftrightarrow A_c\bar{P}^{-1}+\bar{P}^{-1}A_c^T+\bar{G}CQ^{-1}C^T\bar{G}^T=-\bar{Q}\quad(\bar{Q}>0) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c62b77d490c2fb89c0065a176246cf86_l3.png)
ここで、新しいパラメータ![]() を導入し、次の公式を用いています。
を導入し、次の公式を用いています。
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{lll} && \left[\begin{array}{cc} P & M \\ M^T & Q \end{array}\right]<0\\ &\Leftrightarrow& P-MQ^{-1}M^T<0,\ Q<0\\ &\Leftrightarrow& P<0,\ Q-M^TP^{-1}M<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eee622434bc9e2fc505eb899dbb107cb_l3.png) |
いま適当な![]() と
と![]() を与えて、
を与えて、
![]()
![]()
を解いて、![]() と
と![]() を定めるものとします。このとき(7)は
を定めるものとします。このとき(7)は
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]}_{A_c} \underbrace{\left[\begin{array}{cc} \bar{P}_1^{-1} & 0\\ 0 & \bar{P}_2^{-1} \end{array}\right]}_{\bar{P}^{-1}} + \underbrace{\left[\begin{array}{cc} \bar{P}_1^{-1} & 0\\ 0 & \bar{P}_2^{-1} \end{array}\right]}_{\bar{P}^{-1}} \underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]^T}_{A_c^T}\\ +\underbrace{\left[\begin{array}{c} \bar{G}_1\\ \bar{G}_2 \end{array}\right]}_{\bar{G}} \underbrace{CQ^{-1}C^T}_{Q_{22}} \underbrace{\left[\begin{array}{c} \bar{G}_1\\ \bar{G}_2 \end{array}\right]^T}_{\bar{G}^T}\\ = \underbrace{\left[\begin{array}{cc} \bar{A}_{11}\bar{P}_1^{-1} & \bar{A}_{12}\bar{P}_2^{-1}\\ 0 & \Phi \bar{P}_2^{-1} \end{array}\right]}_{A_c\bar{P}^{-1}} + \underbrace{\left[\begin{array}{cc} \bar{A}_{11}\bar{P}_1^{-1} & \bar{A}_{12}\bar{P}_2^{-1}\\ 0 & \Phi \bar{P}_2^{-1} \end{array}\right]^T}_{(A_c\bar{P}^{-1})^T}\\ +\underbrace{\left[\begin{array}{cc} \bar{G}_1Q_{22}\bar{G}_1^T &\bar{G}_1Q_{22}\bar{G}_2^T\\ \bar{G}_2Q_{22}\bar{G}_1^T &\bar{G}_2Q_{22}\bar{G}_2^T \end{array}\right]}_{\bar{G}CQ^{-1}C^T\bar{G}^T}\\ = \left[\begin{array}{cc} \bar{A}_{11}\bar{P}_1^{-1}+\bar{P}_1^{-1}\bar{A}_{11}^T+\bar{G}_1Q_{22}\bar{G}_1^T & \bar{A}_{12}\bar{P}_2^{-1}+\bar{G}_1Q_{22}\bar{G}_2^T\\ \bar{P}_2^{-1}\bar{A}_{12}^T+\bar{G}_2Q_{22}\bar{G}_1^T & \Phi\bar{P}_2^{-1}+\bar{P}_2^{-1}\Phi^T+\bar{G}_2Q_{22}\bar{G}_2^T \end{array}\right]\\ = \left[\begin{array}{cc} -\hat{Q}_1+\bar{G}_1Q_{22}\bar{G}_1^T & \bar{A}_{12}\bar{P}_2^{-1}+\bar{G}_1Q_{22}\bar{G}_2^T\\ \bar{P}_2^{-1}\bar{A}_{12}^T+\bar{G}_2Q_{22}\bar{G}_1^T & -\hat{Q}_2+\bar{G}_2Q_{22}\bar{G}_2^T \end{array}\right]<0\\ \Leftrightarrow \left\{\begin{array}{l} \bar{G}_1Q_{22}\bar{G}_1^T +(\bar{A}_{12}\bar{P}_2^{-1}+\bar{G}_1Q_{22}\bar{G}_2^T)\\ \times(\bar{G}_2Q_{22}\bar{G}_2^T -\hat{Q}_2)^{-1}(\bar{P}_2^{-1}\bar{A}_{12}^T+\bar{G}_2Q_{22}\bar{G}_1^T) <\hat{Q}_1\\ \bar{G}_2Q_{22}\bar{G}_2^T <\hat{Q}_2 \end{array}\right. \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d2a4be3ea4336e3bad8a74302a1a87d8_l3.png)
となります。したがって、この制約を(8)の![]() 、(9)の
、(9)の![]() に付けておきます。
に付けておきます。
●以上の準備の下で次式が示され、閉ループ系のリャプノフ安定性が成り立ちます。

ここで、次の平方完成を行っています。
![]()
また、次が成り立つことを用いています。
![]()
まず、(14.1)は
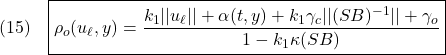
を仮定すると、これを変形して得られる
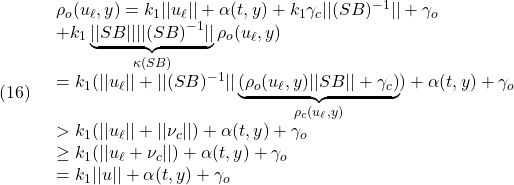
を用いて
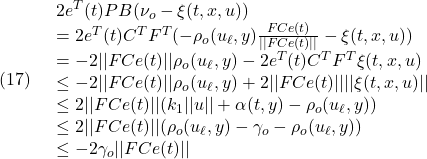
次に、(14.2)は
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \begin{array}{l} 2\bar{e}_z^T(t)\bar{P}\bar{B}(\nu_c+\nu_o+\xi(t,x,u))\\ =2\underbrace{\left[\begin{array}{c} e_{z1}(t)\\ s(t) \end{array}\right]^T}_{\zeta^T(t)} \underbrace{\left[\begin{array}{cc} \bar{P}_1 & 0\\ 0 & \bar{P}_2 \end{array}\right]}_{\bar P} \underbrace{\left[\begin{array}{c} 0\\ S_2B_2 \end{array}\right]}_{\bar{B}}(\nu_c+\nu_o+\xi(t,x,u))\\ =-2s^T(t)\bar{P}_2(S_2B_2)\rho_o(u_\ell,y)\frac{FCe(t)}{||FCe(t)||}\\ -2s^T(t)\bar{P}_2(S_2B_2)(S_2B_2)^{-1}\rho_c(u_\ell,y) \frac{\bar{P}_2s(t)}{||\bar{P}_2s(t)||}+2s^T(t)\bar{P}_2(S_2B_2)\xi(t,x,u)\\ =-2s^T(t)\bar{P}_2(S_2B_2)\rho_o(u_\ell,y)\frac{B^TPe(t)}{||B^TPe(t)||}\\ -2s^T(t)\bar{P}_2\rho_c(u_\ell,y)\frac{\bar{P}_2s(t)}{||\bar{P}_2s(t)||}+2s^T(t)\bar{P}_2(S_2B_2)\xi(t,x,u)\\ \le 2||\bar{P}_2s(t)||||S_2B_2||\rho_o(u_\ell,y)-2\rho_c(u_\ell,y)||\bar{P}_2s(t)||\\ +2||\bar{P}_2s(t)||||S_2B_2||||\xi(t,x,u)||\\ \le 2||\bar{P}_2s(t)||(\rho_o(u_\ell,y)||S_2B_2||-\rho_c(u_\ell,y))\\ +2||\bar{P}_2s(t)||||S_2B_2||(k_1||u||+\alpha(t,y))\\ \le 2||\bar{P}_2s(t)||(\rho_c(u_\ell,y)-\gamma_c-\rho_c(u_\ell,y))\\ +2||\bar{P}_2s(t)||||S_2B_2||(\rho_o(u_\ell,y)-\gamma_o)\\ =-2\underbrace{(\gamma_c-||S_2B_2||(\rho_o(u_\ell,y)-\gamma_o))}_{\gamma_c'}||\bar{P}_2s(t)|| \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b653afff2b1cd408b6383ca8513746bc_l3.png)
追従SMI-OBS制御
SMオブザーバベース・追従SMI制御…Homework
[0] まず準備の復習から始めます。
制御対象の状態空間表現として次式を考えます。
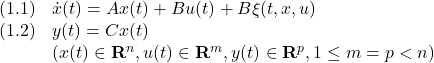
これに対して、積分動作
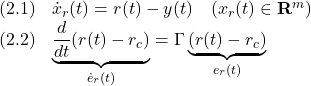
とSM状態オブザーバ
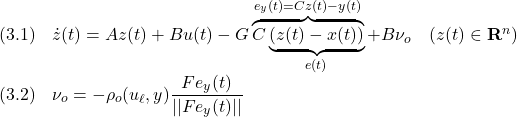
を考えます。
●以下では、![]() の代わりに
の代わりに![]() を用いた制御則
を用いた制御則![]() を
を![]() で表します。
で表します。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \hat{u}(t)=\underbrace{-L\left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right]-L_rr(t)+L_{\dot r}\dot{r}(t)}_{\hat {u}_L}+\hat{\nu}_c\\ \displaystyle{\hat{\nu}_c=L_n\frac{P_2(S\left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right]-S_rr(t))}{||P_2(S\left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right]-S_rr(t))||}}\\ L=(S\tilde{B})^{-1}(S\tilde{A}-\Phi S)\\ L_r=(S\tilde{B})^{-1}(\Phi S_r+S_2MB_r)\\ L_{\dot r}=(S\tilde{B})^{-1}S_r\\ L_n=(S\tilde{B})^{-1}\rho_c(\hat{u}_L,y) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-024f6914b3128301f6c6ae196567ba16_l3.png)
ここでスイッチング関数は、![]() を
を![]() と分割して、次式で表されるとしています。
と分割して、次式で表されるとしています。
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right] %}_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I_m \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right] %}_{x(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-027f6a001ff2fd6efdf5b3456395f8b3_l3.png)
[1] (3.1)から(1.1)を辺々引き算して、誤差方程式
![]()
を得ます。![]() を用いて、(2.1)は
を用いて、(2.1)は
![]()
となります。また(3.1)は、![]() の代わりに
の代わりに![]() を用いることにすれば
を用いることにすれば
![]()
と表せます。
●(7)と(8)をまとめて
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \boxed{\begin{array}{l} \left[\begin{array}{c} \dot x_r(t)\\ \dot z(t) \end{array}\right] = \left[\begin{array}{cc} 0_{m\times m} & -C \\ 0_{n\times m} & A \\ \end{array}\right] \left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right] + \left[\begin{array}{c} I_p\\ -G \end{array}\right] e_y(t)\\ + \left[\begin{array}{c} r(t)\\ B(\hat{u}(t)+\nu_o) \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-65eb681dec39ab633fe7a5bbc2b85d2c_l3.png)
ここで座標変換
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} \left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right]= \underbrace{\left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ S_1 & S_2 \\ \end{array}\right]}_{\bar T} \left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]\\ \Leftrightarrow \left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]= \underbrace{\left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ -M & S_2^{-1} \\ \end{array}\right]}_{\bar{T}^{-1}} \left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right]\quad(M=S_2^{-1}S_1) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4df32cc888cc01697c0d0a7a4a8de076_l3.png)
を行うと
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \bar{T}^{-1} \left[\begin{array}{c} \dot{\tilde{z}}_1(t)\\ \dot{s}(t) \end{array}\right] = \underbrace{\left[\begin{array}{cc|c} 0_{m\times m} & -C_1 & -C_2 \\ 0_{n-m\times m} & A_{11} & A_{12} \\\hline 0_{m\times m} & A_{21} & A_{22} \end{array}\right]}_{\left[\begin{array}{cc} \tilde{A}_{11} & \tilde{A}_{12} \\ \tilde{A}_{21} & \tilde{A}_{22} \end{array}\right]} \left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ -M & S_2^{-1} \\ \end{array}\right] \left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right]\\ + \left[\begin{array}{c} I_p\\ -G_1\\\hline -G_2 \end{array}\right] e_y(t) + \left[\begin{array}{c} r(t)\\ 0\\\hline B_2(\hat{u}(t)+\nu_o) \end{array}\right]\\ = \underbrace{\left[\begin{array}{cc} \tilde{A}_{11}-\tilde{A}_{12}M & \tilde{A}_{12}S_2^{-1}\\ \tilde{A}_{21}-\tilde{A}_{22}M & \tilde{A}_{22}S_2^{-1} \end{array}\right]}_{\tilde{A}\bar{T}^{-1}} \left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right] - \left[\begin{array}{c} \bar{G}_1\\ G_2 \end{array}\right] e_y(t)\\ + \left[\begin{array}{c} B_rr(t)\\ B_2(\hat{u}(t)+\nu_o) \end{array}\right]\\ (\left[\begin{array}{c} G_1\\ G_2 \end{array}\right] =\left[\begin{array}{c} A_{12}C_2^{-1} \\ A_{22}C_2^{-1}-C_2^{-1}A_{22}^S \end{array}\right], \quad\bar{G}_1= \left[\begin{array}{c} -I_p\\ G_1 \end{array}\right]) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-da08553d36abc2e12fd0c39618cc6763_l3.png)
したがって
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \left[\begin{array}{c} \dot{\tilde{z}}_1(t)\\ \dot{s}(t) \end{array}\right] = \underbrace{\left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ S_1 & S_2 \\ \end{array}\right] \left[\begin{array}{cc} \tilde{A}_{11}-\tilde{A}_{12}M & \tilde{A}_{12}S_2^{-1}\\ \tilde{A}_{21}-\tilde{A}_{22}M & \tilde{A}_{22}S_2^{-1} \end{array}\right]}_{\bar{T}\tilde{A}\bar{T}^{-1}} \left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right]\\ - \left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ S_1 & S_2 \\ \end{array}\right] \left[\begin{array}{c} \bar{G}_1\\ G_2 \end{array}\right] e_y(t) + \left[\begin{array}{cc} I_{n} & 0_{n\times m} \\ S_1 & S_2 \\ \end{array}\right] \left[\begin{array}{c} B_rr(t)\\ B_2(\hat{u}(t)+\nu_o) \end{array}\right]\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1da3c1791a8da84361163ffde267324f_l3.png)
すなわち、第1ブロック行は
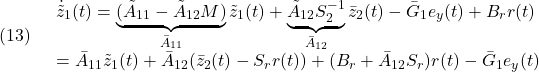
第2ブロック行は(5)を用いて、![]() とおいて
とおいて
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \begin{array}{l} \dot{s}(t)= \underbrace{((S_1\bar{A}_{11}+S_2(\tilde{A}_{21}-\tilde{A}_{22}M))\tilde{z}_1(t)+(S_1\bar{A}_{12}+S_2\tilde{A}_{22}S_2^{-1})s(t)}_{S\tilde{A}\bar{T}^{-1}\left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right]=S\tilde{A}\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]}\\ -\underbrace{(S_1\bar{G}_1+S_2G_2)}_{\bar G_2}e_y(t)+S_1B_rr(t)\\ +\underbrace{S_2B_2}_{\Lambda}(L\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]+L_rr(t)+S_r\dot{r}(t)+\hat{\nu}_c+\nu_o)\\ =S\tilde{A}\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]-\bar{G}_2e_y(t)+S_1B_rr(t)\\ +\Lambda(-\Lambda^{-1}(S\tilde{A}-\Phi S)\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]-\Lambda^{-1}(\Phi S_r+S_2MB_r)r(t)+\Lambda^{-1}S_r\dot{r}(t))\\ +\Lambda(\hat{\nu}_c+\nu_o)\\ =S\tilde{A}\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]-\bar{G}_2e_y(t)+S_1B_rr(t)\\ -(S\tilde{A}-\Phi S)\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]-(\Phi S_r+S_2MB_r)r(t)+S_r\dot{r}(t)+\Lambda(\hat{\nu}_c+\nu_o)\\ =\Phi (\underbrace{S\left[\begin{array}{c} \tilde z_1(t)\\ \tilde z_2(t) \end{array}\right]}_{s(t)}-S_rr(t))+S_r\dot{r}(t)-\bar{G}_2e_y(t)+\Lambda(\hat{\nu}_c+\nu_o) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ebec66163067a3490f53ebceab553d5e_l3.png)
(13)と(14)の結果は、次のようにまとめられます。
![]()
ここで
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \begin{array}{l} \underbrace{\left[\begin{array}{c} \zeta_1(t)\\ \zeta_2(t) \end{array}\right]}_{\zeta(t)}= \left[\begin{array}{c} \tilde z_1(t)\\ s(t) \end{array}\right]+ \left[\begin{array}{c} \bar{A}_{11}^{-1}(\bar{A}_{12}S_r+B_r)r_c\\ -S_rr(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c676bab7a7f2b7c956feb633f175faa2_l3.png)
を定義すると
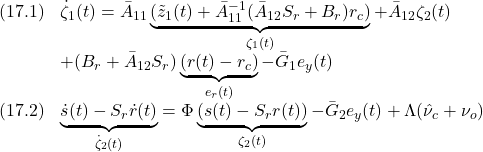
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \begin{array}{l} \underbrace{\left[\begin{array}{c} \dot \zeta_1(t)\\ \dot \zeta_2(t) \end{array}\right]}_{\dot{\zeta}(t)}= \underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]}_{A_c} \underbrace{\left[\begin{array}{c} \zeta_1(t)\\ \zeta_2(t) \end{array}\right]}_{\zeta(t)}\\ - \underbrace{\left[\begin{array}{c} \bar{G}_1\\ \bar{G}_2 \end{array}\right]}_{\bar{G}} \underbrace{e_y(t)}_{Ce(t)} + \underbrace{\left[\begin{array}{c} B_r+\bar{A}_{12}S_r\\ 0 \end{array}\right]}_{\bar{G}_r}e_r(t) + \underbrace{\left[\begin{array}{c} 0\\ \Lambda \end{array}\right]}_{\bar\Lambda}(\hat{\nu}_c+\nu_o) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e698246bb04c91be373318b20c960104_l3.png)
を得ます。これを誤差方程式(6)すなわち
![]()
と合わせて、閉ループ系は次式で表されます。
![Rendered by QuickLaTeX.com \displaystyle{(19)\quad \begin{array}{l} \left[\begin{array}{c} \dot{e}(t)\\ \dot \zeta(t) \end{array}\right]= \underbrace{\left[\begin{array}{cc} A_o & 0\\ -\bar{G}C & A_c \end{array}\right]}_{A_G} \left[\begin{array}{c} e(t)\\ \zeta(t) \end{array}\right]\\ + \left[\begin{array}{c} 0\\ \bar{G}_r \end{array}\right]e_r(t) + \left[\begin{array}{c} B\\ \bar\Lambda \end{array}\right]\nu_o + \left[\begin{array}{c} 0\\ \bar\Lambda \end{array}\right]\hat{\nu}_c - \left[\begin{array}{c} B\\ 0 \end{array}\right]\xi(t,x,\hat{u}) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8e6c6626c17ebcf75a8e1b658d9e4738_l3.png)
ここまでの手順を、関数ob_smiとしてプログラムすることにします。
●以上に基づく設計手順を、数値例で示します。
| MATLAB |
|

図1 SMオブザーバベースSMI追従制御系のシミュレーション例
Note C92 閉ループ系の安定性
●閉ループ系は(19)と(3.2)を合わせて
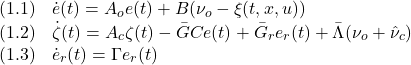
で表されます。これに対して次のリャプノフ関数を考えます。
![]()
ここで、正定行列![]() 、
、![]() 、
、![]() は、それぞれ安定行列
は、それぞれ安定行列![]() 、
、![]() 、
、![]() のリャプノフ行列とし、次のリャプノフ方程式の解とします。
のリャプノフ行列とし、次のリャプノフ方程式の解とします。
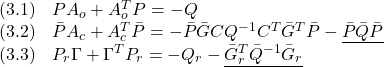
●![]() は、リャプノフ方程式
は、リャプノフ方程式
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \underbrace{\left[\begin{array}{cc} \bar{P}_1 & 0\\ 0 & \bar{P}_2 \end{array}\right]}_{\bar P} \underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]}_{A_c} +\underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]^T}_{A_c^T} \underbrace{\left[\begin{array}{cc} \bar{P}_1 & 0\\ 0 & \bar{P}_2 \end{array}\right]}_{\bar P}<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9f1e612deced36f7c7db9b14fc59dc21_l3.png)
を満足するブロック対角行列とします。ここで、正定行列![]() 、
、![]() は、それぞれ安定行列
は、それぞれ安定行列![]() 、
、![]() に対する次のリャプノフ不等式の解です。
に対する次のリャプノフ不等式の解です。
![]()
![]()
このとき、![]() と
と![]() は、次のリャプノフ不等式の解を構成するとします。
は、次のリャプノフ不等式の解を構成するとします。
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \underbrace{\left[\begin{array}{cc} P & 0\\ 0 & \bar{P} \end{array}\right]}_{P_G} \underbrace{\left[\begin{array}{cc} A_o & 0\\ -\bar{G}C & A_c \end{array}\right]}_{A_G} +\underbrace{\left[\begin{array}{cc} A_o & 0\\ -\bar{G}C & A_c \end{array}\right]^T}_{A_G^T} \underbrace{\left[\begin{array}{cc} P & 0\\ 0 & \bar{P} \end{array}\right]}_{P_G}<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dceeb6208f924a3f6efeaa77bb099a32_l3.png)
これは次式と等価です。
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} PA_o & 0\\ -\bar{P}\bar{G}C & \bar{P}A_c \end{array}\right]}_{P_GA_G}+ \underbrace{\left[\begin{array}{cc} PA_o & 0\\ -\bar{P}\bar{G}C & \bar{P}A_c \end{array}\right]^T}_{(P_GA_G)^T} =\left[\begin{array}{cc} -Q & -C^T\bar{G}^T\bar{P}\\ -\bar{P}\bar{G}C & \bar{P}A_c+A_c^T\bar{P} \end{array}\right]<0\\ \Leftrightarrow \bar{P}A_c+A_c^T\bar{P}+\bar{P}\bar{G}CQ^{-1}C^T\bar{G}^T\bar{P}<0\\ \Leftrightarrow A_c\bar{P}^{-1}+\bar{P}^{-1}A_c^T+\bar{G}CQ^{-1}C^T\bar{G}^T<0\\ \Leftrightarrow A_c\bar{P}^{-1}+\bar{P}^{-1}A_c^T+\bar{G}CQ^{-1}C^T\bar{G}^T=-\bar{Q}\quad(\bar{Q}>0) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c62b77d490c2fb89c0065a176246cf86_l3.png)
ここで、新しいパラメータ![]() を導入し、次の公式を用いています。
を導入し、次の公式を用いています。
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{lll} && \left[\begin{array}{cc} P & M \\ M^T & Q \end{array}\right]<0\\ &\Leftrightarrow& P-MQ^{-1}M^T<0,\ Q<0\\ &\Leftrightarrow& P<0,\ Q-M^TP^{-1}M<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eee622434bc9e2fc505eb899dbb107cb_l3.png) |
いま適当な![]() と
と![]() を与えて、
を与えて、
![]()
![]()
を解いて、![]() と
と![]() を定めるものとします。このとき(7)は
を定めるものとします。このとき(7)は
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]}_{A_c} \underbrace{\left[\begin{array}{cc} \bar{P}_1^{-1} & 0\\ 0 & \bar{P}_2^{-1} \end{array}\right]}_{\bar{P}^{-1}} + \underbrace{\left[\begin{array}{cc} \bar{P}_1^{-1} & 0\\ 0 & \bar{P}_2^{-1} \end{array}\right]}_{\bar{P}^{-1}} \underbrace{\left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12}\\ 0 & \Phi \end{array}\right]^T}_{A_c^T}\\ +\underbrace{\left[\begin{array}{c} \bar{G}_1\\ \bar{G}_2 \end{array}\right]}_{\bar{G}} \underbrace{CQ^{-1}C^T}_{Q_{22}} \underbrace{\left[\begin{array}{c} \bar{G}_1\\ \bar{G}_2 \end{array}\right]^T}_{\bar{G}^T}\\ = \underbrace{\left[\begin{array}{cc} \bar{A}_{11}\bar{P}_1^{-1} & \bar{A}_{12}\bar{P}_2^{-1}\\ 0 & \Phi \bar{P}_2^{-1} \end{array}\right]}_{A_c\bar{P}^{-1}} + \underbrace{\left[\begin{array}{cc} \bar{A}_{11}\bar{P}_1^{-1} & \bar{A}_{12}\bar{P}_2^{-1}\\ 0 & \Phi \bar{P}_2^{-1} \end{array}\right]^T}_{(A_c\bar{P}^{-1})^T}\\ +\underbrace{\left[\begin{array}{cc} \bar{G}_1Q_{22}\bar{G}_1^T &\bar{G}_1Q_{22}\bar{G}_2^T\\ \bar{G}_2Q_{22}\bar{G}_1^T &\bar{G}_2Q_{22}\bar{G}_2^T \end{array}\right]}_{\bar{G}CQ^{-1}C^T\bar{G}^T}\\ = \left[\begin{array}{cc} \bar{A}_{11}\bar{P}_1^{-1}+\bar{P}_1^{-1}\bar{A}_{11}^T+\bar{G}_1Q_{22}\bar{G}_1^T & \bar{A}_{12}\bar{P}_2^{-1}+\bar{G}_1Q_{22}\bar{G}_2^T\\ \bar{P}_2^{-1}\bar{A}_{12}^T+\bar{G}_2Q_{22}\bar{G}_1^T & \Phi\bar{P}_2^{-1}+\bar{P}_2^{-1}\Phi^T+\bar{G}_2Q_{22}\bar{G}_2^T \end{array}\right]\\ = \left[\begin{array}{cc} -\hat{Q}_1+\bar{G}_1Q_{22}\bar{G}_1^T & \bar{A}_{12}\bar{P}_2^{-1}+\bar{G}_1Q_{22}\bar{G}_2^T\\ \bar{P}_2^{-1}\bar{A}_{12}^T+\bar{G}_2Q_{22}\bar{G}_1^T & -\hat{Q}_2+\bar{G}_2Q_{22}\bar{G}_2^T \end{array}\right]<0\\ \Leftrightarrow \left\{\begin{array}{l} \bar{G}_1Q_{22}\bar{G}_1^T +(\bar{A}_{12}\bar{P}_2^{-1}+\bar{G}_1Q_{22}\bar{G}_2^T)\\ \times(\bar{G}_2Q_{22}\bar{G}_2^T -\hat{Q}_2)^{-1}(\bar{P}_2^{-1}\bar{A}_{12}^T+\bar{G}_2Q_{22}\bar{G}_1^T) <\hat{Q}_1\\ \bar{G}_2Q_{22}\bar{G}_2^T <\hat{Q}_2 \end{array}\right. \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d2a4be3ea4336e3bad8a74302a1a87d8_l3.png)
となります。したがって、この制約を(8)の![]() 、(9)の
、(9)の![]() に付けておきます。
に付けておきます。
●以上の準備の下で次式が示され、閉ループ系のリャプノフ安定性が成り立ちます。

ここで、次の平方完成を行っています。
また、次が成り立つことを用いています。
![]()
まず、(14.1)は
![]()
を変形して得られる
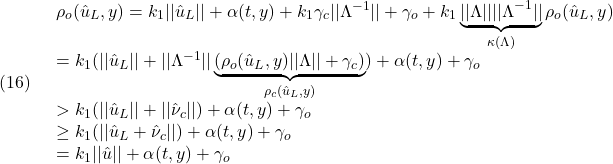
を用いて
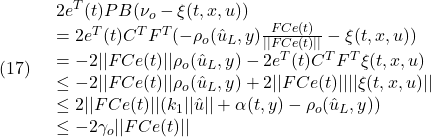
次に、(14.2)は
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \begin{array}{l} 2\zeta^T(t)\bar{P}\bar{\Lambda}(\nu_o+\hat{\nu}_c)\\ =2\underbrace{\left[\begin{array}{c} \zeta_1(t)\\ \zeta_2(t) \end{array}\right]^T}_{\zeta^T(t)} \underbrace{\left[\begin{array}{cc} \bar{P}_1 & 0\\ 0 & \bar{P}_2 \end{array}\right]}_{\bar P} \underbrace{\left[\begin{array}{c} 0\\ \Lambda \end{array}\right]}_{\bar\Lambda}(\nu_o+\hat{\nu}_c)\\ =-2\zeta_2^T(t)\bar{P}_2\Lambda\rho_o(\hat{u}_L,y)\frac{FCe(t)}{||FCe(t)||}-2\zeta_2^T(t)\bar{P}_2\Lambda\rho_c(\hat{u}_L,y)\Lambda^{-1} \frac{\bar{P}_2\zeta_2(t)}{||\bar{P}_2\zeta_2(t)||}\\ \le 2||\bar{P}_2\zeta_2(t)||||\Lambda||\rho_o(\hat{u}_L,y)-2\rho_c(\hat{u}_L,y)||\bar{P}_2\zeta_2(t)||\\ =2||\bar{P}_2\zeta_2(t)||(\rho_o(\hat{u}_L,y)||\Lambda||-\rho_c(\hat{u}_L,y))\\ =2||\bar{P}_2\zeta_2(t)||(\rho_c(\hat{u}_L,y)-\gamma_c-\rho_c(\hat{u}_L,y))\\ =-2\gamma_c||\bar{P}_2\zeta_2(t)|| \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-79955beab6ef0705346e5157fe6ced17_l3.png)
Note C92-2 スライディングモードの検討
このSM制御系では、超平面
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad {\cal S}_c=\left\{\left[\begin{array}{c} e\\ \zeta_1\\ \zeta_2 \end{array}\right]\in{\bf R}^{2n+p}: \left\{\begin{array}{l} e_y(t)=Ce(t)=Cz(t)-y(t)=0\\ \zeta_2(t)=s(t)-S_rr(t)=0 \end{array}\right. \right\} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-198a3c5b246cf20144027bbb223bb2b6_l3.png)
においてスライディングモードが生じることを示します。そのために
に対して次のリャプノフ関数を考えます。
![]()
この時間微分は次のように計算できます。
![]()
(4)の第1項は、![]() より
より
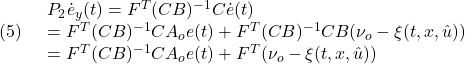
また、(14.1)は![]() を適用して
を適用して
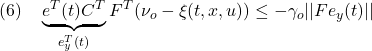
したがって
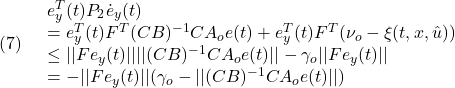
(4)の第2項は、
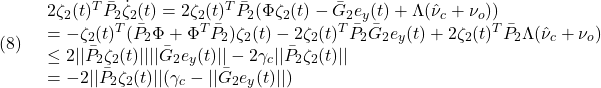
したがって
![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \Omega_\eta=\left\{\left[\begin{array}{c} e\\ \zeta_1\\ \zeta_2 \end{array}\right]\in{\bf R}^{2n+p}: \left\{\begin{array}{l} ||(CB)^{-1}CA_oe(t)||<\gamma_o-\eta\\ ||\bar{G}_2e_y(t)||<\gamma_c-\eta \end{array}\right. \right\} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ba3afedc3c9f5d435d671a0460dfdda4_l3.png)
においては
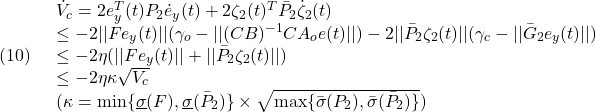
が成り立ち、これより有限時間で![]() となり、超平面
となり、超平面![]() に突入することが分かります(
に突入することが分かります(![]() の表現式はEdwards and Spurgeonによるものです)。
の表現式はEdwards and Spurgeonによるものです)。
準備
SMオブザーバ
[1] 制御対象の状態空間表現として次式を考えます。
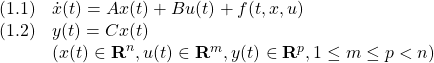
ただし、![]() はモデル誤差、非線形要素、外乱などの影響を表し、次のマッチング条件を満たすとします。
はモデル誤差、非線形要素、外乱などの影響を表し、次のマッチング条件を満たすとします。
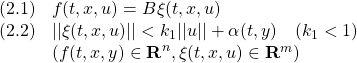
さらに次の3つを仮定します。
仮定![]()
![]() は可制御対
は可制御対
仮定![]()
![]() (相対次数1)
(相対次数1)
仮定![]()
![]() の不変零点は安定(最小位相系)
の不変零点は安定(最小位相系)
一般性を失うことなく、(1)は次のSM標準形であるとします。
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{ll} (3.1) & \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t)\\ (3.2) & y(t) = \underbrace{ \left[\begin{array}{cc} C_1 & C_2 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6ec74dc0c4572a9c7fa91295a5ba283b_l3.png)
●これに対して、次のSMオブザーバを考えます。
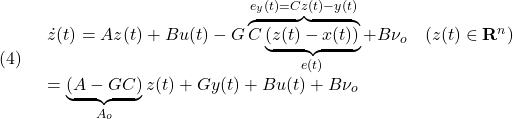
ここで、![]() は
は![]() が安定行列となるように選ばれているとします。また、
が安定行列となるように選ばれているとします。また、
![]()
を満足する![]() と、ある
と、ある![]() に対して
に対して
![]()
が満足されているものとします。このとき、![]() は
は
![]()
のように与えます。上の仮定![]() と
と![]() の下で、SMオブザーバの誤差は次の超平面上でスライディングモードを達成します。
の下で、SMオブザーバの誤差は次の超平面上でスライディングモードを達成します。
![]()
●以下では、![]() を仮定します。座標変換
を仮定します。座標変換
![]()
を行なうと
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} {\cal A}_{11} & {\cal A}_{12}\\ {\cal A}_{21} & {\cal A}_{22} \end{array}\right]}_{{\cal A}}\\ =\underbrace{\left[\begin{array}{cc} {A}_{11}-{A}_{12}C_2^{-1}C_1 & A_{12}C_2^{-1} \\ C_1{\cal A}_{11}+C_2A_{21}-C_2A_{22}C_2^{-1}C_1 & C_1A_{12}C_2^{-1}+C_2A_{22}C_2^{-1} \end{array}\right] }_{T_cAT_c^{-1}}\\ {\cal B}=\underbrace{\left[\begin{array}{c} 0 \\ C_2B_2 \end{array}\right] }_{T_cB}\\ {\cal C}=\underbrace{\left[\begin{array}{cc} 0 & I_p \end{array}\right] }_{CT_c^{-1}}\\ {\cal P}= \underbrace{\left[\begin{array}{cc} I_{n-p} & 0 \\ -C_2^{-1}C_1 & C_2^{-1} \end{array}\right]^T \left[\begin{array}{cc} P_1 & 0\\ 0 & P_2 \end{array}\right] \left[\begin{array}{cc} I_{n-p} & 0 \\ -C_2^{-1}C_1 & C_2^{-1} \end{array}\right] }_{T_c^TPT_c}\\ =\left[\begin{array}{cc} I_{n-p} & -C_1^TC_2^{-T} \\ 0 & C_2^{-T} \end{array}\right]^T \left[\begin{array}{cc} P_1 & 0 \\ -P_2C_2^{-1}C_1 & P_2C_2^{-1} \end{array}\right]\\ =\left[\begin{array}{cc} P_1+C_1^TC_2^{-T}P_2C_2^{-1}C_1 & -C_1^TC_2^{-T}P_2C_2^{-1}\\ -C_2^{-T}P_2C_2^{-1}C_1 & C_2^{-T}P_2C_2^{-1} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-23b25bc8ecbab40ee6e5976ebefccd82_l3.png)
を得ます。したがって
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} G=\underbrace{\left[\begin{array}{cc} I_{n-p} & 0 \\ -C_2^{-1}C_1 & C_2^{-1} \end{array}\right] }_{T_c^{-1}} \underbrace{\left[\begin{array}{c} A_{12}C_2^{-1}\\ C_1A_{12}C_2^{-1}+C_2A_{22}C_2^{-1}-{\cal A}_{22}^s \end{array}\right] }_{\left[\begin{array}{c} {\cal A}_{12}\\ {\cal A}_{22}-{\cal A}_{22}^s \end{array}\right]}\\ =\left[\begin{array}{c} A_{12}C_2^{-1} \\ A_{22}C_2^{-1}-C_2^{-1}A_{22}^S \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6f55e042f0e71a68f90ee8ddf5588d0c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \underbrace{\left[\begin{array}{cc} P_1+C_1^TC_2^{-T}P_2C_2^{-1}C_1 & -C_1^TC_2^{-T}P_2C_2^{-1}\\ -C_2^{-T}P_2C_2^{-1}C_1 & C_2^{-T}P_2C_2^{-1} \end{array}\right] \left[\begin{array}{c} 0 \\ C_2B_2 \end{array}\right] }_{{\cal P}{\cal B}} = \underbrace{\left[\begin{array}{cc} 0 & I_p \end{array}\right]^T }_{{\cal C}^T} F^T\\ \Rightarrow F=(C_2^{-T}P_2C_2^{-1}C_2B_2)^T=B_2^TP_2C_2^{-1} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d8371d4e684ace7595130cce38802819_l3.png)
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \boxed{\begin{array}{l} G= \left[\begin{array}{c} A_{12}C_2^{-1} \\ A_{22}C_2^{-1}-C_2^{-1}A_{22}^S \end{array}\right]\\ F=B_2^TP_2C_2^{-1} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-acc6f79294b0cb173b67e46276765b51_l3.png)
ここまでの手順を、関数smobs3としてプログラムすることにします。
追従SMI制御
[2] 制御対象
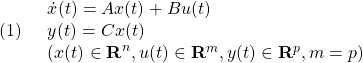
の出力を、コマンド(次式の解)
![]()
に追従させることを考えます(![]() は安定行列)。そのために、積分動作
は安定行列)。そのために、積分動作
![]()
を導入し、次の拡大系を構成します。ここで、(1)はすでに標準形であるとしています。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \left[\begin{array}{c} \dot x_r(t)\\ \dot x(t) \end{array}\right] = \left[\begin{array}{c|cc} 0 & -C_1 & -C_2\\\hline 0 & A_{11} & A_{12} \\ 0 & A_{21} & A_{22} \end{array}\right] \left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right] + \left[\begin{array}{c} 0\\\hline 0\\ B_2 \end{array}\right] u(t) + \left[\begin{array}{c} I_m \\\hline 0 \\ 0 \end{array}\right] r(t)\\ (x_r(t)\in{\rm\bf R}^m, x(t)\in{\rm\bf R}^n) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1ab4b378422eddd1bff475a2408082e2_l3.png)
これを、次のように分割し直しても標準形であることには変わりありません。
![Rendered by QuickLaTeX.com \displaystyle{(5a)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{x}_2(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc|c} 0 & -C_1 & -C_2\\ 0 & A_{11} & A_{12} \\\hline 0 & A_{21} & A_{22} \end{array}\right] }_{\tilde{A}=\left[\begin{array}{cc} \tilde{A}_{11} & \tilde{A}_{12} \\ \tilde{A}_{21} & \tilde{A}_{22} \\ \end{array}\right]} \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0\\ 0\\\hline B_2 \end{array}\right] }_{\tilde{B}} u(t) + \left[\begin{array}{c} I_m \\ 0 \\\hline 0 \end{array}\right] r(t)\\ (x_1(t)\in{\rm\bf R}^n, x_2(t)\in{\rm\bf R}^m) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a01e5393ef83d3a307441de8778d577b_l3.png)
ただし
![]()
●この積分器による拡大系を安定化できれば、積分器の値![]() は定値となり、被積分項
は定値となり、被積分項![]() の値は零となり、
の値は零となり、![]() は
は![]() へ漸近します。そこで、SM制御によって拡大系を安定化し、追従制御系を構成することを考えます。この制御系は特別な
へ漸近します。そこで、SM制御によって拡大系を安定化し、追従制御系を構成することを考えます。この制御系は特別な![]() の場合を含みますので、まずスイッチング関数として、次式を考えます。
の場合を含みますので、まずスイッチング関数として、次式を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] %}_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I_m \\ \end{array}\right] }_{S} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] %}_{x(t)} \ (M=S_2^{-1}S_1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-01bb686061b94fbab2a0ff90e7d23f64_l3.png)
(5)に対して、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} I_n & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right]\\ \Leftrightarrow \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} I_n & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-19e5643bcb296d8a517aba35bc4fe14e_l3.png)
を行って、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(8a)\quad \begin{array}{l} %\underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] %}_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ S_2\bar{A}_{21} & S_2\bar{A}_{22}S_2^{-1} \\ \end{array}\right] }_{T_sA_ET_s^{-1}} %\underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] %}_{x'(t)} + \underbrace{ \left[\begin{array}{cc} 0\\ S_2B_2 \end{array}\right] }_{T_sB_E} u(t)\\ + \left[\begin{array}{cc} B_r \\ S_1B_r \end{array}\right] r(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a23595fe93cd3fb99284c6e90f61bcf1_l3.png)
ただし
![Rendered by QuickLaTeX.com \displaystyle{(8b)\quad \left\{\begin{array}{l} \bar{A}_{11}=\underbrace{ \left[\begin{array}{cc} 0 & -C_1 \\ 0 & A_{11} \end{array}\right]}_{\tilde{A}_{11}} -\underbrace{\left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right]}_{\tilde{A}_{12}}M\quad(M=S_2^{-1}S_1)\\ \bar{A}_{12}= \underbrace{\left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right]}_{\tilde{A}_{12}}S_2^{-1}\\ \bar{A}_{21}=S_2(M\bar{A}_{11} + \left[\begin{array}{cc} 0 & A_{21} \end{array}\right] -A_{22}M)\\ \bar{A}_{22}=S_2(M \left[\begin{array}{c} -C_2\\ A_{12} \end{array}\right] +A_{22})S_2^{-1}\\ B_r=\left[\begin{array}{cc} I_m \\ 0 \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a8cb0e83576eef13d13b8f669a414ae8_l3.png)
ここで、![]() が安定行列となるように行列
が安定行列となるように行列![]() が選ばれているとします。
が選ばれているとします。
●特別な![]() の場合のスライディングモードは
の場合のスライディングモードは![]() で表されますが、一般の
で表されますが、一般の![]() の場合のスライディングモードは
の場合のスライディングモードは
![]()
で表されるとします。ここで、![]() の選び方についてはあとで述べます。
の選び方についてはあとで述べます。
●以上の準備の下で、制御則は次式で表されます。
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \begin{array}{l} u(t)=u_L(t)+\nu_c\\ u_L(t)=-\underbrace{(S\tilde{B})^{-1}(S\tilde{A}-\Phi S)}_{L=L_{eq}+L_\Phi}\left[\begin{array}{c} x_r(t)\\ x(t) \end{array}\right]\\ -\underbrace{(S\tilde{B})^{-1}(\Phi S_r+S_1B_r)}_{L_r} r(t) +\underbrace{(S\tilde{B})^{-1}S_r}_{L_{\dot r}} \dot{r}(t)\\ \nu_c=-\underbrace{(S\tilde{B})^{-1}\rho_c(u_L,y)}_{L_n}\frac{P_2(s(t)-S_rr(t))}{||P_2(s(t)-S_rr(t))||} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4fa5c5c72c2ee8614e09bcaa4631f9d9_l3.png)
これをSMオブザーバを用いて実施する場合は次式を用います(![]() )。
)。
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \hat{u}(t)=\underbrace{-L\left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right]-L_rr(t)+L_{\dot r}\dot{r}(t)}_{\hat{u}_L}+\hat{\nu}_c\\ \displaystyle{\hat{\nu}_c=-L_n\frac{P_2(S\left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right]-S_rr(t))}{||P_2(S\left[\begin{array}{c} x_r(t)\\ z(t) \end{array}\right]-S_rr(t))||}}\\ L=\Lambda^{-1}(S\tilde{A}-\Phi S)\\ L_r=\Lambda^{-1}(\Phi S_r+S_2MB_r)\\ L_{\dot r}=\Lambda^{-1}S_r\\ L_n=\Lambda^{-1}\rho_c(\hat{u}_L,y) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9b9975d5d229ccc8642e2fdd4c1c0561_l3.png)
![]()
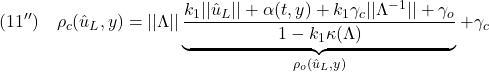
Note C91 ![]() の選び方
の選び方
●積分動作で示した閉ループ系の状態方程式の一部
![]()
を考えます。定常状態でスライディングモードが達成されたとすると
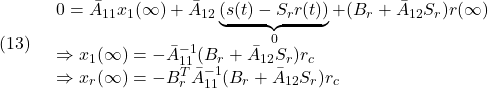
を得ます。![]() とするためには
とするためには
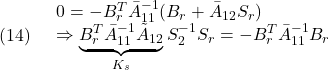
において、![]() が正則であれば、
が正則であれば、![]() を
を
![]()
と求めることができます。そこで次式に注目します。
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \begin{array}{l} \left[\begin{array}{cc} I & 0\\ B_r^T\tilde{A}_{11}^{-1} & -K_s \end{array}\right]= \left[\begin{array}{cc} \tilde{A}_{11} & \tilde{A}_{12}\\ B_r^T & 0 \end{array}\right] \left[\begin{array}{cc} \bar{A}_{11}^{-1} & -\bar{A}_{11}^{-1}\tilde{A}_{12}\\ 0 & I \end{array}\right]\\ = \left[\begin{array}{cc} \tilde{A}_{11} & \tilde{A}_{12}\\ B_r^T & 0 \end{array}\right] \left[\begin{array}{cc} I & 0\\ -M & I \end{array}\right] \left[\begin{array}{cc} \bar{A}_{11}^{-1} & -\bar{A}_{11}^{-1}\tilde{A}_{12}\\ 0 & I \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-359f0d62c20de545dd87152fb1c6a94b_l3.png)
これより![]() が正則であるための条件が次のように求められます。
が正則であるための条件が次のように求められます。
![Rendered by QuickLaTeX.com \displaystyle{(16)\quad \begin{array}{l} {\rm det}\left[\begin{array}{cc} \tilde{A}_{11} & \tilde{A}_{12}\\ B_r^T & 0 \end{array}\right]\ne 0 \Leftrightarrow {\rm det}\left[\begin{array}{cc|c} 0 & -C_1 & -C_2\\ 0 & A_{11} & A_{12}\\\hline I & 0 & 0 \end{array}\right]\ne 0\\ \Leftrightarrow {\rm det}\left[\begin{array}{cc} -C_1 & -C_2\\ A_{11} & A_{12} \end{array}\right]\ne 0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-8d7129e0a72d941b228a1e4ecda1d741_l3.png)
これは不変零点が複素平面原点にはないことを意味しますが、仮定![]() により保証されており、
により保証されており、![]() の正則性が成り立ちます。
の正則性が成り立ちます。
SMオブザーバ
Walcott-Zak’s observer…Homework
[1] 制御対象の状態空間表現として次式を考えます。
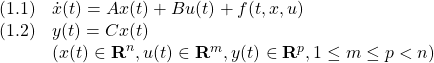
ただし、![]() はモデル誤差、非線形要素、外乱などの影響を表し、次のマッチング条件を満たすとします。
はモデル誤差、非線形要素、外乱などの影響を表し、次のマッチング条件を満たすとします。
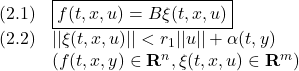
●このとき、Walcott-Zakは次のSMオブザーバを提案しています(![]() )。
)。
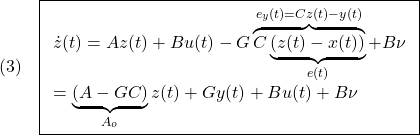
ここで、![]() は
は![]() が安定行列となるように選ばれているとします。また、
が安定行列となるように選ばれているとします。また、
![]()
を満足する![]() と、ある
と、ある![]() に対して
に対して
![]()
が満足されているものとします。このとき、![]() は
は
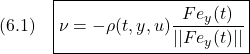
ただし
![]()
のように与えます。
これは、通常のオブザーバと同様に、出力の推定誤差 ![]() をフィードバックした上で、出力の推定誤差のスイッチング動作が加えられています。これにより、モデル誤差、非線形要素、外乱などの影響があるにも拘わらず、
をフィードバックした上で、出力の推定誤差のスイッチング動作が加えられています。これにより、モデル誤差、非線形要素、外乱などの影響があるにも拘わらず、![]() の超平面に載せることが考えられます。
の超平面に載せることが考えられます。
[2] (3)から(1.1)を辺々引き算して、誤差方程式
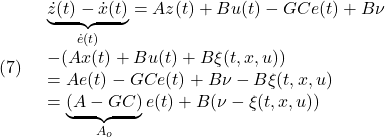
すなわち
![]()
を得ます。このとき、リャプノフ関数
![]()
に対して
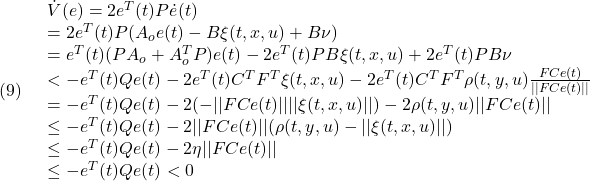
を得て、2次安定性が成り立ちます。したがって、ある有限時間で、次の超平面上でのスライディングモードが達成されます。
![]()
[3] 適当な座標変換を用いて、(1.1)の状態空間表現として次式が得られます。
![Rendered by QuickLaTeX.com \displaystyle{(11.1)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{cc} {\bar A}_{11} & {\bar A}_{12} \\ {\bar A}_{21} & {\bar A}_{22} \\ \end{array}\right] }_{{\bar A}=TAT^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} + \boxed{\underbrace{ \left[\begin{array}{c} 0_{n-p\times p}\\ {\bar B}_{2} \end{array}\right] }_{{\bar B}=TB}} (u(t)+\xi(t))\\ \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-df89f2c8c5027f65f3d1b001df56a333_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11.2)\quad y(t) = \boxed{\underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & I_p \\ \end{array}\right] }_{{\bar C}=CT^{-1}}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d15eb88c68556f6e054c3e64d14d9b4a_l3.png)
ただし、![]() は安定行列です。
は安定行列です。
●これは予備的検討における(3.1)と(3.2)と同じタイプですから、そこでの(18)に相当する
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \dot{\hat x}(t)=A\hat{x}(t)+Bu(t)-G_\ell Ce(t)+G_n\nu\\ G_\ell=T_o^{-1}\left[\begin{array}{c} {\cal A}_{12}\\ {\cal A}_{22}-{\cal A}_{22}^{s} \end{array}\right]\\ G_n=||{\cal D}_{2}||T_o^{-1}\left[\begin{array}{c} 0_{n-p\times p}\\ I_p \end{array}\right]\\ \displaystyle{\nu=-\rho(t,y,u)\frac{P_2e_y(t)}{||P_2e_y(t)||} \quad(P_2{\cal A}_{22}^{s}+{\cal A}_{22}^{s}^TP_2<0)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4b315d5f9deb1d92118c05143cc36e33_l3.png)
を設計できます。これから、(3)と(6.1)における![]() と
と![]() を、次のように定めることが提案されています。
を、次のように定めることが提案されています。
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \boxed{G=(T_LT_bT_c)^{-1}\left[\begin{array}{c} {\cal A}_{12}\\ {\cal A}_{22}-{\cal A}_{22}^{s} \end{array}\right]} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-99565ec8e7483b355f59c24131882a38_l3.png)
![]()
ここまでの手順を、関数smobs2としてプログラムすることにします。
Note C-83: (11)への座標変換
いま
![]()
と分割し、座標変換行列
![]()
を定義します。このとき
![]()
を得ます、また
![]()
と表すと、![]() に注意して
に注意して
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \bar{B}=TB= \left[\begin{array}{cc} I_{n-p} & {P}_{11}^{-1}{P}_{12} \\ 0 & I_p \end{array}\right] \left[\begin{array}{cc} {\tilde P}_{11} & {\tilde P}_{12} \\ {\tilde P}_{21} & {\tilde P}_{22} \end{array}\right] \left[\begin{array}{cc} 0 \\ I_p \end{array}\right] F^T\\ =\left[\begin{array}{cc} {\tilde P}_{12} + {P}_{11}^{-1}{P}_{12}{\tilde P}_{22} \\ {\tilde P}_{22} \end{array}\right] F^T= \underbrace{\left[\begin{array}{cc} 0 \\ {\tilde P}_{22}F^T \end{array}\right] }_{\left[\begin{array}{cc} 0 \\ {\bar B}_{2} \end{array}\right]} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ecf550e6e68e139dfd9b70a2c51821a0_l3.png)
および
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \begin{array}{l} \bar{P}=T^{-T}PT^{-1}\\ = \left[\begin{array}{cc} I_{n-p} & 0 \\ -{P}_{12}^T{P}_{11}^{-1} & I_p \end{array}\right] \left[\begin{array}{cc} {P}_{11} & {P}_{12} \\ {P}_{21} & {P}_{22} \end{array}\right] \left[\begin{array}{cc} I_{n-p} & -{P}_{11}^{-1}{P}_{12} \\ 0 & I_p \end{array}\right]\\ = \left[\begin{array}{cc} {P}_{11} & {P}_{12} \\ 0 & {P}_{22}-{P}_{12}^T{P}_{11}^{-1}{P}_{12} \end{array}\right] \left[\begin{array}{cc} I_{n-p} & -{P}_{11}^{-1}{P}_{12} \\ 0 & I_p \end{array}\right]\\ =\underbrace{\left[\begin{array}{cc} {P}_{11} & 0 \\ 0 & {P}_{22}-{P}_{21}{P}_{11}^{-1}{P}_{12} \end{array}\right] }_{\left[\begin{array}{cc} {\bar P}_{1} & 0 \\ 0 & {\bar P}_{2} \end{array}\right]} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d939c6b48cf57392a69499adfa73c15a_l3.png)
を得ます。また
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \bar{A}=TAT^{-1}\\ = \left[\begin{array}{cc} I_{n-p} & {P}_{11}^{-1}{P}_{12} \\ 0 & I_p \end{array}\right] \left[\begin{array}{cc} {A}_{11} & {A}_{12} \\ {A}_{21} & {A}_{22} \end{array}\right] \left[\begin{array}{cc} I_{n-p} & -{P}_{11}^{-1}{P}_{12} \\ 0 & I_p \end{array}\right]\\ = \left[\begin{array}{cc} {A}_{11}+{P}_{11}^{-1}{P}_{12}{A}_{21} & {A}_{12}+ {P}_{11}^{-1}{P}_{12}{A}_{22}\\ {A}_{21} & {A}_{22} \end{array}\right] \left[\begin{array}{cc} I_{n-p} & -{P}_{11}^{-1}{P}_{12} \\ 0 & I_p \end{array}\right]\\ =\underbrace{\left[\begin{array}{cc} {A}_{11}+{P}_{11}^{-1}{P}_{12}{A}_{21} & * \\ {A}_{21} & {A}_{22}-{A}_{21}{P}_{11}^{-1}{P}_{12} \end{array}\right] }_{\left[\begin{array}{cc} {\bar A}_{11} & {\bar A}_{12} \\ {\bar A}_{21} & {\bar A}_{22} \end{array}\right]} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-818dd08ad7b025fcdf6ac9148b5e312b_l3.png)
より
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \begin{array}{l} \bar{A}_o=\underbrace{TA_oT^{-1} }_{\left[\begin{array}{cc} {\bar A}_{o11} & {\bar A}_{o12} \\ {\bar A}_{o21} & {\bar A}_{o22} \end{array}\right]} =T(A-GC)T^{-1}\\ =\underbrace{TAT^{-1}}_{ \left[\begin{array}{cc} {\bar A}_{11} & {\bar A}_{12} \\ {\bar A}_{21} & {\bar A}_{22} \end{array}\right]} -\underbrace{TGCT^{-1}} _{\left[\begin{array}{cc} 0 & TG \end{array}\right]} = \left[\begin{array}{cc} {\bar A}_{11} & * \\ {\bar A}_{21} & * \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ac09c08dae61878b5898912612961935_l3.png)
すなわち![]() であることに注意します。
であることに注意します。
●本文(4)の左右から、![]() と
と![]() をかけて
をかけて
![]()
また本文(5)の左から、![]() をかけて
をかけて
![]()
を得ます。したがって、座標変換後も、本文(4)と(5)は同様に成り立ちます。
(9)において(6)と(8)を考慮すると
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \left[\begin{array}{cc} {\bar P}_{1} & 0 \\ 0 & {\bar P}_{2} \end{array}\right] \left[\begin{array}{cc} {\bar A}_{o11} & {\bar A}_{o12} \\ {\bar A}_{o21} & {\bar A}_{o22} \ \end{array}\right] +\left[\begin{array}{cc} {\bar A}_{o11} & {\bar A}_{o12} \\ {\bar A}_{o21} & {\bar A}_{o22} \ \end{array}\right]^T \left[\begin{array}{cc} {\bar P}_{1} & 0 \\ 0 & {\bar P}_{2} \end{array}\right]\\ =- \left[\begin{array}{cc} \bar{Q}_{11} & \bar{Q}_{12} \\ \bar{Q}_{12}^T & \bar{Q}_{22} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f9c197610a2dc08d37d7807a77250d9d_l3.png)
すなわち
![]()
したがって、![]() は安定行列となります。
は安定行列となります。
また(10)において(3)と(5)を考慮すると
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \underbrace{\left[\begin{array}{cc} 0 & I_p \end{array}\right]}_{\bar{C}^T}F^T=\underbrace{\left[\begin{array}{cc} {\bar P}_{1} & 0 \\ 0 & {\bar P}_{2} \end{array}\right]}_{\bar P}\underbrace{\left[\begin{array}{cc} 0 \\ {\bar B}_{2} \end{array}\right]}_{\bar B} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-25481cf05987d97cf1d660f8462287a3_l3.png)
すなわち
![]()
予備的検討
[1] 制御対象の状態空間表現として次式を考えます。
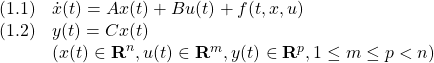
ただし、![]() はモデル誤差、非線形要素、外乱などの影響を表し、次のマッチング条件を満たすとします。
はモデル誤差、非線形要素、外乱などの影響を表し、次のマッチング条件を満たすとします。
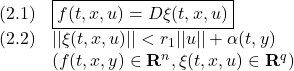
●適当な座標変換![]() によって次式が得られていると仮定します。
によって次式が得られていると仮定します。
![Rendered by QuickLaTeX.com \displaystyle{(3.1)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot y(t) \end{array}\right] }_{\dot{x}'(t)} = \underbrace{ \left[\begin{array}{cc} {\cal A}_{11} & {\cal A}_{12} \\ {\cal A}_{21} & {\cal A}_{22} \\ \end{array}\right] }_{T_oAT_o^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} + \underbrace{ \left[\begin{array}{c} {\cal B}_{1}\\ {\cal B}_{2} \end{array}\right] }_{T_oB} u(t) +\boxed{ \underbrace{ \left[\begin{array}{c} 0_{n-p\times p}\\ {\cal D}_{2} \end{array}\right] }_{T_oD}} \xi(t) \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c84baa48a735c227a2adb1d7a835b4a4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(3.2)\quad y(t) = \boxed{\underbrace{ \left[\begin{array}{cc} 0_{p\times n-p} & I_p \\ \end{array}\right] }_{CT_o^{-1}}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ y(t) \end{array}\right] }_{x'(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-90635122c9b9569be2466b719f5f1954_l3.png)
ただし、![]() は安定行列であることを仮定します。
は安定行列であることを仮定します。
●このとき次のSMオブザーバを考えます。
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \boxed{\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\hat x}_1(t)\\ \dot{\hat y}(t) \end{array}\right] }_{\dot{\hat x}'(t)} = \underbrace{ \left[\begin{array}{cc} {\cal A}_{11} & {\cal A}_{12} \\ {\cal A}_{21} & {\cal A}_{22} \\ \end{array}\right] }_{T_oAT_o^{-1}} \underbrace{ \left[\begin{array}{c} \hat{x}_1(t)\\ \hat{y}(t) \end{array}\right] }_{\hat{x}'(t)} + \underbrace{ \left[\begin{array}{c} {\cal B}_{1}\\ {\cal B}_{2} \end{array}\right] }_{T_oB} u(t)\\ - \left[\begin{array}{c} {\cal A}_{12}\\ {\cal A}_{22}-{\cal A}_{22}^{s} \end{array}\right] \underbrace{(\hat{y}(t)-y(t))}_{e_y(t)} + \left[\begin{array}{c} 0_{n-p\times p}\\ I_p \end{array}\right] \nu \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-66e4a486014204d000a249eb1c1c592b_l3.png)
ここで、![]() は安定行列として選ばれているとします。また、
は安定行列として選ばれているとします。また、
![]()
を満足する![]() を用いて、
を用いて、![]() は
は
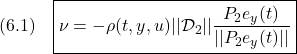
ただし
![]()
のように与えます。
以下では、モデル誤差、非線形要素、外乱などの影響があるにも拘わらず、状態オブザーバを構成できるを検討します。
[2] (4)から(3.1)を辺々引き算して、次の誤差方程式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \left[\begin{array}{c} \dot{\hat x}_1(t)-\dot{x}_1(t)\\ \dot{\hat y}(t)-\dot{y}(t) \end{array}\right] = \left[\begin{array}{cc} {\cal A}_{11} & {\cal A}_{12} \\ {\cal A}_{21} & {\cal A}_{22} \\ \end{array}\right] \left[\begin{array}{c} \hat{x}_1(t)-x_1(t)\\ \hat{y}(t)-y(t) \end{array}\right]\\ - \left[\begin{array}{cc} 0 & {\cal A}_{12}\\ 0 & {\cal A}_{22}-{\cal A}_{22}^{s} \end{array}\right] \left[\begin{array}{c} \hat{x}_1(t)-x_1(t)\\ \hat{y}(t)-y(t) \end{array}\right] + \left[\begin{array}{c} 0_{n-p}\\ \nu-{\cal D}_{2}\xi(t) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0c17498fb75a8ddddcfaced948ff16ca_l3.png)
すなわち
![Rendered by QuickLaTeX.com \displaystyle{(7')\quad \boxed{\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\hat x}_1(t)-\dot{x}_1(t)\\ \dot{\hat y}(t)-\dot{y}(t) \end{array}\right] }_{\left[\begin{array}{c} \dot{e}_1(t)\\ \dot{e}_y(t) \end{array}\right]} = \left[\begin{array}{cc} {\cal A}_{11} & 0_{n-p\times p} \\ {\cal A}_{21} & {\cal A}_{22}^{s} \\ \end{array}\right] \underbrace{ \left[\begin{array}{c} \hat{x}_1(t)-x_1(t)\\ \hat{y}(t)-y(t) \end{array}\right] }_{\left[\begin{array}{c} {e}_1(t)\\ {e}_y(t) \end{array}\right]}\\ + \left[\begin{array}{c} 0_{n-p}\\ \nu-{\cal D}_{2}\xi(t) \end{array}\right] \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eca857318ee4a936235a33d8531cf6bf_l3.png)
●この誤差システムの2次安定性を示します。(5)の解![]() を用いて
を用いて
![]()
を定義し、
![]()
の解![]() を用いて、リャプノフ関数
を用いて、リャプノフ関数
![]()
を考えます。このとき
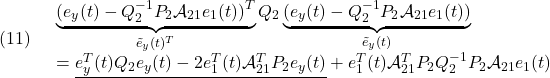
および
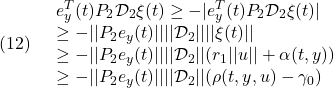
に注意して
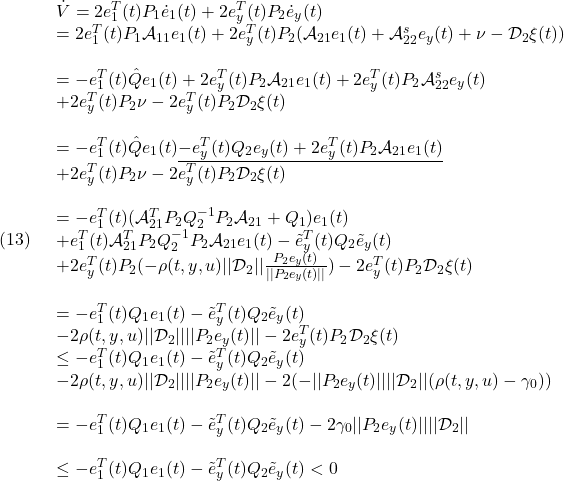
●一方、誤差の振舞いはある有限時間で次の超平面上でのスライディングモードとなることがわかります。
![]()
実際、(10)の第2項
![]()
に対して、(12)に注意して
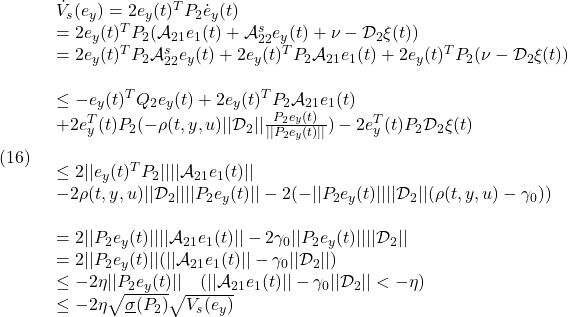
ただし
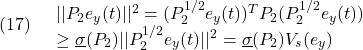
●SMオブザーバ(4)と(6.1)を再掲すると
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{\hat x}_1(t)\\ \dot{\hat y}(t) \end{array}\right] }_{\dot{\hat x}'(t)} = \underbrace{ \left[\begin{array}{cc} {\cal A}_{11} & {\cal A}_{12} \\ {\cal A}_{21} & {\cal A}_{22} \\ \end{array}\right] }_{T_oAT_o^{-1}} \underbrace{ \left[\begin{array}{c} \hat{x}_1(t)\\ \hat{y}(t) \end{array}\right] }_{\hat{x}'(t)} + \underbrace{ \left[\begin{array}{c} {\cal B}_{1}\\ {\cal B}_{2} \end{array}\right] }_{T_oB} u(t)\\ - \left[\begin{array}{c} {\cal A}_{12}\\ {\cal A}_{22}-{\cal A}_{22}^{s} \end{array}\right] \underbrace{(\hat{y}(t)-y(t))}_{e_y(t)} + \left[\begin{array}{c} 0_{n-p\times p}\\ I_p \end{array}\right] \nu \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-47ff921fcda56486a051274cf1f22315_l3.png)
![]()
これは、![]() より
より![]() としてよいので、次のように表すことができます。
としてよいので、次のように表すことができます。
![Rendered by QuickLaTeX.com \displaystyle{(18)\quad \boxed{\begin{array}{l} \dot{\hat x}(t)=A\hat{x}(t)+Bu(t)-G_\ell e_y(t)+G_n\nu\\ G_\ell=T_o^{-1}\left[\begin{array}{c} {\cal A}_{12}\\ {\cal A}_{22}-{\cal A}_{22}^{s} \end{array}\right]\\ G_n=||{\cal D}_{2}||T_o^{-1}\left[\begin{array}{c} 0_{n-p\times p}\\ I_p \end{array}\right]\\ \displaystyle{\nu=-\rho(t,y,u)\frac{P_2e_y(t)}{||P_2e_y(t)||} \quad(P_2{\cal A}_{22}^{s}+{\cal A}_{22}^{s}^TP_2<0)} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7107375b58980fcf0a852de479bd7ce3_l3.png)
[2] 以上の議論は(3.1)と(3.2)の形式を得るための座標変換行列![]() の存在が前提になります。これについて調べるために、出力FB型SM制御(p>m)で得られていた次の結果に注目します。
の存在が前提になります。これについて調べるために、出力FB型SM制御(p>m)で得られていた次の結果に注目します。
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{ll} (18.1*)&(T_aT_bT_c)A(T_aT_bT_c)^{-1}= \left[\begin{array}{cccc} A_{11}^o & A_{12}^o & A_{121}^m & A_{121}\\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m & A_{1221}\\ 0_{p-m\times r} & A_{21}^o & A_{22}^m & A_{1222}\\ A_{2120} & A_{2121} & A_{2122} & A_{22} \end{array}\right]\\ &(A_{11}^o\in{\rm\bf R}^{r\times r},A_{22}^o\in{\rm\bf R}^{n-p-r\times n-p-r},A_{22}^m\in{\rm\bf R}^{p-m\times p-m},A_{22}\in{\rm\bf R}^{m\times m})\\ (18.2*)&(T_aT_bT_c)B= \left[\begin{array}{c} 0_{r\times m} \\ 0_{n-p-r\times m} \\ 0_{p-m\times m} \\ B_2 \end{array}\right]\\ (18.3*)&C(T_aT_bT_c)^{-1}= \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-24aba4138d204a391e18f69edcd60c03_l3.png)
ここで、![]() は可観測対、
は可観測対、![]() の固有値は
の固有値は![]() の不変零点でした。この不変零点は安定であること、
の不変零点でした。この不変零点は安定であること、![]() が仮定されていました。
が仮定されていました。
●これは![]() の場合ですが、
の場合ですが、![]() の場合も、
の場合も、![]() として同様にして次式を得ます。
として同様にして次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{ll} (19.1)&(T_aT_bT_c)A(T_aT_bT_c)^{-1}= \underbrace{ \left[\begin{array}{cc|cc} A_{11}^o & A_{12}^o & A_{121}^m & A_{121}\\ 0_{n-p-r\times r} & A_{22}^o & A_{122}^m & A_{1221}\\\hline 0_{p-q\times r} & A_{21}^o & A_{22}^m & A_{1222}\\ A_{2120} & A_{2121} & A_{2122} & A_{22} \end{array}\right] }_{ \left[\begin{array}{c|c} A_{11} & *\\\hline A_{211} & *\\ * & * \end{array}\right] }\\ &(A_{11}\in{\rm\bf R}^{n-p\times n-p},A_{211}\in{\rm\bf R}^{p-q\times n-p})\\ (19.2)&(T_aT_bT_c)D= \left[\begin{array}{c} 0_{r\times q} \\ 0_{n-p-r\times q} \\ 0_{p-q\times q} \\ D_2 \end{array}\right]\\ (19.3)&C(T_aT_bT_c)^{-1}= \left[\begin{array}{cc} 0_{p\times n-p} & T \\ \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0e35543abcf691542b05178054d4aac2_l3.png)
ここで、![]() は可観測対、
は可観測対、![]() の固有値は
の固有値は![]() の不変零点です。同様に、この不変零点は安定で、
の不変零点です。同様に、この不変零点は安定で、![]() を仮定します。
を仮定します。
●![]() を安定行列とする
を安定行列とする![]() を用いて、追加の座標変換行列を
を用いて、追加の座標変換行列を
![]()
とすると
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{ll} (21.1)&T_L(T_aT_bT_c)A(T_aT_bT_c)^{-1}= \underbrace{\left[\begin{array}{cc} I_{n-p} & \left[\begin{array}{cc} L & 0_{n-p\times q} \end{array}\right] \\ 0_{p\times n-p} & T \end{array}\right]}_{T_L} \left[\begin{array}{c|c} A_{11} & *\\\hline A_{211} & *\\ * & * \end{array}\right]T_L\\ &= \left[\begin{array}{c|c} A_{11}+LA_{211} & *\\\hline * & * \end{array}\right] \underbrace{\left[\begin{array}{cc} I_{n-p} & \left[\begin{array}{cc} L & 0_{n-p\times q} \end{array}\right] \\ 0_{p\times n-p} & T \end{array}\right]}_{T_L}\\ (21.2)&T_L(T_aT_bT_c)D= \underbrace{\left[\begin{array}{cc} I_{n-p} & \left[\begin{array}{cc} L & 0_{n-p\times q} \end{array}\right] \\ 0_{p\times n-p} & T \end{array}\right]}_{T_L} \left[\begin{array}{c} 0_{n-p\times q} \\ 0_{p-q\times q} \\ D_2 \end{array}\right]\\ (21.3)&C(T_aT_bT_c)^{-1}= \left[\begin{array}{cc} 0_{p\times n-p} & I_p \\ \end{array}\right] \underbrace{\left[\begin{array}{cc} I_{n-p} & \left[\begin{array}{cc} L & 0_{n-p\times q} \end{array}\right] \\ 0_{p\times n-p} & T \end{array}\right]}_{T_L} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-68fa24b51933a9c473610573a0e51069_l3.png)
すなわち
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{ll} (22.1)&(T_LT_aT_bT_c)A(T_LT_aT_bT_c)^{-1}= \left[\begin{array}{c|c} A_{11}+LA_{211} & *\\\hline * & * \end{array}\right]\\ (22.2)&(T_LT_aT_bT_c)D= \left[\begin{array}{c} 0_{n-p\times q} \\ T\left[\begin{array}{c} 0_{p-q\times q} \\ D_2 \end{array}\right] \end{array}\right]\\ (22.3)&C(T_LT_aT_bT_c)^{-1}= \left[\begin{array}{cc} 0_{p\times n-p} & I_p \\ \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-92e44180ccc9fb5eea4f190d7391699c_l3.png)
を得ます。したがって、![]() は
は
![]()
と選べばよいことが分かります。
ここまでの手順を、関数ca_form2としてプログラムすることにします。
さらに、関数smobs1としてプログラムすることにします。