以下では、スケジューリングソルバーOptSeqのマニュアルに出てくる例題の分析を行います。
例題(ex1,ex2,ex18,ex8)
●例題ex1:PERT
例題ex1は、作業情報が次表のように与えられるとき、最終作業(出発)の完了時刻(メイクスパン)を求めようとしています。
| # |
作業名 |
作業期間(分) |
後続作業 |
| 1 |
乗客降し |
13 |
3 |
|
| 2 |
荷物降し |
25 |
5 |
4 |
| 3 |
機内清掃 |
15 |
4 |
|
| 4 |
乗客搭乗 |
27 |
6 |
|
| 5 |
荷物積込 |
22 |
6 |
|
| 6 |
出発 |
1 |
0 |
|
#optseq_ex1.py
from optseq import *
#-----データセット
ex1=Model()
data={\
1:[13,[3]],\
2:[25,[5,4]],\
3:[15,[4]],\
4:[27,[6]],\
5:[22,[6]],\
6:[ 1,[0]],\
}
#-----作業とモード
act={}
mode={}
for i in data:
act[i]=ex1.addActivity("Act[{0}]".format(i))
mode[i]=Mode("Mode[{0}]".format(i),data[i][0])
act[i].addModes(mode[i])
#-----先行制約
for i in data:
if data[i][1][0]!=0:
for j in data[i][1]:
ex1.addTemporal(act[i],act[j])
#-----最適化
ex1.Params.TimeLimit=1
ex1.Params.Makespan=True
#ex1.Params.OutputFlag=True
ex1.optimize()
#ex1.writeExcel("ex1_result.csv")
ex1.write("ex1_result.txt")
#-----ex1_result.txt
# activity mode duration 1 2 3 4 5 6 7 8 91011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556
#----------------------------------------------------------------------------------------------------------------------------------------------
# Act[1] Mode[1] 13 ==========================
# Act[2] Mode[2] 25 ==================================================
# Act[3] Mode[3] 15 ==============================
# Act[4] Mode[4] 27 # ======================================================
# Act[5] Mode[5] 22 ============================================
# Act[6] Mode[6] 1 ==
#----------------------------------------------------------------------------------------------------------------------------------------------
# resource usage/capacity
#----------------------------------------------------------------------------------------------------------------------------------------------
このプログラムを実行して、メイクスパンは56分であることが分かります。ex1_result.csvにおいて、■でクリティカルパス(CP)を示すと次のようになりま。

●例題ex2:資源制約付きPERT
例題ex2は例題ex1において、各作業の監督者をアサインする場合を検討しています。
#optseq_ex2.py
from optseq import *
#-----データセット
ex2=Model()
data={\
1:[13,[3]],\
2:[25,[5,4]],\
3:[15,[4]],\
4:[27,[6]],\
5:[22,[6]],\
6:[ 1,[0]],\
}
res=ex2.addResource("worker",capacity={(0,"inf"):1})
#-----作業とモード
act={}
mode={}
for i in data:
act[i]=ex2.addActivity("Act[{0}]".format(i))
mode[i]=Mode("Mode[{0}]".format(i),data[i][0])
mode[i].addResource(res,requirement=1)
act[i].addModes(mode[i])
#-----先行制約
for i in data:
if data[i][1][0]!=0:
for j in data[i][1]:
ex2.addTemporal(act[i],act[j])
#-----最適化
ex2.Params.TimeLimit=1
ex2.Params.Makespan=True
#ex2.Params.OutputFlag=True
ex2.optimize()
#ex2.writeExcel("ex2_result.csv")
#ex2.write("ex2_result.txt")
#-----ex2_result.txt
# activity mode duration 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99100101102103
#---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
# Act[1] Mode[1] 13 =======================================
# Act[2] Mode[2] 25 ===========================================================================
# Act[3] Mode[3] 15 =============================================
# Act[4] Mode[4] 27 =================================================================================
# Act[5] Mode[5] 22 ==================================================================
# Act[6] Mode[6] 1 ===
#---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
# resource usage/capacity
#---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
# worker 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
# 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
#---------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------------
このプログラムを実行して、監督者が1人しかいないと、メイクスパンは103分にまで伸びることが分かります。
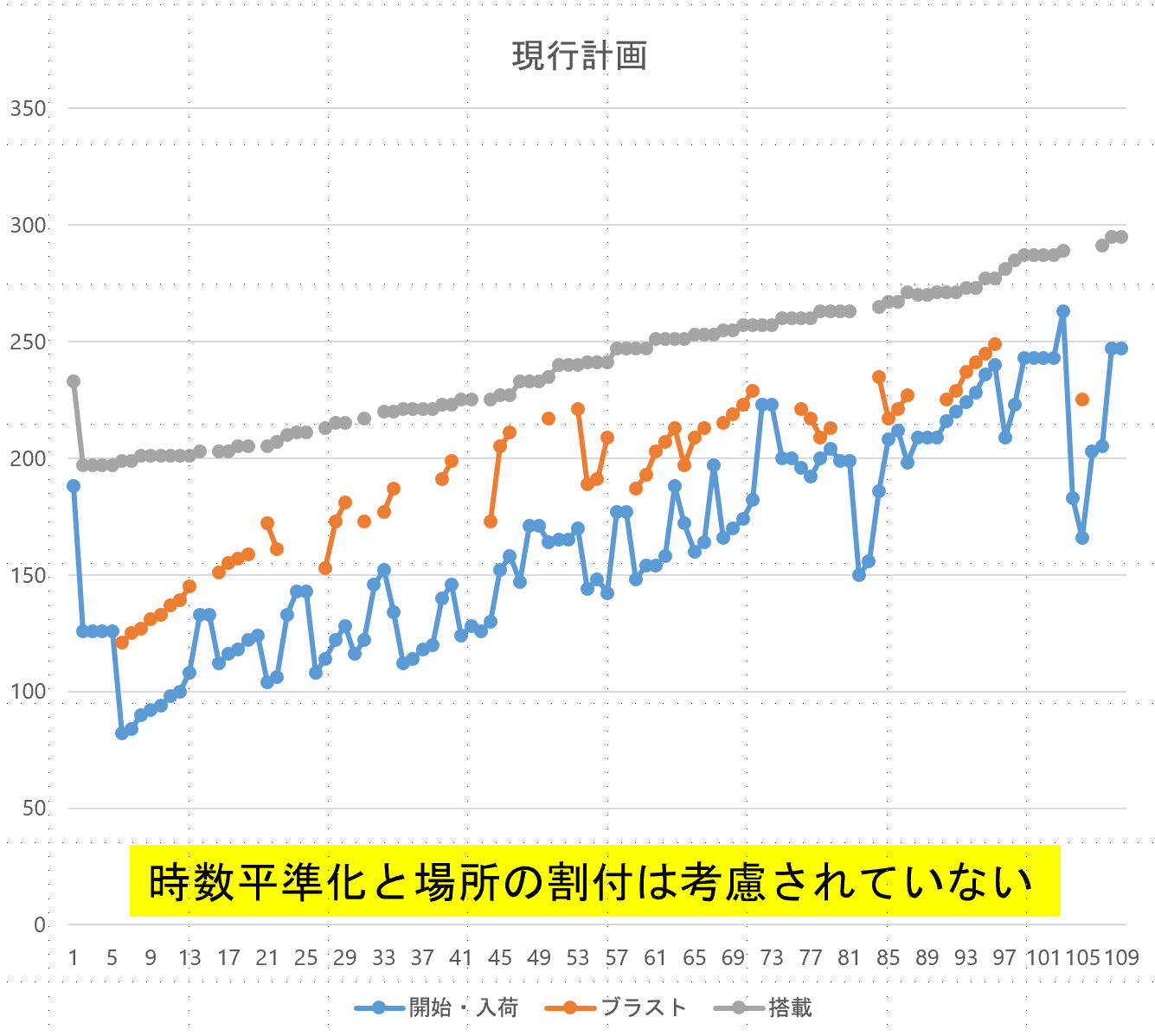
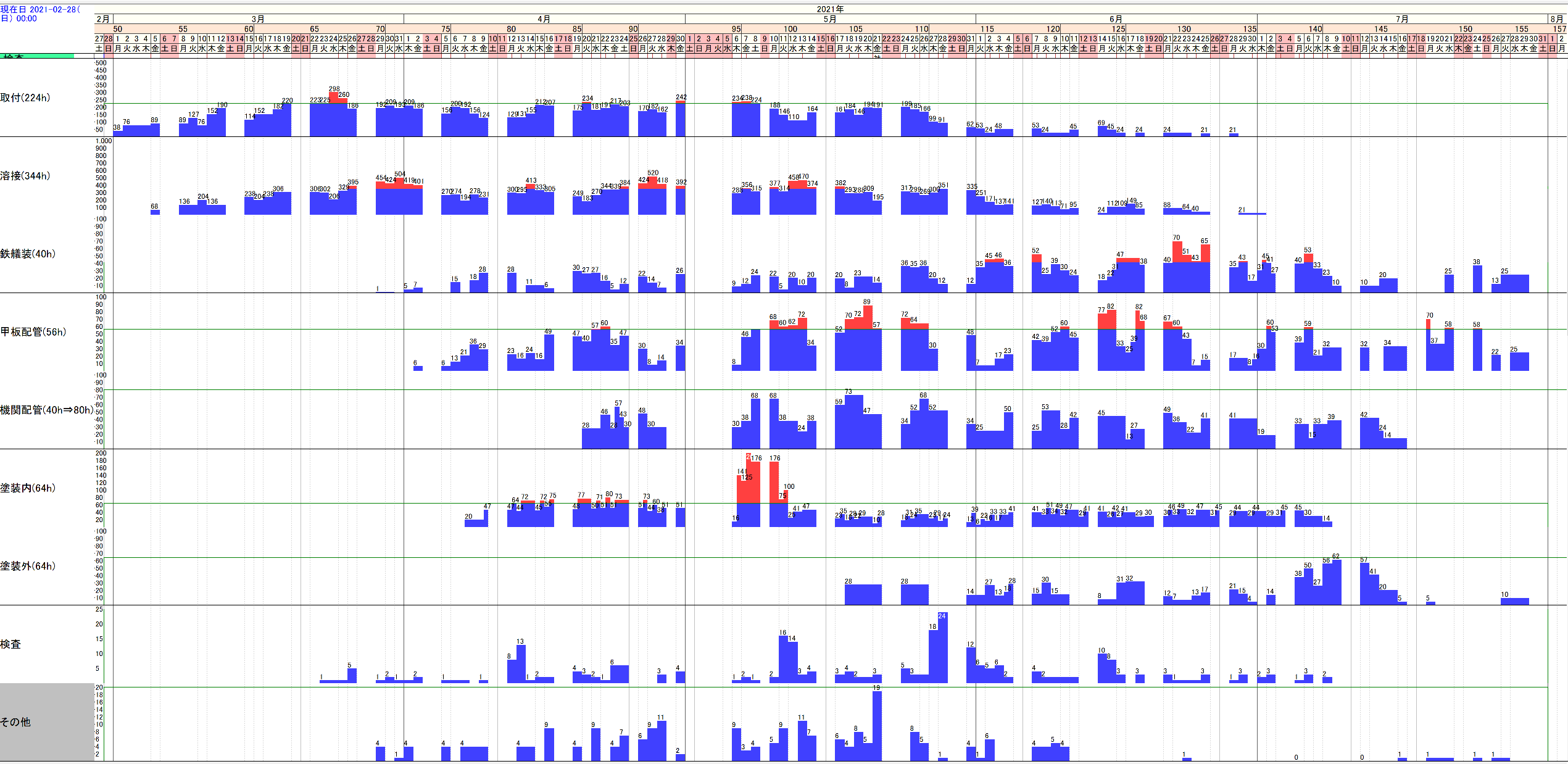
●例題ex18:作業情報の抽出(原題:平準化)
例題ex18は、例題ex2において先行制約を外し、作業員を何人まで増やせば納期52日を満たすかを調べています。
#optseq_ex18.py
from optseq import *
#-----データセット
data={\
1:[13],\
2:[25],\
3:[15],\
4:[27],\
5:[22],\
6:[ 1],\
}
duedate52=52
#=====
for ub in range(1,10):
ex18=Model()
res=ex18.addResource("wor##ker",capacity={(0,"inf"):ub})
#-----作業とモード
act={}
mode={}
for i in data:
act[i]=ex18.addActivity("Act[{0}]".format(i), duedate=duedate52)
mode[i]=Mode("Mode[{0}]".format(i),duration=data[i][0])
mode[i].addResource(res,requirement=1)
act[i].addModes(mode[i])
#-----最適化
ex18.Params.TimeLimit=1
ex18.Params.Makespan=True
#ex18.Params.OutputFlag=True
ex18.optimize()
ex18.writeExcel("ex18_result.csv")
ex18.write("ex18_result.txt")
#-----納期は満たされたか?
completion=0
for a in act:
completion=max(completion, act[a].completion)
if completion<=duedate52: break
#eof
#-----ex18_result.txt
# activity mode duration 1 2 3 4 5 6 7 8 910111213141516171819202122232425262728293031323334353637383940414243444546474849505152
#--------------------------------------------------------------------------------------------------------------------------------------
# Act[1] Mode[1] 13 ==========================
# Act[2] Mode[2] 25 ==================================================
# Act[3] Mode[3] 15 ==============================
# Act[4] Mode[4] 27 ======================================================
# Act[5] Mode[5] 22 ============================================
# Act[6] Mode[6] 1 ==
#--------------------------------------------------------------------------------------------------------------------------------------
# resource usage/capacity
#--------------------------------------------------------------------------------------------------------------------------------------
# worker 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 1
# 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
-----------------------------------------------------------------------------------------
このプログラムを実行して、監督者を1人増やすと、メイクスパンは52分に収まることが分かります。
コマンドdir(作業インスタンス)を用いて、適用可能なメソッドのリストを得るとができます。
:
‘addModes’,
‘autoselect’,
‘backward’,⇒前詰めか後詰めか
‘completion’,⇒完了時刻
‘duedate’,⇒納期
‘execute’,
‘modes’,
‘name’,⇒作業名
‘selected’,⇒選択されたモード
‘start’,⇒開始時刻
‘weight’
●例題ex8:時間制約
例題ex8は、2つの作業の開始のタイミングを揃えたり、ある作業の開始のタイミングを固定する方法を示しています。
#optseq_ex8.py
from optseq import *
#-----データセット
ex8=Model()
data={\
1:[13,[3], 0],\
2:[25,[5,4],0],\
3:[15,[4], 5],\
4:[27,[6], 0],\
5:[22,[6], 0],\
6:[1, [0], 0],\
}
#-----作業とモード
act={}
mode={}
for i in data:
act[i]=ex8.addActivity("Act[{0}]".format(i))
mode[i]=Mode("Mode[{0}]".format(i),duration=data[i][0])
act[i].addModes(mode[i])
#-----先行制約
for i in data:
if data[i][1][0]!=0:
for j in data[i][1]:
ex8.addTemporal(act[i],act[j])
#-----同時開始
for i in data:
if data[i][2]>0:
ex8.addTemporal(act[i],act[data[i][2]],'SS',0)
ex8.addTemporal(act[data[i][2]],act[i],'SS',0)
#-----最適化
ex8.Params.TimeLimit=1
ex8.Params.Makespan=True
#ex8.Params.OutputFlag=True
ex8.optimize()
#ex8.writeExcel("ex8_result.csv")
ex8.write("ex8_result.txt")
#-----ex8_result.txt
# activity mode duration 1 2 3 4 5 6 7 8 91011121314151617181920212223242526272829303132333435363738394041424344454647484950515253545556575859606162636465666768
#----------------------------------------------------------------------------------------------------------------------------------------------------------------------
# Act[1] Mode[1] 13 ==========================
# Act[2] Mode[2] 25 ==================================================
# Act[3] Mode[3] 15 ==============================
# Act[4] Mode[4] 27 ======================================================
# Act[5] Mode[5] 22 ============================================
# Act[6] Mode[6] 1 ==
#----------------------------------------------------------------------------------------------------------------------------------------------------------------------
# resource usage/capacity
----------------------------------------------------------------------------------------------------------------------------------------------------------------------
このプログラムを実行して、作業3と5の開始のタイミングが揃っていることが分かります。ex8_result.csvでは次のように確認できます。

例題(ex3,ex4,ex10)
●例題ex3:並列ショップスケジューリング
例題ex3は、作業間の先行関係が次表のように与えられるとき、最終作業(出発)の完了時刻(メイクスパン)を求めようとしています。
| # |
作業名 |
作業期間 |
後続作業 |
| 1 |
給油準備 |
3 |
9 |
|
|
|
| 2 |
飲料水取替 |
2 |
11 |
|
|
|
| 3 |
ガラス拭き |
2 |
11 |
|
|
|
| 4 |
ジャッキアップ |
2 |
5 |
6 |
7 |
8 |
| 5 |
タイヤ交換(前輪左側) |
4 |
10 |
|
|
|
| 6 |
タイヤ交換(前輪右側) |
4 |
10 |
|
|
|
| 7 |
タイヤ交換(後輪左側) |
4 |
10 |
|
|
|
| 8 |
タイヤ交換(後輪右側) |
4 |
10 |
|
|
|
| 9 |
給油 |
11 |
11 |
|
|
|
| 10 |
ジャッキダウン |
2 |
11 |
|
|
|
| 11 |
出発 |
1 |
0 |
|
|
|
ただし、配員可能な作業員数は次の通りとします。
#optseq_ex3.py
from optseq import *
#-----データセット
ex3=Model()
data={\
1:[3,[9]],\
2:[2,[11]],\
3:[2,[11]],\
4:[2,[5,6,7,8]],\
5:[4,[10]],\
6:[4,[10]],\
7:[4,[10]],\
8:[4,[10]],\
9:[11,[11]],\
10:[2,[11]],\
11:[1,[0]],\
}
res=ex3.addResource("worker",capacity={(0,"inf"):3})
#-----作業とモード
act={}
mode={}
for i in data:
act[i]=ex3.addActivity("Act[{0}]".format(i))
mode[i]=Mode("Mode[{0}]".format(i),duration=data[i][0])
mode[i].addResource(res,requirement=1)
act[i].addModes(mode[i])
#-----先行制約
for i in data:
if i<11:
for j in data[i][1]:
ex3.addTemporal(act[i],act[j])
#-----最適化
ex3.Params.TimeLimit=1
ex3.Params.Makespan=True
#ex3.Params.OutputFlag=True
ex3.optimize()
#ex3.writeExcel("ex3_result.csv")
ex3.write("ex3_result.txt")
#-----ex3_result.txt
# activity mode duration 1 2 3 4 5 6 7 8 9101112131415
# -------------------------------------------------------------
# Act[1] Mode[1] 3 ======
# Act[2] Mode[2] 2 ====
# Act[3] Mode[3] 2 ====
# Act[4] Mode[4] 2 ====
# Act[5] Mode[5] 4 ========
# Act[6] Mode[6] 4 ========
# Act[7] Mode[7] 4 ========
# Act[8] Mode[8] 4 ========
# Act[9] Mode[9] 11 ======================
# Act[10] Mode[10] 2 ====
# Act[11] Mode[11] 1 ==
# -------------------------------------------------------------
# resource usage/capacity
# -------------------------------------------------------------
# worker 3 3 2 2 3 3 3 3 3 3 3 3 2 2 1
# 3 3 3 3 3 3 3 3 3 3 3 3 3 3 3
# -------------------------------------------------------------
このプログラムを実行して、最大配員数の範囲内で作業を並列化する(同時進行させる)ことができています。ex3_result.csvでは次のようになります。

●例題ex4:作業の並列実行(モードの利用)
例題ex4は、作業1についての配員数を変えたモードを複数個設定することで、メイクスパンを短縮するモードを自動選択させています。
#optseq_ex4.py
from optseq import *
#-----データセット
ex4=Model()
data={\
1:[3,[9]],\
2:[2,[11]],\
3:[2,[11]],\
4:[2,[5,6,7,8]],\
5:[4,[10]],\
6:[4,[10]],\
7:[4,[10]],\
8:[4,[10]],\
9:[11,[11]],\
10:[2,[11]],\
11:[1,[0]],\
}
res=ex4.addResource("worker",capacity={(0,"inf"):3})
#-----作業とモード
act={}
mode={}
for i in data:
act[i]=ex4.addActivity("Act[{0}]".format(i))
if i==1:
mode[1,1]=Mode("Mode[1_1]",duration=3)
mode[1,1].addResource(res,requirement=1)
mode[1,2]=Mode("Mode[1_2]",duration=2)
mode[1,2].addResource(res,requirement=2)
mode[1,3]=Mode("Mode[1_3]",duration=1)
mode[1,3].addResource(res,requirement=3)
act[i].addModes(mode[1,1],mode[1,2],mode[1,3])
else:
mode[i]=Mode("Mode[{0}]".format(i),data[i][0])
mode[i].addResource(res,requirement=1)
act[i].addModes(mode[i])
#-----先行制約
for i in data:
if i<11:
for j in data[i][1]:
ex4.addTemporal(act[i],act[j])
#-----最適化
ex4.Params.TimeLimit=1
ex4.Params.Makespan=True
#ex4.Params.OutputFlag=True
ex4.optimize()
#ex4.writeExcel("ex4_result.csv")
ex4.write("ex4.txt")
#-----ex4_result.txt
# activity mode duration 1 2 3 4 5 6 7 8 91011121314
# -----------------------------------------------------------
# Act[1] Mode[1_3] 1 ==
# Act[2] Mode[2] 2 ====
# Act[3] Mode[3] 2 ====
# Act[4] Mode[4] 2 ====
# Act[5] Mode[5] 4 ========
# Act[6] Mode[6] 4 ========
# Act[7] Mode[7] 4 ========
# Act[8] Mode[8] 4 ========
# Act[9] Mode[9] 11 ======================
# Act[10] Mode[10] 2 ====
# Act[11] Mode[11] 1 ==
# -----------------------------------------------------------
# resource usage/capacity
# -----------------------------------------------------------
# worker 3 3 3 3 3 3 3 3 3 3 3 3 2 1
# 3 3 3 3 3 3 3 3 3 3 3 3 3 3
# -----------------------------------------------------------
このプログラムを実行して、作業1について3人を配員するモードmode[1,3]が選ばれています。メイクスパンはex3より1日短くなっています。ex4_result.csvでは次のようになります。
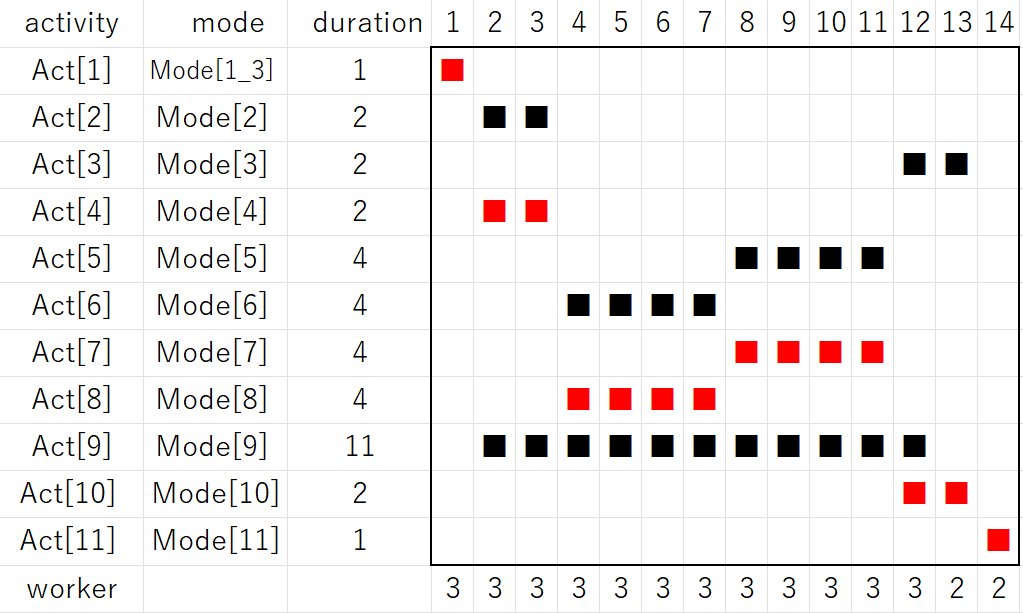
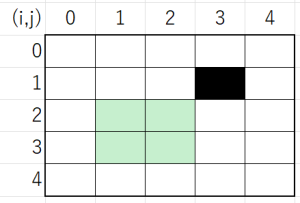
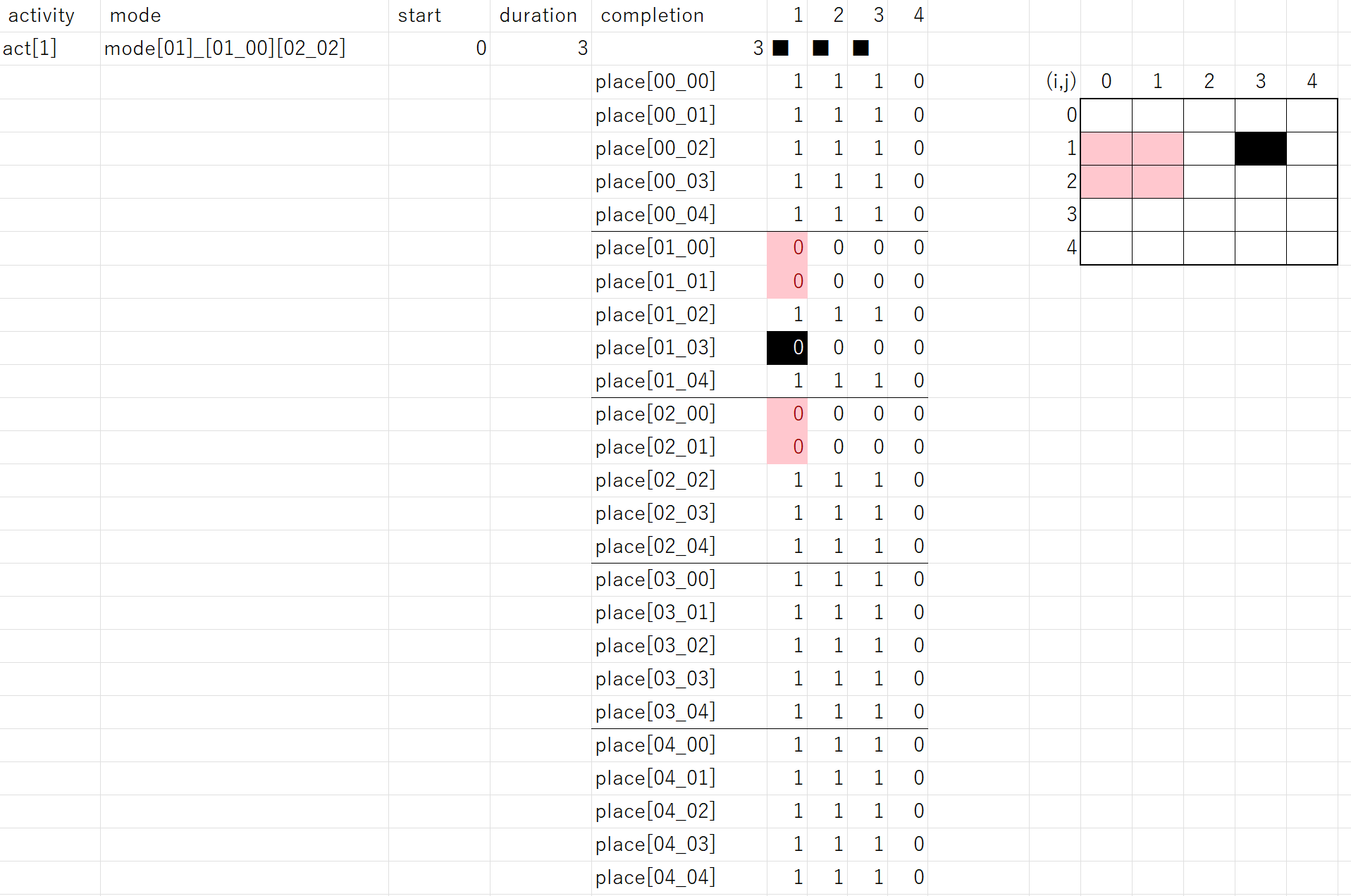
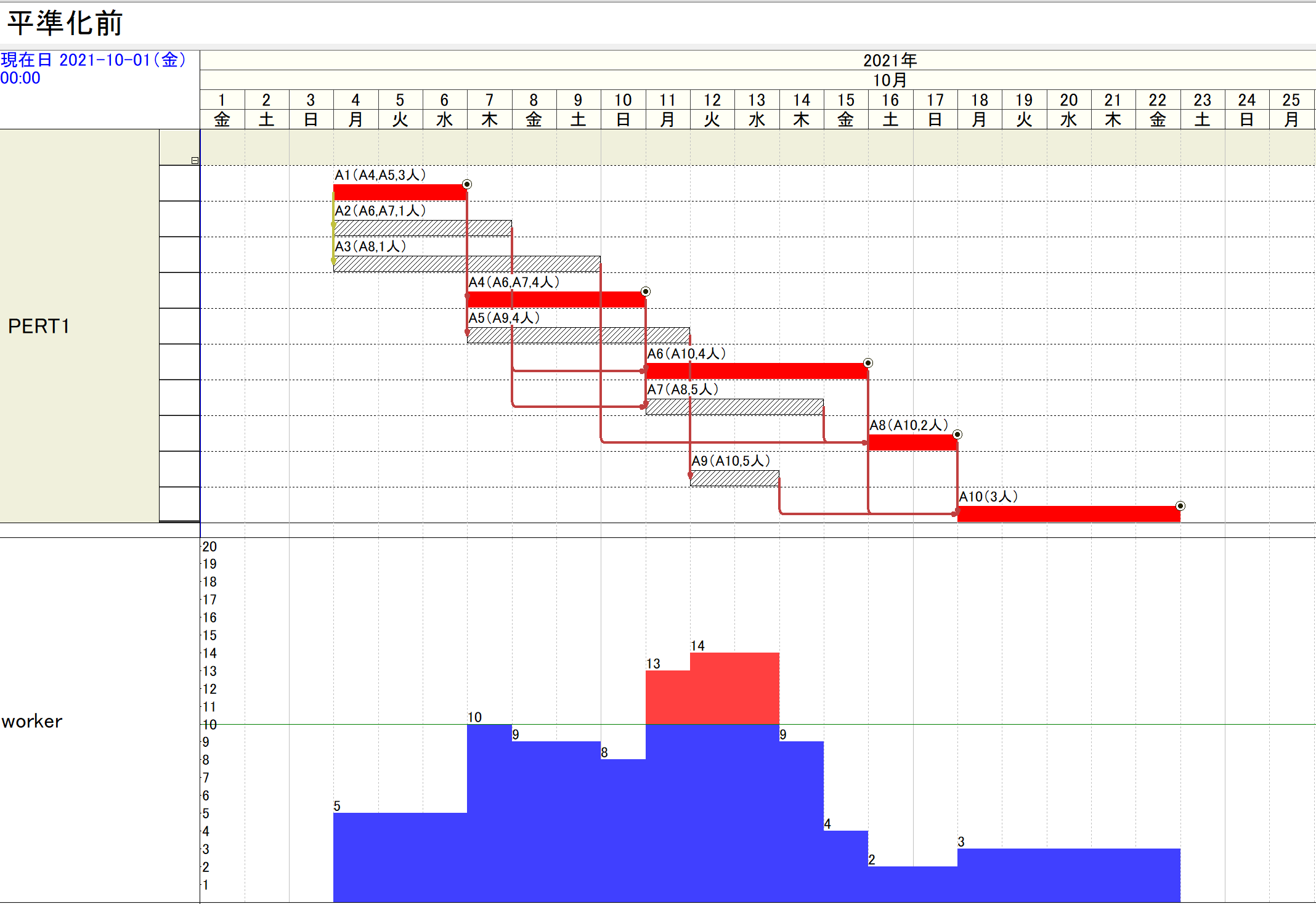
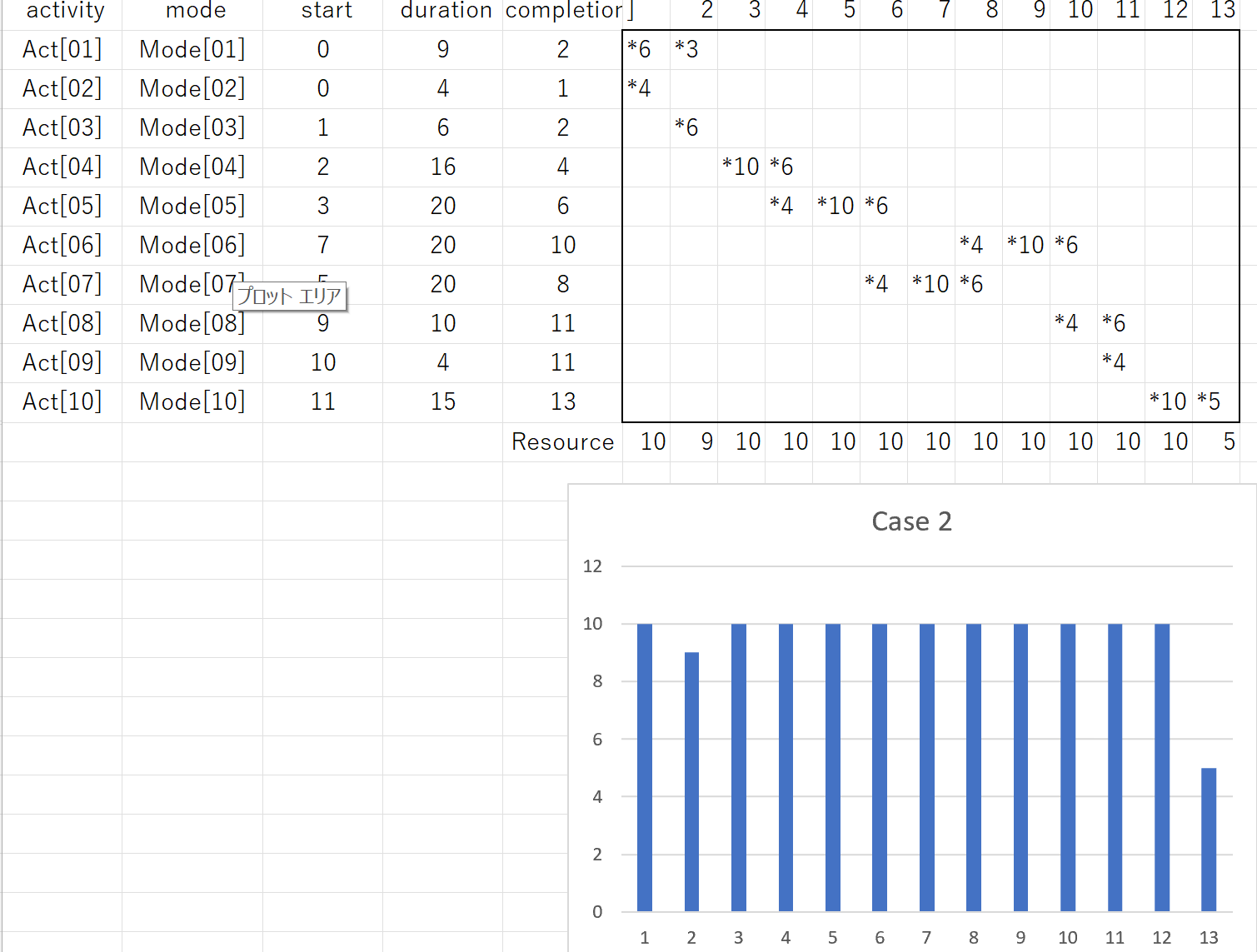
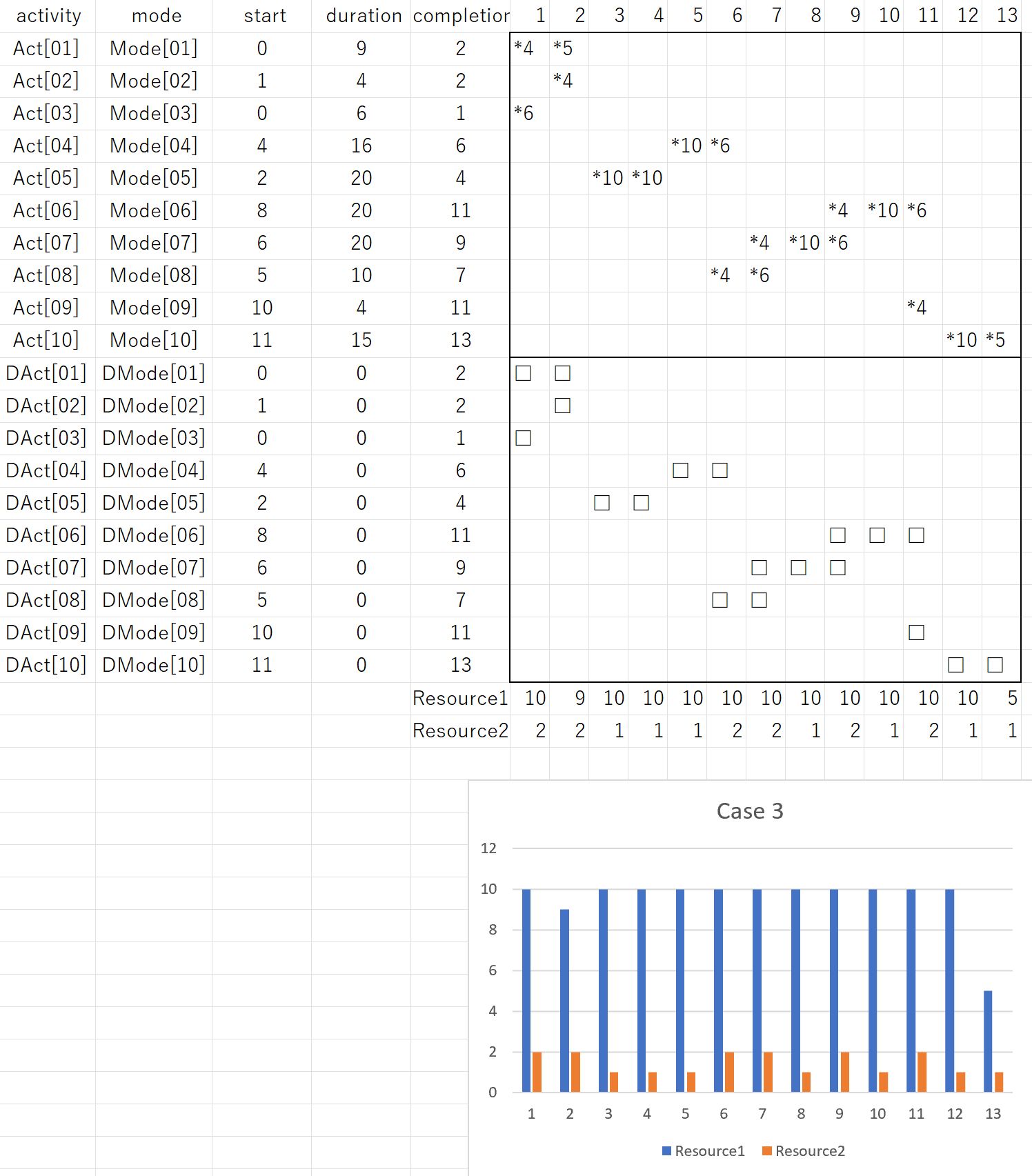
●例題ex10:作業の並列実行(小作業の並列化)
例題ex10は、作業1を1人で行うものとして登録し、これを配員可能な複数人で行って、並列化することを狙っています。この手法は小作業並列化手法と呼ばれ、作業期間が自動調整されることから、高度な平準化手法の基礎となる可能性があります(詳しくは改めて説明します)。
#optseq_ex10.py
from optseq import *
#-----データセット
ex10=Model()
data={\
1:[3,[9]],\
2:[2,[11]],\
3:[2,[11]],\
4:[2,[5,6,7,8]],\
5:[4,[10]],\
6:[4,[10]],\
7:[4,[10]],\
8:[4,[10]],\
9:[11,[11]],\
10:[2,[11]],\
11:[1,[0]],\
}
res=ex10.addResource("worker",capacity={(0,"inf"):3})
#-----作業とモード
act={}
mode={}
for i in data:
act[i]=ex10.addActivity("Act[{0}]".format(i))
mode[i]=Mode("Mode[{0}]".format(i),duration=data[i][0])
mode[i].addResource(res,requirement=1)
if i==1:
mode[i].addParallel(start=1,finish=1,maxparallel=3)
act[i].addModes(mode[i])
#-----先行制約
for i in data:
if i<11:
for j in data[i][1]:
ex10.addTemporal(act[i],act[j])
#-----最適化
ex10.Params.TimeLimit=1
ex10.Params.Makespan=True
#ex10.Params.OutputFlag=True
ex10.optimize()
#ex10.writeExcel("ex10_result.csv")
ex10.write("ex10_result.txt")
#-----ex10_result.txt
# activity mode duration 1 2 3 4 5 6 7 8 910111213
# ---------------------------------------------------------
# Act[1] Mode[1] 3 *3
# Act[2] Mode[2] 2 ====
# Act[3] Mode[3] 2 ====
# Act[4] Mode[4] 2 ====
# Act[5] Mode[5] 4 ========
# Act[6] Mode[6] 4 ========
# Act[7] Mode[7] 4 ========
# Act[8] Mode[8] 4 ========
# Act[9] Mode[9] 11 ======================
# Act[10] Mode[10] 2 ====
# Act[11] Mode[11] 1 ==
# ---------------------------------------------------------
# resource usage/capacity
# ---------------------------------------------------------
# worker 3 3 3 3 3 3 3 3 3 3 3 3 3
# 3 3 3 3 3 3 3 3 3 3 3 3 3
# ---------------------------------------------------------
このプログラムを実行して、作業1は作業員3人で行ない作業期間は1日となっており(■*3)、ex4と同じメイスパンとなっています。ex10_result.csvでは次のようになります。

例題(ex5,ex6,ex20,ex9)
●例題ex5:一般化資源制約付きスケジューリング
例題ex5は、リソースの許容量を期間ごとに決めています。これは休日をもつカレンダーを導入するために役立ちます。
#optseq_ex5.py
from optseq import *
#-----データセット
ex5=Model()
data={\
1:[1,2,[2,4]],\
2:[1,2,[3]],\
3:[2,1,[5]],\
4:[2,1,[7]],\
5:[1,1,[6]],\
6:[1,2,[7]],\
7:[1,1,[0]],\
}
res=ex5.addResource("worker")
res.addCapacity(start=0,finish=2,amount=2)
res.addCapacity(start=2,finish=3,amount=1)
res.addCapacity(start=3,finish="inf",amount=2)
#-----作業とモード
act={}
mode={}
for i in data:
act[i]=ex5.addActivity("Act[{0}]".format(i))
mode[i]=Mode("Mode[{0}]".format(i),duration=data[i][0])
mode[i].addResource(res,requirement=data[i][1])
act[i].addModes(mode[i])
#-----先行制約
for i in data:
if i<7:
for j in data[i][2]:
ex5.addTemporal(act[i],act[j])
#-----最適化
ex5.Params.TimeLimit=1
ex5.Params.Makespan=True
#ex5.Params.OutputFlag=True
ex5.optimize()
#ex5.writeExcel("ex5_result.csv")
ex5.write("ex5.txt")
#-----ex5_result.txt
# activity mode duration 1234567
# --------------------------------------
# Act[1] Mode[1] 1 =
# Act[2] Mode[2] 1 =
# Act[3] Mode[3] 2 ==
# Act[4] Mode[4] 2 ==
# Act[5] Mode[5] 1 =
# Act[6] Mode[6] 1 =
# Act[7] Mode[7] 1 =
# --------------------------------------
# resource usage/capacity
# --------------------------------------
# worker 2212221
# 2212222
# --------------------------------------
このプログラムを実行して、3日目の配員が1名に抑えられていることが分かります。

●例題ex6:納期遅れ最小化スケジューリング
例題ex6は、納期のある複数個の作業を、納期遅れ総和を最小にするためには、どの順番で実施すればよいかを検討しています。
#optseq_ex6.py
from optseq import *
#-----データセット
data={\
ex6=Model()
1:[1,5],\
2:[2,9],\
3:[3,6],\
4:[4,4],\
}
res=ex6.addResource("writer")
res.addCapacity(0,"inf",1)
#-----作業とモード
act={}
mode={}
for i in data:
act[i]=ex6.addActivity("Act[{0}]".format(i),duedate=data[i][1])
mode[i]=Mode("Mode[{0}]".format(i),duration=data[i][0])
mode[i].addResource(res,requirement=1)
act[i].addModes(mode[i])
#-----最適化
ex6.Params.TimeLimit=1
ex6.Params.Makespan=False
#ex6.Params.OutputFlag=True
ex6.optimize()
#ex6.writeExcel("ex6_result.csv")
ex6.write("ex6_result..txt")
#-----ex6_result.txt
# activity mode duration 1 2 3 4 5 6 7 8 910
# ---------------------------------------------------
# Act[1] Mode[1] 1 ==
# Act[2] Mode[2] 2 ====
# Act[3] Mode[3] 3 ======
# Act[4] Mode[4] 4 ========
# ---------------------------------------------------
# resource usage/capacity
# ---------------------------------------------------
# writer 1 1 1 1 1 1 1 1 1 1
# 1 1 1 1 1 1 1 1 1 1
# ---------------------------------------------------
このプログラムを実行して、作業4,1,3,2の順に行うと納期遅れが最小になることが分かります。それでも、ex6_result.csvに■で示すような納期遅れが生じています。

●例題ex20:納期遅れをしない範囲でなるべく多くの仕事をこなす方法
例題ex20では、この目的を達成するために、作業期間0のモードをうまく利用しています。
##optseq_ex20.py
from optseq import *
#-----データセット
ex20= Model()
data={
1:[5,1],\
2:[9,2],\
3:[6,3],\
4:[4,4],\
}
res=ex20.addResource("writer")
res.addCapacity(0,"inf",1)
#-----作業とモード
act={}
mode={}
for i in data:
act[i]=ex20.addActivity(f"Act[{i}]",duedate=data[i][0],weight=100)
mode[i]=Mode(f"Mode[{i}]",duration=data[i][1])
mode[i,0]=Mode(f"Mode[{i}0]",duration=0)
mode[i].addResource(res,1)
act[i].addModes(mode[i],mode[i,0])
#-----モード制約
con1=ex20.addResource("constraint_1",rhs=0,direction="<=",weight=1)
con1.addTerms(coeffs=[1,1,1,1], vars=[act[1],act[2],act[3],act[4]],\
values=[mode[1,0],mode[2,0],mode[3,0],mode[4,0]])
#-----最適化
ex20.Params.TimeLimit=1
ex20.Params.Makespan=False
#ex20.Params.OutputFlag=True
ex20.optimize()
#ex20.writeExcel("ex20_result.csv")
ex20.write("ex20_result.txt")
#-----ex20_result.txt
# activity mode duration 1234567
# --------------------------------------
# Act[1] Mode[1] 1 =
# Act[2] Mode[2] 2 ==
# Act[3] Mode[30] 0
# Act[4] Mode[4] 4 ====
# --------------------------------------
# resource usage/capacity
# --------------------------------------
# writer 1111111
# 1111111
# --------------------------------------
このプログラムを実行して、作業3を行わなければ、他の作業は納期に間に合うことが分かります。
●例題ex9:作業の途中中断
例題ex9は、例題ex6に休業日を考慮する手法を示しています。
#optseq_ex9.py
from optseq import *
#-----データセット
ex9=Model()
data={\
1:[1,5],\
2:[2,9],\
3:[3,6],\
4:[4,4],\
}
res=ex9.addResource("writer")
res.addCapacity(0,3,1)
res.addCapacity(4,6,1)
res.addCapacity(7,10,1)
res.addCapacity(11,"inf",1)
#-----作業とモード
act={}
mode={}
for i in data:
act[i]=ex9.addActivity("Act[{0}]".format(i),duedate=data[i][1])
mode[i]=Mode("Mode[{0}]".format(i),duration=data[i][0])
mode[i].addResource(res,requirement=1)
mode[i].addBreak(start=0,finish='inf',maxtime=1)
mode[i].addResource(res,{(0,"inf"):1},"break") #break中も資源を使う場合
act[i].addModes(mode[i])
#-----最適化
ex9.Params.TimeLimit=1
#ex9.Params.OutputFlag=True
ex9.Params.Makespan=False
ex9.optimize()
#ex9.writeExcel("ex9_result.csv")
ex9.write("ex9_result.txt")
#-----ex9_result.txt
# activity mode duration 1 2 3 4 5 6 7 8 9101112131415
# -------------------------------------------------------------
# Act[1] Mode[1] 1 ==
# Act[2] Mode[2] 2 ====
# Act[3] Mode[3] 3 ======
# Act[4] Mode[4] 4 ========
# -------------------------------------------------------------
# resource usage/capacity
# -------------------------------------------------------------
# writer 1 1 1 0 1 0 0 1 1 0 0 1 1 1 1
# 1 1 1 0 1 1 0 1 1 1 0 1 1 1 1
このプログラムを実行して、次の結果①を得ます。結果②、③,④は中断中のリソースの使用を不可にしたり、中断期間を無制限にしたりして、計画がどのように変わるかを調べています。
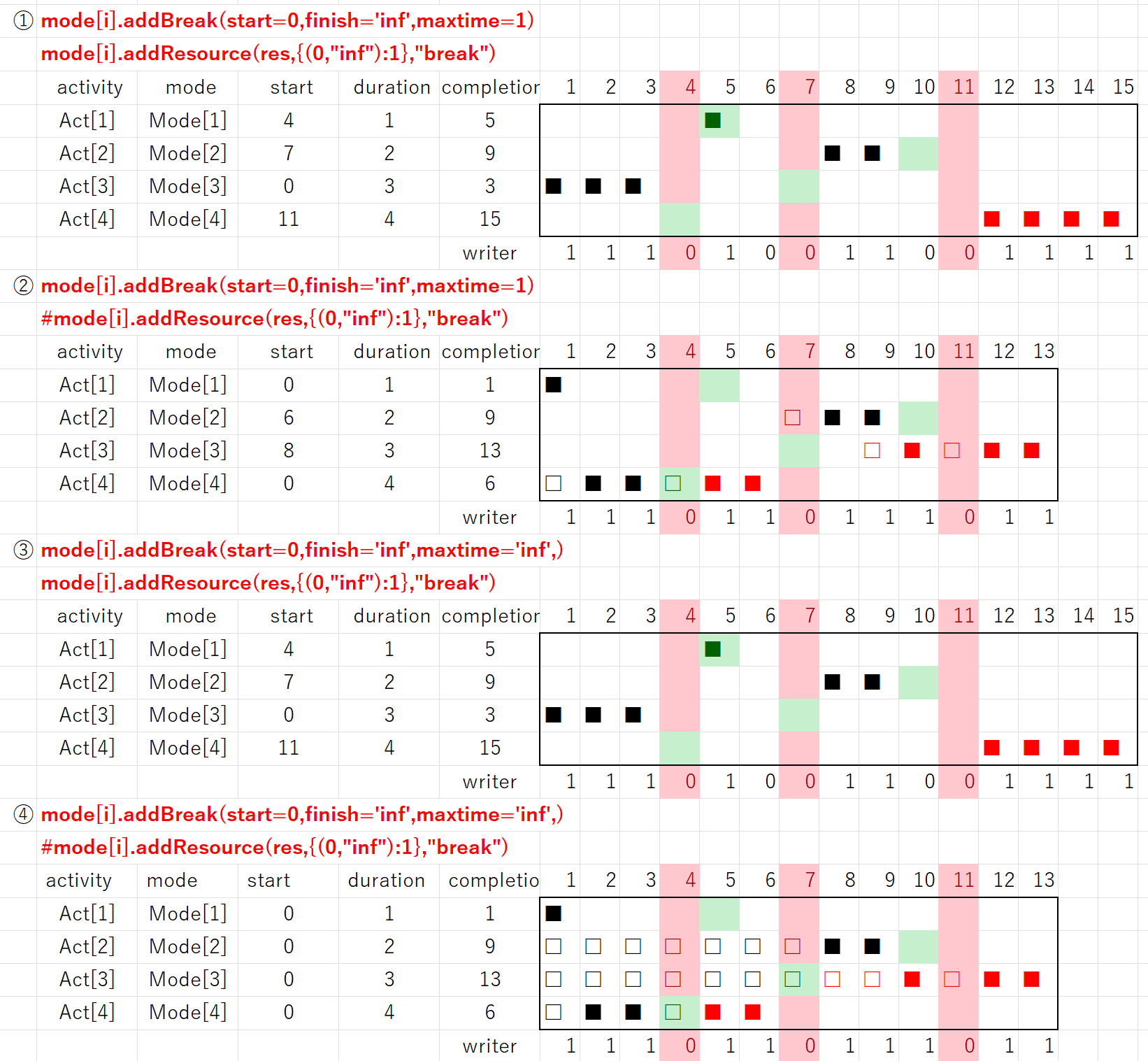
例題(ex7,ex19,ex21)
●例題ex7:クリティカルパス法
例題ex7は、例題ex1の作業時間を、次表のように短縮する可能性を探ろうとしています。ただし、短縮する場合は1万円必要とするとします。
| # |
作業名 |
作業期間 |
後続作業 |
短縮時間 |
| 1 |
乗客降し |
13 |
3 |
|
10 |
| 2 |
荷物降し |
25 |
5 |
4 |
20 |
| 3 |
機内清掃 |
15 |
4 |
|
10 |
| 4 |
乗客搭乗 |
27 |
6 |
|
25 |
| 5 |
荷物積込 |
22 |
6 |
|
20 |
| 6 |
出発 |
1 |
0 |
|
1 |
そのために各作業に通常の作業時間をもつモード1と短縮された作業時間をもつモード2を割り当て、モード2を使う場合は資金rhs万円(再生不能資源)の中から1万円使用するようにします。これは制約式
![Rendered by QuickLaTeX.com \[c_1\times x_{1,2}+c_2\times x_{2,2}+\cdots+c_5\times x_{5,2}\le rhs(man\ yen)\]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-15950d39164897d9ef377f1825e856bd_l3.png)
ただし
![Rendered by QuickLaTeX.com \[c_1=c_2=c_3=c_4=c_5=1(man\ yen)\]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fcf247e96638717034f2f7c5bd11cae6_l3.png)
![Rendered by QuickLaTeX.com \[x_{1,2},\ x_{2,2},\ x_{3,2},\ x_{4,2},\ x_{5,2}=1\ or\ 0\]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-744c142b9249bfdc2c294a04a1ed8694_l3.png)
を課すように問題定式化が行われます。
#optseq_ex7.py
from optseq import *
#-----データセット
ex7=Model()
data={\
1:[13,[3], 10],\
2:[25,[5,4],20],\
3:[15,[4], 10],\
4:[27,[6], 25],\
5:[22,[6], 30],\
6:[ 1,[0], 1],\
}
#-----作業とモード
act={}
mode={}
for i in data:
act[i]=ex7.addActivity("Act[{0}]".format(i))
mode[i,1]=Mode("Mode[{0}][1]".format(i),duration=data[i][0])
mode[i,2]=Mode("Mode[{0}][2]".format(i),duration=data[i][2])
act[i].addModes(mode[i,1],mode[i,2])
#-----モード制約
res=ex7.addResource("money",rhs=5,direction="<=")
for i in data:
if data[i][1][0]!=0:
res.addTerms(1,act[i],mode[i,2])
#-----先行制約
for i in data:
if data[i][1][0]!=0:
for j in data[i][1]:
ex7.addTemporal(act[i],act[j])
#-----最適化
ex7.Params.TimeLimit=1
ex7.Params.Makespan=True
#ex7.Params.OutputFlag=True
ex7.optimize()
#ex7.writeExcel("ex7_result.csv")
#ex7.write("ex7.txt")
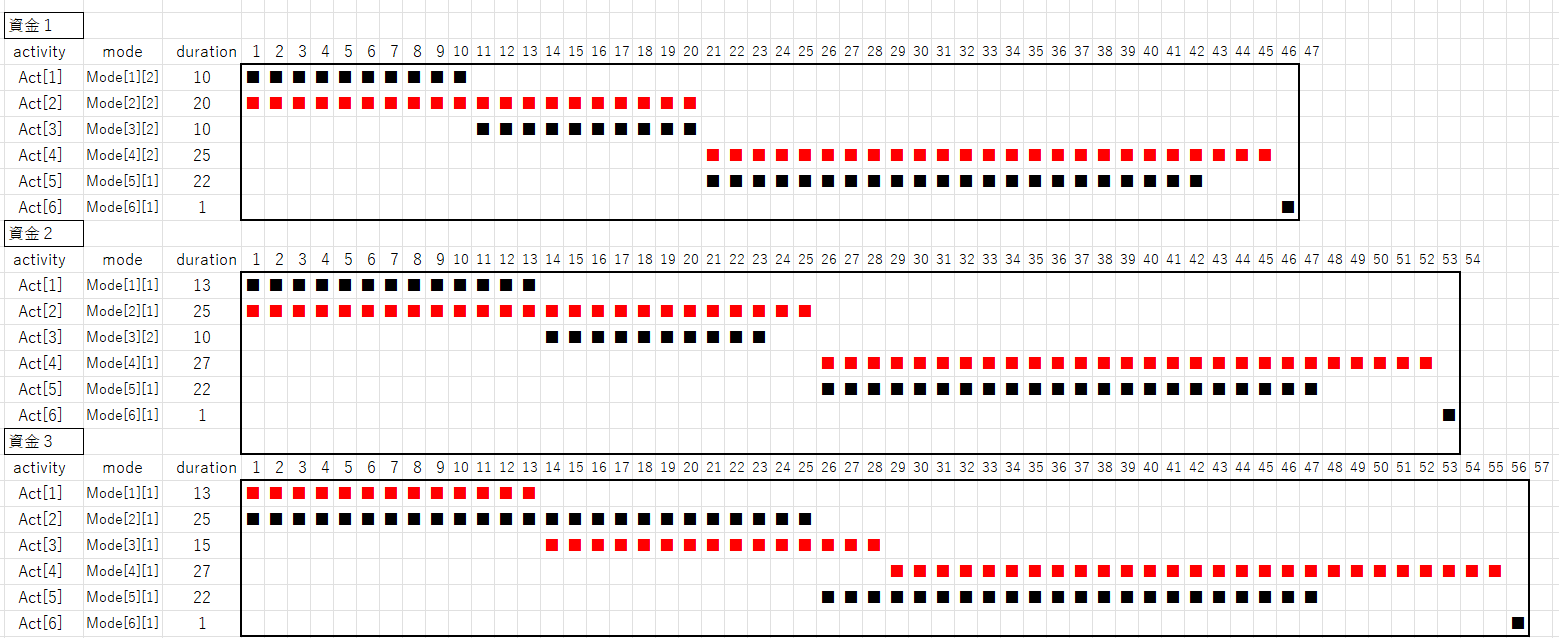
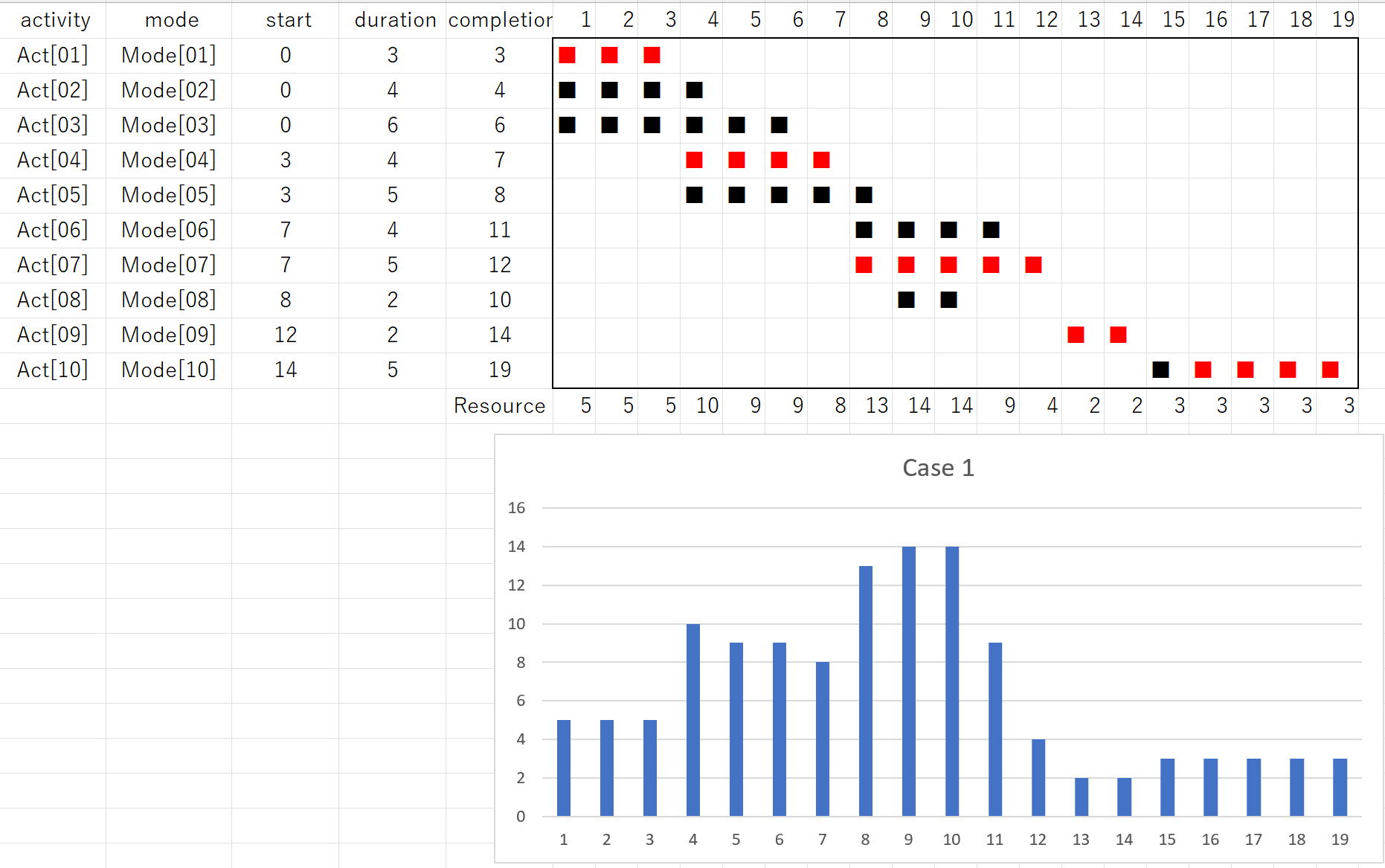
このプログラムを実行して、次の結果を得ます。ただし、資金1,2,3はそれぞれ4万円、1万円、0万円(rhs=4,1,0)に対応しています。
●例題ex19:モード間の関係
#optseq_ex19.py
from optseq import *
#-----データセット
model=Model()
duration ={
("A",0) :10,\
("A",1) :13,\
("A",2) :12,\
("B",0) :15,\
("B",1) :11,\
("B",2) :12,\
("B",3) :14,\
}
#-----作業とモード
act={}
mode={}
act["A"] = model.addActivity("Act[A]")
act["B"] = model.addActivity("Act[B]")
for i,j in duration:
mode[i,j] = Mode(f"Mode[{i},{j}]", duration[i,j])
act["A"].addModes(mode["A",0], mode["A",1], mode["A",2])
act["B"].addModes(mode["B",0], mode["B",1], mode["B",2], mode["B",3] )
#-----モード制約
con1=model.addResource("constraint_1",rhs=0,direction = "=")
con1.addTerms(coeffs=[1,-1], vars= [act["A"], act["B"]],\
values =[mode["A",0],mode["B",0]])
con2=model.addResource("constraint_2",rhs=1,direction = "<=")
con2.addTerms(coeffs=[1,1], vars= [act["A"], act["B"]],\
values =[mode["A",1],mode["B",1]])
con3=model.addResource("constraint_3",rhs=0,direction = "<=")
con3.addTerms(coeffs=[1,-1,-1], vars= [act["A"], act["B"], act["B"]],\
values =[mode["A",2], mode["B",2], mode["B",3]])
#-----最適化
model.Params.TimeLimit=1
model.Params.Makespan=True
model.optimize()
#-----
#eof
任意の作業 がモード
がモード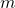 をとるとき値
をとるとき値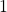 を、
を、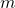 以外のモードをとるとき値
以外のモードをとるとき値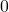 をとる変数を
をとる変数を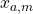 とします。このとき
とします。このとき
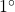 作業
作業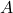 と作業
と作業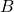 に対して同じモード
に対して同じモード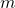 を選択させる制約式は
を選択させる制約式は
![Rendered by QuickLaTeX.com \[x_{A,m}=x_{B,m}\ \Rightarrow\ x_{A,m}+(-1)x_{B,m}=0\]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-47501c759c445df12ec8b419891a6406_l3.png)
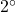 作業
作業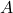 と作業
と作業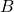 のどちらかにモード
のどちらかにモード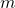 を選択させる制約式は
を選択させる制約式は
![Rendered by QuickLaTeX.com \[x_{A,m}+x_{B,m}\le 1\]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-57fa98ddcd00251228aa5bc7cf603dbb_l3.png)
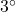 作業
作業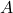 がモード
がモード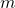 を選択するとき、作業
を選択するとき、作業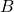 にはモード
にはモード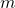 またはモード
またはモード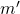 を選択させる制約式は
を選択させる制約式は
![Rendered by QuickLaTeX.com \[x_{A,m}\le x_{B,m}+x_{B,m'}\ \Rightarrow\ x_{A,m}+(-1)x_{B,m}+(-1)x_{B,m'}\le0\]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1db3fbff4e02fd5a3ac864b3e949c731_l3.png)
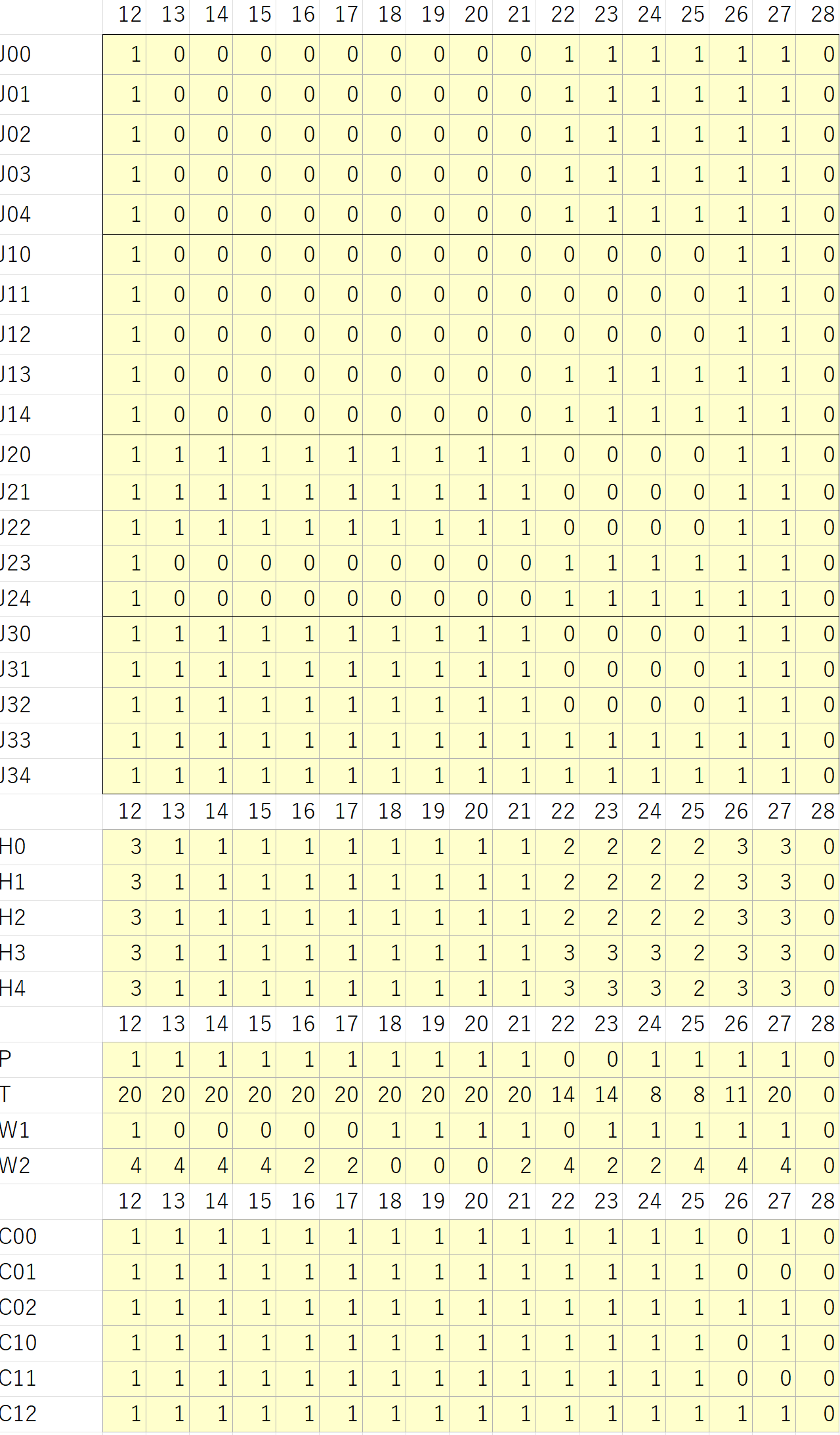
●例題ex21:資源の優先利用の設定法
#optseq_ex21.py
from optseq import *
#-----データセット
ex21=Model()
data={
1:[3,[]],\
2:[2,[]],\
3:[2,[]],\
4:[2,[]],\
5:[4,[]],\
6:[4,[]],\
7:[4,[]],\
8:[4,[]],\
9:[11,[]],\
10:[2,[]],\
}
res={}
for r in range(1,4):
res[r]=ex21.addResource("worker"+str(r), capacity=1)
#-----作業とモード
act={}
mode={}
for i in data:
act[i]=ex21.addActivity("Act[{0}]".format(i))
for r in range(1,4):
mode[i,r]=Mode("Mode[{0}{1}]".format(i,r),duration=data[i][0])
mode[i,r].addResource(res[r],1)
act[i].addModes(mode[i,r])
#-----モード制約
con={}
weight={1:1, 2:2, 3:3}
for r in range(1,4):
con[r]=ex21.addResource(name="Constraint{0}".format(r),\
rhs=0,direction="<=",weight=weight[r])
for i in data:
con[r].addTerms(1,act[i],mode[i,r])
#-----先行制約
ex21.addTemporal(act[1],act[9])
for i in range(5,9):
ex21.addTemporal(act[4],act[i])
ex21.addTemporal(act[i],act[10])
#-----最適化
ex21.Params.TimeLimit=1
ex21.Params.Makespan=True
#ex21.Params.OutputFlag=True
ex21.optimize()
ex21.writeExcel("ex21_result.csv")
#ex21.write("ex21.txt")
#-----
#eof











![Rendered by QuickLaTeX.com \[\displaystyle{\boxed{\begin{array}{cl} {\bf min}&\ Objective\ Function\\ {start\ times}&\\ {\bf subject\ to}&1^\circ\ Precedence\ Constraints\\ &2^\circ\ Resource\ Constraints \end{array}}}\]](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e06beb8547aee1ddb83a85eeb795ffb6_l3.png)