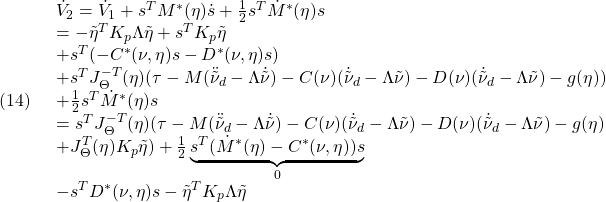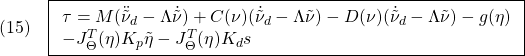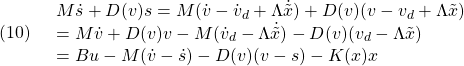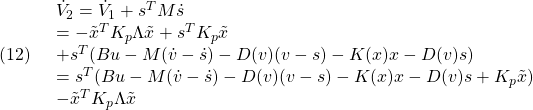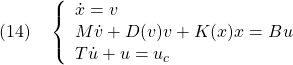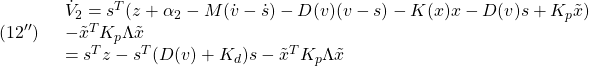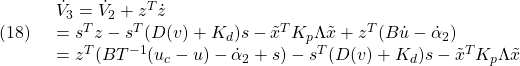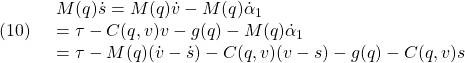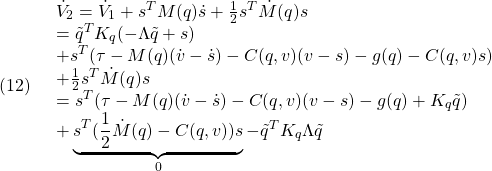制御系CAD

制御を意識したモノつくりを目指して

演習

投稿日時: 2022年8月17日投稿者: cacsd

[1] 次の値を計算せよ。

$1^\circ\ 1-\frac{1}{e}$
$2^\circ\ \cos^{-1}(-1)$

[2] 次の関数のグラフを描け。

$p(x)=\frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}\quad(-3\le x\le 3)$

[3] つぎの行列 $M$ の逆行列 $M^{-1}$ を計算し、 $MM^{-1}=I_2$ を確認せよ。

$M=\left[\begin{array}{cc}a&b\\c&d\end{array}\right]$

[4] 次のA行列の固有値を計算せよ。 ${\rm det}(sI_2-A)=0$ を解け。

$A=\left[\begin{array}{cc}0&1\\-\omega_n^2&-2\zeta\omega_n\end{array}\right]$

[5] $\dot{x}=Ax+Bu$ において、 $A=\left[\begin{array}{cc}1&2\\3&4\end{array}\right]$ 、 $B=\left[\begin{array}{cc}5\\6\end{array}\right]$ のとき、 $A-BF$ の固有値が{-1,-2}となるように状態フィードバック $u=-Fx$ を、次式によって定めよ。また、その妥当性を $A-BF$ の固有値を計算して確かめよ。

$F=[a_2'-a_2,a_1'-a_1]\left[\begin{array}{cc}a_1&1\\1&0\end{array}\right]^{-1}\left[\begin{array}{cc}B&AB\end{array}\right]^{-1}$

ヒント：多項式 $p(s)=s^2+a_1s+a_2$ の係数 $a_1$ と $a_2$ はそれぞれcoeff(p,s,1)とcoeff(p,s,0)で与えられる。

[6] 次の倒立振子の運動方程式を導き、状態空間表現を導け。

基礎事項

投稿日時: 2022年8月17日投稿者: cacsd

[0] はじめに
対話型数式処理プログラムMAXIMAは、次からフリーで入手できます。
http://sourceforge.net/projects/maxima/files/
次のフォントが必要な場合があります。
TeX-fonts-25

[1] 基礎
１）次のコマンドを与えます。最後にshift+enterを押してください。
–> a:1;
こうすると変数aに値1を与えたことになります。MAXIMAでは，「:」は「定義によって等しい」を意味します。確認のため，次のコマンドを与えてみます。
–> a;
また，最後の「;」はコマンド行の区切りを示し（つけない場合は自動的に付加されます），MAXIMAは対応する処理を実行後，その結果を返します。もし，処理結果の表示が不要な場合は，最後に「$」を置きます。次を確かめてください。
–> a:1$
もし，変数aやすべての変数を消去したい場合は，それぞれ次のコマンドを与えます。
–> kill(a);
–> kill(all);

２）さて，四則演算の記法については，通常の言語処理系と同じように，次が用いられます。
–> x+y;
–> x-y;
–> x*y;
–> x/y;
–> x^y;

３）関数 $y=ax^2$ を定義するには，次のコマンドを与えます。
–> y: a*x^2;
yの値を，x=2について計算するときは，次のコマンドを与えます。
–> ev(y,x:2);
または
–> y, x:2

４）一方， $f(x)=ax^2$ のように関数を明示的に定義するには，次のコマンドを与えます。
–> f(x):=a*x^2;
ここで、x=2のときの値は，次のように参照できます。
–> f(2);

[2] 関数のグラフ
１）関数のグラフを描くときは，たとえば次のコマンドを与えます。
–> y1: x^2;
–> plot2d(y1,[x,-2,2]);

２）２つのグラフを重ねて描くときは，続けて次のコマンドを与えます。
–> y2: 2*x;
–> plot2d([y1,y2],[x,-2,2]);

[3] リスト
１）MAXIMAの基本的なデータ構造は，「リスト」と呼ばれるものです。たとえば，次のコマンドを与えます。
–> a1:[a11,a12];
これにより，a1は，２つの要素a11とa12からなるリストとして定義されます。また，要素の区切りは「,」であることに注意してください。

２）ある変数がリストであるかどうかを調べるためには，次のコマンドを与えます。
–> listp(a1);
リストの長さを調べるには，次のコマンドを与えます。
–> length(a1);
リストの要素へのアクセス，たとえば，第１番目の要素を調べるには，次のコマンドを与えます。
–> a1[1];

３）さて，リスト自身を要素にもつリストも定義できます。
–> a2:[a21,a22];
を定義して，次のコマンドを与えてください。
–> A:[a1,a2];
これが，サイズ２×２の行列Ａを定義したことに相当します（行列データについては，あとで詳しく説明します）。たとえば，A[2]はa2を意味しますので，Aの（２，１）要素へのアクセスは次のようにします。
–> A[2][1];

[4] 関数
１）絶対値と平方根については，たとえば次のように得られます。
–> abs(-2);
–> sqrt(2);

２）円周率は，%piで参照することができます。
–> %pi;
–> %pi, numer;
三角関数の計算は，たとえば次の通り実行できます。
–> sin(%pi/4);
–> cos(%pi/4);
–> tan(%pi/4);

３）三角関数の逆関数の計算は，たとえば次の通り実行できます。
–> asin(1);
–> acos(-1);
–> atan(1);
–> atan2(1,-1);
ここで，x>0のときatan2(y,x)=atan(y/x)です。

４）次は，加法定理を示しています。
–> trigexpand(sin(x+y));
–> trigreduce(%)
–> trigexpand(cos(x+y));
–> trigreduce(%)
–> trigexpand(tan(x+y));
–> trigreduce(%)

５）指数関数の計算は，たとえば次の通り実行できます。
–> exp(0);

６）この逆関数(対数関数)の計算は，たとえば次の通り実行できます。
–> log(1);
この底はネイピア数eですが，10の場合は次の関数を定義して用います。
–> log10(x):=log(x)/log(10);
–> log10(1);

７）双曲線関数は，次式で定義されます。
$\sinh=\frac{e^x-e^{-x}}{2},\,\cosh=\frac{e^x+e^{-x}}{2},\,\tanh=\frac{\sinh\,x}{\cosh\,x}$
これらの計算は，たとえば次の通り実行できます。
–> sinh(0);
–> cosh(0);
–> tanh(0);

８）双曲線関数の逆関数の計算は，たとえば次の通り実行できます。
–> asinh(0);
–> acosh(1);
–> atanh(0);

[5] 多項式
１）因数分解
$x^2-1=(x+1)(x-1)$
を行うために，次のコマンドを与えてください。
–> factor(x^2-1);

２）また，式の展開
$(a+1)(x-1)=ax-a+x-1$
を行うために，次のコマンドを与えてください。
–> expand((a+1)*(x-1));
ここで，xだけについて整理して
$(a-1)x-a+1$
としたいときには，次のコマンドを与えまず。
–> ratsimp(%,x);
ここで，「%」は直前の結果を参照しています。

３）さらに，部分分数展開
$\frac{1}{x^2+3x+2}=\frac{1}{x+1}-\frac{1}{x+1}$
を行うために，次のコマンドを与えてみてください。
–> partfrac(1/(x^2+3*x+2),x);

[6] 方程式
１）２次方程式
$x^2+1=0$
を解くために，次のコマンドを与えてください。
–> solve(x^2+1=0,x);
ここで，出力結果における「%i」は虚数単位を表しています。解は2つの要素をもつリストとして得られていることに注意してください。第１番目の解は%[1]，第２番目の解は%[2]でアクセスできます。

２）それでは，２次方程式
$ax^2+bx+c=0$
の解の公式を求めてみましょう。
–> sol: solve(a*x^2+b*x+c=0,x)

３）次に，連立１次方程式
$\left\{\begin{array}{l} x+y=1\\ x+2y=1 \end{array}\right.$
を解くために，次のコマンドを与えてください。
–> solve([x+y=1,x+2*y=1],[x,y])

４）それでは，連立１次方程式
$\left\{\begin{array}{l} ax+by=e\\ cx+dy=f \end{array}\right.$
の解を求めてください。
–> sol: solve([a*x+b*y=e,c*x+d*y=f],[x,y])
解はリストのリストとして得られています。したがって，第１番目の解はsol[1][1],第２番目の解はsol[1][2]でアクセスできることに注意してください。

５）ちなみに，複素数
$1-j$
の実部と虚部は，次のように得られます。
–> realpart(1-%i)
–> imagpart(1-%i)

[7] 論理演算
１）論理和，論理積，否定はそれぞれ
$a\&b$
$a|b$
$\sim\,a$
のように表されます。たとえば
–> true and false;
–> true or false;
–> not true;
これらは，論理式と呼ばれ，trueかfalseのどちらかの値をとります。

２）真理値表を作ってみましょう。
–> [true and true, true and false, false and true, false and false];
–> [true or true, true or false, false or true, false or false];
–> [not true, not false];

３）次の等価な関係は，さまざまな論理展開に有用です。
$\sim (A\Rightarrow\,B)\leftrightarrow\,A\&\sim B$
右辺の真理値表を作ってみましょう。
–> [true and not true, true and not false, false and not true, false and not false];

４）さて，次のように入力してみてください。
–> is(1=1);
–> is(1#1);
これらも論理式です。次も同様です。
–> is(1>1);
–> is(1>=1);
–> is(1<1);
–> is(1<=1);

[8] 微分積分
１）まず極限の例を，いくつか挙げます。
–> limit(exp(-x),x,inf);
–> limit(exp(x),x,inf);
–> limit((1+1/x)^x,x,0);
–> limit(sin(x)/x,x,0);

２）微分の例を，いくつか挙げます。
–> diff(x^2,x);
–> diff(1/x,x);
–> diff(exp(x),x);
–> diff(log(x),x);
–> diff(sin(x),x);
–> diff(atan(x),x)

２）２階微分は，たとえば次のように行います。
–> diff(x^2,x,2);

３）積分の例を，いくつか挙げます。
–> integrate(2*x,x);
–> integrate(-1/x^2,x);
–> integrate(exp(x),x);
–> integrate(1/x,x);
–> integrate(cos(x),x);
–> integrate(1/(x^2+1),x);

４）次のようにtaylor展開を行うことができます。
–> taylor(exp(x),x,0,10);
–> taylor(sin(x),x,0,10);
–> taylor(cos(x),x,0,10);

５）微分方程式
$\frac{dx(t)}{dt}=-x(t)$
を解くために，次のコマンドを与えてください。
–> sol:desolve(’diff(x(t),t)=-x(t),x(t));
ここで，「’diff(x(t),t)」は，
$\frac{dx(t)}{dt}$
を表しています。また，注意しなければないのは，solがリストとなっていないことです。たとえば，x(0)=1のとき，この解のグラフを描くには，次のように，コマンドを与えます。
–> s1:rhs(sol), x(0)=1;
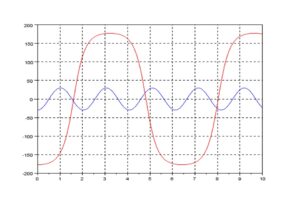
–> plot2d(s1,[t,0,5]);

６）さらに，微分方程式
$\frac{dx(t)}{dt}=-x(t)+\sin(10t)$
の解の構成要素を調べるために，次のコマンドを与えてください。
–> sol:desolve(’diff(x(t),t)=-x(t)+sin(10*t),x(t));
–> s2:rhs(sol), x(0)=1;
–> s3:rhs(sol), x(0)=0;
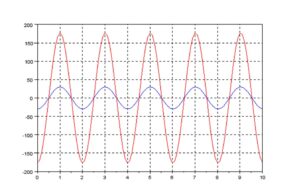
–> plot2d([s1,s2,s3],[t,0,5]);

[9] 行列計算
１）次のコマンドを与えてみましょう。
–> A:matrix([a11,a12],[a21,a22]);
–> B:ident(2);
–> C:zeromatrix(2,2);
–> D:apply(matrix,makelist(ident(2)[i]*[d1,d2][i],i,1,2));
行列Aの（2,1）要素へのアクセスは,A[2][1]またはA[2,1]として行います。
–> A[2,1];

２）行列の結合は次のように行います。
–> addcol(A,B);
–> addrow(A,C);

３）まず，要素ごとの四則演算は，次のように行えます。
–> A+B;
–> A-B;
–> A*B;
–> B/A;
–> A^2;

４）次に，行列としての演算は，次のように行います。
–> A.B;
–> A.invert(A);
–> A^^2;
–> transpose(A);

５）行列の階数，行列式，特性多項式、余因子行列は，次のように求められます。
–> rank(A);
–> determinant(A);
–> charpoly(A,s);
–> adjoint(A);

６）固有値と固有ベクトルは，次のように求められます。
–> Q:matrix([q1,q3],[q3,q2]);
–> eigenvalues(Q);
–> V:eigenvectors(Q);
この固有ベクトルが直交することは、次のように確かめられます。
–> V[2][1][1].V[2][2][1],ratsimp;

倒立振子の安定化制御

投稿日時: 2022年8月17日投稿者: cacsd

[0] このページは、「SCILABによる倒立振子の特性解析」の続きです。以下では、物理定数を次のように仮定します。

$M=0.94$ [kg], $m=0.23$ [m], $\ell=0.6413/2$ [m], $\alpha=5$ [deg]

[1] まず，安定性を調べます。そのために，SCILABの関数specを用いて， $A$ 行列の固有値を求めると，次のように得られます。

$\lambda_1=0,\ \lambda_2=0,\ \lambda_3=+5.181,\ \lambda_4=-5.181$

したがって，３つの固有値の実部が負ではなく，漸近安定性の条件（すべての固有値の実部が負）を満足していません。よって，倒立振子は不安定な制御対象であると判定します。
次に，可制御性の判定を行ないます。そのために，可制御性行列の階数が，制御対象の次数４に等しいか，すなわち

${\rm rank}[B\ A-\lambda_i I_4]=4\quad(i=1,2,3,4)$

が成り立つかどうかを調べます。行列 $[B\ A-\lambda_iI_4]$ の最小特異値を求めると，次のように得られます。

$\begin{tabular}{l|l}\hline eigenvalues of A & minimum singular values of $[B\ A-\lambda_iI_4]$\\\hline \lambda_1=0 & \sigma_{min}=0.849\\ \lambda_2=0 & \sigma_{min}=0.849\\ \lambda_3=+5.181 & \sigma_{min}=0.434\\ \lambda_4=-5.181 & \sigma_{min}=0.434\\\hline \end{tabular}$

すべての最小特異値は正なので，倒立振子の可制御性は成り立つと判定します。

次に，可観測性の判定を行ないます。そのために，可観測性行列の階数が，制御対象の次数４に等しいか，すなわち

${\rm rank}\left[\begin{array}{c}C\\ A-\lambda_i I_4\end{array}\right]=4\quad(i=1,2,3,4)$

が成り立つかどうかを調べます。行列 $\left[\begin{array}{c}C\\ A-\lambda_i I_4\end{array}\right]$ の最小特異値を求めると，次のように得られます。

$\begin{tabular}{l|l}\hline eigenvalues of A & minimum singular values of $\left[\begin{array}{c}C\\ A-\lambda_i I_4\end{array}\right]$\\\hline \lambda_1=0 & \sigma_{min}=1\\ \lambda_2=0 & \sigma_{min}=1\\ \lambda_3=+5.181 & \sigma_{min}=0.189\\ \lambda_4=-5.181 & \sigma_{min}=0.189\\\hline \end{tabular}$

すべての最小特異値は正なので，倒立振子の可観測性は成り立つと判定します。

以上の計算を，SCILABで行うためのプログラムを，次に示します。

//cip.sce
M=0.94; m=0.23; ell=0.6413/2; g=9.8;
alpha=5/180*%pi
a32=-6*m*g/(8*M+(5-3*cos(2*alpha))*m);
b3=8/(8*M+(5-3*cos(2*alpha))*m);
a42=6*(M+m)*g/(8*M+(5-3*cos(2*alpha))*m)/ell;
b4=-6*cos(alpha)/(8*M+(5-3*cos(2*alpha))*m)/ell;
A=[0 0 1 0;0 0 0 1;0 a32 0 0;0 a42 0 0];
B=[0;0;b3;b4];
C=eye(2,4);
r=spec(A)
for i=1:4, min(svd([B A-r(i)*eye(4,4)])), end
for i=1:4, min(svd([C; A-r(i)*eye(4,4)])), end

[2] 不安定な倒立振子を安定化するための状態フィードバック

$u=-Fx$

を決定することを考えます。そのために安定な閉ループ系

$\dot{x}=(A-BF)x$

の応答に対して，２次形式評価関数

$\displaystyle{J=\int_0^\infty (q_1^2r^2(t)+q_2^2\dot{r}^2(t)+q_3^2\theta^2(t)+q_4^2\dot{\theta}^2(t)+\rho^2r_1^2u^2(t))dt}$

ただし、

$\displaystyle{q_1=\frac{1}{\max |r|},\ q_2=\frac{1}{\max |\dot{r}|},\ q_3=\frac{1}{\max |\theta|},\ q_4=\frac{1}{\max |\dot{\theta}|},\ r_1=\frac{1}{\max |u|}}$

を最小化するものを選ぶことを考えます。そのような安定化状態フードバックのゲイン行列 $F$ は，リッカチ方程式CARE

$\Pi A+A^T\Pi -\Pi B R^{-1} B^T\Pi+Q=0$

ただし、

$Q={\rm diag}\{q_1^2,q_2^2,q_3^2.q_4^2\},\ R=\rho^2r_1^2$

の解 $\Pi>0$ を用いて，次のように与えられます。

$F=R^{-1}B\Pi$

以上の計算を，SCILABで行うためのプログラムを，次に示します。

Mr=1; Tr=0.1; Mth=5/180*%pi;
Tth=(1/4)*(2*%pi*sqrt(4/3*ell/g)); Mu=5;
q1=1/Mr; q2=1/Mth; q3=Tr/Mr; q4=Tth/Mth; r1=1/Mu; rho=1;
Q=diag([q1^2,q2^2,q3^2,q4^2]); R=rho^2*r1^2;
//—–
function [F,p]=opt(A,B,C,Q,R)
w2=R\B’;
[v,p]=spec([A -B*w2;-C’*Q*C -A’]); p=diag(p);
[dummy,index]=sort(real(p));
n=size(A,1); j=index(n+1:n+n);
p=p(j); x=v(1:n,j); y=v(n+1:n+n,j);
X=real(y/x); F=w2*X;
endfunction
//—–
[F,p]=opt(A,B,eye(4,4),Q,R);
function dz=clps1(t,z),dz=(A-B*F)*z,endfunction
t0=0; t=0:0.01:10; x0=[0;3/180*%pi;0;0];
z=ode(x0,t0,t,clps1);
scf(0);
subplot(211),plot(t,diag([100 180/%pi])*C*z); mtlb_grid
subplot(212),plot(t,-F*z); mtlb_grid

計算工学演習第一レポート（２）

単振り子のアニメーション

投稿日時: 2022年8月17日投稿者: cacsd

次の単振り子を考えます。

この運動方程式は

$\begin{array}{ll} \displaystyle{m\ddot{r}=\underbrace{-mg\sin\theta}_f\quad(r=\ell\theta)} \end{array}$

すなわち

$\begin{array}{ll} \displaystyle{\ddot{\theta}=-\frac{g}{\ell}\sin\theta} \end{array}$

となります。ここで、 $\theta\simeq0$ 　と近似すると

$\begin{array}{ll} \displaystyle{\ddot{\theta}=-\frac{g}{\ell}\theta} \end{array}$

となります。この解は、 $\dot{\theta}(0)=0$ 　を仮定すると

$\theta(t)=\theta(0)\cos\left(\sqrt{\frac{g}{\ell}}t\right)$

のように表されます。ここで、単振り子の周期は次式で与えられます。

$\frac{2\pi}{T}=\sqrt{\frac{g}{\ell}} \Rightarrow T=2\pi\sqrt{\frac{\ell}{g}}$

この線形シミュレーションを行うために、次のプログラムを実行してみてください。

function dx=f(t,x),
dx=A*x,
endfunction
g=9.8; L=1;
A=[0 1;-g/L 0];
t0=0; t1=10; nt=100; td=(t1-t0)/nt; t=t0:td:t1;
x0=[-30/180*%pi;0];
x1=ode(x0,t0,t,f);
x0=[-177/180*%pi;0];
x2=ode(x0,t0,t,f);
clf(0),scf(0);
plot(t,180/%pi*x1(1,:),’b’,t,180/%pi*x2(1,:),’r’),
mtlb_grid

次のようなグラフが現れるでしょう。初期値は２通り設定しています。

次に、非線形シミュレーションを行うために、次のプログラムを実行してみてください。

function dx=f1(t,x)
th=x(1);
dth=x(2);
dx(1)=dth;
dx(2)=-g/ell*sin(th);
endfunction
g=9.8; ell=1; T=2*%pi*1/sqrt(g/ell)
t0=0; t1=10; nt=100; td=(t1-t0)/nt; t=t0:td:t1;
x=[-30/180*%pi;0];
for i=1:nt, x=[x ode(x(:,i),t(i),t(i+1),f1)]; end
x1=x;
x=[-177/180*%pi;0];
for i=1:nt, x=[x ode(x(:,i),t(i),t(i+1),f1)]; end
x2=x;
clf(0),scf(0);
plot(t,180/%pi*x1(1,:),’b’,t,180/%pi*x2(1,:),’r’),
mtlb_grid

次のようなグラフが現れるでしょう。初期値は２通り設定しています。

線形と非線形では、シミュレーション結果が全く違います！

それでは、これらをアニメーションで比較してみましょう。まず、線形シミュレーションの場合です。

function dx=f1(t,x),
dx=A*x,
endfunction
g=9.8; L=1;
A=[0 1;-g/L 0];
t0=0; t1=10; nt=2000; td=(t1-t0)/nt; t=t0:td:t1;
x0=[-30/180*%pi;0];
x1=ode(x0,t0,t,f1);
x0=[-177/180*%pi;0];
x2=ode(x0,t0,t,f1);
x=L*sin(x2(1,:)+%pi);
y=L*cos(x2(1,:)+%pi);
figure(1);
plot([0;x(1)],[0;y(1)],’o-‘);
h_compound = gce();
h_compound.children.thickness = 2
h_compound.children.mark_size = 10;
h_compound.children.mark_background = 2;
h_axes = gca();
h_axes.data_bounds = [-1.5,-1.5;1.5,1.5];
i = 1;
while i<=length(t)
drawlater();
h_compound.children.data = [0 0;x(i),y(i)];
drawnow();
i = i+1;
end

次に、非線形シミュレーションの場合です。

function dx=f2(t,x)
th=x(1);
dth=x(2);
dx(1)=dth;
dx(2)=-g/ell*sin(th);
endfunction
g=9.8; ell=0.5; T=2*%pi*1/sqrt(g/ell);
t0=0; t1=10; nt=2000; td=(t1-t0)/nt; t=t0:td:t1;
x0=[-30/180*%pi;0];
x1=ode(x0,t0,t,f2);
x0=[-177/180*%pi;0];
x2=ode(x0,t0,t,f2);
x=2*ell*sin(x2(1,:)+%pi);
y=2*ell*cos(x2(1,:)+%pi);
figure(1);
plot([0;x(1)],[0;y(1)],’o-‘);
h_compound = gce();
h_compound.children.thickness = 2
h_compound.children.mark_size = 10;
h_compound.children.mark_background = 2;
h_axes = gca();
h_axes.data_bounds = [-1.5,-1.5;1.5,1.5];
i = 1;
while i<=length(t)
drawlater();
h_compound.children.data = [0 0;x(i),y(i)];
drawnow();
i = i+1;
end

このアニメーションの作成には、次のサイトを参考にさせていただきました。

Scilabでアニメーション作成

【参考】　バネで拘束されている台車のアニメーションを以下に示します。

clear; xdel(winsid());
function dx=f(t,x),
dx=A*x,
endfunction
A=[0 1;-1 0];
t0=0; t1=10; nt=2000; td=(t1-t0)/nt; t=t0:td:t1;
x0=[0;1];
x1=ode(x0,t0,t,f);
x=0.2*[0 1 1 0 0]’;
y=0.2*[0 0 1 1 0]’;
figure(1);
plot(x,y);
mtlb_grid
h_compound = gce();
h_compound.children.thickness = 2
h_compound.children.mark_size = 10;
h_compound.children.mark_background = 2;
h_axes = gca();
h_axes.data_bounds = [-1.5,-1;1.5,1];
i = 1;
while i<=length(t)
drawlater();
h_compound.children.data = [x+x1(1,i) y];
drawnow();
i = i+1;
end

線形系の応答計算

投稿日時: 2022年8月17日投稿者: cacsd

[1]自由系の時間応答
a) 次の１次自由系の時間応答を重ねて描け。
$\dot{x}=-\frac{1}{T}x,\quad x(0)=1$
$\quad(T=0.5,1,2; K=1)$
b) 次の２次自由系の時間応答を重ねて描け。
$\dot{x}= \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right]x ,\quad x(0)= \left[\begin{array}{cc} 1 \\ 0 \end{array}\right]$
$y=\left[\begin{array}{cc} 1 & 0 \end{array}\right]x$
$\quad(\zeta=0.01,\frac{1}{\sqrt{2}},1; \omega_n=1)$

//resp1.sce
//—–
function dx=f(t,x),dx=a*x,endfunction
x0=1; t0=0;t=0:0.1:10;
a=-1/0.5;
x1=ode(x0,t0,t,f);
a=-1/1;
x2=ode(x0,t0,t,f);
a=-1/2;
x3=ode(x0,t0,t,f);
scf(1);
plot(t,x1,t,x2,t,x3)
mtlb_grid
//—–
function dx=f(t,x),dx=A*x,endfunction
x0=[1;0];t0=0;t=0:0.1:10;
A=[0 1;-1 -0.02]; C=[1 0];
x1=ode(x0,t0,t,f); y1=C*x1;
A=[0 1;-1 -sqrt(2)]; C=[1 0];
x2=ode(x0,t0,t,f); y2=C*x2;
A=[0 1;-1 -2]; C=[1 0];
x3=ode(x0,t0,t,f); y3=C*x3;
scf(2);
plot(t,y1,t,y2,t,y3)
mtlb_grid
//—–
//eof

[2]インパルス応答
a) 次の１次系のインパルス応答を重ねて描け。
$\dot{x}=-\frac{1}{T}x+\frac{K}{T}u$
$\quad(T=0.5,1,2; K=1)$
b) 次の２次系のインパルス応答を重ねて描け。
$\dot{x}= \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right]x + \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right]u$
$y=\left[\begin{array}{cc} 1 & 0 \end{array}\right]x$
$\quad(\zeta=0.01,\frac{1}{\sqrt{2}},1; \omega_n=1)$

//resp2.sce
//—–
function dx=f(t,x),dx=a*x,endfunction
t0=0; t=0:0.01:5;
a=-1/0.5; b=1/0.5;
x1=ode(b,t0,t,f);
a=-1; b=1;
x2=ode(b,t0,t,f);
a=-1/2; b=1/2;
x3=ode(b,t0,t,f);
scf(1);
plot(t,x1,t,x2,t,x3)
mtlb_grid
//—–
function dx=f(t,x),dx=A*x,endfunction
t0=0;t=0:0.1:10;
A=[0 1;-1 -0.02]; B=[0;1]; C=[1 0];
x1=ode(B,t0,t,f); y1=C*x1;
A=[0 1;-1 -sqrt(2)]; B=[0;1]; C=[1 0];
x2=ode(B,t0,t,f); y2=C*x2;
A=[0 1;-1 -2]; B=[0;1]; C=[1 0];
x3=ode(B,t0,t,f); y3=C*x3;
scf(2);
plot(t,y1,t,y2,t,y3,t,1)
mtlb_grid
//—–
//eof

[3]正弦波入力に対する時間応答
a) 次の１次自由系の $u=\sin\,10t$ に対する時間応答を，零入力応答と零状態応答と重ねて描け。
$\dot{x}=-\frac{1}{T}x+\frac{K}{T}u,\quad x(0)=1$
$\quad(T=1; K=1)$
b) 次の２次自由系の $u=\sin\,10t$ に対する時間応答を，零入力応答と零状態応答と重ねて描け。
$\dot{x}= \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right]x + \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right]u ,\quad x(0)= \left[\begin{array}{cc} 1 \\ 0 \end{array}\right]$
$y=\left[\begin{array}{cc} 1 & 0 \end{array}\right]x$
$\quad(\zeta=\frac{1}{\sqrt{2}}; \omega_n=1)$

//resp3.sce
//—–
function dx=f1(t,x),dx=a*x,endfunction
function dx=f2(t,x),dx=a*x+b*u(t),endfunction
function ut=u(t),ut=sin(10*t),endfunction
a=-1; b=1;
x0=1; t0=0; t=0:0.01:5;
x1=ode(x0,t0,t,f1);
x0=0; t0=0; t=0:0.01:5;
x2=ode(x0,t0,t,f2);
x0=1; t0=0; t=0:0.01:5;
x3=ode(x0,t0,t,f2);
scf(1);
plot(t,x1,t,x2,t,x3)
mtlb_grid
//—–
function dx=f1(t,x),dx=A*x,endfunction
function dx=f2(t,x),dx=A*x+B*u(t),endfunction
function ut=u(t),ut=sin(10*t),endfunction
A=[0 1;-1 -sqrt(2)]; B=[0;1]; C=[1 0];
x0=[1;0]; t0=0; t=0:0.1:10;
x1=ode(x0,t0,t,f1); y1=C*x1;
x0=[0;0]; t0=0; t=0:0.1:10;
x2=ode(x0,t0,t,f2); y2=C*x2;
x0=[1;0]; t0=0; t=0:0.1:10;
x3=ode(x0,t0,t,f2); y3=C*x3;
scf(2);
plot(t,y1,t,y2,t,y3,t,1)
mtlb_grid
//—–
//eof

[4]ステップ応答
a) 次の１次系のステップ応答を重ねて描け。
$\dot{x}=-\frac{1}{T}x+\frac{K}{T}u$
$\quad(T=-0.5,-1,2; K=1)$
b) 次の２次系のステップ応答を重ねて描け。
$\dot{x}= \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right]x + \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right]u$
$y=\left[\begin{array}{cc} 1 & 0 \end{array}\right]x$
$\quad(\zeta=0.01,\frac{1}{\sqrt{2}},1; \omega_n=1)$

//resp4.sce
//—–
function dx=f(t,x),dx=a*x+b*u(t),endfunction
function ut=u(t),ut=1,endfunction
x0=0; t0=0; t=0:0.01:5;
a=-1/0.5; b=1/0.5;
x1=ode(x0,t0,t,f);
a=-1; b=1;
x2=ode(x0,t0,t,f);
a=-1/2; b=1/2;
x3=ode(x0,t0,t,f);
scf(1);
plot(t,x1,t,x2,t,x3,t,1-1/%e)
mtlb_grid
//—–
function dx=f(t,x),dx=A*x+B*u(t),endfunction
function ut=u(t),ut=1,endfunction
x0=[0;0];t0=0;t=0:0.1:10;
A=[0 1;-1 -0.02]; B=[0;1]; C=[1 0];
x1=ode(x0,t0,t,f); y1=C*x1;
A=[0 1;-1 -sqrt(2)]; B=[0;1]; C=[1 0];
x2=ode(x0,t0,t,f); y2=C*x2;
A=[0 1;-1 -2]; B=[0;1]; C=[1 0];
x3=ode(x0,t0,t,f); y3=C*x3;
scf(2);
plot(t,y1,t,y2,t,y3,t,1)
mtlb_grid
//—–
//eof

[5]周波数応答
a) 次の１次系の周波数応答を重ねて描け。
$\dot{x}=-\frac{1}{T}x+\frac{K}{T}u$
$\quad(T=-0.5,-1,2; K=1)$
b) 次の２次系の周波数応答を重ねて描け。
$\dot{x}= \left[\begin{array}{cc} 0 & 1\\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right]x + \left[\begin{array}{cc} 0 \\ \omega_n^2 \end{array}\right]u$
$y=\left[\begin{array}{cc} 1 & 0 \end{array}\right]x$
$\quad(\zeta=0.01,\frac{1}{\sqrt{2}},1; \omega_n=1)$

//resp5.sce
//—–
function g=f(a,b,w), g=b./(%i*w-a), endfunction
w=logspace(-1,1);
a=-1/2; b=1/2; g=f(a,b,w); ga1=20*log10(abs(g));
ph1=180/%pi*atan(imag(g),real(g));
a=-1/1; b=1/1; g=f(a,b,w); ga2=20*log10(abs(g));
ph2=180/%pi*atan(imag(g),real(g));
a=-1/0.5; b=1/0.5; g=f(a,b,w); ga3=20*log10(abs(g));
ph3=180/%pi*atan(imag(g),real(g));
scf(1);
subplot(211),plot2d(w,ga1,logflag=’ln’),
plot2d(w,ga2,logflag=’ln’),
plot2d(w,ga3,logflag=’ln’),mtlb_grid
subplot(212),plot2d(w,ph1,logflag=’ln’),
plot2d(w,ph2,logflag=’ln’),
plot2d(w,ph3,logflag=’ln’),mtlb_grid
//—–
function g=f(A,B,C,w),
g=[]; N=length(w)
for i=1:N, g=[g C*((%i*w(i)*eye(A)-A)\B)]; end
endfunction
B=[0;1]; C=[1 0]; w=logspace(-1,1,200);
A=[0 1;-1 -2*0.01]; g=f(A,B,C,w); ga1=20*log10(abs(g));
ph1=180/%pi*atan(imag(g),real(g));
A=[0 1;-1 -2/sqrt(2)]; g=f(A,B,C,w); ga2=20*log10(abs(g));
ph2=180/%pi*atan(imag(g),real(g));
A=[0 1;-1 -2*1]; g=f(A,B,C,w); ga3=20*log10(abs(g));
ph3=180/%pi*atan(imag(g),real(g));
scf(2);
subplot(211),plot2d(w,ga1,logflag=’ln’),
plot2d(w,ga2,logflag=’ln’),
plot2d(w,ga3,logflag=’ln’),mtlb_grid
subplot(212),plot2d(w,ph1,logflag=’ln’),
plot2d(w,ph2,logflag=’ln’)
plot2d(w,ph3,logflag=’ln’),mtlb_grid
//—–
//eof

演習

投稿日時: 2022年8月17日投稿者: cacsd

[1] 次の行列を定義せよ。

$1^\circ\ A=\left[\begin{array}{cc} 0 & 1 \\ -1 & -0.02 \end{array}\right],\ B=\left[\begin{array}{cc} 0 \\ 1 \end{array}\right],\ C=\left[\begin{array}{cc} 1 & 0 \end{array}\right]$

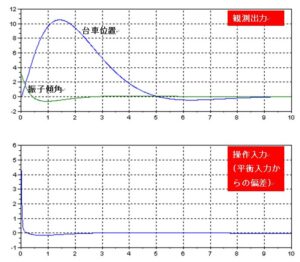
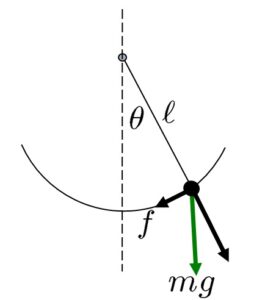
$2^\circ\ A=\left[\begin{array}{cccc} 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \end{array}\right],\ B=\left[\begin{array}{cc} 0 & 0 \\ 0 & 0 \\ 1 & 1 \\ 1 & -1 \end{array}\right]$

$3^\circ\ A=\left[\begin{array}{cccc} 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \\ -1 & -4 & -6 & -4 \end{array}\right],\ B=\left[\begin{array}{cc} 0 \\ 0 \\ 0 \\ 1 \end{array}\right]$

[2] 行列

$E=\left[\begin{array}{ccccc} 1 & 2 & 1 & 0 & 0\\ 3 & 4 & 0 & 1 & 0\\ 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 2 & 0\\ 0 & 0 & 0 & 0 & 3 \end{array}\right]$

に対して

$1^\circ$ 行列Eの列ベクトルを逆順に並べよ。

$2^\circ$ 行列Eの行ベクトルを逆順に並べよ。

$3^\circ$ 行列Eの奇数番目の列ベクトルと偶数番目の行ベクトルからなる小行列を求めよ。

[3]

$1^\circ$ 行列

$A=\left[\begin{array}{ccccc} 0 & 1 \\ -2 & -3 \end{array}\right]$

の固有値分解 $VRV^{-1}$ を求め，つぎを確かめよ。

$A=VRV^{-1}$

$2^\circ$ 行列

$C=\left[\begin{array}{ccccc} 1 & 0 & 0 & 0 \\ 1 & 1 & 0 & 0 \end{array}\right]$

の特異値分解 $USV^T$ を求め，つぎを確かめよ。

$C=USV^T$
$U^TU=I$
$V^TV=I$

$3^\circ$ x=[3 1 5 4 2] の要素を大きい順に並べよ。

[4] 平均 $\mu$ ，分散 $\sigma^2$ の正規分布密度関数

$p(x)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{(x-\mu)^2}{2\sigma^2}} \quad(-3\le x\le3)$

に対して

(1) $\mu=0$ ， $\sigma=1$ ,
(2) $\mu=1$ ， $\sigma=0.5$ ,
(3) $\mu=-1$ ， $\sigma=2$

の場合のグラフを重ねて描け。

[5] 与えられた中心の座標 $(x,y)$ と半径 $r$ に対して，円を描く関数を作成し

(1) $(x,y)=(0,0)$ ， $r=1$
(2) $(x,y)=(1,1)$ ， $r=2$
(3) $(x,y)=(-1,-1)$ ， $r=3$

の場合の円を重ねて描け。

SCILABの基礎事項

投稿日時: 2022年8月17日投稿者: cacsd

[0] はじめに
SCILABは対話型数値計算プログラムで、次からフリーで入手できます。
http://www.scilab.org/products/scilab/download

[1] 行列データの入力
１）サイズ２×２の行列
$A=\left[\begin{array}{cc}1&2\\3&4\end{array}\right]$
を定義するために、次を入力してみます。
–> A=[1 2;3 4]
ここで、行列データは[ ]で囲み、要素の区切りはスペースまたはカンマ、行替えはセミコロン；を用いることに注意してください。次のように最後に；を置くと、出力が抑制されます。
–> A=[1 2;3 4];
すでに入力した行列データへのアクセスは、次のように行います。
–> A
また、特定の要素へのアクセスや修正は、次のように行います。
–> A(2,1)
–> A(2,1)=-5

２）２次の単位行列
$B=\left[\begin{array}{cc}1&0\\0&1\end{array}\right]$
は、次により入力できます。
–> B=eye(2,2)
便利なのは、次のように異なる行数と列数が許されることです。
–> B=eye(2,3)
これは、次のサイズ２×３の行列
$B=\left[\begin{array}{ccc}1&0&0\\0&1&0\end{array}\right]$
の定義を意味します。

３）サイズ３×２の零行列
$C=\left[\begin{array}{cc}0&0\\0&0\\0&0\end{array}\right]$
は、次により定義できます。
–> C=zeros(3,2)

４）３次の対角行列
$D=\left[\begin{array}{ccc}1&0&0\\0&2&0\\0&0&3\end{array}\right]$
は、次により定義できます。
–> D=diag([1 2 3])
すなわち、ベクトルにdiagを作用させているわけですが、行列にdiagを作用させ、対角成分を抽出することもできます。
–> d=diag(D)

５）行列A,B,C,Dを小行列としてもつブロック行列
$E=\left[\begin{array}{cc}A&B\\C&D\end{array}\right]$
を定義するためには、次のように入力します。
–> E=[A B;C D]

６）サイズ２×２の複素行列
$F=\left[\begin{array}{cc}1+i&2+3i\\3+2i&4+4i\end{array}\right]$
も、次により定義できます。
–> F=[1+%i, 2+3*%i;3+2*%i, 4+4*%i]
ここで、%iは虚数単位を意味します。

７）SCILABでは、空行列を定義できます。
–> G=[]

８）すべての要素が1である行列
$H=\left[\begin{array}{cc}1&1\\1&1\end{array}\right]$
は、次により定義できます。
–> H=ones(2,2)

[2] 行列データの管理
１）現時点でどのような行列を定義したかを調べるためには、次のように入力します。
–> who_user
また、たとえば入力した行列データdを消去するためには、次のように入力します。
–> clear d
すべてのデータを消去するときは、次のように入力します。
–> clear

２）行列データEのサイズを調べるには、次のように入力します。
–> [m,n]=size(E)

３）浮動小数点表示を行うためには、次のように入力します。
–> format(’e’)
これを固定小数点表示に戻すためには、次のように入力します。
–> format(’v’)

４）カレントディレクトリのチェックを行うためには、次のコマンドが使えます
–> pwd
–> ls
カレントディレクトリの変更のためには、次のコマンドを与えます。
–> cd(’dname’)

５）メモリ上のデータのセーブとロードのためには、次のコマンドを与えます。
–> save(’fname’)
–> load(’fname’)

[3] コロン記法
１）まず、次を入力してみてください。
–> h=1:3
これは、「form 1 to 3」を意味します。すなわちサイズ1×5の行列h=[1 2 3]が生成されます。コロン「:」はtoの意味で使われ、colon notationと呼ばれています。

２）それでは、次はどうでしょう。
–> h=0:0.5:3
これは、「form 1 to 3 by 0.5」を意味します。すなわち、２つのコロンで挟まれた0.5は増分を意味し、サイズ1×5の行列h=[1 1.5 2 2.5 3]が生成されます。ちなみに、h=1:3はh=1:1:3と同じと考えておきましょう。

３）それでは、次はどうでしょう。
–> h=0:-2
これは、h=1:1:-2の意味になりますが、1から-2まで、増分1では到達できないので、空行列となります。

[4] 小行列の抽出
１）コロン記法の利点は，行列の添え字部分に適用できることにあります。たとえば，行列Eの(2,3)要素には
–> E(2,3)
でアクセスできるのですが，この2と3は，スカラーである必要はなく，ベクトルが使えます。たとえば，次を確かめてください。
–> E([1 3],: )
これは第１行と弟２行からなるサイズ2×5の小行列が取り出されることに注意してください。列を指定する「：」はすべての列を意味しています。

２）次はどうでしょう。
–> E(:,2:4 )
ここで、2:4は[2 3 4]というベクトルでしたよね。第2～4列からなるサイズ5×3の小行列が取り出されることに注意してください。行を指定する「：」はすべての行を意味しています。

３）それでは，次はどうでしょう。
–> E([1 3],2:4 )

[5] 行列の分割
１）いろいろな応用では、ある行列を分割する必要が出てきます。これは小行列の抽出の観点から、たとえば次のようにできます。
–> [m,n]=size(E); i=2; j=2;
–> A=E(1:i,1:j);
–> B=E(1:i,j+1:n);
–> C=E(i+1:m,1:j);
–> D=E(i+1:m,j+1:n);
ここで、i=0のときは1:i=[]、i=mのときはi+1:m=[]などに注意してください。

[6] 行列演算
いま、行列Aが次のように定義されていることを確認してください。
$A=\left[\begin{array}{cc}1&2\\-5&4\end{array}\right]$
また、行列Bを新しく定義します。
–> B=eye(A)

１）行列A,Bの和、差、乗算は次のように計算できます。
–> X=A+B
–> X=A-B
–> X=A*B

２）行列Aが正則のとき、その逆行列は
–> X=inv(A)
で計算されます。しかし、これは逆行列の要素が欲しいとき以外は使わないようにしましょう。
多くの場合、逆行列は次の連立一次方程式
$AX=B$
または
$XA=B$
を解くときに用いますが、SCILABでは、次のように計算します。
–> X=A\B
–> X=B/A
それぞれ左からの割り算、右からの割り算と呼ばれます。
これは数値的に安定な数値計算アルゴリズムを得るためは直交行列だけの演算ですませることが必要だからです。

３）行列Aのべき乗と転置共役は次のように計算でされます。
–> X=A^2
–> X=A’

４）それでは、次の演算結果と比較してみましょう。
–> X=A.*B
–> X=A.\B
–> X=B./A
–> X=A.^2
–> X=A.’
すなわち、演算子の前に「ドット．」をおくと、要素ごとの演算やただの転置になります。

５）次に、組み込み関数としては、次が使えます。
sin,cos,tan
asin,acos,atan
sinh,cosh,tanh
asinh,acosh,atanh
sqrt
exp,log,log10
abs
real,imag

６）行列関数としては次が準備されています。
–> X=expm(A)
–> X=norm(A)
–> X=rank(A)
–> X=det(A)
ぞれぞれ、行列指数関数、ノルム、階数、行列式を計算します。

７）また、固有値問題を解くには次の関数を用います。
–> [V,R]=spec(A)
単に固有値だけを求めるのであれば
–> r=spec(A)
でＯＫです。

８）さらに、特異値問題を解くには次の関数を用います。
–> [U,S,V]=svd(A)
単に特異値だけを求めるのであれば
–> s=svd(A)
でＯＫです。

９）多項式 $x+1$ と $x+2$ の掛け算は、次のように行います。
–> r=convol([1 1],[1 2])

１０）いま、次のベクトルを定義します。
–> x=[3 1 5 4 2]
このとき、次はxの要素を大きい順番に並べ替えます。
–> [y,i]=gsort(x)
yがソーティングされた結果、iが元のどの位置にあったかを示すインデックスです。たとえば
–> x（i)
としてみるとyと同じ結果が出ます。

１１）次は、ベクトルの要素和、最大値、最小値を求める関数です。
–> y=sum(x)
–> y=max(x)
–> y=min(x)

[7] 関数のグラフ
１）次の関数のグラフを描いてみます。
$p(x)=\frac{1}{2\pi}e^{-\frac{x^2}{2}}\quad(-3\le x\le3)$
次のコマンドを与えてください。
–> x=-3:0.1:3;
–> y=1/sqrt(2*%pi)*exp(-x.*x/2)；
–> plot(x,y)
ここで，なぜx*xでなく，x.*xとしているか考えてみてください。

２）描画範囲（-3<=x<=3, 0<=ｙ<=0.4）を指定し，グリッドを描画するには，次のようなコマンドを追加します。
–> mtlb_grid
–> mtlb_axis([-3 3 0 0.5])
–> xtitle(’N(0,1)’)
ここで，「mtlb_」はMATLABのコマンド相当という意味です。

３）次の１次系の周波数応答を片対数グラフを描いてみましょう。
$|\hat{g}(j\omega)|=20\log_{10}\frac{1}{\sqrt{1+\omega^2}}\quad(0.1\le x\le10)$
次のコマンドを与えてください。
–> w=logspace(-1,1);
–> ga=20*log10(sqrt(1+w.^2).^(-1));
–> plot2d(w,ga,logflag=’ln’)
–> mtlb_grid

[8] プログラミング
これまでは対話型入力を行ってきましたが，一連のコマンドをエディタを用いてあらかじめ編集しておいて一括処理する，すなわちscilabでのプログラミングについて学びます。まず，白紙を示すアイコンをクリックして，エディタscipadを起動してください。

１） 1から9までの奇数の和を求める次のプログラムを入力し，ファイル名ex1.sceでセーブします。
//ex1.sce
//—–
s=0;
for i=1:2:9, s=s+i; end
disp(s,’sum=’)
//—–
//eof
scipadのexecuteコマンドをクリックして実行します。答えは25のはずです。

２）マシンイプシロン(machine epsilon)と呼ばれる特別な定数を求めてみましょう。次のプログラムをファイル名ex2.sceでセーブします。
//ex2.sce
//—–
s=1;
while 1+s>1, s=s/2; end
s=s*2;
disp(s,’eps=’),
//—–
//eof
scipadのexecuteコマンドをクリックして実行します。epsは次の%epsと等しくなります。
–-> %eps
次を実行してみてください。
–> 1+%eps/2==1
すなわち，
マシンイプシロン%eps=2^{-k}は，1+2^{-k-1}>1が成り立たなくなる最小のkを用いて定義されます。浮動小数点による数値計算では，1+%eps=1となる正数が存在することに注意してください。

３）次は，if文を使った例です。次のプログラムをファイル名ex3.sceでセーブします。
//ex3.sce
//—–
x=input(’x= ‘);
if imag(x)~=0, disp(’complex number’)
elseif x>0, disp(’positive real number’)
elseif x<0, disp(’negative real number’)
else disp(’zero’)
end
//—–
//eof
scipadのexecuteコマンドをクリックして実行します。

４）関数の例として，行列の階数を計算するものを示しましょう。次のプログラムをファイル名rank2.sceでセーブします。
//rank2.sce
//—–
function r=rank2(A)
s=svd(A); tol=max(size(A))*s(1)*%eps; r=sum(s>tol);
endfunction
//—–
//eof
このとき，次を入力してください。
–> exec(‘rank2.sce’)
–> r=rank2([1 2;3 4])

５）次の微分方程式の解を求めることを考えます。
$\dot{x}(t)=-x(t)+\sin(10t)$
次のプログラムをファイル名ex4.sceでセーブします。
//ex4.sce
//—–
function dx=f(t,x), dx=-x+sin(10*t); endfunction
x0=1; t0=0; t=0:0.01:5;
x=ode(x0,t0,t,f);
plot(t,x), mtlb_grid
//—–
//eof
scipadのexecuteコマンドをクリックして実行します。

MATLABの基礎事項

投稿日時: 2022年8月17日投稿者: cacsd

[1] 行列データの入力 　
１）サイズ２×２の行列
$A=\left[\begin{array}{cc}1&2\\3&4\end{array}\right]$
を定義するために、次を入力してみます。
>> A=[1 2;3 4]
ここで、行列データは[ ]で囲み、要素の区切りはスペースまたはカンマ、行替えはセミコロン；を用いることに注意してください。次のように最後に；を置くと、出力が抑制されます。
>> A=[1 2;3 4];
すでに入力した行列データへのアクセスは、次のように行います。
>> A
また、特定の要素へのアクセスや修正は、次のように行います。
>> A(2,1)
>> A(2,1)=-5

２）２次の単位行列
$B=\left[\begin{array}{cc}1&0\\0&1\end{array}\right]$
は、次により入力できます。
>> B=eye(2,2)
便利なのは、次のように異なる行数と列数が許されることです。
>> B=eye(2,3)
これは、次のサイズ２×３の行列
$B=\left[\begin{array}{ccc}1&0&0\\0&1&0\end{array}\right]$
の定義を意味します。

３）サイズ３×２の零行列
$C=\left[\begin{array}{cc}0&0\\0&0\\0&0\end{array}\right]$
は、次により定義できます。
>> C=zeros(3,2)

４）３次の対角行列
$D=\left[\begin{array}{ccc}1&0&0\\0&2&0\\0&0&3\end{array}\right]$
は、次により定義できます。
>> D=diag([1 2 3])
すなわち、ベクトルにdiagを作用させているわけですが、行列にdiagを作用させ、対角成分を抽出することもできます。
>> d=diag(D)

５）行列A,B,C,Dを小行列としてもつブロック行列
$E=\left[\begin{array}{cc}A&B\\C&D\end{array}\right]$
を定義するためには、次のように入力します。
>> E=[A B;C D]

６）サイズ２×２の複素行列
$F=\left[\begin{array}{cc}1+i&2+3i\\3+2i&4+4i\end{array}\right]$
も、次により定義できます。
>> F=[1+i, 2+3*i;3+2*i, 4+4*i]
ここで、iは虚数単位として定義されています。もちろん再定義可能です。

７）MATLABでは、空行列を定義できます。
>> G=[]

８）すべての要素が1である行列
$H=\left[\begin{array}{cc}1&1\\1&1\end{array}\right]$
は、次により定義できます。
>> H=ones(2,2)

[2] 行列データの管理
１）現時点でどのような行列を定義したかを調べるためには、次のように入力します。
>> who
行列のザイズを合わせて表示するには、次のように入力します。
>> whos
また、たとえば入力した行列データdを消去するためには、次のように入力します。
>>clear d
すべてのデータを消去するときは、次のように入力します。
>>clear

２）行列データEのサイズを調べるには、次のように入力します。
>> [m,n]=size(E)

３）浮動小数点表示を行うためには、次のように入力します。
>> format short e
これを固定小数点表示に戻すためには、次のように入力します。
>> format

４）カレントディレクトリのチェックを行うためには、次のコマンドが使えます
>> pwd
>> ls
カレントディレクトリの変更のためには、次のコマンドを与えます。
>> cd dname

５）メモリ上のデータのセーブとロードのためには、次のコマンドを与えます。
>> save filename
>> load filename

[3] コロン記法
１）まず、次を入力してみてください。
>> h=1:3
これは、「form 1 to 3」を意味します。すなわちサイズ1×5の行列h=[1 2 3]が生成されます。コロン「:」はtoの意味で使われ、colon notationと呼ばれています。

２）それでは、次はどうでしょう。
>> h=0:0.5:3
これは、「form 1 to 3 by 0.5」を意味します。すなわち、２つのコロンで挟まれた0.5は増分を意味し、サイズ1×5の行列h=[1 1.5 2 2.5 3]が生成されます。ちなみに、h=1:3はh=1:1:3と同じと考えておきましょう。

３）それでは、次はどうでしょう。
>> h=0:-2
これは、h=1:1:-2の意味になりますが、1から-2まで、増分1では到達できないので、空行列となります。

[4] 小行列の抽出
１）コロン記法の利点は，行列の添え字部分に適用できることにあります。たとえば，行列Eの(2,3)要素には
>> E(2,3)
でアクセスできるのですが，この2と3は，スカラーである必要はなく，ベクトルが使えます。たとえば，次を確かめてください。
>> E([1 3],: )
これは第１行と弟２行からなるサイズ2×5の小行列が取り出されることに注意してください。列を指定する「：」はすべての列を意味しています。

２）次はどうでしょう。
>> E(:,2:4 )
ここで、2:4は[2 3 4]というベクトルでしたよね。第2～4列からなるサイズ5×3の小行列が取り出されることに注意してください。行を指定する「：」はすべての行を意味しています。

３)それでは，次はどうでしょう。
>> E([1 3],2:4 )

[5] 行列の分割
１）いろいろな応用では、ある行列を分割する必要が出てきます。これは小行列の抽出の観点から、たとえば次のようにできます。
>> [m,n]=size(E); i=2; j=2;
>> A=E(1:i,1:j);
>> B=E(1:i,j+1:n);
>> C=E(i+1:m,1:j);
>> D=E(i+1:m,j+1:n);
ここで、i=0のときは1:i=[]、i=mのときはi+1:m=[]などに注意してください。

[6] 行列演算
いま、行列Aが次のように定義されていることを確認してください。
$A=\left[\begin{array}{cc}1&2\\-5&4\end{array}\right]$
また、行列Bを新しく定義します。
>> B=eye(A)

１）行列A,Bの和、差、乗算は次のように計算できます。
>> X=A+B
>> X=A-B
>> X=A*B

２）行列Aが正則のとき、その逆行列は
>> X=inv(A)
で計算されます。しかし、これは逆行列の要素が欲しいとき以外は使わないようにしましょう。
多くの場合、逆行列は次の連立一次方程式
$AX=B$
または
$XA=B$
を解くときに用いますが、MATLABでは、次のように計算します。
>> X=A\B
>> X=B/A
それぞれ左からの割り算、右からの割り算と呼ばれます。
これは数値的に安定な数値計算アルゴリズムを得るためは直交行列だけの演算ですませることが必要だからです。

３）行列Aのべき乗と転置共役は次のように計算でされます。
>> X=A^2
>> X=A’

４）それでは、次の演算結果と比較してみましょう。
>> X=A.+B
>> X=A.-B
>> X=A.*B
>> X=A.\B
>> X=B./A
>> X=A.^2
>> X=A.’
すなわち、演算子の前に「ドット．」をおくと、要素ごとの演算やただの転置になります。

５）次に、組み込み関数としては、次が使えます。
sin,cos,tan,asin,acos,atan,sinh,cosh,tanh,asinh,acosh,atanh,sqrt,exp,log,log10,abs,real,imag

６）行列関数としては次が準備されています。
>> X=expm(A)
>> X=norm(A)
>> X=rank(A)
>> X=det(A)
ぞれぞれ、行列指数関数、ノルム、階数、行列式を計算します。

７）また、固有値問題を解くには次の関数を用います。
–>[V,R]=eig(A)
単に固有値だけを求めるのであれば
–>r=eig(A)
でＯＫです。

８）さらに、特異値問題を解くには次の関数を用います。
–>[U,S,V]=svd(A)
単に特異値だけを求めるのであれば
–>s=svd(A)
でＯＫです。

９）多項式 $x+1$ と $x+2$ の掛け算は、次のように行います。
–>r=convol([1 1],[1 2])

１０）いま、次のベクトルを定義します。
–>x=[3 1 5 4 2]
このとき、次はxの要素を小さい順番に並べ替えます。
–>[y,i]=sort(x)
yがソーティングされた結果、iが元のどの位置にあったかを示すインデックスです。たとえば
–>x（i)
としてみるとyと同じ結果が出ます。

１１）次は、ベクトルの要素和、最大値、最小値を求める関数です。
–>y=sum(x)
–>y=max(x)
–>y=min(x)

[7] 関数のグラフ
１）次の関数のグラフを描いてみます。
$p(x)=\frac{1}{2\pi}e^{-\frac{x^2}{2}}\quad(-3\le x\le3)$
次のコマンドを与えてください。
>> x=-3:0.1:3;
>> y=1/sqrt(2*pi)*exp(-x.*x/2)；
>> plot(x,y)
ここで，なぜx*xでなく，x.*xとしているか考えてみてください。またpiは $\pi$ として定義されています。

２）描画範囲（-3<=x<=3, 0<=ｙ<=0.4）を指定し，グリッドを描画するには，次のようなコマンドを追加します。
>> grid
>> axis([-3 3 0 0.5])
>> xtitle(’N(0,1)’)

３）次の１次系の周波数応答を片対数グラフび描いてみましょう。
$|\hat{g}(j\omega)|=20\log_{10}\frac{1}{\sqrt{1+\omega^2}}\quad(0.1\le x\le10)$
次のコマンドを与えてください。
>> w=logspace(-1,1);
>> ga=20*log10(sqrt(1+w.^2).^(-1));
>> semilogx(w,ga)
>> grid

[8] プログラミング
これまでは対話型入力を行ってきましたが，一連のコマンドをエディタを用いてあらかじめ編集しておいて一括処理する，すなわちMATLABでのプログラミングについて学びます。まず，新規スクリプトを示すアイコンをクリックして，エディタを起動してください。

１） 1から9までの奇数の和を求める次のプログラムを入力し，ファイル名ex1.mでセーブします。
//ex1.m
//—–
s=0;
for i=1:2:9,
s=s+i;
end
disp(s,’sum=’)
//—–
//eof
エディタの実行ボタンをクリックします。答えは25のはずです。

２）マシンイプシロン(machine epsilon)と呼ばれる特別な定数を求めてみましょう。次のプログラムをファイル名ex2.mでセーブします。
//ex2.m
//—–
s=1;
while 1+s>1,
s=s/2;
end
s=s*2;
disp(s,’eps=’),
//—–
//eof
エディタの実行ボタンをクリックします。このsは次のepsと等しくなります。
>> eps
次を実行してみてください。
>> 1+eps/2==1
すなわち，
マシンイプシロンeps=a^{-k}は，1+a^{-k-1}>1が成り立たなくなる最小のkを用いて定義されます。浮動小数点による数値計算では，1+eps=1となる正数が存在することに注意してください。

３）次は，if文を使った例です。次のプログラムをファイル名ex3.mでセーブします。
//ex3.m
//—–
x=input(’x= ‘);
if imag(x)~=0,
disp(’complex number’)
elseif x>0,
disp(’positive real number’)
elseif x<0,
disp(’negative real number’)
else
disp(’zero’)
end
//—–
//eof
エディタの実行ボタンをクリックします。。

４）関数の例として，行列の階数を計算するものを示しましょう。次のプログラムをファイル名rank2.mでセーブします。
//rank2.m
//—–
function r=rank2(A)
s=svd(A);
tol=max(size(A))*s(1)*eps; r=sum(s>tol);
endfunction
//—–
//eof
このとき，次を入力してください。
>> r=rank([1 2;3 4])

５）次の微分方程式の解を求めることを考えます。
$\dot{x}(t)=-x(t)+\sin(10t)$
次のプログラムをファイル名ex4.mでセーブします。
//ex4.m
//—–
function dx=f(t,x),dx=-x+sin(10*t), endfunction
x0=1; t0=0;
t=0:0.01:5;
x=ode(x0,t0,t,f);
plot(t,x),
mtlb_grid
//—–
//eof
エディタの実行ボタンをクリックします。

SVD

投稿日時: 2022年8月14日投稿者: cacsd

制御系CADに関わる数値計算では実行列の特異値分解(Singular-Value Decomposition, SVD)を多用しますが、データ駆動分野の計算でも基盤技術となっています。

●いまデータは次の複素行列にまとめられているとします。

$\displaystyle{(1)\quad X=\left[\begin{array}{ccccc} x_1 & x_2 & \cdots & x_m \end{array}\right]\in{\bf C}^{n\times m} \quad(x_1,x_2,\cdots,x_n\in{\bf C}^n) }$

ここで列ベクトル $x_1,x_2,\cdots,x_n$ はn次元数ベクトルですが、データ駆動分野では、nの値は数個ではなく、数千、数万のオーダーになります。

● $X$ をサイズ $n\times m$ の複素行列（ ${\rm rank}\,X=k$ ）とします。このとき、ユニタリ行列 $U$ と $V$ が存在して

$\displaystyle{(2.1)\quad X=U\Sigma V^H\quad(U\in{\bf C}^{n\times n},\Sigma\in{\bf R}^{n\times m},V\in{\bf C}^{m\times m}) }$

が成り立ちます（ $V^H=V^{*T}$ ）。ここで、実行列 $\Sigma$ は次のように表されます。

$\displaystyle{(2.2)\quad \Sigma= \left[\begin{array}{cc} \widehat{\Sigma} & 0_{k\times m-k}\\ 0_{n-k\times k} & 0_{n-k\times m-k} \end{array}\right]\in{\bf R}^{n\times m} }$

$\displaystyle{(2.3)\quad \widehat{\Sigma} ={\rm diag}\{\sigma_1,\cdots,\sigma_k\}\quad(\sigma_1\ge\cdots\ge\sigma_k>0) }$

MATLABのコマンドでは、次のように求めます。

>> [U,S,V]=svd(X)

●いま $\boxed{n\ge m}$ とします。このとき(2)は次式となります。

$\displaystyle{(3.1)\quad X= \underbrace{\left[\begin{array}{cc} U_1 & U_2 \end{array}\right]}_{U} \underbrace{\left[\begin{array}{cc} \Sigma_1 \\ 0_{n-m\times m} \end{array}\right]}_{\Sigma}V^H =U_1\Sigma_1V^H }$

$\displaystyle{(3.2)\quad \Sigma_1={\rm diag}\{\sigma_1,\cdots,\sigma_k, 0,\cdots,0\}\in{\bf R}^{m\times m} }$

MATLABのコマンドでは、次のように求めます。

>> [U1,S1,V]=svd(X,’econ’)

(2)の場合は $U$ は大規模な行列となりますが、(3)の場合はスリムな行列となりますので、Economic SVDと呼ぶことがあります。

●いま実効階数を $r$ とします。すなわち微小な $\epsilon>0$ に対して

$\displaystyle{(4)\quad \sigma_1\ge\cdots\ge\sigma_r> \epsilon >\sigma_{r+1}\ge\cdots\ge\sigma_k>0 }$

とします。このとき(3)から次式のように近似できます。

$\displaystyle{(5.1)\quad X\approx \widetilde{X}= \underbrace{\left[\begin{array}{cc} \widetilde{U} & \cdot \end{array}\right]}_{U} \underbrace{\left[\begin{array}{cc} \widetilde{\Sigma} & 0_{r\times m-r} \\ 0_{n-r\times r} & 0_{n-r\times m-r} \end{array}\right]}_{\Sigma'} \underbrace{\left[\begin{array}{c} \widetilde{V}^H\\ \cdot \end{array}\right]}_{V^H} =\widetilde{U}\widetilde{\Sigma}\widetilde{V}^H }$

$\displaystyle{(5.2)\quad \widetilde{\Sigma} ={\rm diag}\{\sigma_1,\cdots,\sigma_r\}\quad(\sigma_1\ge\cdots\ge\sigma_r>\epsilon) }$

●(2.1)、(3.1)、(5.1)の関係はダイアディック形式を用いて次のように表されます。

$\displaystyle{(6)\quad \underbrace{\sum_{i=1}^{m}\sigma_iu_iv_i^H}_{U\Sigma V^H} =\underbrace{\sum_{i=1}^{k}\sigma_iu_iv_i^H}_{U_1\Sigma_1 V^H} \approx \underbrace{\sum_{i=1}^{r}\sigma_iu_iv_i^H}_{\widetilde{U}\widetilde{\Sigma}\widetilde{V}^H} }$

●相関行列 $XX^H$ または $X^HX$ は、(3.1)より、次式のように表されます。

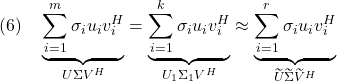
$\displaystyle{(7.1)\quad \begin{array}{l} XX^H=U\left[\begin{array}{cc} \Sigma_1 \\ 0_{n-m\times m} \end{array}\right] \underbrace{V^HV}_{I_m}\left[\begin{array}{cc} \Sigma_1 & 0_{m\times n-m} \end{array}\right] U^H\\=U\left[\begin{array}{cc} \Sigma_1^2 & 0_{m\times n-m} \\ 0_{n-m\times m} & 0_{n-m\times n-m} \end{array}\right] U^H \end{array} }$

$\displaystyle{(7.2)\quad X^HX=V\left[\begin{array}{cc} \Sigma_1 & 0_{m\times n-m} \end{array}\right] \underbrace{U^HU}_{I_n}\left[\begin{array}{cc} \Sigma_1 \\ 0_{n-m\times m} \end{array}\right] V^H=V\Sigma_1^2 V^H }$

これらより

$\displaystyle{(8.1)\quad \begin{array}{l} XX^HU=U\left[\begin{array}{cc} \Sigma_1^2 & 0_{m\times n-m} \\ 0_{n-m\times m} & 0_{n-m\times n-m} \end{array}\right] \end{array} }$

$\displaystyle{(8.2)\quad X^HXV=V\Sigma_1^2 }$

すなわち、非零の特異値は相関行列 $XX^H$ または $X^HX$ の固有値の正の平方根です。もし $X=X^H$ の場合は $X$ の特異値は $X$ の固有値の絶対値となります。これはスカラの場合、次式を意味しています。

$\displaystyle{(9)\quad \sigma=\sqrt{xx^*}=\sqrt{(x_R+jx_I)(x_R-jx_I)}=\sqrt{x_R^2+x_I^2}=|x| }$

データ駆動分野では、nの値は数個ではなく、数千、数万のオーダーになります。一方、ｍの値はそのように大きな値とはなりません。したがって、(8.2)の小規模な固有値問題を解いて $\Sigma_1$ と $V$ を求め、(3.1)に基づいて、(8.1)の大規模な固有値問題の固有ベクトルの一部 $U_1$ を、次式により求めることが行われます。

$\displaystyle{(10)\quad U_1=XV\Sigma_1^{-1} }$

(5.1)に基づく場合は次式となります。

$\displaystyle{(11)\quad \widetilde{U}=X\widetilde{V}\widetilde{\Sigma}^{-1} }$

このような手法はスナップショットと呼ばれています。

●観測データを行ベクトルとしてもつ $X$ を考えます。

$\displaystyle{(12)\quad X=\left[\begin{array}{c} X_{11},\cdots,X_{1m}\\ \vdots\\ %X_{i1},\cdots,X_{im}\\ %\vdots\\ X_{n1},\cdots,X_{nm}\\ \end{array}\right] }$

ここで、 $n$ 回の観測が行われ、各観測では $m$ 個のデータを得るものとしています。これから

$\displaystyle{(13)\quad \bar{X}=\left[\begin{array}{c} 1\\ \vdots\\ 1 \end{array}\right] \left[\begin{array}{c} \displaystyle{\frac{1}{n}\sum_{i=1}^nX_{i1},\cdots,\frac{1}{n}\sum_{i=1}^nX_{im}} \end{array}\right] }$

を引いた行列 $B$ の特異値分解を

$\displaystyle{(14)\quad B=X-\bar{X}=U\Sigma V^H }$

とします。このとき、共分散行列は

$\displaystyle{(15)\quad C=\frac{1}{n-1}BB^H=\frac{1}{n-1}V\Sigma^2 V^H\Rightarrow D=\frac{1}{n-1}\Sigma^2 }$

のように表されます。すなわち共分散行列の主成分ベクトルと、その方向に沿う不変分散値が、行列 $B$ の特異値分解から得られることに留意します。

Marine Craft

投稿日時: 2022年2月10日投稿者: cacsd

Marine Craft

$\displaystyle{(1)\quad \left\{\begin{array}{l} \dot{\eta}=J_\Theta(\eta)\nu\\ M\dot{\nu}+C(\nu)\nu+D(\nu)\nu+g(\eta)=\tau\\ \tau=Bu \end{array}\right. }$

$1^\circ$ $M=M^T$ , $\dot{M}=0$
$2^\circ$ $C(\nu)=-C^T(\nu)$
$3^\circ$ $D(\nu)>0$
$4^\circ$ $BB^T$ は正則
$5^\circ$ $J_\Theta(\eta)$ はオイラー角変換行列

$\displaystyle{(1')\quad \left\{\begin{array}{l} M^*(\eta)\ddot{\eta}+C^*(\nu,\eta)\dot{\eta}+D^*(\nu,\eta)\dot{\eta}+g^*(\eta)=J^{-T}_\Theta(\eta)\tau\\ M^*(\eta)=J^{-T}_\Theta(\eta)MJ^{-1}_\Theta(\eta)\\ C^*(\nu,\eta)=J^{-T}_\Theta(\eta)(C(\nu)-MJ^{-1}_\Theta(\eta)\dot{J}_\Theta(\eta))J^{-1}_\Theta(\eta)\\ D^*(\nu,\eta)=J^{-T}_\Theta(\eta)D(\nu)J^{-1}_\Theta(\eta)\\ g^*(\eta)=J^{-T}_\Theta(\eta)g(\eta) \end{array}\right. }$

●Step 1

$\displaystyle{(2)\quad \boxed{\tilde{\eta}=\eta-\eta_d,\ \tilde{\nu}=\nu-\nu_d}\quad\Rightarrow\quad\dot{\tilde{\eta}}=J_\Theta(\eta)\tilde{\nu} }$

$\displaystyle{(3)\quad \dot{\eta}=s+\alpha_1 }$

$\displaystyle{(4)\quad \boxed{s=\dot{\tilde{\eta}}+\Lambda\tilde{\eta}}=\dot{\eta}-\dot{\eta}_d+\Lambda\tilde{\eta}}\quad(\Lambda={\rm diag}\{\lambda_1,\dots,\lambda_m\}) }$

$\displaystyle{(5)\quad \boxed{\alpha_1=\dot{\eta}-s=\dot{\eta}_d-\Lambda\tilde{\eta}} }$

$\displaystyle{(6)\quad \dot{\tilde{\eta}}=\dot{\eta}-\dot{\eta}_d=-\Lambda\tilde{\eta}+s }$

$\displaystyle{(7)\quad \boxed{V_1=\frac{1}{2}\tilde{\eta}^TK_p\tilde{\eta}}\quad(K_p>0) }$

$\displaystyle{(8)\quad \dot{V}_1=\tilde{\eta}^TK_p\dot{\tilde{\eta}}=\tilde{\eta}^TK_p(-\Lambda\tilde{\eta}+s) \quad\Rightarrow\quad \boxed{\dot{V}_1=-\tilde{\eta}^TK_p\Lambda\tilde{\eta}+s^TK_p\tilde{\eta}} }$

●Step 2

$\displaystyle{(9)\quad s=\dot{\tilde{\eta}}+\Lambda\tilde{\eta}=\dot{\eta}-\dot{\eta}_d+\Lambda\tilde{\eta} \quad\Rightarrow\quad\dot{\eta}=s+\dot{\eta}_d-\Lambda\tilde{\eta} }$

$\displaystyle{(10)\quad \dot{s}=\ddot{\tilde{\eta}}+\Lambda\dot{\tilde{\eta}}=\ddot{\eta}-\ddot{\eta}_d+\Lambda\dot{\tilde{\eta}} \quad\Rightarrow\quad\ddot{\eta}=\dot{s}+\ddot{\eta}_d-\Lambda\dot{\tilde{\eta}} }$

$\displaystyle{(11)\quad \begin{array}{l} M^*(\eta)(\dot{s}+\ddot{\eta}_d-\Lambda\dot{\tilde{\eta}})\\ +C^*(\nu,\eta)(s+\dot{\eta}_d-\Lambda\tilde{\eta}) +D^*(\nu,\eta)(s+\dot{\eta}_d-\Lambda\tilde{\eta}) +g^*(\eta)=J^{-T}_\Theta(\eta)\tau \end{array} }$

$\displaystyle{(1')\quad \left\{\begin{array}{l} M^*(\eta)=J^{-T}_\Theta(\eta)MJ^{-1}_\Theta(\eta)\\ C^*(\nu,\eta)=J^{-T}_\Theta(\eta)(C(\nu)-MJ^{-1}_\Theta(\eta)\dot{J}_\Theta(\eta))J^{-1}_\Theta(\eta)\\ D^*(\nu,\eta)=J^{-T}_\Theta(\eta)D(\nu)J^{-1}_\Theta(\eta)\\ g^*(\eta)=J^{-T}_\Theta(\eta)g(\eta) \end{array}\right. }$

$\displaystyle{(12)\quad \begin{array}{l} M^*(\eta)\dot{s}=-C^*(\nu,\eta)s-D^*(\nu,\eta)s+J^{-T}_\Theta(\eta)\tau\\ -M^*(\eta)(\ddot{\tilde{\eta}}_d-\Lambda\dot{\tilde{\eta}})-C^*(\nu,\eta)(\dot{\tilde{\eta}}_d-\Lambda\tilde{\eta})-D^*(\nu,\eta)(\dot{\tilde{\eta}}_d-\Lambda\tilde{\eta})-g^*(\eta)\\ =-C^*(\nu,\eta)s-D^*(\nu,\eta)s\\ +J^{-T}_\Theta(\eta)(\tau -\underbrace{J^{T}_\Theta(\eta)M^*(\eta)J_\Theta(\eta)}_{M} \underbrace{J^{-1}_\Theta(\eta)(\ddot{\tilde{\eta}}_d-\Lambda\dot{\tilde{\eta}})}_ {\ddot{\tilde{\nu}}_d-\Lambda\dot{\tilde{\nu}}}\\ -\underbrace{J^{T}_\Theta(\eta)C^*(\nu,\eta)J_\Theta(\eta)}_{C(\nu)-MJ^{-1}_\Theta(\eta)\dot{J}_\Theta(\eta)} \underbrace{J^{-1}_\Theta(\eta)(\dot{\tilde{\eta}}_d-\Lambda\tilde{\eta})}_ {\ddot{\tilde{\nu}}_d-\Lambda\dot{\tilde{\nu}}}\\ -\underbrace{J^{T}_\Theta(\eta)D^*(\nu,\eta)J_\Theta(\eta)}_{D(\nu)} \underbrace{J^{-1}_\Theta(\eta)(\dot{\tilde{\eta}}_d-\Lambda\tilde{\eta})}_ {\ddot{\tilde{\nu}}_d-\Lambda\dot{\tilde{\nu}}}\\ -\underbrace{J^{T}_\Theta(\eta)g^*(\eta)}_{g(\eta)})\\ =-C^*(\nu,\eta)s-D^*(\nu,\eta)s\\ +J^{-T}_\Theta(\eta)(\tau-M(\ddot{\tilde{\nu}}_d-\Lambda\dot{\tilde{\nu}})-C(\nu)(\dot{\tilde{\nu}}_d-\Lambda\tilde{\nu})-D(\nu)(\dot{\tilde{\nu}}_d-\Lambda\tilde{\nu})-g(\eta)) \end{array} }$

$\displaystyle{(13)\quad \boxed{V_2=V_1+\frac{1}{2}s^TM^*(\eta)s} }$

$\displaystyle{(14)\quad \begin{array}{l} \dot{V}_2=\dot{V}_1+s^TM^*(\eta)\dot{s}+\frac{1}{2}s^T\dot{M}^*(\eta)s\\ =-\tilde{\eta}^TK_p\Lambda\tilde{\eta}+s^TK_p\tilde{\eta}\\ +s^T(-C^*(\nu,\eta)s-D^*(\nu,\eta)s)\\ +s^TJ^{-T}_\Theta(\eta)(\tau-M(\ddot{\tilde{\nu}}_d-\Lambda\dot{\tilde{\nu}}) -C(\nu)(\dot{\tilde{\nu}}_d-\Lambda\tilde{\nu}) -D(\nu)(\dot{\tilde{\nu}}_d-\Lambda\tilde{\nu})-g(\eta))\\ +\frac{1}{2}s^T\dot{M}^*(\eta)s\\ =s^TJ^{-T}_\Theta(\eta)(\tau-M(\ddot{\tilde{\nu}}_d-\Lambda\dot{\tilde{\nu}})-C(\nu)(\dot{\tilde{\nu}}_d-\Lambda\tilde{\nu})-D(\nu)(\dot{\tilde{\nu}}_d-\Lambda\tilde{\nu})-g(\eta)\\+J^{T}_\Theta(\eta)K_p\tilde{\eta}) +\frac{1}{2}\underbrace{s^T(\dot{M}^*(\eta)-C^*(\nu,\eta))s}_{0}\\ -s^TD^*(\nu,\eta)s-\tilde{\eta}^TK_p\Lambda\tilde{\eta} \end{array} }$

$\displaystyle{(15)\quad \boxed{\begin{array}{l} \tau=M(\ddot{\tilde{\nu}}_d-\Lambda\dot{\tilde{\nu}})+C(\nu)(\dot{\tilde{\nu}}_d-\Lambda\tilde{\nu})-D(\nu)(\dot{\tilde{\nu}}_d-\Lambda\tilde{\nu})-g(\eta)\\ -J^{T}_\Theta(\eta)K_p\tilde{\eta}-J^{T}_\Theta(\eta)K_ds \end{array}} }$

$\displaystyle{(14')\quad \boxed{\dot{V}_2=-s^T(D^*(\nu,\eta)+K_d)s-\tilde{x}^TK_p\Lambda\tilde{x} }$