SM制御則…Homework
[1] 制御対象の状態方程式として次式を考えます。
![]()
ここで、![]() はモデル誤差、非線形要素、外乱などの影響を表し、有界かつ未知とします。これに対し、次のスイッチング関数を定義します。
はモデル誤差、非線形要素、外乱などの影響を表し、有界かつ未知とします。これに対し、次のスイッチング関数を定義します。
![]()
以下では、状態方程式とスイッチング関数は次のSM標準形(regular form)をとるように座標変換されているとします(Note C22-1参照)。
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad \boxed{\underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot x_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t) + \underbrace{ \left[\begin{array}{l} f_u(t,x)\\ f_m(t,x,u) \end{array}\right] }_{f(t,x,u)}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7d9915e30ab5eebb009f8eba1931c74b_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \boxed{s(t)= \underbrace{ \left[\begin{array}{cc} S_1 & S_2 \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{S_2 \left[\begin{array}{cc} M & I_m \\ \end{array}\right] }_{S} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} \ (M=S_2^{-1}S_1)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-fd9d30f50f0b1a358dd111e982cf142d_l3.png)
ここで、![]() と
と![]() はともにサイズ
はともにサイズ![]() の正則行列とします。したがって、
の正則行列とします。したがって、![]() はマッチング条件を満たしますが、
はマッチング条件を満たしますが、![]() はマッチング条件を満たさないことに留意します。
はマッチング条件を満たさないことに留意します。
これに対して、座標変換
![Rendered by QuickLaTeX.com \displaystyle{(5)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)}\\ \Leftrightarrow \underbrace{ \left[\begin{array}{c} x_1(t)\\ x_2(t) \end{array}\right] }_{x(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ -S_2^{-1}S_1 & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9b7409c24983e2cf677cd893ab39c8b1_l3.png)
を行うために、まず(5)を(3)に代入して
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{cc} I & 0 \\ -M & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{\bar{x}}(t)}\\ = \underbrace{ \left[\begin{array}{cc} A_{11} & A_{12} \\ A_{21} & A_{22} \\ \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{cc} I & 0 \\ -M & S_2^{-1} \\ \end{array}\right] }_{T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t)\\ + \underbrace{ \left[\begin{array}{l} f_u(t,x)\\ f_m(t,x,u) \end{array}\right] }_{f(t,x,u)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2603c79f9420895b735d182a315f4d6a_l3.png)
左から![]() をかけて
をかけて
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{\bar{x}}(t)} = \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{cc} A_{11}-A_{12}M & A_{12}S_2^{-1} \\ A_{21}-A_{22}M & A_{22}S_2^{-1} \\ \end{array}\right] }_{AT_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}\\ + \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{c} 0\\ B_2 \end{array}\right] }_{B} u(t) + \underbrace{ \left[\begin{array}{cc} I & 0 \\ S_1 & S_2 \\ \end{array}\right] }_{T_s} \underbrace{ \left[\begin{array}{l} f_u(t,x)\\ f_m(t,x,u) \end{array}\right] }_{f(t,x,u)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-97d89cd7503cc935f956b67dce447b04_l3.png)
すなわち、次式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \boxed{ \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot x_1(t)\\ \dot s(t) \end{array}\right] }_{\dot{\bar{x}}(t)} = \underbrace{ \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ \bar{A}_{21} & \bar{A}_{22}\\ \end{array}\right] }_{\bar{A}=T_s A T_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \bar{B}_2 \end{array}\right] }_{\bar{B}=T_sB} u(t)\\ + \underbrace{ \left[\begin{array}{c} f_u(t,x)\\ S_1f_u(t,x)+S_2f_m(t,x,u) \end{array}\right] }_{T_sf(t,x,u)} \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-00ef0c4a7e2512e1cdc58d5395f78586_l3.png)
ただし
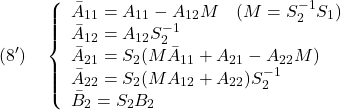
以下では、![]() がサイズ
がサイズ![]() の安定行列となるようにスイッチング関数が選ばれていると仮定します。
の安定行列となるようにスイッチング関数が選ばれていると仮定します。
●このとき、スライディングモード制御則(SM制御則、SMC則)
![]()
を、2次安定性
![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \boxed{ \begin{array}{lll} V(\bar{x})= \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} P_1 & 0\\ 0 & P_2 \end{array}\right] }_{P} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}\\ \Rightarrow \dot{V}(\bar{x})\le - \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]^T }_{\bar{x}^T(t)} \underbrace{ \left[\begin{array}{cc} Q_1 & 0\\ 0 & I \end{array}\right] }_{Q} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)} \end{array}}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b728547541ea693965c4fb59721e61ea_l3.png)
すなわち
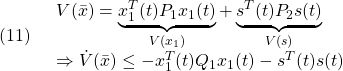
が成り立つように決定します(![]() ,
, ![]() ,
, ![]() )。
)。
[2] 可到達性の検討
ここでは、スライディングモード制御則(9)の具体的な表現を求め、スライディングモードに到達する時刻![]() の見積もりを行います。
の見積もりを行います。
●等価制御は、(7)において![]() として
として
![Rendered by QuickLaTeX.com \displaystyle{ \begin{array}{cl} (12.1) & s(t)=0\\ \Downarrow &\\ (12.2) & \dot{s}(t)=0\\ \Downarrow &\\ (12.3) & \bar{A}_{21}x_1(t)+\bar{A}_{22}s(t)+\bar{B}_{2}u(t)=0\\ \Downarrow &\\ (12.4) & u_{eq}(t)=-\underbrace{\bar{B}_{2}^{-1}}_{([0\ I]T_sB)^{-1}} \underbrace{\left[\begin{array}{cc} \bar{A}_{21} & \bar{A}_{22} \\ \end{array}\right]}_{[0\ I]T_sAT_s^{-1}} \underbrace{ \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right] }_{\bar{x}(t)}\\ \Downarrow & by\ S=[0\ I]T_s, x=T_s^{-1}\bar{x}\\ (12.5) & u_{eq}(t)=-(SB)^{-1}SAx(t)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aa7375ffaeacc584b4d99f678aa447a2_l3.png)
のように得られます。(9)の線形制御![]() は、この等価制御をベースして
は、この等価制御をベースして
![]()
すなわち
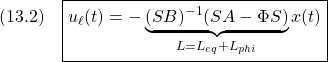
のように構成します。ここで、![]() は適当に設定されたサイズ
は適当に設定されたサイズ![]() の安定行列です。
の安定行列です。
●このとき閉ループ系は次式で与えられます。
![Rendered by QuickLaTeX.com \displaystyle{(14)\quad \begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t)\\ \dot{s}(t) \end{array}\right] = \left[\begin{array}{cc} \bar{A}_{11} & \bar{A}_{12} \\ 0 & \Phi \\ \end{array}\right] \left[\begin{array}{c} x_1(t)\\ s(t) \end{array}\right]\\ + \left[\begin{array}{c} f_u(t,x)\\ \bar{B}_{2}u_n(t)+S_2(Mf_u(t,x)+f_m(t,x,u)) \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1b7f283e78147327758f740eb0f3d38a_l3.png)
すなわち
![]()
閉ループ系の状態は![]() と
と![]() から成りますが、(15.2)は
から成りますが、(15.2)は![]() だけに関係しているので、まずその下線部に抗してスライディングモード
だけに関係しているので、まずその下線部に抗してスライディングモード![]() を達成する
を達成する![]() を明らかにします。
を明らかにします。
さて、![]() は安定行列なので
は安定行列なので
![]()
を満たす![]() を選ぶことができます。これを用いて、(7)のスイッチング項
を選ぶことができます。これを用いて、(7)のスイッチング項![]() を
を
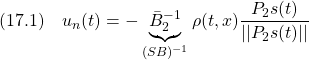
すなわち
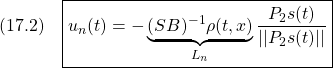
と定めます。
●![]() は、仮定
は、仮定
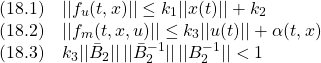
のもとで
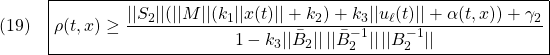
のように選びます。このとき
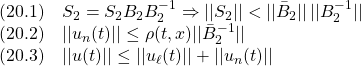
に注意して
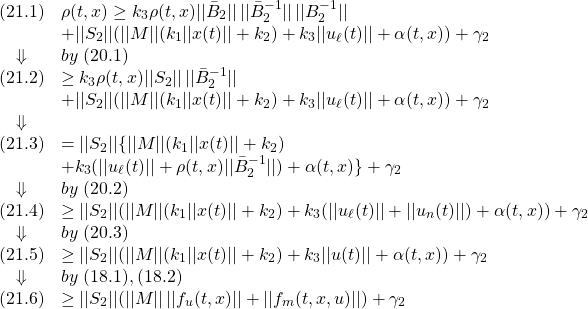
を得て、次式が成り立ちます。(15.2)は![]() だけに関係しているので、リャプノフ関数
だけに関係しているので、リャプノフ関数![]() の微分について調べます。
の微分について調べます。
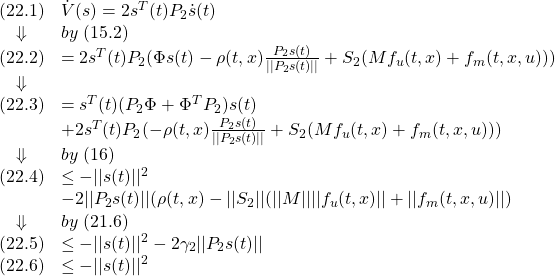
これより(15.2)における2次安定性が成り立つことが分かります。2次安定であれば状態![]() は0に漸近します。しかし興味深いのは、ある時刻
は0に漸近します。しかし興味深いのは、ある時刻![]() 以降は
以降は![]() を保持するような振舞いをすることです。
を保持するような振舞いをすることです。
●その到達時刻![]() を見積もるために、(22.5)から
を見積もるために、(22.5)から
![]()
も成り立つことと
![]()
に注意して
![]()
よって
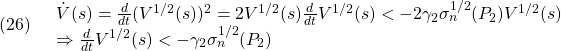
この両辺を積分すると
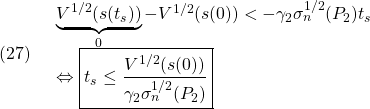
を得て、![]() に到達する時刻
に到達する時刻![]() を見積もることができます。
を見積もることができます。
[2] スライディングモードの検討
次に![]() のもとで、(15.1)から
のもとで、(15.1)から![]() の振舞いについて調べます。
の振舞いについて調べます。
![]() は安定行列なので
は安定行列なので
![]()
を満たす![]() を選ぶことができます。そこで、(15.1)に対するリャプノフ関数
を選ぶことができます。そこで、(15.1)に対するリャプノフ関数![]() の微分について調べます。
の微分について調べます。
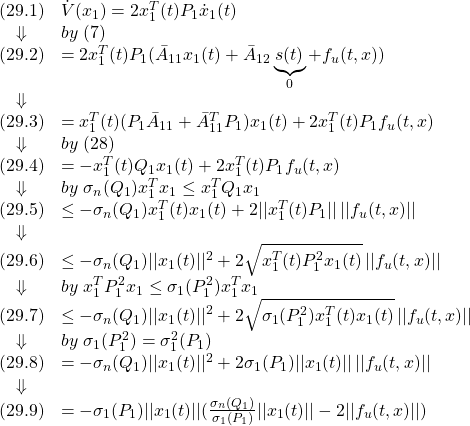
ここで
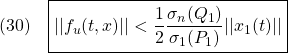
のとき
![]()
となって、リヤプノフ安定性が成り立ちます。したがって、ロバスト性での議論と同様に、![]() が発散することはないことが分かります。
が発散することはないことが分かります。
Note C22-1 SM標準形について
列フルランクをもつ![]() は、サイズ
は、サイズ![]() の直交行列
の直交行列![]() とサイズ
とサイズ![]() の直交行列
の直交行列![]() を用いて
を用いて
![]()
のように特異値分解できます。ただし
![]()
![]()
いま
![]()
と分割するとき、本論(1)に対する座標変換
![]()
を行うと(![]() に注意)
に注意)
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{x}_{r1}(t)\\ \dot{x}_{r2}(t) \end{array}\right] }_{\dot{x}_r(t)} = \underbrace{ \left[\begin{array}{cc} A_{r11} & A_{r12} \\ A_{r21} & A_{r22} \\ \end{array}\right] }_{A_r=T_rAT_r^T} \underbrace{ \left[\begin{array}{c} x_{r1}(t)\\ x_{r2}(t) \end{array}\right] }_{x_r(t)} + \underbrace{ \left[\begin{array}{c} 0\\ \Sigma_1V^T \end{array}\right] }_{B_r=T_rB} u(t)\\ + \underbrace{ \left[\begin{array}{l} f_{ru}(t,x)\\ f_{rm}(t,x,u) \end{array}\right] }_{f_r(t,x,u)=T_rf(t,x,u)} \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-37c0842a8446b8a7abc1cbf016179aba_l3.png)
のように本論(3)が得られます。ちなみに本論(4)は次式に相当します。
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad s(t)= \underbrace{ \left[\begin{array}{cc} S_{r1} & S_{r2} \\ \end{array}\right] }_{S_r=ST_r^T} \underbrace{ \left[\begin{array}{c} x_{r1}(t)\\ x_{r2}(t) \end{array}\right] }_{x_r(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-988fe8c3933d54a6b2a2343fa71b6828_l3.png)
これから、標準形に対して求めたスイッチング関数を元の状態方程式に関するものに戻すには
![]()
とすればよいことが分かります。
Note C22-2 条件(18)について
次式で表されるDCモータを考えます。
![]()
これより、次の状態方程式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \underbrace{ \left[\begin{array}{c} \dot{\theta}\\ \dot{\omega}\\ \dot{i}_a \end{array}\right] }_{\dot{x}} = \underbrace{ \left[\begin{array}{cc|c} 0 & 1 & 0\\ 0 & 0 & \frac{K_t}{J_0}\\\hline 0 & -\frac{K_e}{L_0} & -\frac{R}{L_0} \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} \theta\\ \omega\\ i_a \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{c} 0\\ 0\\\hline \frac{1}{L_0} \end{array}\right] }_{B} \underbrace{ v_a }_{u} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f34e214e8999446dc4f74a57bf7ab251_l3.png)
またスイッチング関数として次式を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad s= \underbrace{ \left[\begin{array}{ccc} \frac{J_0}{K_t}\omega_n^2 & 2\frac{J_0}{K_t}\zeta\omega_n & 1 \end{array}\right] }_{S}x \quad(M= \left[\begin{array}{ccc} \frac{J_0}{K_t}\omega_n^2 & 2\frac{J_0}{K_t}\zeta\omega_n \end{array}\right]) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-37b3f655680fcf1663a507a6815010ae_l3.png)
さらに次式のようなパラメータの不確かさを考えます。
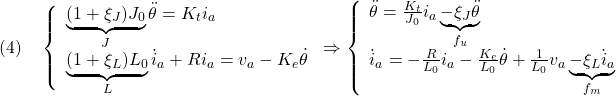
ただし、次を仮定します。
![]()
これにより状態方程式は次式となります。
![Rendered by QuickLaTeX.com \displaystyle{(6)\quad \dot{x}=Ax+Bu+ \left[\begin{array}{c} 0\\ f_{u}\\ f_{m} \end{array}\right]%} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-403044bf0348dcd88eba34f879facf92_l3.png)
まず![]() は
は
![]()
と表されるので、仮定(18)の第2式における![]() と
と![]() は次のように特定できます。
は次のように特定できます。
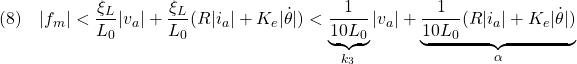
また![]() については、閉ループ系では
については、閉ループ系では
![]()
と考えられるので、仮定(18)の第1式における![]() と
と![]() は次のように特定できます。
は次のように特定できます。
![]()
さて、(19)を見積もってみます。
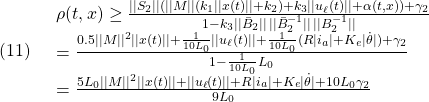
以上に基づいて、DCモータに対するSMCのシミュレーションを行ってみます。
| MATLAB |
|
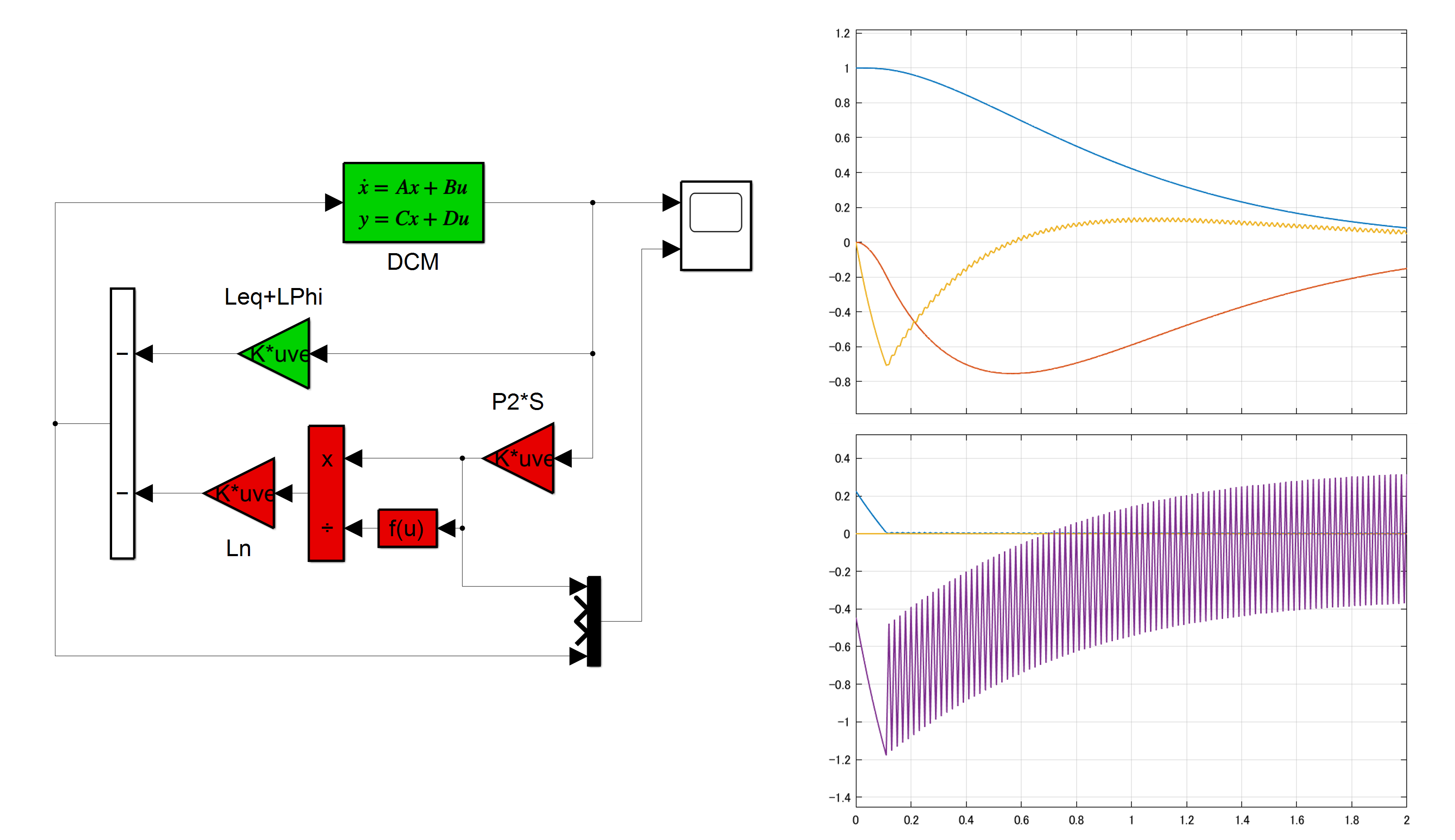
図1 DCモータに対するSMCのシミュレーション例
Note C22-4 スライディングモード制御系の安定性について
スライディングモード制御系の振舞いは、スライディングモードへの突入動作と、そこでの滑り動作から成ります。前者は、![]() を達成することですから、2次安定性
を達成することですから、2次安定性
![]()
を検討します。これが可到達条件となります。ただ、これではまだ原点![]() への収束は保証されないので、2次安定性
への収束は保証されないので、2次安定性
![]()
を検討します。
Note C22-5 安定行列![]() について
について
●「![]() が可制御対
が可制御対 ![]()
![]() も可制御対」
も可制御対」
実際、
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \begin{array}{l} {\rm rank}\left[\begin{array}{cc} B & \lambda I_n-A \end{array}\right]\\ = {\rm rank}\left[\begin{array}{ccc} 0 & A_{11}-\lambda I_m & A_{12}\\ B_{2} & A_{21} & A_{22}-\lambda I_m \end{array}\right]\\ = {\rm rank}\left[\begin{array}{ccc} A_{11}-\lambda I_m & A_{12} \end{array}\right]+m \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-585e01601ba9a848826ac5abbfdf9019_l3.png)
これより
![]()
●「![]() の固有値はスイッチング関数を出力方程式としたときの不変零点に等しい」
の固有値はスイッチング関数を出力方程式としたときの不変零点に等しい」
まず、線形系
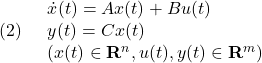
の不変零点とは、行列![]() の一般化固有値すなわち
の一般化固有値すなわち
![]()
を満足する![]() として定義されます。これから次式が成り立ちます。
として定義されます。これから次式が成り立ちます。
![]()
詳しい説明は省きますが、これは指数関数入力![]() に対する応答が零になることを意味しています。
に対する応答が零になることを意味しています。
(3)が非自明な解をもつためには次式が必要十分となります。
![]()
さて、次の線形系を考えます。
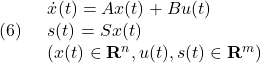
この不変零点を求めます。
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \begin{array}{l} {\rm det}\left[\begin{array}{cc} \lambda I_n-A & -B\\ -S & 0 \end{array}\right]\\ = {\rm det}\left[\begin{array}{ccc} \lambda I_{n-m}-A_{11} & -A_{12} & 0\\ -A_{21} & \lambda I_m-A_{22} & -B_{2}\\ -S_1 & -S_2 & 0 \end{array}\right]=0\\ \Leftrightarrow {\rm det}\left[\begin{array}{ccc} \lambda I_{n-m}-A_{11} & -A_{12} \\ -S_1 & -S_2 \end{array}\right]=0\\ \Leftrightarrow{\rm det} \left[\begin{array}{cc} I_{n-m} & -A_{12}S_2^{-1} \\ 0 & I_m \end{array}\right]\left[\begin{array}{cc} \lambda I_{n-m}-\bar{A}_{11} & 0 \\ 0 & -S_2 \end{array}\right] \left[\begin{array}{cc} I_{n-m} & 0 \\ M & I_m \end{array}\right]\\ ={\rm det}(\lambda I_{n-m}-\bar{A}_{11}){\rm det}(-S_2)=0\\ \Leftrightarrow {\rm det}(\lambda I_{n-m}-\bar{A}_{11})=0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-571e2b9312a22e1a6842d8c5bcbcb33f_l3.png)
すなわち、スイッチング関数を出力方程式とするシステム(6)の不変零点は、行列![]() の固有値と一致します。この行列
の固有値と一致します。この行列![]() はスライディングモードの振舞いを決めるので、
はスライディングモードの振舞いを決めるので、![]() は安定行列とすることが前提となります。したがって、どのようなスイッチング関数が望ましいかは、どのような超平面上をどのようにスライディングさせるかに関わっていると言えます。
は安定行列とすることが前提となります。したがって、どのようなスイッチング関数が望ましいかは、どのような超平面上をどのようにスライディングさせるかに関わっていると言えます。