線形系の2次安定性…Homework
対象が平衡状態にあることは線形状態方程式![]() において、
において、![]() を意味します。そこで平衡状態が乱されて
を意味します。そこで平衡状態が乱されて![]() となる時刻を
となる時刻を![]() にとると、線形状態方程式は次式となります。
にとると、線形状態方程式は次式となります。
![]()
これに出力方程式
![]()
を考慮する場合も含めると、漸近安定性の判定法は次のようにまとめられます。
|
【漸近安定性の定義とその等価な条件】
定義DA: 条件A0: 条件A1: 条件A2: 条件A3: 条件A4: |
条件A2のリャプノフ方程式から次式を得ます。
![]()
線形系(1)に対してリャプノフ関数
![]()
を考えるとき、(3)は2次安定性の条件
![]()
を意味します。これから漸近安定な線形系(1)は2次安定であることが分かります。
●条件A2の両辺から![]() をかけて
をかけて
![]()
を得ます。![]() は可観測対なので条件A3を適用して(
は可観測対なので条件A3を適用して(![]() をはずして)
をはずして)
条件A2′: ![]() ただし、
ただし、![]()
も漸近安定性の条件となることに注意します。
モデルの不確かさがある場合…Homework
いま漸近安定な線形系(1)において次のようなモデルの不確かさがあるとします。
![]()
条件A2’より、適当な![]() と
と![]() に対して
に対して
![]()
が成り立ちます。このとき
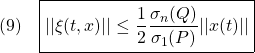
ならば、リャプノフ関数
![]()
に対して
![]()
となって、リャプノフ安定となります。
●実際、
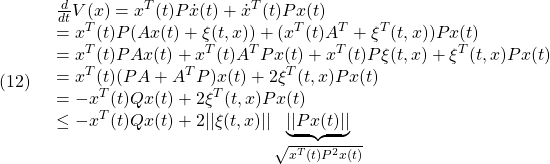
ここで、
![]()
に注意して、(9)の下では
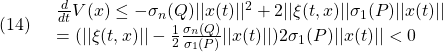
となります。
●次の数値例を考えてみます。
![Rendered by QuickLaTeX.com \displaystyle{(15)\quad \left[\begin{array}{c} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -4 & -1 \end{array}\right] }_{A} \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right] + \underbrace{\left[\begin{array}{c} 0 \\ 1 \end{array}\right]}_{D}\underbrace{\sin(2t)}_{\xi(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-686b73217e57bd77cd759540d3fae61f_l3.png)
![]() は安定行列なので、リャプノフ方程式
は安定行列なので、リャプノフ方程式![]() を満足する
を満足する![]() は
は
![]()
のように求まります。
この![]() をもつリャプノフ関数(10)に対して
をもつリャプノフ関数(10)に対して
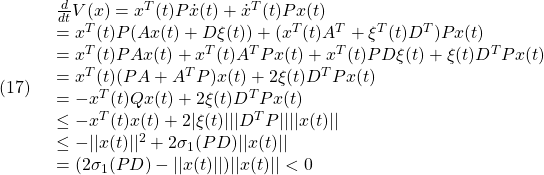
これから
![]()
のときは![]() となって原点に漸近していきますが、
となって原点に漸近していきますが、![]() になるとそれは保証されないことが分かります(図1参照)。
になるとそれは保証されないことが分かります(図1参照)。
 図1 モデルの不確かさがある場合の解軌道
図1 モデルの不確かさがある場合の解軌道
演習C12…Flipped Classroom
![]() smc17.slxを用いて、図1のシミュレーションを行え。
smc17.slxを用いて、図1のシミュレーションを行え。
Note C12 振り子の安定性
振り子の運動方程式
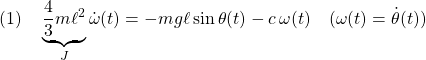
から得られる非線形状態方程式
![Rendered by QuickLaTeX.com \displaystyle{(2)\quad \frac{d}{dt} \underbrace{\left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right]}_{x} = \underbrace{ \left[\begin{array}{c} \omega(t) \\ -\frac{mg\ell}{J}\sin\theta(t)-\frac{c}{J}\omega(t) \end{array}\right] }_{f(x)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3b7ba41f7598be72c8ae81339591673c_l3.png)
に対して、次のリャプノフ関数の候補を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(3)\quad V=\frac{1}{2} \underbrace{ \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right]^T \left[\begin{array}{cc} \frac{1}{2}\frac{c^2}{J} & \frac{1}{2}c \\ \frac{1}{2}c & J \end{array}\right] \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right] }_{x^T(t)Px(t)} +mg\ell(1-\cos\theta(t))>0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-98c8ff12c9923ef1a298272fc344e4e4_l3.png)
この時間微分を計算すると
![Rendered by QuickLaTeX.com \displaystyle{(4)\quad \begin{array}{l} \dot{V}(t)=\frac{1}{2}(x^TP\dot{x}+\dot{x}^TPx)+mg\ell\omega\sin\theta =x^TP\dot{x}+mg\ell\omega\sin\theta\\ =\left[\begin{array}{c} \theta \\ \omega \end{array}\right]^T \left[\begin{array}{cc} p_1 & p_3 \\ p_3 & p_2 \end{array}\right] \left[\begin{array}{c} \omega \\ -\frac{mg\ell}{J}\sin\theta-\frac{c}{J}\omega \end{array}\right]+mg\ell\omega\sin\theta\\ =\left[\begin{array}{cc} \theta &\omega \end{array}\right] \left[\begin{array}{cc} p_1\omega -p_3(\frac{mg\ell}{J}\sin\theta+\frac{c}{J}\omega) \\ p_3\omega -p_2(\frac{mg\ell}{J}\sin\theta+\frac{c}{J}\omega) \end{array}\right]+mg\ell\omega\sin\theta\\ =p_1\theta\omega -p_3(\frac{mg\ell}{J}\theta\sin\theta+\frac{c}{J}\theta\omega)+ p_3\omega^2 -p_2(\frac{mg\ell}{J}\omega\sin\theta+\frac{c}{J}\omega^2)+mg\ell\omega\sin\theta\\ =-\frac{mg\ell}{J}\sin\theta(p_3\theta+p_2\omega-J\omega) +(p_3-p_2\frac{c}{J})\omega^2+(p_1-p_3\frac{c}{J})\theta\omega \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6c783b4a46a73e78fb425f69bfa45499_l3.png)
ここで、![]() 、
、![]() 、
、![]() を代入して
を代入して
![]()
となります。ここで
![]()
だから、(5)は負値をとります。したがって、(3)はリャプノフ関数となっています。
●ちなみに(2)を次のように書き直してみます。
![Rendered by QuickLaTeX.com \displaystyle{(7)\quad \left[\begin{array}{c} \dot{\theta}(t) \\ \dot{\omega}(t) \end{array}\right] = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\frac{mg\ell}{J} & -\frac{c}{J} \end{array}\right] }_{A} \left[\begin{array}{c} \theta(t) \\ \omega(t) \end{array}\right] + \underbrace{ \left[\begin{array}{c} 0 \\ \frac{mg\ell}{J} \end{array}\right] }_{D} \underbrace{ (\theta(t)-\sin\theta(t)) }_{\xi(x)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-0c7be17a5704d87667dc74b647c5f7da_l3.png)
我々は軸摩擦をもつ振り子の角度は十分時間がたてば零に収束することを知っています。上の議論に沿って解釈すれば、モデルの不確かさ![]() 自体が限りなく零に近づき(
自体が限りなく零に近づき(![]() )、線形系となると考えられます。
)、線形系となると考えられます。
Note C12 MATLABによるリャプノフ方程式の求解
たとえば、安定行列![]()
が与えられるとき、リャプノフ方程式![]() を満足する
を満足する![]() は
は
![]()
のように求まります。これはMATLABで次のコマンドを用いました。
P=lyap(A’,eye(2))
ここで、P=lyap(A,Q) はリャプノフ方程式![]() の解を求めることに注意します。この解を
の解を求めることに注意します。この解を![]() に対するリャプノフ行列と呼ぶことがあります。
に対するリャプノフ行列と呼ぶことがあります。
![]()