| MATLAB |
%of_syn_lmi6.m
%-----
A=[0 1;-1 -2*0.01]; B1=[0;1]; B2=B1;
C1=[1 0;0 0]; D11=[0;0]; D12=[0;1];
C2=[1 0]; D21=0; D22=0;
%-----
setlmis([]);
gam=lmivar(1,[1 0]);
R=lmivar(1,[2 1]);
S=lmivar(1,[2 1]);
Ak=lmivar(2,[2 2]);
Bk=lmivar(2,[2 1]);
Ck=lmivar(2,[1 2]);
Dk=lmivar(2,[1 1]);
%-----
lmiRS=newlmi;
lmiterm([lmiRS 1 1 R],A,1,'s'); %#1:R*A'+AR
lmiterm([lmiRS 1 1 Ck],B2,1,'s'); %#1:Ck'*B2'+B2*Ck
lmiterm([lmiRS 2 1 0],A'); %#1:A'
lmiterm([lmiRS 2 1 Ak],1,1); %#1:Ak
lmiterm([lmiRS 2 1 -Dk],C2',B2'); %#1:C2'*Dk'*B2'
lmiterm([lmiRS 2 2 S],1,A,'s'); %#1:A'*S+S*A
lmiterm([lmiRS 2 2 Bk],1,C2,'s'); %#1:C2'*Bk'+Bk*C2
lmiterm([lmiRS 1 3 0],B1); %#1:B1
lmiterm([lmiRS 1 3 Dk],B2,D21); %#1:B2*Dk*D21
lmiterm([lmiRS 2 3 S],1,B1); %#1:S*B1
lmiterm([lmiRS 2 3 Bk],1,D21); %#1:Bk*D21
lmiterm([lmiRS 3 3 gam],-1,1); %#1:-gam
lmiterm([lmiRS 4 1 R],C1,1); %#1:C1*R
lmiterm([lmiRS 4 1 Ck],D12,1); %#1:D12*Ck
lmiterm([lmiRS 4 2 0],C1); %#1:C1
lmiterm([lmiRS 4 2 Dk],D12,C2); %#1:D12*Dk*C2
lmiterm([lmiRS 4 3 0],D11); %#1:D11
lmiterm([lmiRS 4 3 Dk],D12,D21); %#1:D12*Dk*D21
lmiterm([lmiRS 4 4 gam],-1,1); %#1:-gam
%-----
alpha=0.1;
lmiPL1=newlmi;
lmiterm([lmiPL1 1 1 R],A,1,'s'); %#2:R*A'+A*R
lmiterm([lmiPL1 1 1 Ck],B2,1,'s'); %#2:Ck'*B2'+B2*Ck
lmiterm([lmiPL1 2 1 Ak],1,1); %#2:Ak
lmiterm([lmiPL1 1 2 0],A); %#2:A
lmiterm([lmiPL1 1 2 Dk],B2,C2); %#2:B2*Dk*C2
lmiterm([lmiPL1 2 2 S],1,A,'s'); %#2:A'*S+S*A
lmiterm([lmiPL1 2 2 Bk],1,C2,'s'); %#2:C2'*Bk'+Bk*C2
%
lmiterm([lmiPL1 1 1 R],2*alpha,1); %#2:2*alpha*R
lmiterm([lmiPL1 2 1 0],2*alpha); %#2:2*alpha*I
lmiterm([lmiPL1 2 2 S],2*alpha,1); %#2:2*alpha*S
%-----
r=2;
lmiPL2=newlmi;
lmiterm([lmiPL2 1 1 R],-r,1); %#3:-r*R
lmiterm([lmiPL2 2 1 0],-r); %#3:-r*I
lmiterm([lmiPL2 2 2 S],-r,1); %#3:-r*S
%
lmiterm([lmiPL2 1 3 R],A,1); %#3:A*R
lmiterm([lmiPL2 1 3 Ck],B2,1); %#3:B2*Ck
lmiterm([lmiPL2 2 3 Ak],1,1); %#3:Ak
lmiterm([lmiPL2 1 4 0],A); %#3:A
lmiterm([lmiPL2 1 4 Dk],B2,C2); %#3:B2*Dk*C2
lmiterm([lmiPL2 2 4 S],1,A); %#3:S*A
lmiterm([lmiPL2 2 4 Bk],1,C2); %#3:Bk*C2
%
lmiterm([lmiPL2 3 3 R],-r,1); %#3:-r*R
lmiterm([lmiPL2 4 3 0],-r); %#3:-r*I
lmiterm([lmiPL2 4 4 S],-r,1); %#3:-r*S
%-----
th=0.4*pi; sth=sin(th); cth=cos(th);
lmiPL3=newlmi;
lmiterm([lmiPL3 1 1 R],sth*A,1,'s'); %#4:sth*(R*A'+A*R)
lmiterm([lmiPL3 1 1 Ck],sth*B2,1,'s');%#4:sth*(Ck'*B2'+B2*Ck)
lmiterm([lmiPL3 2 1 Ak],sth,1); %#4:sth*(Ak)
lmiterm([lmiPL3 1 2 0],sth*A); %#4:sth*(A)
lmiterm([lmiPL3 1 2 Dk],sth*B2,C2); %#4:sth*(B2*Dk*C2)
lmiterm([lmiPL3 2 2 S],1,sth*A,'s'); %#4:sth*(A'*S+S*A)
lmiterm([lmiPL3 2 2 Bk],1,sth*C2,'s');%#4:sth*(C2'*Bk'+Bk*C2)
%
% lmiterm([lmiPL3 1 3 R],1,cth*A'); %#4:cth*(R*A')
% lmiterm([lmiPL3 1 3 R],-cth*A,1); %#4:cth*(-A*R)
% lmiterm([lmiPL3 1 3 -Ck],cth*B2',1);%#4:cth*(Ck'*B2')
% lmiterm([lmiPL3 1 3 Ck],-cth*B2,1); %#4:cth*(-B2*Ck)
lmiterm([lmiPL3 1 3 R],cth*A,1); %#1:cth*(A*R)
lmiterm([lmiPL3 1 3 R],1,-cth*A'); %#1:cth*(-R*A')
lmiterm([lmiPL3 1 3 Ck],cth*B2,1); %#1:cth*(B*Ck)
lmiterm([lmiPL3 1 3 -Ck],-cth*B2',1); %#1:cth*(-Ck'*B')
lmiterm([lmiPL3 2 3 Ak],cth,1); %#4:cth*(Ak)
lmiterm([lmiPL3 1 4 -Ak],-cth,1); %#4:cth*(-Ak')
lmiterm([lmiPL3 1 4 0],A); %#4:cth*(A)
lmiterm([lmiPL3 2 3 0],-A'); %#4:cth*(-A')
lmiterm([lmiPL3 1 4 Dk],cth*B2,C2); %#4:cth*(B2*Dk*C2)
lmiterm([lmiPL3 2 3 -Dk],-cth*C2',B2');%#4:cth*(-C2'*Dk'*B2')
lmiterm([lmiPL3 2 4 S],1,cth*A); %#4:cth*(S*A)
lmiterm([lmiPL3 2 4 S],-cth*A',1); %#4:cth*(-A'*S)
lmiterm([lmiPL3 2 4 Bk],1,cth*C2); %#4:cth*(Bk*C2)
lmiterm([lmiPL3 2 4 -Bk],-cth*C2',1); %#4:cth*(-C2'*Bk')
%
lmiterm([lmiPL3 3 3 R],sth*A,1,'s'); %#4:sth*(R*A'+A*R)
lmiterm([lmiPL3 3 3 Ck],sth*B2,1,'s');%#4:sth*(Ck'*B2'+B2*Ck)
lmiterm([lmiPL3 4 3 Ak],sth,1); %#4:sth*(Ak)
lmiterm([lmiPL3 3 4 0],sth*A); %#4:sth*(A)
lmiterm([lmiPL3 3 4 Dk],sth*B2,C2); %#4:sth*(B2*Dk*C2)
lmiterm([lmiPL3 4 4 S],1,sth*A,'s'); %#4:sth*(A'*S+S*A)
lmiterm([lmiPL3 4 4 Bk],1,sth*C2,'s');%#4:sth*(C2'*Bk'+Bk*C2)
%-----
posX=-newlmi;
lmiterm([posX 1 1 R],1,1); %#5:R
lmiterm([posX 2 1 0],1); %#5:I
lmiterm([posX 2 2 S],1,1); %#5:S
%-----
lmiDk=-newlmi;
lmiterm([lmiDk 1 1 0],1e2); %#6:1e2
lmiterm([lmiDk 2 2 0],1e2); %#6:1e2
lmiterm([lmiDk 2 1 Dk],1,1); %#6:Dk
%-----
lmig=newlmi;
lmiterm([lmig,1,1,gam],1,1); %#7:gam
lmiterm([lmig,1,1,0],-1e3); %#7:1e3
%-----
LMIs=getlmis;
cobj=zeros(1,decnbr(LMIs));
cobj(1)=1;
[cost,xopt]=mincx(LMIs,cobj);
%-----
gopt=dec2mat(LMIs,xopt,gam)
R=dec2mat(LMIs,xopt,R);
S=dec2mat(LMIs,xopt,S);
ak=dec2mat(LMIs,xopt,Ak);
bk=dec2mat(LMIs,xopt,Bk);
ck=dec2mat(LMIs,xopt,Ck);
dk=dec2mat(LMIs,xopt,Dk);
[u,sd,v]=svd(eye(size(A,1)-S*R);
sd=diag(sqrt(1./diag(sd)));
Ni=sd*u'; Mti=v*sd;
AK=Ni*(ak-S*(A-B2*dk*C2)*R-bk*C2*R-S*B2*ck)*Mti;
BK=Ni*(bk-S*B2*dk);
CK=(ck-dk*C2*R)*Mti;
DK=dk;
%-----
pl=eig(A)
ACL=[A+B2*DK*C2 B2*CK;
BK*C2 AK];
plCL=eig(ACL)
close all,figure(1)
dregion(alpha,0,r,th,r*[-1,1,-1,1])
plot(real(pl),imag(pl),'x',real(plCL),imag(plCL),'*')
BCL=[B1+B2*DK*D21;
BK*D21];
CCL=[C1+D12*DK*C2 D12*CK];
DCL=D11+D12*DK*D21;
figure(2)
ol=ltisys(A,B1,C1,D11);
cl=ltisys(ACL,BCL,CCL,DCL);
om=logspace(-1,1,100);
splot(cl,'sv',om),hold on
splot(ol,'sv',om),grid
%-----
%eof
|
![]() 次系
次系![]() の
の![]() ノルムが
ノルムが![]() より小となるためのLMI条件は、次の通りでした。
より小となるためのLMI条件は、次の通りでした。![Rendered by QuickLaTeX.com \displaystyle{(1) \begin{array}{lll} && \sup_{\omega\in{\rm\bf R}}||\hat{G}(j\omega)||_2<\gamma \nonumber\\ &\Leftrightarrow& \exists X>0:\ \left[\begin{array}{ccc} A^TX+XA & XB & C^T \\ B^TX & -\gamma I & D^T \\ C & D & -\gamma I \end{array}\right]<0 \nonumber\\ &\Leftrightarrow& \exists Y>0:\ \left[\begin{array}{ccc} YA^T+AY & B & YC^T \\ B^T & -\gamma I & D^T \\ CY & D & -\gamma I \end{array}\right]<0\nonumber \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-eb1de97e8a1b06912197472c90ad05e5_l3.png)
![]()

![]() 次系を考えます。
次系を考えます。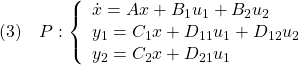
![]()
![Rendered by QuickLaTeX.com \displaystyle{(5) \begin{array}{l} P_{CL}: \\ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x} \\ \dot{x}_K \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} A+B_2D_KC_2 & B_2C_K \\ B_KC_2 & A_K \end{array}\right] }_{A_{CL}} \left[\begin{array}{c} x \\ x_K \end{array}\right] + \underbrace{ \left[\begin{array}{ccc} B_1+B_2D_KD_{21} \\ B_KD_{21} \end{array}\right] }_{B_{CL}} u_1\\ y_1 = \underbrace{ \left[\begin{array}{ccc} C_1+D_{12}D_KC_2 & D_{12}C_K \end{array}\right] }_{C_{CL}} \left[\begin{array}{c} x \\ x_K \end{array}\right] + \underbrace{ (D_{11}+D_{12}D_KD_{21}) }_{D_{CL}} u_1 \end{array}\right. \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2dd70838946d03d3ab984179f3b7d3f4_l3.png)
![]() ノルムが
ノルムが![]() より小、すなわち
より小、すなわち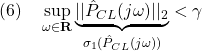
![]()
![]() を求める問題を考えます。
を求める問題を考えます。![Rendered by QuickLaTeX.com \displaystyle{(8)\quad \exists Y_{CL}>0:\ \left[\begin{array}{ccc} Y_{CL}A_{CL}^T+A_{CL}Y_{CL} & B_{CL} & Y_{CL}C_{CL}^T \\ B_{CL}^T & -\gamma I & D_{CL}^T \\ C_{CL}Y_{CL} & D_{CL} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ccc6bd8e5c1593548f942810686e27e0_l3.png)
![]() を代入して
を代入して![Rendered by QuickLaTeX.com \displaystyle{(9)\quad \exists \Pi_1\Pi_2^{-1}>0:\ \left[\begin{array}{ccc} \Pi_2^{-T}\Pi_1^TA_{CL}^T+A_{CL}\Pi_1\Pi_2^{-1} & B_{CL} & \Pi_2^{-T}\Pi_1^TC_{CL}^T \\ B_{CL}^T & -\gamma I & D_{CL}^T \\ C_{CL}\Pi_1\Pi_2^{-1} & D_{CL} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d63a7b09fc6927497933c2d9ac659f7e_l3.png)
![]() 、右から
、右から![]() をかけると、次のようなLMIとなります。
をかけると、次のようなLMIとなります。![Rendered by QuickLaTeX.com \displaystyle{(10)\quad \exists \Pi_2^T\Pi_1>0:\ \left[\begin{array}{ccc} \Pi_1^TA_{CL}^T\Pi_2+\Pi_2^TA_{CL}\Pi_1 & \Pi_2^TB_{CL} & \Pi_1^TC_{CL}^T \\ B_{CL}^T\Pi_2 & -\gamma I & D_{CL}^T \\ C_{CL}\Pi_1 & D_{CL} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7976677da89389b0f79fb5b4a9aac527_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(11)\quad \begin{array}{l} \Pi_2^TA_{CL}\Pi_1= \left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] \left[\begin{array}{ccc} A+B_2D_KC_2 & B_2C_K \\ B_KC_2 & A_K \end{array}\right] \left[\begin{array}{cc} R & I \\ M^T & 0 \end{array}\right] \\ =\left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] \left[\begin{array}{ccc} (A+B_2D_KC_2)R+B_2C_KM^T & A+B_2D_KC_2 \\ B_KC_2R+A_KM^T & B_KC_2 \end{array}\right] \\ =\left[\begin{array}{ccc} (A+B_2D_KC_2)R+B_2C_KM^T & \\ S(A+B_2D_KC_2)R+SB_2C_KM^T+NB_KCR+NA_KM^T & \end{array}\right. \\ \left.\begin{array}{ccc} & A+B_2D_KC_2 \\ & S(A+B_2D_KC_2)+NB_KC_2 \end{array}\right] \\ =\left[\begin{array}{cc} AR+B_2{\cal C}_K & A+B_2D_KC_2 \\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d79e51c89c40ae80b0c6446a23daa362_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(12)\quad \begin{array}{l} \Pi_2^TB_{CL}= \left[\begin{array}{cc} I & 0 \\ S & N \end{array}\right] \left[\begin{array}{ccc} B_1+B_2D_KD_{21} \\ B_KD_{21} \end{array}\right] \\ =\left[\begin{array}{ccc} B_1+B_2D_KD_{21} \\ S(B_1+B_2D_KD_{21})+NB_KD_{21} \end{array}\right] =\left[\begin{array}{ccc} B_1+B_2D_KD_{21} \\ SB_1+{\cal B}_KD_{21} \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a426811990f69d6297aaad7f2544eb65_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(13)\quad \begin{array}{l} C_{CL}\Pi_1= \left[\begin{array}{ccc} C_1+D_{12}D_KC_2 & D_{12}C_K \end{array}\right] \left[\begin{array}{cc} R & I \\ M^T & 0 \end{array}\right] \\ =\left[\begin{array}{ccc} (C_1+D_{12}D_KC_2)R+D_{12}C_KM^T & C_1+D_{12}D_KC_2 \end{array}\right] \\ =\left[\begin{array}{ccc} C_1R+D_{12}{\cal C}_K & C_1+D_{12}D_KC_2 \end{array}\right] \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-913e7b88945a8ea6aee40b1542674159_l3.png)
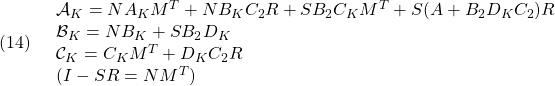
![]() を最小化し、
を最小化し、 ![]() を求め、次式によって出力フィードバックのゲインを決定します。
を求め、次式によって出力フィードバックのゲインを決定します。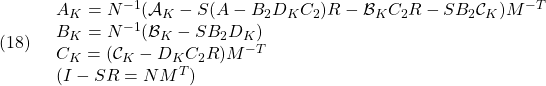
![]() 次のコードを参考にして、
次のコードを参考にして、![]() 制御(出力FB)を求める関数を作成せよ。
制御(出力FB)を求める関数を作成せよ。![]() 上の2次振動系の
上の2次振動系の![]() 制御について、閉ループ系の固有値に制約を付けた場合の効果を確かめよ。
制御について、閉ループ系の固有値に制約を付けた場合の効果を確かめよ。![Rendered by QuickLaTeX.com \displaystyle{(16) \left[\begin{array}{ccc} \left[\begin{array}{cc} AR+B_2{\cal C}_K & A+B_2D_KC_2\\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right]+(*)^T & \left[\begin{array}{c} B_1+B_2D_KD_{21} \\ SB_1+{\cal B}_KD_{21} \end{array}\right] & (*)^T \\ (*)^T & -\gamma I & (*)^T \\ \left[\begin{array}{cc} C_1R+D_{12}{\cal C}_K & C_1+D_{12}D_KC_2 \end{array}\right] & D_{11} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3070fcd4f3d258cf999951fbb4f9fbe5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(17) \begin{array}{l} \left[\begin{array}{cc} AR+B_2{\cal C}_K & A+B_2D_KC_2\\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right] +(*)^T %\nonumber\\&& +\alpha \left[\begin{array}{cc} R & I \\ I & S \end{array}\right]<0} \\ \left[\begin{array}{cc} -r \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] & \left[\begin{array}{cc} AR+B_2{\cal C}_K & A+B_2D_KC_2\\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right] \\ (*)^T & -r \left[\begin{array}{cc} R & I \\ I & S \end{array}\right] \end{array}\right] <0 \\ \left[\begin{array}{cc} \sin\theta & \cos\theta \\ -\cos\theta & \sin\theta \end{array}\right]\otimes \left[\begin{array}{cc} AR+B_2{\cal C}_K & A+B_2D_KC_2\\ {\cal A}_K & SA+{\cal B}_KC_2 \end{array}\right]+ (*)^T <0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7d7cb3c0df233a8a04c1e6b3e9b25962_l3.png)