伝達特性…Homework
[0] ![]() 次系の応答の相互関係は次のようにまとめることができました。
次系の応答の相互関係は次のようにまとめることができました。
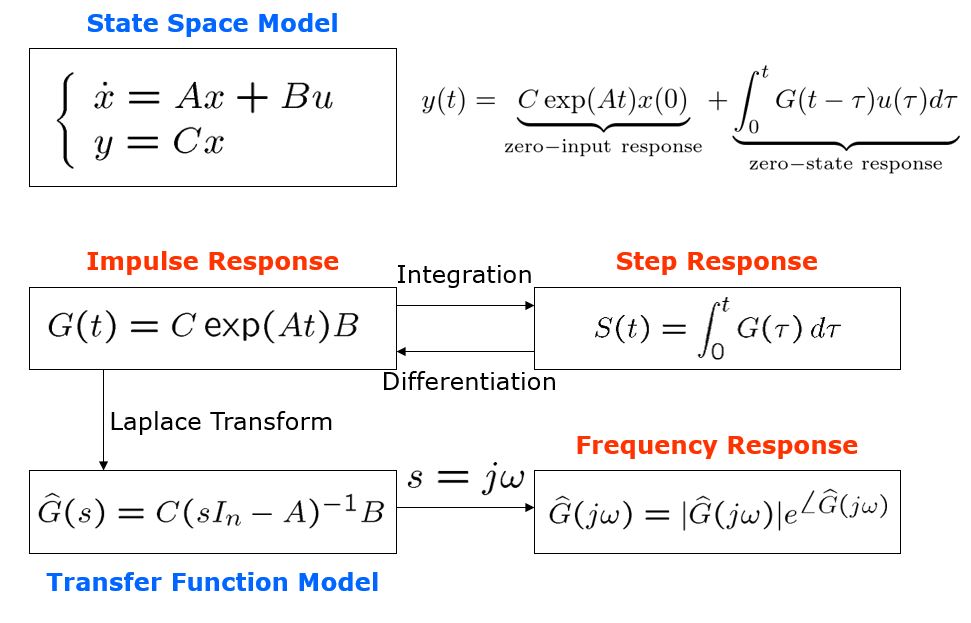
図1 線形系の時間応答
ここで、![]() 次系のインパルス応答が分かれば、どのような入力を与えられても出力を計算できます。または伝達関数が分かれば同様のことが言えます。したがって
次系のインパルス応答が分かれば、どのような入力を与えられても出力を計算できます。または伝達関数が分かれば同様のことが言えます。したがって![]() 次系は漸近安定であるとして、その性能(伝達特性)の評価はインパルス応答または伝達関数を用いて行われます。伝達関数は状態空間表現のうち可制御かつ可観測な部分しか反映しないので、以下では
次系は漸近安定であるとして、その性能(伝達特性)の評価はインパルス応答または伝達関数を用いて行われます。伝達関数は状態空間表現のうち可制御かつ可観測な部分しか反映しないので、以下では![]() は可制御対、
は可制御対、![]() は可観測対と仮定しておきます。
は可観測対と仮定しておきます。
[1] ![]() から
から![]() への写像
への写像![]() の「伝達特性」をどう測るかを考えます。これはスカラの場合は正比例の関係
の「伝達特性」をどう測るかを考えます。これはスカラの場合は正比例の関係![]() ですから、比例定数
ですから、比例定数![]() に相当する量を求める話になります。
に相当する量を求める話になります。
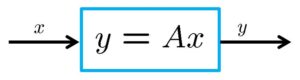
図2 線形写像
サイズ![]() の行列
の行列![]() の次の特異値分解を考えます。
の次の特異値分解を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(1)\quad \boxed{\begin{array}{l} A= \underbrace{ \left[\begin{array}{cc} U_1 & U_2 \end{array}\right] }_{U(m\times m)} \underbrace{ \left[\begin{array}{cc} {\rm diag}\{\sigma_1,\cdots,\sigma_k\} & 0_{k\times (n-k)} \\ 0_{(m-k)\times k} & 0_{(m-k)\times (n-k)} \end{array}\right] }_{\Sigma= \left[\begin{array}{cc} \Sigma_1 & 0 \\ 0 & 0 \end{array}\right] \quad(\sigma_1\ge\cdots\ge\sigma_k) } \underbrace{ \left[\begin{array}{cc} V_1^T \\ V_2^T \end{array}\right] }_{V(n\times n)^T}\\ =U_1(m\times k)\Sigma_1(k\times k)V_1(n\times k)^T \end{array}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1a8bdd72019cbda663e2a40b3a70d3b6_l3.png)
ここで、![]() で、
で、![]() と
と![]() は直交行列です。
は直交行列です。
![]()
したがって、次のような3つの線形写像に分解されます。
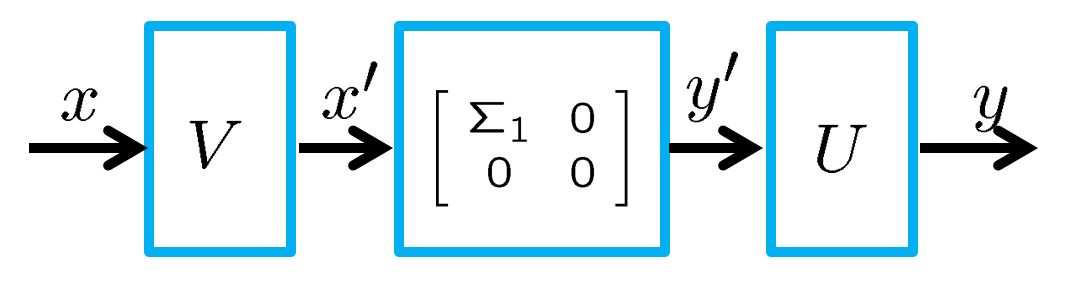 図3 特異値分解
図3 特異値分解
![]() 次元ベクトル
次元ベクトル![]() のノルムとして、次の3通りがよく用いられ、それぞれ1ノルム、2ノルム、
のノルムとして、次の3通りがよく用いられ、それぞれ1ノルム、2ノルム、![]() ノルムと呼ばれます。
ノルムと呼ばれます。

以下では、ベクトルのノルムとして、2番目の2ノルムを考えます。
このとき、次が成り立ちます。
![]()
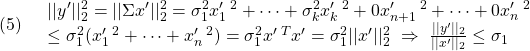
![]()
すなわち
![]()
したがって、線形写像![]() の伝達特性は、行列
の伝達特性は、行列![]() の2ノルム
の2ノルム
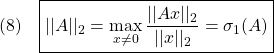
すなわち行列![]() の最大特異値
の最大特異値![]() (行列
(行列![]() または
または![]() の最大固有値の正の平方根)によって測られます。
の最大固有値の正の平方根)によって測られます。
[2] 入力![]() から出力
から出力![]() への漸近安定な
への漸近安定な![]() 次系の「伝達特性」をどう測るかを考えます。
次系の「伝達特性」をどう測るかを考えます。
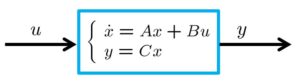
図4 n次系
![]() 次系の入出力応答は次式で表されます。ただし、
次系の入出力応答は次式で表されます。ただし、![]() とします。
とします。
![]()
これをフーリエ変換しますと次式を得ます。
![]()
いま時間関数![]() のノルムを次のように定義し、このノルムが有界な時間関数の集合を
のノルムを次のように定義し、このノルムが有界な時間関数の集合を![]() と表記します。
と表記します。
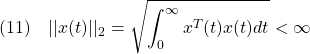
このとき、次のパーセバルの定理
![]()
および周波数伝達関数行列![]() の2ノルムに関する不等式
の2ノルムに関する不等式
![]()
に注意して、次式が成り立ちます。
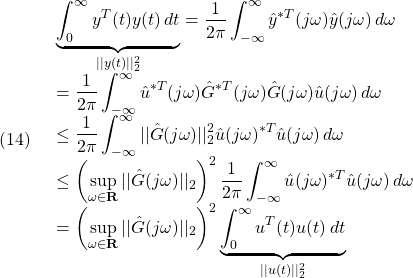
すなわち
![]()
これに基づいて、![]() 次系の
次系の![]() ノルムを次式で定義します。
ノルムを次式で定義します。
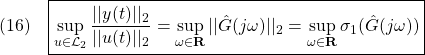
●いま、任意の複素数![]() の特異値は
の特異値は![]() であることに注意すると、スカラ系の
であることに注意すると、スカラ系の![]() ノルムは、ゲイン曲線の最大値であることがわかります。多変数系に対して
ノルムは、ゲイン曲線の最大値であることがわかります。多変数系に対して![]() をプロットした曲線は
をプロットした曲線は![]() プロットと呼ばれています。
プロットと呼ばれています。
●次の直達項をもつn次系を考えます。

図5 直達項をもつn次系
このとき、インパルス応答と周波数伝達関数は、それぞれ
![]()
![]()
となりますが、上の議論はそのまま成り立ち、![]() ノルムを定義できます。
ノルムを定義できます。
[3] 漸近安定な![]() 次系の「伝達特性」を測るもう一つの方法は、すべてのインパルス応答の2乗面積の総和によるものです。
次系の「伝達特性」を測るもう一つの方法は、すべてのインパルス応答の2乗面積の総和によるものです。![]() 入力
入力![]() 出力
出力![]() 次系のインパルス応答は
次系のインパルス応答は
![]()
の![]() 個あります。いま任意の行列
個あります。いま任意の行列![]() のすべての要素の2乗和
のすべての要素の2乗和![]() はまたは
はまたは![]() で表されることに注意します。すべてのインパルス応答の2乗面積の総和は
で表されることに注意します。すべてのインパルス応答の2乗面積の総和は
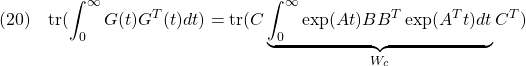
または
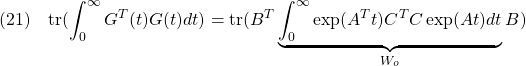
のように表されます。ここで、![]() と
と![]() はそれぞれリャプノフ方程式
はそれぞれリャプノフ方程式
![]()
![]()
の解であることに注意しておきます。![]() に注意して
に注意して
![]()
の正の平方根を![]() 次系の
次系の![]() ノルムと呼びます。
ノルムと呼びます。
●直達項をもつn次系の場合は、インパルス応答
![]()
の2乗面積の総和は発散してしまうので、![]() ノルムはできないことに注意します。
ノルムはできないことに注意します。
Note B21 1次系のパーセバルの定理
1次系
![]()
のインパルス応答と周波数伝達関数の絶対値は
![]()
となります。まずパーセバルの定理
![]()
が成り立つことは次のように確かめられます。
![]()
![]()
また1次系のノルムは、複素数![]() の特異値がその絶対値であることに注意して
の特異値がその絶対値であることに注意して
![]()