LPV制御…Homework
[1] 回転体は次の運動方程式で表されます。
![]()
ここで、次のパラメータ変動を想定します。
![]()
次の状態方程式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{(3) \underbrace{ \left[\begin{array}{c} \dot{\omega}_1(t) \\ \dot{\omega}_2(t) \end{array}\right] }_{\dot{x}(t)} = \underbrace{ \left[\begin{array}{cc} 0 & \Omega(t)\frac{J_2-J_3}{J_1} \\ \Omega(t)\frac{J_3-J_1}{J_2} & 0 \end{array}\right] }_{A(\Omega(t))} \underbrace{ \left[\begin{array}{c} \omega_1(t) \\ \omega_2(t) \end{array}\right] }_{x(t)} + \underbrace{ \left[\begin{array}{cc} \frac{1}{J_1} & 0 \\ 0 & \frac{1}{J_2} \end{array}\right] }_{B} \underbrace{ \left[\begin{array}{c} \tau_1(t) \\ \tau_2(t) \end{array}\right] }_{u(t)} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-06d0d0706f122470d4466143aac157d2_l3.png)
●そのために、![]() は次式で表されることに着目します。
は次式で表されることに着目します。
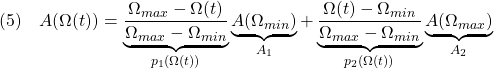
ただし
![]()
このとき上の状態方程式は、端点(vertex)モデルとよばれる
![]()
を、係数![]() によって重み付けて
によって重み付けて
![]()
のように得られることが分かります。これをLPV(Linear Parameter Varying)モデルと呼びます。
[2] 状態フィートバックによるパラメータ変動抑制について考えます。そのために端点モデルに対応した端点コントローラとよばれる
![]()
を、係数![]() によって重み付けた
によって重み付けた
![]()
のようなLPV(Linear Parameter Varying)制御を考えます。これは次のように図示されます。
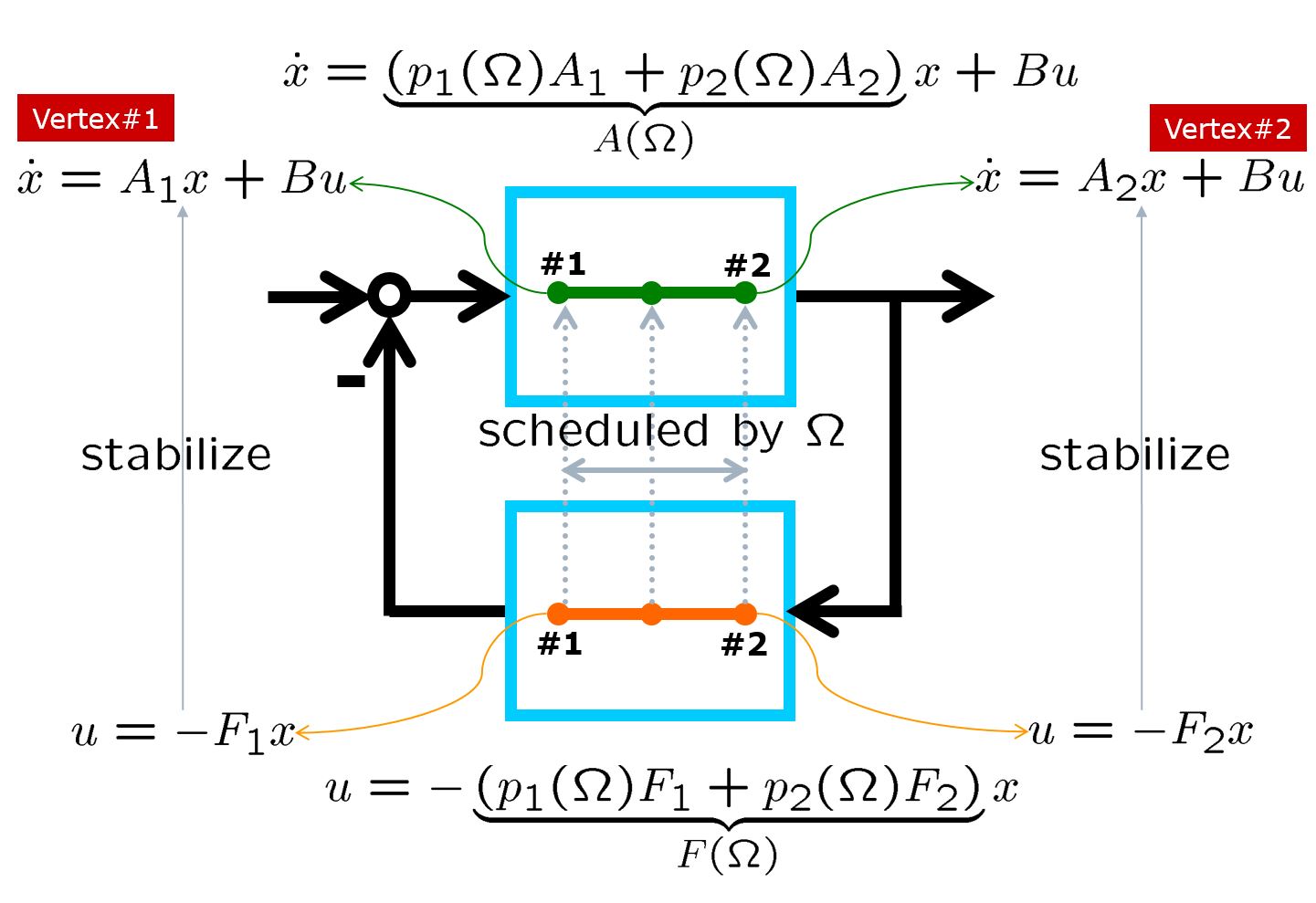 図3 LPV制御の枠組み
図3 LPV制御の枠組み
この閉ループ系は次式で表されます。
![]()
ここで、![]() と
と![]() は安定行列となるように設計しますが、閉ループ系の時変系としての安定性が保証されるかの検討が必要になります。
は安定行列となるように設計しますが、閉ループ系の時変系としての安定性が保証されるかの検討が必要になります。
[3] そのための準備として、次の時変自由系の漸近安定性を考えます。
![]()
平衡状態![]() の近傍
の近傍![]() において、リャプノフ関数とよばれる
において、リャプノフ関数とよばれる
![]()
を構成して
![]()
を示すことができれば、平衡状態は漸近安定となることが知られています。リャプノフ関数の存在は十分条件であること、またリャプノフ関数も時変でなく時不変としていることに注意してください。
●ちなみに、時不変自由系
![]()
の漸近安定性![]() のLMI条件は
のLMI条件は
![]()
でした(前者がX-LMI、後者がY-LMI)。このときは
![]()
と選べば
![]()
となっていることが分かります。
[4] いま、上の![]() と
と![]() を個別に安定行列としたとすると
を個別に安定行列としたとすると
![]()
![]()
から、個別にリャプノフ関数の候補
![]()
![]()
が得られますが、閉ループ系
![]()
のリャプノフ関数を構成したことにはなりません。一方
![]()
となる共通の![]() を見つけることができれば
を見つけることができれば
![]()
に対して、LPV制御では
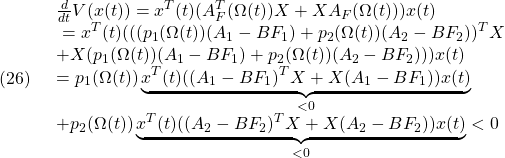
となって、リャプノフ関数を構成したことになります。
[5] LPVモデル
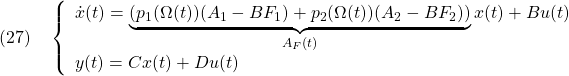
に対して、各端点モデルの閉ループ系において、![]() ノルムは
ノルムは![]() より小であるとすると
より小であるとすると
![Rendered by QuickLaTeX.com \displaystyle{(28)\quad \exists X_1>0:\ \left[\begin{array}{ccc} (A_1-BF_1)^TX_1+X_1(A_1-BF_1) & X_1B & C^T \\ B^TX_1 & -\gamma I & D^T \\ C & D & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4e0b94de7fd261c64c1ad459ff663479_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(29)\quad \exists X_2>0:\ \left[\begin{array}{ccc} (A_2-BF_2)^TX_2+X_2(A_2-BF_2) & X_2B & C^T \\ B^TX_2 & -\gamma I & D^T \\ C & D & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e6b89cd6a762615e4cf1bf7d4196430f_l3.png)
が成り立ちます。いま、共通解![]() が求まっているとしますと
が求まっているとしますと
![Rendered by QuickLaTeX.com \displaystyle{(30)\quad \left[\begin{array}{ccc} (A_1-BF_1)^TX+X(A_1-BF_1) & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D &-I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-54dee83aaf14f44301eff55fc1606abe_l3.png)
![]()
![Rendered by QuickLaTeX.com \displaystyle{(31)\quad \left[\begin{array}{ccc} (A_1-BF_1)^TX+X(A_1-BF_1) & XB & C^T \\ B^TX & -\gamma^2 I & D^T \\ C & D &-I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-740c33f1cb04f1a96dba09b1d8f767da_l3.png)
![]()
に注意して、LPV制御では
![]()
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right]^T \left[\begin{array}{cc} \begin{array}{c} ( p_1(\Omega(t))(A_1-BF_1)+p_2(\Omega(t))(A_2-BF_2) )^TX\\ +X( p_1(\Omega(t))(A_1-BF_1)+p_2(\Omega(t))(A_2-BF_2) ) \end{array} & XB \\ B^TX & 0 \end{array}\right] \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-1fc23d0a361803d365380b86a013ae6e_l3.png)
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{ < \underbrace{(p_1(\Omega(t))+p_2(\Omega(t)))}_1 \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right]^T \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right]^T \left[\begin{array}{cc} - I & 0 \\ 0 & \gamma^2 I \end{array}\right] \left[\begin{array}{cc} C & D \\ 0 & I \end{array}\right] \left[\begin{array}{c} x(t) \\ u(t) \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2d9183af6071904863cbae048501209a_l3.png)
![]()
を得ます。すなわち時変系としての閉ループ系において、消散性の条件
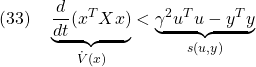
が成り立ち
![]()
が成り立ちます。これは時不変系の場合には![]() ノルムですが、時変系の場合は
ノルムですが、時変系の場合は![]() ゲインとよびます。
ゲインとよびます。
(28)と(29)の共通解![]() が求まれば、(24)は自動的に満足されるので、閉ループ系の時変系としての安定性が保証されることになります。
が求まれば、(24)は自動的に満足されるので、閉ループ系の時変系としての安定性が保証されることになります。
[6] いま、次の2ポート表現かつポリトピック表現された![]() 次系を考えます。
次系を考えます。
![Rendered by QuickLaTeX.com \displaystyle{(35)\quad P: \left\{\begin{array}{l} \dot{x}(t)=\underbrace{(p_1(\Omega(t))A_1+p_2(\Omega(t))A_2)}_{A(\Omega(t))}x(t)+B_1u_1(t)+B_2u_2(t) \\ \underbrace{ \left[\begin{array}{c} y(t)\\ u(t) \end{array}\right] }_{y_1(t)} = \underbrace{ \left[\begin{array}{c} C\\ 0 \end{array}\right] }_{C_1} x(t)+ \underbrace{ \left[\begin{array}{c} 0\\ 0 \end{array}\right] }_{D_{11}}u_1(t)+ \underbrace{ \left[\begin{array}{c} 0\\ I \end{array}\right] }_{D_{12}} u_2(t) \\ y_2(t)=x(t) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-427d73db7b01554c5df63c0e87878e0a_l3.png)
これに対する状態フィードバック
![]()
による閉ループ系
![Rendered by QuickLaTeX.com \displaystyle{(37)\quad P_{CL}: \left\{\begin{array}{l} \dot{x}(t)=(A(\Omega(t))-B_2F(\Omega(t)))x(t)+B_1u_1(t) \\ y_1(t)= \underbrace{ \left[\begin{array}{c} C\\ -F \end{array}\right] }_{C_1-D_{12}F} x(t) \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d78f3f099b3133c3acad786e1bf139f9_l3.png)
において、その![]() ゲインが
ゲインが![]() より小、すなわち
より小、すなわち
![]()
となるように状態フィードバックゲイン![]() を求める問題を考えます。
を求める問題を考えます。
●詳しい説明はあとで行いますが、この問題は次のように、線形行列不等式を制約条件にもつ線形計画問題として定式化されます。
|
Minimize
|
この最小化問題の解 ![]() を用いて、次のように
を用いて、次のように![]() を定めます。
を定めます。
![]()
![]()
[6] LPV制御のイメージを次に示します。LPVモデルとして表すことができる制御対象に対して、端点コントローラを求め、これを変動パラメータでスケジューリングする仕組みを表しています。
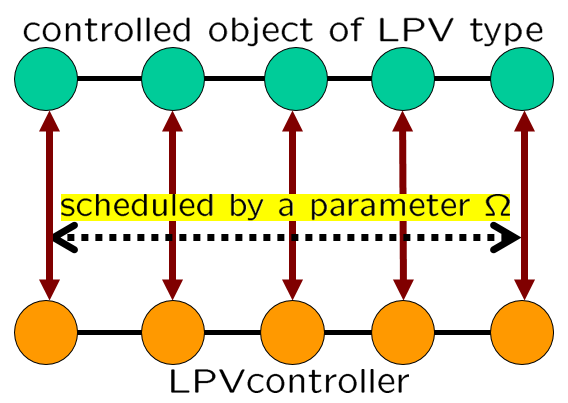 図4 LPV制御のイメージ
図4 LPV制御のイメージ
これに対して従来型のPID制御、LQI制御などのLTI制御は、次のように表すことができます。このようにピンポイントの制御が可能なので、一般には優れた性能を示しますが、パラメータ変動を考慮していないのでロバスト性は劣ると考えられます。
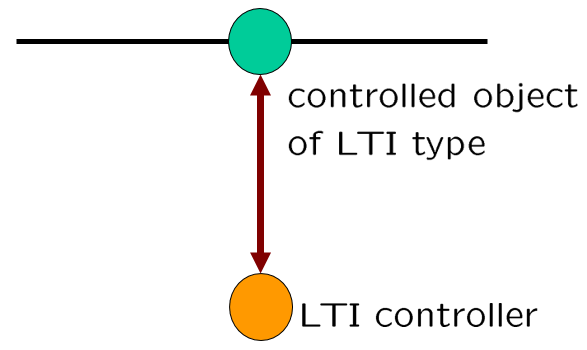 図5 LTI制御のイメージ
図5 LTI制御のイメージ
また、LPV制御の副産物として、スケジューリングを止めるとLTI制御方式が得られ、実装上の観点からメリットがあります。
 図6 LPV制御においてスケジューリングを止めた場合
図6 LPV制御においてスケジューリングを止めた場合
演習B03…Flipped Classroom
![]() 回転体のパラメータ変動を状態FBによるLPV制御で抑制したシミュレーションプログラムを以下に示す。これを実行し効果を確かめよ。
回転体のパラメータ変動を状態FBによるLPV制御で抑制したシミュレーションプログラムを以下に示す。これを実行し効果を確かめよ。
| MATLAB |
|
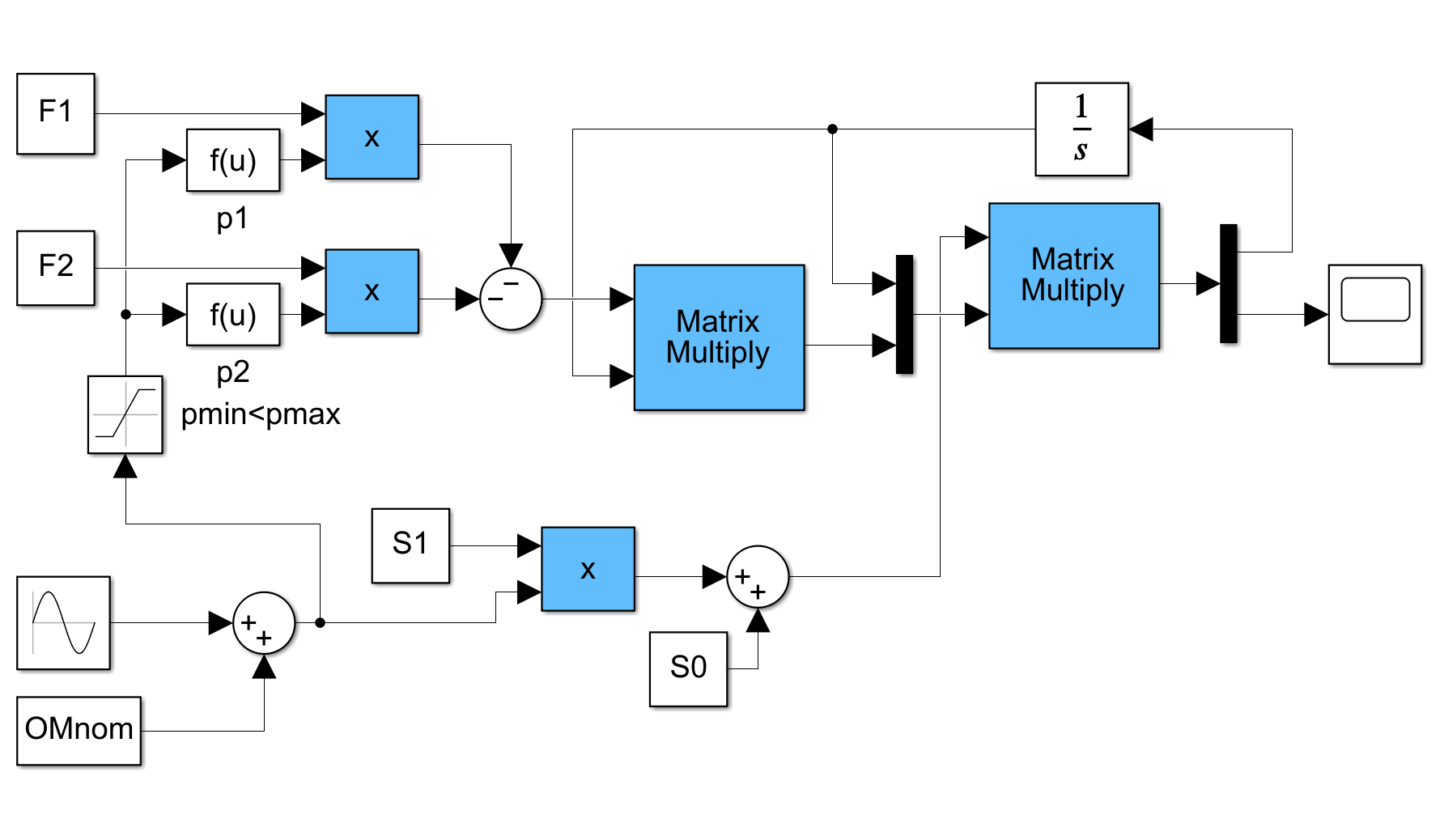
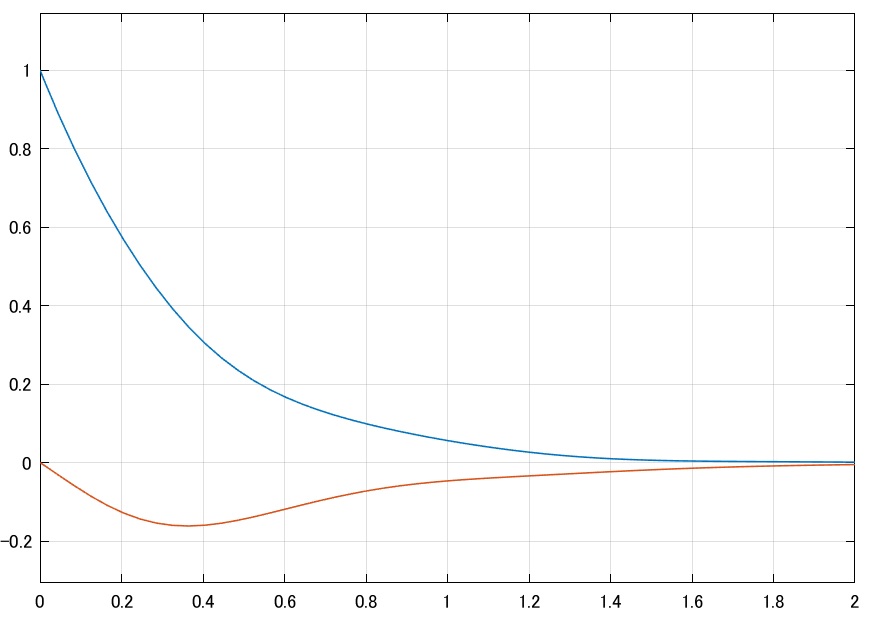 図7 回転体のLPV制御
図7 回転体のLPV制御
![]() 回転体のパラメータ変動を状態FBによる
回転体のパラメータ変動を状態FBによる![]() 制御で抑制したシミュレーションプログラムを以下に示す。これを実行し
制御で抑制したシミュレーションプログラムを以下に示す。これを実行し![]() と比較せよ。
と比較せよ。
| MATLAB |
|

 図8 回転体の
図8 回転体の![]() 制御
制御
![]()
![]() のLPV制御において、次のようにスケジューリングを止めた場合、これを実行し
のLPV制御において、次のようにスケジューリングを止めた場合、これを実行し![]() と
と![]() と比較せよ。
と比較せよ。

図9 回転体のLPV制御においてスケジューリングを止めた場合
![Rendered by QuickLaTeX.com \displaystyle{(40)\quad \left[\begin{array}{ccc} (A_1Y-B_2Z_1)^T+A_1Y-B_2Z_1 & B_1 & (C_1Y-D_{12}Z_1)^T \\ B_1^T & -\gamma I & D_{11}^T \\ C_1Y-D_{12}Z_1 & D_{11} & -\gamma I \end{array}\right]<0 }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c7466d89622c237467830e9e7a4dde4f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(41)\quad \begin{array}{l} 2\alpha Y+A_1Y-B_2Z_1+(A_1Y-B_2Z_1)^T<0 \\ \left[\begin{array}{cc} -rY & A_1Y-B_2Z_1 \\ (A_1Y-B_2Z_1)^T & -rY \end{array}\right]<0 \\ \left[\begin{array}{cc} \sin\theta(A_1Y-B_2Z_1+(A_1Y-B_2Z_1)^T) & \\ -\cos\theta(A_1Y-B_2Z_1-(A_1Y-B_2Z_1)^T) & \end{array}\right. \\ \left.\begin{array}{cc} & \cos\theta(A_1Y-B_2Z_1-(A_1Y-B_2Z_1)^T) \\ & \sin\theta(A_1Y-B_2Z_1+(A_1Y-B_2Z_1)^T) \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-e8f398812655a3aa43af25d448acd033_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(42)\quad \left[\begin{array}{ccc} (A_2Y-B_2Z_2)^T+A_2Y-B_2Z_2 & B_1 & (C_1Y-D_{12}Z_2)^T \\ B_1^T & -\gamma I & D_{11}^T \\ C_1Y-D_{12}Z_2 & D_{11} & -\gamma I \end{array}\right]<0 \\ }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-4cce98efcffcefcc62a9d413a65d4bc4_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(43)\quad \begin{array}{l} 2\alpha Y+A_1Y-B_2Z_2+(A_1Y-B_2Z_2)^T<0 \\ \left[\begin{array}{cc} -rY & A_1Y-B_2Z_2 \\ (A_1Y-B_2Z_2)^T & -rY \end{array}\right]<0 \\ \left[\begin{array}{cc} \sin\theta(A_2Y-B_2Z_2+(A_2Y-B_2Z_2)^T) & \\ -\cos\theta(A_2Y-B_2Z_2-(A_2Y-B_2Z_2)^T) & \end{array}\right. \\ \left.\begin{array}{cc} & \cos\theta(A_2Y-B_2Z_2-(A_2Y-B_2Z_2)^T) \\ & \sin\theta(A_2Y-B_2Z_2+(A_2Y-B_2Z_2)^T) \end{array}\right]<0 \end{array} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-748f7d965c9e2ec369f760ff7e4cfe8d_l3.png)