可安定性と可制御性…Homework
[1] ある平衡状態周りの挙動が線形状態方程式
![]()
で表される制御対象に対して、状態フィードバック
![]()
による閉ループ系
![]()
を安定化できる条件について調べます。
●状態フィーバックにより安定化できることを可安定性と言います。
|
【可安定性の定義とその等価な条件】
定義DS: 状態フィードバックにより安定化可能 条件S1: 条件S2: |
証明はあとで述べますが、可安定性の判定は行列![]() と
と![]() を用いて行われるので、可安定性が成り立つとき、対
を用いて行われるので、可安定性が成り立つとき、対![]() は可安定対という言い方をします。
は可安定対という言い方をします。
●可安定性の十分条件として次の可制御性が知られています。
|
【可制御性の定義とその等価な条件】
定義DC: 任意初期状態を,任意有限時間内に,任意状態に移動可能 条件C1: 条件C2: 条件C3: 条件C4: 条件C5: |
可制御性の判定も行列![]() と
と![]() を用いて行われるので、可制御性が成り立つとき、対
を用いて行われるので、可制御性が成り立つとき、対![]() は可制御対という言い方をします。条件C1の積分式を可制御性グラミアン行列、条件C2の行列を可制御性行列と呼びます。また条件C4を満足する
は可制御対という言い方をします。条件C1の積分式を可制御性グラミアン行列、条件C2の行列を可制御性行列と呼びます。また条件C4を満足する![]() の固有値を
の固有値を![]() は可制御固有値、満足しない固有値を不可制御固有値と呼びます。
は可制御固有値、満足しない固有値を不可制御固有値と呼びます。
[2] 以下では、可制御性の条件について、まず
定義DC![]() 条件C1
条件C1![]() 条件C2
条件C2
を証明します。特に、命題![]() を証明するのに、
を証明するのに、
![]()
を用いて矛盾が出ることを示していることに注意してください。
●<定義C0![]() 条件C1> ある時刻
条件C1> ある時刻![]() で可制御性グラミアン行列が正定でないとします。このとき,
で可制御性グラミアン行列が正定でないとします。このとき,![]() 次元ベクトル
次元ベクトル![]() が存在して
が存在して
![]()
が成り立ちます。これより
![]()
を得ます。いま,初期状態![]() を
を![]() に移すことを考えると
に移すことを考えると
![]()
と書けます。ここで,変数変換により
![]()
となることに注意して,(6)の左から![]() をかけると
をかけると
![]()
を得ます。ここで,![]() のとき
のとき![]() となり,矛盾が生じます。よって条件C1が成り立ちます。
となり,矛盾が生じます。よって条件C1が成り立ちます。
●<定義DC![]() 条件C1> (1)に対して,
条件C1> (1)に対して,![]() において,入力を
において,入力を
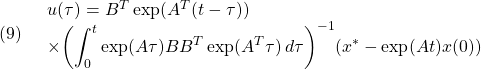
と定めれば,初期状態![]() が移される先の状態
が移される先の状態![]() は、(9)を(1)の解
は、(9)を(1)の解
![]()
に代入して,次式に注意すれば,![]() と計算されます。
と計算されます。
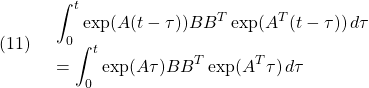
以上で,![]() は任意であるので、定義DCを得ていることになります。
は任意であるので、定義DCを得ていることになります。
●<条件C1![]() 条件C2> 可制御性行列は行フルランク(行数に等しい階数)とはならないとすします。このとき,ある
条件C2> 可制御性行列は行フルランク(行数に等しい階数)とはならないとすします。このとき,ある![]() 次元ベクトル
次元ベクトル![]() が存在して
が存在して
![]()
が成り立ちます。ケーリー・ハミルトンの定理を用いて
![]()
したがって
![]()
が成り立ちます。これより,ある時刻![]() に対して
に対して
![]()
を得ますが,これは条件C1と矛盾です。よって条件C2が成り立ちます。
●<条件C1![]() 条件C2> ある時刻
条件C2> ある時刻![]() で可制御性グラミアン行列が正定でないとします。このとき,
で可制御性グラミアン行列が正定でないとします。このとき,![]() に対して(14)が成り立ちます。この第
に対して(14)が成り立ちます。この第![]() 回微分を求めて,
回微分を求めて,![]() とおくと
とおくと
![]()
これより,(12)を得ますが,これは条件C2と矛盾しています。よって条件C1が成り立ちます。
●あとで<条件C3![]() 条件C4
条件C4![]() 条件C5
条件C5![]() 条件C2>を可制御標準形を求めて、<条件C2
条件C2>を可制御標準形を求めて、<条件C2![]() 条件C3>を可制御正準形を求めて示します。
条件C3>を可制御正準形を求めて示します。
●上の可制御性と可安定性のさまざまな条件のうち、理論展開では条件C5と条件S2が、数値計算では条件C4と条件S1がよく用いられます。特に、条件C5と条件S2による判定法は、PBH(Popov-Blevitch-Hautus)法と呼ばれています。
演習 A32-1…Flipped Classroom
次のコードは、PBH法の骨格となる部分を示している。これを実行して得られる変数contとstabの解釈を行え。
| MATLAB |
|
演習 A32-2…Flipped Classroom
倒立振子CIP、CIP2、AIP、PIP、DIPの可制御性を調べよ。
| MATLAB |
|
Note A32 可制御性は状態フィードバックにより不変
![]() が可制御対ならば
が可制御対ならば![]() も可制御対であることは次のように証明されます。
も可制御対であることは次のように証明されます。
条件C5より,任意の![]() に対して
に対して
![]()
成り立つので,これを仮定して
![]()
を示します。実際,![]() より
より
![]()
を得ますが,このような![]() は,仮定(1)より,
は,仮定(1)より,![]() でなければなりません。
でなければなりません。