
上図のようなドローンについて、次の文献をフォローしていきます。
Randal Beard: Quadrotor Dynamics and Control, Rev0.1, Brigham Young University, 2008
以下では、![]() 、
、![]() をそれぞれ
をそれぞれ![]() 、
、![]() と略記します。
と略記します。
準備

●上図のように、ベクトル![]() を、ベクトル
を、ベクトル![]() のまわりに
のまわりに![]() だけ回転して得られるベクトル
だけ回転して得られるベクトル![]() の表現式を求めます。
の表現式を求めます。
![]()
ただし
![]()
![]()
![]()
から、次式を得ます。
![]()
ここで
![]()
![]()
![]()
とおくと
![]()
![Rendered by QuickLaTeX.com \displaystyle{\hat{n}\times{\bf p}= {\rm det} \left[\begin{array}{ccc} \hat{i}^0 & \hat{j}^0 & \hat{k}^0\\ \hat{n}_x & \hat{n}_y & \hat{n}_z\\ p_x^0 & p_y^0 & p_z^0 \end{array}\right]}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-987b3b87c684eb8f160259eccaed8b8c_l3.png)
![]()
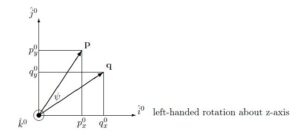
●![]() の場合(left-handed rotation about z-axis)
の場合(left-handed rotation about z-axis)
![]()
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} q_x^0 \\ q_y^0 \\ q_z^0 \end{array}\right] }_{{\bf q}} =(1-C_\psi) p_z^0 \underbrace{ \left[\begin{array}{c} 0 \\ 0 \\ 1 \end{array}\right] }_{\hat{i}} \hat{n}+C_\psi \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] -S_\psi \left[\begin{array}{c} -p_y^0 \\ p_x^0 \\ 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-12d5ca14cbcc4c55826c7d6d8f899987_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \underbrace{ \left[\begin{array}{ccc} C_\psi & S_\psi & 0 \\ -S_\psi & C_\psi & 0 \\ 0 & 0 & 1 \end{array}\right] }_{R(\phi)} \underbrace{ \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] }_{{\bf p}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-034528a2aacb8e95ad6d97e767cee015_l3.png)
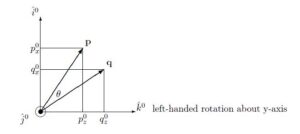
●![]() の場合(left-handed rotation about y-axis)
の場合(left-handed rotation about y-axis)
![]()
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} q_x^0 \\ q_y^0 \\ q_z^0 \end{array}\right] }_{{\bf q}} =(1-C_\theta) p_y^0 \underbrace{ \left[\begin{array}{c} 0 \\ 1 \\ 0 \end{array}\right] }_{\hat{j}} \hat{n}+C_\theta \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] -S_\theta \left[\begin{array}{c} p_z^0 \\ 0\\ -p_x^0 \\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a989718664a4f406a703678aa7bce25c_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ =\underbrace{ \left[\begin{array}{ccc} C_\theta & 0 & -S_\theta \\ 0 & 1 & 0 \\ S_\theta & 0 & C_\theta \end{array}\right] }_{R(\theta)} \underbrace{ \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] }_{{\bf p}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-77d80bf487c6766d1c677f8791183be6_l3.png)
●![]() の場合(left-handed rotation about x-axis)
の場合(left-handed rotation about x-axis)
![]()
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} q_x^0 \\ q_y^0 \\ q_z^0 \end{array}\right] }_{{\bf q}} =(1-C_\phi) p_x^0 \underbrace{ \left[\begin{array}{c} 1 \\ 0 \\ 0 \end{array}\right] }_{\hat{k}} \hat{n}+C_\phi \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] -S_\phi \left[\begin{array}{c} 0\\ -p_z^0 \\ p_y^0 \\ \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-59bae1ad5756ab21b2c3dfbfa893e055_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ =\underbrace{ \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & C_\phi & S_\phi \\ 0 & -S_\phi & C_\phi \end{array}\right] }_{R(\psi)} \underbrace{ \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] }_{{\bf p}} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d1ab1c6a193d60691e385bcb0e30cfb3_l3.png)

以上のようなベクトルの回転は、相対的に座標軸を回転させても、把握できます。
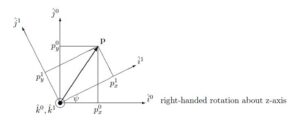
●right-handed rotation about z-axis
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} p_x^1 \\ p_y^1 \\ p_z^1 \end{array}\right] }_{{\bf p}^1} = \underbrace{ \left[\begin{array}{ccc} \hat{i}^1\cdot\hat{i}^0&\hat{i}^1\cdot\hat{j}^0&\hat{i}^1\cdot\hat{k}^0\\ \hat{j}^1\cdot\hat{i}^0&\hat{j}^1\cdot\hat{j}^0&\hat{j}^1\cdot\hat{k}^0\\ \hat{k}^1\cdot\hat{i}^0&\hat{k}^1\cdot\hat{j}^0&\hat{k}^1\cdot\hat{k}^0 \end{array}\right] }_{R_0^1(\psi)} \underbrace{ \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] }_{{\bf p}^0} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9e097cfdaee9cbb694b4d1748693d3c6_l3.png)
![]()
![Rendered by QuickLaTeX.com \displaystyle{ R_0^1(\psi)= \left[\begin{array}{ccc} C_\psi & S_\psi & 0 \\ -S_\psi & C_\psi & 0 \\ 0 & 0 & 1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-58ac6cd544f764f340163f5d9e7d61aa_l3.png)
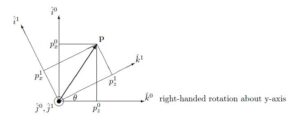
●right-handed rotation about y-axis
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} p_x^1 \\ p_y^1 \\ p_z^1 \end{array}\right] }_{{\bf p}^1} = \underbrace{ \left[\begin{array}{ccc} \hat{i}^1\cdot\hat{i}^0&\hat{i}^1\cdot\hat{j}^0&\hat{i}^1\cdot\hat{k}^0\\ \hat{j}^1\cdot\hat{i}^0&\hat{j}^1\cdot\hat{j}^0&\hat{j}^1\cdot\hat{k}^0\\ \hat{k}^1\cdot\hat{i}^0&\hat{k}^1\cdot\hat{j}^0&\hat{k}^1\cdot\hat{k}^0 \end{array}\right] }_{R_0^1(\theta)} \underbrace{ \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] }_{{\bf p}^0} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-aceb055a39624b49b00c52ba93b2fafc_l3.png)
![]()
![Rendered by QuickLaTeX.com \displaystyle{ R_0^1(\theta)= \left[\begin{array}{ccc} C_\theta & 0 & -S_\theta \\ 0 & 1 & 0 \\ S_\theta & 0 & C_\theta \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bc434799df6aa0435586745ed76ca371_l3.png)
●right-handed rotation about x-axis
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} p_x^1 \\ p_y^1 \\ p_z^1 \end{array}\right] }_{{\bf p}^1} = \underbrace{ \left[\begin{array}{ccc} \hat{i}^1\cdot\hat{i}^0&\hat{i}^1\cdot\hat{j}^0&\hat{i}^1\cdot\hat{k}^0\\ \hat{j}^1\cdot\hat{i}^0&\hat{j}^1\cdot\hat{j}^0&\hat{j}^1\cdot\hat{k}^0\\ \hat{k}^1\cdot\hat{i}^0&\hat{k}^1\cdot\hat{j}^0&\hat{k}^1\cdot\hat{k}^0 \end{array}\right] }_{R_0^1(\phi)} \underbrace{ \left[\begin{array}{c} p_x^0 \\ p_y^0 \\ p_z^0 \end{array}\right] }_{{\bf p}^0} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-be939844208f01e80bd96a4578eb7d9c_l3.png)
![]()
![Rendered by QuickLaTeX.com \displaystyle{ R_0^1(\phi)= \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & C_\phi & S_\phi \\ 0 & -S_\phi & C_\phi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-9e26ef5f7bc02c2f2f19b14327fc67f6_l3.png)
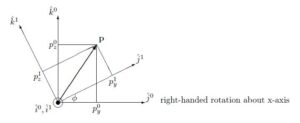
座標系
●ドローンの運動の記述にあたっては、次のような地上座標系![]() と機体固定座標系
と機体固定座標系![]() を用います。
を用います。

![]() における機体の位置は次の変数で表します。
における機体の位置は次の変数で表します。
![]() : the inertial (north) position of the aircraft along
: the inertial (north) position of the aircraft along ![]() in
in ![]()
![]() : the inertial (east) position of the aircraft along
: the inertial (east) position of the aircraft along ![]() in
in ![]()
![]() : the altitude of the aircraft measured along
: the altitude of the aircraft measured along ![]() in
in ![]()
また、![]() は、
は、![]() から、次のオイラー角
から、次のオイラー角
![]() : the roll angle defined with respect to
: the roll angle defined with respect to ![]()
![]() : the pitch angle defined with respect to
: the pitch angle defined with respect to ![]()
![]() : the yaw angle defined with respect to
: the yaw angle defined with respect to ![]()
を用いて、次のように逐次回転して得られます。
![]()
ここで、![]() は原点を機体重心にもつ回転前の座標系(
は原点を機体重心にもつ回転前の座標系(![]() に平行)を表しています。
に平行)を表しています。
●![]() における任意ベクトル
における任意ベクトル![]() (後出の位置ベクトル、速度ベクトルなど)は、
(後出の位置ベクトル、速度ベクトルなど)は、![]() から、次のような変換を行って得られます。
から、次のような変換を行って得られます。
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{= \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & C_\phi & S_\phi \\ 0 & -S_\phi & C_\phi \end{array}\right] \left[\begin{array}{ccc} C_\theta & 0 & -S_\theta \\ 0 & 1 & 0 \\ S_\theta & 0 & C_\theta \end{array}\right] \left[\begin{array}{ccc} C_\psi & S_\psi & 0 \\ -S_\psi & C_\psi & 0 \\ 0 & 0 & 1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-cbcf941c508f91c6e056f42732084bf5_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \left[\begin{array}{ccc} C_\theta C_\psi & C_\theta S_\psi & -S_\theta \\ S_\phi S_\theta C_\psi - C_\phi S_\psi & S_\phi S_\theta S_\psi + C_\phi C_\psi & S_\phi C_\theta \\ C_\phi S_\theta C_\psi + C_\phi S_\psi & C_\phi S_\theta S_\psi - S_\phi C_\psi & C_\phi C_\theta \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-bb9eeb9b54c7ae5be019eb255e6bdbd8_l3.png)
●![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{ R_v^{v1}(\psi)= \left[\begin{array}{ccc} C_\psi & S_\psi & 0 \\ -S_\psi & C_\psi & 0 \\ 0 & 0 & 1 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-62a0d9a3674b84f4cc7fd9463923b711_l3.png)

●![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{ R_{v1}^{v2}(\theta)= \left[\begin{array}{ccc} C_\theta & 0 & -S_\theta \\ 0 & 1 & 0 \\ S_\theta & 0 & C_\theta \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-882fd5b2077da6bcc03598d35349e31f_l3.png)
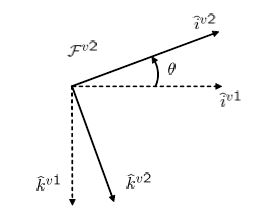
●![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{ R_{v2}^b(\phi)= \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & C_\phi & S_\phi \\ 0 & -S_\phi & C_\phi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-65b7f87e8d6ceac41cc3eed6be19136b_l3.png)

●![]() における任意ベクトル
における任意ベクトル![]() (後出の位置ベクトル、速度ベクトルなど)の時間変化がどのように表されるかを調べます。
(後出の位置ベクトル、速度ベクトルなど)の時間変化がどのように表されるかを調べます。
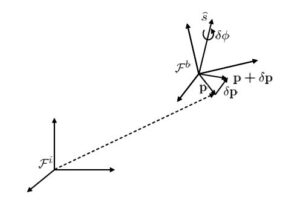
これは、次式で表されます。
![]()
実際
![]()
![]()
![]()
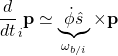
運動方程式
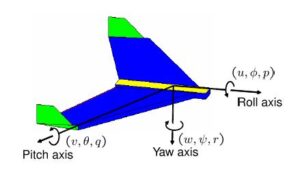
![]() における運動は次の変数を用いて表されます。
における運動は次の変数を用いて表されます。
![]() : the body frame velocity measured along
: the body frame velocity measured along ![]() in
in ![]()
![]() : the body frame velocity measured along
: the body frame velocity measured along ![]() in
in ![]()
![]() : the body frame velocity measured along
: the body frame velocity measured along ![]() in
in ![]()
![]() : the roll rate measured along
: the roll rate measured along ![]() in
in ![]()
![]() : the pitch rate measured along
: the pitch rate measured along ![]() in
in ![]()
![]() : the yaw rate measured along
: the yaw rate measured along ![]() in
in ![]()
これらが![]() からどう表されるか、すなわち次の変数の微分とどう関係するか(キネマティックス)を調べます。
からどう表されるか、すなわち次の変数の微分とどう関係するか(キネマティックス)を調べます。
![]() : the inertial (north) position of the quadrotor along
: the inertial (north) position of the quadrotor along ![]() in
in ![]()
![]() : the inertial (east) position of the quadrotor along
: the inertial (east) position of the quadrotor along ![]() in
in ![]()
![]() : the altitude of the aircraft measured along
: the altitude of the aircraft measured along ![]() in
in ![]()
![]() : the roll angle defined with respect to
: the roll angle defined with respect to ![]()
![]() : the pitch angle defined with respect to
: the pitch angle defined with respect to ![]()
![]() : the yaw angle defined with respect to
: the yaw angle defined with respect to ![]()
●![]() と
と![]() における速度ベクトルについては
における速度ベクトルについては
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} u \\ v \\ w \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} C_\theta C_\psi & C_\theta S_\psi & -S_\theta \\ S_\phi S_\theta C_\psi - C_\phi S_\psi & S_\phi S_\theta S_\psi + C_\phi C_\psi & S_\phi C_\theta \\ C_\phi S_\theta C_\psi + C_\phi S_\psi & C_\phi S_\theta S_\psi - S_\phi C_\psi & C_\phi C_\theta \end{array}\right] }_{R_v^b} \left[\begin{array}{c} \dot{p}_n \\ \dot{p}_e \\ -\dot{h} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-de39a8b9bd05d0eb4e506e36a8e0fa0a_l3.png)
の関係が成り立ちます。したがって、
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{p}_n \\ \dot{p}_e \\ -\dot{h} \end{array}\right] = \underbrace{ \left[\begin{array}{ccc} C_\theta C_\psi &S_\phi S_\theta C_\psi - C_\phi S_\psi &C_\phi S_\theta C_\psi + C_\phi S_\psi \\ C_\theta S_\psi &S_\phi S_\theta S_\psi + C_\phi C_\psi &C_\phi S_\theta S_\psi - S_\phi C_\psi \\ -S_\theta &S_\phi C_\theta &C_\phi C_\theta \end{array}\right] }_{R_b^v=(R_v^b)^T} \left[\begin{array}{c} u \\ v \\ w \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d363a281bdd4e8b2b988be4d3069aa11_l3.png)
●![]() と
と![]() における角速度ベクトルについては
における角速度ベクトルについては
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} p \\ q \\ r \end{array}\right] = \underbrace{R_{v2}^b(\dot{\phi})}_{I} \left[\begin{array}{c} \dot{\phi} \\ 0 \\ 0 \end{array}\right] + R_{v2}^b(\phi)\underbrace{R_{v1}^{v2}(\dot{\theta})}_{I} \left[\begin{array}{c} 0 \\ \dot{\theta} \\ 0 \end{array}\right] + R_{v2}^b(\phi)R_{v1}^{v2}(\theta)\underbrace{R_{v}^{v1}(\dot{\psi})}_{I} \left[\begin{array}{c} 0 \\ 0 \\ \dot{\psi} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a04c24d997a7e6874afdd3b415001501_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \left[\begin{array}{c} \dot{\phi} \\ 0 \\ 0 \end{array}\right] + \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & C_\phi & S_\phi \\ 0 & -S_\phi & C_\phi \end{array}\right] \left[\begin{array}{c} 0 \\ \dot{\theta} \\ 0 \end{array}\right] + \left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & C_\phi & S_\phi \\ 0 & -S_\phi & C_\phi \end{array}\right] \left[\begin{array}{ccc} C_\theta & 0 & -S_\theta \\ 0 & 1 & 0 \\ S_\theta & 0 & C_\theta \end{array}\right] \left[\begin{array}{c} 0 \\ 0 \\ \dot{\psi} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-97c20a9db7f00180754feff31ee807c8_l3.png)
の関係が成り立ちます。したがって、
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} p \\ q \\ r \end{array}\right]= \left[\begin{array}{ccc} 1 & 0 & -S_\theta \\ 0 & C_\phi & S_\phi C_\theta \\ 0 & -S_\phi & C_\phi C_\theta \end{array}\right] \left[\begin{array}{c} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-061d5edae9ebd68d687e9549b5a5a40b_l3.png)
すなわち、次の関係式を得ます。
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{array}\right] = \left[\begin{array}{ccc} 1 & S_\phi T_\theta & C_\phi T_\theta \\ 0 & C_\phi & -S_\phi \\ 0 & \frac{S_\phi}{C_\theta} & \frac{C_\phi}{C_\theta} \end{array}\right] \left[\begin{array}{c} p \\ q \\ r \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-10b9bc4111bd976ca0649bb42dfacd55_l3.png)
●次に並進運動(ダイナミックス)は次式で表されます。
![]()
![Rendered by QuickLaTeX.com \displaystyle{ \frac{d}{dt}_b \left[\begin{array}{c} u\\ v\\ w \end{array}\right] + \left[\begin{array}{c} p\\ q\\ r \end{array}\right] \times \left[\begin{array}{c} u\\ v\\ w \end{array}\right] =\frac{1}{m} \left[\begin{array}{c} f_x\\ f_y\\ f_z \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f49c0967c1c1583628163273d1cc944f_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{u}\\ \dot{v}\\ \dot{w} \end{array}\right] =- \underbrace{ \left[\begin{array}{ccc} 0 & -r & q\\ r & 0 &-p\\ -q & p & 0 \end{array}\right] \left[\begin{array}{c} u\\ v\\ w \end{array}\right] }_{\left[\begin{array}{c} qw-rv \\ ru-pw\\ pv-qu \end{array}\right]} +\frac{1}{m} \left[\begin{array}{c} f_x\\ f_y\\ f_z \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-6e5e479c4745afec971e8a449e1d7113_l3.png)
●また回転運動(ダイナミックス)は次式で表されます。
![]()
![]()
![Rendered by QuickLaTeX.com \displaystyle{J= \left[\begin{array}{ccc} \int(y^2+z^2)dm & -\int xydm & -\int xzdm \\ -\int yxdm & \int(x^2+z^2)dm & -\int yzdm \\ -\int zxdm & -\int zydm & \int(x^2+y^2)dm \end{array}\right] =\left[\begin{array}{ccc} J_x & 0 & 0 \\ 0 & J_y & 0 \\ 0 & 0 & J_z \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-16d24597f8387fec8c1eb565263ad684_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \frac{d}{dt}_bJ \left[\begin{array}{c} p\\ q\\ r \end{array}\right] + \left[\begin{array}{c} p\\ q\\ r \end{array}\right] \times J \left[\begin{array}{c} p\\ q\\ r \end{array}\right] = \left[\begin{array}{c} \tau_\phi\\ \tau_\theta\\ \tau_\psi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3a28be1d9f68276f11ece9ae89a59304_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} J_x\dot{p}\\ J_y\dot{q}\\ J_z\dot{r} \end{array}\right] + \underbrace{ \left[\begin{array}{ccc} 0 & -r & q\\ r & 0 &-p\\ -q & p & 0 \end{array}\right] \left[\begin{array}{c} J_xp\\ J_yq\\ J_zr \end{array}\right] }_{\left[\begin{array}{c} (J_z-J_y)qr \\ (J_x-J_z)pr\\ (J_y-J_x)pq \end{array}\right]} = \left[\begin{array}{c} \tau_\phi\\ \tau_\theta\\ \tau_\psi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-11a81fab1a1c7f81823c26120d6d2b21_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{p}\\ \dot{q}\\ \dot{r} \end{array}\right] =- \underbrace{ \left[\begin{array}{ccc} 0 & 0 & \frac{J_z-J_y}{J_x}q\\ \frac{J_x-J_z}{J_y} r & 0 & 0\\ 0 & \frac{J_y-J_x}{J_z}p & 0 \end{array}\right] \left[\begin{array}{c} p\\ q\\ r \end{array}\right] }_{ \left[\begin{array}{c} \frac{J_z-J_y}{J_x}qr \\ \frac{J_x-J_z}{J_y}pr \\ \frac{J_y-J_x}{J_z}pq \end{array}\right] } + \left[\begin{array}{c} \frac{1}{J_x}\tau_\phi\\ \frac{1}{J_y}\tau_\theta\\ \frac{1}{J_z}\tau_\psi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-3eb533fddc2cdc3acb2986b508ba0373_l3.png)
外力
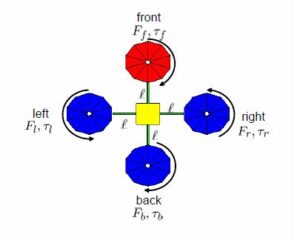
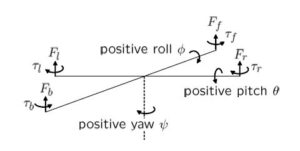
4つのモータへの回転指令を![]() とします。このとき、各モータによる推力とトルクは次式で表されます。
とします。このとき、各モータによる推力とトルクは次式で表されます。
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
また、4つのモータの合推力と各軸回りのトルクは次式で表されます。
![]()
![]()
![]()
![]()
すなわち
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} F\\ \tau_\phi\\ \tau_\theta\\ \tau_\psi \end{array}\right] = \underbrace{ \left[\begin{array}{cccc} k_1 & k_1 & k_1 & k_1 \\ 0 & -\ell k_1 & 0 & \ell k_1 \\ \ell k_1 & 0 & -\ell k_1 & 0 \\ -k_2 & k_2 & -k_2 & k_2 \end{array}\right] }_{{\cal M}} \left[\begin{array}{c} \delta_f\\ \delta_r\\ \delta_b\\ \delta_\ell \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-2189a79e26837861510a7bb0f99f2a55_l3.png)
また、並進運動方程式の外力項は次式となります。
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} f_x\\ f_y\\ f_z \end{array}\right] = R_v^b \left[\begin{array}{c} 0\\ 0\\ mg \end{array}\right] + \left[\begin{array}{c} 0\\ 0\\ -F \end{array}\right] =mg \left[\begin{array}{ccc} -S_\theta \\ S_\phi C_\theta \\ C_\phi C_\theta \end{array}\right] + \left[\begin{array}{c} 0\\ 0\\ -F \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-46b8705ff1f44fac694d366bf9bfc130_l3.png)
このときドローンの運動方程式に基づく状態方程式は次式となります。
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{p}_n \\ \dot{p}_e \\ -\dot{h} \\ \hline \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \\ \hline \dot{u}\\ \dot{v}\\ \dot{w} \\ \hline \dot{p}\\ \dot{q}\\ \dot{r} \end{array}\right] = \left[\begin{array}{ccc|ccc} 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array}\right.}](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c057cf51cb84ad35be913e5f72b6b095_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left.\begin{array}{ccc|ccc} C_\theta C_\psi &S_\phi S_\theta C_\psi - C_\phi S_\psi &C_\phi S_\theta C_\psi + C_\phi S_\psi & 0 & 0 & 0\\ C_\theta S_\psi &S_\phi S_\theta S_\psi + C_\phi C_\psi &C_\phi S_\theta S_\psi - S_\phi C_\psi & 0 & 0 & 0\\ -S_\theta &S_\phi C_\theta &C_\phi C_\theta & 0 & 0 & 0\\ \hline 0 & 0 & 0 & 1 & S_\phi T_\theta & C_\phi T_\theta \\ 0 & 0 & 0 & 0 & C_\phi & -S_\phi \\ 0 & 0 & 0 & 0 & \frac{S_\phi}{C_\theta} & \frac{C_\phi}{C_\theta}\\ \hline 0 & r &- q & 0 & 0 & 0\\ r- & 0 &p & 0 & 0 & 0\\ q & -p & 0 & 0 & 0 & 0\\ \hline 0 & 0 & 0 & 0 & 0 & -\frac{J_z-J_y}{J_x}q\\ 0 & 0 & 0 & -\frac{J_x-J_z}{J_y} r & 0 & 0\\ 0 & 0 & 0 & 0 & -\frac{J_y-J_x}{J_z}p & 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-ac9a7943b0d77c3ef3dcaeb6016011e8_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \times \left[\begin{array}{c} p_n \\ p_e \\ -h \\ \hline \phi \\ \theta \\ \psi \\ \hline u\\ v\\ w \\ \hline p\\ q\\ r \end{array}\right] + \left[\begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \hline 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ \frac{1}{m} & 0 & 0 & 0 \\ \hline 0 & \frac{1}{J_x} & 0 & 0 \\ 0 & 0 & \frac{1}{J_y} & 0 \\ 0 & 0 & 0 & \frac{1}{J_z} \\ \end{array}\right] \left[\begin{array}{cccc} k_1 & k_1 & k_1 & k_1 \\ 0 & -\ell k_1 & 0 & \ell k_1 \\ \ell k_1 & 0 & -\ell k_1 & 0 \\ -k_2 & k_2 & -k_2 & k_2 \end{array}\right]^{-1} \left[\begin{array}{c} \delta_f\\ \delta_r\\ \delta_b\\ \delta_\ell \end{array}\right] + \left[\begin{array}{c} 0 \\ 0 \\ 0 \\ \hline 0 \\ 0 \\ 0 \\ \hline -gS_\theta \\ gS_\phi C_\theta \\ gC_\phi C_\theta \\ \hline 0 \\ 0 \\ 0 \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dfbd76199ec24769a2fab7d91200e5dc_l3.png)
これを見ると、![]() 行列に状態変数が絡んでおり、複雑なダイナミクスをもっていることが分かります。
行列に状態変数が絡んでおり、複雑なダイナミクスをもっていることが分かります。
運動方程式の簡単化
次の仮定のもとで、運動方程式の簡単化を行ないます。
仮定1: ![]() 、
、![]() 、
、![]() は小さく無視できる
は小さく無視できる
仮定2: ![]() 、
、![]() は小さく無視できる
は小さく無視できる
まず、仮定1のもとで、次の近似が可能です。
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{p}\\ \dot{q}\\ \dot{r} \end{array}\right] =- \left[\begin{array}{c} \frac{J_z-J_y}{J_x}qr \\ \frac{J_x-J_z}{J_y}pr \\ \frac{J_y-J_x}{J_z}pq \end{array}\right] + \left[\begin{array}{c} \frac{1}{J_x}\tau_\phi\\ \frac{1}{J_y}\tau_\theta\\ \frac{1}{J_z}\tau_\psi \end{array}\right] \simeq \left[\begin{array}{c} \frac{1}{J_x}\tau_\phi\\ \frac{1}{J_y}\tau_\theta\\ \frac{1}{J_z}\tau_\psi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-f6a1e8b9f0e32ed0de052e40acd5d9e8_l3.png)
このとき、仮定2をおけば次の近似が可能です。
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \end{array}\right] = \left[\begin{array}{ccc} 1 & S_\phi T_\theta & C_\phi T_\theta \\ 0 & C_\phi & -S_\phi \\ 0 & \frac{S_\phi}{C_\theta} & \frac{C_\phi}{C_\theta} \end{array}\right] \left[\begin{array}{c} p \\ q \\ r \end{array}\right] \simeq \left[\begin{array}{c} p \\ q \\ r \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7588cb998bf45f4453bd790068da25cd_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \ddot{\phi} \\ \ddot{\theta} \\ \ddot{\psi} \end{array}\right] \simeq \left[\begin{array}{c} \dot{p}\\ \dot{q}\\ \dot{r} \end{array}\right] \simeq \left[\begin{array}{c} \frac{1}{J_x}\tau_\phi\\ \frac{1}{J_y}\tau_\theta\\ \frac{1}{J_z}\tau_\psi \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c00140559d247b19ba35379d4f2fc7d2_l3.png)
これは、機体の傾きを独立して制御できることを示しています。
さらに次のような近似が可能です。
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \dot{p}_x \\ \dot{p}_y \\ \dot{p}_z \end{array}\right] = {R}_{v1}^b \left[\begin{array}{c} u \\ v \\ w \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-07b55ee0eb520a01571a66c82273a1b1_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \ddot{p}_x \\ \ddot{p}_y \\ \ddot{p}_z \end{array}\right] = \underbrace{\dot{R}_{v1}^b}_{\simeq0} \left[\begin{array}{c} {u}\\ {v}\\ {w} \end{array}\right] + {R}_{v1}^b \left[\begin{array}{c} \dot{u}\\ \dot{v}\\ \dot{w} \end{array}\right] \simeq {R}_{v1}^b \left[\begin{array}{c} \dot{u}\\ \dot{v}\\ \dot{w} \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b6a4f91764dbe1ccc821cb66b6c128a3_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ \left[\begin{array}{c} \ddot{p}_x \\ \ddot{p}_y \\ \ddot{p}_z \end{array}\right] \simeq \left[\begin{array}{ccc} C_\theta & S_\phi S_\theta & C_\phi S_\theta \\ 0 & C_\phi & -S_\phi \\ -S_\theta &S_\phi C_\theta &C_\phi C_\theta \end{array}\right] (g \left[\begin{array}{c} -S_\theta \\ S_\phi C_\theta \\ C_\phi C_\theta \end{array}\right] +\frac{1}{m} \left[\begin{array}{c} 0\\ 0\\ -F \end{array}\right]) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-806c2333ecc5b9e2f2176af3d06ac631_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{ = \left[\begin{array}{c} 0 \\ 0 \\ g \end{array}\right] -\frac{1}{m}F \left[\begin{array}{ccc} C_\phi S_\theta \\ -S_\phi \\ C_\phi C_\theta \end{array}\right] \simeq \left[\begin{array}{c} 0 \\ 0 \\ g-\frac{1}{m}F \end{array}\right] }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-a012c160125fa47849e9b54d7a6be80e_l3.png)
結局、ドローンの運動方程式は、次式のように簡単化されます。
![]()
![]()
![]()
![]()
いま,重力補償のために![]() から決まる
から決まる![]() を各操作入力に前もって加えておくことにすると、次式が成り立ちます。
を各操作入力に前もって加えておくことにすると、次式が成り立ちます。
![]()
![]()
![]()
![]()
![]()
![]()
このときドローンの線形状態方程式は次式となります。
![Rendered by QuickLaTeX.com \displaystyle{ \underbrace{ \left[\begin{array}{c} \dot{p}_z \\ \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \\\hline \ddot{z} \\ \ddot{\phi} \\ \ddot{\theta} \\ \ddot{\psi} \\ \end{array}\right] }_{\dot{x}} = \underbrace{ \left[\begin{array}{cccc|cccc} 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\\hline 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ \end{array}\right] }_{A} % \left[\begin{array}{c|c} % 0_{4\times4} & I_4 \\\hline % 0_{4\times4} & 0_{4\times4} % \end{array}\right] \underbrace{ \left[\begin{array}{c} {p_z} \\ {\phi} \\ {\theta} \\ {\psi} \\\hline \dot{z} \\ \dot{\phi} \\ \dot{\theta} \\ \dot{\psi} \\ \end{array}\right] }_{x} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-c2d526861def4102dd037941437ebbd2_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{+ \underbrace{ \left[\begin{array}{cccc} 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\\hline -\frac{k_f}{m} & -\frac{k_f}{m} & -\frac{k_f}{m} & -\frac{k_f}{m} \\ 0 & -\frac{\ell k_f}{J_x} & 0 & \frac{\ell k_f}{J_x} \\ \frac{\ell k_f}{J_y} & 0 & -\frac{\ell k_f}{J_y} & 0 \\ -\frac{k_\tau}{J_z} & \frac{k_\tau}{J_z} & -\frac{k_\tau}{J_z} & \frac{k_\tau}{J_z} \\ \end{array}\right] }_{B} % \left[\begin{array}{c} % 0_{4\times4} \\ % B_2 \\ % \end{array}\right] \underbrace{ \left[\begin{array}{c} \delta_f-\delta^* \\ \delta_r-\delta^* \\ \delta_b-\delta^* \\ \delta_\ell-\delta^* \\ \end{array}\right] }_{u} }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b01d89585d73ec5fff8e27c5c03036e2_l3.png)