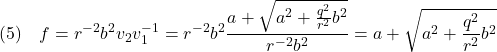Home Work 7.1
[P] 平衡状態から外れたとき、これを戻すためには、いろいろな「軌道(時系列)」があると思うけど、何かリーズナブルな決め方はあるのかな?
[C] 状態変数の振る舞い(2乗面積)と操作変数の振る舞い(2乗面積)のトレードオフを計ることがよく行われているよ。
[M] トレードオフの意味だけど、高校で、次の関数の最小値を求める問題があったね。
![]()
右辺第1項は増加関数、第2項は減少関数だから、グラフを描いてみると、最小値が生まれているよね。
Flipped Classroom 7.1
[1]
評価関数はスカラ値を取るので、定数倍してもOKだから、![]() で割ると、
で割ると、
![]()
これから![]() は操作のためのコストとみなせます。すなわちコスト
は操作のためのコストとみなせます。すなわちコスト![]() がより小さくなると、操作はより大きな振る舞いが許されます。
がより小さくなると、操作はより大きな振る舞いが許されます。![]() のときはcheap controlと呼ばれます。
のときはcheap controlと呼ばれます。
[2]
![]()
を解くと
![]()
![]() の場合の固有ベクトルは
の場合の固有ベクトルは
![]()
すなわち
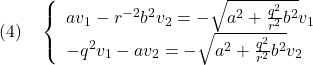
![]() の場合(と規格化する場合)は
の場合(と規格化する場合)は
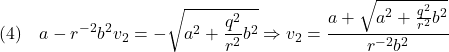
したがって