|
【本章のねらい】 ・ 状態空間表現を用いて漸近安定性の判定を行う。 ・ 状態空間表現を用いて時間応答の計算を行う。 |
2.1 漸近安定性
|
いま制御対象は平衡状態(物理的な釣り合いの状態)にあるとし,何らかの要因でこれが乱されたとき,その振舞いはつぎの
このとき,もし元の平衡状態に戻るならば,その平衡状態は漸近安定,または
の時間応答
となれば,漸近安定である。もし
ならば,漸近安定ではない,すなわち不安定である。 例題2.1 1次自由系 演習2.1 つぎの1次系が漸近安定となる定数 ●
で与えられる(テキスト「線形システム制御入門」の 定理2.2参照)。ここで,
で定義される。たとえば
のように計算される(テキスト「線形システム制御入門」の 定理2.4参照)。これらを用いて,次の例題を考える。 例題2.2 つぎの2次自由系の時間応答を求め,漸近安定性を判定せよ。
解答
これより,つぎが成り立つ。
したがって,漸近安定である。 (2) 式(??)を用いて,時間応答は次式となる。
これより,つぎが成り立つ。 たとえば したがって,漸近安定でない。 (3) 式(??)を用いて,時間応答は次式となる。
これより,つぎが成り立つ。
したがって,漸近安定である。 演習2.2 つぎの2次自由系の時間応答を求め,漸近安定性を判定せよ。
一般に, 例題2.3 つぎの行列
解答 (1) 行列
の解として, (2) 行列
の解として, (3) 行列
の解として, 演習2.3 例題2.2と演習2.2の2次系の漸近安定性を,行列 MATLABを用いて漸近安定性を判定するには,たとえば例題2.3(3)に対しては,つぎのコマンドを与えればよい。 %stability_check.m |
SCILABを用いて漸近安定性を判定するには,たとえば例題2.3(3)に対しては,つぎのコマンドを与えればよい。
//stability_check.m
A=[0 1;1 -1]; n=size(A,1); //行列データの定義と次数の取得
poles=spec(A) //行列の固有値の計算
sum(real(poles)<0)==n //論理式による漸近安定性の判定
2.2 時間応答
ただし,
すなわち,時間応答は零入力応答と零状態応答の和となる(テキスト「線形システム制御入門」の定理2.3参照)。 以下では,簡単のために,1入力1出力の場合を考える。
は,ステップ応答と呼ばれる。したがって,ステップ応答はインパルス応答を積分して,逆にインパルス応答はステップ応答を微分して得られる。 まず,次式で表される1次系を考える。
例題2.4 1次系(??)のステップ応答を求めよ。 解答 インパルス応答は
で表わされる。または,インパルス応答を直接積分して
演習2.4 つぎの1次系のステップ応答を求めよ。 (1) 1次系(??)のステップ応答
において,
すなわち,時定数は,応答が定常値 例題2.5 つぎの1次系のステップ応答をMATLABで計算し,図示せよ。
解答 MATLABに,つぎのコマンドを与えればよい。 %step_resp1.m |
SCILABに,つぎのコマンドを与えればよい。
//step_resp1.m
sys=syslin(‘c’,-1,1,1,0); //状態空間表現のデータ構造体の定義
t=0:0.1:5; //ステップ応答を計算する時刻の定義
plot(t,csim(‘step’,t,sys)), ,mtlb_grid //ステップ応答の計算と図示
|
演習2.5 例題2.5の図上に,時定数を求めるための補助線を引き,交点の座標をginput(1)を使って読み取れ。
つぎに,次式で表される2次系を考える。
ここで,
これらに対応して,
これらに対応して,インパルス応答
は,次式で与えられる。
これらに対応して,ステップ応答は,次式で与えられる。
特に,
ただし
このとき,ステップ応答の行き過ぎ時間
したがって,図上で第1番目のオーバーシュートの頂点の座標
例題2.6 つぎの2次系のステップ応答をMATLABで計算し,図示せよ。
解答 MATLABに,つぎのコマンドを与えればよい。 %step_resp2.m |
SCILABに,つぎのコマンドを与えればよい。
//step_resp2.m
A=[0 1;-1 -0.02]; B=[0;1]; C=[1 0];
sys=syslin(‘c’,A,B,C);
t=0:0.1:10; plot2d(t,csim(‘step’,t,sys)), mtlb_grid
| 演習2.6 例題2.6の図上で,第1番目のオーバーシュートの頂点の座標をginput(1)を使って読み込み,固有角周波数と減衰係数を同定せよ。
さて,もう一つ重要な 例題2.7 つぎの1次系の時間応答をMATLABで計算し,図示せよ。
ただし, 解答 MATLABに,つぎのコマンドを与えればよい。 %sin_resp.m |
SCILABに,つぎのコマンドを与えればよい。。
//sin_resp.m
sys=syslin(‘c’,-1,1,1,0); x0=1;
t=0:0.05:10; u=sin(10*t); //入力を指定
y=csim(u,t,sys,x0); //時間応答の計算
plot2d(t,y), mtlb_grid //時間応答の図示
| 演習2.7 例題2.7の図上に,零入力応答と零状態応答を重ねて表示せよ。
この例が示すように,
ここで,周波数伝達関数
で与えられる。古典制御で用いられるボード線図は,角周波数毎にゲイン 例題2.8 つぎの1次系のボード線図をMATLABで図示せよ。
解答 MATLABに,つぎのコマンドを与えればよい。 %bode_diag.m |
SCILABに,つぎのコマンドを与えればよい。
//bode_diag.m
sys=syslin(‘c’,-1,1,1,0);
fmin=1e-1/(2*%pi); fmax=1e1/(2*%pi); //周波数範囲の指定
bode(sys,fmin,fmax) //ボード線図の計算と図示
| 演習2.8 例題2.6の2次系のボード線図をMATLABで図示せよ。
最後に,自由系の時間応答(初期値応答)の計算法を示す。 例題2.9 つぎの1次自由系の時間応答をMATLABで計算し,図示せよ。
解答 MATLABに,つぎのコマンドを与えればよい。 %free_resp.m |
SCILABに,つぎのコマンドを与えればよい。
//free_resp.m
sys=syslin(‘c’,-1,0,1,0); x0=1;
t=0:0.1:5; u=zeros(1,length(t)); //零入力を指定
y=csim(u,t,sys,x0); //初期値応答の計算
plot2d(t,y), mtlb_grid //初期値応答の図示
| 演習2.9 例題(2.6)の2次系のインパルス応答をMATLABで図示せよ。 |
演習問題の解答
|
演習2.1
(1) 漸近安定であるための条件は, 演習2.2
これより,つぎが成り立つ。
したがって,漸近安定でない。 (2) (??)式を用いて,時間応答は次式となる。
これより,つぎが成り立つ。
したがって,漸近安定である。 (3) (??)式を用いて,時間応答は次式となる。
これより,つぎが成り立つ。
したがって,漸近安定でない。 演習2.3 例題1.2について: 演習1.2について: 演習2.4 (1) 演習2.5 定常ゲインは1.したがって,横線 %step_resp1_cont.m |
//step_resp1_cont.m
plot2d([0 5],(1-exp(-1))*[1 1]) %レベル1-1/e=0.632の表示
w=locate(1)
|
演習2.6
%step_resp2_cont.m |
//step_resp2_cont.m
w=locate(1); Tp=w(1); p0=w(2)-1;
zeta=sqrt(log(p0)^2/(log(p0)^2+%pi^2));
wn=sqrt(log(p0)^2+%pi^2)/Tp;
|
演習2.7
%sin_resp_cont.m |
//sin_resp_cont.m
x0=1; u=zeros(1,length(t)); y1=csim(u,t,sys,x0); %零入力応答の計算
x0=0; u=sin(10*t); y2=csim(u,t,sys,x0); %零状態応答の計算
hold on, plot2d(t,y1,’g’,t,y2,’r’)
|
演習2.8
%bode_diag2.m |
//bode_diag2.m
A=[0 1;-1 -0.02]; B=[0;1]; C=[1 0]; sys=syslin(‘c’,A,B,C,0);
fmin=1e-1/(2*%pi); fmax=1e1/(2*%pi);
bode(sys,fmin,fmax)
|
演習2.9
%impulse_resp.m |
//impulse_resp.m
A=[0 1;-1 -0.02]; B=[0;1]; C=[1 0]; sys=syslin(‘c’,A,B,C,0);
t=0:0.1:5; u=zeros(1,length(t));
y=csim(u,t,sys,B);
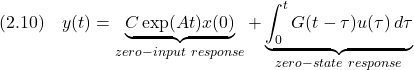
![Rendered by QuickLaTeX.com \displaystyle{(2.17)\quad \left\{\begin{array}{l} \underbrace{ \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right] }_{\dot x} = \underbrace{ \left[\begin{array}{cc} 0 & 1 \\ -\omega_n^2 & -2\zeta\omega_n \end{array}\right] }_{A} \underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] }_{x} + \underbrace{ \left[\begin{array}{c} 0 \\ \omega_n^2 \end{array}\right] }_{B} u(t) \\ y(t)= \underbrace{ \left[\begin{array}{cc} 1 & 0 \end{array}\right] }_{C} \underbrace{ \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] }_{x} \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-d6fa93bcbfb96d93d94f9d66f5d59230_l3.png)
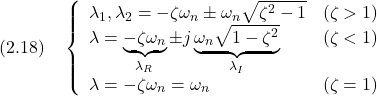
![Rendered by QuickLaTeX.com \displaystyle{(2.19)\quad A= \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda_1 & \lambda_2 \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda_1& 0\\ 0 & \lambda_2 \end{array}\right] }_{\Lambda} \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda_1 & \lambda_2 \end{array}\right]^{-1} }_{V^{-1}} \quad (\zeta>1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-dc4be3c5282d75dff407233f401f3cae_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2.20)\quad A= \underbrace{ \left[\begin{array}{cc} 1 & 0 \\ \lambda_R & \lambda_I \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda_R & \lambda_I \\ -\lambda_I & \lambda_R \end{array}\right] }_{\Lambda} \underbrace{ \frac{1}{\lambda_I} \left[\begin{array}{cc} \lambda_I & 0 \\ -\lambda_R & 1 \end{array}\right] }_{V^{-1}} \quad (\zeta<1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-b54e86b94889450f0dc10eed7c12eb0a_l3.png)
![Rendered by QuickLaTeX.com \displaystyle{(2.21)\quad A= \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda & \lambda+1 \end{array}\right] }_{V} \underbrace{ \left[\begin{array}{cc} \lambda & 1\\ 0 & \lambda \end{array}\right] }_{\Lambda} \underbrace{ \left[\begin{array}{cc} 1 & 1\\ \lambda & \lambda+1 \end{array}\right]^{-1} }_{V^{-1}} \quad (\zeta<1)(\zeta=1) }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-7de86a3d34cbcf41a4444cfcb326f29b_l3.png)
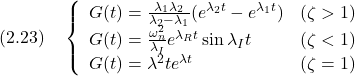
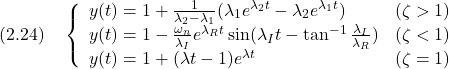
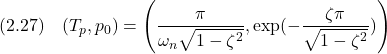
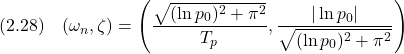
![Rendered by QuickLaTeX.com \displaystyle{ \left\{\begin{array}{l} \left[\begin{array}{c} \dot{x}_1(t) \\ \dot{x}_2(t) \end{array}\right]= \left[\begin{array}{cc} 0 & 1 \\ -1 & -0.02 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] + \left[\begin{array}{c} 0 \\ 1 \end{array}\right]u(t)\\ y(t)= \left[\begin{array}{cc} 1 & 0 \end{array}\right] \left[\begin{array}{c} x_1(t) \\ x_2(t) \end{array}\right] \end{array}\right. }](https://cacsd1.sakura.ne.jp/wp/wp-content/ql-cache/quicklatex.com-05f0daf3113d159b35c6b96888f71b3a_l3.png)